10.3 平行线的性质 同步达标测评(含答案)沪科版七年级数学下册
文档属性
| 名称 | 10.3 平行线的性质 同步达标测评(含答案)沪科版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 279.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览




文档简介
沪科版七年级数学下册《 平行线的性质》同步达标测评
一.选择题(共8小题,满分32分)
1.小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA=( )
A.20° B.40° C.50° D.60°
2.某学员在驾校练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则两次拐弯的角度可能是( )
A.第一次向左拐30°,第二次向右拐30°
B.第一次向左拐45°,第二次向左拐45°
C.第一次向左拐60°,第二次向右拐120°
D.第一次向左拐53°,第二次向左拐127°
3.如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为E,若∠CBD=35°,则∠AFB的度数为( )
A.70° B.75° C.80° D.85°
4.如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E与BF交于点G.已知∠BGD′=26°,则∠α的度数是( )
A.77° B.64° C.26° D.87°
5.一把直尺和一个直角三角板(含30°角的直角三角形板)按如图所示放置,若∠1=15°,则∠2的度数为( )
A.60° B.50° C.45° D.40°
6.如图,AB∥DE,∠1=135°,∠C为直角.则∠D的度数为( )
A.35° B.40° C.45° D.55°
7.如图所示,若AB∥DE,且∠E=55°,则∠B+∠C的度数是( )
A.135° B.125° C.55° D.45°
8.如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=32°,则∠2的度数为( )
A.32° B.68° C.58° D.34°
二.填空题(共5小题,满分20分)
9.如图,已知AB∥CD,∠1=55°,则∠2的度数为 .
10.如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF,若∠1=32°,则∠2= .
11.已知直线a∥b,把一块含30°角的直角三角板按如图方式放置,若∠1=43°,则∠2= .
12.如图,AB∥CD,CB∥DE,∠B=65°,则∠D的度数为 度.
13.如图,AB∥CD,AB⊥AE,∠CAE=35°,则∠ACD的度数为 .
三.解答题(共7小题,满分68分)
16.如图,BE∥CF,∠A=30°,∠C=80°,求∠B的度数.
20.如图,点D、E、F、G均在△ABC的边上,连接BD、DE、FG,∠3=∠CBA,FG∥BD.
(1)求证:∠1+∠2=180°;
(2)若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.
13.如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?
14.已知:两直线AB∥CD,E是平面内任一点(不在AB、CD上).
(1)如图1所示,E在射线AB与CD之间时,请说明∠AEC=∠A+∠C的理由.
(2)如图2所示,点E在AB与CD的上方时,请探索∠A,∠C,∠AEC三者的数量关系,并说明理由.
17.(1)如图1,l1∥l2,求∠A1+∠A2+∠A3= .(直接写出结果)
(2)如图2,l1∥l2,求∠A1+∠A2+∠A3+∠A4= .(直接写出结果)
(3)如图3,l1∥l2,求∠A1+∠A2+∠A3+∠A4+∠A5= .(直接写出结果)
(4)如图4,l1∥l2,求∠A1+∠A2+…+∠An= .(直接写出结果)
18.已知直线AB∥CD,P为平面内一点,连接PA、PD.
(1)如图1,已知∠A=50°,∠D=150°,求∠APD的度数;
(2)如图2,判断∠PAB、∠CDP、∠APD之间的数量关系为 .
(3)如图3,在(2)的条件下,AP⊥PD,DN平分∠PDC,若∠PAN+∠PAB=∠APD,求∠AND的度数.
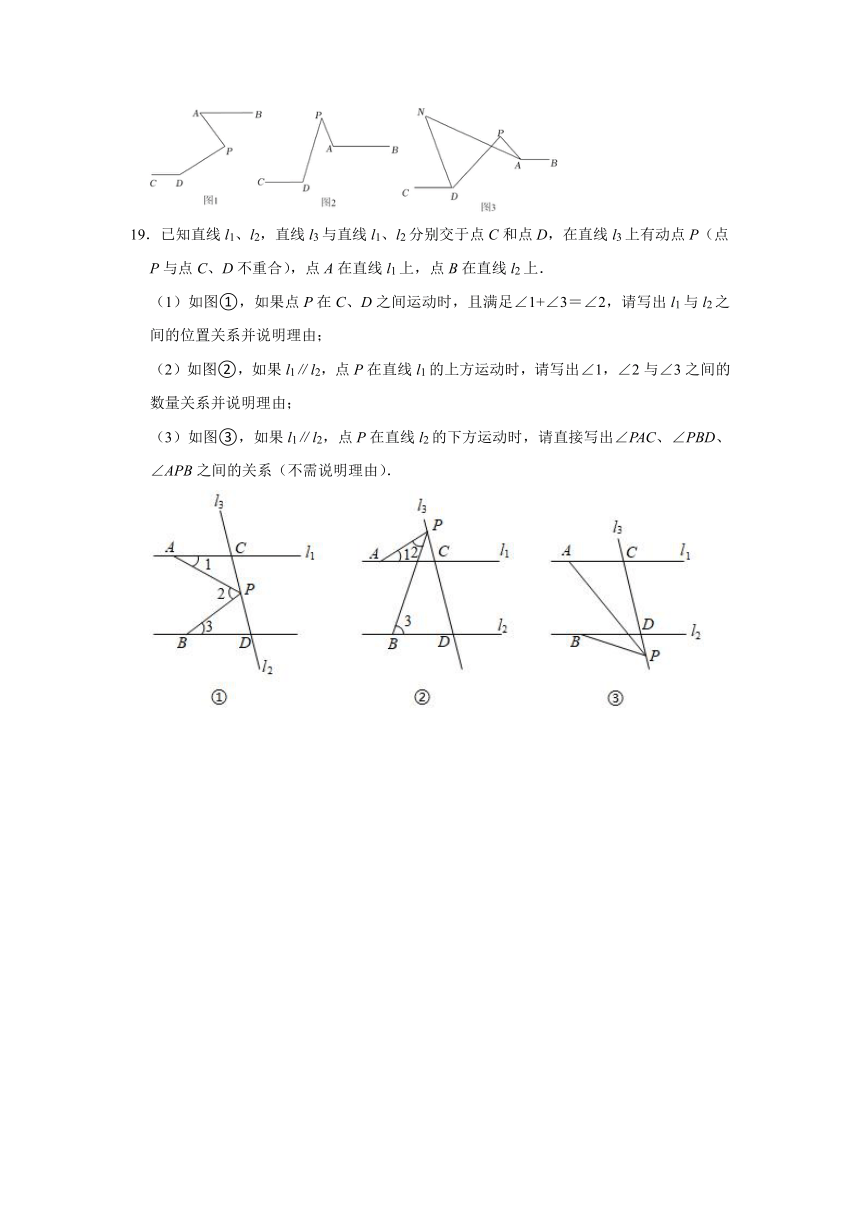
19.已知直线l1、l2,直线l3与直线l1、l2分别交于点C和点D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)如图①,如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系并说明理由;
(2)如图②,如果l1∥l2,点P在直线l1的上方运动时,请写出∠1,∠2与∠3之间的数量关系并说明理由;
(3)如图③,如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系(不需说明理由).
参考答案
一.选择题(共8小题,满分32分)
1.解:由图可得,∠AEF=50°,
又∵DC∥EF,
∴∠BAC=50°,
∵∠B=30°,
∴∠BDA=50°﹣30°=20°,
故选:A.
2.解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同旁内角,且互补,
故选:D.
3.解:由折叠的性质得到,∠EBD=∠CBD,
∵∠CBD=35°,
∴∠EBC=2∠CBD=70°,
∵AD∥BC,
∴∠AFB=∠EBC=70°,
故选:A.
4.解:∵矩形纸条ABCD中,AD∥BC,
∴∠AEG=∠BGD'=26°,
∴∠DEG=180°﹣26°=154°,
由折叠可得,∠α=∠DEG=×154°=77°,
故选:A.
5.解:如图,过点A作AF∥DE,
∴∠1=∠BAF=15°,
∵∠B=30°,∠ACB=90°,
∴∠BAC=60°,
∴∠CAF=60°﹣15°=45°,
∵DE∥MN,AF∥DE,
∴AF∥MN,
∴∠CAF=∠2=45°,
故选:C.
6.解:过点C作CF∥AB,如图所示:
∵∠1=135°,
∴∠BAC=180°﹣∠1=45°,
∵CF∥AB,AB∥DE,
∴∠ACF=∠BAC=45°,CF∥DE,
∴∠DCF=∠D,
∵∠ACD为直角,
∴∠DCF=90°﹣∠ACF=45°,
∴∠D=45°.
故选:C.
7.解:∵AB∥DE,
∴∠E=∠BFE=55°,
∵∠BFE=∠B+∠C,
∴∠B+∠C=55°,
故选:C.
8.解:∵直线a∥b,
∴∠2+∠BAC+∠1=180°,
∵AC⊥BA,
∴∠BAC=90°,
∴∠2=180°﹣∠1﹣∠BAC=180°﹣90°﹣32°=58°,
故选:C.
二.填空题(共5小题,满分20分)
9.解:∵AB∥CD,∠1=55°,
∴∠3=∠1=55°,
∴∠2=180°﹣∠3=125°,
故答案为:125°.
10.解:∵AB∥CD,
∴∠1=∠AEG.
∵EG平分∠AEF,
∴∠AEF=2∠AEG,
∴∠AEF=2∠1=64°.
∴∠2=64°.
故答案为:64°.
11.解:如图所示:
由题意得∠CAB=30°,
∵a∥b,∠1=43°,
∴∠DAB=180°﹣∠1=137°,
∵∠DAB=∠2+∠CAB,
∴∠2=∠DAB﹣∠CAB=107°.
故答案为:107°.
12.解:∵AB∥CD,∠B=65°,
∴∠C=∠B=65°,
∵CB∥DE,
∴∠D+∠C=180°,
∴∠D=180°﹣65°=115°;
故答案为:115.
13.解:∵AB⊥AE,
∴∠BAE=90°.
∴∠BAC=∠BAE﹣∠CAE=90°﹣35°=55°.
又∵AB∥CD,
∴∠BAC+∠ACD=180°.
∴∠ACD=180°﹣∠BAC=180°﹣55°=125°.
故答案为:125°.
三.解答题(共7小题,满分58分)
14.解:∵BE∥CF,∠C=80°,
∴∠ADE=∠C=80°,
∵∠ADE是△ABD的一个外角,
∴∠ADE=∠A+∠B,
∵∠C=30°,
∴∠B=50°.
15.解:(1)∵∠3=∠CBA,
∴AB∥DE,
∴∠2=∠DBA,
∵FG∥BD,
∴∠1+∠DBA=180°,
∴∠1+∠2=180°;
(2)∵AB∥DE,
∴∠CDE=∠A=35°,
∵DE平分∠BDC,
∴∠2=∠CDE=35°,
∴∠DBA=35°,
∵BD平分∠CBA,
∴∠CBA=70°,
∴∠C=180°﹣∠A﹣∠CBA=75°.
16.AB∥CD,要证明AB∥CD,即要证明∠ABC=∠BCD,即要证明∠1+∠2=∠3+∠4,由已知条件不难证明∠1+∠2=∠3+∠4.
解:AB∥CD,理由如下:
∵MN∥EF,
∴∠2=∠3,
∵∠1=∠2,∠2=∠3,∠3=∠4,
∴∠1+∠2=∠3+∠4,
∵∠1+∠ABC+∠2=180°,∠3+∠BCD+∠4=180°,
∴∠ABC=∠BCD,
∴AB∥CD.
17.解:(1)如图a,过点E作EF∥AB;,
∴∠A=∠AEF(两直线平行,内错角相等),
∵AB∥CD(已知),
∴EF∥CD(平行的传递性),
∴∠FEC=∠C(两直线平行,内错角相等),
∵∠AEC=∠AEF+∠FEC(图上可知),
∴∠AEC=∠A+∠C(等量代换);
(2)∠A+∠C﹣∠AEC=180°,
理由如下:如图b,过点E作EF∥AB,
∴∠AEF+∠1=180°(两直线平行,同旁内角互补),
∵AB∥CD(已知),
∴EF∥CD(平行的传递性),
∴∠FEC=∠2(两直线平行,内错角相等),
即∠CEA+∠AEF=∠2,
∴∠AEF=∠2﹣∠CEA(等式性质),
∴∠2﹣∠CEA+∠1=180°(等量代换),
即∠1+∠2﹣∠AEC=180°,
即∠A+∠C﹣∠AEC=180°.
18.解:(1)如图1,过A2作直线l3∥直线l1,
则l3∥直线l2,
∴∠1+∠3=∠4+∠2=180°,
∴∠A1+∠A2+∠A3=360°;
故答案为360°;
(2)如图2:过A2作直线l3∥直线l1,l4∥l1
则l3∥l1∥l4∥l2,
∴∠1+∠3=∠4+∠5=∠6+∠2=180°,
∴∠A1+∠A2+∠A3+∠A4=540°,
故答案为:540°;
(3)如图3:过A2作直线l3∥直线l1,l4∥l1,l5∥l1,
则l3∥l1∥l4∥l5∥l2,
∴∠1+∠3=∠4+∠5=∠6+∠7=∠8+∠2=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=720°,
故答案为:720°;
(4)如图4:由图1,图2,图3归纳得出,∠A1+∠A2+…+∠An=(n﹣1) 180°,
故答案为:(n﹣1) 180°.
19.解:(1)如图1,过点P作EF∥AB,
∵∠A=50°,
∴∠APE=∠A=50°,
∵AB∥CD,
∴EF∥CD,
∴∠CDP+∠EPD=180°,
∵∠D=150°,
∴∠EPD=180°﹣150°=30°,
∴∠APD=∠APE+∠EPD=50°+30°=80°;
(2)如图2,过点P作EF∥AB,则AB∥EF∥CD,
∴∠CDP=∠DPF,∠FPA+∠PAB=180°,
∵∠FPA=∠DPF﹣APD,
∴∠DPF﹣APD+∠PAB=180°,
∴∠CDP+∠PAB﹣APD=180°,
故答案为:∠CDP+∠PAB﹣APD=180°;
(3)如图3,PD交AN于点O,
∵AP⊥PD,
∴∠APO=90°,
∵∠PAN+∠PAB=∠APD,
∴∠PAN+∠PAB=90°,
∵∠POA+∠PAN=90°,
∴∠POA=∠PAB,
∵∠POA=∠NOD,
∴∠NOD=∠PAB,
∵DN平分∠PDC,
∴∠ODN=∠PDC,
∴∠AND=180°﹣∠NOD﹣∠ODN
=180°﹣(∠PAB+∠PDC),
由(2)得:∠CDP+∠PAB﹣APD=180°,
∴∠CDP+∠PAB=180°+∠APD,
∴∠AND=180°﹣(∠PAB+∠PDC)
=180°﹣(180°+∠APD)
=180°﹣(180°+90°)
=45°.
20.(1)解:l1∥l2,理由如下:
如图①,过点P作PE∥l1,
∵PE∥l1,
∴∠1=∠APE,
∴∠2=∠APE+∠BPE=∠1+∠BPE,
∵∠1+∠3=∠2,
∴∠BPE=∠3,
∴PE∥l2,
∴l1∥l2;
(2)解:如图②所示,当点P在直线l1的上方运动时,∠2=∠3﹣∠1,
理由:过点P作PF∥l1,
∴∠FPA=∠1,
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠2=∠FPB﹣∠PFA=∠3﹣∠1;
(3)解:如图③所示,当点P在直线l2的下方运动时,∠APB+∠PBD=∠PAC,
理由:过点P作PM∥l1,
∴∠MPA=∠PAC,
∵l1∥l2,
∴PM∥l2,
∴∠MPB=∠PBD,
∴∠APB=∠MPA﹣∠BPM=∠PAC﹣∠PBD,
即∠APB+∠PBD=∠PAC.
一.选择题(共8小题,满分32分)
1.小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA=( )
A.20° B.40° C.50° D.60°
2.某学员在驾校练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则两次拐弯的角度可能是( )
A.第一次向左拐30°,第二次向右拐30°
B.第一次向左拐45°,第二次向左拐45°
C.第一次向左拐60°,第二次向右拐120°
D.第一次向左拐53°,第二次向左拐127°
3.如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为E,若∠CBD=35°,则∠AFB的度数为( )
A.70° B.75° C.80° D.85°
4.如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E与BF交于点G.已知∠BGD′=26°,则∠α的度数是( )
A.77° B.64° C.26° D.87°
5.一把直尺和一个直角三角板(含30°角的直角三角形板)按如图所示放置,若∠1=15°,则∠2的度数为( )
A.60° B.50° C.45° D.40°
6.如图,AB∥DE,∠1=135°,∠C为直角.则∠D的度数为( )
A.35° B.40° C.45° D.55°
7.如图所示,若AB∥DE,且∠E=55°,则∠B+∠C的度数是( )
A.135° B.125° C.55° D.45°
8.如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=32°,则∠2的度数为( )
A.32° B.68° C.58° D.34°
二.填空题(共5小题,满分20分)
9.如图,已知AB∥CD,∠1=55°,则∠2的度数为 .
10.如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF,若∠1=32°,则∠2= .
11.已知直线a∥b,把一块含30°角的直角三角板按如图方式放置,若∠1=43°,则∠2= .
12.如图,AB∥CD,CB∥DE,∠B=65°,则∠D的度数为 度.
13.如图,AB∥CD,AB⊥AE,∠CAE=35°,则∠ACD的度数为 .
三.解答题(共7小题,满分68分)
16.如图,BE∥CF,∠A=30°,∠C=80°,求∠B的度数.
20.如图,点D、E、F、G均在△ABC的边上,连接BD、DE、FG,∠3=∠CBA,FG∥BD.
(1)求证:∠1+∠2=180°;
(2)若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.
13.如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?
14.已知:两直线AB∥CD,E是平面内任一点(不在AB、CD上).
(1)如图1所示,E在射线AB与CD之间时,请说明∠AEC=∠A+∠C的理由.
(2)如图2所示,点E在AB与CD的上方时,请探索∠A,∠C,∠AEC三者的数量关系,并说明理由.
17.(1)如图1,l1∥l2,求∠A1+∠A2+∠A3= .(直接写出结果)
(2)如图2,l1∥l2,求∠A1+∠A2+∠A3+∠A4= .(直接写出结果)
(3)如图3,l1∥l2,求∠A1+∠A2+∠A3+∠A4+∠A5= .(直接写出结果)
(4)如图4,l1∥l2,求∠A1+∠A2+…+∠An= .(直接写出结果)
18.已知直线AB∥CD,P为平面内一点,连接PA、PD.
(1)如图1,已知∠A=50°,∠D=150°,求∠APD的度数;
(2)如图2,判断∠PAB、∠CDP、∠APD之间的数量关系为 .
(3)如图3,在(2)的条件下,AP⊥PD,DN平分∠PDC,若∠PAN+∠PAB=∠APD,求∠AND的度数.
19.已知直线l1、l2,直线l3与直线l1、l2分别交于点C和点D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)如图①,如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系并说明理由;
(2)如图②,如果l1∥l2,点P在直线l1的上方运动时,请写出∠1,∠2与∠3之间的数量关系并说明理由;
(3)如图③,如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系(不需说明理由).
参考答案
一.选择题(共8小题,满分32分)
1.解:由图可得,∠AEF=50°,
又∵DC∥EF,
∴∠BAC=50°,
∵∠B=30°,
∴∠BDA=50°﹣30°=20°,
故选:A.
2.解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同旁内角,且互补,
故选:D.
3.解:由折叠的性质得到,∠EBD=∠CBD,
∵∠CBD=35°,
∴∠EBC=2∠CBD=70°,
∵AD∥BC,
∴∠AFB=∠EBC=70°,
故选:A.
4.解:∵矩形纸条ABCD中,AD∥BC,
∴∠AEG=∠BGD'=26°,
∴∠DEG=180°﹣26°=154°,
由折叠可得,∠α=∠DEG=×154°=77°,
故选:A.
5.解:如图,过点A作AF∥DE,
∴∠1=∠BAF=15°,
∵∠B=30°,∠ACB=90°,
∴∠BAC=60°,
∴∠CAF=60°﹣15°=45°,
∵DE∥MN,AF∥DE,
∴AF∥MN,
∴∠CAF=∠2=45°,
故选:C.
6.解:过点C作CF∥AB,如图所示:
∵∠1=135°,
∴∠BAC=180°﹣∠1=45°,
∵CF∥AB,AB∥DE,
∴∠ACF=∠BAC=45°,CF∥DE,
∴∠DCF=∠D,
∵∠ACD为直角,
∴∠DCF=90°﹣∠ACF=45°,
∴∠D=45°.
故选:C.
7.解:∵AB∥DE,
∴∠E=∠BFE=55°,
∵∠BFE=∠B+∠C,
∴∠B+∠C=55°,
故选:C.
8.解:∵直线a∥b,
∴∠2+∠BAC+∠1=180°,
∵AC⊥BA,
∴∠BAC=90°,
∴∠2=180°﹣∠1﹣∠BAC=180°﹣90°﹣32°=58°,
故选:C.
二.填空题(共5小题,满分20分)
9.解:∵AB∥CD,∠1=55°,
∴∠3=∠1=55°,
∴∠2=180°﹣∠3=125°,
故答案为:125°.
10.解:∵AB∥CD,
∴∠1=∠AEG.
∵EG平分∠AEF,
∴∠AEF=2∠AEG,
∴∠AEF=2∠1=64°.
∴∠2=64°.
故答案为:64°.
11.解:如图所示:
由题意得∠CAB=30°,
∵a∥b,∠1=43°,
∴∠DAB=180°﹣∠1=137°,
∵∠DAB=∠2+∠CAB,
∴∠2=∠DAB﹣∠CAB=107°.
故答案为:107°.
12.解:∵AB∥CD,∠B=65°,
∴∠C=∠B=65°,
∵CB∥DE,
∴∠D+∠C=180°,
∴∠D=180°﹣65°=115°;
故答案为:115.
13.解:∵AB⊥AE,
∴∠BAE=90°.
∴∠BAC=∠BAE﹣∠CAE=90°﹣35°=55°.
又∵AB∥CD,
∴∠BAC+∠ACD=180°.
∴∠ACD=180°﹣∠BAC=180°﹣55°=125°.
故答案为:125°.
三.解答题(共7小题,满分58分)
14.解:∵BE∥CF,∠C=80°,
∴∠ADE=∠C=80°,
∵∠ADE是△ABD的一个外角,
∴∠ADE=∠A+∠B,
∵∠C=30°,
∴∠B=50°.
15.解:(1)∵∠3=∠CBA,
∴AB∥DE,
∴∠2=∠DBA,
∵FG∥BD,
∴∠1+∠DBA=180°,
∴∠1+∠2=180°;
(2)∵AB∥DE,
∴∠CDE=∠A=35°,
∵DE平分∠BDC,
∴∠2=∠CDE=35°,
∴∠DBA=35°,
∵BD平分∠CBA,
∴∠CBA=70°,
∴∠C=180°﹣∠A﹣∠CBA=75°.
16.AB∥CD,要证明AB∥CD,即要证明∠ABC=∠BCD,即要证明∠1+∠2=∠3+∠4,由已知条件不难证明∠1+∠2=∠3+∠4.
解:AB∥CD,理由如下:
∵MN∥EF,
∴∠2=∠3,
∵∠1=∠2,∠2=∠3,∠3=∠4,
∴∠1+∠2=∠3+∠4,
∵∠1+∠ABC+∠2=180°,∠3+∠BCD+∠4=180°,
∴∠ABC=∠BCD,
∴AB∥CD.
17.解:(1)如图a,过点E作EF∥AB;,
∴∠A=∠AEF(两直线平行,内错角相等),
∵AB∥CD(已知),
∴EF∥CD(平行的传递性),
∴∠FEC=∠C(两直线平行,内错角相等),
∵∠AEC=∠AEF+∠FEC(图上可知),
∴∠AEC=∠A+∠C(等量代换);
(2)∠A+∠C﹣∠AEC=180°,
理由如下:如图b,过点E作EF∥AB,
∴∠AEF+∠1=180°(两直线平行,同旁内角互补),
∵AB∥CD(已知),
∴EF∥CD(平行的传递性),
∴∠FEC=∠2(两直线平行,内错角相等),
即∠CEA+∠AEF=∠2,
∴∠AEF=∠2﹣∠CEA(等式性质),
∴∠2﹣∠CEA+∠1=180°(等量代换),
即∠1+∠2﹣∠AEC=180°,
即∠A+∠C﹣∠AEC=180°.
18.解:(1)如图1,过A2作直线l3∥直线l1,
则l3∥直线l2,
∴∠1+∠3=∠4+∠2=180°,
∴∠A1+∠A2+∠A3=360°;
故答案为360°;
(2)如图2:过A2作直线l3∥直线l1,l4∥l1
则l3∥l1∥l4∥l2,
∴∠1+∠3=∠4+∠5=∠6+∠2=180°,
∴∠A1+∠A2+∠A3+∠A4=540°,
故答案为:540°;
(3)如图3:过A2作直线l3∥直线l1,l4∥l1,l5∥l1,
则l3∥l1∥l4∥l5∥l2,
∴∠1+∠3=∠4+∠5=∠6+∠7=∠8+∠2=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=720°,
故答案为:720°;
(4)如图4:由图1,图2,图3归纳得出,∠A1+∠A2+…+∠An=(n﹣1) 180°,
故答案为:(n﹣1) 180°.
19.解:(1)如图1,过点P作EF∥AB,
∵∠A=50°,
∴∠APE=∠A=50°,
∵AB∥CD,
∴EF∥CD,
∴∠CDP+∠EPD=180°,
∵∠D=150°,
∴∠EPD=180°﹣150°=30°,
∴∠APD=∠APE+∠EPD=50°+30°=80°;
(2)如图2,过点P作EF∥AB,则AB∥EF∥CD,
∴∠CDP=∠DPF,∠FPA+∠PAB=180°,
∵∠FPA=∠DPF﹣APD,
∴∠DPF﹣APD+∠PAB=180°,
∴∠CDP+∠PAB﹣APD=180°,
故答案为:∠CDP+∠PAB﹣APD=180°;
(3)如图3,PD交AN于点O,
∵AP⊥PD,
∴∠APO=90°,
∵∠PAN+∠PAB=∠APD,
∴∠PAN+∠PAB=90°,
∵∠POA+∠PAN=90°,
∴∠POA=∠PAB,
∵∠POA=∠NOD,
∴∠NOD=∠PAB,
∵DN平分∠PDC,
∴∠ODN=∠PDC,
∴∠AND=180°﹣∠NOD﹣∠ODN
=180°﹣(∠PAB+∠PDC),
由(2)得:∠CDP+∠PAB﹣APD=180°,
∴∠CDP+∠PAB=180°+∠APD,
∴∠AND=180°﹣(∠PAB+∠PDC)
=180°﹣(180°+∠APD)
=180°﹣(180°+90°)
=45°.
20.(1)解:l1∥l2,理由如下:
如图①,过点P作PE∥l1,
∵PE∥l1,
∴∠1=∠APE,
∴∠2=∠APE+∠BPE=∠1+∠BPE,
∵∠1+∠3=∠2,
∴∠BPE=∠3,
∴PE∥l2,
∴l1∥l2;
(2)解:如图②所示,当点P在直线l1的上方运动时,∠2=∠3﹣∠1,
理由:过点P作PF∥l1,
∴∠FPA=∠1,
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠2=∠FPB﹣∠PFA=∠3﹣∠1;
(3)解:如图③所示,当点P在直线l2的下方运动时,∠APB+∠PBD=∠PAC,
理由:过点P作PM∥l1,
∴∠MPA=∠PAC,
∵l1∥l2,
∴PM∥l2,
∴∠MPB=∠PBD,
∴∠APB=∠MPA﹣∠BPM=∠PAC﹣∠PBD,
即∠APB+∠PBD=∠PAC.
