北师大版八年级数学下册 1.1 等腰三角形复习题---常用作辅助线方法(含解析)
文档属性
| 名称 | 北师大版八年级数学下册 1.1 等腰三角形复习题---常用作辅助线方法(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:24:38 | ||
图片预览



文档简介
1.1 等腰三角形复习题---常用作辅助线方法
【题型1 作中线构造三线合一模型】
1.已知:三角形ABC中,∠A=90°,AB=AC,D为BC边的中点,
(1)如图①,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图②,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
2.如图,在中,,点在上,且连接,,若,,则的大小是( )
A. B. C. D.
3.如图,中,,平分,且求证:.
4.如图,四边形中,,平分,,求证:.
【题型2 作垂线构造等腰三角形】
1.如图,在中,平分,是上一点,,且.
(1)如果,则的度数为
(2)求证:.
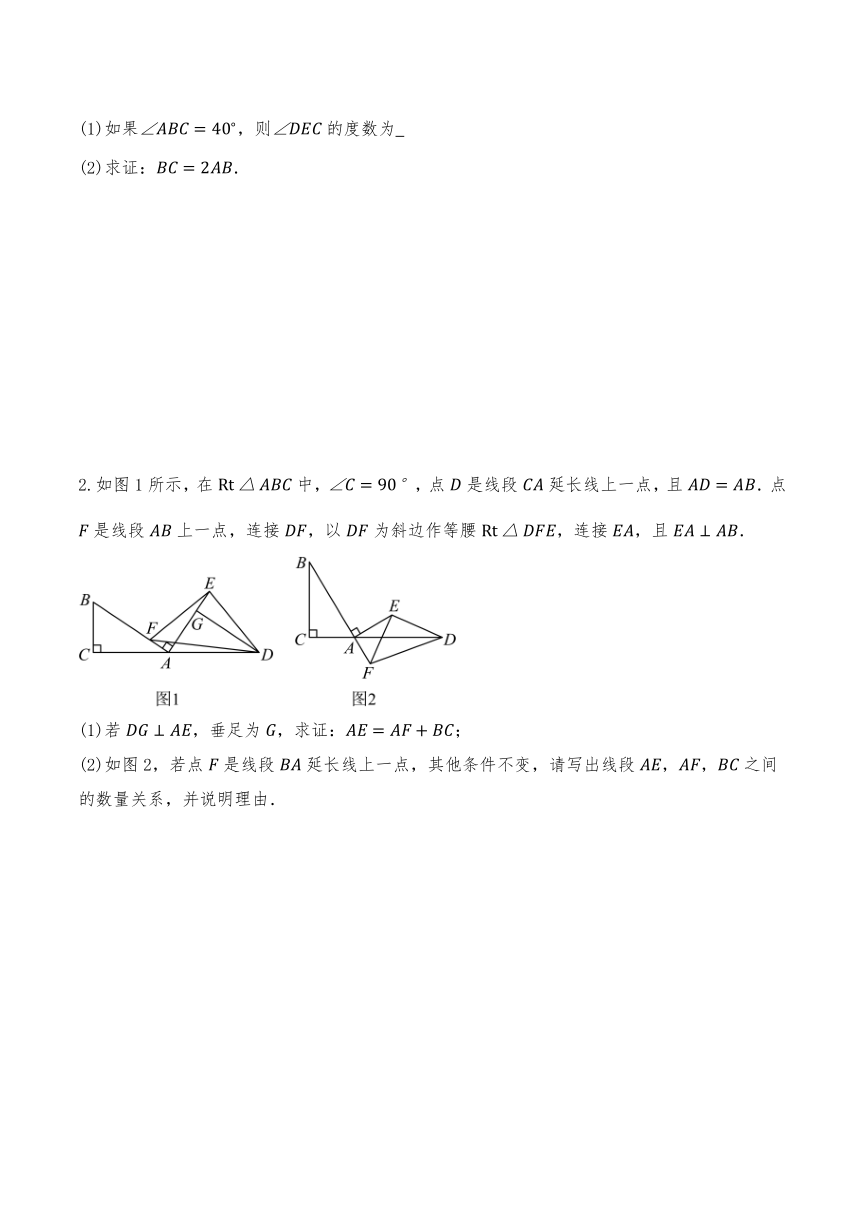
2.如图1所示,在中,,点是线段延长线上一点,且.点是线段上一点,连接,以为斜边作等腰,连接,且.
(1)若,垂足为,求证:;
(2)如图2,若点是线段延长线上一点,其他条件不变,请写出线段,,之间的数量关系,并说明理由.
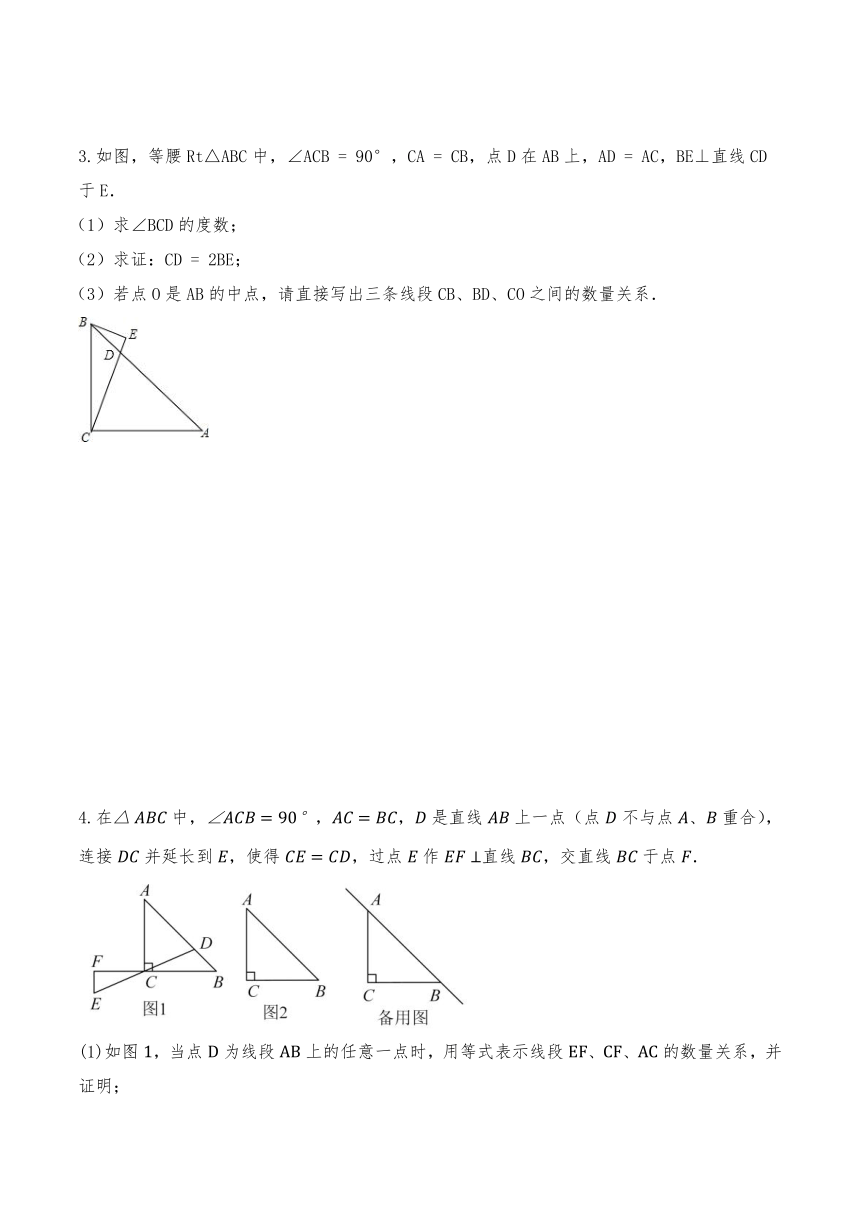
3.如图,等腰Rt△ABC中,∠ACB = 90°,CA = CB,点D在AB上,AD = AC,BE⊥直线CD于E.
(1)求∠BCD的度数;
(2)求证:CD = 2BE;
(3)若点O是AB的中点,请直接写出三条线段CB、BD、CO之间的数量关系.
4.在中,,,是直线上一点(点不与点、重合),连接并延长到,使得,过点作直线,交直线于点.
(1)如图,当点为线段上的任意一点时,用等式表示线段、、的数量关系,并证明;
(2)如图,当点为线段的延长线上一点时,依题意补全图,猜想线段、、的数量关系是否发生改变,并证明;
(3)如图,当点在线段的延长线上时,直接写出线段、、之间的数量关系.
【题型3 构造等腰(直角)三角形】
1.如图,中,,垂直的角平分线于,为的中点,则图中两个阴影部分面积之差的最大值为( )
A. B. C. D.
2.如图,在中,平分,,的面积为,的面积为,则的面积为________.
3.如图,是等腰直角三角形,是其底边上的高,是上的一点,以为边向上作等边三角形,连接,则的度数为 .
4.如图,在中,,、为内的两点,平分,,若,,则的长为_______;
如图,,,则的度数为________.
【题型4 作平行线构造等腰三角形】
1.如图,是边长为2的等边三角形,点在上,过点作,垂足为,延长到点,使,连接交于点,则的长为( )
A.0.5 B.0.9 C.1 D.1.25
2.如图1,P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于
点D.
(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=2,求DE的长.
3.在中,,点D在射线上,点E在的延长线上,且.连接,与边所在的直线交于点F.
(1)当点D在线段上时,如图所示,求证:.
(2)过点D作交直线于点H.若,求的长是多少?
4.【问题提出】
(1)如图1,在中,,点是上一点,交于点,点是的中点,连接并延长交的延长线于点,求证:;
【问题探究】
(2)如图2,在四边形中,,点是的中点,连接,,与的延长线交于点.探究线段与、之间的数量关系,并说明理由.
【问题解决】
(3)如图3,某校有一块四边形空地,现将这块空地规划为实践活动区域,在的中点处修建入口,沿修建一条小路(小路的宽度忽略不计),将这块空地分成两部分,在内种植蔬菜,在四边形内种植果树,已知,恰好平分,,,求的长.
【题型5 倍长中线构造等腰三角形】
1.如图,点是的中点,点在上,且求证:.
2.如图,是的中线,在上取一点,连接并延长交于点,使.求证:.
3.如图,中,点在边上,,,垂直于的延长线于点,,,则边的长为______.
4.如图,中,为中线,点为上一点,,交于点,且若,则( )
A. B. C. D.
【题型6 截长补短构造等腰三角形】
1.在中,于点,平分,,,则______.
2.如图,已知平分的外角,为上一点,.
如图,求证:;
判断的形状并证明;
如图,过点作于点,若,,求线段的长.
3.已知在中,,平分交于点,点在线段上点不与点,重合,且.
如图,若,且,则 , .
如图,求证:;若,且,求的度数.
4.如图,四边形中,是上一点,,,,探究、、之间的数量关系,并证明.
【题型7 旋转构造等腰三角形】
1.如图,在等腰直角中,,,、为斜边上的点,,若,,则的长是( )
A. B. C. D.
2.如图,中,,是内一点,连接、、,,求证.
3.如图,在中,,,以为边在的下方作等边,求的最大值.
4.如图,已知在等腰中,,点、是斜边上的两点不包括端点,且,若,,则_______________
参考答案
【题型1 作中线构造三线合一模型】
1.(1)证明:连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,BD=AD.
∴∠B=∠DAC=45° 又BE=AF,
∴△BDE≌△ADF(SAS).
∴ED=FD,∠BDE=∠ADF.
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°.
∴△DEF为等腰直角三角形.
(2)△DEF为等腰直角三角形.
证明:若E,F分别是AB,CA延长线上的点,如图所示:连接AD,
∵AB=AC,
∴△ABC为等腰三角形,
∵∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC(三线合一),
∴∠DAC=∠ABD=45°.
∴∠DAF=∠DBE=135°.又AF=BE,
∴△DAF≌△DBE(SAS).
∴FD=ED,∠FDA=∠EDB.
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF仍为等腰直角三角形.
2.C
【分析】
本题考查直角三角形斜边中线的性质,四边形内角和定理,等腰三角形的判定与性质有关知识,如图,取的中点,连接,想办法证明,推出进而可解决问题.
【解答】
解:如图,取的中点,连接,.
,,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
故选C.
3.证明:如图,取的中点,连接,则.
,.
平分,.
在和中,
.
.
,,,
.
.
又,
.
,
.
4.解:如图,取中点连接,
,
是等腰三角形,
垂直且平分,
,
,
,
是角平分线,
在和中,
,
,
,
垂直,
,
.
【题型2 作垂线构造等腰三角形】
1.(1)解:,平分,
,
,
,
是的一个外角,
;
故答案为:
(2)证明:过点作于点,
平分,,
,
在和中,
,
(全等三角形的对应边相等),
,,
,
.
2.(1)证明:如图1,,,
,
,
,,
在和中,
,
,
,
是以为斜边的等腰直角三角形,
,,
,
在和中,
,
,
,
,
,
;
(2)解:,
理由:如图2,作交的延长线于点,则,
,
在和中,
,
,
,
,
,
在和中,
,
,
,
,
.
3.解:(1)∵等腰Rt△ABC中,∠ACB = 90°,CA = CB,
∴∠A =∠CBA = 45°,
∵AD = AC,
∴∠ACD = 67.5°,
∴∠BCD =90°-∠ACD = 22.5°;
(2)作AH⊥CD于H,如图:
∵BE⊥直线CD于E,AD = AC,
∴CD = 2CH,∠BEC =∠AHC = 90°,
∵∠BCE +∠DCA = ∠HAC +∠DCA = 90°,
∴∠BCE =∠HAC,
在△CBE与△ACH中,
∴△CBE≌△ACH(AAS),
∴CH = BE,即CD = 2CH = 2BE;
(3)如图,
在Rt△ACB中,∵AO = OB,
∴AB = 2OC,
∵BD = AB-AD,AB = 2OC,AD = AC = BC,
∴BD =2OC-BC.
4.(1)解:结论:.
理由如下:过作于,
∴,
∵,
∴,
在和中,
∴,
∴,,
∵,,
∴,
∵,
∴,
∴,
∵,
∴;
(2)依题意补全图形,结论:,
理由如下:
过作交的延长线于,
∵,
∴,
在和中,
∴,
∴,,
∵,
∴,
∴,
∵,
∴;
(3).
如图,过作交的延长线于,
同理可证,
∴,,
∵,
∴,
∴,
∵,
∴.
【题型3 构造等腰(直角)三角形】
1.C
【解析】解:延长交于点设交于点.
,
,
,,
,
,
,
,
,
,
,
,,
,
,
,
,,
,
,
当时,的面积最大,最大面积为.
图中两个阴影部分面积之差的最大值为,
故选:.
2.
【分析】
本题考查了等腰三角形的判定与性质、全等三角形的判定与性质、三角形面积的计算;证明三角形全等得出是解决问题的关键.延长交于,由证明≌,得出,得出的面积的面积,的面积的面积,即可得出结果.
【解答】
解:延长交于,如图所示:
平分,垂直于,
,,
在和中,
≌,
,
的面积的面积,的面积的面积,
的面积的面积的面积的面积,
故答案为.
3.
如图,连接并延长交于点,
是等腰直角三角形,为上的高,
是的垂直平分线,
,
是等边三角形,
,,
,
,,
,
.
解:延长交于,延长交于,
,
为等边三角形,
,,
又,
,
,平分,
,,
,
,
,
.
故答案为:.
(2)解:延长到,使,连接,
,
,
又,
是等边三角形,
,,
又,,
,
在和中,
≌,
.
故答案为:.
【题型4 作平行线构造等腰三角形】
1.C
【分析】本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键.过作的平行线交于,通过证明,得,再由是等边三角形,即可得出.
【详解】解:过作的平行线交于,如图所示:
∴,
∵是等边三角形,
∴,
∴是等边三角形,
∴,
∵,
在中和中,
,
∴,
∴,
∵于,是等边三角形,
∴,
∴,
∴,
∵,
∴,
故选:C.
2.
证明:如图1,过点P作PF∥BC交AC于点F;
∵PF∥BC,
∴△APF∽△ABC,
又∵△ABC是等边三角形,
∴△APF是等边三角形,
∴∠APF=∠BCA=60°,AP=PF=AF=CQ,
∴∠FDP=∠DCQ,∠FDP=∠CDQ,
∵在△PDF和△QDC中,
∴△PDF≌△QDC(AAS),
∴PD=DQ;
(2)解:如图2,过P作PF∥BC交AC于F.
∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ.
由(1)可知∴△PFD≌△QCD(AAS),
∴FD=CD,
∵AE=EF,
∴EF+FD=AE+CD,∴AE+CD=DE= AC,又∵AC=2,
∴DE=1.
3.(1)证明:过点D作,交于点G.
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
(2)解:如图所示,当点D在线段上时,过点E作,交延长线于O,点D作,
∵,
∴,
又∵,
∴,
∴,
∴,
∵,
由(1)得:
∴,
∴,
∵,
∴;
当点D在的延长线上时,过点E作交的延长线于点O,过点D作,如图,
同理可证,,
∴,
∴,
∵,
∴;
综上所述,的长为1或3.
4.(1)证明:∵,,
∴,,
,
∵点F是的中点,
∴,
,,,
∴,
∴,
∴.
(2)解:.
理由:分别延长与的延长线交于点G.
∵,
∴,,
∵E为边的中点,
∴,
∴,
∴,
又∵,
∴,
∴,
∴.
(3)解:过C作交的延长线于点M,延长交于点N,连接,
∵点E是的中点,,
∴,
∵,,
∴,,,
,,,
∴,
∴,
∵平分,
∴,
∴,
又,
∴平分,
∴,
∵,,
∴,
,,,
∴,
∴.
【题型5 倍长中线构造等腰三角形】
1.证明:延长到,使,连接,
是的中点,
,
在和中
,
≌.
,.
,
.
,
又,
.
2.证明:如图,延长至H,使得,连接,如图所示:
∵是的中线,
∴,
∵,
,
,
∴,
∴.
3.
【解析】解:延长到,使得,连接,如图所示:
,
是等腰三角形,
,
过点作,交于点,
,
,
,
,
,
,,
,
,
,
,
,,
,
,
在中,由勾股定理得:,
在中,由勾股定理得:,
故答案为:.
4.B
解:如图,延长至点,使,连接.
因为,,
所以.
所以,.
因为,
所以.
又因为,
所以,
所以.
所以.
故选B.
【题型6 截长补短构造等腰三角形】
1.
解:在上截取,连接,
,
,
即,
设,则,
,
平分,
,
,
,
,
,
,
,
,
故答案为:.
2.解:证明:如图,设交于点.
,,
又,,
结论:是等腰三角形.
理由:在射线上截取,连接.
平分,
.
在和中,
BA=BH,∠ABD=∠HBD,BD=BD,
≌,
,.
,
,
,即为等腰三角形;
如图,作于点.
平分,,,
.
在和中,
≌,
.
在和中,
≌,
,
.
3.(1)54°;99°
(2)①如图,在CB上截取CF,使得FC=AC,连接EF.
因为CD平分∠ACB,
所以∠1=∠2.
在△ACE和△FCE中,因为AC=FC,∠1=∠2,EC=EC,
所以△ACE≌△FCE,
所以∠3=∠4,AE=FE.
因为∠4=∠5+∠6,
所以∠3=∠5+∠6.
因为∠3=2∠6,
所以∠5=∠6,
所以FB=FE.
所以AE=FB,
所以AE+AC=FB+FC=BC.
②如图,连接AF.
因为∠1=∠2=30°,
所以∠ACF=∠1+∠2=60°.
因为AC=FC,
所以△ACF是等边三角形,
所以AF=AC,∠FAC=60°.
因为AC=BE,
所以BE=AF.
在△BFE和△AEF中,因为BF=AE,FE=EF,BE=AF,
所以△BFE≌△AEF,
所以∠6=∠7.
因为∠7+∠3=60°,
所以∠6+∠3=60°.
因为∠3=2∠6,
所以∠6+2∠6=60°,
所以∠6=20°,即∠EBC=20°.
4.
证明:在上截取,使得,连接,
,,
且,
;
在和中,
,
,,
,
,
,
,
.
【题型7 旋转构造等腰三角形】
1.D
【解析】解:,,
,
如图,将绕点逆时针旋转,得到,连接.
由旋转的性质得,,,,,
,,
,
,
在和中,
,
≌,
,
,
是直角三角形,
,
,
,
;
故选:.
2.解:将顺时针旋转到的位置,使和重合,变为,连接
,
,,
,
,
,
,
,
.
3.解:如图,逆时针旋转得到,
,,
是等边三角形,
,
在中,,即,
则当点、三点共线时,,即,
即的最大值是.
4.
【解析】【分析】
本题考查了旋转的性质,全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,难度适中.准确作出旋转后的图形是解题的关键.将绕点逆时针旋转,得到,连接,根据旋转的性质可得,,,,然后求出,从而得到,再利用“边角边”证明和全等,根据全等三角形对应边相等可得,再求出是直角三角形,然后由勾股定理得出,求出、的长度,即可解决问题.
【解答】
解:如图,将绕点逆时针旋转,得到,连接.
由旋转的性质得,,,,,
,,
,
,
在和中,
≌,
,
,
是直角三角形,
,
,
,
,
,
.
故答案为.
【题型1 作中线构造三线合一模型】
1.已知:三角形ABC中,∠A=90°,AB=AC,D为BC边的中点,
(1)如图①,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图②,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
2.如图,在中,,点在上,且连接,,若,,则的大小是( )
A. B. C. D.
3.如图,中,,平分,且求证:.
4.如图,四边形中,,平分,,求证:.
【题型2 作垂线构造等腰三角形】
1.如图,在中,平分,是上一点,,且.
(1)如果,则的度数为
(2)求证:.
2.如图1所示,在中,,点是线段延长线上一点,且.点是线段上一点,连接,以为斜边作等腰,连接,且.
(1)若,垂足为,求证:;
(2)如图2,若点是线段延长线上一点,其他条件不变,请写出线段,,之间的数量关系,并说明理由.
3.如图,等腰Rt△ABC中,∠ACB = 90°,CA = CB,点D在AB上,AD = AC,BE⊥直线CD于E.
(1)求∠BCD的度数;
(2)求证:CD = 2BE;
(3)若点O是AB的中点,请直接写出三条线段CB、BD、CO之间的数量关系.
4.在中,,,是直线上一点(点不与点、重合),连接并延长到,使得,过点作直线,交直线于点.
(1)如图,当点为线段上的任意一点时,用等式表示线段、、的数量关系,并证明;
(2)如图,当点为线段的延长线上一点时,依题意补全图,猜想线段、、的数量关系是否发生改变,并证明;
(3)如图,当点在线段的延长线上时,直接写出线段、、之间的数量关系.
【题型3 构造等腰(直角)三角形】
1.如图,中,,垂直的角平分线于,为的中点,则图中两个阴影部分面积之差的最大值为( )
A. B. C. D.
2.如图,在中,平分,,的面积为,的面积为,则的面积为________.
3.如图,是等腰直角三角形,是其底边上的高,是上的一点,以为边向上作等边三角形,连接,则的度数为 .
4.如图,在中,,、为内的两点,平分,,若,,则的长为_______;
如图,,,则的度数为________.
【题型4 作平行线构造等腰三角形】
1.如图,是边长为2的等边三角形,点在上,过点作,垂足为,延长到点,使,连接交于点,则的长为( )
A.0.5 B.0.9 C.1 D.1.25
2.如图1,P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于
点D.
(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=2,求DE的长.
3.在中,,点D在射线上,点E在的延长线上,且.连接,与边所在的直线交于点F.
(1)当点D在线段上时,如图所示,求证:.
(2)过点D作交直线于点H.若,求的长是多少?
4.【问题提出】
(1)如图1,在中,,点是上一点,交于点,点是的中点,连接并延长交的延长线于点,求证:;
【问题探究】
(2)如图2,在四边形中,,点是的中点,连接,,与的延长线交于点.探究线段与、之间的数量关系,并说明理由.
【问题解决】
(3)如图3,某校有一块四边形空地,现将这块空地规划为实践活动区域,在的中点处修建入口,沿修建一条小路(小路的宽度忽略不计),将这块空地分成两部分,在内种植蔬菜,在四边形内种植果树,已知,恰好平分,,,求的长.
【题型5 倍长中线构造等腰三角形】
1.如图,点是的中点,点在上,且求证:.
2.如图,是的中线,在上取一点,连接并延长交于点,使.求证:.
3.如图,中,点在边上,,,垂直于的延长线于点,,,则边的长为______.
4.如图,中,为中线,点为上一点,,交于点,且若,则( )
A. B. C. D.
【题型6 截长补短构造等腰三角形】
1.在中,于点,平分,,,则______.
2.如图,已知平分的外角,为上一点,.
如图,求证:;
判断的形状并证明;
如图,过点作于点,若,,求线段的长.
3.已知在中,,平分交于点,点在线段上点不与点,重合,且.
如图,若,且,则 , .
如图,求证:;若,且,求的度数.
4.如图,四边形中,是上一点,,,,探究、、之间的数量关系,并证明.
【题型7 旋转构造等腰三角形】
1.如图,在等腰直角中,,,、为斜边上的点,,若,,则的长是( )
A. B. C. D.
2.如图,中,,是内一点,连接、、,,求证.
3.如图,在中,,,以为边在的下方作等边,求的最大值.
4.如图,已知在等腰中,,点、是斜边上的两点不包括端点,且,若,,则_______________
参考答案
【题型1 作中线构造三线合一模型】
1.(1)证明:连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,BD=AD.
∴∠B=∠DAC=45° 又BE=AF,
∴△BDE≌△ADF(SAS).
∴ED=FD,∠BDE=∠ADF.
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°.
∴△DEF为等腰直角三角形.
(2)△DEF为等腰直角三角形.
证明:若E,F分别是AB,CA延长线上的点,如图所示:连接AD,
∵AB=AC,
∴△ABC为等腰三角形,
∵∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC(三线合一),
∴∠DAC=∠ABD=45°.
∴∠DAF=∠DBE=135°.又AF=BE,
∴△DAF≌△DBE(SAS).
∴FD=ED,∠FDA=∠EDB.
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF仍为等腰直角三角形.
2.C
【分析】
本题考查直角三角形斜边中线的性质,四边形内角和定理,等腰三角形的判定与性质有关知识,如图,取的中点,连接,想办法证明,推出进而可解决问题.
【解答】
解:如图,取的中点,连接,.
,,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
故选C.
3.证明:如图,取的中点,连接,则.
,.
平分,.
在和中,
.
.
,,,
.
.
又,
.
,
.
4.解:如图,取中点连接,
,
是等腰三角形,
垂直且平分,
,
,
,
是角平分线,
在和中,
,
,
,
垂直,
,
.
【题型2 作垂线构造等腰三角形】
1.(1)解:,平分,
,
,
,
是的一个外角,
;
故答案为:
(2)证明:过点作于点,
平分,,
,
在和中,
,
(全等三角形的对应边相等),
,,
,
.
2.(1)证明:如图1,,,
,
,
,,
在和中,
,
,
,
是以为斜边的等腰直角三角形,
,,
,
在和中,
,
,
,
,
,
;
(2)解:,
理由:如图2,作交的延长线于点,则,
,
在和中,
,
,
,
,
,
在和中,
,
,
,
,
.
3.解:(1)∵等腰Rt△ABC中,∠ACB = 90°,CA = CB,
∴∠A =∠CBA = 45°,
∵AD = AC,
∴∠ACD = 67.5°,
∴∠BCD =90°-∠ACD = 22.5°;
(2)作AH⊥CD于H,如图:
∵BE⊥直线CD于E,AD = AC,
∴CD = 2CH,∠BEC =∠AHC = 90°,
∵∠BCE +∠DCA = ∠HAC +∠DCA = 90°,
∴∠BCE =∠HAC,
在△CBE与△ACH中,
∴△CBE≌△ACH(AAS),
∴CH = BE,即CD = 2CH = 2BE;
(3)如图,
在Rt△ACB中,∵AO = OB,
∴AB = 2OC,
∵BD = AB-AD,AB = 2OC,AD = AC = BC,
∴BD =2OC-BC.
4.(1)解:结论:.
理由如下:过作于,
∴,
∵,
∴,
在和中,
∴,
∴,,
∵,,
∴,
∵,
∴,
∴,
∵,
∴;
(2)依题意补全图形,结论:,
理由如下:
过作交的延长线于,
∵,
∴,
在和中,
∴,
∴,,
∵,
∴,
∴,
∵,
∴;
(3).
如图,过作交的延长线于,
同理可证,
∴,,
∵,
∴,
∴,
∵,
∴.
【题型3 构造等腰(直角)三角形】
1.C
【解析】解:延长交于点设交于点.
,
,
,,
,
,
,
,
,
,
,
,,
,
,
,
,,
,
,
当时,的面积最大,最大面积为.
图中两个阴影部分面积之差的最大值为,
故选:.
2.
【分析】
本题考查了等腰三角形的判定与性质、全等三角形的判定与性质、三角形面积的计算;证明三角形全等得出是解决问题的关键.延长交于,由证明≌,得出,得出的面积的面积,的面积的面积,即可得出结果.
【解答】
解:延长交于,如图所示:
平分,垂直于,
,,
在和中,
≌,
,
的面积的面积,的面积的面积,
的面积的面积的面积的面积,
故答案为.
3.
如图,连接并延长交于点,
是等腰直角三角形,为上的高,
是的垂直平分线,
,
是等边三角形,
,,
,
,,
,
.
解:延长交于,延长交于,
,
为等边三角形,
,,
又,
,
,平分,
,,
,
,
,
.
故答案为:.
(2)解:延长到,使,连接,
,
,
又,
是等边三角形,
,,
又,,
,
在和中,
≌,
.
故答案为:.
【题型4 作平行线构造等腰三角形】
1.C
【分析】本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键.过作的平行线交于,通过证明,得,再由是等边三角形,即可得出.
【详解】解:过作的平行线交于,如图所示:
∴,
∵是等边三角形,
∴,
∴是等边三角形,
∴,
∵,
在中和中,
,
∴,
∴,
∵于,是等边三角形,
∴,
∴,
∴,
∵,
∴,
故选:C.
2.
证明:如图1,过点P作PF∥BC交AC于点F;
∵PF∥BC,
∴△APF∽△ABC,
又∵△ABC是等边三角形,
∴△APF是等边三角形,
∴∠APF=∠BCA=60°,AP=PF=AF=CQ,
∴∠FDP=∠DCQ,∠FDP=∠CDQ,
∵在△PDF和△QDC中,
∴△PDF≌△QDC(AAS),
∴PD=DQ;
(2)解:如图2,过P作PF∥BC交AC于F.
∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ.
由(1)可知∴△PFD≌△QCD(AAS),
∴FD=CD,
∵AE=EF,
∴EF+FD=AE+CD,∴AE+CD=DE= AC,又∵AC=2,
∴DE=1.
3.(1)证明:过点D作,交于点G.
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
(2)解:如图所示,当点D在线段上时,过点E作,交延长线于O,点D作,
∵,
∴,
又∵,
∴,
∴,
∴,
∵,
由(1)得:
∴,
∴,
∵,
∴;
当点D在的延长线上时,过点E作交的延长线于点O,过点D作,如图,
同理可证,,
∴,
∴,
∵,
∴;
综上所述,的长为1或3.
4.(1)证明:∵,,
∴,,
,
∵点F是的中点,
∴,
,,,
∴,
∴,
∴.
(2)解:.
理由:分别延长与的延长线交于点G.
∵,
∴,,
∵E为边的中点,
∴,
∴,
∴,
又∵,
∴,
∴,
∴.
(3)解:过C作交的延长线于点M,延长交于点N,连接,
∵点E是的中点,,
∴,
∵,,
∴,,,
,,,
∴,
∴,
∵平分,
∴,
∴,
又,
∴平分,
∴,
∵,,
∴,
,,,
∴,
∴.
【题型5 倍长中线构造等腰三角形】
1.证明:延长到,使,连接,
是的中点,
,
在和中
,
≌.
,.
,
.
,
又,
.
2.证明:如图,延长至H,使得,连接,如图所示:
∵是的中线,
∴,
∵,
,
,
∴,
∴.
3.
【解析】解:延长到,使得,连接,如图所示:
,
是等腰三角形,
,
过点作,交于点,
,
,
,
,
,
,,
,
,
,
,
,,
,
,
在中,由勾股定理得:,
在中,由勾股定理得:,
故答案为:.
4.B
解:如图,延长至点,使,连接.
因为,,
所以.
所以,.
因为,
所以.
又因为,
所以,
所以.
所以.
故选B.
【题型6 截长补短构造等腰三角形】
1.
解:在上截取,连接,
,
,
即,
设,则,
,
平分,
,
,
,
,
,
,
,
,
故答案为:.
2.解:证明:如图,设交于点.
,,
又,,
结论:是等腰三角形.
理由:在射线上截取,连接.
平分,
.
在和中,
BA=BH,∠ABD=∠HBD,BD=BD,
≌,
,.
,
,
,即为等腰三角形;
如图,作于点.
平分,,,
.
在和中,
≌,
.
在和中,
≌,
,
.
3.(1)54°;99°
(2)①如图,在CB上截取CF,使得FC=AC,连接EF.
因为CD平分∠ACB,
所以∠1=∠2.
在△ACE和△FCE中,因为AC=FC,∠1=∠2,EC=EC,
所以△ACE≌△FCE,
所以∠3=∠4,AE=FE.
因为∠4=∠5+∠6,
所以∠3=∠5+∠6.
因为∠3=2∠6,
所以∠5=∠6,
所以FB=FE.
所以AE=FB,
所以AE+AC=FB+FC=BC.
②如图,连接AF.
因为∠1=∠2=30°,
所以∠ACF=∠1+∠2=60°.
因为AC=FC,
所以△ACF是等边三角形,
所以AF=AC,∠FAC=60°.
因为AC=BE,
所以BE=AF.
在△BFE和△AEF中,因为BF=AE,FE=EF,BE=AF,
所以△BFE≌△AEF,
所以∠6=∠7.
因为∠7+∠3=60°,
所以∠6+∠3=60°.
因为∠3=2∠6,
所以∠6+2∠6=60°,
所以∠6=20°,即∠EBC=20°.
4.
证明:在上截取,使得,连接,
,,
且,
;
在和中,
,
,,
,
,
,
,
.
【题型7 旋转构造等腰三角形】
1.D
【解析】解:,,
,
如图,将绕点逆时针旋转,得到,连接.
由旋转的性质得,,,,,
,,
,
,
在和中,
,
≌,
,
,
是直角三角形,
,
,
,
;
故选:.
2.解:将顺时针旋转到的位置,使和重合,变为,连接
,
,,
,
,
,
,
,
.
3.解:如图,逆时针旋转得到,
,,
是等边三角形,
,
在中,,即,
则当点、三点共线时,,即,
即的最大值是.
4.
【解析】【分析】
本题考查了旋转的性质,全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,难度适中.准确作出旋转后的图形是解题的关键.将绕点逆时针旋转,得到,连接,根据旋转的性质可得,,,,然后求出,从而得到,再利用“边角边”证明和全等,根据全等三角形对应边相等可得,再求出是直角三角形,然后由勾股定理得出,求出、的长度,即可解决问题.
【解答】
解:如图,将绕点逆时针旋转,得到,连接.
由旋转的性质得,,,,,
,,
,
,
在和中,
≌,
,
,
是直角三角形,
,
,
,
,
,
.
故答案为.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
