北师大版八年级数学下册 1.2 直角三角形复习题--直角三角形全等的判定 (含解析)
文档属性
| 名称 | 北师大版八年级数学下册 1.2 直角三角形复习题--直角三角形全等的判定 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:25:21 | ||
图片预览




文档简介
1.2 直角三角形复习题--直角三角形全等的判定
【题型1 用HL证全等】
1.如图,,,要根据“”证明,还应添加一个条件是( )
A. B. C. D.
2.用三角尺可以画角平分线:如图所示,在已知的两边上分别取点M,N,使,再过点M画的垂线,过点N画的垂线,两垂线交于点P,画射线 ,可以得到,所以.那么射线就是的平分线.的依据是( ).
A. B. C. D.
3.如图,在和中,,,若要用“斜边、直角边”直接证明,则还需补充条件: .
4.如图,于点C,,,连接,射线于点A,点P在线段上移动,点Q在射线上随着点P移动,且始终保持,当 时,才能使与全等.
5.如图,在和中,,,与分别为,边上的中线,且,求证:.
6.如图,,,于点E,于点F,求证:.
7.如图,,是上的一点,且,.求证:.
8.如图,,点B,E,F在同一直线上,,,求证.
9.如图,、是的高,且,求证:
10.如图,在中,,,是延长线上一点,点在上,且.求证:.
【题型2 全等的性质和HL综合】
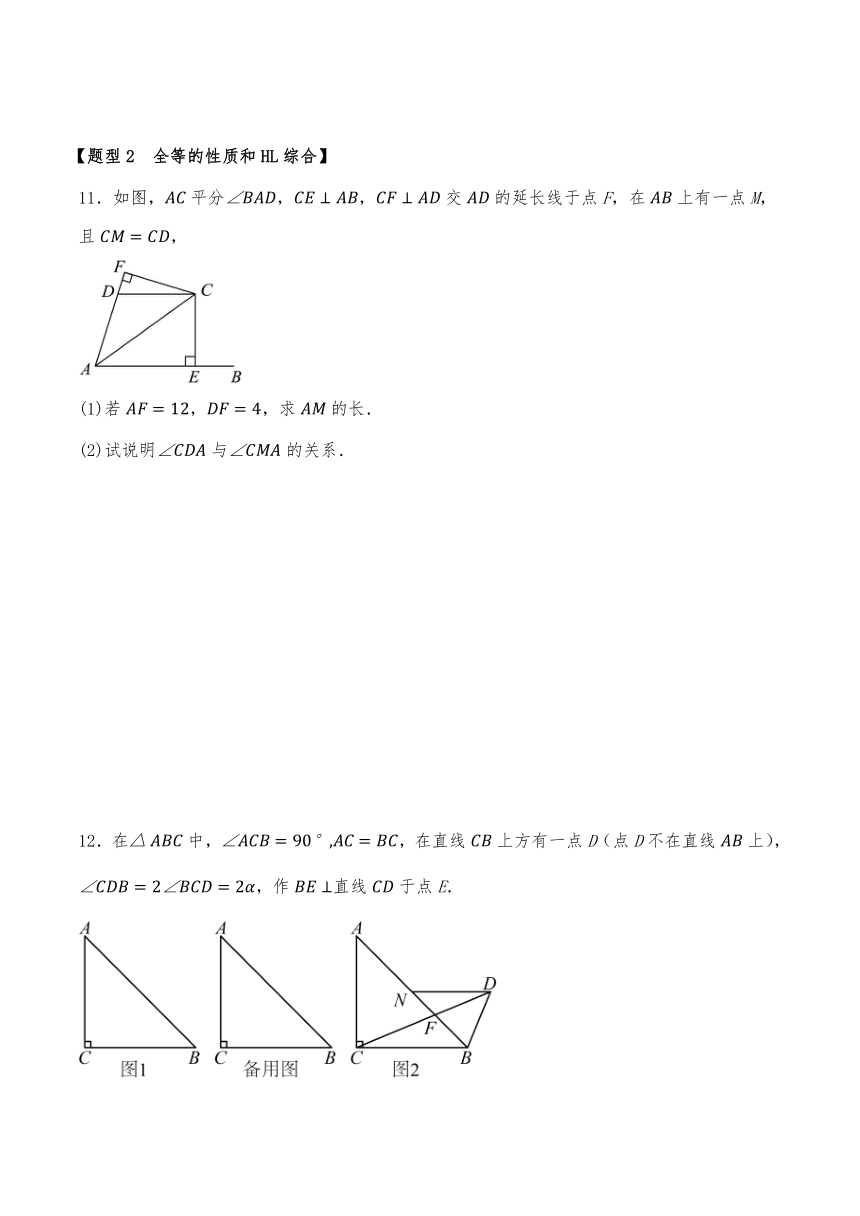
11.如图,平分,,交的延长线于点F,在上有一点M,且,
(1)若,,求的长.
(2)试说明与的关系.
12.在中,,在直线上方有一点D(点D不在直线上),,作直线于点E.
(1)在图1中自己完成画图,探索线段三者的数量关系并证明;
(2)如图2,点D在直线右面,交于点F,作交于N,若点N恰为的中点,求的值.
13.如图,D是的外角平分线上的一点,.
(1)求证:;
(2)若是等腰直角三角形,,,,与交于点F,求的度数.
14.如图,,,,,,垂足分别是,,求证:
(1);
(2).
15.如图,是的平分线,,点P在上,,,垂足分别是M,N.求证:.
16.如图,点在线段上,点在线段上,,,,点,分别在线段,边上,且满足,猜测与的数量关系并说明理由.
17.如图①所示,在一条直线上,,过分别作,,若.
(1)请猜想线段的数量关系,不用说明理由.
(2)若将的边沿方向移动,变为图时,其余条件不变,上述结论是否成立?请说明理由.
18.完成下列各题
(1)如图1,,点在上,且,则的度数为______;
(2)如图2,是的角平分线,于,于,连接交于点.
①求证:垂直平分线段;
②若的面积为8,,,求的长.
19.已知:如图,点,,在同一条直线上,平分,,于,于.
(1)求证:;
(2)若,,求的长.
20.如图,在中,,为上一点,为外一点,,连接,连接交于,且分.
(1)用尺规完成以下基本作图:过点作的垂线,垂足为;(不写作法,不下结论,保留作图痕迹)
(2)求证:.请根据下列证明思路完成填空:
证明:,
.
平分,,,
,.
在和中,
( ).
,,
.
21.与均为等婹直角三角形,.
(1)如图1,当,,在同一直线上时,的延长线与交于点,则______.
(2)当与的位置如图2时,的延长线与交于点,猜想的大小并证明你的结论.
(3)如图3,当A,,在同一直线上时(A,在点的异侧),与交于点,,请直接写出,,之间的数量关系.
22.
学完《全等三角形》一章后,我们知道“斜边和一条直角边分别相等的两个直角三角形全等(简称‘’定理)”是判定直角三角形全等的特有方法.
【简单应用】
如图(1),在中,,,点D、E分别在边、上.若,则线段和线段的数量关系是 .
【拓展延伸】
(1)如图(2),在中,为钝角,,点D、E分别在边、上.若,则线段和线段相等吗?如果相等,请给出证明;如果不相等,请说明理由;
(2)在中,,,点D在边上,点E在的延长线上,且.则线段与线段的数量关系为 (用含m的式子表示).
23.如图1,在和中,,,.
(1)求证:.
(2)在图1的基础上,过点作,交延长线于点,作,交延长线于点,延长线交于点.
①与有什么数量关系,请说明理由.
②若四边形的面积为35,,点为的中点,则的长为多少?请直接写出答案.
24.如图,已知在中,,D是上的一点,,点P从B点出发沿射线方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连接.
(1)当时,则______;
(2)当为以为腰的等腰三角形时,求t的值;
(3)过点D作于点E.在点P的运动过程中,当t为何值时,能使?
25.已知和,其中,.
(1)将和按如图1所示位置摆放,点落在上,的延长线交于点,连接,且平分.
①求证;
②猜想,与之间的数量关系是__________;
(2)若将图1中的按如图2所示位置摆放,交于点,的延长线交于点,,连接,且平分.试判断(1)中②猜想的结论还成立吗?并说明理由;
(3)若将图1中的按如图3所示位置摆放,,分别交的延长线于点,,连接,且平分.你认为(1)中②猜想的结论还成立吗?若成立,写出证明过程;若不成立,请直接写出,与之间的数量关系.
26.已知:等腰和等腰中,,,.
(1)如图1,延长交于点,若,则的度数为 ;
(2)如图2,连接、,延长交于点,若,点为中点,求证:;
(3)如图3,连接、,点是的中点,连接,交于点,,,则的面积为 .
27.如图,在中,,,是的角平分线, 于点.是线段上一动点(不与点,重合),连接,作,交延长线于点,延长至点,使,连接.
(1)若,求的长;
(2)猜想与之间的数量关系,并证明你的猜想;
(3)在点运动过程中,与之间的数量关系是否会发生变化?若不变化,写出它们之间的数量关系并证明;若变化,请说明理由.
28.(1)阅读理解:问题:如图1,在四边形中,对角线平分,.求证:.
思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在上截取,连接,得到全等三角形,进而解决问题;
方法2:延长到点,使得,连接,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种,添加辅助线并完成证明.
(2)问题解决:如图2,在(1)的条件下,连接,当时,探究线段,,之间的数量关系,并说明理由;
(3)问题拓展:如图3,在四边形中,,,过点作,垂足为点,请写出线段、、之间的数量关系.
29.在中,,,是的角平分线.过点作于点,以未顶点作,使的两边分别交直线于点,交直线于点,请解答下列问题:
(1)如图1,当点在线段上,点在线段上且时,求证:;
(2)求出图1中的度数,并判断线段、、之间的数量关系,加以证明;
(3)不改变图1中的大小.
①如图2,当点在线段上,点在线段的延长线时,线段、、之间的数量关系为________;
②如图3,当点在线段的延长线上,点在线段上时,线段、、之间的数量关系为________.
30.已知△ABC等边三角形,△BDC是顶角120°的等腰三角形,以D为顶点作60°的角,它的两边分别与AB.AC所在的直线相交于点M和N,连接MN.
(1)如图1,当点M、点N在边AB、AC上且DM=DN时,探究:BM、MN、NC之间的关系,并直接写出你的结论;
(2)如图2,当点M、点N在边AB、AC上,但DM≠DN时,(1)中的结论还成立吗?写出你的猜想并加以证明;
(3)如图3,若点M、N分别在射线AB、CA上,其他条件不变,(1)中的结论还成立吗?若成立,写出你的猜想;若不成立,请直接写出新的结论.
【题型1 用HL证全等】
1.C
【分析】本题考查了全等三角形的判定定理.根据垂直定义求出,再根据全等三角形的判定定理推出即可.
【详解】解:还需要添加的条件是,
理由是:∵,,
,
在和中,
,
∴,
故选:C.
2.C
【分析】本题考查全等三角形的判定和性质,角平分线的判定等知识,解题的关键是正确寻找全等三角形解决问题.
根据作图过程可以证明,进而可得结论.
【详解】∵,
在Rt和Rt中,
,
∴,
∴,
∴射线就是的平分线.
故选:C.
3.
【分析】由,,即可推出,于是得到答案.本题考查直角三角形全等的判定,关键是掌握直角三角形全等的判定方法.
【详解】证明:在和中,
,
∴.
故答案为:.
4.3或6
【分析】本题考查了直角三角形全等的判定,正确分类、熟练掌握利用证明直角三角形全等的方法是关键.根据即可解答.
【详解】解:,
,
,
∴当或时,都可以根据证明与全等;
故答案为:3或6.
5.证明:∵与分别为,边上的中线,
∴,,
∵,
∴,
在和中,
,
∴.
6.证明:,,
.
,,,
∴.
在和中,
.
7.∵,
∴,
∵,
∴在和中,
,
∴.
8.证明:∵,
∴,
即,
∵,
在和中,
,
∴.
9.证明:∵、是的高,
∴,
在和中,,
∴.
10.证明:,
,
,
为等腰直角三角形,
在和中,
【题型2 全等的性质和HL综合】
11.(1)解:∵平分,,,
∴,
在和中,
,
∴,
∴,
∵在和中,
,
∴,
∴,
当点M在点E左边时,,
当点M在点E右边时,,
综上:或.
12.(1)解:.理由:
延长至R,使,连接.
∴.
∵,
又,
∴,
∴,
∴,
∵,
∴.
∴.
(2)解:连接,过C作,过C作,交延长线于Q.延长交于M.连接,
∵,
∴,
∵,
∴,
∴,即垂直平分,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∴.
∵,,
∴,
∴.
13.如图,D是的外角平分线上的一点,.
(1)证明:如下图,过点作于点,作于点,
∴,
∵平分,,,
∴,
又∵,
∴,
∴;
(2)证明:∵,
∴,
∵,,
∴,
∴,
又∵平分,
∴,
∴,
∴,
由(1)可知,,
∴,即,
∴,
∴.
14.(1)解:,,
,
在和中,
,
;
(2),
,
于点,于点,
,
.
15.解:∵是的平分线,
∴,
在和中,
∴,
∴,
∴是的平分线,
∵,,
∴,
在和中,
∴,
∴.
16.解:,
证明:∵点在线段上,,
∴,
在中,
∴
∴,
又∵
∴
又,即
在中,
∴,
∴.
17.(1)解:.
理由:,,
,
,
,
即,
在和中,,
,
,
在和中,
,
,
;
(2)解:结论依然成立.
理由:,,
,
,
,
即,
在和中,,
,
,
在和中,
,
,
.
18.(1)解:设,
∵,
∴,
∴,
又∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
故答案为:;
(2)①∵平分,,,
∴,
∵,
∴,
∴,
∴垂直平分线段.
②∵的面积为8,,,,
∴的面积的面积,
∴,
∴,
解得:,
∴的长为2.
19.(1)证明:∵平分,,
∴,,
在和中,
,
∴;
(2)解:在和中,
,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
20.(1)解:如图,点即为所求;
(2)证明:,
.
平分,,,
,
,.
在和中,
().
,
,,
,
.
故答案为:,, ,.
21.
(1)证明:∵和是等腰直角三角形,
∴,
在和中,
,
∴,
∴,
∵,
又∵,
∴.
(2)解:.证明如下:
同(1)可证,
∴,
∴.
(3)解:如图:过点G作于点H,同(2)可知,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴.
解:简单应用:∵,,,
∴,
∴.
故答案为:;
拓展延伸:(1).理由如下:
如图(2)中,过点作交的延长线于,过点作交的延长线于.
∵,,,
∴,
∴,,
∵,,,
∴,
∴,
∵,
∴.
(2)在上取一点,使得,由(1)可知则.
过点作于.
∵,,
∴,
∵,
∴,
∴,
则,
∵,则,
∴,
∴,
∴,
故答案为:.
23.(1)证明:,
,
,
在和中
,
.
.
(2)①,理由如下:
连结,如图:
,,
是边上的高,是边上的高,
,
,
,,
又,
,
在和中,
,
,
.
②由①得,
,,
在和中,
,
,
,
,
,即:,
,
,
,
点为的中点,
,
设,则,
,
即:,
,
.
24.(1)当时,如图:
由题意,得:,
∴,
在中,,
在中,,
在中,,
∴,即:,
解得:,
∴;
故答案为:20.
(2)①当时,如图
∵
∴,
∴;
②若,则,
在直角三角形中,,
∴
解得:;
综上所述:t的值16或5;
(3)∵,
∴,
①若P在C点的左侧,则,
∴.
又,,且,
∴,
∴,
∴,
则,
解得:;
②若P在C点的右侧,则,
∴,
同法可得:,
∴,
∴,
解得,
综上所述:或11.
25.已知和,其中,.
(1)证明:①∵平分,,
∴,.
②∵,,,
∴,
∴,
∵,,
∴,
∴,
∵,而,
∴;
(2)∵平分,,
∴,,
∵,
∴,
∴.
∵,,
∴,
∴,
∵,而,
∴;
(3)②的结论不成立,结论为:,理由如下:
∵平分,,
∴,,
∵,
∴,
∴.
∵,,
∴,
∴,
∵,而,
∴;
26.(1)解:,
,即,
,
,
故答案为:;
(2)证明:如图2,延长至点,使,连接,
在和中,
,
,
,,
,
在和中,
,
,
;
(3)解:如图3,延长至,使,连接、、,设交于点,
,
,
,
是等腰直角三角形,是等腰直角三角形,
,,
在与中,
,
,
,,
点是的中点,
,
,,
,
,,
,,
,
,,
,
,即,
,
,
,
,
故答案为:16.
27.(1)解:∵,,是的角平分线,,
∴,
∴,
∴,
∴,
解得,,
∴,
∴的长为6;
(2)解:,证明如下;
∵,
∴,
∴;
(3)解:不变化,,证明如下;
由题意知,,
∴,
∵,
∴是等边三角形,
∴,,
∵,
∴,即,
∵,
∴,
∴,
∵,,,
∴,
∴.
28.解:(1)方法1:在上截取,连接,
平分,
,
在和中,
,
,
,,
,,
,
,
;
方法2:延长到,使,连接,
平分,
,
在和中,
,
,
,,
,,
,
,
;
(2),,之间的数量关系为.
方法1:理由如下:
如图,在上截取,连接,
由(1)知,
,
,
,
,
为等边三角形,
,,
,
为等边三角形,
,,
,
,
,
.
方法:理由:延长到,使,连接,
由(1)知,
,
是等边三角形,
,,
,
,
,
,
为等边三角形,
,,
,
,
即,
在和中,
,
,
,
,
;
(3)线段、、之间的数量关系为.
连接,过点作于点,
,,
,
在和中,
,
,
,,
在和中,
,
,
,
,
.
29.(1)证明:∵BP是△ABC的角平分线,PD⊥AB,PC⊥BC,
∴PD=PC,
在Rt△EPD与Rt△FPC中,
,
∴Rt△EPD≌Rt△FPC(HL);
(2)解:∵Rt△PDE≌Rt△PCF,
∴∠DPE=∠CPF,
∴∠EPF=∠DPC,
∵∠ABC=45°,
∴∠DPC=360° 90° 90° 45°=135°,
∴∠EPF=135°;
CP=CF+AE;理由如下:
∵Rt△PDE≌Rt△PCF,
∴DE=CF,
∵△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∴∠APD=∠A=45°,
∴AD=PD,
∴AD=CP,
∵CP=AD=DE+AE=CF+AE;
(3)解:①CF+CP=AE,理由如下:
由(1)知Rt△EPD≌Rt△FPC,
∴∠EPD=∠FPC,ED=FC,PD=PC,
在△ABC中,∠C=90°,AC=BC,
∴∠A=45°,
∵PD⊥AB,
∴∠APD=45°,AD=PD,
∴CP+CF=AD+ED=AE,
故答案为:CP+CF=AE;
②CF AE=CP,理由如下:
由(1)知Rt△EPD≌Rt△FPC,
∴∠EPD=∠FPC,ED=FC,PD=PC,
在△ABC中,∠C=90°,AC=BC,
∴∠A=45°,
∵PD⊥AB,
∴∠APD=45°,AD=PD,
∴CF AE=DE AE=AD=CP,
故答案为:CF AE=CP.
30.如图1,当点M、点N在边AB、AC上且DM=DN时,探究:BM、MN、NC之间的关系,并直接写出你的结论;
(2)如图2,当点M、点N在边AB、AC(1)∵△ABC是正三角形,
∴∠ABC=∠ACB=60°,
∵△BDC是顶角∠BDC=120°的等腰三角形,
∴∠DBC=∠DCB=30°,
∴∠DBM=∠DCN=90°,
∵在Rt△BDM和Rt△CDN中,
,
∴Rt△BDM≌Rt△CDN(HL),
∴BM=CN,∠BDM=∠CDN,
∵∠MDN=60°,,
∴△DMN是等边三角形,∠BDM=∠CDN=30°,
∴NC=BM=DM=MN,
∴MN=MB+NC;
(2)成立.理由如下:
延长AC至E,使CE=BM,连接DE,
∵△BDC是顶角∠BDC=120°的等腰三角形,△ABC是等边三角形,
∴∠BCD=30°,
∴∠ABD=∠ACD=90°,
即∠ECD=∠MBD=90°,
∵在Rt△DCE和Rt△DBM中,
,
∴Rt△DCE≌Rt△DBM(SAS),
∴∠BDM=∠CDE,DE= DM,
又∵∠BDC=120°,∠MDN=60°,
∴∠BDM+∠NDC=∠BDC -∠MDN=60°,
∴∠CDE+∠NDC=60°,即∠NDE=60°,
∴∠MDN=∠NDE=60°,
∵在△DMN和△DEN中,
,
∴△DMN≌△DEN(SAS),
∴NE=NM,即CE+CN=NM,
∴BM+CN=NM;
(2)MN=CN -BM,理由如下:
在CA上截取CE=BM,连接DM,
同理可证明:Rt△DCE≌Rt△DBM(SAS),
∴DE=DM,∠EDC=∠BDM,
∵∠MDN=∠MDB+∠BDN=60°,
∴∠BDN+∠CDE=60°,
∴∠NDE=∠NDM=60°,
∵在△MDN和△EDN中,
=60°,
∴△MDN≌△EDN(SAS),
∴MN=NE=NC -CE=NC -BM.
【题型1 用HL证全等】
1.如图,,,要根据“”证明,还应添加一个条件是( )
A. B. C. D.
2.用三角尺可以画角平分线:如图所示,在已知的两边上分别取点M,N,使,再过点M画的垂线,过点N画的垂线,两垂线交于点P,画射线 ,可以得到,所以.那么射线就是的平分线.的依据是( ).
A. B. C. D.
3.如图,在和中,,,若要用“斜边、直角边”直接证明,则还需补充条件: .
4.如图,于点C,,,连接,射线于点A,点P在线段上移动,点Q在射线上随着点P移动,且始终保持,当 时,才能使与全等.
5.如图,在和中,,,与分别为,边上的中线,且,求证:.
6.如图,,,于点E,于点F,求证:.
7.如图,,是上的一点,且,.求证:.
8.如图,,点B,E,F在同一直线上,,,求证.
9.如图,、是的高,且,求证:
10.如图,在中,,,是延长线上一点,点在上,且.求证:.
【题型2 全等的性质和HL综合】
11.如图,平分,,交的延长线于点F,在上有一点M,且,
(1)若,,求的长.
(2)试说明与的关系.
12.在中,,在直线上方有一点D(点D不在直线上),,作直线于点E.
(1)在图1中自己完成画图,探索线段三者的数量关系并证明;
(2)如图2,点D在直线右面,交于点F,作交于N,若点N恰为的中点,求的值.
13.如图,D是的外角平分线上的一点,.
(1)求证:;
(2)若是等腰直角三角形,,,,与交于点F,求的度数.
14.如图,,,,,,垂足分别是,,求证:
(1);
(2).
15.如图,是的平分线,,点P在上,,,垂足分别是M,N.求证:.
16.如图,点在线段上,点在线段上,,,,点,分别在线段,边上,且满足,猜测与的数量关系并说明理由.
17.如图①所示,在一条直线上,,过分别作,,若.
(1)请猜想线段的数量关系,不用说明理由.
(2)若将的边沿方向移动,变为图时,其余条件不变,上述结论是否成立?请说明理由.
18.完成下列各题
(1)如图1,,点在上,且,则的度数为______;
(2)如图2,是的角平分线,于,于,连接交于点.
①求证:垂直平分线段;
②若的面积为8,,,求的长.
19.已知:如图,点,,在同一条直线上,平分,,于,于.
(1)求证:;
(2)若,,求的长.
20.如图,在中,,为上一点,为外一点,,连接,连接交于,且分.
(1)用尺规完成以下基本作图:过点作的垂线,垂足为;(不写作法,不下结论,保留作图痕迹)
(2)求证:.请根据下列证明思路完成填空:
证明:,
.
平分,,,
,.
在和中,
( ).
,,
.
21.与均为等婹直角三角形,.
(1)如图1,当,,在同一直线上时,的延长线与交于点,则______.
(2)当与的位置如图2时,的延长线与交于点,猜想的大小并证明你的结论.
(3)如图3,当A,,在同一直线上时(A,在点的异侧),与交于点,,请直接写出,,之间的数量关系.
22.
学完《全等三角形》一章后,我们知道“斜边和一条直角边分别相等的两个直角三角形全等(简称‘’定理)”是判定直角三角形全等的特有方法.
【简单应用】
如图(1),在中,,,点D、E分别在边、上.若,则线段和线段的数量关系是 .
【拓展延伸】
(1)如图(2),在中,为钝角,,点D、E分别在边、上.若,则线段和线段相等吗?如果相等,请给出证明;如果不相等,请说明理由;
(2)在中,,,点D在边上,点E在的延长线上,且.则线段与线段的数量关系为 (用含m的式子表示).
23.如图1,在和中,,,.
(1)求证:.
(2)在图1的基础上,过点作,交延长线于点,作,交延长线于点,延长线交于点.
①与有什么数量关系,请说明理由.
②若四边形的面积为35,,点为的中点,则的长为多少?请直接写出答案.
24.如图,已知在中,,D是上的一点,,点P从B点出发沿射线方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连接.
(1)当时,则______;
(2)当为以为腰的等腰三角形时,求t的值;
(3)过点D作于点E.在点P的运动过程中,当t为何值时,能使?
25.已知和,其中,.
(1)将和按如图1所示位置摆放,点落在上,的延长线交于点,连接,且平分.
①求证;
②猜想,与之间的数量关系是__________;
(2)若将图1中的按如图2所示位置摆放,交于点,的延长线交于点,,连接,且平分.试判断(1)中②猜想的结论还成立吗?并说明理由;
(3)若将图1中的按如图3所示位置摆放,,分别交的延长线于点,,连接,且平分.你认为(1)中②猜想的结论还成立吗?若成立,写出证明过程;若不成立,请直接写出,与之间的数量关系.
26.已知:等腰和等腰中,,,.
(1)如图1,延长交于点,若,则的度数为 ;
(2)如图2,连接、,延长交于点,若,点为中点,求证:;
(3)如图3,连接、,点是的中点,连接,交于点,,,则的面积为 .
27.如图,在中,,,是的角平分线, 于点.是线段上一动点(不与点,重合),连接,作,交延长线于点,延长至点,使,连接.
(1)若,求的长;
(2)猜想与之间的数量关系,并证明你的猜想;
(3)在点运动过程中,与之间的数量关系是否会发生变化?若不变化,写出它们之间的数量关系并证明;若变化,请说明理由.
28.(1)阅读理解:问题:如图1,在四边形中,对角线平分,.求证:.
思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在上截取,连接,得到全等三角形,进而解决问题;
方法2:延长到点,使得,连接,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种,添加辅助线并完成证明.
(2)问题解决:如图2,在(1)的条件下,连接,当时,探究线段,,之间的数量关系,并说明理由;
(3)问题拓展:如图3,在四边形中,,,过点作,垂足为点,请写出线段、、之间的数量关系.
29.在中,,,是的角平分线.过点作于点,以未顶点作,使的两边分别交直线于点,交直线于点,请解答下列问题:
(1)如图1,当点在线段上,点在线段上且时,求证:;
(2)求出图1中的度数,并判断线段、、之间的数量关系,加以证明;
(3)不改变图1中的大小.
①如图2,当点在线段上,点在线段的延长线时,线段、、之间的数量关系为________;
②如图3,当点在线段的延长线上,点在线段上时,线段、、之间的数量关系为________.
30.已知△ABC等边三角形,△BDC是顶角120°的等腰三角形,以D为顶点作60°的角,它的两边分别与AB.AC所在的直线相交于点M和N,连接MN.
(1)如图1,当点M、点N在边AB、AC上且DM=DN时,探究:BM、MN、NC之间的关系,并直接写出你的结论;
(2)如图2,当点M、点N在边AB、AC上,但DM≠DN时,(1)中的结论还成立吗?写出你的猜想并加以证明;
(3)如图3,若点M、N分别在射线AB、CA上,其他条件不变,(1)中的结论还成立吗?若成立,写出你的猜想;若不成立,请直接写出新的结论.
【题型1 用HL证全等】
1.C
【分析】本题考查了全等三角形的判定定理.根据垂直定义求出,再根据全等三角形的判定定理推出即可.
【详解】解:还需要添加的条件是,
理由是:∵,,
,
在和中,
,
∴,
故选:C.
2.C
【分析】本题考查全等三角形的判定和性质,角平分线的判定等知识,解题的关键是正确寻找全等三角形解决问题.
根据作图过程可以证明,进而可得结论.
【详解】∵,
在Rt和Rt中,
,
∴,
∴,
∴射线就是的平分线.
故选:C.
3.
【分析】由,,即可推出,于是得到答案.本题考查直角三角形全等的判定,关键是掌握直角三角形全等的判定方法.
【详解】证明:在和中,
,
∴.
故答案为:.
4.3或6
【分析】本题考查了直角三角形全等的判定,正确分类、熟练掌握利用证明直角三角形全等的方法是关键.根据即可解答.
【详解】解:,
,
,
∴当或时,都可以根据证明与全等;
故答案为:3或6.
5.证明:∵与分别为,边上的中线,
∴,,
∵,
∴,
在和中,
,
∴.
6.证明:,,
.
,,,
∴.
在和中,
.
7.∵,
∴,
∵,
∴在和中,
,
∴.
8.证明:∵,
∴,
即,
∵,
在和中,
,
∴.
9.证明:∵、是的高,
∴,
在和中,,
∴.
10.证明:,
,
,
为等腰直角三角形,
在和中,
【题型2 全等的性质和HL综合】
11.(1)解:∵平分,,,
∴,
在和中,
,
∴,
∴,
∵在和中,
,
∴,
∴,
当点M在点E左边时,,
当点M在点E右边时,,
综上:或.
12.(1)解:.理由:
延长至R,使,连接.
∴.
∵,
又,
∴,
∴,
∴,
∵,
∴.
∴.
(2)解:连接,过C作,过C作,交延长线于Q.延长交于M.连接,
∵,
∴,
∵,
∴,
∴,即垂直平分,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∴.
∵,,
∴,
∴.
13.如图,D是的外角平分线上的一点,.
(1)证明:如下图,过点作于点,作于点,
∴,
∵平分,,,
∴,
又∵,
∴,
∴;
(2)证明:∵,
∴,
∵,,
∴,
∴,
又∵平分,
∴,
∴,
∴,
由(1)可知,,
∴,即,
∴,
∴.
14.(1)解:,,
,
在和中,
,
;
(2),
,
于点,于点,
,
.
15.解:∵是的平分线,
∴,
在和中,
∴,
∴,
∴是的平分线,
∵,,
∴,
在和中,
∴,
∴.
16.解:,
证明:∵点在线段上,,
∴,
在中,
∴
∴,
又∵
∴
又,即
在中,
∴,
∴.
17.(1)解:.
理由:,,
,
,
,
即,
在和中,,
,
,
在和中,
,
,
;
(2)解:结论依然成立.
理由:,,
,
,
,
即,
在和中,,
,
,
在和中,
,
,
.
18.(1)解:设,
∵,
∴,
∴,
又∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
故答案为:;
(2)①∵平分,,,
∴,
∵,
∴,
∴,
∴垂直平分线段.
②∵的面积为8,,,,
∴的面积的面积,
∴,
∴,
解得:,
∴的长为2.
19.(1)证明:∵平分,,
∴,,
在和中,
,
∴;
(2)解:在和中,
,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
20.(1)解:如图,点即为所求;
(2)证明:,
.
平分,,,
,
,.
在和中,
().
,
,,
,
.
故答案为:,, ,.
21.
(1)证明:∵和是等腰直角三角形,
∴,
在和中,
,
∴,
∴,
∵,
又∵,
∴.
(2)解:.证明如下:
同(1)可证,
∴,
∴.
(3)解:如图:过点G作于点H,同(2)可知,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴.
解:简单应用:∵,,,
∴,
∴.
故答案为:;
拓展延伸:(1).理由如下:
如图(2)中,过点作交的延长线于,过点作交的延长线于.
∵,,,
∴,
∴,,
∵,,,
∴,
∴,
∵,
∴.
(2)在上取一点,使得,由(1)可知则.
过点作于.
∵,,
∴,
∵,
∴,
∴,
则,
∵,则,
∴,
∴,
∴,
故答案为:.
23.(1)证明:,
,
,
在和中
,
.
.
(2)①,理由如下:
连结,如图:
,,
是边上的高,是边上的高,
,
,
,,
又,
,
在和中,
,
,
.
②由①得,
,,
在和中,
,
,
,
,
,即:,
,
,
,
点为的中点,
,
设,则,
,
即:,
,
.
24.(1)当时,如图:
由题意,得:,
∴,
在中,,
在中,,
在中,,
∴,即:,
解得:,
∴;
故答案为:20.
(2)①当时,如图
∵
∴,
∴;
②若,则,
在直角三角形中,,
∴
解得:;
综上所述:t的值16或5;
(3)∵,
∴,
①若P在C点的左侧,则,
∴.
又,,且,
∴,
∴,
∴,
则,
解得:;
②若P在C点的右侧,则,
∴,
同法可得:,
∴,
∴,
解得,
综上所述:或11.
25.已知和,其中,.
(1)证明:①∵平分,,
∴,.
②∵,,,
∴,
∴,
∵,,
∴,
∴,
∵,而,
∴;
(2)∵平分,,
∴,,
∵,
∴,
∴.
∵,,
∴,
∴,
∵,而,
∴;
(3)②的结论不成立,结论为:,理由如下:
∵平分,,
∴,,
∵,
∴,
∴.
∵,,
∴,
∴,
∵,而,
∴;
26.(1)解:,
,即,
,
,
故答案为:;
(2)证明:如图2,延长至点,使,连接,
在和中,
,
,
,,
,
在和中,
,
,
;
(3)解:如图3,延长至,使,连接、、,设交于点,
,
,
,
是等腰直角三角形,是等腰直角三角形,
,,
在与中,
,
,
,,
点是的中点,
,
,,
,
,,
,,
,
,,
,
,即,
,
,
,
,
故答案为:16.
27.(1)解:∵,,是的角平分线,,
∴,
∴,
∴,
∴,
解得,,
∴,
∴的长为6;
(2)解:,证明如下;
∵,
∴,
∴;
(3)解:不变化,,证明如下;
由题意知,,
∴,
∵,
∴是等边三角形,
∴,,
∵,
∴,即,
∵,
∴,
∴,
∵,,,
∴,
∴.
28.解:(1)方法1:在上截取,连接,
平分,
,
在和中,
,
,
,,
,,
,
,
;
方法2:延长到,使,连接,
平分,
,
在和中,
,
,
,,
,,
,
,
;
(2),,之间的数量关系为.
方法1:理由如下:
如图,在上截取,连接,
由(1)知,
,
,
,
,
为等边三角形,
,,
,
为等边三角形,
,,
,
,
,
.
方法:理由:延长到,使,连接,
由(1)知,
,
是等边三角形,
,,
,
,
,
,
为等边三角形,
,,
,
,
即,
在和中,
,
,
,
,
;
(3)线段、、之间的数量关系为.
连接,过点作于点,
,,
,
在和中,
,
,
,,
在和中,
,
,
,
,
.
29.(1)证明:∵BP是△ABC的角平分线,PD⊥AB,PC⊥BC,
∴PD=PC,
在Rt△EPD与Rt△FPC中,
,
∴Rt△EPD≌Rt△FPC(HL);
(2)解:∵Rt△PDE≌Rt△PCF,
∴∠DPE=∠CPF,
∴∠EPF=∠DPC,
∵∠ABC=45°,
∴∠DPC=360° 90° 90° 45°=135°,
∴∠EPF=135°;
CP=CF+AE;理由如下:
∵Rt△PDE≌Rt△PCF,
∴DE=CF,
∵△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∴∠APD=∠A=45°,
∴AD=PD,
∴AD=CP,
∵CP=AD=DE+AE=CF+AE;
(3)解:①CF+CP=AE,理由如下:
由(1)知Rt△EPD≌Rt△FPC,
∴∠EPD=∠FPC,ED=FC,PD=PC,
在△ABC中,∠C=90°,AC=BC,
∴∠A=45°,
∵PD⊥AB,
∴∠APD=45°,AD=PD,
∴CP+CF=AD+ED=AE,
故答案为:CP+CF=AE;
②CF AE=CP,理由如下:
由(1)知Rt△EPD≌Rt△FPC,
∴∠EPD=∠FPC,ED=FC,PD=PC,
在△ABC中,∠C=90°,AC=BC,
∴∠A=45°,
∵PD⊥AB,
∴∠APD=45°,AD=PD,
∴CF AE=DE AE=AD=CP,
故答案为:CF AE=CP.
30.如图1,当点M、点N在边AB、AC上且DM=DN时,探究:BM、MN、NC之间的关系,并直接写出你的结论;
(2)如图2,当点M、点N在边AB、AC(1)∵△ABC是正三角形,
∴∠ABC=∠ACB=60°,
∵△BDC是顶角∠BDC=120°的等腰三角形,
∴∠DBC=∠DCB=30°,
∴∠DBM=∠DCN=90°,
∵在Rt△BDM和Rt△CDN中,
,
∴Rt△BDM≌Rt△CDN(HL),
∴BM=CN,∠BDM=∠CDN,
∵∠MDN=60°,,
∴△DMN是等边三角形,∠BDM=∠CDN=30°,
∴NC=BM=DM=MN,
∴MN=MB+NC;
(2)成立.理由如下:
延长AC至E,使CE=BM,连接DE,
∵△BDC是顶角∠BDC=120°的等腰三角形,△ABC是等边三角形,
∴∠BCD=30°,
∴∠ABD=∠ACD=90°,
即∠ECD=∠MBD=90°,
∵在Rt△DCE和Rt△DBM中,
,
∴Rt△DCE≌Rt△DBM(SAS),
∴∠BDM=∠CDE,DE= DM,
又∵∠BDC=120°,∠MDN=60°,
∴∠BDM+∠NDC=∠BDC -∠MDN=60°,
∴∠CDE+∠NDC=60°,即∠NDE=60°,
∴∠MDN=∠NDE=60°,
∵在△DMN和△DEN中,
,
∴△DMN≌△DEN(SAS),
∴NE=NM,即CE+CN=NM,
∴BM+CN=NM;
(2)MN=CN -BM,理由如下:
在CA上截取CE=BM,连接DM,
同理可证明:Rt△DCE≌Rt△DBM(SAS),
∴DE=DM,∠EDC=∠BDM,
∵∠MDN=∠MDB+∠BDN=60°,
∴∠BDN+∠CDE=60°,
∴∠NDE=∠NDM=60°,
∵在△MDN和△EDN中,
=60°,
∴△MDN≌△EDN(SAS),
∴MN=NE=NC -CE=NC -BM.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
