第二次月考卷(3-4单元)(含答案)-2024-2025学年五年级数学下册阶段质量检测卷(北师大版)
文档属性
| 名称 | 第二次月考卷(3-4单元)(含答案)-2024-2025学年五年级数学下册阶段质量检测卷(北师大版) |

|
|
| 格式 | docx | ||
| 文件大小 | 93.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览




文档简介
保密★启用前
2024-2025学年北师大版数学下册第二次月考卷
(五年级)
考试范围:3-4单元 考试时间:90分钟
注意事项:
1.答题前,填写好自己的姓名、班级、考号等信息,请写在答题卡规定的位置上。
2.所有题目必须在答题卡上作答,在试卷上作答无效。
3.考试结束后将试卷和答题卡一并交回。
一、单选题(10分)
1.a是非0自然数,下列算式中,得数最小的是( )。
A.a× B.a+ C.a× D.a×
2.假分数的倒数都( )1。
A.小于 B.等于 C.大于 D.不大于
3.用分数表示下图涂色部分( )。
A. B. C. D.
4.姐姐装了杯纯果汁,兑满了温水后给弟弟喝了半杯,弟弟喝了( )杯纯果汁。
A. B. C. D.
5.两根同样长的线段,第1段先擦去,再延长dm,第二段先延长dm,再擦去。那么,现在这两条线段的长度( )。
A.第1段长 B.第2段长 C.一样长 D.无法判断
6.正方体的棱长扩大到原来的3倍,它的体积扩大到原来的( )。
A.3倍 B.9倍 C.27倍
7.一个长10cm、宽8cm、高4cm的长方体木块,能切成( )个棱长是2cm的小正方体木块。
A.40 B.80 C.160 D.120
8.用来表示一块橡皮擦的体积,下面的计量单位中( )最合适.
A.立方分米 B.平方分米 C.立方厘米 D.平方厘米
9.一根方木的体积是 80dm3,长是 20dm,这根方木的横截面积是( )。
A.4dm B.4dm2 C.4dm3
10.将一块长方体橡皮泥捏成一个正方体,正方体和长方体相比( )。
A.体积相等,表面积不相等 B.体积和表面积都不相等
C.表面积相等,体积不相等 D.体积和表面积都相等
二、判断题(5分)
11.1立方米铁块的体积和它的占地面积相等。( )
12.两个体积相等的长方体,它们的形状一定相同.( )
13.棱长是3dm的正方体,正好能分割成3000个棱长是1cm的小正方体。( )
14.把一根木料锯成两段需要分钟,如果锯成8段需要 分钟。( )
15.1kg的比4kg的重一些。( )
三、填空题(20分)
16. 3个是 ,5个 和11个相等。
17.如果两个数相乘的积是1,那么这两个数 。
18.学校一个月节约用水 吨,照这样计算,这所学校一个季度节约用水 吨,一年节约用水 吨。
19.一袋白糖千克,用了千克,还剩 千克;如果用了这袋糖的,还剩 千克。
20. 的倒数是 , 的倒数是 。
21.在横线上填上合适的单位名称:
(1)一个粉笔盒的体积约是 1 。
(2)一台冰箱的容积约是 200 。
22. 0.06升= 毫升 2立方米40立方分米= 立方米。
23.一个长方体,如果高减少2厘米,就变成一个正方体,这时表面积比原来减少64平方厘米。原来长方体的体积是 立方厘米。
24.一个正方体的棱长之和是72分米,它的表面积是 ,体积是 。
25.物体所占 是物体的体积,容器所能容纳物体的 是容器的容积。
26.一根长方体钢材的横截面是边长为2cm的正方形,它的长是5m。这根钢材的体积是 dm3。
四、计算题(23分)
27.直接写得数.
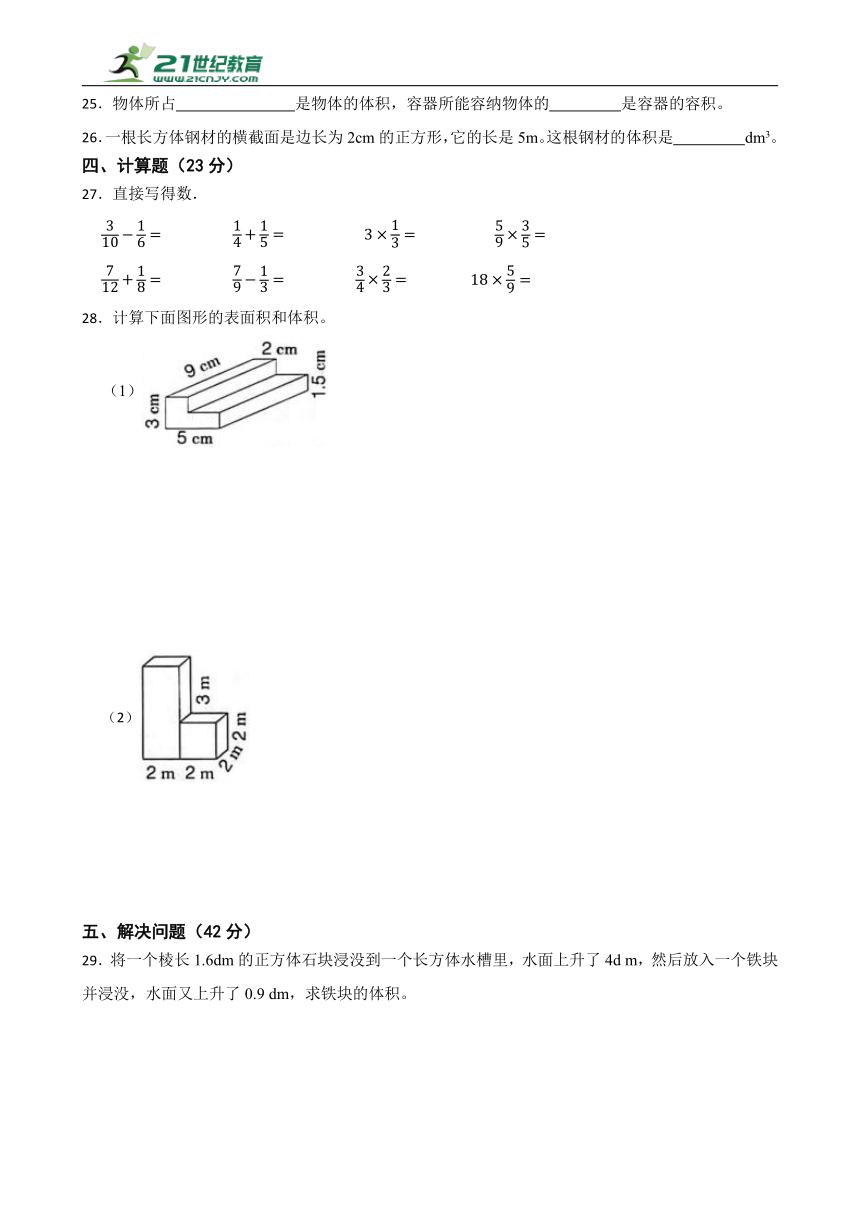
28.计算下面图形的表面积和体积。
(1)
五、解决问题(42分)
29.将一个棱长1.6dm的正方体石块浸没到一个长方体水槽里,水面上升了4d m,然后放入一个铁块并浸没,水面又上升了0.9 dm,求铁块的体积。
30.有一块棱长是 80 厘米的正方体的铁块,现在要把它熔铸成一个横截面积是 20 平方厘米的长方体,这个长方体的长是多少厘米?
31.一个长方体的沙坑,长40分米,宽2 米,深0.5米,需要多少立方米的黄沙才能填满?如果每立方米黄沙重 1.4吨,这些黄沙重多少吨?
32.用铁皮做一个无盖的长方体水箱,长10 分米,宽0.8米,高5 分米,至少需要多少平方分米的铁皮?这个水箱的容积是多少升?
33.春雷小学去年毕业的学生有160人,今年毕业的学生人数比去年增加了 今年毕业的学生比去年多多少人?
34.”节约资源从我做起”。实验小学上个月开展了收集空矿泉水瓶的活动。五年级收集了165个,是六年级的,四年级收集的个数是六年级的,实验小学四、六年级各收集了多少个空矿泉水瓶?
答案解析部分
1.A
解:A项:因为<1,所以a×<a;
B项:a+ >a;
C项:因为 <1,所以a×<a;
D项:因为 >1,所以a×>a。
<,则a×的得数最小。
故答案为:A。
一个非0的数乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。
2.D
解:假分数的倒数都不大于1。
故答案为:D。
因为假分数的值大于或等于1,那么假分数的倒数就小于或等于1。
3.B
解:×=,涂色部分用分数表示为。
故答案为:B。
三角形先被平均分成四份,其中的一个三角形占大三角形的,其中的一个三角形又被平均分成4份,这份占1个三角形的,占大三角形的。
4.B
解:×=(杯),
弟弟喝了杯纯果汁。
故答案为:B。
兑满了温水后给弟弟喝了半杯,弟弟喝了这杯果汁水的一半,也是喝了纯果汁的一半;杯纯果汁的一半是杯纯果汁 。
5.A
解:假设线段长a分米,
第1段剩下:a×(1-)+=a+;
第2段剩下:(a+)×(1-)=(a+)×=a+;
不管a是几,a+>a+,所以剩下的长度,第1段长 。
故答案为:A。
先计算,再通过计算的结果判断。
6.C
解:正方体的棱长扩大到原来的3倍,它的体积扩大到原来的3×3×3=27倍。
故答案为:C。
正方体体积=棱长×棱长×棱长,所以正方体体积扩大的倍数是棱长扩大倍数的立方倍。
7.A
解:因为长宽高都是2厘米的倍数,所以不浪费,
(10×8×4)÷(2×2×2)=320÷8=40(个)
能切成40个棱长是2cm的小正方体木块。
故答案为:A。
长方体木块的体积÷小正方体木块的体积=能切成的块数。
8.C
解:一块橡皮擦的体积用立方厘米最合适。
故答案为:C。
体积的常用单位有立方米、立方分米、立方厘米;根据实际情况并结合题中的数字选择合适的单位。
9.B
解:80÷20=4(dm2)
故答案为:B。
长方体体积=底面积×高,也可以用横截面面积乘长求出体积,因此用方木的体积除以长即可求出方木横截面的面积。
10.A
解:将一块长方体橡皮泥捏成一个正方体,正方体和长方体所占空间的大小不变,也就是体积相等,表面积不相等。
故答案为:A。
将一块长方体橡皮泥捏成一个正方体后体积相等,还是橡皮泥的体积,表面积不相等。
11.错误
解:1立方米铁块的体积和它的占地面积无法比较大小,原题干说法错误。
故答案为:错误。
体积是物体所占空间的大小,占地面积是它的底面积,体积和面积无法比较大小。
12.错误
解:两个体积相等的长方体,它们的形状不一定相同。原题说法错误。
故答案为:错误。
两个体积相等的长方体,只能说明它们长、宽、高的乘积相等,并不能确定长、宽、高分别相等,所以两个长方体不一定相同。
13.错误
解:棱长是3dm的正方体,正好能分割成27000个棱长是1cm的小正方体。原题说法错误。
故答案为:错误。
棱长3dm的正方体,体积是27立方分米,棱长是1厘米的小正方体,体积是1立方厘米,27立方分米=27000立方厘米,所以能割成27000个小正方体。
14.错误
解:锯成8段需要锯 8 1 = 7 (次),
锯成两段需要分钟,说明锯1次需要分钟,
×7=(分钟),锯成8段需要分钟,原题说法错误。
故答案为:错误。
锯一次需要的时间×7=锯7次需要的时间。
15.错误
解:1kg×=kg,4kg×=kg,一样重。原题说法错误。
故答案为:错误。
求一个数的几分之几是多少用乘法。据此解答。
16.;
解:3个是,11个是1,所以5个和11个相等。
故答案为:;。
分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数和的简便运算。
17.互为倒数
解:如果两个数相乘的积是1,那么这两个数互为倒数。
故答案为:互为倒数。
互为倒数的两个数,积是1。
18.8;32
解:一年=12个月
一季度=3个月
×3=8(吨)
×12=32(吨)。
故答案为:8;32。
这所学校一个季度节约用水的吨数=平均每个月节约用水的吨数×一季度的月数;一年节约用水的吨数=平均每个月节约用水的吨数×一年的月数。
19.;
解:-=(千克),还剩千克;
×(1-)=×=(千克)。
故答案为:;。
第一空:一袋白糖的质量-用去的质量=还剩的质量;
第二空:一袋白糖的质量×(1-用去的分率)=还剩的质量。
20.;
的倒数是 , 的倒数是 。
据倒数的定义,乘积是1的两个数互为倒数, × =1, × =1,即可得解。
21.(1)立方分米
(2)升
解:(1)一个粉笔盒的体积约是1立方分米;
(2)一台冰箱的容积约是 200升。
故答案为:(1)立方分米;(2)升。
根据实际生活经验以及题干中的具体数据来进行填空。
22.60;2.04
解:0.06升=60毫升;2立方米40立方分米=2.04立方米。
故答案为:60;2.04。
1升=1000毫升,1立方米=1000立方分米,根据这些单位之间的进率换算单位即可。
23.640
解:减少的表面积是高为2厘米的侧面积,侧面积是4个相同的长方形,
64÷4÷2=16÷2=8(厘米)
8×8×(8+2)=8×8×10=640(立方厘米)
原来长方体的体积是640立方厘米。
故答案为:640。
减少的表面积÷4=减少的1个面的面积,减少的1个面的面积÷高=原来长方体的长和宽,原来长方体的长+2厘米=原来长方体的高,原来长方体的长×宽×高=原来长方体的体积。
24.216平方分米;216立方米
解:棱长:72÷12=6(分米)
表面积:6×6×6=36×6=216(平方分米)
体积:6×6×6=216(立方分米)
故答案为:216平方分米;216立方分米。
正方体的棱长 = 棱长总和 ÷ 12,表面积 = 6 × (棱长 × 棱长),体积 = 棱长 × 棱长 × 棱长。
25.空间的大小;体积
解:物体所占空间的大小是物体的体积,
容器所能容纳物体的体积是容器的容积。
故答案为:空间的大小;体积。
本题关键区分体积与容积:体积描述物体自身占据的空间,容积描述容器容纳其他物体的体积。
26.2
解:2厘米=0.2分米,5米=50分米;
0.2×0.2×50
=0.04×50
=2(立方分米)。
故答案为:2。
先单位换算2厘米=0.2分米,5米=50分米;这根钢材的体积=底面边长×边长×高。
27.
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的法则进行计算,计算结果能约分的要约成最简分数;
分数乘整数,整数与分子相乘的乘积作分子,分母不变,能约分的要先约分,再计算;
分数乘分数,能约分的先约分,然后用分子相乘的积作分子,分母相乘的积作分母,据此解答。
28.(1)解:表面积:
(9×5+9×3+5×3)×2-(5-2)×(3-1.5)×2
=(45+27+15)×2-3×1.5×2
=87×2-9
=174-9
=165(cm2)
体积:
9×2×(3-1.5)+9×5×1.5
=18×1.5+45×1.5
=27+67.5
=94.5(cm3)
(2)解:表面积:
2×2×6+2×(2+3)×4
=24+40
=64(m2)
体积:
2×2×(3+2)+2×2×2
=20+8
=28(m3)
(1)图形的表面积比长9cm、宽5cm、高3cm的长方体的表面积少了两个长方形面的面积,这两个长方形的长都是(5-2)cm,宽都是(3-1.5)cm,由此计算表面积。图形的体积是下面长9cm、宽5cm、高1.5cm的长方体体积,加上上面长9cm、宽2cm、高是(3-1.5)cm的长方体体积。
(2)图形的表面积是左边长方体的表面积加上右边正方体4个面的面积,因此2×2的面一共有6个,2×(2+3)的面一共有4个。用左边长方体的体积加上右边正方体的体积就是它的体积。
29.解:1.6×1.6×1.6÷4×0.9
=4.096÷4×0.9
=1.024×0.9
=0.9216(立方分米)
答:铁块的体积是0.9216立方分米。
铁块的体积=长方体水槽的底面积×放入这个铁块后水面上升的高度,其中,长方体水槽的底面积=正方体石块的棱长×棱长×棱长÷水面上升的高度。
30.解:(80×80×80)÷20
=512000÷20
=25600(厘米)
答:这个长方体的长是25600厘米。
这个长方体的长=这个长方体的体积÷横截面的面积;其中,这个长方体的体积=正方体铁块的体积=棱长×棱长×棱长。
31.解:40分米=4米
4×2×0.5
=8×0.5
=4(立方米)
4×1.4=5.6(吨)
答:这些黄沙重5.6吨。
需要黄沙的体积=长方体沙坑的长×宽×高,这些黄沙的质量=这些黄沙的体积×平均每立方米的质量。
32.解:0.8米=8分米
10×8+(10×5+8×5)×2
=80+90×2
=80+180
=260(平方分米)
10×8×5
=80×5
=400(立方分米)
400立方分米=400升
答:至少需要260平方分米的铁皮,这个水箱的容积是400升。
至少需要铁皮的面积=长方体水箱的长×宽+(长×高+宽×高)×2,这个水箱的容积=长×宽×高。然后再单位换算。
33.解:(人)
答:今年毕业的学生比去年多48人
去年毕业的学生数×增加的分率=增加的人数。
34.解:165÷= 275(个)
275×=99(个)
答:实验小学四收集了99个空矿泉水瓶;六年级收集了275个空矿泉水瓶。
五年级收集的个数÷对应六年级收集个数的分率=六年级收集个数;六年级收集个数×=四年级收集的个数。
2024-2025学年北师大版数学下册第二次月考卷
(五年级)
考试范围:3-4单元 考试时间:90分钟
注意事项:
1.答题前,填写好自己的姓名、班级、考号等信息,请写在答题卡规定的位置上。
2.所有题目必须在答题卡上作答,在试卷上作答无效。
3.考试结束后将试卷和答题卡一并交回。
一、单选题(10分)
1.a是非0自然数,下列算式中,得数最小的是( )。
A.a× B.a+ C.a× D.a×
2.假分数的倒数都( )1。
A.小于 B.等于 C.大于 D.不大于
3.用分数表示下图涂色部分( )。
A. B. C. D.
4.姐姐装了杯纯果汁,兑满了温水后给弟弟喝了半杯,弟弟喝了( )杯纯果汁。
A. B. C. D.
5.两根同样长的线段,第1段先擦去,再延长dm,第二段先延长dm,再擦去。那么,现在这两条线段的长度( )。
A.第1段长 B.第2段长 C.一样长 D.无法判断
6.正方体的棱长扩大到原来的3倍,它的体积扩大到原来的( )。
A.3倍 B.9倍 C.27倍
7.一个长10cm、宽8cm、高4cm的长方体木块,能切成( )个棱长是2cm的小正方体木块。
A.40 B.80 C.160 D.120
8.用来表示一块橡皮擦的体积,下面的计量单位中( )最合适.
A.立方分米 B.平方分米 C.立方厘米 D.平方厘米
9.一根方木的体积是 80dm3,长是 20dm,这根方木的横截面积是( )。
A.4dm B.4dm2 C.4dm3
10.将一块长方体橡皮泥捏成一个正方体,正方体和长方体相比( )。
A.体积相等,表面积不相等 B.体积和表面积都不相等
C.表面积相等,体积不相等 D.体积和表面积都相等
二、判断题(5分)
11.1立方米铁块的体积和它的占地面积相等。( )
12.两个体积相等的长方体,它们的形状一定相同.( )
13.棱长是3dm的正方体,正好能分割成3000个棱长是1cm的小正方体。( )
14.把一根木料锯成两段需要分钟,如果锯成8段需要 分钟。( )
15.1kg的比4kg的重一些。( )
三、填空题(20分)
16. 3个是 ,5个 和11个相等。
17.如果两个数相乘的积是1,那么这两个数 。
18.学校一个月节约用水 吨,照这样计算,这所学校一个季度节约用水 吨,一年节约用水 吨。
19.一袋白糖千克,用了千克,还剩 千克;如果用了这袋糖的,还剩 千克。
20. 的倒数是 , 的倒数是 。
21.在横线上填上合适的单位名称:
(1)一个粉笔盒的体积约是 1 。
(2)一台冰箱的容积约是 200 。
22. 0.06升= 毫升 2立方米40立方分米= 立方米。
23.一个长方体,如果高减少2厘米,就变成一个正方体,这时表面积比原来减少64平方厘米。原来长方体的体积是 立方厘米。
24.一个正方体的棱长之和是72分米,它的表面积是 ,体积是 。
25.物体所占 是物体的体积,容器所能容纳物体的 是容器的容积。
26.一根长方体钢材的横截面是边长为2cm的正方形,它的长是5m。这根钢材的体积是 dm3。
四、计算题(23分)
27.直接写得数.
28.计算下面图形的表面积和体积。
(1)
五、解决问题(42分)
29.将一个棱长1.6dm的正方体石块浸没到一个长方体水槽里,水面上升了4d m,然后放入一个铁块并浸没,水面又上升了0.9 dm,求铁块的体积。
30.有一块棱长是 80 厘米的正方体的铁块,现在要把它熔铸成一个横截面积是 20 平方厘米的长方体,这个长方体的长是多少厘米?
31.一个长方体的沙坑,长40分米,宽2 米,深0.5米,需要多少立方米的黄沙才能填满?如果每立方米黄沙重 1.4吨,这些黄沙重多少吨?
32.用铁皮做一个无盖的长方体水箱,长10 分米,宽0.8米,高5 分米,至少需要多少平方分米的铁皮?这个水箱的容积是多少升?
33.春雷小学去年毕业的学生有160人,今年毕业的学生人数比去年增加了 今年毕业的学生比去年多多少人?
34.”节约资源从我做起”。实验小学上个月开展了收集空矿泉水瓶的活动。五年级收集了165个,是六年级的,四年级收集的个数是六年级的,实验小学四、六年级各收集了多少个空矿泉水瓶?
答案解析部分
1.A
解:A项:因为<1,所以a×<a;
B项:a+ >a;
C项:因为 <1,所以a×<a;
D项:因为 >1,所以a×>a。
<,则a×的得数最小。
故答案为:A。
一个非0的数乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。
2.D
解:假分数的倒数都不大于1。
故答案为:D。
因为假分数的值大于或等于1,那么假分数的倒数就小于或等于1。
3.B
解:×=,涂色部分用分数表示为。
故答案为:B。
三角形先被平均分成四份,其中的一个三角形占大三角形的,其中的一个三角形又被平均分成4份,这份占1个三角形的,占大三角形的。
4.B
解:×=(杯),
弟弟喝了杯纯果汁。
故答案为:B。
兑满了温水后给弟弟喝了半杯,弟弟喝了这杯果汁水的一半,也是喝了纯果汁的一半;杯纯果汁的一半是杯纯果汁 。
5.A
解:假设线段长a分米,
第1段剩下:a×(1-)+=a+;
第2段剩下:(a+)×(1-)=(a+)×=a+;
不管a是几,a+>a+,所以剩下的长度,第1段长 。
故答案为:A。
先计算,再通过计算的结果判断。
6.C
解:正方体的棱长扩大到原来的3倍,它的体积扩大到原来的3×3×3=27倍。
故答案为:C。
正方体体积=棱长×棱长×棱长,所以正方体体积扩大的倍数是棱长扩大倍数的立方倍。
7.A
解:因为长宽高都是2厘米的倍数,所以不浪费,
(10×8×4)÷(2×2×2)=320÷8=40(个)
能切成40个棱长是2cm的小正方体木块。
故答案为:A。
长方体木块的体积÷小正方体木块的体积=能切成的块数。
8.C
解:一块橡皮擦的体积用立方厘米最合适。
故答案为:C。
体积的常用单位有立方米、立方分米、立方厘米;根据实际情况并结合题中的数字选择合适的单位。
9.B
解:80÷20=4(dm2)
故答案为:B。
长方体体积=底面积×高,也可以用横截面面积乘长求出体积,因此用方木的体积除以长即可求出方木横截面的面积。
10.A
解:将一块长方体橡皮泥捏成一个正方体,正方体和长方体所占空间的大小不变,也就是体积相等,表面积不相等。
故答案为:A。
将一块长方体橡皮泥捏成一个正方体后体积相等,还是橡皮泥的体积,表面积不相等。
11.错误
解:1立方米铁块的体积和它的占地面积无法比较大小,原题干说法错误。
故答案为:错误。
体积是物体所占空间的大小,占地面积是它的底面积,体积和面积无法比较大小。
12.错误
解:两个体积相等的长方体,它们的形状不一定相同。原题说法错误。
故答案为:错误。
两个体积相等的长方体,只能说明它们长、宽、高的乘积相等,并不能确定长、宽、高分别相等,所以两个长方体不一定相同。
13.错误
解:棱长是3dm的正方体,正好能分割成27000个棱长是1cm的小正方体。原题说法错误。
故答案为:错误。
棱长3dm的正方体,体积是27立方分米,棱长是1厘米的小正方体,体积是1立方厘米,27立方分米=27000立方厘米,所以能割成27000个小正方体。
14.错误
解:锯成8段需要锯 8 1 = 7 (次),
锯成两段需要分钟,说明锯1次需要分钟,
×7=(分钟),锯成8段需要分钟,原题说法错误。
故答案为:错误。
锯一次需要的时间×7=锯7次需要的时间。
15.错误
解:1kg×=kg,4kg×=kg,一样重。原题说法错误。
故答案为:错误。
求一个数的几分之几是多少用乘法。据此解答。
16.;
解:3个是,11个是1,所以5个和11个相等。
故答案为:;。
分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数和的简便运算。
17.互为倒数
解:如果两个数相乘的积是1,那么这两个数互为倒数。
故答案为:互为倒数。
互为倒数的两个数,积是1。
18.8;32
解:一年=12个月
一季度=3个月
×3=8(吨)
×12=32(吨)。
故答案为:8;32。
这所学校一个季度节约用水的吨数=平均每个月节约用水的吨数×一季度的月数;一年节约用水的吨数=平均每个月节约用水的吨数×一年的月数。
19.;
解:-=(千克),还剩千克;
×(1-)=×=(千克)。
故答案为:;。
第一空:一袋白糖的质量-用去的质量=还剩的质量;
第二空:一袋白糖的质量×(1-用去的分率)=还剩的质量。
20.;
的倒数是 , 的倒数是 。
据倒数的定义,乘积是1的两个数互为倒数, × =1, × =1,即可得解。
21.(1)立方分米
(2)升
解:(1)一个粉笔盒的体积约是1立方分米;
(2)一台冰箱的容积约是 200升。
故答案为:(1)立方分米;(2)升。
根据实际生活经验以及题干中的具体数据来进行填空。
22.60;2.04
解:0.06升=60毫升;2立方米40立方分米=2.04立方米。
故答案为:60;2.04。
1升=1000毫升,1立方米=1000立方分米,根据这些单位之间的进率换算单位即可。
23.640
解:减少的表面积是高为2厘米的侧面积,侧面积是4个相同的长方形,
64÷4÷2=16÷2=8(厘米)
8×8×(8+2)=8×8×10=640(立方厘米)
原来长方体的体积是640立方厘米。
故答案为:640。
减少的表面积÷4=减少的1个面的面积,减少的1个面的面积÷高=原来长方体的长和宽,原来长方体的长+2厘米=原来长方体的高,原来长方体的长×宽×高=原来长方体的体积。
24.216平方分米;216立方米
解:棱长:72÷12=6(分米)
表面积:6×6×6=36×6=216(平方分米)
体积:6×6×6=216(立方分米)
故答案为:216平方分米;216立方分米。
正方体的棱长 = 棱长总和 ÷ 12,表面积 = 6 × (棱长 × 棱长),体积 = 棱长 × 棱长 × 棱长。
25.空间的大小;体积
解:物体所占空间的大小是物体的体积,
容器所能容纳物体的体积是容器的容积。
故答案为:空间的大小;体积。
本题关键区分体积与容积:体积描述物体自身占据的空间,容积描述容器容纳其他物体的体积。
26.2
解:2厘米=0.2分米,5米=50分米;
0.2×0.2×50
=0.04×50
=2(立方分米)。
故答案为:2。
先单位换算2厘米=0.2分米,5米=50分米;这根钢材的体积=底面边长×边长×高。
27.
异分母分数加减法计算方法:先通分,然后按照同分母分数加减法的法则进行计算,计算结果能约分的要约成最简分数;
分数乘整数,整数与分子相乘的乘积作分子,分母不变,能约分的要先约分,再计算;
分数乘分数,能约分的先约分,然后用分子相乘的积作分子,分母相乘的积作分母,据此解答。
28.(1)解:表面积:
(9×5+9×3+5×3)×2-(5-2)×(3-1.5)×2
=(45+27+15)×2-3×1.5×2
=87×2-9
=174-9
=165(cm2)
体积:
9×2×(3-1.5)+9×5×1.5
=18×1.5+45×1.5
=27+67.5
=94.5(cm3)
(2)解:表面积:
2×2×6+2×(2+3)×4
=24+40
=64(m2)
体积:
2×2×(3+2)+2×2×2
=20+8
=28(m3)
(1)图形的表面积比长9cm、宽5cm、高3cm的长方体的表面积少了两个长方形面的面积,这两个长方形的长都是(5-2)cm,宽都是(3-1.5)cm,由此计算表面积。图形的体积是下面长9cm、宽5cm、高1.5cm的长方体体积,加上上面长9cm、宽2cm、高是(3-1.5)cm的长方体体积。
(2)图形的表面积是左边长方体的表面积加上右边正方体4个面的面积,因此2×2的面一共有6个,2×(2+3)的面一共有4个。用左边长方体的体积加上右边正方体的体积就是它的体积。
29.解:1.6×1.6×1.6÷4×0.9
=4.096÷4×0.9
=1.024×0.9
=0.9216(立方分米)
答:铁块的体积是0.9216立方分米。
铁块的体积=长方体水槽的底面积×放入这个铁块后水面上升的高度,其中,长方体水槽的底面积=正方体石块的棱长×棱长×棱长÷水面上升的高度。
30.解:(80×80×80)÷20
=512000÷20
=25600(厘米)
答:这个长方体的长是25600厘米。
这个长方体的长=这个长方体的体积÷横截面的面积;其中,这个长方体的体积=正方体铁块的体积=棱长×棱长×棱长。
31.解:40分米=4米
4×2×0.5
=8×0.5
=4(立方米)
4×1.4=5.6(吨)
答:这些黄沙重5.6吨。
需要黄沙的体积=长方体沙坑的长×宽×高,这些黄沙的质量=这些黄沙的体积×平均每立方米的质量。
32.解:0.8米=8分米
10×8+(10×5+8×5)×2
=80+90×2
=80+180
=260(平方分米)
10×8×5
=80×5
=400(立方分米)
400立方分米=400升
答:至少需要260平方分米的铁皮,这个水箱的容积是400升。
至少需要铁皮的面积=长方体水箱的长×宽+(长×高+宽×高)×2,这个水箱的容积=长×宽×高。然后再单位换算。
33.解:(人)
答:今年毕业的学生比去年多48人
去年毕业的学生数×增加的分率=增加的人数。
34.解:165÷= 275(个)
275×=99(个)
答:实验小学四收集了99个空矿泉水瓶;六年级收集了275个空矿泉水瓶。
五年级收集的个数÷对应六年级收集个数的分率=六年级收集个数;六年级收集个数×=四年级收集的个数。
同课章节目录
