第4章 平面内的两条直线 单元整合练习 (含答案)2024-2025学年湘教版七年级数学下册
文档属性
| 名称 | 第4章 平面内的两条直线 单元整合练习 (含答案)2024-2025学年湘教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 323.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:30:47 | ||
图片预览




文档简介
平台中小学教育资源及组卷应用
第4章 平面内的两条直线 单元整合练习
一、选择题(每小题3分,共30分)
1.定义法下列说法不正确的是 ( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
2.如图,直线AB 和 CD 交于点 O,∠1-∠2=70°,则∠3 的度数为 ( )
A.55° B.50° C.45° D.40°
3.如图,直线AB,CD 被直线EF 所截,交点分别是点 M,N,则∠AME 与∠ENC是 ( )
A.同位角 B.同旁内角
C.内错角 D.对顶角
4.(2024青海中考)如图,一段弯曲管道中,AB∥CD,∠ABC=120°,则∠BCD的度数是( )
A.120° B.30° C.60° D.150°
5.(2024北京中考)如图,直线AB 和 CD 相交于点O,OE⊥OC.若∠AOC=58°,则∠EOB的大小为 ( )
A.29° B.32° C.45° D.58°
6.情境题·现实生活(2022 江苏常州中考)如图,斑马线的作用是引导行人安全地通过马路.小丽觉得行人沿垂直于马路的方向走过斑马线更为合理,这一想法的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
7.一块电脑主板的示意图如图(单位:mm),其中每个角都是直角,则这块主板的周长是 ( )
A.48 mm B.80 mm
C.96 mm D.100 mm
8.平行线拐点模型一条公路修到湖边时,需拐弯绕道而过,第一次拐弯∠A 的度数为α,第二次拐弯∠B 的度数为β,到了点 C 后需要继续拐弯,且拐弯后的道路与第一次拐弯之前的道路平行,则∠C的度数为 ( )
A.α-β B.180°-β+α
C.360°-β-α D.β-α
9.(2024广东深圳盐田期末)利用如图所示的方法,可以折出“过已知直线外一点 P 且与已知直线AB 平行”的直线.下列解释正确的是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.以上解释都正确
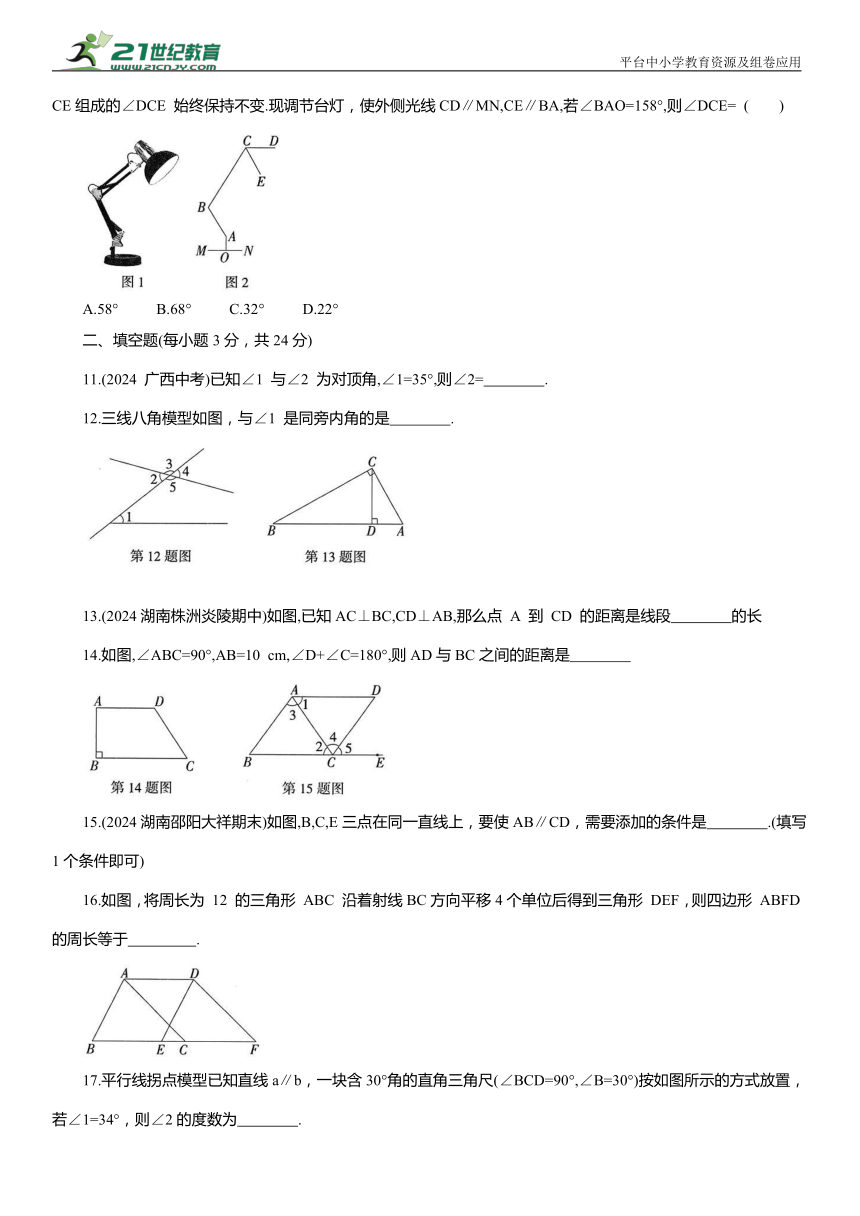
10.如图所示的是一盏可调节台灯(如图1)及其示意图(如图2).固定支撑杆AO 垂直于底座MN于点O,AB 与BC是分别可绕点 A 和B 旋转的调节杆,台灯灯罩可绕点 C 旋转调节光线角度,在调节过程中,最外侧光线CD、CE组成的∠DCE 始终保持不变.现调节台灯,使外侧光线CD∥MN,CE∥BA,若∠BAO=158°,则∠DCE= ( )
A.58° B.68° C.32° D.22°
二、填空题(每小题3分,共24分)
11.(2024 广西中考)已知∠1 与∠2 为对顶角,∠1=35°,则∠2= .
12.三线八角模型如图,与∠1 是同旁内角的是 .
13.(2024湖南株洲炎陵期中)如图,已知AC⊥BC,CD⊥AB,那么点 A 到 CD 的距离是线段 的长
14.如图,∠ABC=90°,AB=10 cm,∠D+∠C=180°,则AD与BC之间的距离是
15.(2024湖南邵阳大祥期末)如图,B,C,E三点在同一直线上,要使AB∥CD,需要添加的条件是 .(填写1个条件即可)
16.如图,将周长为 12 的三角形 ABC 沿着射线BC方向平移4个单位后得到三角形 DEF,则四边形 ABFD 的周长等于 .
17.平行线拐点模型已知直线a∥b,一块含30°角的直角三角尺(∠BCD=90°,∠B=30°)按如图所示的方式放置,若∠1=34°,则∠2的度数为 .
18. 新考向·规律探究试题在同一平面内有足够多条直线,记作a ,a ,a ,…, an,如果 那么a 与a 的位置关系是 .
三、解答题(共46分)
19.(8分)如图,直线AB,CD相交于点 O,OC平分∠AOM,且∠AOM=88°,射线 ON在∠BOM的内部.
(1)求∠AOD的度数.
(2)若∠BOC=4∠NOB,求∠MON的度数.
20.(2023湖南湘西州龙山期末)(8分)如图,在三角形ABC中,BC=4cm,把三角形ABC 沿BC所在直线向右平移2cm 得到三角形DEF.
(1)图中与∠A 相等的角有多少个
(2)图中的平行线共有多少组 请分别写出来.
(3)求BE:BC:BF的值.
21.(8分)如图所示,已知 AD 平分∠CAE,AD∥BC,试说明:∠B=∠C.
22.(2024 湖南湘潭雨湖期末)(10分)如图,AB∥CD,E 是直线 FD 上的一点,∠ABC=140°,∠CDF=40°.
(1)求证:BC∥EF.
(2)连接BD,若BD∥AE,∠BAE=110°,则BD是否平分∠ABC 请说明理由.
23.分类讨论思想 (2024山东泰安期末)(12分)直线AB,CD 相交于点 O,过点O 作OE⊥CD.
(1)如图1,若∠BOD=27°,求∠AOE的度数.
(2)如图2,作射线 OF,使∠EOF=∠AOE,则OD 是∠BOF 的平分线.请说明理由.
(3)在图 1 上作 OG⊥AB,写出∠COG 与∠AOE 的数量关系,并说明理由.
1A 若点在直线上,则过该点不能作出已知直线的平行线,故A 选项说法错误,B、C、D选项说法正确.故选A.
2A ∵∠1-∠2=70°,∠1+∠2=180°,∴∠2=55°,∵∠3=∠2,∴∠3=55°,故选 A.
3A 根据同位角、内错角、同旁内角、对顶角的定义解答即可.
4C∵AB∥CD,∴∠BCD+∠ABC=180°,
∵∠ABC=120°,∴∠BCD=60°.故选 C.
5B ∵OE⊥OC,∴∠COE=∠DOE=90°,∵∠BOD=∠AOC=58°,∴∠EOB=90°-58°=32°.故选 B.
6A 小丽觉得行人沿垂直于马路的方向走过斑马线更为合理,这一想法的数学依据是垂线段最短,故选 A.
7C(16+24)×2+4×4=40×2+16=96(mm),∴这块主板的周长是96 mm,故选 C.
8B 如图,过B作 BF∥AD,∵CE∥AD,∴AD∥BF∥CE,∴∠ABF=∠A=α,∠FBC=180°-∠C,∵∠ABC=∠ABF+∠FBC=β,∴α+180°-∠C=β,
∴∠C=180°-β+α,故选 B.
9 D如图,
由图2的操作可知PE⊥AE,所以∠PEA=90°,由图3的操作可知MN⊥PE,所以∠MPE=∠NPE=90°,所以∠MPE=∠NPE=∠AEP=∠BEP=∠AEQ=∠BEQ=90°,所以可依据同位角相等,两直线平行或内错角相等,两直线平行或同旁内角互补,两直线平行判定AB∥MN,故选 D.
10B 如图所示,过点A作AG∥MN,过点B作BH∥CD,
∵CD∥MN,∴AG∥MN∥BH∥CD,
∵OA⊥MN,∴AG⊥OA,即∠OAG=90°,
∵∠BAO=158°,∴∠BAG=∠BAO-∠OAG=68°,
∴∠ABH=∠BAG=68°,
∵CE∥AB,BH∥CD,∴ ∠ABC+∠BCE = 180°=∠CBH+∠BCD,∴ ∠ABH+∠CBH+∠BCE=180°=∠CBH+∠BCE+∠DCE,∴∠DCE=∠ABH=68°,故选 B.
11答案 35°
解析 ∵∠1与∠2为对顶角,∠1=35°,∴∠2=∠1=35°.故答案为35°.
12答案 ∠5
解析 根据“两条直线被第三条直线所截,位于这两条直线的内部且在截线同侧,这样的两个角叫作同旁内角”进行判断即可.
13答案 AD
解析 ∵CD⊥AB,∴点A到 CD 的距离是线段AD的长.
14答案 10 cm
解析 ∵∠D+∠C=180°,∴ AD∥BC,∵ ∠ABC=90°,∴AB 的长即为AD 与BC 之间的距离,∵AB=10 cm,∴AD 与 BC 之间的距离是 10 cm.
15答案 ∠3=∠4(答案不唯一)
解析 当∠3=∠4时,根据内错角相等,两直线平行可以判定AB∥CD.答案不唯一.
16答案 20
解析 根据题意,将周长为12 的三角形 ABC 沿边BC向右平移4个单位后得到三角形DEF,∴AD=4,BF=BC+CF=BC+4,DF=AC,又∵AB+BC+AC=12,∴四边形 ABFD 的周长=AD+AB+BF+DF=4+AB+BC+4+AC=20.故答案为20.
17答案 26°
解析 如图,过D作DM∥a,∵a∥b,
∴DM∥a∥b,∴∠BDM=∠1=34°,∠2=∠CDM,
∴ ∠CDM=60°-34°=26°,∴∠2=26°.
故答案为26°.
18答案 a ∥a 024
解析 由题意知a ⊥a ,a ⊥a ,a ∥a ,a ∥a ,……,易知位置关系以4次为一循环.规律:对于直线 an,下标n除以4,当余数为2或3时,直线 an与a 的位置关系为垂直,当余数为1或整除时,直线an与a 的位置关系为平行,2 024÷4=506,所以a ∥a 024·
19解析 (1)∵OC平分∠AOM,且∠AOM=88°,
(2)∵∠AOD=136°,∴∠BOC=136°,
∵∠BOC=4∠NOB,∴∠NOB=34°,
∵∠COM=44°,
∴∠MON=∠BOC-∠NOB-∠COM=136°-34°-44°=58°.
20解析 (1)∵三角形 DEF 是由三角形ABC 平移得到的,∴∠D=∠A,AB∥DE,
∴∠EMC=∠A,∠AMD=∠A,
∴图中与∠A 相等的角有3个.
(2)图中的平行线共有2组.由平移的性质可得,AB∥DE,AC∥DF.
(3)由平移的性质可知BE=2cm,CF=2cm,
∵BC=4cm,∴BF=6cm,
∴BE:BC: BF=2:4:6=1:2:3.
21证明 ∵AD∥BC,∴∠B=∠EAD,∠DAC=∠C,∵AD平分∠CAE,∴∠EAD=∠DAC,∴∠B=∠C.
22解析 (1)证明:∵AB∥CD,∴∠ABC+∠BCD=180°,
∵∠ABC=140°,∴∠BCD=40°,
∵∠CDF=40°,∴∠BCD=∠CDF,∴BC∥EF.
(2)BD 平分∠ABC.理由:∵ AE∥BD,∴ ∠BAE+∠ABD= 180°,∵ ∠BAE = 110°,∴ ∠ABD =70°,∵∠ABC=140°,∴ ∠ABD=∠DBC=70°,∴ BD 平分∠ABC.
23解析 (1)∵OE⊥CD,
∴∠COE=90°,即∠AOC+∠AOE=90°,
∵∠AOC=∠BOD=27°,
∴ ∠AOE=90°-27°=63°.
(2)理由:∵ OE⊥CD,∴∠COE=∠DOE=90°,即∠AOC+∠AOE=∠DOF+∠EOF=90°,
∵∠EOF=∠AOE,
∴∠AOC=∠DOF,
又∵∠AOC=∠BOD,
∴∠BOD=∠DOF,即OD 是∠BOF的平分线.
(3)∠COG+∠AOE=180°或∠COG=∠AOE,理由如下:
①当OG在AB下方时,如图1,
∵OG⊥AB,∴∠AOG=∠BOG=90°,即∠AOE+∠EOG=∠DOG+∠BOD=90°,
∵OE⊥CD,
∴∠COE=90°,即∠AOC+∠AOE=90°,
∴∠BOD=∠AOC=∠EOG,
∴∠AOE=∠DOG,
∵∠COG+∠DOG=180°,
∴∠COG+∠AOE=180°.
②当OG在AB上方时,如图2,
∵OG⊥AB,∴∠AOG=90°=∠AOC+∠COG,
∵OE⊥CD,∴∠COE=90°=∠AOC+∠AOE,
∴∠COG=∠AOE.
第4章 平面内的两条直线 单元整合练习
一、选择题(每小题3分,共30分)
1.定义法下列说法不正确的是 ( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
2.如图,直线AB 和 CD 交于点 O,∠1-∠2=70°,则∠3 的度数为 ( )
A.55° B.50° C.45° D.40°
3.如图,直线AB,CD 被直线EF 所截,交点分别是点 M,N,则∠AME 与∠ENC是 ( )
A.同位角 B.同旁内角
C.内错角 D.对顶角
4.(2024青海中考)如图,一段弯曲管道中,AB∥CD,∠ABC=120°,则∠BCD的度数是( )
A.120° B.30° C.60° D.150°
5.(2024北京中考)如图,直线AB 和 CD 相交于点O,OE⊥OC.若∠AOC=58°,则∠EOB的大小为 ( )
A.29° B.32° C.45° D.58°
6.情境题·现实生活(2022 江苏常州中考)如图,斑马线的作用是引导行人安全地通过马路.小丽觉得行人沿垂直于马路的方向走过斑马线更为合理,这一想法的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
7.一块电脑主板的示意图如图(单位:mm),其中每个角都是直角,则这块主板的周长是 ( )
A.48 mm B.80 mm
C.96 mm D.100 mm
8.平行线拐点模型一条公路修到湖边时,需拐弯绕道而过,第一次拐弯∠A 的度数为α,第二次拐弯∠B 的度数为β,到了点 C 后需要继续拐弯,且拐弯后的道路与第一次拐弯之前的道路平行,则∠C的度数为 ( )
A.α-β B.180°-β+α
C.360°-β-α D.β-α
9.(2024广东深圳盐田期末)利用如图所示的方法,可以折出“过已知直线外一点 P 且与已知直线AB 平行”的直线.下列解释正确的是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.以上解释都正确
10.如图所示的是一盏可调节台灯(如图1)及其示意图(如图2).固定支撑杆AO 垂直于底座MN于点O,AB 与BC是分别可绕点 A 和B 旋转的调节杆,台灯灯罩可绕点 C 旋转调节光线角度,在调节过程中,最外侧光线CD、CE组成的∠DCE 始终保持不变.现调节台灯,使外侧光线CD∥MN,CE∥BA,若∠BAO=158°,则∠DCE= ( )
A.58° B.68° C.32° D.22°
二、填空题(每小题3分,共24分)
11.(2024 广西中考)已知∠1 与∠2 为对顶角,∠1=35°,则∠2= .
12.三线八角模型如图,与∠1 是同旁内角的是 .
13.(2024湖南株洲炎陵期中)如图,已知AC⊥BC,CD⊥AB,那么点 A 到 CD 的距离是线段 的长
14.如图,∠ABC=90°,AB=10 cm,∠D+∠C=180°,则AD与BC之间的距离是
15.(2024湖南邵阳大祥期末)如图,B,C,E三点在同一直线上,要使AB∥CD,需要添加的条件是 .(填写1个条件即可)
16.如图,将周长为 12 的三角形 ABC 沿着射线BC方向平移4个单位后得到三角形 DEF,则四边形 ABFD 的周长等于 .
17.平行线拐点模型已知直线a∥b,一块含30°角的直角三角尺(∠BCD=90°,∠B=30°)按如图所示的方式放置,若∠1=34°,则∠2的度数为 .
18. 新考向·规律探究试题在同一平面内有足够多条直线,记作a ,a ,a ,…, an,如果 那么a 与a 的位置关系是 .
三、解答题(共46分)
19.(8分)如图,直线AB,CD相交于点 O,OC平分∠AOM,且∠AOM=88°,射线 ON在∠BOM的内部.
(1)求∠AOD的度数.
(2)若∠BOC=4∠NOB,求∠MON的度数.
20.(2023湖南湘西州龙山期末)(8分)如图,在三角形ABC中,BC=4cm,把三角形ABC 沿BC所在直线向右平移2cm 得到三角形DEF.
(1)图中与∠A 相等的角有多少个
(2)图中的平行线共有多少组 请分别写出来.
(3)求BE:BC:BF的值.
21.(8分)如图所示,已知 AD 平分∠CAE,AD∥BC,试说明:∠B=∠C.
22.(2024 湖南湘潭雨湖期末)(10分)如图,AB∥CD,E 是直线 FD 上的一点,∠ABC=140°,∠CDF=40°.
(1)求证:BC∥EF.
(2)连接BD,若BD∥AE,∠BAE=110°,则BD是否平分∠ABC 请说明理由.
23.分类讨论思想 (2024山东泰安期末)(12分)直线AB,CD 相交于点 O,过点O 作OE⊥CD.
(1)如图1,若∠BOD=27°,求∠AOE的度数.
(2)如图2,作射线 OF,使∠EOF=∠AOE,则OD 是∠BOF 的平分线.请说明理由.
(3)在图 1 上作 OG⊥AB,写出∠COG 与∠AOE 的数量关系,并说明理由.
1A 若点在直线上,则过该点不能作出已知直线的平行线,故A 选项说法错误,B、C、D选项说法正确.故选A.
2A ∵∠1-∠2=70°,∠1+∠2=180°,∴∠2=55°,∵∠3=∠2,∴∠3=55°,故选 A.
3A 根据同位角、内错角、同旁内角、对顶角的定义解答即可.
4C∵AB∥CD,∴∠BCD+∠ABC=180°,
∵∠ABC=120°,∴∠BCD=60°.故选 C.
5B ∵OE⊥OC,∴∠COE=∠DOE=90°,∵∠BOD=∠AOC=58°,∴∠EOB=90°-58°=32°.故选 B.
6A 小丽觉得行人沿垂直于马路的方向走过斑马线更为合理,这一想法的数学依据是垂线段最短,故选 A.
7C(16+24)×2+4×4=40×2+16=96(mm),∴这块主板的周长是96 mm,故选 C.
8B 如图,过B作 BF∥AD,∵CE∥AD,∴AD∥BF∥CE,∴∠ABF=∠A=α,∠FBC=180°-∠C,∵∠ABC=∠ABF+∠FBC=β,∴α+180°-∠C=β,
∴∠C=180°-β+α,故选 B.
9 D如图,
由图2的操作可知PE⊥AE,所以∠PEA=90°,由图3的操作可知MN⊥PE,所以∠MPE=∠NPE=90°,所以∠MPE=∠NPE=∠AEP=∠BEP=∠AEQ=∠BEQ=90°,所以可依据同位角相等,两直线平行或内错角相等,两直线平行或同旁内角互补,两直线平行判定AB∥MN,故选 D.
10B 如图所示,过点A作AG∥MN,过点B作BH∥CD,
∵CD∥MN,∴AG∥MN∥BH∥CD,
∵OA⊥MN,∴AG⊥OA,即∠OAG=90°,
∵∠BAO=158°,∴∠BAG=∠BAO-∠OAG=68°,
∴∠ABH=∠BAG=68°,
∵CE∥AB,BH∥CD,∴ ∠ABC+∠BCE = 180°=∠CBH+∠BCD,∴ ∠ABH+∠CBH+∠BCE=180°=∠CBH+∠BCE+∠DCE,∴∠DCE=∠ABH=68°,故选 B.
11答案 35°
解析 ∵∠1与∠2为对顶角,∠1=35°,∴∠2=∠1=35°.故答案为35°.
12答案 ∠5
解析 根据“两条直线被第三条直线所截,位于这两条直线的内部且在截线同侧,这样的两个角叫作同旁内角”进行判断即可.
13答案 AD
解析 ∵CD⊥AB,∴点A到 CD 的距离是线段AD的长.
14答案 10 cm
解析 ∵∠D+∠C=180°,∴ AD∥BC,∵ ∠ABC=90°,∴AB 的长即为AD 与BC 之间的距离,∵AB=10 cm,∴AD 与 BC 之间的距离是 10 cm.
15答案 ∠3=∠4(答案不唯一)
解析 当∠3=∠4时,根据内错角相等,两直线平行可以判定AB∥CD.答案不唯一.
16答案 20
解析 根据题意,将周长为12 的三角形 ABC 沿边BC向右平移4个单位后得到三角形DEF,∴AD=4,BF=BC+CF=BC+4,DF=AC,又∵AB+BC+AC=12,∴四边形 ABFD 的周长=AD+AB+BF+DF=4+AB+BC+4+AC=20.故答案为20.
17答案 26°
解析 如图,过D作DM∥a,∵a∥b,
∴DM∥a∥b,∴∠BDM=∠1=34°,∠2=∠CDM,
∴ ∠CDM=60°-34°=26°,∴∠2=26°.
故答案为26°.
18答案 a ∥a 024
解析 由题意知a ⊥a ,a ⊥a ,a ∥a ,a ∥a ,……,易知位置关系以4次为一循环.规律:对于直线 an,下标n除以4,当余数为2或3时,直线 an与a 的位置关系为垂直,当余数为1或整除时,直线an与a 的位置关系为平行,2 024÷4=506,所以a ∥a 024·
19解析 (1)∵OC平分∠AOM,且∠AOM=88°,
(2)∵∠AOD=136°,∴∠BOC=136°,
∵∠BOC=4∠NOB,∴∠NOB=34°,
∵∠COM=44°,
∴∠MON=∠BOC-∠NOB-∠COM=136°-34°-44°=58°.
20解析 (1)∵三角形 DEF 是由三角形ABC 平移得到的,∴∠D=∠A,AB∥DE,
∴∠EMC=∠A,∠AMD=∠A,
∴图中与∠A 相等的角有3个.
(2)图中的平行线共有2组.由平移的性质可得,AB∥DE,AC∥DF.
(3)由平移的性质可知BE=2cm,CF=2cm,
∵BC=4cm,∴BF=6cm,
∴BE:BC: BF=2:4:6=1:2:3.
21证明 ∵AD∥BC,∴∠B=∠EAD,∠DAC=∠C,∵AD平分∠CAE,∴∠EAD=∠DAC,∴∠B=∠C.
22解析 (1)证明:∵AB∥CD,∴∠ABC+∠BCD=180°,
∵∠ABC=140°,∴∠BCD=40°,
∵∠CDF=40°,∴∠BCD=∠CDF,∴BC∥EF.
(2)BD 平分∠ABC.理由:∵ AE∥BD,∴ ∠BAE+∠ABD= 180°,∵ ∠BAE = 110°,∴ ∠ABD =70°,∵∠ABC=140°,∴ ∠ABD=∠DBC=70°,∴ BD 平分∠ABC.
23解析 (1)∵OE⊥CD,
∴∠COE=90°,即∠AOC+∠AOE=90°,
∵∠AOC=∠BOD=27°,
∴ ∠AOE=90°-27°=63°.
(2)理由:∵ OE⊥CD,∴∠COE=∠DOE=90°,即∠AOC+∠AOE=∠DOF+∠EOF=90°,
∵∠EOF=∠AOE,
∴∠AOC=∠DOF,
又∵∠AOC=∠BOD,
∴∠BOD=∠DOF,即OD 是∠BOF的平分线.
(3)∠COG+∠AOE=180°或∠COG=∠AOE,理由如下:
①当OG在AB下方时,如图1,
∵OG⊥AB,∴∠AOG=∠BOG=90°,即∠AOE+∠EOG=∠DOG+∠BOD=90°,
∵OE⊥CD,
∴∠COE=90°,即∠AOC+∠AOE=90°,
∴∠BOD=∠AOC=∠EOG,
∴∠AOE=∠DOG,
∵∠COG+∠DOG=180°,
∴∠COG+∠AOE=180°.
②当OG在AB上方时,如图2,
∵OG⊥AB,∴∠AOG=90°=∠AOC+∠COG,
∵OE⊥CD,∴∠COE=90°=∠AOC+∠AOE,
∴∠COG=∠AOE.
同课章节目录
