第5章 轴对称与旋转单元整合练习 (含答案)2024-2025学年湘教版七年级数学下册
文档属性
| 名称 | 第5章 轴对称与旋转单元整合练习 (含答案)2024-2025学年湘教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 240.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:31:47 | ||
图片预览




文档简介
第5章 轴对称与旋转单元整合练习
一、选择题(每小题3分,共30分)
1.端午节是中国传统节日,下列与端午节有关的文创图案中,是轴对称图形的是 ( )
2.下列图形中,点A 与点B关于直线l对称的是 ( )
3.正方形的对称轴的条数为 ( )
A.1 B.2 C.3 D.4
4.在图形的平移和旋转变换中,下列说法正确的是 ( )
A.对应点所连线段都平行
B.对应线段都平行
C.对应点所连线段都相等
D.对应线段都相等
5.(2024 四川南充期末)如图,直线 MN 是四边形AMBN的对称轴,点 P 是直线 MN上的点,下列判断错误的是 ( )
A. AM=BM B. AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
6.如图,将△ABC 绕点 C顺时针旋转90°得到△EDC,若∠ACB=20°,则∠ACD的度数是 ( )
A.55° B.60° C.65° D.70°
7.如图,△ABC绕点O顺时针旋转角度α后得到△DEF,若∠COE=15°,∠BOF=85°,则旋转角α的值为( )
A.40° B.45° C.50° D.55°
8.小华在镜中看到身后墙上的时钟,你认为实际时间最接近8点的是 ( )
9. P是∠AOB内一点,分别作点 P 关于直线OA、OB的对称点 P 、P ,连接OP 、OP ,则下列结论一定正确的是 ( )
且
平台中小学教育资源及组卷应用
10.如图所示的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有 ( )
A.1个
二、填空题(每小题3分,共24分)
11.下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 (填序号).(M7205002)
12.(2024湖南邵阳大祥期末)如图,将△AOB 绕点O按逆时针方向旋转一定的角度后得到△COD,若∠AOB=15°,∠BOC=35°,则图中的旋转角的度数是 .
13.新考法(2024甘肃白银期末)如图,以虚线为对称轴,那么“甲”字的对称图形可看成是 字.
甲
14.(2024 江西吉安期末)如图,在△ABC 中,AB =8cm,AC=4cm,BC=5cm,点D,E分别在AC,AB上,且△BCD与△BED关于BD所在直线对称,则△ADE的周长为 cm.
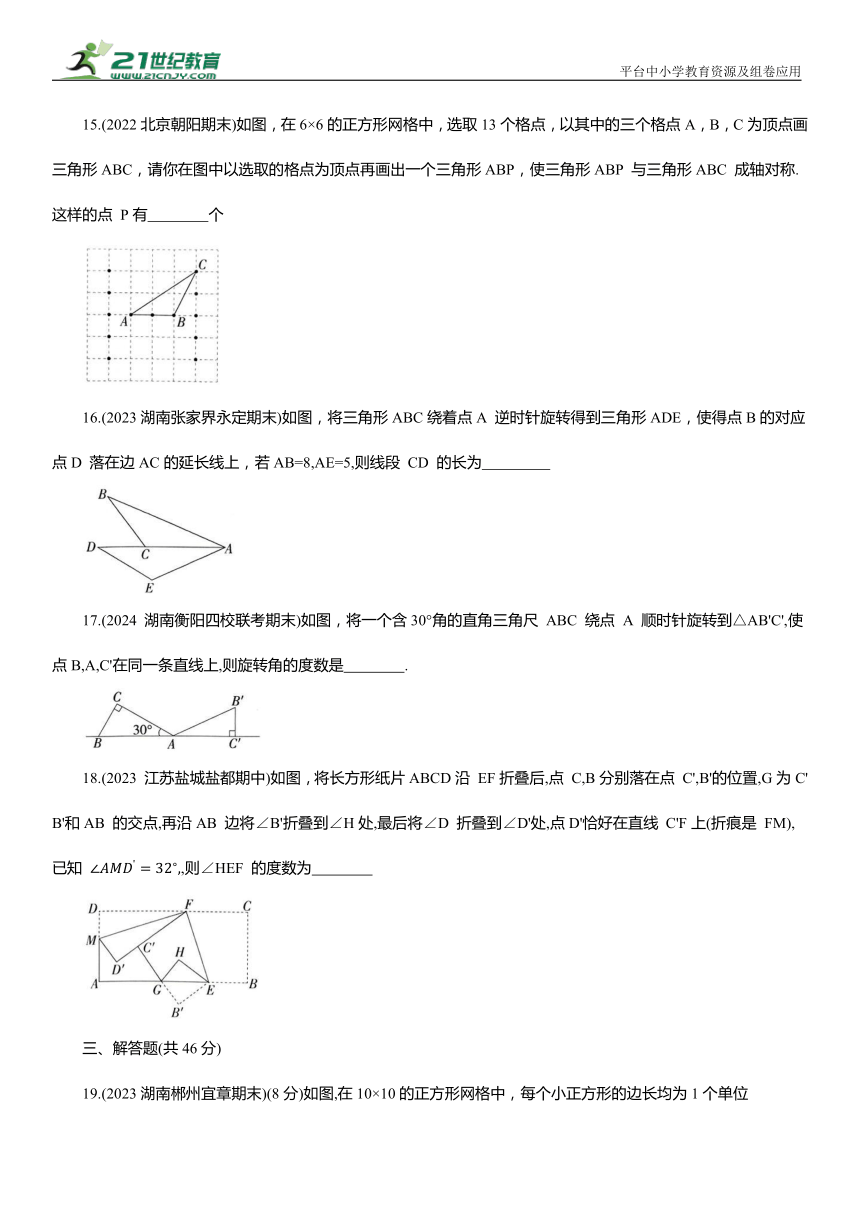
15.(2022北京朝阳期末)如图,在6×6的正方形网格中,选取13个格点,以其中的三个格点A,B,C为顶点画三角形ABC,请你在图中以选取的格点为顶点再画出一个三角形ABP,使三角形ABP 与三角形ABC 成轴对称.这样的点 P有 个
16.(2023湖南张家界永定期末)如图,将三角形ABC绕着点A 逆时针旋转得到三角形ADE,使得点B的对应点D 落在边AC的延长线上,若AB=8,AE=5,则线段 CD 的长为
17.(2024 湖南衡阳四校联考期末)如图,将一个含30°角的直角三角尺 ABC 绕点 A 顺时针旋转到△AB'C',使点B,A,C'在同一条直线上,则旋转角的度数是 .
18.(2023 江苏盐城盐都期中)如图,将长方形纸片ABCD沿 EF折叠后,点 C,B分别落在点 C',B'的位置,G为C'B'和AB 的交点,再沿AB 边将∠B'折叠到∠H处,最后将∠D 折叠到∠D'处,点D'恰好在直线 C'F上(折痕是 FM),已知 ,则∠HEF 的度数为
三、解答题(共46分)
19.(2023湖南郴州宜章期末)(8分)如图,在10×10的正方形网格中,每个小正方形的边长均为1个单位
(1)将三角形ABC向下平移6个单位,得到三角形A'B'C',请你画出三角形A'B'C'.
(2)将三角形A'B'C'绕点 C'顺时针旋转90°,得到三角形 A"B"C',请你画出三角形A"B"C'.
20.(8分)如图,△ABC和△ADE关于直线 MN对称,BC 与 DE 的交点 F 在直线 MN 上
(1)图中点 D 的对应点是 ,AE 的对应边是 .
(2)若∠DAE=108°,∠EAF=39°,求∠DAC的度数.
21.(9分)如图,三角形ABC 和三角形A'B'C'关于直线 m对称
(1)结合图形指出对称点.
(2)连接AA',直线m与线段AA'有什么关系
(3)延长线段AC与A'C',它们的交点与直线m有怎样的关系 其他对应线段(或其延长线)的交点呢 你发现了什么规律
22.(9分)如图,点 P 是∠AOB外的一点,点E 与点 P 关于直线OA 对称,点F 与点 P 关于直线OB 对称,直线 FE 分别交 OA、OB 于点 C、D,连接PC,PD,PE,PF
(1)若∠OCP=∠F=20°,求∠CPD的度数(提示:三角形三个内角的和等于180°).
(2)若CP=DP,CF=13,DE=3,求CP的长.
23.新考法 分类讨论思想(12 分)已知,∠AOB 是直角,过点O 作射线 OC(OC在直线 OA的上方),设 ,且α≠90°),将射线 OC 绕点 O 逆时针旋转 45°得到射线OD.
(1)如图1,若0°<α<45°,则∠AOC+∠BOD= °.
(2)如图2,若
(i)请你直接写出∠AOC 与∠BOD 之间的数量关系.
(ii)作∠AOD的平分线OE,试判断∠COE与∠BOD 之间的数量关系,并说明理由.
(3)若OF 平分∠BOC,请你直接写出∠DOF的度数(用含α的代数式表示).
1B A,C,D选项中的图形都不能找到一条直线,使图形沿这条直线折叠,直线两旁的部分互相重合,所以不是轴对称图形;B选项中的图形能找到一条直线,使图形沿这条直线折叠,直线两旁的部分互相重合,所以是轴对称图形,故选 B.
2A 若点A与点 B 关于直线l对称,则要满足AB垂直于直线l且点A,点B到直线l的距离相等,故选 A.
3D 正方形有4条对称轴,故选 D.
4D 在图形的平移变换中,对应点所连线段互相平行(或在同一直线上),对应线段都相等,但不一定平行,在图形的旋转变换中,对应点所连线段不一定相等,但对应线段都相等,故选 D.
5B ∵直线 MN是四边形 AMBN 的对称轴,∴ AM=BM,AN=BN,∠ANM=∠BNM,∵点P是直线MN上的点,∴∠MAP=∠MBP,∴选项 A,C,D正确,选项B错误,故选 B.
6D ∵△ABC绕点 C顺时针旋转90°得到△EDC,∴∠BCD=90°,∵∠ACB=20°,∴ ∠ACD=∠BCD-∠ACB=90°-20°=70°.故选D.
7C ∵ △ABC 绕点 O 顺时针旋转角度 α后得到△DEF,∴∠BOE=∠COF=α,
∵∠BOF=∠BOE+∠COF-∠COE,
∴α+α-15°=85°,解得α=50°.故选 C.
8D由对称的性质得8点的时钟在镜子中看到应该是4点,所以答案应该是 C选项或D 选项图形中的一个,这两个图形中更接近4点的是D选项.故选 D.
9B ∵点 P 关于直线OA、OB 的对称点分别为点 P 、P ,∴ OP =OP =OP,∠AOP =∠AOP ,∠BOP = +∠BOP =2(∠AOP+∠BOP)=2∠AOB,∵ ∠AOB 的度数不确定,∴OP 与OP 不一定垂直.故选 B.
10D第1个图案可以旋转90°得到,也可以经过轴对称,沿对称轴对折得到;
第2个图案可以旋转180°得到,也可以经过轴对称,沿对称轴对折得到;
第3个图案可以旋转180°得到,也可以经过轴对称,沿对称轴对折得到;
第4个图案可以旋转90°得到,也可以经过轴对称,沿对称轴对折得到.
综上所述,题目中四个图案均满足条件.故选 D.
11答案 ①②③④
解析 根据轴对称图形的概念,可知①②③④均为轴对称图形.故答案为①②③④.
12答案 50°
解析 ∵将△AOB 绕点 O 按逆时针方向旋转一定的角度后得到△COD,
∴∠AOC 为旋转角,∵ ∠AOB=15°,∠BOC=35°, ,即旋转角的度数是50°.
13答案 由
解析 根据轴对称的性质可得出答案.
14答案 7
解析 ∵ △BCD 与△BED关于BD 所在直线对称,AB=8cm,AC=4cm,BC=5cm,
∴BC=BE=5cm,CD=DE,∴AE=AB-BE=8-5=3(cm),
∴△ADE 的周长=AD+DE+AE=AC+AE=4+3=7(cm).故答案为7.
15答案 2
解析 如图,满足条件的点 P有2个.
16答案 3
解析 ∵ 将三角形ABC 绕着点 A 逆时针旋转得到三角形ADE,∴AB=AD,AC=AE,∵AB=8,AE=5,∴AD=8,AC=5,∴CD=AD-AC=8-5=3.
17答案 150°
解析 由题意知旋转角是∠CAC',∵∠CAC'=180°- .旋转角的度数是150°.
18答案 42°
解析 由折叠性质可知∠DMF=∠D'MF,∵ ∠AMD'=32°,∴∠DMF=∠D'MF=74°,∴∠DFM=∠D'FM=16°,∴∠CFE=∠C'FE=74°,∵AB∥CD,∴∠FEB=106°,∠FEG = 74°,∴ ∠FEB' = 106°, ∴∠B'EG =∠FEB'-∠FEG=106°-74°=32°,∴∠HEG=∠B'EG=32°,∴ ∠HEF=∠FEG-∠HEG=74°-32°=42°.
19解析 (1)如图所示,三角形A'B'C'即为所求.
(2)如图所示,三角形A"B"C'即为所求.
20解析 (1)∵ △ABC 和△ADE 关于直线 MN 对称,∴题图中点 D 的对应点是 B,AE 的对应边是AC.故答案为B;AC.
(2)∵∠EAF=39°,
∴根据对称性得∠CAF=∠EAF=39°,
∴∠CAE=78°,∵ ∠DAE=108°,∴ ∠DAC=∠DAE-
21解析 (1)对称点:A和A',B和B',C和C'.
(2)线段AA'被直线m垂直平分.
(3)线段AC与A'C'的延长线的交点在直线m上,其他对应线段(或其延长线)的交点也在直线m上.
规律:若两线段关于某直线对称,且不平行,则它们的交点或它们的延长线的交点在对称轴上.
22解析 (1)∵点E与点 P 关于直线OA 对称,点F与点 P 关于直线OB 对称,∠OCP=∠F=20°,
∴∠OCE=∠OCP=20°,∠DPF=∠F=20°,
∴∠PCF=40°,∠CPF=180°-∠F-∠PCF=120°,
∴∠CPD=∠CPF-∠DPF=100°,即∠CPD 的度数为100°.
(2)∵点E与点P 关于直线OA对称,点 F与点P关于直线OB对称,CP=DP,
∴CE=CP=DP,DP=DF,∴CE=DF,
∴CF=CE+DE+DF=2CE+3=13,∴CE=5,
∴CP=5,即CP的长为5.
23解析 本题主要考查旋转的性质,角度的和、差关系及分类讨论思想.
(1)∵∠AOB=90°,∴∠BOD+∠DOC+∠AOC=90°,∵∠DOC=45°,∴∠AOC+∠BOD=90°-45°=45°.故答案为45.
(2)(i)∠AOC-∠BOD=45°.
理由:如图1,∵∠AOD=α+45°,OE 是∠AOD 的平分线,
由(i)得,∠BOD=α-45°,
(3)①当0°<α<90°时,如图2,
∠DOF=∠DOC-∠COF=∠DOC- ∠BOC
②当 时,如图3,
综上,∠DOF的度数为- α.
一、选择题(每小题3分,共30分)
1.端午节是中国传统节日,下列与端午节有关的文创图案中,是轴对称图形的是 ( )
2.下列图形中,点A 与点B关于直线l对称的是 ( )
3.正方形的对称轴的条数为 ( )
A.1 B.2 C.3 D.4
4.在图形的平移和旋转变换中,下列说法正确的是 ( )
A.对应点所连线段都平行
B.对应线段都平行
C.对应点所连线段都相等
D.对应线段都相等
5.(2024 四川南充期末)如图,直线 MN 是四边形AMBN的对称轴,点 P 是直线 MN上的点,下列判断错误的是 ( )
A. AM=BM B. AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
6.如图,将△ABC 绕点 C顺时针旋转90°得到△EDC,若∠ACB=20°,则∠ACD的度数是 ( )
A.55° B.60° C.65° D.70°
7.如图,△ABC绕点O顺时针旋转角度α后得到△DEF,若∠COE=15°,∠BOF=85°,则旋转角α的值为( )
A.40° B.45° C.50° D.55°
8.小华在镜中看到身后墙上的时钟,你认为实际时间最接近8点的是 ( )
9. P是∠AOB内一点,分别作点 P 关于直线OA、OB的对称点 P 、P ,连接OP 、OP ,则下列结论一定正确的是 ( )
且
平台中小学教育资源及组卷应用
10.如图所示的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有 ( )
A.1个
二、填空题(每小题3分,共24分)
11.下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 (填序号).(M7205002)
12.(2024湖南邵阳大祥期末)如图,将△AOB 绕点O按逆时针方向旋转一定的角度后得到△COD,若∠AOB=15°,∠BOC=35°,则图中的旋转角的度数是 .
13.新考法(2024甘肃白银期末)如图,以虚线为对称轴,那么“甲”字的对称图形可看成是 字.
甲
14.(2024 江西吉安期末)如图,在△ABC 中,AB =8cm,AC=4cm,BC=5cm,点D,E分别在AC,AB上,且△BCD与△BED关于BD所在直线对称,则△ADE的周长为 cm.
15.(2022北京朝阳期末)如图,在6×6的正方形网格中,选取13个格点,以其中的三个格点A,B,C为顶点画三角形ABC,请你在图中以选取的格点为顶点再画出一个三角形ABP,使三角形ABP 与三角形ABC 成轴对称.这样的点 P有 个
16.(2023湖南张家界永定期末)如图,将三角形ABC绕着点A 逆时针旋转得到三角形ADE,使得点B的对应点D 落在边AC的延长线上,若AB=8,AE=5,则线段 CD 的长为
17.(2024 湖南衡阳四校联考期末)如图,将一个含30°角的直角三角尺 ABC 绕点 A 顺时针旋转到△AB'C',使点B,A,C'在同一条直线上,则旋转角的度数是 .
18.(2023 江苏盐城盐都期中)如图,将长方形纸片ABCD沿 EF折叠后,点 C,B分别落在点 C',B'的位置,G为C'B'和AB 的交点,再沿AB 边将∠B'折叠到∠H处,最后将∠D 折叠到∠D'处,点D'恰好在直线 C'F上(折痕是 FM),已知 ,则∠HEF 的度数为
三、解答题(共46分)
19.(2023湖南郴州宜章期末)(8分)如图,在10×10的正方形网格中,每个小正方形的边长均为1个单位
(1)将三角形ABC向下平移6个单位,得到三角形A'B'C',请你画出三角形A'B'C'.
(2)将三角形A'B'C'绕点 C'顺时针旋转90°,得到三角形 A"B"C',请你画出三角形A"B"C'.
20.(8分)如图,△ABC和△ADE关于直线 MN对称,BC 与 DE 的交点 F 在直线 MN 上
(1)图中点 D 的对应点是 ,AE 的对应边是 .
(2)若∠DAE=108°,∠EAF=39°,求∠DAC的度数.
21.(9分)如图,三角形ABC 和三角形A'B'C'关于直线 m对称
(1)结合图形指出对称点.
(2)连接AA',直线m与线段AA'有什么关系
(3)延长线段AC与A'C',它们的交点与直线m有怎样的关系 其他对应线段(或其延长线)的交点呢 你发现了什么规律
22.(9分)如图,点 P 是∠AOB外的一点,点E 与点 P 关于直线OA 对称,点F 与点 P 关于直线OB 对称,直线 FE 分别交 OA、OB 于点 C、D,连接PC,PD,PE,PF
(1)若∠OCP=∠F=20°,求∠CPD的度数(提示:三角形三个内角的和等于180°).
(2)若CP=DP,CF=13,DE=3,求CP的长.
23.新考法 分类讨论思想(12 分)已知,∠AOB 是直角,过点O 作射线 OC(OC在直线 OA的上方),设 ,且α≠90°),将射线 OC 绕点 O 逆时针旋转 45°得到射线OD.
(1)如图1,若0°<α<45°,则∠AOC+∠BOD= °.
(2)如图2,若
(i)请你直接写出∠AOC 与∠BOD 之间的数量关系.
(ii)作∠AOD的平分线OE,试判断∠COE与∠BOD 之间的数量关系,并说明理由.
(3)若OF 平分∠BOC,请你直接写出∠DOF的度数(用含α的代数式表示).
1B A,C,D选项中的图形都不能找到一条直线,使图形沿这条直线折叠,直线两旁的部分互相重合,所以不是轴对称图形;B选项中的图形能找到一条直线,使图形沿这条直线折叠,直线两旁的部分互相重合,所以是轴对称图形,故选 B.
2A 若点A与点 B 关于直线l对称,则要满足AB垂直于直线l且点A,点B到直线l的距离相等,故选 A.
3D 正方形有4条对称轴,故选 D.
4D 在图形的平移变换中,对应点所连线段互相平行(或在同一直线上),对应线段都相等,但不一定平行,在图形的旋转变换中,对应点所连线段不一定相等,但对应线段都相等,故选 D.
5B ∵直线 MN是四边形 AMBN 的对称轴,∴ AM=BM,AN=BN,∠ANM=∠BNM,∵点P是直线MN上的点,∴∠MAP=∠MBP,∴选项 A,C,D正确,选项B错误,故选 B.
6D ∵△ABC绕点 C顺时针旋转90°得到△EDC,∴∠BCD=90°,∵∠ACB=20°,∴ ∠ACD=∠BCD-∠ACB=90°-20°=70°.故选D.
7C ∵ △ABC 绕点 O 顺时针旋转角度 α后得到△DEF,∴∠BOE=∠COF=α,
∵∠BOF=∠BOE+∠COF-∠COE,
∴α+α-15°=85°,解得α=50°.故选 C.
8D由对称的性质得8点的时钟在镜子中看到应该是4点,所以答案应该是 C选项或D 选项图形中的一个,这两个图形中更接近4点的是D选项.故选 D.
9B ∵点 P 关于直线OA、OB 的对称点分别为点 P 、P ,∴ OP =OP =OP,∠AOP =∠AOP ,∠BOP = +∠BOP =2(∠AOP+∠BOP)=2∠AOB,∵ ∠AOB 的度数不确定,∴OP 与OP 不一定垂直.故选 B.
10D第1个图案可以旋转90°得到,也可以经过轴对称,沿对称轴对折得到;
第2个图案可以旋转180°得到,也可以经过轴对称,沿对称轴对折得到;
第3个图案可以旋转180°得到,也可以经过轴对称,沿对称轴对折得到;
第4个图案可以旋转90°得到,也可以经过轴对称,沿对称轴对折得到.
综上所述,题目中四个图案均满足条件.故选 D.
11答案 ①②③④
解析 根据轴对称图形的概念,可知①②③④均为轴对称图形.故答案为①②③④.
12答案 50°
解析 ∵将△AOB 绕点 O 按逆时针方向旋转一定的角度后得到△COD,
∴∠AOC 为旋转角,∵ ∠AOB=15°,∠BOC=35°, ,即旋转角的度数是50°.
13答案 由
解析 根据轴对称的性质可得出答案.
14答案 7
解析 ∵ △BCD 与△BED关于BD 所在直线对称,AB=8cm,AC=4cm,BC=5cm,
∴BC=BE=5cm,CD=DE,∴AE=AB-BE=8-5=3(cm),
∴△ADE 的周长=AD+DE+AE=AC+AE=4+3=7(cm).故答案为7.
15答案 2
解析 如图,满足条件的点 P有2个.
16答案 3
解析 ∵ 将三角形ABC 绕着点 A 逆时针旋转得到三角形ADE,∴AB=AD,AC=AE,∵AB=8,AE=5,∴AD=8,AC=5,∴CD=AD-AC=8-5=3.
17答案 150°
解析 由题意知旋转角是∠CAC',∵∠CAC'=180°- .旋转角的度数是150°.
18答案 42°
解析 由折叠性质可知∠DMF=∠D'MF,∵ ∠AMD'=32°,∴∠DMF=∠D'MF=74°,∴∠DFM=∠D'FM=16°,∴∠CFE=∠C'FE=74°,∵AB∥CD,∴∠FEB=106°,∠FEG = 74°,∴ ∠FEB' = 106°, ∴∠B'EG =∠FEB'-∠FEG=106°-74°=32°,∴∠HEG=∠B'EG=32°,∴ ∠HEF=∠FEG-∠HEG=74°-32°=42°.
19解析 (1)如图所示,三角形A'B'C'即为所求.
(2)如图所示,三角形A"B"C'即为所求.
20解析 (1)∵ △ABC 和△ADE 关于直线 MN 对称,∴题图中点 D 的对应点是 B,AE 的对应边是AC.故答案为B;AC.
(2)∵∠EAF=39°,
∴根据对称性得∠CAF=∠EAF=39°,
∴∠CAE=78°,∵ ∠DAE=108°,∴ ∠DAC=∠DAE-
21解析 (1)对称点:A和A',B和B',C和C'.
(2)线段AA'被直线m垂直平分.
(3)线段AC与A'C'的延长线的交点在直线m上,其他对应线段(或其延长线)的交点也在直线m上.
规律:若两线段关于某直线对称,且不平行,则它们的交点或它们的延长线的交点在对称轴上.
22解析 (1)∵点E与点 P 关于直线OA 对称,点F与点 P 关于直线OB 对称,∠OCP=∠F=20°,
∴∠OCE=∠OCP=20°,∠DPF=∠F=20°,
∴∠PCF=40°,∠CPF=180°-∠F-∠PCF=120°,
∴∠CPD=∠CPF-∠DPF=100°,即∠CPD 的度数为100°.
(2)∵点E与点P 关于直线OA对称,点 F与点P关于直线OB对称,CP=DP,
∴CE=CP=DP,DP=DF,∴CE=DF,
∴CF=CE+DE+DF=2CE+3=13,∴CE=5,
∴CP=5,即CP的长为5.
23解析 本题主要考查旋转的性质,角度的和、差关系及分类讨论思想.
(1)∵∠AOB=90°,∴∠BOD+∠DOC+∠AOC=90°,∵∠DOC=45°,∴∠AOC+∠BOD=90°-45°=45°.故答案为45.
(2)(i)∠AOC-∠BOD=45°.
理由:如图1,∵∠AOD=α+45°,OE 是∠AOD 的平分线,
由(i)得,∠BOD=α-45°,
(3)①当0°<α<90°时,如图2,
∠DOF=∠DOC-∠COF=∠DOC- ∠BOC
②当 时,如图3,
综上,∠DOF的度数为- α.
同课章节目录
