4.5 垂线 同步练习(含答案)2024-2025学年湘教版七年级数学下册
文档属性
| 名称 | 4.5 垂线 同步练习(含答案)2024-2025学年湘教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 294.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:44:09 | ||
图片预览




文档简介
4.5 垂 线
平台中小学教育资源及组卷应用
第1 课时 垂线及垂线的性质
基础过关全练
知识点 1 垂线与斜线
1.(2024贵州贵阳月考)如图,点O 在直线BD上,已知∠1=25°,OC⊥OA,则∠BOC 的度数为( )
A.55° B.65° C.75° D.155°
2.(2024四川雅安中考)如图,直线AB,CD交于点O,OE⊥AB 于点 O,若∠1=35°,则∠2 的度数是 ( )
A.55° B.45° C.35° D.30°
3.如图,直线AB,CD 相交于点O,OE平分∠BOD,OF⊥OE.若∠AOC=46°,则∠COF 的度数为 ( )
A.67° B.92° C.113° D.134°
4.已知直线AB,CD 交于点 O,EO⊥CD,垂足为O,且 OB 平分∠EOD,则∠AOC 的度数为 .
5.如图,直线AB,CD 相交于点O,EO⊥CD,垂足为O,OF平分∠BOD.
(1)若∠AOC=40°,求∠EOF 的度数.
(2)试猜想∠EOF 与∠AOC 之间的数量关系,并说明理由.
6.如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.
(1)试说明:BD∥EF.
(2)试说明:∠AMD=∠AGH.
知识点2 垂线的性质
7.在同一平面内的三条直线a,b,c,a⊥b,b⊥c,则a与c 的位置关系是 ( )
A. a⊥c B.a∥c
C.相交但不垂直 D.不能确定
8.如图,AB⊥BD,CD⊥BD,垂足分别为B,D,∠A+∠AEF=180°,试说明CD∥EF.
能力提升全练
9.(2024辽宁沈阳于洪期末,6,☆)阅读下列材料,①~④步中推导依据错误的是( )
已知:如图,直线b∥c,b⊥a.
求证:c⊥a.
证明:①∵b⊥a(已知),∴∠1=90°(垂直的定义),
②又∵b∥c(已知),∴∠1=∠2(同位角相等,两直线平行),
③∴∠2=90°(等量代换),
④∴c⊥a(垂直的定义).
A.① B.② C.③ D.④
10.(2024湖南常德桃源期末,15, )直线AB 上有点O,过O作射线OC、OD,使OC⊥OD,如果∠AOC = 30°, 那么 ∠BOD = .
11如图,已知直线AB、CD、EF交于点O,( 且OE平分∠AOM
(1)若 求 的度数.
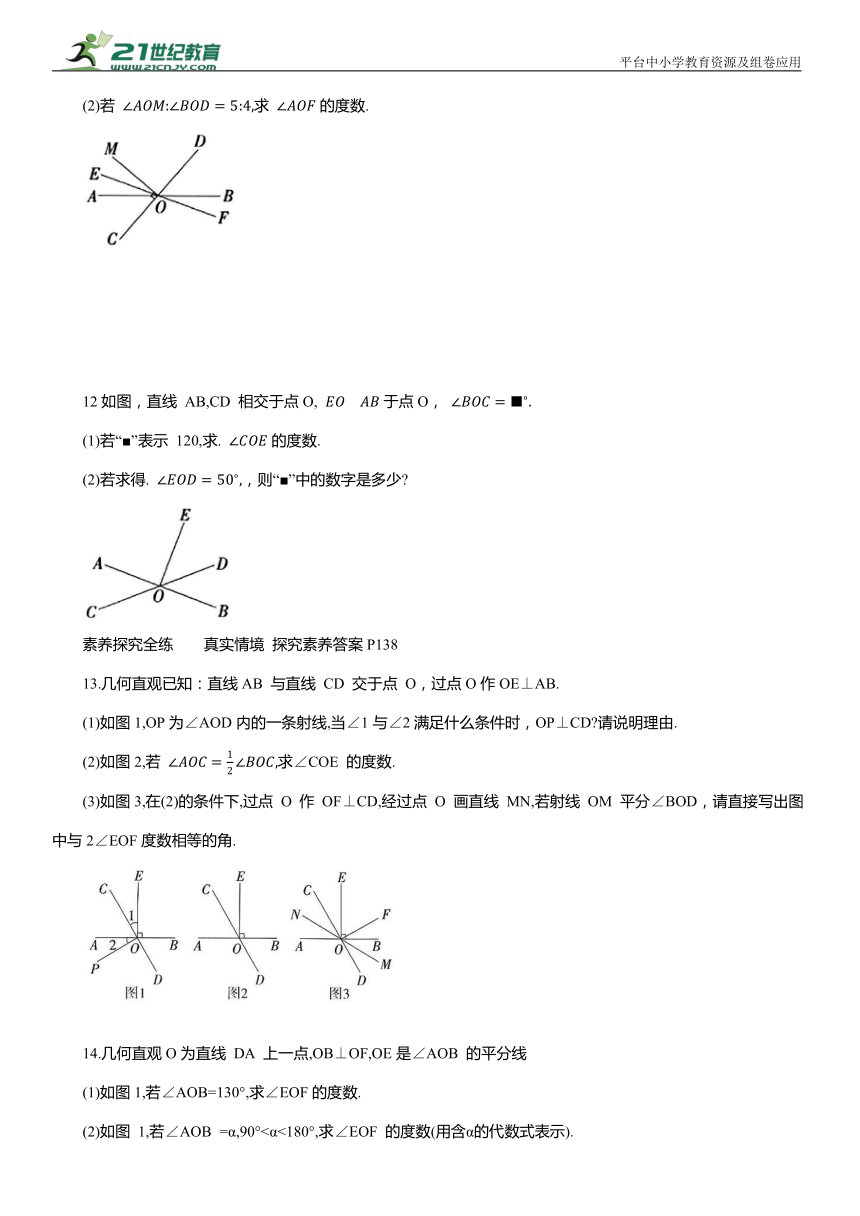
(2)若 求 的度数.
12如图,直线 AB,CD 相交于点O, 于点O,
(1)若“■”表示 120,求. 的度数.
(2)若求得. ,则“■”中的数字是多少
素养探究全练 真实情境 探究素养答案P138
13.几何直观已知:直线AB 与直线 CD 交于点 O,过点O作OE⊥AB.
(1)如图1,OP为∠AOD内的一条射线,当∠1与∠2满足什么条件时,OP⊥CD 请说明理由.
(2)如图2,若 求∠COE 的度数.
(3)如图3,在(2)的条件下,过点 O 作 OF⊥CD,经过点 O 画直线 MN,若射线 OM 平分∠BOD,请直接写出图中与2∠EOF度数相等的角.
14.几何直观O为直线 DA 上一点,OB⊥OF,OE是∠AOB 的平分线
(1)如图1,若∠AOB=130°,求∠EOF的度数.
(2)如图 1,若∠AOB =α,90°<α<180°,求∠EOF 的度数(用含α的代数式表示).
(3)若∠AOB=α,0°<α<90°,请在图2中画出射线OF,使得(2)中∠EOF 的结果仍然成立.
第2课时 点到直线的距离
基础过关全练
知识点3 垂线的画法及基本事实
1.过点 P 作直线l的垂线CD,下面三角尺的摆放正确的是 ( )
2.小明与小刚在讨论数学问题时,有如下对话:
小明:在同一平面内,过一点A有且只有一条直线与已知直线m平行.
小刚:在同一平面内,过一点A有且只有一条直线与已知直线m垂直.
对于两个人的说法,正确的是 ( )
A.小明对 B.小刚对
C.两人均对 D.两人均不对
知识点 4 垂线段及点到直线的距离
3.(2024湖南郴州宜章期末)如图,直线l表示一条河,点P 表示蓄水池,现要从河道内向蓄水池 P引水,设计了四条水渠开挖路线 PA,PB,PC,PD,其中PB⊥l,要使路线最短,可以选择的路线是 ( )
A. PA B. PB C. PC D. PD
4.教材变式如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为D,AC=10,AB=6,BC=8,则点A到BC的距离为 ,点 C到AB 的距离为 ,点B到AC的距离为 .
能力提升全练
5.(2024 湖南郴州宜章期末,14,☆)如图,已知ON⊥l,OM⊥l,所以 OM 所在直线与 ON所在直线重合,其理由是
6.(2024安徽黄山期中,23, )如图,为了解决A、B、C、D四个小区的缺水问题,市政府准备投资修建一个水厂.
(1)不考虑其他因素,请你画图确定水厂 H的位置,使之与四个小区的距离之和最小.
(2)若计划把河流EF中的水引入水厂H中,且水厂H到EF的距离最短,请你画图确定铺设引水管道的位置,并说明理由.
素养探究全练
7.几何直观如图,已知三角形ABC,按要求作图.
(1)过点A作BC边上的高AD.
(2)过点 C作AB、AC的垂线分别交直线 AB 于点 E、F.
(3)AB=15,BC=7,AD=12,求点 C 到直线AB的距离.
第1 课时 垂线及垂线的性质
基础过关全练
1B ∵OC⊥OA,∴∠AOC=90°,∵∠1=25°,
∴∠BOC=∠AOC-∠1=90°-25°=65°,故选 B.
2A∵OE⊥AB,∠1=35°,∴∠AOC=90°-∠1=55°,∴∠2=∠AOC=55°,故选 A.
3C∵∠AOC=46°,∴∠AOC=∠BOD=46°,
∵OE平分∠
∵ OE⊥OF,∴ ∠EOF=90°,∴ ∠DOF=90°-23°=67°,∴∠COF=180°-67°=113°,故选 C.
4答案 45°
解析 ∵EO⊥CD,∴∠EOD=90°,
∵OB平分∠
∴∠AOC=∠BOD=45°.
5解析 (1)∵∠AOC=40°,∴∠BOD=∠AOC=40°,∵OF平分∠BOD,∴∠BOF=∠DOF=20°,
∵ EO⊥CD,∴ ∠DOE= 90°,∴ ∠EOF =∠DOE-
理由:已知∠BOD = ∠AOC,∵ EO⊥CD,OF 平分
6证明 (1)∵BD⊥AC,EF⊥AC,
∴∠CFE=∠CDB=90°,∴BD∥EF.
(2)∵BD∥EF,∴∠2=∠CBD,∵∠1=∠2,
∴∠CBD=∠1,∴GF∥BC,
∵DM∥BC,∴DM∥GF,∴∠AMD=∠AGH.
7B 在同一平面内,垂直于同一条直线的两条直线平行.
8证明 因为∠A+∠AEF=180°,所以AB∥EF,又因为AB⊥BD,所以 EF⊥BD,又因为 CD⊥BD,所以CD∥EF.
能力提升全练
9B ①∵b⊥a(已知),∴∠1=90°(垂直的定义),②又∵b∥c(已知),∴∠1=∠2(两直线平行,同位角相等),③∴∠2=90°(等量代换),④∴c⊥a(垂直的定义).推导依据错误的是②,故选 B.
10答案 60°或120°
解析 如图1,∵OC⊥OD,∴∠COD=90°,∵∠AOC=30°,∴∠BOD=180°-30°-90°=60°.
如图2,∵OC⊥OD,∴∠COD=90°,
∵∠AOC=30°,∴∠AOD=90°-30°=60°,
∴∠BOD=180°-60°=120°.
故答案为60°或120°.
11解析 (1)∵∠BOF=20°,∠BOF=∠AOE,
∴∠AOE=20°.
∵OE平分∠AOM,∴∠AOM=2∠AOE=40°.
∵OM⊥CD,∴∠COM=90°,
∴ ∠AOC=∠COM-∠AOM=50°.
(2)∵OM⊥CD,∴∠DOM=90°,∴∠AOM+∠BOD=90°,
∵∠AOM:∠BOD=5:4,
∴∠AOM=50°,∠BOD=40°,
∵OE平分∠
∴∠AOF=180°-∠AOE=155°.
12解析 (1)∵EO⊥AB,∴∠AOE=90°.
∵∠BOC=120°,∴∠AOC=180°-∠BOC=60°,
∴ ∠COE=∠AOC+∠AOE=60°+90°=150°.
(2)∵EO⊥AB,∴∠AOE=90°,∵∠EOD=50°,
∴ ∠AOD=∠AOE+∠EOD=90°+50°=140°,
∴∠BOC=∠AOD=140°,
∴“■”中的数字是140.
素养探究全练
13解析 (1)当∠1=∠2时,OP⊥CD,理由如下:∵OE⊥AB,∴∠AOC+∠1=90°,∵∠1=∠2,∴ ∠AOC+∠2=∠COP=90°,∴OP⊥CD.
(2)∵ ∠AOC+∠BOC=180°,且
∴∠AOC=60°,∵OE⊥AB,∴∠AOE=90°,
(3)由(2)知∠AOC=60°,∵射线OM平分∠BOD,∴∠BOM=∠DOM=∠AON=∠CON=30°,∵ OE⊥AB,OF⊥CD,∴ ∠AOE=∠COF=90°,∴ ∠AOC= ∠BOC = ∠FON = ∠EOM = 180°-60°= 120°=2∠EOF,∴ 与 2∠EOF 度数相等的角是∠AOD、∠BOC、∠FON、∠EOM.
14解析 (1)∵∠AOB=130°,OE 是∠AOB的平分线,
∵OB⊥OF,∴∠BOF=90°,
∴∠AOF=∠AOB-∠BOF=130°-90°=40°,
∴ ∠EOF=∠AOE-∠AOF=65°-40°=25°.
(2)∵∠AOB=α,90°<α<180°,OE 是∠AOB 的平分线,∴∠AOE= α,∵ ∠BOF=90°,∴ ∠AOF=α-
(3)如图,∵∠AOB=α,∴∠BOE=∠AOE= α,∵∠BOF=90°,∴∠EOF=∠BOF-∠BOE=90°- α.
第2 课时 点到直线的距离
基础过关全练
1A 点P在三角尺的一条直角边上,三角尺的另一直角边落在直线l上,只有 A选项符合.
2B ∵在同一平面内,过直线外一点有且只有一条直线与已知直线平行;在同一平面内,过一点有且只有一条直线与已知直线垂直,∴小明错,小刚对,故选 B.
3B∵在PA,PB,PC,PD四条路线中只有PB⊥l,∴路线PB 最短.故选 B.
4答案 6;8;4.8
解析 ∵∠ABC=90°,∴AB⊥BC,∴点A到BC的距离为AB 的长,点C到AB 的距离为CB 的长,∴点 A到BC的距离为6,点 C到AB的距离为8,
∵BD⊥AC,
∴点B到AC的距离为BD的长,. 点B到AC.的距离为4.8.
能力提升全练
5答案 在同一平面内,过一点有且只有一条直线与已知直线垂直
解析 已知ON⊥l,OM⊥l,OM与ON都经过点O,所以OM 所在直线与ON所在直线重合,理由是在同一平面内,过一点有且只有一条直线与已知直线垂直.
6解析 (1)如图,连接AC和BD,线段AC和BD的交点H就是水厂的位置.
(2)饮水管道(HM)位置如图,理由是垂线段最短.
素养探究全练
7解析 (1)如图所示.
(2)如上图所示.
即点 C 到直线AB 的距离为2
平台中小学教育资源及组卷应用
第1 课时 垂线及垂线的性质
基础过关全练
知识点 1 垂线与斜线
1.(2024贵州贵阳月考)如图,点O 在直线BD上,已知∠1=25°,OC⊥OA,则∠BOC 的度数为( )
A.55° B.65° C.75° D.155°
2.(2024四川雅安中考)如图,直线AB,CD交于点O,OE⊥AB 于点 O,若∠1=35°,则∠2 的度数是 ( )
A.55° B.45° C.35° D.30°
3.如图,直线AB,CD 相交于点O,OE平分∠BOD,OF⊥OE.若∠AOC=46°,则∠COF 的度数为 ( )
A.67° B.92° C.113° D.134°
4.已知直线AB,CD 交于点 O,EO⊥CD,垂足为O,且 OB 平分∠EOD,则∠AOC 的度数为 .
5.如图,直线AB,CD 相交于点O,EO⊥CD,垂足为O,OF平分∠BOD.
(1)若∠AOC=40°,求∠EOF 的度数.
(2)试猜想∠EOF 与∠AOC 之间的数量关系,并说明理由.
6.如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.
(1)试说明:BD∥EF.
(2)试说明:∠AMD=∠AGH.
知识点2 垂线的性质
7.在同一平面内的三条直线a,b,c,a⊥b,b⊥c,则a与c 的位置关系是 ( )
A. a⊥c B.a∥c
C.相交但不垂直 D.不能确定
8.如图,AB⊥BD,CD⊥BD,垂足分别为B,D,∠A+∠AEF=180°,试说明CD∥EF.
能力提升全练
9.(2024辽宁沈阳于洪期末,6,☆)阅读下列材料,①~④步中推导依据错误的是( )
已知:如图,直线b∥c,b⊥a.
求证:c⊥a.
证明:①∵b⊥a(已知),∴∠1=90°(垂直的定义),
②又∵b∥c(已知),∴∠1=∠2(同位角相等,两直线平行),
③∴∠2=90°(等量代换),
④∴c⊥a(垂直的定义).
A.① B.② C.③ D.④
10.(2024湖南常德桃源期末,15, )直线AB 上有点O,过O作射线OC、OD,使OC⊥OD,如果∠AOC = 30°, 那么 ∠BOD = .
11如图,已知直线AB、CD、EF交于点O,( 且OE平分∠AOM
(1)若 求 的度数.
(2)若 求 的度数.
12如图,直线 AB,CD 相交于点O, 于点O,
(1)若“■”表示 120,求. 的度数.
(2)若求得. ,则“■”中的数字是多少
素养探究全练 真实情境 探究素养答案P138
13.几何直观已知:直线AB 与直线 CD 交于点 O,过点O作OE⊥AB.
(1)如图1,OP为∠AOD内的一条射线,当∠1与∠2满足什么条件时,OP⊥CD 请说明理由.
(2)如图2,若 求∠COE 的度数.
(3)如图3,在(2)的条件下,过点 O 作 OF⊥CD,经过点 O 画直线 MN,若射线 OM 平分∠BOD,请直接写出图中与2∠EOF度数相等的角.
14.几何直观O为直线 DA 上一点,OB⊥OF,OE是∠AOB 的平分线
(1)如图1,若∠AOB=130°,求∠EOF的度数.
(2)如图 1,若∠AOB =α,90°<α<180°,求∠EOF 的度数(用含α的代数式表示).
(3)若∠AOB=α,0°<α<90°,请在图2中画出射线OF,使得(2)中∠EOF 的结果仍然成立.
第2课时 点到直线的距离
基础过关全练
知识点3 垂线的画法及基本事实
1.过点 P 作直线l的垂线CD,下面三角尺的摆放正确的是 ( )
2.小明与小刚在讨论数学问题时,有如下对话:
小明:在同一平面内,过一点A有且只有一条直线与已知直线m平行.
小刚:在同一平面内,过一点A有且只有一条直线与已知直线m垂直.
对于两个人的说法,正确的是 ( )
A.小明对 B.小刚对
C.两人均对 D.两人均不对
知识点 4 垂线段及点到直线的距离
3.(2024湖南郴州宜章期末)如图,直线l表示一条河,点P 表示蓄水池,现要从河道内向蓄水池 P引水,设计了四条水渠开挖路线 PA,PB,PC,PD,其中PB⊥l,要使路线最短,可以选择的路线是 ( )
A. PA B. PB C. PC D. PD
4.教材变式如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为D,AC=10,AB=6,BC=8,则点A到BC的距离为 ,点 C到AB 的距离为 ,点B到AC的距离为 .
能力提升全练
5.(2024 湖南郴州宜章期末,14,☆)如图,已知ON⊥l,OM⊥l,所以 OM 所在直线与 ON所在直线重合,其理由是
6.(2024安徽黄山期中,23, )如图,为了解决A、B、C、D四个小区的缺水问题,市政府准备投资修建一个水厂.
(1)不考虑其他因素,请你画图确定水厂 H的位置,使之与四个小区的距离之和最小.
(2)若计划把河流EF中的水引入水厂H中,且水厂H到EF的距离最短,请你画图确定铺设引水管道的位置,并说明理由.
素养探究全练
7.几何直观如图,已知三角形ABC,按要求作图.
(1)过点A作BC边上的高AD.
(2)过点 C作AB、AC的垂线分别交直线 AB 于点 E、F.
(3)AB=15,BC=7,AD=12,求点 C 到直线AB的距离.
第1 课时 垂线及垂线的性质
基础过关全练
1B ∵OC⊥OA,∴∠AOC=90°,∵∠1=25°,
∴∠BOC=∠AOC-∠1=90°-25°=65°,故选 B.
2A∵OE⊥AB,∠1=35°,∴∠AOC=90°-∠1=55°,∴∠2=∠AOC=55°,故选 A.
3C∵∠AOC=46°,∴∠AOC=∠BOD=46°,
∵OE平分∠
∵ OE⊥OF,∴ ∠EOF=90°,∴ ∠DOF=90°-23°=67°,∴∠COF=180°-67°=113°,故选 C.
4答案 45°
解析 ∵EO⊥CD,∴∠EOD=90°,
∵OB平分∠
∴∠AOC=∠BOD=45°.
5解析 (1)∵∠AOC=40°,∴∠BOD=∠AOC=40°,∵OF平分∠BOD,∴∠BOF=∠DOF=20°,
∵ EO⊥CD,∴ ∠DOE= 90°,∴ ∠EOF =∠DOE-
理由:已知∠BOD = ∠AOC,∵ EO⊥CD,OF 平分
6证明 (1)∵BD⊥AC,EF⊥AC,
∴∠CFE=∠CDB=90°,∴BD∥EF.
(2)∵BD∥EF,∴∠2=∠CBD,∵∠1=∠2,
∴∠CBD=∠1,∴GF∥BC,
∵DM∥BC,∴DM∥GF,∴∠AMD=∠AGH.
7B 在同一平面内,垂直于同一条直线的两条直线平行.
8证明 因为∠A+∠AEF=180°,所以AB∥EF,又因为AB⊥BD,所以 EF⊥BD,又因为 CD⊥BD,所以CD∥EF.
能力提升全练
9B ①∵b⊥a(已知),∴∠1=90°(垂直的定义),②又∵b∥c(已知),∴∠1=∠2(两直线平行,同位角相等),③∴∠2=90°(等量代换),④∴c⊥a(垂直的定义).推导依据错误的是②,故选 B.
10答案 60°或120°
解析 如图1,∵OC⊥OD,∴∠COD=90°,∵∠AOC=30°,∴∠BOD=180°-30°-90°=60°.
如图2,∵OC⊥OD,∴∠COD=90°,
∵∠AOC=30°,∴∠AOD=90°-30°=60°,
∴∠BOD=180°-60°=120°.
故答案为60°或120°.
11解析 (1)∵∠BOF=20°,∠BOF=∠AOE,
∴∠AOE=20°.
∵OE平分∠AOM,∴∠AOM=2∠AOE=40°.
∵OM⊥CD,∴∠COM=90°,
∴ ∠AOC=∠COM-∠AOM=50°.
(2)∵OM⊥CD,∴∠DOM=90°,∴∠AOM+∠BOD=90°,
∵∠AOM:∠BOD=5:4,
∴∠AOM=50°,∠BOD=40°,
∵OE平分∠
∴∠AOF=180°-∠AOE=155°.
12解析 (1)∵EO⊥AB,∴∠AOE=90°.
∵∠BOC=120°,∴∠AOC=180°-∠BOC=60°,
∴ ∠COE=∠AOC+∠AOE=60°+90°=150°.
(2)∵EO⊥AB,∴∠AOE=90°,∵∠EOD=50°,
∴ ∠AOD=∠AOE+∠EOD=90°+50°=140°,
∴∠BOC=∠AOD=140°,
∴“■”中的数字是140.
素养探究全练
13解析 (1)当∠1=∠2时,OP⊥CD,理由如下:∵OE⊥AB,∴∠AOC+∠1=90°,∵∠1=∠2,∴ ∠AOC+∠2=∠COP=90°,∴OP⊥CD.
(2)∵ ∠AOC+∠BOC=180°,且
∴∠AOC=60°,∵OE⊥AB,∴∠AOE=90°,
(3)由(2)知∠AOC=60°,∵射线OM平分∠BOD,∴∠BOM=∠DOM=∠AON=∠CON=30°,∵ OE⊥AB,OF⊥CD,∴ ∠AOE=∠COF=90°,∴ ∠AOC= ∠BOC = ∠FON = ∠EOM = 180°-60°= 120°=2∠EOF,∴ 与 2∠EOF 度数相等的角是∠AOD、∠BOC、∠FON、∠EOM.
14解析 (1)∵∠AOB=130°,OE 是∠AOB的平分线,
∵OB⊥OF,∴∠BOF=90°,
∴∠AOF=∠AOB-∠BOF=130°-90°=40°,
∴ ∠EOF=∠AOE-∠AOF=65°-40°=25°.
(2)∵∠AOB=α,90°<α<180°,OE 是∠AOB 的平分线,∴∠AOE= α,∵ ∠BOF=90°,∴ ∠AOF=α-
(3)如图,∵∠AOB=α,∴∠BOE=∠AOE= α,∵∠BOF=90°,∴∠EOF=∠BOF-∠BOE=90°- α.
第2 课时 点到直线的距离
基础过关全练
1A 点P在三角尺的一条直角边上,三角尺的另一直角边落在直线l上,只有 A选项符合.
2B ∵在同一平面内,过直线外一点有且只有一条直线与已知直线平行;在同一平面内,过一点有且只有一条直线与已知直线垂直,∴小明错,小刚对,故选 B.
3B∵在PA,PB,PC,PD四条路线中只有PB⊥l,∴路线PB 最短.故选 B.
4答案 6;8;4.8
解析 ∵∠ABC=90°,∴AB⊥BC,∴点A到BC的距离为AB 的长,点C到AB 的距离为CB 的长,∴点 A到BC的距离为6,点 C到AB的距离为8,
∵BD⊥AC,
∴点B到AC的距离为BD的长,. 点B到AC.的距离为4.8.
能力提升全练
5答案 在同一平面内,过一点有且只有一条直线与已知直线垂直
解析 已知ON⊥l,OM⊥l,OM与ON都经过点O,所以OM 所在直线与ON所在直线重合,理由是在同一平面内,过一点有且只有一条直线与已知直线垂直.
6解析 (1)如图,连接AC和BD,线段AC和BD的交点H就是水厂的位置.
(2)饮水管道(HM)位置如图,理由是垂线段最短.
素养探究全练
7解析 (1)如图所示.
(2)如上图所示.
即点 C 到直线AB 的距离为2
同课章节目录
