期末素养测试卷(二) (含答案)2024-2025学年湘教版七年级数学下册
文档属性
| 名称 | 期末素养测试卷(二) (含答案)2024-2025学年湘教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 247.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览



文档简介
期末素养测试卷(二)
一、选择题(每小题3分,共30分)
1.(2024山西大同期末)下列调查方式适合采用全面调查的是 ( )
A.检测某品牌汽车的抗撞击能力
B.监测大同市御河的水质情况
C.调查某班学生安全教育平台学习任务的完成情况
D.调查6月份大同市二手房市场的均价
2.(2024 四川自贡中考)在0,-2,- ,π四个数中,最大的数是 ( )
A.-2 B.0 C.π
3.如图,与∠1成同位角的角共有 ( )
A.1个 B.2个 C.3个 D.4个
4.(多选题)(2022湖南湘潭中考,9,62)若a>b,则下列四个选项中一定成立的是 ( )
A. a+2>b+2 B.-3a>-3b
D. a-15.(2024湖南邵阳大祥期末)下列运算中,正确的是( )
D.5a-2a=3
6.如图所示的是某种工具模型的示意图.已知AB∥CD,∠ABE=50°,则∠CDF 的度数为 ( )
A.40° B.50° C.55° D.60°
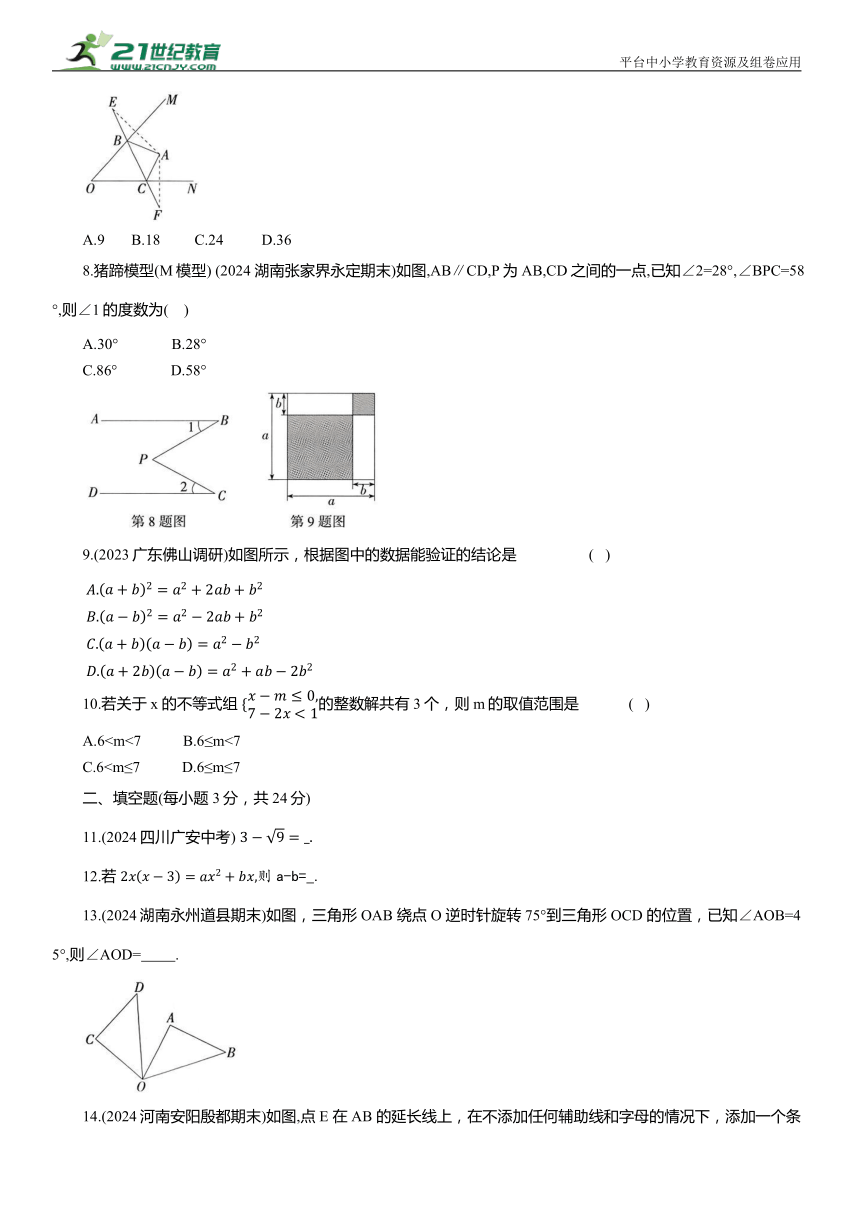
7.(2024湖南湘潭雨湖期末)如图,点A 是∠MON内一点,点E,F分别是点A 关于直线OM,ON的对称点,连接EF 交 OM,ON于点 B,C,连接AB,AC.已知EF=18,则△ABC的周长为 ( )
A.9 B.18 C.24 D.36
8.猪蹄模型(M模型) (2024 湖南张家界永定期末)如图,AB∥CD,P为AB,CD之间的一点,已知∠2=28°,∠BPC=58°,则∠1的度数为( )
A.30° B.28°
C.86° D.58°
9.(2023广东佛山调研)如图所示,根据图中的数据能验证的结论是 ( )
10.若关于x 的不等式组 的整数解共有3个,则m的取值范围是 ( )
A.6平台中小学教育资源及组卷应用
C.6二、填空题(每小题3分,共24分)
11.(2024四川广安中考)
12.若则a-b= .
13.(2024湖南永州道县期末)如图,三角形OAB 绕点O 逆时针旋转75°到三角形 OCD 的位置,已知∠AOB=45°,则∠AOD= .
14.(2024河南安阳殷都期末)如图,点 E 在AB 的延长线上,在不添加任何辅助线和字母的情况下,添加一个条件 ,使AB∥DC(填一个即可).
15.(2024湖南永州江华期末)若x+y=2, xy=1,则
16.(2024湖南常德期末)已知m+2n-3=0,!则2"·4"的值为 .
17.(2023 山 东 聊 城 中 考 )若 不 等 式 组 的解集为x≥m,则m的取值范围是 .
18.(2024湖南岳阳期末)小林乘车进入车库时仔细观察了车库门口的曲臂直杆道闸,曲臂直杆道闸的示意图如图所示,已知AB 垂直于水平地面AE,当车牌被自动识别后,曲臂直杆道闸的BC段绕点 B 缓慢向上旋转,CD 段则一直保持水平状态上升(即CD 与AE 始终平行),在该过程中,∠ABC+∠BCD始终等于 .
三、解答题(共66分)
19.(6分)先化简,再求值: (x+2)(x-2)+x(x-4),其中x=-2.
20.(2024 湖南张家界桑植期末)(6分)如图,已知△ABC的顶点都在格点上,直线l与网格线重合(每个小正方形的边长均为1个单位长度).
(1)画出△ABC关于直线l对称的△A B C .
(2)将△ABC向右平移6个单位长度,再向上平移3 个单位长度,得到△A B C ,画出△A B C .
(3)画出△ABC绕点A 逆时针旋转90°后得到的△AB C .
21.(2024 甘肃兰州中考 ) (8 分) 解不 等式组
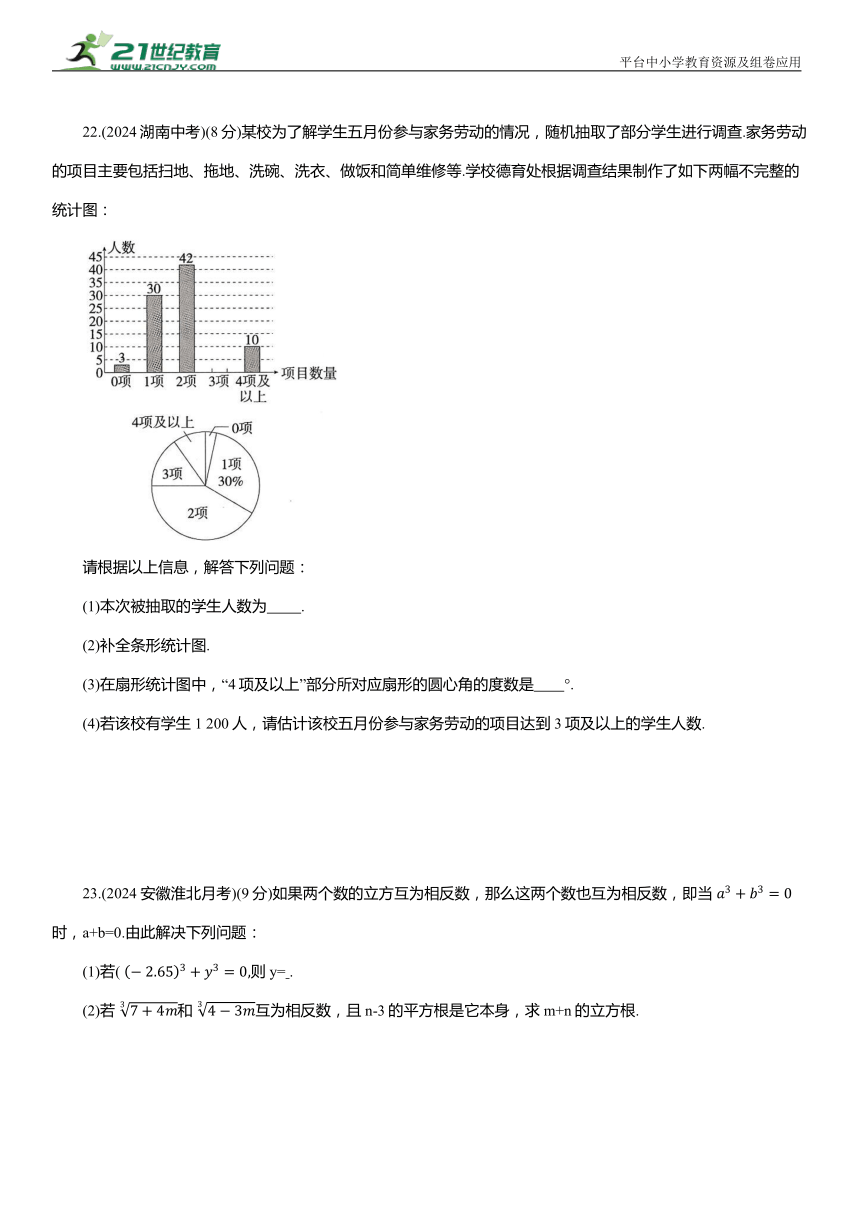
22.(2024湖南中考)(8分)某校为了解学生五月份参与家务劳动的情况,随机抽取了部分学生进行调查.家务劳动的项目主要包括扫地、拖地、洗碗、洗衣、做饭和简单维修等.学校德育处根据调查结果制作了如下两幅不完整的统计图:
请根据以上信息,解答下列问题:
(1)本次被抽取的学生人数为 .
(2)补全条形统计图.
(3)在扇形统计图中,“4项及以上”部分所对应扇形的圆心角的度数是 °.
(4)若该校有学生1 200人,请估计该校五月份参与家务劳动的项目达到3项及以上的学生人数.
23.(2024 安徽淮北月考)(9分)如果两个数的立方互为相反数,那么这两个数也互为相反数,即当 时,a+b=0.由此解决下列问题:
(1)若( 则y= .
(2)若 和 互为相反数,且n-3的平方根是它本身,求m+n的立方根.
24.(2024湖南中考)(9分)刺绣是我国的民间传统手工艺,湘绣作为中国四大刺绣之一,闻名中外.在巴黎奥运会开幕倒计时50天之际,某国际旅游公司计划购买A、B两种奥运主题的湘绣作品作为纪念品.已知购买1件A 种湘绣作品与2件B种湘绣作品共需要700元,购买2件A种湘绣作品与3件 B种湘绣作品共需要1 200元.
(1)求A种湘绣作品和B种湘绣作品的单价分别为多少元.
(2)该国际旅游公司计划购买A 种湘绣作品和B种湘绣作品共200件,总费用不超过50 000元,那么最多能购买A种湘绣作品多少件
25.(2024 重庆奉节期末)(10分)数形结合是我们解决数学问题常用到的思想方法.如图2,我们通过两种不同的方法计算阴影部分的面积,可以得到一个数学公式.
操作:如图1 所示的是一个长为2m、宽为2n的长方形,沿图中虚线剪开,均分成四个小长方形,然后按图2的方式拼成一个正方形.
计算:
请用两种不同的方法求出图2中阴影部分的面积.
(1)方法1: .
(2)方法2: .
(3)总结观察图2并结合前面的计算,我们可以得出((m+n) ,(m-n) ,mn三个代数式之间的等量关系为 .
应用:
运用你所得到的公式,解决下列问题:
(4)若 mn=5,m-n=4,求( 的值.
(5)若(a-2023)(2024-a)=-12,求[(a-2 023)-(2024-a)] 的值.
26.(2024湖南永州双牌期末)(10分)在综合与实践课上,老师让同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动.已知两直线a,b,且a∥b,直角三角尺ABC中,∠BCA=90°,∠BAC=30°.
(1)【操作发现】
如图①,当三角尺的顶点 B 在直线 b 上时,若∠1=55°,则∠2= °.
(2)【探索证明】
如图②,当三角尺的顶点 C 在直线b 上时,请写出∠1 与∠2之间的数量关系,并说明理由.
(3)【拓展应用】
如图③,把三角尺的顶点 B放在直线b上且保持不动,旋转三角尺,点A 始终在直线BD(D为直线b上一点)的上方,若存在∠1=5∠CBD(∠CBD<60°),请直接写出射线 BA 与直线a所夹锐角的度数.
1C 检测某品牌汽车的抗撞击能力,适合采用抽样调查;监测大同市御河的水质情况,适合采用抽样调查;调查某班学生安全教育平台学习任务的完成情况,适合采用全面调查;调查6月份大同市二手房市场的均价,适合采用抽样调查.故选C.
2 ,∴这四个数中最大的数为π,故选 C.
3 C题图中与∠1 成同位角的角有∠DAB,∠EBH,∠FGH,共3个,故选 C.
4 AC A.在不等式a>b的两边同时加上2,不等号的方向不变,即a+2>b+2,故A项符合题意;B.在不等式a>b的两边同时乘-3,不等号的方向改变,即-3a<-3b,故B项不合题意;C.在不等式a>b的两边同时除以4,不等号的方向不变,即 故C 项符合题意;D.在不等式a>b的两边同时减去1,不等号的方向不变,即(a-1>b-1,故 D项不合题意.故选 AC.
故选项 A 错误; 故选项 B错误; 故选项 C正确;5a-2a=3a,故选项D错误.故选 C.
6B ∵AB∥CD,∴∠ABD=∠BDC,∵∠ABE+∠ABD=180°,∠BDC+∠CDF= 180°,∴ ∠CDF =∠ABE =50°,故选 B.
7B ∵点E,A关于直线OM对称,∴OM垂直平分AE,
∴AB=BE,同理,FC=AC,
∴△ABC的周长=BC+AB+AC=BC+BE+CF=EF=18故选 B.
8A 如图,过P作PQ∥AB,
∵AB∥CD,∴PQ∥CD∥AB,
∴∠CPQ=∠2=28°,∠BPQ=∠1,
∵ ∠BPQ=∠BPC-∠CPQ=58°-28°=30°,
∴∠1=30°.故选 A.
9B 题图中,较大阴影正方形的边长为a-b,因此面积为 ,较小阴影正方形的边长为b,因此面积为b ,整体正方形的边长为a,因此面积为a ,由题图中各个部分的面积之间的关系可得, 故选 B.
由①得x≤m,由②得x>3,故原不等式组的解集为311答案 0
解析 原式=3-3=0,故答案为0.
12答案 8
解析 · ∴a=2,b=-6,∴a-b=2+6=8.故答案为8.
13答案 30°
解析 ∵ 三角形 OAB 绕点 O 逆时针旋转75°到三角形OCD的位置,∠AOB=45°,∴∠AOC=75°,∠COD=∠AOB=45°,∴ ∠AOD=∠AOC-∠COD=75°-45°=30°,故答案为30°.
14答案 ∠A+∠D=180°(答案不唯一)
解析 根据平行线的判定定理即可得到结论,答案不唯一.
15答案 2
解析
16答案 8
解析 由m+2n-3=0可得m+2n=3,
17答案 m≥-1
解析 解 得x≥-1,解2x-m≥x得x≥m.
∵不等式组 的解集为x≥m,
∴m≥-1.故答案为m≥-1.
18答案 270°
解析 如图,过点B作BG∥AE,
∵AE∥CD,∴AE∥CD∥BG,
∴∠BAE+∠ABG=180°,∠BCD+∠CBG=180°,
∴∠BAE+∠ABG+∠CBG+∠BCD=360°,
∴∠BAE+∠ABC+∠BCD=360°.
∵BA⊥AE,∴∠BAE=90°,
∴∠ABC+∠BCD=360°-∠BAE=270°.
19解析
2分
4分
5分
当x=-2时,原式 …… 6分
20解析 (1)如图,△A B C 即为所求. ………… 2分
(2)如图,△A B C 即为所求. 4分
(3)如图,△AB C 即为所求. …………………… 6分
21解析 解不等式①得x>-6,…… 3分解不等式②得x<1, 6分∴该不等式组的解集为-622解析 (1)本次被抽取的学生人数为30÷30%=100.故答案为100. 2分
(2)参与家务劳动的项目为3项的人数为100-3-30-42-10=15,……………………………………… 3分
补全条形统计图如下: 4分
(3)在扇形统计图中,“4项及以上”部分所对应扇形的圆心角的度数是
故答案为36. 6分
(人). … 7分
答:估计该校五月份参与家务劳动的项目达到3项及以上的学生人数为300. 8分
23解析 (1)根据题意可知-2.65与y互为相反数,故y=2.65.故答案为2.65. 3分
(2)根据题意,得7+4m+4-3m=0,…………… 4分
解得m=-11.……………………………………… 5分
∵n-3的平方根是它本身,
∴n-3=0, 6分
解得n=3. ………………………………………… 7分
∴m+n=-11+3=-8,
∴m+n的立方根为 … 9分
24解析 (1)设A种湘绣作品的单价为x元,B种湘绣作品的单价为y元,
根据题意得 解得
答:A种湘绣作品的单价为300元,B种湘绣作品的单价为200元. 4分
(2)设购买A种湘绣作品m件,则购买B种湘绣作品(200-m)件,
根据题意得300m+200(200-m)≤50000,解得m≤100,
故最多能购买A种湘绣作品100件. 9分
25解析 (1)题图2中阴影部分是边长为m-n的正方形,因此面积为( 故答案为(m-n) . … 1分
(2)题图2中阴影部分的面积可以看成边长为m+n的大正方形的面积减去题图1中长方形的面积,即 故填 …………… 2分
(3)由(1)(2)可以得出
故答案为 … 3分
(4)∵mn=5,m-n=4,
. …… 6分
(5)设.x=a-2023,y=2024-a,,则x+y=1, … 7分
由(a-2023)(2024-a)=-12可得 xy=-12, ………………… 8分
=1+48=49.……………………………………… 10分
26解析 (1)过点 C作CD∥a,如图1所示.
∵a∥b,∴CD∥a∥b,
∴∠2=∠ACD,∠1=∠BCD,
∴∠1+∠2=∠ACD+∠BCD=∠BCA,
∴∠2=∠BCA-∠1,
∵∠BCA=90°,∠1=55°,
故答案为35. 2分
(2)∠2-∠1=120°. 4分
理由:如图2所示,
∵∠BCA=90°,∠BAC=30°,
∴∠B=180°-∠BCA-∠BAC=60°,
由(1)可知∠B=∠1+∠3,
∴∠1+∠3=60°,
∴∠3=60°-∠1,
∵∠2+∠3=180°,
即∠2-∠1=120°.………………………………… 6分
(3)80°或30°. 10分
详解:依题意有以下两种情况:
①当BC在直线BD的上方时,如图3所示,
∵∠BCA=90°,∠BAC=30°,
∴∠ABC=180°-∠BCA-∠BAC=60°,设∠CBD=α(α<60°),则∠1=5∠CBD=5α,
∵点B 在直线b上且保持不动,
∴∠1+∠ABC+∠CBD=180°,
,解得α=20°,
∴∠1=5α=100°,
∵直线a∥b,∴∠1+∠2=180°,
②当BC在直线BD的下方时,如图4所示,同理得∠ABC=60°,
设∠CBD=β(β<60°),则∠1=5∠CBD=5β,
∴∠ABD=∠ABC-∠CBD=60°-β,
∵点B在直线b上且保持不动,
∴∠1+∠ABD=180°,
解得β=30°,∴∠1=5β=150°,
∵直线a∥b,
∴∠1+∠2=180°,
∴∠2=180°-∠1=30°.
综上所述,射线 BA与直线a所夹锐角的度数为80°或30°.
一、选择题(每小题3分,共30分)
1.(2024山西大同期末)下列调查方式适合采用全面调查的是 ( )
A.检测某品牌汽车的抗撞击能力
B.监测大同市御河的水质情况
C.调查某班学生安全教育平台学习任务的完成情况
D.调查6月份大同市二手房市场的均价
2.(2024 四川自贡中考)在0,-2,- ,π四个数中,最大的数是 ( )
A.-2 B.0 C.π
3.如图,与∠1成同位角的角共有 ( )
A.1个 B.2个 C.3个 D.4个
4.(多选题)(2022湖南湘潭中考,9,62)若a>b,则下列四个选项中一定成立的是 ( )
A. a+2>b+2 B.-3a>-3b
D. a-1
D.5a-2a=3
6.如图所示的是某种工具模型的示意图.已知AB∥CD,∠ABE=50°,则∠CDF 的度数为 ( )
A.40° B.50° C.55° D.60°
7.(2024湖南湘潭雨湖期末)如图,点A 是∠MON内一点,点E,F分别是点A 关于直线OM,ON的对称点,连接EF 交 OM,ON于点 B,C,连接AB,AC.已知EF=18,则△ABC的周长为 ( )
A.9 B.18 C.24 D.36
8.猪蹄模型(M模型) (2024 湖南张家界永定期末)如图,AB∥CD,P为AB,CD之间的一点,已知∠2=28°,∠BPC=58°,则∠1的度数为( )
A.30° B.28°
C.86° D.58°
9.(2023广东佛山调研)如图所示,根据图中的数据能验证的结论是 ( )
10.若关于x 的不等式组 的整数解共有3个,则m的取值范围是 ( )
A.6
C.6
11.(2024四川广安中考)
12.若则a-b= .
13.(2024湖南永州道县期末)如图,三角形OAB 绕点O 逆时针旋转75°到三角形 OCD 的位置,已知∠AOB=45°,则∠AOD= .
14.(2024河南安阳殷都期末)如图,点 E 在AB 的延长线上,在不添加任何辅助线和字母的情况下,添加一个条件 ,使AB∥DC(填一个即可).
15.(2024湖南永州江华期末)若x+y=2, xy=1,则
16.(2024湖南常德期末)已知m+2n-3=0,!则2"·4"的值为 .
17.(2023 山 东 聊 城 中 考 )若 不 等 式 组 的解集为x≥m,则m的取值范围是 .
18.(2024湖南岳阳期末)小林乘车进入车库时仔细观察了车库门口的曲臂直杆道闸,曲臂直杆道闸的示意图如图所示,已知AB 垂直于水平地面AE,当车牌被自动识别后,曲臂直杆道闸的BC段绕点 B 缓慢向上旋转,CD 段则一直保持水平状态上升(即CD 与AE 始终平行),在该过程中,∠ABC+∠BCD始终等于 .
三、解答题(共66分)
19.(6分)先化简,再求值: (x+2)(x-2)+x(x-4),其中x=-2.
20.(2024 湖南张家界桑植期末)(6分)如图,已知△ABC的顶点都在格点上,直线l与网格线重合(每个小正方形的边长均为1个单位长度).
(1)画出△ABC关于直线l对称的△A B C .
(2)将△ABC向右平移6个单位长度,再向上平移3 个单位长度,得到△A B C ,画出△A B C .
(3)画出△ABC绕点A 逆时针旋转90°后得到的△AB C .
21.(2024 甘肃兰州中考 ) (8 分) 解不 等式组
22.(2024湖南中考)(8分)某校为了解学生五月份参与家务劳动的情况,随机抽取了部分学生进行调查.家务劳动的项目主要包括扫地、拖地、洗碗、洗衣、做饭和简单维修等.学校德育处根据调查结果制作了如下两幅不完整的统计图:
请根据以上信息,解答下列问题:
(1)本次被抽取的学生人数为 .
(2)补全条形统计图.
(3)在扇形统计图中,“4项及以上”部分所对应扇形的圆心角的度数是 °.
(4)若该校有学生1 200人,请估计该校五月份参与家务劳动的项目达到3项及以上的学生人数.
23.(2024 安徽淮北月考)(9分)如果两个数的立方互为相反数,那么这两个数也互为相反数,即当 时,a+b=0.由此解决下列问题:
(1)若( 则y= .
(2)若 和 互为相反数,且n-3的平方根是它本身,求m+n的立方根.
24.(2024湖南中考)(9分)刺绣是我国的民间传统手工艺,湘绣作为中国四大刺绣之一,闻名中外.在巴黎奥运会开幕倒计时50天之际,某国际旅游公司计划购买A、B两种奥运主题的湘绣作品作为纪念品.已知购买1件A 种湘绣作品与2件B种湘绣作品共需要700元,购买2件A种湘绣作品与3件 B种湘绣作品共需要1 200元.
(1)求A种湘绣作品和B种湘绣作品的单价分别为多少元.
(2)该国际旅游公司计划购买A 种湘绣作品和B种湘绣作品共200件,总费用不超过50 000元,那么最多能购买A种湘绣作品多少件
25.(2024 重庆奉节期末)(10分)数形结合是我们解决数学问题常用到的思想方法.如图2,我们通过两种不同的方法计算阴影部分的面积,可以得到一个数学公式.
操作:如图1 所示的是一个长为2m、宽为2n的长方形,沿图中虚线剪开,均分成四个小长方形,然后按图2的方式拼成一个正方形.
计算:
请用两种不同的方法求出图2中阴影部分的面积.
(1)方法1: .
(2)方法2: .
(3)总结观察图2并结合前面的计算,我们可以得出((m+n) ,(m-n) ,mn三个代数式之间的等量关系为 .
应用:
运用你所得到的公式,解决下列问题:
(4)若 mn=5,m-n=4,求( 的值.
(5)若(a-2023)(2024-a)=-12,求[(a-2 023)-(2024-a)] 的值.
26.(2024湖南永州双牌期末)(10分)在综合与实践课上,老师让同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动.已知两直线a,b,且a∥b,直角三角尺ABC中,∠BCA=90°,∠BAC=30°.
(1)【操作发现】
如图①,当三角尺的顶点 B 在直线 b 上时,若∠1=55°,则∠2= °.
(2)【探索证明】
如图②,当三角尺的顶点 C 在直线b 上时,请写出∠1 与∠2之间的数量关系,并说明理由.
(3)【拓展应用】
如图③,把三角尺的顶点 B放在直线b上且保持不动,旋转三角尺,点A 始终在直线BD(D为直线b上一点)的上方,若存在∠1=5∠CBD(∠CBD<60°),请直接写出射线 BA 与直线a所夹锐角的度数.
1C 检测某品牌汽车的抗撞击能力,适合采用抽样调查;监测大同市御河的水质情况,适合采用抽样调查;调查某班学生安全教育平台学习任务的完成情况,适合采用全面调查;调查6月份大同市二手房市场的均价,适合采用抽样调查.故选C.
2 ,∴这四个数中最大的数为π,故选 C.
3 C题图中与∠1 成同位角的角有∠DAB,∠EBH,∠FGH,共3个,故选 C.
4 AC A.在不等式a>b的两边同时加上2,不等号的方向不变,即a+2>b+2,故A项符合题意;B.在不等式a>b的两边同时乘-3,不等号的方向改变,即-3a<-3b,故B项不合题意;C.在不等式a>b的两边同时除以4,不等号的方向不变,即 故C 项符合题意;D.在不等式a>b的两边同时减去1,不等号的方向不变,即(a-1>b-1,故 D项不合题意.故选 AC.
故选项 A 错误; 故选项 B错误; 故选项 C正确;5a-2a=3a,故选项D错误.故选 C.
6B ∵AB∥CD,∴∠ABD=∠BDC,∵∠ABE+∠ABD=180°,∠BDC+∠CDF= 180°,∴ ∠CDF =∠ABE =50°,故选 B.
7B ∵点E,A关于直线OM对称,∴OM垂直平分AE,
∴AB=BE,同理,FC=AC,
∴△ABC的周长=BC+AB+AC=BC+BE+CF=EF=18故选 B.
8A 如图,过P作PQ∥AB,
∵AB∥CD,∴PQ∥CD∥AB,
∴∠CPQ=∠2=28°,∠BPQ=∠1,
∵ ∠BPQ=∠BPC-∠CPQ=58°-28°=30°,
∴∠1=30°.故选 A.
9B 题图中,较大阴影正方形的边长为a-b,因此面积为 ,较小阴影正方形的边长为b,因此面积为b ,整体正方形的边长为a,因此面积为a ,由题图中各个部分的面积之间的关系可得, 故选 B.
由①得x≤m,由②得x>3,故原不等式组的解集为3
解析 原式=3-3=0,故答案为0.
12答案 8
解析 · ∴a=2,b=-6,∴a-b=2+6=8.故答案为8.
13答案 30°
解析 ∵ 三角形 OAB 绕点 O 逆时针旋转75°到三角形OCD的位置,∠AOB=45°,∴∠AOC=75°,∠COD=∠AOB=45°,∴ ∠AOD=∠AOC-∠COD=75°-45°=30°,故答案为30°.
14答案 ∠A+∠D=180°(答案不唯一)
解析 根据平行线的判定定理即可得到结论,答案不唯一.
15答案 2
解析
16答案 8
解析 由m+2n-3=0可得m+2n=3,
17答案 m≥-1
解析 解 得x≥-1,解2x-m≥x得x≥m.
∵不等式组 的解集为x≥m,
∴m≥-1.故答案为m≥-1.
18答案 270°
解析 如图,过点B作BG∥AE,
∵AE∥CD,∴AE∥CD∥BG,
∴∠BAE+∠ABG=180°,∠BCD+∠CBG=180°,
∴∠BAE+∠ABG+∠CBG+∠BCD=360°,
∴∠BAE+∠ABC+∠BCD=360°.
∵BA⊥AE,∴∠BAE=90°,
∴∠ABC+∠BCD=360°-∠BAE=270°.
19解析
2分
4分
5分
当x=-2时,原式 …… 6分
20解析 (1)如图,△A B C 即为所求. ………… 2分
(2)如图,△A B C 即为所求. 4分
(3)如图,△AB C 即为所求. …………………… 6分
21解析 解不等式①得x>-6,…… 3分解不等式②得x<1, 6分∴该不等式组的解集为-6
(2)参与家务劳动的项目为3项的人数为100-3-30-42-10=15,……………………………………… 3分
补全条形统计图如下: 4分
(3)在扇形统计图中,“4项及以上”部分所对应扇形的圆心角的度数是
故答案为36. 6分
(人). … 7分
答:估计该校五月份参与家务劳动的项目达到3项及以上的学生人数为300. 8分
23解析 (1)根据题意可知-2.65与y互为相反数,故y=2.65.故答案为2.65. 3分
(2)根据题意,得7+4m+4-3m=0,…………… 4分
解得m=-11.……………………………………… 5分
∵n-3的平方根是它本身,
∴n-3=0, 6分
解得n=3. ………………………………………… 7分
∴m+n=-11+3=-8,
∴m+n的立方根为 … 9分
24解析 (1)设A种湘绣作品的单价为x元,B种湘绣作品的单价为y元,
根据题意得 解得
答:A种湘绣作品的单价为300元,B种湘绣作品的单价为200元. 4分
(2)设购买A种湘绣作品m件,则购买B种湘绣作品(200-m)件,
根据题意得300m+200(200-m)≤50000,解得m≤100,
故最多能购买A种湘绣作品100件. 9分
25解析 (1)题图2中阴影部分是边长为m-n的正方形,因此面积为( 故答案为(m-n) . … 1分
(2)题图2中阴影部分的面积可以看成边长为m+n的大正方形的面积减去题图1中长方形的面积,即 故填 …………… 2分
(3)由(1)(2)可以得出
故答案为 … 3分
(4)∵mn=5,m-n=4,
. …… 6分
(5)设.x=a-2023,y=2024-a,,则x+y=1, … 7分
由(a-2023)(2024-a)=-12可得 xy=-12, ………………… 8分
=1+48=49.……………………………………… 10分
26解析 (1)过点 C作CD∥a,如图1所示.
∵a∥b,∴CD∥a∥b,
∴∠2=∠ACD,∠1=∠BCD,
∴∠1+∠2=∠ACD+∠BCD=∠BCA,
∴∠2=∠BCA-∠1,
∵∠BCA=90°,∠1=55°,
故答案为35. 2分
(2)∠2-∠1=120°. 4分
理由:如图2所示,
∵∠BCA=90°,∠BAC=30°,
∴∠B=180°-∠BCA-∠BAC=60°,
由(1)可知∠B=∠1+∠3,
∴∠1+∠3=60°,
∴∠3=60°-∠1,
∵∠2+∠3=180°,
即∠2-∠1=120°.………………………………… 6分
(3)80°或30°. 10分
详解:依题意有以下两种情况:
①当BC在直线BD的上方时,如图3所示,
∵∠BCA=90°,∠BAC=30°,
∴∠ABC=180°-∠BCA-∠BAC=60°,设∠CBD=α(α<60°),则∠1=5∠CBD=5α,
∵点B 在直线b上且保持不动,
∴∠1+∠ABC+∠CBD=180°,
,解得α=20°,
∴∠1=5α=100°,
∵直线a∥b,∴∠1+∠2=180°,
②当BC在直线BD的下方时,如图4所示,同理得∠ABC=60°,
设∠CBD=β(β<60°),则∠1=5∠CBD=5β,
∴∠ABD=∠ABC-∠CBD=60°-β,
∵点B在直线b上且保持不动,
∴∠1+∠ABD=180°,
解得β=30°,∴∠1=5β=150°,
∵直线a∥b,
∴∠1+∠2=180°,
∴∠2=180°-∠1=30°.
综上所述,射线 BA与直线a所夹锐角的度数为80°或30°.
同课章节目录
