平行线中与学具或折叠有关的问题 (含答案)2024-2025学年湘教版七年级数学下册
文档属性
| 名称 | 平行线中与学具或折叠有关的问题 (含答案)2024-2025学年湘教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 169.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:46:16 | ||
图片预览

文档简介
平台中小学教育资源及组卷应用
平行线中与学具或折叠有关的问题
类型一 三角尺与直尺组合
1.如图1,把一块含30°角的直角三角尺ABC 的边 BC放置于长方形直尺DEFG的边EF 上.
(1)根据图1填空:∠1= °,∠2= °.
(2)现把三角尺绕 B 点逆时针旋转,旋转角的度数为 n.
①如图2,当 n=25°,且点 C 恰好落在 DG上时,求∠1、∠2 的度数.
②当( 时,是否存在三角尺某一边所在的直线与直尺某一边(直尺有四条边)所在的直线垂直 如果存在,请直接写出所有n的值和对应的那两条边;如果不存在,请说明理由.
类型二 两个三角尺组合
2.(2024山东临沂河东期末)如图,MN∥PQ.将两块直角三角尺(一块含30°角,一块含45°角)按如下方式进行摆放,恰好满足∠MAE=∠CBQ.
(1)若∠NAC=16°,求∠CBQ 的度数.
(2)试判断AB 与 DE 的位置关系,并说明理由.
3.如图所示,将两个三角尺的直角顶点重合.
(1)写出全部以 C 为顶点的相等的角.
(2)若∠ACB=150°,求∠DCE的度数.
(3)写出∠ACB与∠DCE之间的数量关系.
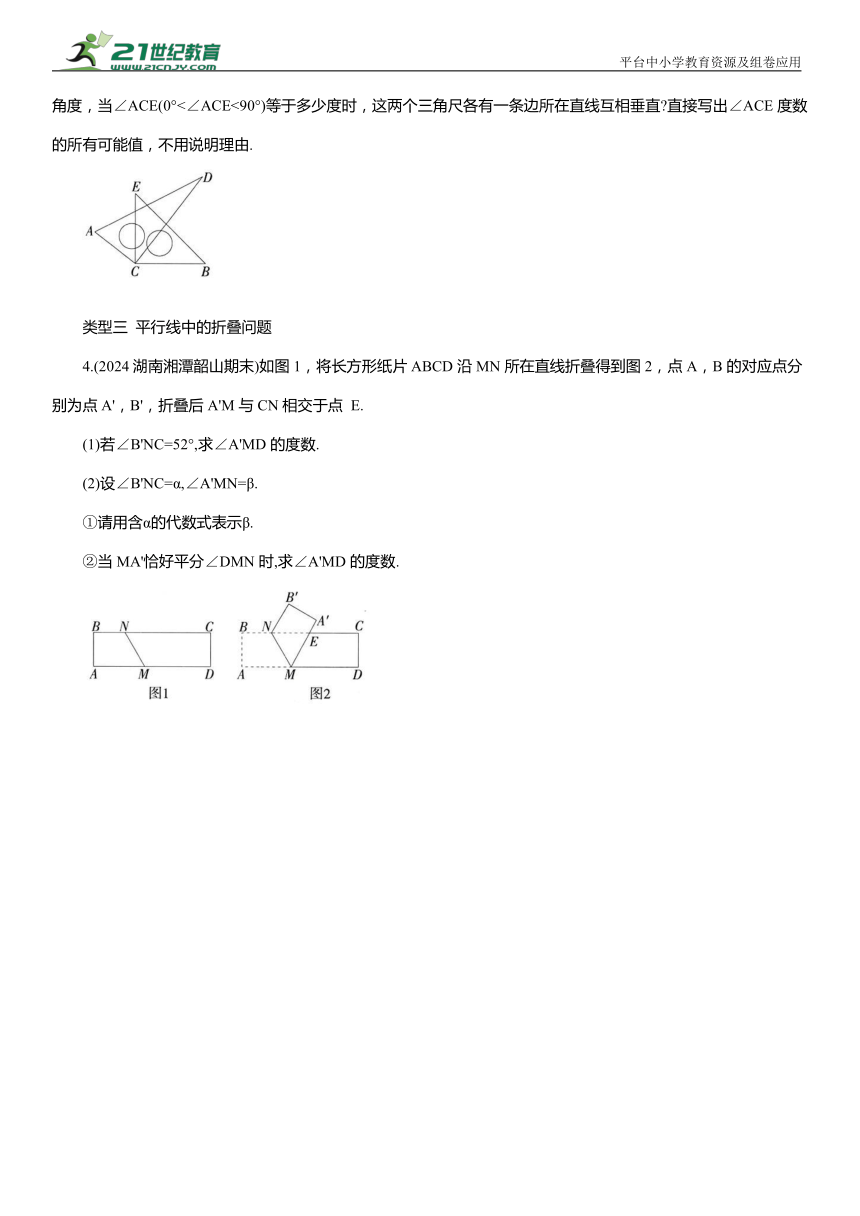
(4)按住三角尺ACD不动,将三角尺ECB 的边EC与AC重合,然后绕点 C 按顺时针或逆时针任意转动一个角度,当∠ACE(0°<∠ACE<90°)等于多少度时,这两个三角尺各有一条边所在直线互相垂直 直接写出∠ACE度数的所有可能值,不用说明理由.
类型三 平行线中的折叠问题
4.(2024湖南湘潭韶山期末)如图1,将长方形纸片ABCD沿MN所在直线折叠得到图2,点A,B的对应点分别为点A',B',折叠后A'M与CN相交于点 E.
(1)若∠B'NC=52°,求∠A'MD的度数.
(2)设∠B'NC=α,∠A'MN=β.
①请用含α的代数式表示β.
②当MA'恰好平分∠DMN时,求∠A'MD的度数.
1解析 (1)根据三角尺三个角的角度和直尺上、下边平行可知,
(2)①∵∠ABC=60°,n=25°,
∴∠ABE=180°-60°-25°=95°,
∵ DG∥EF,∴ ∠1=∠ABE=95°,∠BCG=180°-
∵∠ACB+∠BCG+∠2=360°,∴∠2=360°-∠ACB-
②当n=30°时,AB⊥DG(EF);当n=90°时,BC⊥DG(EF),AC⊥DE(GF);当n=120°时,AB⊥DE(GF).
2解析 (1)∵∠NAC=16°,∠BAC=45°,
∴ ∠CBQ=∠ABQ-∠ABC=119°-90°=29°.
(2)AB∥DE.理由:∵ MN∥PQ,∴∠MAB=∠ABQ.
∵∠MAE=∠CBQ,∴∠MAB-∠MAE=∠ABQ-∠CBQ,即∠EAB=∠ABC=90°.
∵∠AED=90°,∴∠EAB+∠AED=180°,∴AB∥DE.
3解析 (1)∠ACE=∠BCD,∠ACD=∠ECB.
(2)∵∠ACB=150°,∠BCE=90°,
∴ ∠DCE=90°-∠ACE=90°-60°=30°.
(3)∠ACB+∠DCE=∠BCE+∠ACE+∠DCE=90°+ ,即∠ACB+∠DCE=180°.
(4)CE⊥AD时,∠ACE=30°;EB⊥CD(或BE⊥AC)时,∠ACE=45°;BE⊥AD时,∠ACE=75°;CB⊥AD时,∠ACE=60°,即∠ACE 度数所有可能的值为30°、45°、60°、75°.
4解析 (1)∵NB'∥A'M,∴∠A'EC=∠B'NC=52°,∵ CN∥MD,∴ ∠A'MD=∠A'EC=52°.
(2)①由(1)得∠A'MD=∠B'NC=α,由题意知∠A'MN=∠AMN=β,
②∵ MA'恰好平分∠DMN,∴∠NMA'=∠A'MD,
∴∠AMN=∠NMA'=∠A'MD,
平行线中与学具或折叠有关的问题
类型一 三角尺与直尺组合
1.如图1,把一块含30°角的直角三角尺ABC 的边 BC放置于长方形直尺DEFG的边EF 上.
(1)根据图1填空:∠1= °,∠2= °.
(2)现把三角尺绕 B 点逆时针旋转,旋转角的度数为 n.
①如图2,当 n=25°,且点 C 恰好落在 DG上时,求∠1、∠2 的度数.
②当( 时,是否存在三角尺某一边所在的直线与直尺某一边(直尺有四条边)所在的直线垂直 如果存在,请直接写出所有n的值和对应的那两条边;如果不存在,请说明理由.
类型二 两个三角尺组合
2.(2024山东临沂河东期末)如图,MN∥PQ.将两块直角三角尺(一块含30°角,一块含45°角)按如下方式进行摆放,恰好满足∠MAE=∠CBQ.
(1)若∠NAC=16°,求∠CBQ 的度数.
(2)试判断AB 与 DE 的位置关系,并说明理由.
3.如图所示,将两个三角尺的直角顶点重合.
(1)写出全部以 C 为顶点的相等的角.
(2)若∠ACB=150°,求∠DCE的度数.
(3)写出∠ACB与∠DCE之间的数量关系.
(4)按住三角尺ACD不动,将三角尺ECB 的边EC与AC重合,然后绕点 C 按顺时针或逆时针任意转动一个角度,当∠ACE(0°<∠ACE<90°)等于多少度时,这两个三角尺各有一条边所在直线互相垂直 直接写出∠ACE度数的所有可能值,不用说明理由.
类型三 平行线中的折叠问题
4.(2024湖南湘潭韶山期末)如图1,将长方形纸片ABCD沿MN所在直线折叠得到图2,点A,B的对应点分别为点A',B',折叠后A'M与CN相交于点 E.
(1)若∠B'NC=52°,求∠A'MD的度数.
(2)设∠B'NC=α,∠A'MN=β.
①请用含α的代数式表示β.
②当MA'恰好平分∠DMN时,求∠A'MD的度数.
1解析 (1)根据三角尺三个角的角度和直尺上、下边平行可知,
(2)①∵∠ABC=60°,n=25°,
∴∠ABE=180°-60°-25°=95°,
∵ DG∥EF,∴ ∠1=∠ABE=95°,∠BCG=180°-
∵∠ACB+∠BCG+∠2=360°,∴∠2=360°-∠ACB-
②当n=30°时,AB⊥DG(EF);当n=90°时,BC⊥DG(EF),AC⊥DE(GF);当n=120°时,AB⊥DE(GF).
2解析 (1)∵∠NAC=16°,∠BAC=45°,
∴ ∠CBQ=∠ABQ-∠ABC=119°-90°=29°.
(2)AB∥DE.理由:∵ MN∥PQ,∴∠MAB=∠ABQ.
∵∠MAE=∠CBQ,∴∠MAB-∠MAE=∠ABQ-∠CBQ,即∠EAB=∠ABC=90°.
∵∠AED=90°,∴∠EAB+∠AED=180°,∴AB∥DE.
3解析 (1)∠ACE=∠BCD,∠ACD=∠ECB.
(2)∵∠ACB=150°,∠BCE=90°,
∴ ∠DCE=90°-∠ACE=90°-60°=30°.
(3)∠ACB+∠DCE=∠BCE+∠ACE+∠DCE=90°+ ,即∠ACB+∠DCE=180°.
(4)CE⊥AD时,∠ACE=30°;EB⊥CD(或BE⊥AC)时,∠ACE=45°;BE⊥AD时,∠ACE=75°;CB⊥AD时,∠ACE=60°,即∠ACE 度数所有可能的值为30°、45°、60°、75°.
4解析 (1)∵NB'∥A'M,∴∠A'EC=∠B'NC=52°,∵ CN∥MD,∴ ∠A'MD=∠A'EC=52°.
(2)①由(1)得∠A'MD=∠B'NC=α,由题意知∠A'MN=∠AMN=β,
②∵ MA'恰好平分∠DMN,∴∠NMA'=∠A'MD,
∴∠AMN=∠NMA'=∠A'MD,
同课章节目录
