4.1 平面内两条直线的位置关系 同步练习(含答案)2024-2025学年湘教版七年级数学下册
文档属性
| 名称 | 4.1 平面内两条直线的位置关系 同步练习(含答案)2024-2025学年湘教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 189.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:20:38 | ||
图片预览




文档简介
4.1 平面内两条直线的位置关系
4.1.1平行线
基础过关全练
知识点 1 相交线与平行线
1.(2024.江苏淮安期中)在同一平面内,不重合的两条直线的位置关系是 ( )
A.平行 B.相交
C.平行或相交 D.不能确定
2.易错题(2024 黑龙江大庆肇源月考)下列说法正确的是 ( )
A.同一个平面内,不相交的两条线段是平行线
B.同一个平面内,两条直线不相交就重合
C.同一个平面内,没有公共点的两条直线是平行线
D.不相交的两条直线是平行线
3.下列关于平行线的表示方法正确的是 ( )
A. a∥A B. AB∥cd C. A∥B D.a∥b
4.下列图形中,AB 不平行于 CD 的是( )
5.在同一平面内,任意三条直线有几种不同的位置关系 你能画图说明吗
下面是小明的解题过程:
解:有两种位置关系,如图所示.
小明的解答正确吗 如果不正确,请你给出正确的解答.
知识点 2 平行线的画法
6.根据下列要求画图:
(1)如图1,过点A画MN∥BC.
(2)如图2,过点C画CE∥DA,与AB交于点E,连接DE,过点C画 CF∥DE,与AB的延长线交于点 F.
知识点3 平行线的基本事实
7.教材变式如图,过点A画直线l的平行线,能画 ( )
A.无数条 B.2条 C.1条 D.0条
8.若a∥b,l∥a,则l与b的位置关系是 .
9.在同一平面内,直线l的同侧有A、B、C三点,如果AB∥l,BC∥l,那么A、B、C三点是否在同一直线上 为什么
10.如图,已知直线a,点B,点 C.
(1)过点 B画直线a的平行线,能画几条
(2)过点 C画直线a的平行线,它与过点 B 的平行线平行吗 请说明理由.
能力提升全练
11.(2024河南周口西华月考,9,☆☆)下列说法中,正确的个数为 ( )
(1)过一点有无数条直线与已知直线平行.
(2)如果a∥b,a∥c,那么b∥c.
(3)如果两条线段不相交,那么它们就平行.
(4)如果两条直线不相交,那么它们就平行.
A.1 B.2 C.3 D.4
12.(2024山东聊城冠县期中,3, )若直线a,b,c,d有下列关系,则推理正确的是( )
A.∵a∥b,b∥c,∴c∥d
B.∵a∥c,b∥d,∴c∥d
C.∵a∥b,a∥c,∴b∥c
D.∵a∥b,c∥d,∴a∥c
13.(2024湖南永州道县期中,5, )如图,PC∥AB,QC∥AB,则点 P、C、Q在一条直线上.理由是 .
素养探究全练
14.几何直观如图所示,在同一平面内,两条直线相交时有1个交点,三条直线相交时最多有3个交点,四条直线相交时最多有6个交点.
(1)当五条直线相交时最多会有多少个交点
(2)当n条直线相交时最多有多少个交点 (用含n的代数式表示)
(3)算一算,同一平面内10条直线相交时最多有多少个交点
(4)平面上有10条直线,没有任意3条及3条以上直线交于同一点,也无重合,它们能有31个交点吗 如果能,给出一个画法;如果不能,请说明理由.
平台中小学教育资源及组卷应用
4.1.2 相交直线所成的角
基础过关全练
知识点1 对顶角的定义及其性质
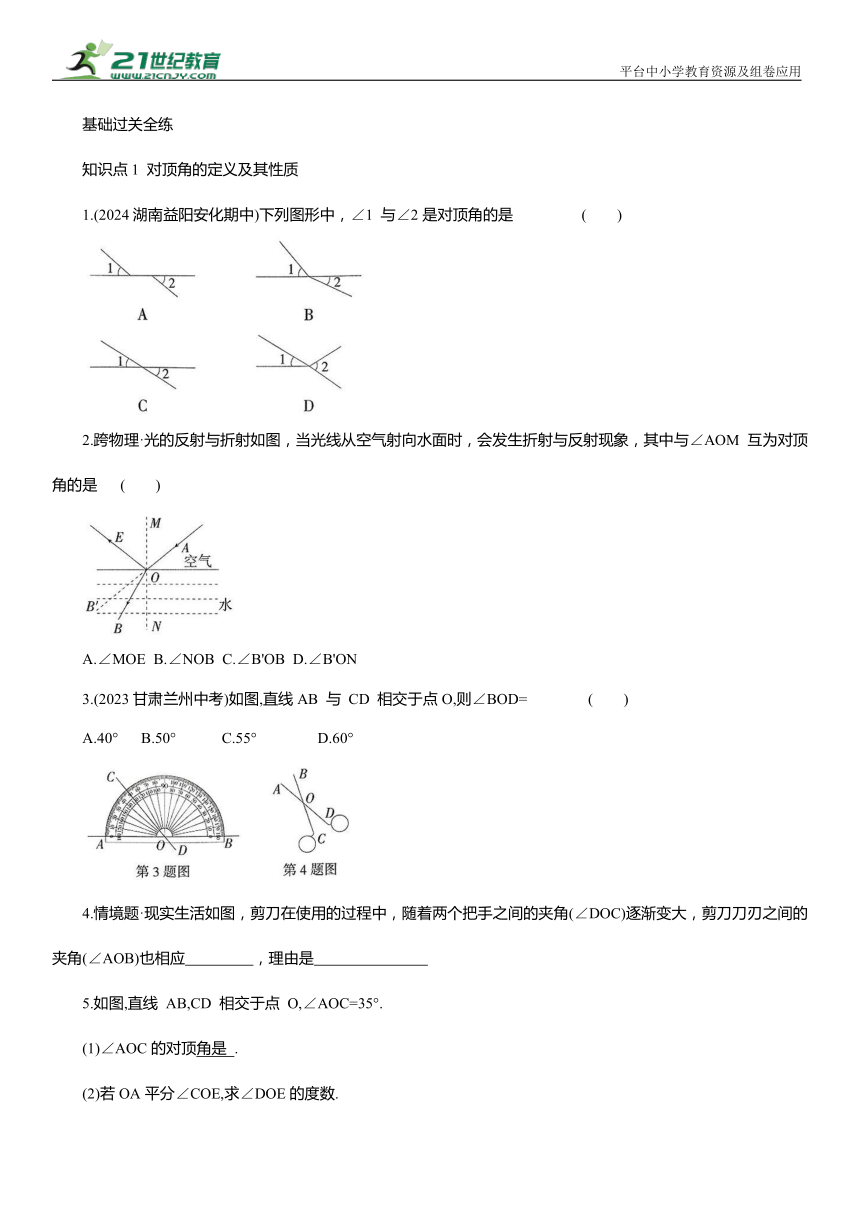
1.(2024湖南益阳安化期中)下列图形中,∠1 与∠2是对顶角的是 ( )
2.跨物理·光的反射与折射如图,当光线从空气射向水面时,会发生折射与反射现象,其中与∠AOM 互为对顶角的是 ( )
A.∠MOE B.∠NOB C.∠B'OB D.∠B'ON
3.(2023甘肃兰州中考)如图,直线AB 与 CD 相交于点O,则∠BOD= ( )
A.40° B.50° C.55° D.60°
4.情境题·现实生活如图,剪刀在使用的过程中,随着两个把手之间的夹角(∠DOC)逐渐变大,剪刀刀刃之间的夹角(∠AOB)也相应 ,理由是
5.如图,直线 AB,CD 相交于点 O,∠AOC=35°.
(1)∠AOC的对顶角是 .
(2)若OA平分∠COE,求∠DOE的度数.
知识点2 同位角、内错角、同旁内角
6.(2024河北石家庄新华期末)如图,∠1 与∠2 是 ( )
A.同位角 B.内错角
C.同旁内角 D.对顶角
7.三线八角模型如图所示,与∠1 是内错角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
8.(2024湖南株洲荷塘期中)如图,直线 EF 与直线AB,CD 相交.图中所示的各个角中,能看作∠1的同旁内角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
9.教材变式如图所示.
(1)∠AED 和∠ABC 可看成是直线 、 被直线 所截得的 角.
(2)∠EDB 和∠DBC可看成是直线 、 被直线 所截得的 角.
(3)∠EDC 和∠C 可看成是直线 、 被直线 所截得的 角.
10.如图,找出∠1~∠8中所有的同位角、内错角和同旁内角.
能力提升全练
11.情境题·现实生活(2024 湖南永州零陵期中,5,22)如图所示的是某品牌椅子的实物图及示意图,DE与地面(AB)平行,若∠ACB=48°,则∠DCE= ( )
A.48° B.132° C.42° D.32°
12.(2024北京平谷期末,2,)两条直线被第三条直线所截,形成了“三线八角”,为了便于记忆,同学们可用双手表示“三线八角”(两大拇指代表被截直线,食指代表截线).下列三幅图依次表示 ( )
A.同位角、同旁内角、内错角
B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角
D.同位角、内错角、对顶角
13.(2023湖南岳阳平江二中月考,16,☆)如图.
(1)当直线AC、DG被直线 CD所截时,∠2 的内错角是 .
(2)∠AEF的所有同位角是 .
(3)∠1的所有同旁内角是 .
14.方程思想(2024 河南师大附中期中,18, )如图,直线AB、CD 相交于点 O,OE 把∠BOD分成两部分.(M7204002)
(1)图中∠AOD 的对顶角为 .
(2)若OE平分∠BOD,∠DOE:∠AOD=1∶4,求∠EOC的度数.
15.几何直观下列各图中,直线都交于一点,请探究同一平面内交于一点的直线的条数与所形成的对顶角的对数之间的规律.
(1)请观察上图并填写下表:
交于一点的直线的条数 2 3 4
对顶角的对数 ___ ___ ___
(2)若n条直线交于一点,则共有 对对顶角(用含 n的代数式表示).
(3)当100条直线交于一点时,共有 对对顶角.
4.1.1 平行线
基础过关全练
1C同一平面内不重合的两条直线有平行和相交这两种位置关系.故选 C.
2C 根据平行线的定义,A.应该是不相交的两条直线,故错误;B.在同一个平面内,两条直线的位置关系有相交和平行两种,故错误;C.正确;D.缺少在同一平面内的前提条件,故错误.故选 C.
3D一条直线可以用两个大写字母或者一个小写字母表示,据此可排除A、B、C,故选 D.
4D 观察题中图形可知选项D中AB 不平行于 CD.
5解析 不正确,如图所示,在同一平面内,任意三条直线有四种不同的位置关系.
6解析 (1)如图1所示.
(2)如图2所示.
7C 因为过直线外一点有且只有一条直线与这条直线平行,所以过点A画直线l的平行线,能画1条.故选C.
8答案 l∥b
解析 由“平行于同一条直线的两条直线平行”可知,当a∥b,l∥a时,l∥b.故答案为l∥b.
9解析 A、B、C三点在同一直线上,理由:∵过直线外一点有且只有一条直线与已知直线平行,∴经过点B且与直线l平行的直线AB、BC是同一条直线,即A、B、C三点共线.
10解析 (1)如图,过直线a外的一点 B 画直线a的平行线,有且只有一条直线与直线a平行.
(2)过点C画直线a的平行线c,它与过点B的平行线b平行.理由:如图,∵b∥a,c∥a,∴c∥b.
能力提升全练
11 A 过直线外一点有且只有一条直线与已知直线平行,说法(1)错误;根据“平行于同一条直线的两条直线平行”可知,说法(2)正确;线段的长度是有限的,不相交也不一定平行,说法(3)错误;在同一平面内,如果两条直线不相交,那么它们就平行,说法(4)错误.正确的只有一个,故选 A.
12 C∵a∥b,b∥c,∴c∥a,故A不符合题意;a∥c,b∥d,c与d不一定平行,故B不符合题意;∵a∥b,a∥c,∴b∥c,故C符合题意;a∥b,c∥d,a与c不一定平行,故D 不符合题意.故选 C.
13答案 过直线外一点有且只有一条直线与已知直线平行解析 ∵ PC∥AB,QC∥AB,PC 和 CQ 都过点 C,∴点 P、C、Q在一条直线上(过直线外一点有且只有一条直线与已知直线平行).
素养探究全练
14解析 (1)∵两条直线相交,有1个交点,三条直线相交,最多有1+2=3个交点,四条直线相交,最多有1+2+3=6个交点,∴五条直线相交,最多有1+2+3+4=10个交点.
(2)n条直线相交,最多有1+2+3+…+(n-1)= 个交点.
(3)10条直线相交,最多有 个交点.
(4)会出现31个交点,如图所示.
4.1.2 相交直线所成的角
基础过关全练
1C只有两直线相交时,才产生对顶角,故选 C.
2D根据对顶角的定义可知∠B'ON与∠AOM 互为对顶角,故选 D.
3B ∵直线AB与CD相交于点O,∴∠BOD=∠AOC,∵∠AOC=50°,∴ ∠BOD=50°,故选 B.
4 答案 变大;对顶角相等
解析 ∵两直线相交,对顶角相等,且对顶角中两个角的变化一致,∴随着两个把手之间的夹角(∠DOC)逐渐变大,剪刀刀刃之间的夹角(∠AOB)也相应变大,理由是对顶角相等.
5 解析 (1)由对顶角的定义可得∠AOC 的对顶角是∠BOD,故答案为∠BOD.
(2)∵ OA 平分∠COE,∠AOC=35°,∴ ∠COE=2∠AOC=70°,∴∠DOE=180°-∠COE=110°.
6A 根据同位角的定义可知,图形中的∠1与∠2是同位角,故选 A.
7B 根据内错角的定义可知,∠3与∠1是内错角.
8D 两条直线被第三条直线所截形成的角中,若两个角都在两直线(被截线)之间,并且在第三条直线(截线)的同一旁,则这样一对角叫作同旁内角.由题图可知,能看作∠1的同旁内角的是∠5,故选D.
9答案 (1)ED;BC;AB;同位 (2)ED;BC;BD;内错(3)ED;BC;AC;同旁内
解析 (1)∠AED 和∠ABC 分别在直线 ED、BC 的同一方(上方),并且都在直线AB的同侧(右侧),故∠AED 和∠ABC是同位角.
(2)∠EDB 和∠DBC 都在直线 ED、BC之间,并且分别在直线 BD 的两侧(∠EDB 在直线 BD 上方,∠DBC在直线 BD下方),故∠EDB 和∠DBC 是内错角.
(3)∠EDC和∠C都在直线 ED、BC之间,并且都在直线 AC 的同侧(左侧),故∠EDC 和∠C 是同旁内角.
10解析 同位角:∠1与∠8,∠4 与∠7,∠2与∠5,∠3 与∠6.
内错角:∠3与∠8,∠4与∠5.
同旁内角:∠3与∠5,∠4与∠8.
能力提升全练
11 A 根据对顶角的性质有∠DCE=∠ACB=48°.故选 A.
12 B 根据同位角、内错角、同旁内角的概念,可知第一个图是同位角,第二个图是内错角,第三个图是同旁内角.故选 B.
13解析 (1)当直线AC、DG被直线 CD所截时,∠2的内错角是∠ACD.
(2)∠AEF 的同位角是∠ACD、∠ACB.
(3)∠1 的同旁内角是∠ACD、∠ACB、∠EFD.
14解析 (1)由题意得∠AOD的对顶角为∠BOC,故答案为∠BOC.
(2)设∠DOE=x,则∠AOD=4x,
∵OE平分∠BOD,∴∠BOE=∠DOE=x,
∴x+x+4x=180°,解得x=30°,
∴∠BOE=30°,∠AOD=4x=120°,
∴∠BOC=∠AOD=120°,
∴∠EOC=∠BOE+∠BOC=150°.
·方法解读
题中等量关系比较复杂或有比例关系时,常列方程来求解.
素养探究全练
15解析 (1)根据题图可得2条直线交于一点时,共有1×2=2对对顶角;3条直线交于一点时,共有2×3=6对对顶角;4条直线交于一点时,共有3×4=12对对顶角.
(2)当n条直线交于一点时,共有n(n-1)对对顶角.
(3)当n=100时,n(n-1)=100×99=9900,故共有9 900对对顶角.
4.1.1平行线
基础过关全练
知识点 1 相交线与平行线
1.(2024.江苏淮安期中)在同一平面内,不重合的两条直线的位置关系是 ( )
A.平行 B.相交
C.平行或相交 D.不能确定
2.易错题(2024 黑龙江大庆肇源月考)下列说法正确的是 ( )
A.同一个平面内,不相交的两条线段是平行线
B.同一个平面内,两条直线不相交就重合
C.同一个平面内,没有公共点的两条直线是平行线
D.不相交的两条直线是平行线
3.下列关于平行线的表示方法正确的是 ( )
A. a∥A B. AB∥cd C. A∥B D.a∥b
4.下列图形中,AB 不平行于 CD 的是( )
5.在同一平面内,任意三条直线有几种不同的位置关系 你能画图说明吗
下面是小明的解题过程:
解:有两种位置关系,如图所示.
小明的解答正确吗 如果不正确,请你给出正确的解答.
知识点 2 平行线的画法
6.根据下列要求画图:
(1)如图1,过点A画MN∥BC.
(2)如图2,过点C画CE∥DA,与AB交于点E,连接DE,过点C画 CF∥DE,与AB的延长线交于点 F.
知识点3 平行线的基本事实
7.教材变式如图,过点A画直线l的平行线,能画 ( )
A.无数条 B.2条 C.1条 D.0条
8.若a∥b,l∥a,则l与b的位置关系是 .
9.在同一平面内,直线l的同侧有A、B、C三点,如果AB∥l,BC∥l,那么A、B、C三点是否在同一直线上 为什么
10.如图,已知直线a,点B,点 C.
(1)过点 B画直线a的平行线,能画几条
(2)过点 C画直线a的平行线,它与过点 B 的平行线平行吗 请说明理由.
能力提升全练
11.(2024河南周口西华月考,9,☆☆)下列说法中,正确的个数为 ( )
(1)过一点有无数条直线与已知直线平行.
(2)如果a∥b,a∥c,那么b∥c.
(3)如果两条线段不相交,那么它们就平行.
(4)如果两条直线不相交,那么它们就平行.
A.1 B.2 C.3 D.4
12.(2024山东聊城冠县期中,3, )若直线a,b,c,d有下列关系,则推理正确的是( )
A.∵a∥b,b∥c,∴c∥d
B.∵a∥c,b∥d,∴c∥d
C.∵a∥b,a∥c,∴b∥c
D.∵a∥b,c∥d,∴a∥c
13.(2024湖南永州道县期中,5, )如图,PC∥AB,QC∥AB,则点 P、C、Q在一条直线上.理由是 .
素养探究全练
14.几何直观如图所示,在同一平面内,两条直线相交时有1个交点,三条直线相交时最多有3个交点,四条直线相交时最多有6个交点.
(1)当五条直线相交时最多会有多少个交点
(2)当n条直线相交时最多有多少个交点 (用含n的代数式表示)
(3)算一算,同一平面内10条直线相交时最多有多少个交点
(4)平面上有10条直线,没有任意3条及3条以上直线交于同一点,也无重合,它们能有31个交点吗 如果能,给出一个画法;如果不能,请说明理由.
平台中小学教育资源及组卷应用
4.1.2 相交直线所成的角
基础过关全练
知识点1 对顶角的定义及其性质
1.(2024湖南益阳安化期中)下列图形中,∠1 与∠2是对顶角的是 ( )
2.跨物理·光的反射与折射如图,当光线从空气射向水面时,会发生折射与反射现象,其中与∠AOM 互为对顶角的是 ( )
A.∠MOE B.∠NOB C.∠B'OB D.∠B'ON
3.(2023甘肃兰州中考)如图,直线AB 与 CD 相交于点O,则∠BOD= ( )
A.40° B.50° C.55° D.60°
4.情境题·现实生活如图,剪刀在使用的过程中,随着两个把手之间的夹角(∠DOC)逐渐变大,剪刀刀刃之间的夹角(∠AOB)也相应 ,理由是
5.如图,直线 AB,CD 相交于点 O,∠AOC=35°.
(1)∠AOC的对顶角是 .
(2)若OA平分∠COE,求∠DOE的度数.
知识点2 同位角、内错角、同旁内角
6.(2024河北石家庄新华期末)如图,∠1 与∠2 是 ( )
A.同位角 B.内错角
C.同旁内角 D.对顶角
7.三线八角模型如图所示,与∠1 是内错角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
8.(2024湖南株洲荷塘期中)如图,直线 EF 与直线AB,CD 相交.图中所示的各个角中,能看作∠1的同旁内角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
9.教材变式如图所示.
(1)∠AED 和∠ABC 可看成是直线 、 被直线 所截得的 角.
(2)∠EDB 和∠DBC可看成是直线 、 被直线 所截得的 角.
(3)∠EDC 和∠C 可看成是直线 、 被直线 所截得的 角.
10.如图,找出∠1~∠8中所有的同位角、内错角和同旁内角.
能力提升全练
11.情境题·现实生活(2024 湖南永州零陵期中,5,22)如图所示的是某品牌椅子的实物图及示意图,DE与地面(AB)平行,若∠ACB=48°,则∠DCE= ( )
A.48° B.132° C.42° D.32°
12.(2024北京平谷期末,2,)两条直线被第三条直线所截,形成了“三线八角”,为了便于记忆,同学们可用双手表示“三线八角”(两大拇指代表被截直线,食指代表截线).下列三幅图依次表示 ( )
A.同位角、同旁内角、内错角
B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角
D.同位角、内错角、对顶角
13.(2023湖南岳阳平江二中月考,16,☆)如图.
(1)当直线AC、DG被直线 CD所截时,∠2 的内错角是 .
(2)∠AEF的所有同位角是 .
(3)∠1的所有同旁内角是 .
14.方程思想(2024 河南师大附中期中,18, )如图,直线AB、CD 相交于点 O,OE 把∠BOD分成两部分.(M7204002)
(1)图中∠AOD 的对顶角为 .
(2)若OE平分∠BOD,∠DOE:∠AOD=1∶4,求∠EOC的度数.
15.几何直观下列各图中,直线都交于一点,请探究同一平面内交于一点的直线的条数与所形成的对顶角的对数之间的规律.
(1)请观察上图并填写下表:
交于一点的直线的条数 2 3 4
对顶角的对数 ___ ___ ___
(2)若n条直线交于一点,则共有 对对顶角(用含 n的代数式表示).
(3)当100条直线交于一点时,共有 对对顶角.
4.1.1 平行线
基础过关全练
1C同一平面内不重合的两条直线有平行和相交这两种位置关系.故选 C.
2C 根据平行线的定义,A.应该是不相交的两条直线,故错误;B.在同一个平面内,两条直线的位置关系有相交和平行两种,故错误;C.正确;D.缺少在同一平面内的前提条件,故错误.故选 C.
3D一条直线可以用两个大写字母或者一个小写字母表示,据此可排除A、B、C,故选 D.
4D 观察题中图形可知选项D中AB 不平行于 CD.
5解析 不正确,如图所示,在同一平面内,任意三条直线有四种不同的位置关系.
6解析 (1)如图1所示.
(2)如图2所示.
7C 因为过直线外一点有且只有一条直线与这条直线平行,所以过点A画直线l的平行线,能画1条.故选C.
8答案 l∥b
解析 由“平行于同一条直线的两条直线平行”可知,当a∥b,l∥a时,l∥b.故答案为l∥b.
9解析 A、B、C三点在同一直线上,理由:∵过直线外一点有且只有一条直线与已知直线平行,∴经过点B且与直线l平行的直线AB、BC是同一条直线,即A、B、C三点共线.
10解析 (1)如图,过直线a外的一点 B 画直线a的平行线,有且只有一条直线与直线a平行.
(2)过点C画直线a的平行线c,它与过点B的平行线b平行.理由:如图,∵b∥a,c∥a,∴c∥b.
能力提升全练
11 A 过直线外一点有且只有一条直线与已知直线平行,说法(1)错误;根据“平行于同一条直线的两条直线平行”可知,说法(2)正确;线段的长度是有限的,不相交也不一定平行,说法(3)错误;在同一平面内,如果两条直线不相交,那么它们就平行,说法(4)错误.正确的只有一个,故选 A.
12 C∵a∥b,b∥c,∴c∥a,故A不符合题意;a∥c,b∥d,c与d不一定平行,故B不符合题意;∵a∥b,a∥c,∴b∥c,故C符合题意;a∥b,c∥d,a与c不一定平行,故D 不符合题意.故选 C.
13答案 过直线外一点有且只有一条直线与已知直线平行解析 ∵ PC∥AB,QC∥AB,PC 和 CQ 都过点 C,∴点 P、C、Q在一条直线上(过直线外一点有且只有一条直线与已知直线平行).
素养探究全练
14解析 (1)∵两条直线相交,有1个交点,三条直线相交,最多有1+2=3个交点,四条直线相交,最多有1+2+3=6个交点,∴五条直线相交,最多有1+2+3+4=10个交点.
(2)n条直线相交,最多有1+2+3+…+(n-1)= 个交点.
(3)10条直线相交,最多有 个交点.
(4)会出现31个交点,如图所示.
4.1.2 相交直线所成的角
基础过关全练
1C只有两直线相交时,才产生对顶角,故选 C.
2D根据对顶角的定义可知∠B'ON与∠AOM 互为对顶角,故选 D.
3B ∵直线AB与CD相交于点O,∴∠BOD=∠AOC,∵∠AOC=50°,∴ ∠BOD=50°,故选 B.
4 答案 变大;对顶角相等
解析 ∵两直线相交,对顶角相等,且对顶角中两个角的变化一致,∴随着两个把手之间的夹角(∠DOC)逐渐变大,剪刀刀刃之间的夹角(∠AOB)也相应变大,理由是对顶角相等.
5 解析 (1)由对顶角的定义可得∠AOC 的对顶角是∠BOD,故答案为∠BOD.
(2)∵ OA 平分∠COE,∠AOC=35°,∴ ∠COE=2∠AOC=70°,∴∠DOE=180°-∠COE=110°.
6A 根据同位角的定义可知,图形中的∠1与∠2是同位角,故选 A.
7B 根据内错角的定义可知,∠3与∠1是内错角.
8D 两条直线被第三条直线所截形成的角中,若两个角都在两直线(被截线)之间,并且在第三条直线(截线)的同一旁,则这样一对角叫作同旁内角.由题图可知,能看作∠1的同旁内角的是∠5,故选D.
9答案 (1)ED;BC;AB;同位 (2)ED;BC;BD;内错(3)ED;BC;AC;同旁内
解析 (1)∠AED 和∠ABC 分别在直线 ED、BC 的同一方(上方),并且都在直线AB的同侧(右侧),故∠AED 和∠ABC是同位角.
(2)∠EDB 和∠DBC 都在直线 ED、BC之间,并且分别在直线 BD 的两侧(∠EDB 在直线 BD 上方,∠DBC在直线 BD下方),故∠EDB 和∠DBC 是内错角.
(3)∠EDC和∠C都在直线 ED、BC之间,并且都在直线 AC 的同侧(左侧),故∠EDC 和∠C 是同旁内角.
10解析 同位角:∠1与∠8,∠4 与∠7,∠2与∠5,∠3 与∠6.
内错角:∠3与∠8,∠4与∠5.
同旁内角:∠3与∠5,∠4与∠8.
能力提升全练
11 A 根据对顶角的性质有∠DCE=∠ACB=48°.故选 A.
12 B 根据同位角、内错角、同旁内角的概念,可知第一个图是同位角,第二个图是内错角,第三个图是同旁内角.故选 B.
13解析 (1)当直线AC、DG被直线 CD所截时,∠2的内错角是∠ACD.
(2)∠AEF 的同位角是∠ACD、∠ACB.
(3)∠1 的同旁内角是∠ACD、∠ACB、∠EFD.
14解析 (1)由题意得∠AOD的对顶角为∠BOC,故答案为∠BOC.
(2)设∠DOE=x,则∠AOD=4x,
∵OE平分∠BOD,∴∠BOE=∠DOE=x,
∴x+x+4x=180°,解得x=30°,
∴∠BOE=30°,∠AOD=4x=120°,
∴∠BOC=∠AOD=120°,
∴∠EOC=∠BOE+∠BOC=150°.
·方法解读
题中等量关系比较复杂或有比例关系时,常列方程来求解.
素养探究全练
15解析 (1)根据题图可得2条直线交于一点时,共有1×2=2对对顶角;3条直线交于一点时,共有2×3=6对对顶角;4条直线交于一点时,共有3×4=12对对顶角.
(2)当n条直线交于一点时,共有n(n-1)对对顶角.
(3)当n=100时,n(n-1)=100×99=9900,故共有9 900对对顶角.
同课章节目录
