北京市昌平区2024~2025学年八年级下册期中数学试卷(无答案)
文档属性
| 名称 | 北京市昌平区2024~2025学年八年级下册期中数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 930.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 17:26:50 | ||
图片预览



文档简介
2025北京昌平初二(下)期中
数 学
本试卷共8页,三道大题,28个小题,满分100分.考试时间120分钟.考生务必将答案填涂或书写在答题卡上,在试卷上作答无效.考试结束后,请交回答题卡.
一、选择题(共16分,每题2分,第1-8题均有四个选项,符合题意的选项只有一个)
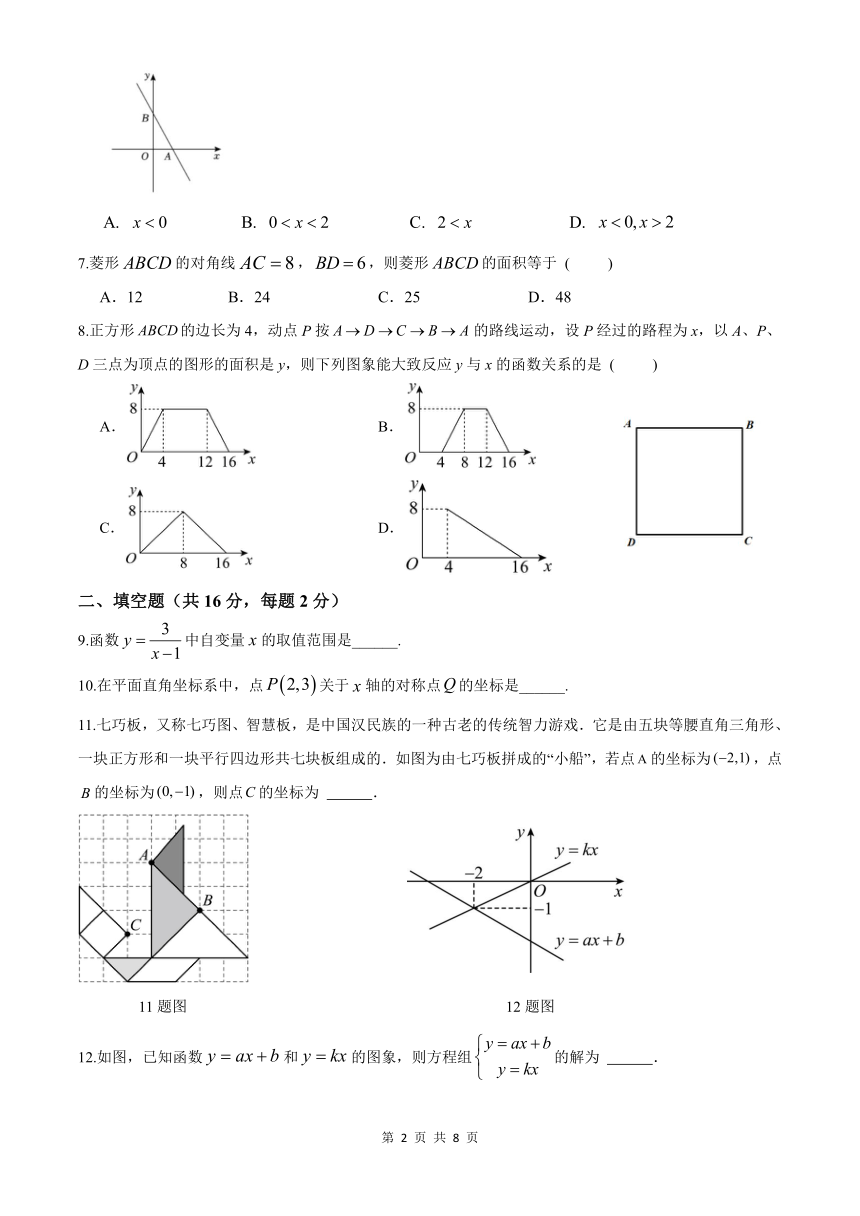
1.下列图形中, 既是轴对称图形又是中心对称图形的是 ( )
B. C.
点所在的象限是 ( )
第一象限 B. 第二象限 C. 第三象限 第四象限
3.下列图象中,表示y是x的函数的是 ( )
A. B. C. D.
4.若一个正多边形的内角和为°, 则这个正多边形共有 ( ) 条边.
5.依据所标数据, 下列一定为平行四边形的是 ( )
A. B.
C. D.
6.一次函数的图象与轴交于点,与轴交于点,根据图象可知的解集为 ( )
7.菱形的对角线,,则菱形的面积等于 ( )
A.12 B.24 C.25 D.48
8.正方形的边长为4,动点P按的路线运动,设P经过的路程为x,以A、P、D三点为顶点的图形的面积是y,则下列图象能大致反应y与x的函数关系的是 ( )
A. B.
C. D.
二、填空题(共16分,每题2分)
9.函数中自变量x的取值范围是______.
10.在平面直角坐标系中,点关于x轴的对称点的坐标是______.
11.七巧板,又称七巧图、智慧板,是中国汉民族的一种古老的传统智力游戏.它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图为由七巧板拼成的“小船”,若点的坐标为,点的坐标为,则点的坐标为 .
11题图 12题图
12.如图,已知函数和的图象,则方程组的解为 .
若点,在一次函数图象上,则______(填,或).
14.如图,平行四边形中,,平分交边于点,则等于______.
15.已知,如图,边长为8的正方形ABCD中,点E为边DC上一点,DE=2,点P在对角线AC上运动,连接DP,EP,则DP+EP的最小值为______.
16.长方形的边OA在x轴的正半轴上,A、C两点的坐标分别为,点B在第一象限,将直线沿y轴向上平移个单位,若平移后的直线将长方形的面积分成1:5的两部分,则m的值为 .
三、解答题(本题共12道小题,第17~22题,每小题5分,第23~26题,每小题6分,第27~28题,每小题7分,共68分)
17.如图, 点, 分别是平行四边形的边、上的一点, 连接, 若. 求证: 四边形是平行四边形.
18.在平面直角坐标系中,一次函数的图象分别交轴, 轴于,两点.
(1)求点, 的坐标;
(2)画出该函数的图象;
(3)若点, 连接, , 求的面积.
19.下面是小明设计的“作矩形”的尺规作图过程:
已知: 在中,.
求作: 矩形.
作法: 如图,
①分别以点, 为圆心, 大于的长为半径作弧, 两弧相交于, 两点;
②作直线交于点;
③作射线BP,在射线BP上截取PD=BP;
④连接, .
则四边形是矩形.
根据小明设计的尺规作图过程,解决以下问题:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明
证明: 连接, , , .
, ,
是线段的垂直平分线.
= .
,
四边形是平行四边形( )(填推理的依据).
四边形是矩形( )(填推理的依据).
20.在平面直角坐标系xOy中,直线与直线交于点.
(1)求点A的坐标及直线的表达式;
(2)若P是坐标轴上一点(不与点O重合),且满足,直接写出点P的坐标.
21.如图, 在正方形网格中, 的三个顶点都在格点上, 点, 的坐标分别为, , 结合所给的平面直角坐标系解答下列问题:
(1)点的坐标是 ;
(2)画出关于原点对称的, 点坐标是 ;
(3)求出的长.
22.李师傅将容量为60升的货车油箱加满后, 从工厂出发运送一批物资到某地, 行驶过程中, 货车离目的地的路程(千米)与行驶时间(小时)的关系如图所示, 当油箱中剩余油量为10升时, 货车会自动显示加油提醒,设货车平均耗油量为0.1升/千米, 请根据图象解答下列问题:
(1)工厂距目的地的路程为 ;
(2)求关于的函数表达式;
(3)运输过程中,当货车显示加油提醒时, t是多少?
23.在平面直角坐标系中,一次函数的图象由函数的图象平移得到,且经过点.
(1)求该一次函数的解析式;
(2)当时,对于的每一个值,函数的值大于一次函数的值,直接写出的取值范围.
24.数学课上,我们探究过三角形中位线性质定理:三角形的中位线平行于第三边,且等于第三边的一半.
以下,是对此定理的探究及证明过程:
已知,如图,在中,分别是的中点.
求证:且.
(1)【定理探究】某数学小组有甲、乙、丙、丁四位同学.他们在思考后说出了添加的辅助线:
甲:延长至点,使,连接.
乙:延长到点,使,连接.
丙:作,延长,使,延长,使.
丁:过点作,交于点,过点作的平行线交延长线于点.
则四位同学所作的辅助线能证明三角形中位线性质定理的是________;
A.甲、乙、丁 B.乙、丙 C.乙、丁 D.全正确
(2)【定理证明】请你按“乙同学”所作的辅助线将证明过程补充完整;
(3)【定理应用】
如图,两地被池塘隔开,不能直接测量它们之间的距离.小颖在地面上选了点和点,使,连接.并分别找到和的中点.若测得米,米,则两地间的距离________米(用含的代数式表示).
25.某学校要购买一种笔记本,供学生研学时使用. 在甲文具店不管一次购买多少本,每本价格为2元. 在乙文具店购买同样的笔记本,一次购买数量不超过20时,每本价格为2.4元;一次购买数量超过20时,超过的部分每本价格为1.8元.设在同一家文具店,一次购买这种笔记本的数量为(为非负数).
(1)设在甲文具店购买这种笔记本的付款金额为元,在乙文具店购买这种笔记本的付款金额为元,分别写出,关于的函数关系式;
(2)当时,在哪家文具店购买这种笔记本的花费少?请说明理由.
26.描点画图是探究未知函数图象变化规律的一个重要方法,下面是通过描点画图感知函数图象的变化规律的过程:
……
……
请根据学习函数的经验,利用上述表格所反映的与之间的变化规律,对该函数的图象与性质进行探究.
(1)表中是与的对应值,则 ;
(2)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,请你先描出点,然后画出该函数的图象;
(3)若关于的不等式的解集是,则的值为 .
27.如图,在正方形中,是边上的一点(不与,重合),点关于的对称点是点,连接AF,BF,直线,交于点,连接.
(1)在图1中补全图形;
(2)求的度数,写出求解过程;
(3)用等式表示线段之间的数量关系,并证明.
28.在平面直角坐标系中,对于点P与图形W给出如下定义:N为图形W上任意一点,P,N两点间距离的最小值称为点P与图形W的“近点距离”.特别的,当点P在图形W上时,点P与图形W的“近点距离”为零.如图1,点,.
(1)点与线段的“近点距离”是 ;点与线段的“近点距离”是 ;
(2)点P在直线上,如果点P与线段的“近点距离”为2,求点P的坐标;
(3)如图2,将线段向右平移3个单位,得到线段,连接,,若直线上存在点G,使得点G与四边形的“近点距离”小于或等于,直接写出b的取值范围.
数 学
本试卷共8页,三道大题,28个小题,满分100分.考试时间120分钟.考生务必将答案填涂或书写在答题卡上,在试卷上作答无效.考试结束后,请交回答题卡.
一、选择题(共16分,每题2分,第1-8题均有四个选项,符合题意的选项只有一个)
1.下列图形中, 既是轴对称图形又是中心对称图形的是 ( )
B. C.
点所在的象限是 ( )
第一象限 B. 第二象限 C. 第三象限 第四象限
3.下列图象中,表示y是x的函数的是 ( )
A. B. C. D.
4.若一个正多边形的内角和为°, 则这个正多边形共有 ( ) 条边.
5.依据所标数据, 下列一定为平行四边形的是 ( )
A. B.
C. D.
6.一次函数的图象与轴交于点,与轴交于点,根据图象可知的解集为 ( )
7.菱形的对角线,,则菱形的面积等于 ( )
A.12 B.24 C.25 D.48
8.正方形的边长为4,动点P按的路线运动,设P经过的路程为x,以A、P、D三点为顶点的图形的面积是y,则下列图象能大致反应y与x的函数关系的是 ( )
A. B.
C. D.
二、填空题(共16分,每题2分)
9.函数中自变量x的取值范围是______.
10.在平面直角坐标系中,点关于x轴的对称点的坐标是______.
11.七巧板,又称七巧图、智慧板,是中国汉民族的一种古老的传统智力游戏.它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图为由七巧板拼成的“小船”,若点的坐标为,点的坐标为,则点的坐标为 .
11题图 12题图
12.如图,已知函数和的图象,则方程组的解为 .
若点,在一次函数图象上,则______(填,或).
14.如图,平行四边形中,,平分交边于点,则等于______.
15.已知,如图,边长为8的正方形ABCD中,点E为边DC上一点,DE=2,点P在对角线AC上运动,连接DP,EP,则DP+EP的最小值为______.
16.长方形的边OA在x轴的正半轴上,A、C两点的坐标分别为,点B在第一象限,将直线沿y轴向上平移个单位,若平移后的直线将长方形的面积分成1:5的两部分,则m的值为 .
三、解答题(本题共12道小题,第17~22题,每小题5分,第23~26题,每小题6分,第27~28题,每小题7分,共68分)
17.如图, 点, 分别是平行四边形的边、上的一点, 连接, 若. 求证: 四边形是平行四边形.
18.在平面直角坐标系中,一次函数的图象分别交轴, 轴于,两点.
(1)求点, 的坐标;
(2)画出该函数的图象;
(3)若点, 连接, , 求的面积.
19.下面是小明设计的“作矩形”的尺规作图过程:
已知: 在中,.
求作: 矩形.
作法: 如图,
①分别以点, 为圆心, 大于的长为半径作弧, 两弧相交于, 两点;
②作直线交于点;
③作射线BP,在射线BP上截取PD=BP;
④连接, .
则四边形是矩形.
根据小明设计的尺规作图过程,解决以下问题:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明
证明: 连接, , , .
, ,
是线段的垂直平分线.
= .
,
四边形是平行四边形( )(填推理的依据).
四边形是矩形( )(填推理的依据).
20.在平面直角坐标系xOy中,直线与直线交于点.
(1)求点A的坐标及直线的表达式;
(2)若P是坐标轴上一点(不与点O重合),且满足,直接写出点P的坐标.
21.如图, 在正方形网格中, 的三个顶点都在格点上, 点, 的坐标分别为, , 结合所给的平面直角坐标系解答下列问题:
(1)点的坐标是 ;
(2)画出关于原点对称的, 点坐标是 ;
(3)求出的长.
22.李师傅将容量为60升的货车油箱加满后, 从工厂出发运送一批物资到某地, 行驶过程中, 货车离目的地的路程(千米)与行驶时间(小时)的关系如图所示, 当油箱中剩余油量为10升时, 货车会自动显示加油提醒,设货车平均耗油量为0.1升/千米, 请根据图象解答下列问题:
(1)工厂距目的地的路程为 ;
(2)求关于的函数表达式;
(3)运输过程中,当货车显示加油提醒时, t是多少?
23.在平面直角坐标系中,一次函数的图象由函数的图象平移得到,且经过点.
(1)求该一次函数的解析式;
(2)当时,对于的每一个值,函数的值大于一次函数的值,直接写出的取值范围.
24.数学课上,我们探究过三角形中位线性质定理:三角形的中位线平行于第三边,且等于第三边的一半.
以下,是对此定理的探究及证明过程:
已知,如图,在中,分别是的中点.
求证:且.
(1)【定理探究】某数学小组有甲、乙、丙、丁四位同学.他们在思考后说出了添加的辅助线:
甲:延长至点,使,连接.
乙:延长到点,使,连接.
丙:作,延长,使,延长,使.
丁:过点作,交于点,过点作的平行线交延长线于点.
则四位同学所作的辅助线能证明三角形中位线性质定理的是________;
A.甲、乙、丁 B.乙、丙 C.乙、丁 D.全正确
(2)【定理证明】请你按“乙同学”所作的辅助线将证明过程补充完整;
(3)【定理应用】
如图,两地被池塘隔开,不能直接测量它们之间的距离.小颖在地面上选了点和点,使,连接.并分别找到和的中点.若测得米,米,则两地间的距离________米(用含的代数式表示).
25.某学校要购买一种笔记本,供学生研学时使用. 在甲文具店不管一次购买多少本,每本价格为2元. 在乙文具店购买同样的笔记本,一次购买数量不超过20时,每本价格为2.4元;一次购买数量超过20时,超过的部分每本价格为1.8元.设在同一家文具店,一次购买这种笔记本的数量为(为非负数).
(1)设在甲文具店购买这种笔记本的付款金额为元,在乙文具店购买这种笔记本的付款金额为元,分别写出,关于的函数关系式;
(2)当时,在哪家文具店购买这种笔记本的花费少?请说明理由.
26.描点画图是探究未知函数图象变化规律的一个重要方法,下面是通过描点画图感知函数图象的变化规律的过程:
……
……
请根据学习函数的经验,利用上述表格所反映的与之间的变化规律,对该函数的图象与性质进行探究.
(1)表中是与的对应值,则 ;
(2)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,请你先描出点,然后画出该函数的图象;
(3)若关于的不等式的解集是,则的值为 .
27.如图,在正方形中,是边上的一点(不与,重合),点关于的对称点是点,连接AF,BF,直线,交于点,连接.
(1)在图1中补全图形;
(2)求的度数,写出求解过程;
(3)用等式表示线段之间的数量关系,并证明.
28.在平面直角坐标系中,对于点P与图形W给出如下定义:N为图形W上任意一点,P,N两点间距离的最小值称为点P与图形W的“近点距离”.特别的,当点P在图形W上时,点P与图形W的“近点距离”为零.如图1,点,.
(1)点与线段的“近点距离”是 ;点与线段的“近点距离”是 ;
(2)点P在直线上,如果点P与线段的“近点距离”为2,求点P的坐标;
(3)如图2,将线段向右平移3个单位,得到线段,连接,,若直线上存在点G,使得点G与四边形的“近点距离”小于或等于,直接写出b的取值范围.
同课章节目录
