第18章 平行四边形 单元试卷(含答案) 2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 第18章 平行四边形 单元试卷(含答案) 2024-2025学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 328.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 11:13:54 | ||
图片预览



文档简介
第18章平行四边形 单元试卷 2024-2025学年人教版数学八年级下册
一、单选题
1.已知菱形的对角线长分别为、,则菱形的面积为( )
A. B. C. D.
2.顺次连接一个四边形四边的中点得到的四边形是矩形,则原四边形一定是( )
A.矩形 B.平行四边形
C.对角线互相垂直的四边形 D.任意四边形
3.如图,已知四边形ABCD是矩形,对角线交于点P,则下列结论正确的是()
A.AC是的平分线 B.
C. D.
4.如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( )
A.11 B.16 C.19 D.22
5.如图,点是矩形的对角线的中点,交于点,若,,则的长为( )
A.5 B.4 C. D.
6.如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴上;,且,若A的坐标为,OC长为6,则点B的坐标是( )
A. B. C. D.
7.在中,点D是边上的点(与B,C两点不重合),过点D作,,分别交,于E,F两点,下列说法正确的是( )
A.若,则四边形是矩形
B.若垂直平分,则四边形是矩形
C.若,则四边形是菱形
D.若平分,则四边形是菱形
8.如图,在正方形中,,E,F分别为边的中点,连接,点G,H分别为的中点,连接,则的长为( )
A. B.1 C. D.2
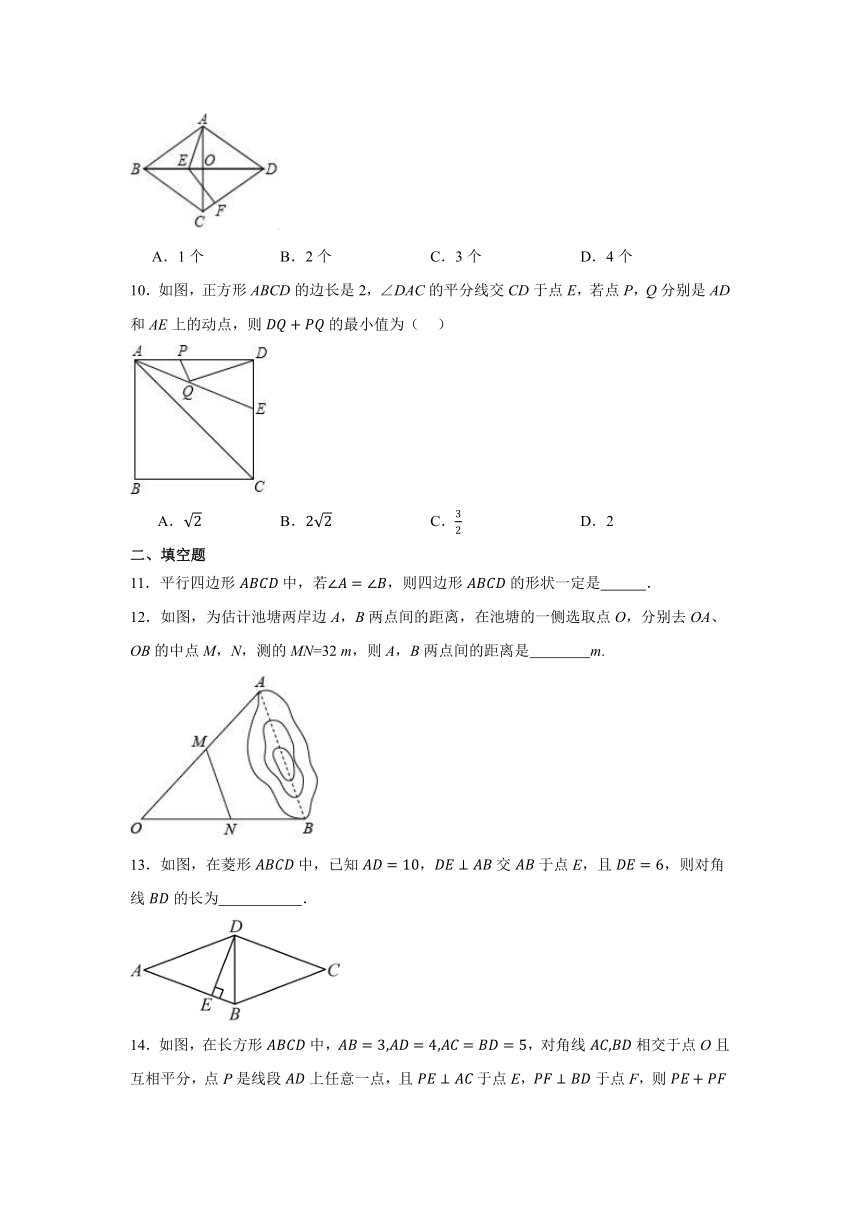
9.如图,菱形ABCD中,∠ABC=60°,AB=4,对角线AC、BD交于点O,E是线段BO上一动点,F是射线DC上一动点,若∠AEF=120°,则线段EF的长度的整数值的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形ABCD的边长是2,∠DAC的平分线交CD于点E,若点P,Q分别是AD和AE上的动点,则的最小值为( )
A. B. C. D.2
二、填空题
11.平行四边形中,若,则四边形的形状一定是 .
12.如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别去OA、OB的中点M,N,测的MN=32 m,则A,B两点间的距离是 m.
13.如图,在菱形中,已知,交于点E,且,则对角线的长为 .
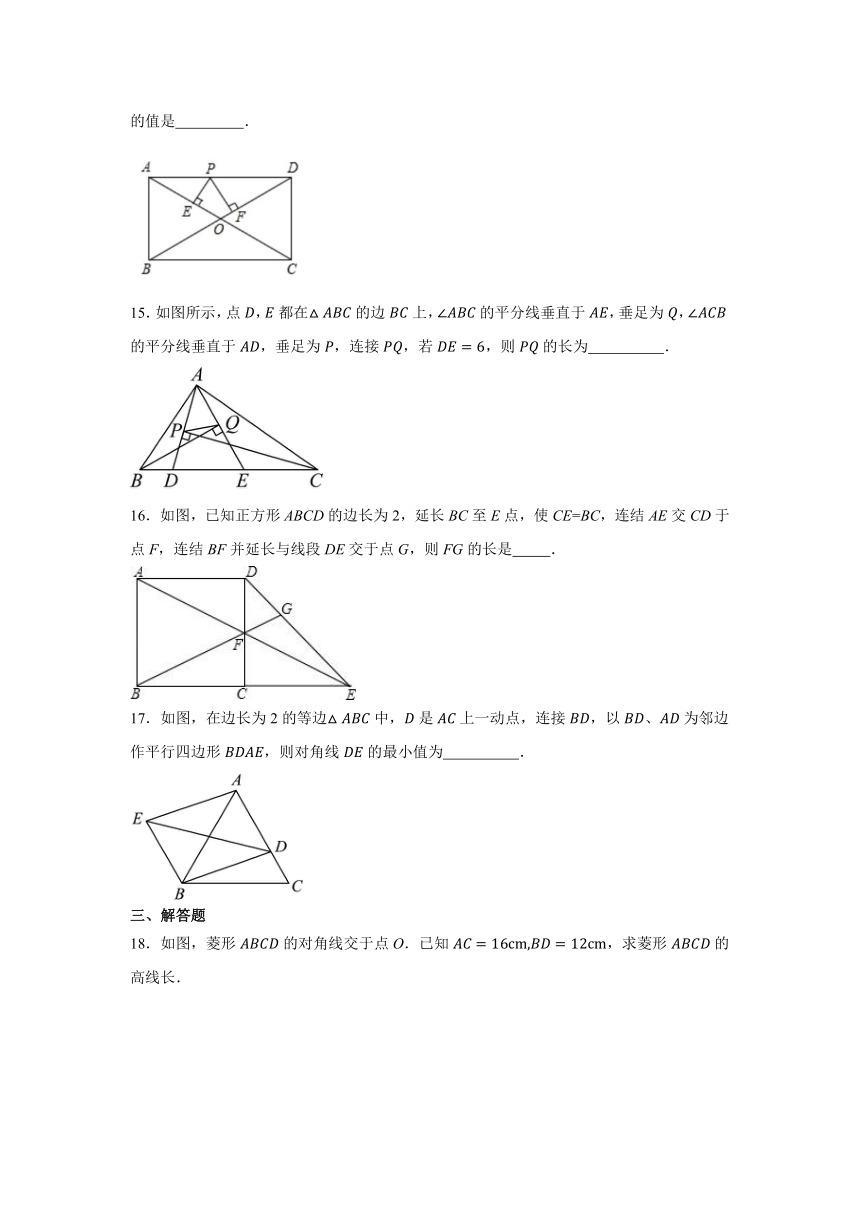
14.如图,在长方形中,,对角线相交于点O且互相平分,点P是线段上任意一点,且于点E,于点F,则的值是 .
15.如图所示,点,都在的边上,的平分线垂直于,垂足为,的平分线垂直于,垂足为,连接,若,则的长为 .
16.如图,已知正方形ABCD的边长为2,延长BC至E点,使CE=BC,连结AE交CD于点F,连结BF并延长与线段DE交于点G,则FG的长是 .
17.如图,在边长为2的等边中,是上一动点,连接,以、为邻边作平行四边形,则对角线的最小值为 .
三、解答题
18.如图,菱形的对角线交于点O.已知,求菱形的高线长.
19.如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
20.(1)如图,在中,点是的中点,点,分别在线段及其延长线上,且,给出下列条件:①;②;③.从中选择一个条件使四边形是菱形,你认为这个条件是______(只填写序号).
(2)已知在中,对角线,相交于点,请你添加一个适当的条件,使成为一个菱形.你添加的条件是______.
21.如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24 cm,△ECF的周长为8 cm,求四边形纸片ABCD的周长.
22.如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;
(2)如图2,当点P在线段OC上时(点P不与点O、C重合),(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.
参考答案
1.B
2.C
3.C
4.D
5.D
6.C
7.D
8.C
9.C
10.A
11.矩形
12.64
13.
14.
15.3
16..
17.
18.解:设菱形的高线长为,
∵菱形的对角线交于点O.已知,
∴,
∴菱形的边长,
菱形的面积为:,
∴,
∴
19.(1)∵DF∥BE,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∵O为AC的中点,
∴OA=OC,
∵AE=CF,
∴OA-AE=OC-CF,
即OE=OF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(AAS);
(2)若OD=AC,则四边形ABCD是矩形,理由为:
证明:∵△BOE≌△DOF,
∴OB=OD,
∵OD=AC,
∴OA=OB=OC=OD,且BD=AC,
∴四边形ABCD为矩形.
20.(1)证明:
为等腰三角形
点是的中点
ADBC,且
四边形是菱形.
(2)根据对角线互相垂直的平行四边形是菱形,可得,或一组邻边相等的平行四边形是菱形,可得.
21.解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
AD+DC+BC+AB=AD+DF+FC+CE+BE+AB=(AD+DF+AF)+(FC+CE+FE)=24+8=32(cm).
22.(1)解:PE=PD,PE⊥PD;
当点P在线段AO上时,
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP=45°,
在△ABP和△ADP中,
∴△ABP≌△ADP(SAS),
∴BP=DP,
∵PB=PE,
∴PE=PD,
过点P作PM⊥CD于点M,作PN⊥BC于点N,
∵四边形ABCD是正方形,
∴∠BCP=90°,∠BCP=∠DCP=45°,
∴四边形PNCM是矩形,
∵∠BCP=∠DCP=45°=∠CNP,
∴PN=CN,
∴四边形PNCM是正方形,
∴PN=PM,∠MPN=90°,
∵PE=PD,
∴Rt△PNE≌Rt△PMD(HL),
∴∠DPM=∠EPN,
∵∠MPN=90°,
∴∠DPE=90°,
故PE⊥PD,
PE与PD的数量关系和位置关系分别为:PE=PD,PE⊥PD;
(2)解:(1)中结论还成立,理由如下:
如图.
同理可证△ABP≌△ADP (SAS),
∴PB=PD,
又∵PB=PE,
∴PE=PD.
∵△ADP≌△ABP,
∴∠ADP=∠ABP,
∴∠CDP=∠CBP,
∵BP=PE,
∴∠CBP=∠PEC,
∴∠PEC=∠PDC,
∵∠1=∠2,
∴∠DPE=∠DCE=90°,
∴PE⊥PD.
(3)解:(1)中结论还成立,如图.
同理可证△ABP≌△ADP (SAS),
∴PB=PD,
又∵PB=PE,
∴PE=PD.
∵△ADP≌△ABP,
∴∠ADP=∠ABP,
∴∠CDP=∠CBP,
∵BP=PE,
∴∠CBP=∠PEC,
∴∠PEC=∠PDC,
∵∠1=∠2,
∴∠DPE=∠DCE=90°,
∴PE⊥PD.
一、单选题
1.已知菱形的对角线长分别为、,则菱形的面积为( )
A. B. C. D.
2.顺次连接一个四边形四边的中点得到的四边形是矩形,则原四边形一定是( )
A.矩形 B.平行四边形
C.对角线互相垂直的四边形 D.任意四边形
3.如图,已知四边形ABCD是矩形,对角线交于点P,则下列结论正确的是()
A.AC是的平分线 B.
C. D.
4.如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( )
A.11 B.16 C.19 D.22
5.如图,点是矩形的对角线的中点,交于点,若,,则的长为( )
A.5 B.4 C. D.
6.如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴上;,且,若A的坐标为,OC长为6,则点B的坐标是( )
A. B. C. D.
7.在中,点D是边上的点(与B,C两点不重合),过点D作,,分别交,于E,F两点,下列说法正确的是( )
A.若,则四边形是矩形
B.若垂直平分,则四边形是矩形
C.若,则四边形是菱形
D.若平分,则四边形是菱形
8.如图,在正方形中,,E,F分别为边的中点,连接,点G,H分别为的中点,连接,则的长为( )
A. B.1 C. D.2
9.如图,菱形ABCD中,∠ABC=60°,AB=4,对角线AC、BD交于点O,E是线段BO上一动点,F是射线DC上一动点,若∠AEF=120°,则线段EF的长度的整数值的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形ABCD的边长是2,∠DAC的平分线交CD于点E,若点P,Q分别是AD和AE上的动点,则的最小值为( )
A. B. C. D.2
二、填空题
11.平行四边形中,若,则四边形的形状一定是 .
12.如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别去OA、OB的中点M,N,测的MN=32 m,则A,B两点间的距离是 m.
13.如图,在菱形中,已知,交于点E,且,则对角线的长为 .
14.如图,在长方形中,,对角线相交于点O且互相平分,点P是线段上任意一点,且于点E,于点F,则的值是 .
15.如图所示,点,都在的边上,的平分线垂直于,垂足为,的平分线垂直于,垂足为,连接,若,则的长为 .
16.如图,已知正方形ABCD的边长为2,延长BC至E点,使CE=BC,连结AE交CD于点F,连结BF并延长与线段DE交于点G,则FG的长是 .
17.如图,在边长为2的等边中,是上一动点,连接,以、为邻边作平行四边形,则对角线的最小值为 .
三、解答题
18.如图,菱形的对角线交于点O.已知,求菱形的高线长.
19.如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
20.(1)如图,在中,点是的中点,点,分别在线段及其延长线上,且,给出下列条件:①;②;③.从中选择一个条件使四边形是菱形,你认为这个条件是______(只填写序号).
(2)已知在中,对角线,相交于点,请你添加一个适当的条件,使成为一个菱形.你添加的条件是______.
21.如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24 cm,△ECF的周长为8 cm,求四边形纸片ABCD的周长.
22.如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;
(2)如图2,当点P在线段OC上时(点P不与点O、C重合),(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.
参考答案
1.B
2.C
3.C
4.D
5.D
6.C
7.D
8.C
9.C
10.A
11.矩形
12.64
13.
14.
15.3
16..
17.
18.解:设菱形的高线长为,
∵菱形的对角线交于点O.已知,
∴,
∴菱形的边长,
菱形的面积为:,
∴,
∴
19.(1)∵DF∥BE,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∵O为AC的中点,
∴OA=OC,
∵AE=CF,
∴OA-AE=OC-CF,
即OE=OF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(AAS);
(2)若OD=AC,则四边形ABCD是矩形,理由为:
证明:∵△BOE≌△DOF,
∴OB=OD,
∵OD=AC,
∴OA=OB=OC=OD,且BD=AC,
∴四边形ABCD为矩形.
20.(1)证明:
为等腰三角形
点是的中点
ADBC,且
四边形是菱形.
(2)根据对角线互相垂直的平行四边形是菱形,可得,或一组邻边相等的平行四边形是菱形,可得.
21.解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
AD+DC+BC+AB=AD+DF+FC+CE+BE+AB=(AD+DF+AF)+(FC+CE+FE)=24+8=32(cm).
22.(1)解:PE=PD,PE⊥PD;
当点P在线段AO上时,
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP=45°,
在△ABP和△ADP中,
∴△ABP≌△ADP(SAS),
∴BP=DP,
∵PB=PE,
∴PE=PD,
过点P作PM⊥CD于点M,作PN⊥BC于点N,
∵四边形ABCD是正方形,
∴∠BCP=90°,∠BCP=∠DCP=45°,
∴四边形PNCM是矩形,
∵∠BCP=∠DCP=45°=∠CNP,
∴PN=CN,
∴四边形PNCM是正方形,
∴PN=PM,∠MPN=90°,
∵PE=PD,
∴Rt△PNE≌Rt△PMD(HL),
∴∠DPM=∠EPN,
∵∠MPN=90°,
∴∠DPE=90°,
故PE⊥PD,
PE与PD的数量关系和位置关系分别为:PE=PD,PE⊥PD;
(2)解:(1)中结论还成立,理由如下:
如图.
同理可证△ABP≌△ADP (SAS),
∴PB=PD,
又∵PB=PE,
∴PE=PD.
∵△ADP≌△ABP,
∴∠ADP=∠ABP,
∴∠CDP=∠CBP,
∵BP=PE,
∴∠CBP=∠PEC,
∴∠PEC=∠PDC,
∵∠1=∠2,
∴∠DPE=∠DCE=90°,
∴PE⊥PD.
(3)解:(1)中结论还成立,如图.
同理可证△ABP≌△ADP (SAS),
∴PB=PD,
又∵PB=PE,
∴PE=PD.
∵△ADP≌△ABP,
∴∠ADP=∠ABP,
∴∠CDP=∠CBP,
∵BP=PE,
∴∠CBP=∠PEC,
∴∠PEC=∠PDC,
∵∠1=∠2,
∴∠DPE=∠DCE=90°,
∴PE⊥PD.
