湖北省恩施市板桥中学2024-2025学年八年级下学期期中考试数学试题(图片版,含答案)
文档属性
| 名称 | 湖北省恩施市板桥中学2024-2025学年八年级下学期期中考试数学试题(图片版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 07:23:29 | ||
图片预览




文档简介
参考答案
一、选择题(共10小题,每题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A D A C B B A
二、填空题(共5小题,每题3分,共15分)
11.
12.x≤2024
13.1.5
14.
15.24
三、解答题(共9题,共75分,解答应写出文字说明,证明过程或演算步骤)
16.解:(1)原式=3—2+=;----------------------------------------------(4分)
(2)原式=3﹣4+=3﹣4+2=1.----------------------------------------------(8分)
17.解:∵三角形周长为,两边长为,
∴第三边长为-------------------------------------------------------(2分)
(cm),
答:第三边长为2cm.-------------------------------------------------------(6分)
证明:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°,--------------------------------------------(1分)
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,--------------------------------------------(2分)
在Rt△BFA和Rt△DEC中,
,
∴Rt△BFA≌Rt△DEC(HL),--------------------------------------------(4分)
∴∠FAB=∠ECD,
∴AB∥CD,-------------------------------------------(5分)
又∵AB=CD,
∴四边形ABCD是平行四边形.--------------------------------------------(7分)
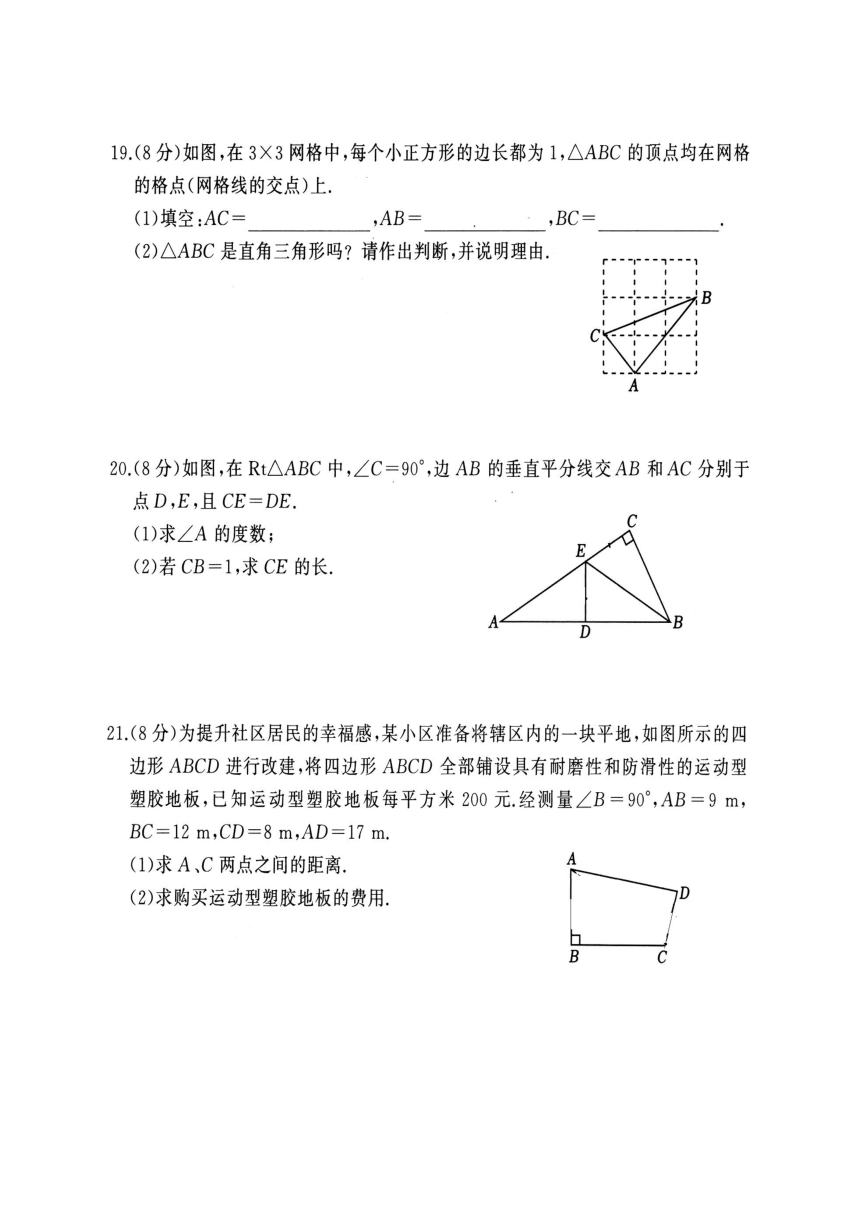
19.解:(1),2,-------------------------------------------------------(3分)
(2)△ABC是直角三角形,理由如下:
由(1)知,AC=,AB=2,BC=,
∵,
,------------------------------------------------(5分)
∴AC2+AB2=BC2, ∴△ABC是直角三角形.---------------------------------------------(8分)
20.解:(1)∵∠C=90°,DE⊥AB,CE=DE,
∴BE平分∠ABC,∴∠CBE=∠ABE,
∵DE的垂直平分AB,∴EA=EB,∴∠ABE=∠A.
∴∠CBE=∠ABE=∠A,∵∠C=90°,∴∠CBE+∠ABE+∠A=90°,
即3∠A=90°,∴∠A=30°;-------------------------------------------------(4分)
(2)∵∠CBE=∠ABE=∠A=30°,∠C=90°,∴BE=2CE,
在Rt△BCE中,根据勾股定理得CE2+BC2=BE2,
∵BC=1, ∴CE2+12=(2CE)2,解得CE=.--------------------------------------(8分)
21.解:(1)如图,连接AC,-------------------------------------(1分)
∵∠B=90°,AB=9m,BC=12m,
∴,
答:A、C两点之间的距离15m.-------------------------------------(4分)
(2)由(1)已得:AC=15m,
∵CD=8m,AD=17m,
∴CD2+AC2=82+152=289=172=AD2,
∴△ACD是直角三角形,且∠ACD=90°,-------------------------------------(5分)
∴四边形ABCD的面积为114(m2),------------------------------------(7分)
∵运动型塑胶地板每平方米200元,
∴购买运动型塑胶地板的费用为114×200=22800(元),
答:购买运动型塑胶地板的费用为22800元.-------------------------------------(8分)
22.解:(1)由题意,得BQ=t,DP=t,
∵四边形ABCD是矩形, ∴CD=AB=4,AD=BC=8, ∴AP=8﹣t,
当四边形ABQP是矩形时,BQ=AP,
∴t=8-t, 解得t=4,∴当t=4 s时,四边形ABQP是矩形;---------------------------------(5分)
(2)四边形AQCP是菱形,-------------------------------------------------------(6分)
理由:∵AB=4,BQ=PD=t=3,∠B=90°, ∴AQ5,
此时,CQ=CB-BQ=5,AP=AD-PD=5,
∵四边形ABCD是矩形, ∴AD∥BC,
∵CQ=AP, ∴四边形AQCP为平行四边形,
∵AQ=CQ=5, ∴四边形AQCP为菱形.--------------------------------------(10分)
23.解:(1)5 -------------------------------------------------------(1分)
证明如下:
.-------------------------------------------------------(4分)
,-------------------------------------------------------(5分)
证明如下,
.-------------------------------------------------------(8分)
(3)71-------------------------------------------------------(10分)
24.解:(1)证明:由题意得,AC=6 m,BC=8 m,AB=10 m,
∵62+82=102,∴AC2+BC2=AB2,----------------------------------------------(2分)
∴△ABC是直角三角形,且∠ACB=90°,∴AC⊥BC;-----------------------------------------(4分)
(2)解:从节约水管的角度考虑,应选择八(1)班铺设方案,理由如下:
∵CD⊥AB, ∴,
∴,---------------------------------------------------(6分)
∴(m),----------------------------------------------(7分)
∵AC+BC=6+8=14,-------------------------------------------------------(8分)
又∵ ,
∴八(1)班方案中水管的长度小于八(2)班方案中水管的长度,
∴从节约水管的角度考虑,应选择八(1)班铺设方案.----------------------------------------(10分)
一、选择题(共10小题,每题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A D A C B B A
二、填空题(共5小题,每题3分,共15分)
11.
12.x≤2024
13.1.5
14.
15.24
三、解答题(共9题,共75分,解答应写出文字说明,证明过程或演算步骤)
16.解:(1)原式=3—2+=;----------------------------------------------(4分)
(2)原式=3﹣4+=3﹣4+2=1.----------------------------------------------(8分)
17.解:∵三角形周长为,两边长为,
∴第三边长为-------------------------------------------------------(2分)
(cm),
答:第三边长为2cm.-------------------------------------------------------(6分)
证明:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°,--------------------------------------------(1分)
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,--------------------------------------------(2分)
在Rt△BFA和Rt△DEC中,
,
∴Rt△BFA≌Rt△DEC(HL),--------------------------------------------(4分)
∴∠FAB=∠ECD,
∴AB∥CD,-------------------------------------------(5分)
又∵AB=CD,
∴四边形ABCD是平行四边形.--------------------------------------------(7分)
19.解:(1),2,-------------------------------------------------------(3分)
(2)△ABC是直角三角形,理由如下:
由(1)知,AC=,AB=2,BC=,
∵,
,------------------------------------------------(5分)
∴AC2+AB2=BC2, ∴△ABC是直角三角形.---------------------------------------------(8分)
20.解:(1)∵∠C=90°,DE⊥AB,CE=DE,
∴BE平分∠ABC,∴∠CBE=∠ABE,
∵DE的垂直平分AB,∴EA=EB,∴∠ABE=∠A.
∴∠CBE=∠ABE=∠A,∵∠C=90°,∴∠CBE+∠ABE+∠A=90°,
即3∠A=90°,∴∠A=30°;-------------------------------------------------(4分)
(2)∵∠CBE=∠ABE=∠A=30°,∠C=90°,∴BE=2CE,
在Rt△BCE中,根据勾股定理得CE2+BC2=BE2,
∵BC=1, ∴CE2+12=(2CE)2,解得CE=.--------------------------------------(8分)
21.解:(1)如图,连接AC,-------------------------------------(1分)
∵∠B=90°,AB=9m,BC=12m,
∴,
答:A、C两点之间的距离15m.-------------------------------------(4分)
(2)由(1)已得:AC=15m,
∵CD=8m,AD=17m,
∴CD2+AC2=82+152=289=172=AD2,
∴△ACD是直角三角形,且∠ACD=90°,-------------------------------------(5分)
∴四边形ABCD的面积为114(m2),------------------------------------(7分)
∵运动型塑胶地板每平方米200元,
∴购买运动型塑胶地板的费用为114×200=22800(元),
答:购买运动型塑胶地板的费用为22800元.-------------------------------------(8分)
22.解:(1)由题意,得BQ=t,DP=t,
∵四边形ABCD是矩形, ∴CD=AB=4,AD=BC=8, ∴AP=8﹣t,
当四边形ABQP是矩形时,BQ=AP,
∴t=8-t, 解得t=4,∴当t=4 s时,四边形ABQP是矩形;---------------------------------(5分)
(2)四边形AQCP是菱形,-------------------------------------------------------(6分)
理由:∵AB=4,BQ=PD=t=3,∠B=90°, ∴AQ5,
此时,CQ=CB-BQ=5,AP=AD-PD=5,
∵四边形ABCD是矩形, ∴AD∥BC,
∵CQ=AP, ∴四边形AQCP为平行四边形,
∵AQ=CQ=5, ∴四边形AQCP为菱形.--------------------------------------(10分)
23.解:(1)5 -------------------------------------------------------(1分)
证明如下:
.-------------------------------------------------------(4分)
,-------------------------------------------------------(5分)
证明如下,
.-------------------------------------------------------(8分)
(3)71-------------------------------------------------------(10分)
24.解:(1)证明:由题意得,AC=6 m,BC=8 m,AB=10 m,
∵62+82=102,∴AC2+BC2=AB2,----------------------------------------------(2分)
∴△ABC是直角三角形,且∠ACB=90°,∴AC⊥BC;-----------------------------------------(4分)
(2)解:从节约水管的角度考虑,应选择八(1)班铺设方案,理由如下:
∵CD⊥AB, ∴,
∴,---------------------------------------------------(6分)
∴(m),----------------------------------------------(7分)
∵AC+BC=6+8=14,-------------------------------------------------------(8分)
又∵ ,
∴八(1)班方案中水管的长度小于八(2)班方案中水管的长度,
∴从节约水管的角度考虑,应选择八(1)班铺设方案.----------------------------------------(10分)
同课章节目录
