苏科版2024—2025学年七年级下册数学期中考试模拟试卷(一)(含答案)
文档属性
| 名称 | 苏科版2024—2025学年七年级下册数学期中考试模拟试卷(一)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 298.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
苏科版2024—2025学年七年级下册数学期中考试模拟试卷(一)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.下列选项是二元一次方程的是( )
A.x﹣3y B.xy+y=﹣1 C.x+y=z﹣2 D.1
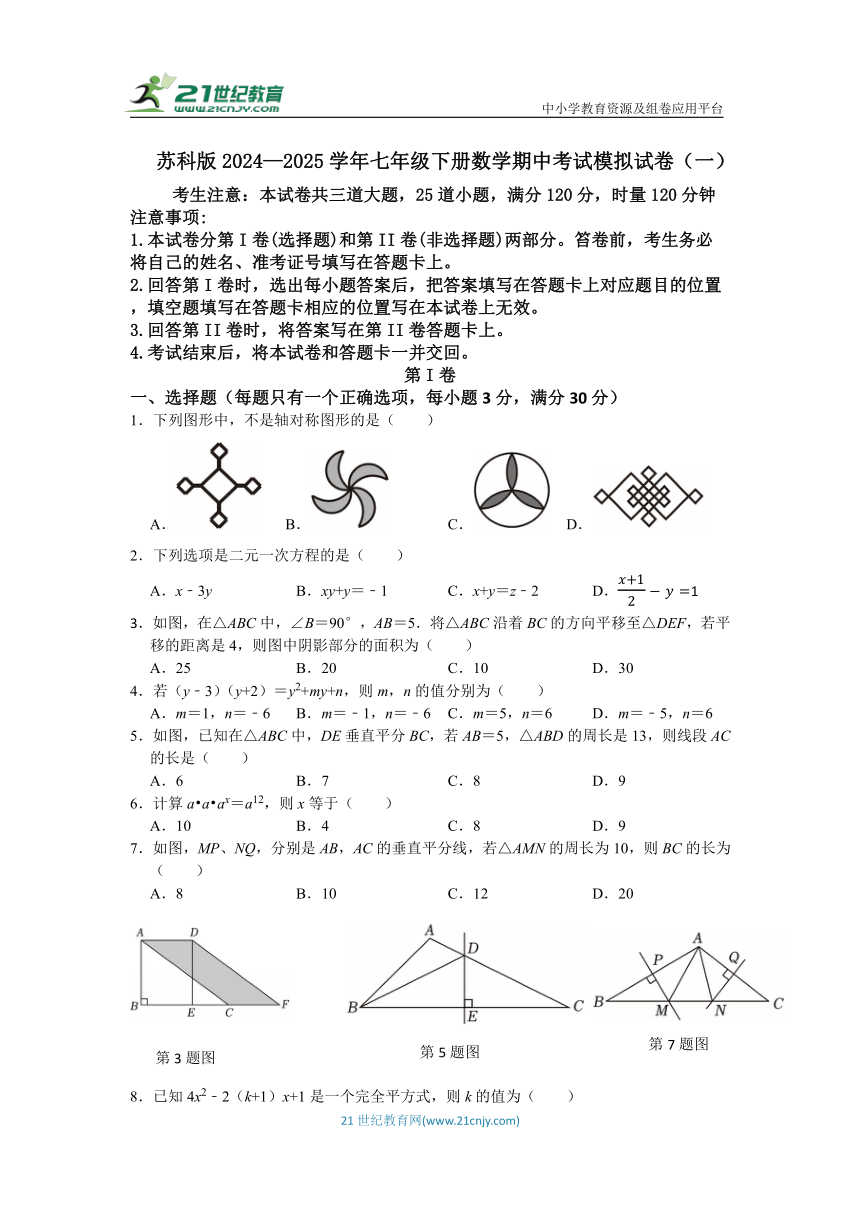
3.如图,在△ABC中,∠B=90°,AB=5.将△ABC沿着BC的方向平移至△DEF,若平移的距离是4,则图中阴影部分的面积为( )
A.25 B.20 C.10 D.30
4.若(y﹣3)(y+2)=y2+my+n,则m,n的值分别为( )
A.m=1,n=﹣6 B.m=﹣1,n=﹣6 C.m=5,n=6 D.m=﹣5,n=6
5.如图,已知在△ABC中,DE垂直平分BC,若AB=5,△ABD的周长是13,则线段AC的长是( )
A.6 B.7 C.8 D.9
6.计算a a ax=a12,则x等于( )
A.10 B.4 C.8 D.9
7.如图,MP、NQ,分别是AB,AC的垂直平分线,若△AMN的周长为10,则BC的长为( )
A.8 B.10 C.12 D.20
8.已知4x2﹣2(k+1)x+1是一个完全平方式,则k的值为( )
A.2 B.±2 C.1 D.1或﹣3
9.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
10.已知(x﹣2024)2+(x﹣2026)2=38,则(x﹣2025)2的值是( )
A.4 B.18 C.12 D.16
二、填空题(6小题,每题3分,共18分)
11.目前世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为 .
12.已知a2+ab+b2=6,a2﹣ab+b2=10,则a+b= .
13.若x+3y﹣3=0,则3x 27y= .
14.若关于x,y的二元一次方程组的解也是方程3x﹣2y=8的解,则k的值为 .
15.甲、乙两人共同解方程组由于甲看错了方程①中的a,得到方程组的解为,乙看错了方程②中的b,得到方程组的解为,则10a+b的值 .
16.若方程组的解是,则方程组的解是 .
第II卷
苏科版2024—2025学年七年级下册数学期中考试模拟试卷(一)
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:(a﹣b)2﹣2a(a﹣3b)+(a﹣b)(b﹣a),其中a=﹣1,b=1.
18.解方程组:
(1); (2).
19.在一次测试中,甲、乙两同学计算同一道整式乘法:(2x+a)(3x+b),甲由于抄错了第一个多项式中a的符号,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)试求出式子中a,b的值;
(2)请你计算出这道整式乘法的正确结果.
20.已知(3x﹣m)(x2+x+1)的展开式中不含x的二次项,a2+5b2+4(ab+b+1)=0,求:
(1)m的值;
(2)(a﹣b)m的值.
21.如图,已知在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC,若△ADE的周长为8cm,△OBC的周长为18cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
22.某校七年级400名学生到郊外参加植树活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金150元,大客车每辆租金250元,请选出最省钱的租车方案,并求出最少租金.
23.已知关于x,y的二元一次方程组,甲由于看错了方程组中的a,得到的方程组的解为,乙由于看错了b,得到方程组的解为.
(1)求a,b的值;
(2)若方程组的解与方程组的解相同,求2m﹣n的值.
24.阅读理解:
若x满足(60﹣x)(x﹣40)=20,求(60﹣x)2+(x﹣40)2的值.
解:设60﹣x=a,x﹣40=b,
则ab=20,a+b=60﹣x+x﹣40=20.
∴(60﹣x)2+(x﹣40)2
=a2+b2
=(a+b)2﹣2ab
=202﹣2×20=360;
类比探究:
(1)若x满足(70﹣x)(x﹣20)=﹣30,求(70﹣x)2+(x﹣20)2的值.
(2)若x满足(3﹣4x)(2x﹣5),求(3﹣4x)2+4(2x﹣5)2的值.
友情提示(2)中的4(2x﹣5)2可通过逆用积的乘方公式变成[2(2x﹣5)]2.
(3)若x满足(2023﹣x)2+(2020﹣x)2=2061,求(2023﹣x)(2020﹣x)的值.
解决问题:
(4)如图,正方形AEGO和长方形KLMC重叠,重叠部分是长方形BEFC其面积是300,分别延长FC、BC交AO和OG于D、H两点,构成的四边形ABCD和CFGH都是正方形,四边形ODCH是长方形.设CM=x,KC=3CM=3x,KB=54,FM=20,延长AO至P,使OP=2OD,延长AE至R,使RE=2BE,过点P、R作AP、AR垂线,两垂线交于点N,求正方形ARNP的面积.(结果是一个具体的数值)
25.我们定义:如果两个多项式M与N的和为常数,则称M与N互为“对消多项式”,这个常数称为它们的“对消值”.如MF=2x2﹣x+6与N=﹣2x2+x﹣1互为“对消多项式”,它们的“对消值”为5.
(1)下列各组多项式互为“对消多项式”的是 (填序号):
①3x2+2x与3x2+2;
②x﹣6与﹣x+2;
③﹣5x2y3+2xy与5x2y3﹣2xy﹣1.
(2)多项式A=(x﹣a)2与多项式B=﹣bx2﹣2x+b(a,b为常数)互为“对消多项式”,求它们的“对消值”;
(3)关于x的多项式C=mx2+6x+4与D=﹣m(x+1)(x+n)互为“对消多项式”,“对消值”为t.若a﹣b=m,b﹣c=mn,求代数式a2+b2+c2﹣ab﹣bc﹣ac+2t的最小值.
参考答案
一、选择题
1—10:BDBBC ABDBB
二、填空题
11.【解答】解:0.000000076=7.6×10﹣8.
故答案为:7.6×10﹣8.
12.【解答】解:两式相减,得2ab=﹣4,
解得ab=﹣2,
∴(a+b)2=a2+2ab+b2=6+ab=6﹣2=4,
∴a+b=2或﹣2.
故答案为:2或﹣2.
13.【解答】解:∵x+3y﹣3=0,
∴x+3y=3,
∴3x 27y=3x+3y=33=27,
故答案为:27.
14.【解答】解:,
①+②,得3x=6k,
∴x=2k.
把x=2k代入②,得2k+y=k,
∴y=﹣k.
又∵3x﹣2y=8,
∴6k+2k=8.
∴k=1.
故答案为:1.
15.【解答】解:根据方程的解的概念得出是方程②的解,
将代入4x﹣by=﹣2,
可得:﹣12+b=﹣2,
解得:b=10,
将代入ax+5y=15,
可得:5a+20=15,
解得:a=﹣1,
当a=﹣1,b=10时,10a+b=﹣10+10=0.
故答案为:0.
16.【解答】解:∵,
∴,
∵方程组的解是,
∴,
∴,
∴方程组的解是.
故答案为:.
三、解答题
17.【解答】解:(a﹣b)2﹣2a(a﹣3b)+(a﹣b)(b﹣a)
=a2﹣2ab+b2﹣2a2+6ab﹣a2+2ab﹣b2
=﹣2a2+6ab,
∵a=﹣1,b=1,
∴原式=﹣2a2+6ab=﹣2×(﹣1)2+6×(﹣1)×1=﹣8.
18.【解答】解:(1),
①+②得:5x=10,
解得:x=2,
将x=2代入①得:3×2+y=9,
解得:y=3,
∴方程组的解为:;
(2),
将②代入①得:3(3﹣2y)﹣4y=4,
解得:,
将代入②得:,
解得:x=2,
∴方程组的解为:.
19.【解答】解:(1)∵(3x﹣m)(x2+x+1)
=3x3+(3﹣m)x2+(3﹣m)x﹣m
由题意得3﹣m=0,
解得m=3,
即m的值为3;
(2)∵a2+5b2+4(ab+b+1)
=(a2+4ab+4b2)+(b2+4b+4)
=(a+2b)2+(b+2)2
=0
∴a+2b=0,b+2=0,
解得a=4,b=﹣2,
∴(a﹣b)m
=[4﹣(﹣2)]3
=63
=216.
20.【解答】解:(1)由题意得(2x﹣a)(3x+b)
=6x2+(2b﹣3a)x﹣ab
=6x2+11x﹣10,
(2x+a)(x+b)
=2x2+(a+2b)x+ab
=2x2﹣9x+10,
所以2b﹣3a=11,①
a+2b=﹣9.②
由②得2b=﹣9﹣a,代入①得﹣9﹣a﹣3a=11,
所以a=﹣5.
所以2b=﹣4.
所以b=﹣2.
(2)当a=﹣5,b=﹣2时,由(1)得(2x+a)(3x+b)=(2x﹣5)(3x﹣2)=6x2﹣19x+10.
21.【解答】解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=8(cm);
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=18cm,
∴OA=OB=OC=5(cm);
(3)∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=60°.
22.【解答】解:(1)设每辆小客车能坐x人,每辆大客车能坐y人,
据题意:,
解得:,
答:每辆小客车能坐20人,每辆大客车能坐45人;
(2)①由题意得:20m+45n=400,
∴n,
∵m、n为非负整数,
∴或 或,
∴租车方案有三种:
方案一:小客车20车、大客车0辆,
方案二:小客车11辆,大客车4辆,
方案三:小客车2辆,大客车8辆;
②方案一租金:150×20=3000(元),
方案二租金:150×11+250×4=2650(元),
方案三租金:150×2+250×8=2300(元),
∴方案三租金最少,最少租金为2300元.
23.【解答】解:(1)由于甲看错了关于x,y的二元一次方程组中的a,得到的方程组的解为,
∴满足方程5x+by=42,即5×12﹣3b=42,
解得b=6,
由于乙看错了关于x,y的二元一次方程组中的吧,得到的方程组的解为,
∴满足方程ax﹣4y=10,即2a﹣4×(﹣1)=10,
解得a=3,
答:a=3;b=6;
(2)当a=3,b=6时,原方程可变为,
解得,
把代入方程组得,,
解得,
∴2m﹣n=2+3=5.
24.【解答】解:(1)设70﹣x=a,x﹣20=b,
则ab=﹣30,a+b=70﹣x+x﹣20=50,
∴(70﹣x)2+(x﹣20)2
=a2+b2
=(a+b)2﹣2ab
=502﹣2×(﹣30)
=2500+60
=2560,
∴(70﹣x)2+(x﹣20)2的值为2560;
(2)∵(3﹣4x)(2x﹣5),
∴(3﹣4x)[2(2x﹣5)]=9,
∴(3﹣4x)(4x﹣10)=9,
设3﹣4x=m,4x﹣10=n,
则m+n=3﹣4x+4x﹣10=﹣7,mn=9,
∴(3﹣4x)2+4(2x﹣5)2
=(3﹣4x)2+[2(2x﹣5)]2
=(3﹣4x)2+(4x﹣10)2
=m2+n2
=(m+n)2﹣2mn
=(﹣7)2﹣2×9
=49﹣18
=31,
∴(3﹣4x)2+4(2x﹣5)2的值为31;
(3)设2023﹣x=p,2020﹣x=q,
则p﹣q=2023﹣x﹣(2020﹣x)=3,p2+q2=2061,
∴2pq=p2+q2﹣(p﹣q)2
=2061﹣32
=2061﹣9
=2052,
∴(2023﹣x)(2020﹣x)=pq=1026,
∴(2023﹣x)(2020﹣x)的值为1026;
(4)∵CM=x,KC=3CM=3x,KB=54,FM=20,
∴BC=KC﹣KB=3x﹣54,CF=CM﹣FM=x﹣20,
∵长方形BEFC的面积是300,
∴BC CF=(3x﹣54)(x﹣20)=300,
由题意得:AB=BC=3x﹣54,CF=BE=x﹣20,
∵ER=2BE,
∴BR=3BE=3(x﹣20),
∴AR=AB+BR=(3x﹣54)+3(x﹣20)=(3x﹣54)+(3x﹣60),
∵(3x﹣54)(x﹣20)=300,
∴(3x﹣54)[3(x﹣20)]=900,
∴(3x﹣54)(3x﹣60)=900,
设3x﹣54=a,3x﹣60=b,
则a﹣b=3x﹣54﹣(3x﹣60)=6,ab=900,
∴正方形ARNP的面积=AR2
=[(3x﹣54)+(3x﹣60)]2
=(a+b)2
=(a﹣b)2+4ab
=62+4×900
=36+3600
=3636,
∴正方形ARNP的面积为3636.
25.【解答】解:(1)∵3x2+2x+3x2+2=6x2+2x+2,
x﹣6﹣x+2=﹣4,
﹣5x2y3+2xy+5x2y3﹣2xy﹣1=﹣1,
∴①组多项式不是互为“对消多项式”,
②③组多项式是互为“对消多项式”,
故答案为:②③;
(2)∵A=(x﹣a)2=x2﹣2ax+a2,B=﹣bx2﹣2x+b,
∴A+B
=x2﹣2ax+a2﹣bx2﹣2x+b
=(1﹣b)x2+(﹣2a﹣2)x+(a2+b),
∵A与B互为“对消多项式”,
∴1﹣b=0,﹣2a﹣2=0,
解得a=﹣1,b=1.
∴a2+b
=(﹣1)2+1
=1+1
=2,
∴它们的“对消值”是2;
(3)∵C=mx2+6x+4,D=﹣m(x+1)(x+n)=﹣mx2+(﹣mn﹣m)x﹣mn,
∴C+D=(6﹣mn﹣m)x+(4﹣mn),
∵C与D互为“对消多项式”且“对消值”为t,
∵a﹣b=m,b﹣c=mn,
∴a﹣c=(a﹣b)+(b﹣c)=m+mn=6,
∴a2+b2+c2﹣ab﹣bc﹣ac+2t
=m2﹣4m+32
=(m﹣2)2+28≥28,
∴代数式 a2+b2+c2=ab=bc=ac+2 的最小值是28.
21世纪教育网(www.21cnjy.com)
苏科版2024—2025学年七年级下册数学期中考试模拟试卷(一)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.下列选项是二元一次方程的是( )
A.x﹣3y B.xy+y=﹣1 C.x+y=z﹣2 D.1
3.如图,在△ABC中,∠B=90°,AB=5.将△ABC沿着BC的方向平移至△DEF,若平移的距离是4,则图中阴影部分的面积为( )
A.25 B.20 C.10 D.30
4.若(y﹣3)(y+2)=y2+my+n,则m,n的值分别为( )
A.m=1,n=﹣6 B.m=﹣1,n=﹣6 C.m=5,n=6 D.m=﹣5,n=6
5.如图,已知在△ABC中,DE垂直平分BC,若AB=5,△ABD的周长是13,则线段AC的长是( )
A.6 B.7 C.8 D.9
6.计算a a ax=a12,则x等于( )
A.10 B.4 C.8 D.9
7.如图,MP、NQ,分别是AB,AC的垂直平分线,若△AMN的周长为10,则BC的长为( )
A.8 B.10 C.12 D.20
8.已知4x2﹣2(k+1)x+1是一个完全平方式,则k的值为( )
A.2 B.±2 C.1 D.1或﹣3
9.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
10.已知(x﹣2024)2+(x﹣2026)2=38,则(x﹣2025)2的值是( )
A.4 B.18 C.12 D.16
二、填空题(6小题,每题3分,共18分)
11.目前世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为 .
12.已知a2+ab+b2=6,a2﹣ab+b2=10,则a+b= .
13.若x+3y﹣3=0,则3x 27y= .
14.若关于x,y的二元一次方程组的解也是方程3x﹣2y=8的解,则k的值为 .
15.甲、乙两人共同解方程组由于甲看错了方程①中的a,得到方程组的解为,乙看错了方程②中的b,得到方程组的解为,则10a+b的值 .
16.若方程组的解是,则方程组的解是 .
第II卷
苏科版2024—2025学年七年级下册数学期中考试模拟试卷(一)
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:(a﹣b)2﹣2a(a﹣3b)+(a﹣b)(b﹣a),其中a=﹣1,b=1.
18.解方程组:
(1); (2).
19.在一次测试中,甲、乙两同学计算同一道整式乘法:(2x+a)(3x+b),甲由于抄错了第一个多项式中a的符号,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)试求出式子中a,b的值;
(2)请你计算出这道整式乘法的正确结果.
20.已知(3x﹣m)(x2+x+1)的展开式中不含x的二次项,a2+5b2+4(ab+b+1)=0,求:
(1)m的值;
(2)(a﹣b)m的值.
21.如图,已知在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC,若△ADE的周长为8cm,△OBC的周长为18cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
22.某校七年级400名学生到郊外参加植树活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金150元,大客车每辆租金250元,请选出最省钱的租车方案,并求出最少租金.
23.已知关于x,y的二元一次方程组,甲由于看错了方程组中的a,得到的方程组的解为,乙由于看错了b,得到方程组的解为.
(1)求a,b的值;
(2)若方程组的解与方程组的解相同,求2m﹣n的值.
24.阅读理解:
若x满足(60﹣x)(x﹣40)=20,求(60﹣x)2+(x﹣40)2的值.
解:设60﹣x=a,x﹣40=b,
则ab=20,a+b=60﹣x+x﹣40=20.
∴(60﹣x)2+(x﹣40)2
=a2+b2
=(a+b)2﹣2ab
=202﹣2×20=360;
类比探究:
(1)若x满足(70﹣x)(x﹣20)=﹣30,求(70﹣x)2+(x﹣20)2的值.
(2)若x满足(3﹣4x)(2x﹣5),求(3﹣4x)2+4(2x﹣5)2的值.
友情提示(2)中的4(2x﹣5)2可通过逆用积的乘方公式变成[2(2x﹣5)]2.
(3)若x满足(2023﹣x)2+(2020﹣x)2=2061,求(2023﹣x)(2020﹣x)的值.
解决问题:
(4)如图,正方形AEGO和长方形KLMC重叠,重叠部分是长方形BEFC其面积是300,分别延长FC、BC交AO和OG于D、H两点,构成的四边形ABCD和CFGH都是正方形,四边形ODCH是长方形.设CM=x,KC=3CM=3x,KB=54,FM=20,延长AO至P,使OP=2OD,延长AE至R,使RE=2BE,过点P、R作AP、AR垂线,两垂线交于点N,求正方形ARNP的面积.(结果是一个具体的数值)
25.我们定义:如果两个多项式M与N的和为常数,则称M与N互为“对消多项式”,这个常数称为它们的“对消值”.如MF=2x2﹣x+6与N=﹣2x2+x﹣1互为“对消多项式”,它们的“对消值”为5.
(1)下列各组多项式互为“对消多项式”的是 (填序号):
①3x2+2x与3x2+2;
②x﹣6与﹣x+2;
③﹣5x2y3+2xy与5x2y3﹣2xy﹣1.
(2)多项式A=(x﹣a)2与多项式B=﹣bx2﹣2x+b(a,b为常数)互为“对消多项式”,求它们的“对消值”;
(3)关于x的多项式C=mx2+6x+4与D=﹣m(x+1)(x+n)互为“对消多项式”,“对消值”为t.若a﹣b=m,b﹣c=mn,求代数式a2+b2+c2﹣ab﹣bc﹣ac+2t的最小值.
参考答案
一、选择题
1—10:BDBBC ABDBB
二、填空题
11.【解答】解:0.000000076=7.6×10﹣8.
故答案为:7.6×10﹣8.
12.【解答】解:两式相减,得2ab=﹣4,
解得ab=﹣2,
∴(a+b)2=a2+2ab+b2=6+ab=6﹣2=4,
∴a+b=2或﹣2.
故答案为:2或﹣2.
13.【解答】解:∵x+3y﹣3=0,
∴x+3y=3,
∴3x 27y=3x+3y=33=27,
故答案为:27.
14.【解答】解:,
①+②,得3x=6k,
∴x=2k.
把x=2k代入②,得2k+y=k,
∴y=﹣k.
又∵3x﹣2y=8,
∴6k+2k=8.
∴k=1.
故答案为:1.
15.【解答】解:根据方程的解的概念得出是方程②的解,
将代入4x﹣by=﹣2,
可得:﹣12+b=﹣2,
解得:b=10,
将代入ax+5y=15,
可得:5a+20=15,
解得:a=﹣1,
当a=﹣1,b=10时,10a+b=﹣10+10=0.
故答案为:0.
16.【解答】解:∵,
∴,
∵方程组的解是,
∴,
∴,
∴方程组的解是.
故答案为:.
三、解答题
17.【解答】解:(a﹣b)2﹣2a(a﹣3b)+(a﹣b)(b﹣a)
=a2﹣2ab+b2﹣2a2+6ab﹣a2+2ab﹣b2
=﹣2a2+6ab,
∵a=﹣1,b=1,
∴原式=﹣2a2+6ab=﹣2×(﹣1)2+6×(﹣1)×1=﹣8.
18.【解答】解:(1),
①+②得:5x=10,
解得:x=2,
将x=2代入①得:3×2+y=9,
解得:y=3,
∴方程组的解为:;
(2),
将②代入①得:3(3﹣2y)﹣4y=4,
解得:,
将代入②得:,
解得:x=2,
∴方程组的解为:.
19.【解答】解:(1)∵(3x﹣m)(x2+x+1)
=3x3+(3﹣m)x2+(3﹣m)x﹣m
由题意得3﹣m=0,
解得m=3,
即m的值为3;
(2)∵a2+5b2+4(ab+b+1)
=(a2+4ab+4b2)+(b2+4b+4)
=(a+2b)2+(b+2)2
=0
∴a+2b=0,b+2=0,
解得a=4,b=﹣2,
∴(a﹣b)m
=[4﹣(﹣2)]3
=63
=216.
20.【解答】解:(1)由题意得(2x﹣a)(3x+b)
=6x2+(2b﹣3a)x﹣ab
=6x2+11x﹣10,
(2x+a)(x+b)
=2x2+(a+2b)x+ab
=2x2﹣9x+10,
所以2b﹣3a=11,①
a+2b=﹣9.②
由②得2b=﹣9﹣a,代入①得﹣9﹣a﹣3a=11,
所以a=﹣5.
所以2b=﹣4.
所以b=﹣2.
(2)当a=﹣5,b=﹣2时,由(1)得(2x+a)(3x+b)=(2x﹣5)(3x﹣2)=6x2﹣19x+10.
21.【解答】解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=8(cm);
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=18cm,
∴OA=OB=OC=5(cm);
(3)∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=60°.
22.【解答】解:(1)设每辆小客车能坐x人,每辆大客车能坐y人,
据题意:,
解得:,
答:每辆小客车能坐20人,每辆大客车能坐45人;
(2)①由题意得:20m+45n=400,
∴n,
∵m、n为非负整数,
∴或 或,
∴租车方案有三种:
方案一:小客车20车、大客车0辆,
方案二:小客车11辆,大客车4辆,
方案三:小客车2辆,大客车8辆;
②方案一租金:150×20=3000(元),
方案二租金:150×11+250×4=2650(元),
方案三租金:150×2+250×8=2300(元),
∴方案三租金最少,最少租金为2300元.
23.【解答】解:(1)由于甲看错了关于x,y的二元一次方程组中的a,得到的方程组的解为,
∴满足方程5x+by=42,即5×12﹣3b=42,
解得b=6,
由于乙看错了关于x,y的二元一次方程组中的吧,得到的方程组的解为,
∴满足方程ax﹣4y=10,即2a﹣4×(﹣1)=10,
解得a=3,
答:a=3;b=6;
(2)当a=3,b=6时,原方程可变为,
解得,
把代入方程组得,,
解得,
∴2m﹣n=2+3=5.
24.【解答】解:(1)设70﹣x=a,x﹣20=b,
则ab=﹣30,a+b=70﹣x+x﹣20=50,
∴(70﹣x)2+(x﹣20)2
=a2+b2
=(a+b)2﹣2ab
=502﹣2×(﹣30)
=2500+60
=2560,
∴(70﹣x)2+(x﹣20)2的值为2560;
(2)∵(3﹣4x)(2x﹣5),
∴(3﹣4x)[2(2x﹣5)]=9,
∴(3﹣4x)(4x﹣10)=9,
设3﹣4x=m,4x﹣10=n,
则m+n=3﹣4x+4x﹣10=﹣7,mn=9,
∴(3﹣4x)2+4(2x﹣5)2
=(3﹣4x)2+[2(2x﹣5)]2
=(3﹣4x)2+(4x﹣10)2
=m2+n2
=(m+n)2﹣2mn
=(﹣7)2﹣2×9
=49﹣18
=31,
∴(3﹣4x)2+4(2x﹣5)2的值为31;
(3)设2023﹣x=p,2020﹣x=q,
则p﹣q=2023﹣x﹣(2020﹣x)=3,p2+q2=2061,
∴2pq=p2+q2﹣(p﹣q)2
=2061﹣32
=2061﹣9
=2052,
∴(2023﹣x)(2020﹣x)=pq=1026,
∴(2023﹣x)(2020﹣x)的值为1026;
(4)∵CM=x,KC=3CM=3x,KB=54,FM=20,
∴BC=KC﹣KB=3x﹣54,CF=CM﹣FM=x﹣20,
∵长方形BEFC的面积是300,
∴BC CF=(3x﹣54)(x﹣20)=300,
由题意得:AB=BC=3x﹣54,CF=BE=x﹣20,
∵ER=2BE,
∴BR=3BE=3(x﹣20),
∴AR=AB+BR=(3x﹣54)+3(x﹣20)=(3x﹣54)+(3x﹣60),
∵(3x﹣54)(x﹣20)=300,
∴(3x﹣54)[3(x﹣20)]=900,
∴(3x﹣54)(3x﹣60)=900,
设3x﹣54=a,3x﹣60=b,
则a﹣b=3x﹣54﹣(3x﹣60)=6,ab=900,
∴正方形ARNP的面积=AR2
=[(3x﹣54)+(3x﹣60)]2
=(a+b)2
=(a﹣b)2+4ab
=62+4×900
=36+3600
=3636,
∴正方形ARNP的面积为3636.
25.【解答】解:(1)∵3x2+2x+3x2+2=6x2+2x+2,
x﹣6﹣x+2=﹣4,
﹣5x2y3+2xy+5x2y3﹣2xy﹣1=﹣1,
∴①组多项式不是互为“对消多项式”,
②③组多项式是互为“对消多项式”,
故答案为:②③;
(2)∵A=(x﹣a)2=x2﹣2ax+a2,B=﹣bx2﹣2x+b,
∴A+B
=x2﹣2ax+a2﹣bx2﹣2x+b
=(1﹣b)x2+(﹣2a﹣2)x+(a2+b),
∵A与B互为“对消多项式”,
∴1﹣b=0,﹣2a﹣2=0,
解得a=﹣1,b=1.
∴a2+b
=(﹣1)2+1
=1+1
=2,
∴它们的“对消值”是2;
(3)∵C=mx2+6x+4,D=﹣m(x+1)(x+n)=﹣mx2+(﹣mn﹣m)x﹣mn,
∴C+D=(6﹣mn﹣m)x+(4﹣mn),
∵C与D互为“对消多项式”且“对消值”为t,
∵a﹣b=m,b﹣c=mn,
∴a﹣c=(a﹣b)+(b﹣c)=m+mn=6,
∴a2+b2+c2﹣ab﹣bc﹣ac+2t
=m2﹣4m+32
=(m﹣2)2+28≥28,
∴代数式 a2+b2+c2=ab=bc=ac+2 的最小值是28.
21世纪教育网(www.21cnjy.com)
同课章节目录
