第九章中心对称图形—平行四边形期中复习(含答案)
文档属性
| 名称 | 第九章中心对称图形—平行四边形期中复习(含答案) |

|
|
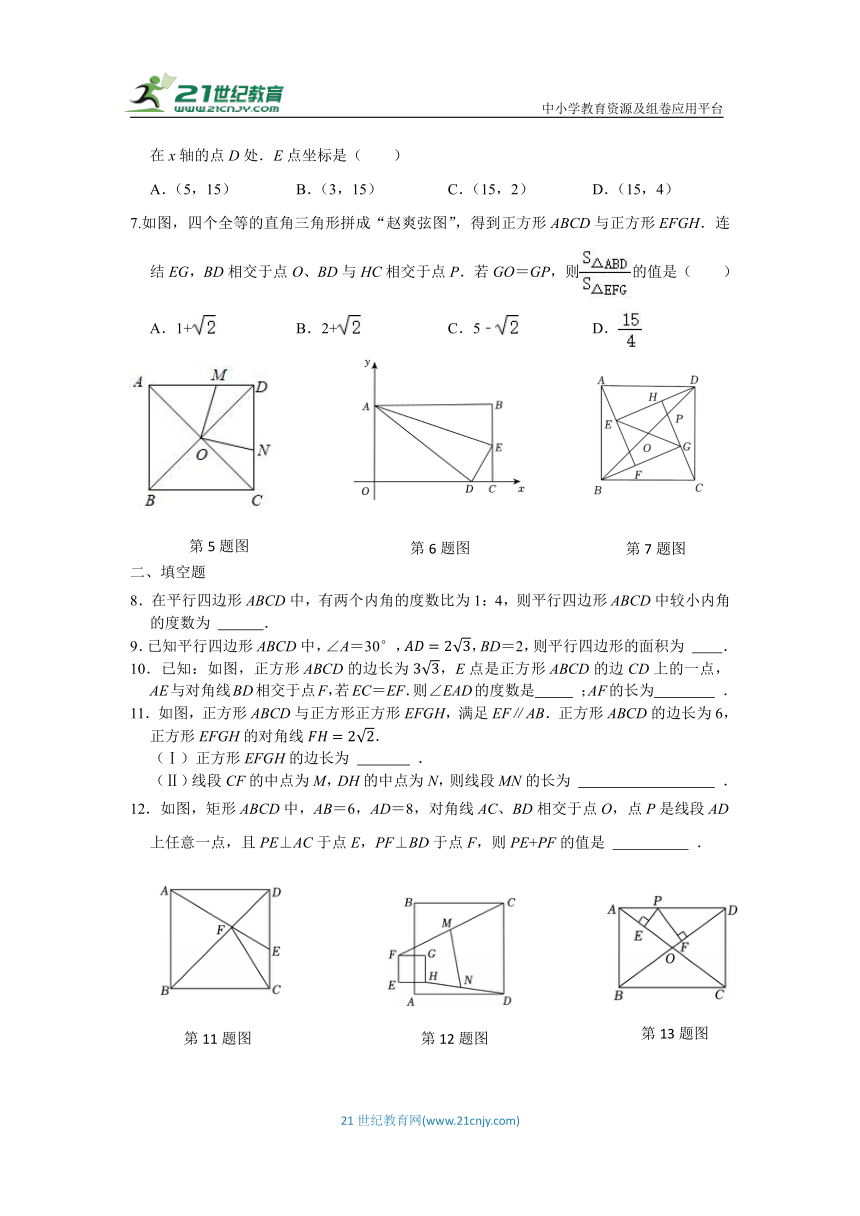
| 格式 | docx | ||
| 文件大小 | 627.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章中心对称图形—平行四边形期中复习苏科版2024—2025学年八年级下册
一、选择题
1.下列图形既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.如图,在四边形ABCD中,AC与BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AB=DC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
3.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
4.如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;
②若AC⊥BD,则四边形EFGH为菱形;
③若四边形EFGH是平行四边形,则AC与BD互相平分;
④若四边形EFGH是正方形,则AC与BD互相垂直且相等.
其中正确的个数是( )
A.1 B.2 C.3 D.4
5.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
6.如图,在矩形OABC中,OA=9,AB=15,E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处.E点坐标是( )
A.(5,15) B.(3,15) C.(15,2) D.(15,4)
7.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则的值是( )
A.1+ B.2+ C.5﹣ D.
二、填空题
8.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 .
9.已知平行四边形ABCD中,∠A=30°,,BD=2,则平行四边形的面积为 .
10.已知:如图,正方形ABCD的边长为,E点是正方形ABCD的边CD上的一点,AE与对角线BD相交于点F,若EC=EF.则∠EAD的度数是 ;AF的长为 .
11.如图,正方形ABCD与正方形正方形EFGH,满足EF∥AB.正方形ABCD的边长为6,正方形EFGH的对角线.
(Ⅰ)正方形EFGH的边长为 .
(Ⅱ)线段CF的中点为M,DH的中点为N,则线段MN的长为 .
12.如图,矩形ABCD中,AB=6,AD=8,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值是 .
三、解答题
13.如图,△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
(1)求证:DM(AC﹣AB);
(2)若AD=6,BD=8,DM=2,求AC的长.
14.已知:如图,在 ABCD中,E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AECF是平行四边形;
(2)若AD⊥BD,AB=5,AD=3,且EF﹣AF=2,求DE的长.
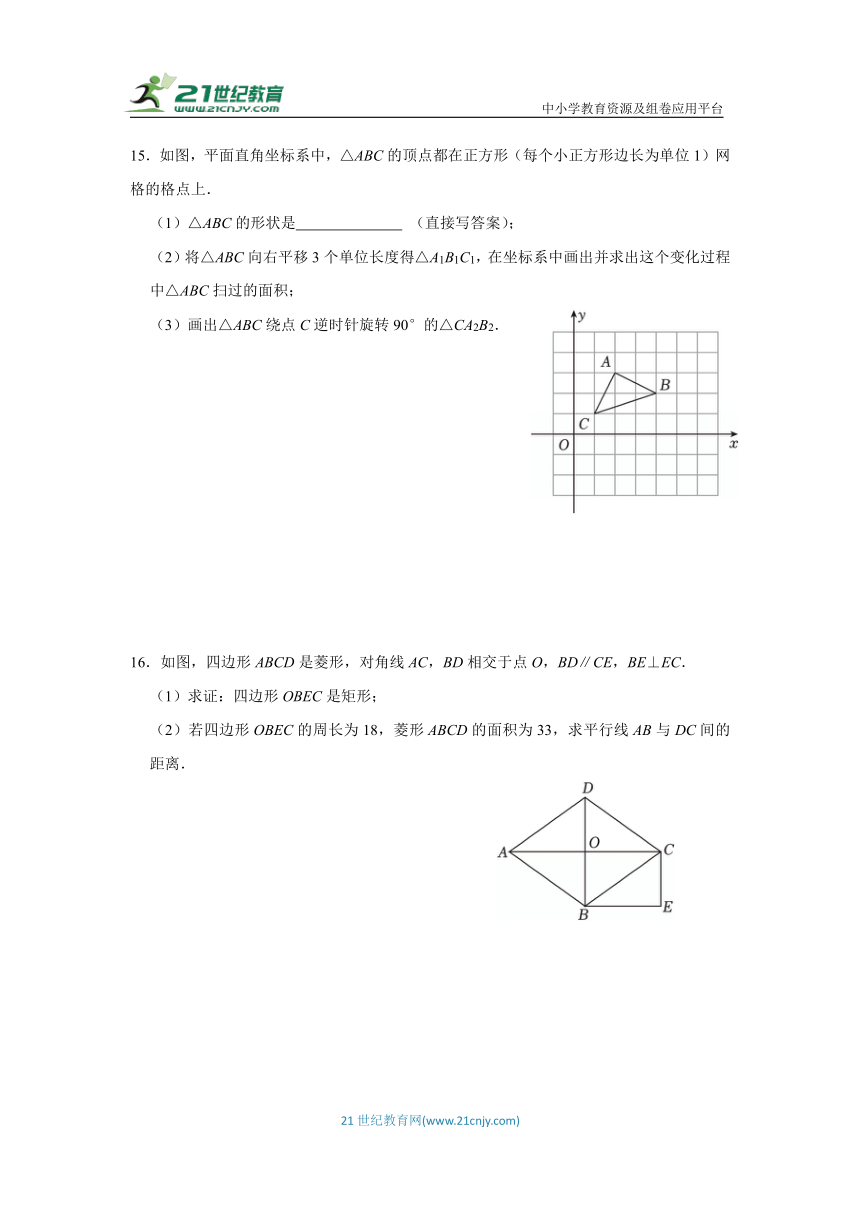
15.如图,平面直角坐标系中,△ABC的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
(1)△ABC的形状是 (直接写答案);
(2)将△ABC向右平移3个单位长度得△A1B1C1,在坐标系中画出并求出这个变化过程中△ABC扫过的面积;
(3)画出△ABC绕点C逆时针旋转90°的△CA2B2.
16.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,BD∥CE,BE⊥EC.
(1)求证:四边形OBEC是矩形;
(2)若四边形OBEC的周长为18,菱形ABCD的面积为33,求平行线AB与DC间的距离.
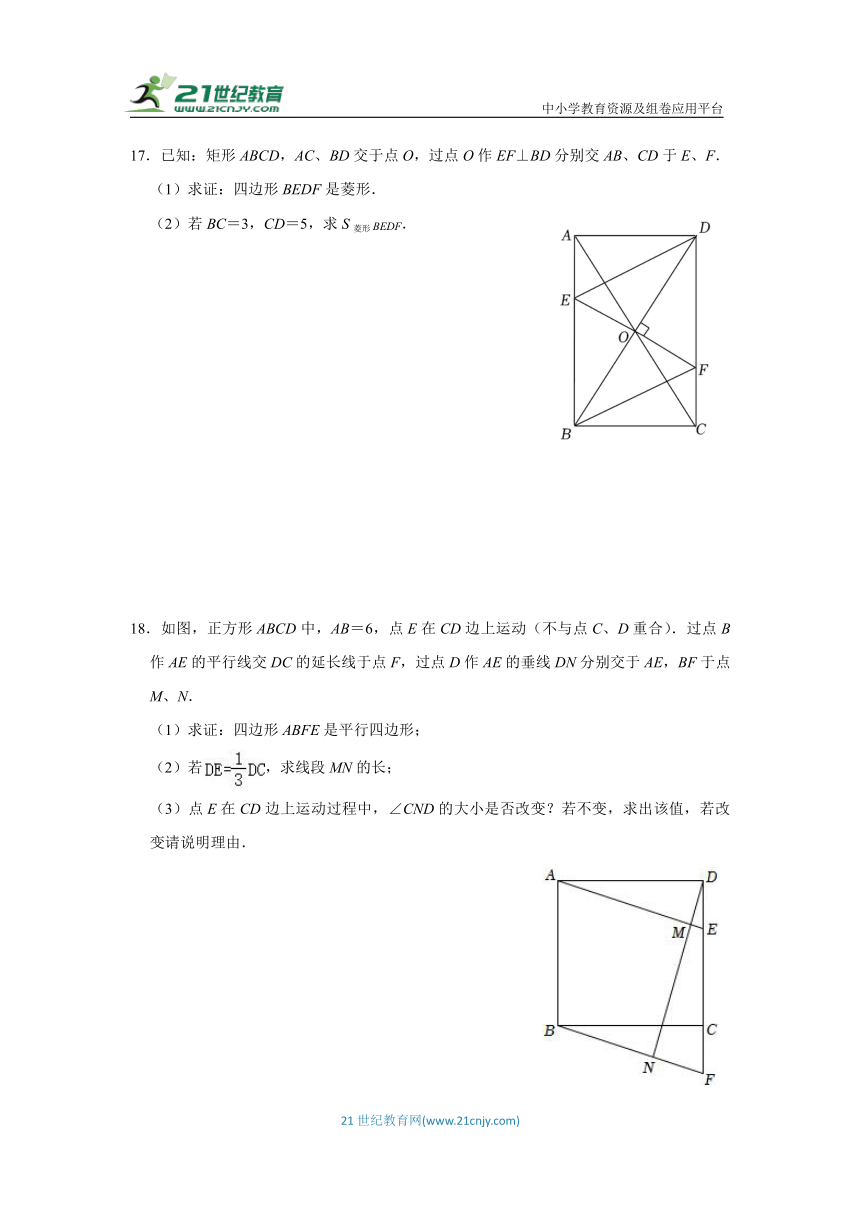
17.已知:矩形ABCD,AC、BD交于点O,过点O作EF⊥BD分别交AB、CD于E、F.
(1)求证:四边形BEDF是菱形.
(2)若BC=3,CD=5,求S菱形BEDF.
18.如图,正方形ABCD中,AB=6,点E在CD边上运动(不与点C、D重合).过点B作AE的平行线交DC的延长线于点F,过点D作AE的垂线DN分别交于AE,BF于点M、N.
(1)求证:四边形ABFE是平行四边形;
(2)若,求线段MN的长;
(3)点E在CD边上运动过程中,∠CND的大小是否改变?若不变,求出该值,若改变请说明理由.
参考答案
一、选择题
1-7:DCBAC DB
二、填空题
8.【解答】解:如图:
∵四边形ABCD为平行四边形,有两个内角的度数比为1:4,
∴AD∥BC,∠A=4∠B,
∴∠A+∠B=180°,
∴4∠B+∠B=180°,
∴∠B=36°,
∴∠A=144°,
∴平行四边形ABCD中较小内角的度数为36°,
故答案为:36°.
9.【解答】解:过D作DE⊥AB于E,
在Rt△ADE中,∵∠A=30°,AD=2,
∴DEAD,AEAD=3,
在Rt△BDE中,
∵BD=2,
∴BE2,
如图1,∴AB=4,
∴平行四边形ABCD的面积=AB DE=4;
如图2,AB=2,
∴平行四边形ABCD的面积=AB DE=2.
故答案为:2或4.
10.【解答】解:∵四边形ABCD是正方形,AC是对角线,
∴AD=CD,∠ADC=90°,
∴,
在△ADF和△CDF中,
,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF,
∵EC=EF,
∴∠ECF=∠EFC,
∴∠AED=2∠ECF,则∠AED=2∠EAD,
在Rt△ADE中,∠EAD+∠AED=90°,
∴∠EAD+2∠EAD=90°,
解得∠EAD=30°;
在Rt△ADE中,,
∴AE=2DE,
由勾股定理得:AE2=AD2+DE2,即,
解得DE=3(负值舍去),
∴AE=6,,
∴;
故答案为:30°;.
11.【解答】解:(Ⅰ)∵正方形EFGH的对角线.
∴EF2,
故答案为:2;
(Ⅱ)连接HM并延长至点P,使MP=MH,作PQ⊥CD于点Q,连接PC、FH、PD,
∵M是线段CF的中点,
∴MF=MC,
在△FHM和△CPM中,
∴△FHM≌△CPM(SAS),
∴FH=PC=2,∠HFM=∠PCM,
∵FG∥BC,
∴∠GFM=∠BCM,
∴∠HFG=∠PCB=45°
∴∠PCQ=45°,
∴PQ=QC=2,
∴DQ=CD+CQ=8,
∴,
∵线段HP的中点为M,DH的中点为N,
∴.
故答案为:.
12.【解答】解:连接OP,过点D作DH⊥AC于点H,如图所示:
∵四边形ABCD为矩形,且AB=6,AD=8,
∴CD=AB=6,OA=OC=OD=OB,∠ADC=90°,
在Rt△ACD中,由勾股定理得:AC10,
∴OA=OC=OD=1/2AC=5,
∵PE⊥AC,PF⊥BD,
∴S△OAPOA PEPE,S△ODPOD PFPF,S△OADOA DHDH,
∵S△OAP+S△ODP=S△OAD,
∴PEPFDH,
∴PE+PF=DH,
∵∠ADC=90°,DH⊥AC,
∴由三角形的面积公式得:S△ACDAC DHAD CD,
∴DH4.8,
∴PE+PF=4.8.
故答案为:4.8.
三、解答题
13.解:(1)证明:延长BD交AC于E,
∵AD⊥BD,
∴∠ADB=∠ADE=90°,
∵AD为∠BAC的平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中,
,
∴△BAD≌△EAD(ASA),
∴AB=AE,BD=DE,
∵M为BC的中点,
∴DMCE(AC﹣AB);
(2)∵在Rt△ADB中,∠ADB=90°,AD=6,BD=8,
∴由勾股定理得:AE=AB10,
∵DM=2,DMCE,
∴CE=4,
∴AC=10+4=14.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADB=∠CBD.
∴∠ADE=∠CBF.
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
∴AE=CF,∠AED=∠CBF.
∴AE∥CF,
∴四边形AFCE是平行四边形;
(2)解:∵BD⊥AD,AB=5,BC=AD=3,
∴BD4,
连接AC交EF于O,如图,
∴DO=OBBD=2,
∵四边形AECF是平行四边形,
∴EO=OFEF,
∴DE=BF,
设DE=BF=x,
∴EF=2x+4,
∵EF﹣AF=2,
∴AF=2x+2,
∵AF2=AD2+DF2,
∴(2x+2)2=32+(4+x)2,
∴x(负值舍去),
∴DE的长为.
15.【解答】解:(1)由勾股定理得,AB,AC,BC,
∴AB=AC,AB2+AC2=BC2,
∴∠BAC=90°,
∴△ABC为等腰直角三角形.
故答案为:等腰直角三角形.
(2)如图,△A1B1C1即为所求.
这个变化过程中△ABC扫过的面积为.
(3)如图,△CA2B2即为所求.
16.【解答】(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∵BD∥CE,
∴CE⊥AC,
又∵BE⊥EC,
∴∠BOC=∠OCE=∠CEB=90°,
∴四边形OBEC是矩形;
(2)解:∵四边形OBEC的周长为18,四边形OBEC是矩形,
∴OC+OB=9,
∵菱形ABCD的面积为33,
∴AC BD=33,
即2OB×2OC=33,
∴2OB OC=33,
∵OC+OB=9,
∴(OC+OB)2=81,
∴OC2+2OB OC+OB2=81,
∴OC2+OB2=48,
∴BC4,
∵四边形ABCD是菱形,
∴AB=BC=4,
设平行线AB与DC间的距离为x,
则AB x=33,
即4x=33,
解得x,
即平行线AB与DC间的距离为.
17.【解答】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,OB=OD,
∴∠EBD=∠FDB,
在△EBO和△FDO中,
,
∴△EBO≌△FDO(ASA),
∴OE=OF,
∵OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠BCD=90°,
∵四边形BEDF是菱形,
∴BF=DF,
∵BC=3,CD=5,
∴FC=CD﹣DF=5﹣BF,
在Rt△BCF中,根据勾股定理得:
BF2=BC2+FC2,
∴BF2=32+(5﹣BF)2,
∴BF=,
∴S菱形BEDF=DF BC=BF BC=×3=.
18.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB∥DC,
∵AE∥BF,
∴四边形ABFE是平行四边形;
(2)解:在正方形ABCD中,AB=6,
∴BC=CD=AD=AB=6,∠ADC=∠BCD=90°,
∵,
∴DE=2,CE=4,
∴AE=2,
对于△AED,∠ADE=90°,DM⊥AE,
∴AD DE=AE DM,
解得DM=.
连接BD,
∵AE∥BF,
∴DN⊥BF,
∴∠DNF=90°.
∴BC DF=BF DN,
由(1)知,四边形ABFE是平行四边形,
∴EF=AB=6,BF=AE=2,
∴DF=8,
∴6×8=2 DN,
∴DN=.
∴MN=DN﹣DM=.
(3)不变,∠CND=45°,理由如下:
如图,在DN上取点G,使DG=BN,连接CG,CN,
∵∠NDF+∠F=∠CBF+∠F=90°,
∴∠NDF=∠CBF,
∵DC=BC,DG=BN,
∴△CDG≌△CBN(SAS),
∴CG=CN,∠DCG=∠BCN,
∵∠DCG+∠BCG=90°,
∴∠BCN+∠BCG=90°,即∠GCN=90°.
∴∠CNG=45°,即∠CND=45°.
21世纪教育网(www.21cnjy.com)
第九章中心对称图形—平行四边形期中复习苏科版2024—2025学年八年级下册
一、选择题
1.下列图形既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.如图,在四边形ABCD中,AC与BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AB=DC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
3.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
4.如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;
②若AC⊥BD,则四边形EFGH为菱形;
③若四边形EFGH是平行四边形,则AC与BD互相平分;
④若四边形EFGH是正方形,则AC与BD互相垂直且相等.
其中正确的个数是( )
A.1 B.2 C.3 D.4
5.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
6.如图,在矩形OABC中,OA=9,AB=15,E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处.E点坐标是( )
A.(5,15) B.(3,15) C.(15,2) D.(15,4)
7.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则的值是( )
A.1+ B.2+ C.5﹣ D.
二、填空题
8.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 .
9.已知平行四边形ABCD中,∠A=30°,,BD=2,则平行四边形的面积为 .
10.已知:如图,正方形ABCD的边长为,E点是正方形ABCD的边CD上的一点,AE与对角线BD相交于点F,若EC=EF.则∠EAD的度数是 ;AF的长为 .
11.如图,正方形ABCD与正方形正方形EFGH,满足EF∥AB.正方形ABCD的边长为6,正方形EFGH的对角线.
(Ⅰ)正方形EFGH的边长为 .
(Ⅱ)线段CF的中点为M,DH的中点为N,则线段MN的长为 .
12.如图,矩形ABCD中,AB=6,AD=8,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值是 .
三、解答题
13.如图,△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
(1)求证:DM(AC﹣AB);
(2)若AD=6,BD=8,DM=2,求AC的长.
14.已知:如图,在 ABCD中,E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AECF是平行四边形;
(2)若AD⊥BD,AB=5,AD=3,且EF﹣AF=2,求DE的长.
15.如图,平面直角坐标系中,△ABC的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
(1)△ABC的形状是 (直接写答案);
(2)将△ABC向右平移3个单位长度得△A1B1C1,在坐标系中画出并求出这个变化过程中△ABC扫过的面积;
(3)画出△ABC绕点C逆时针旋转90°的△CA2B2.
16.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,BD∥CE,BE⊥EC.
(1)求证:四边形OBEC是矩形;
(2)若四边形OBEC的周长为18,菱形ABCD的面积为33,求平行线AB与DC间的距离.
17.已知:矩形ABCD,AC、BD交于点O,过点O作EF⊥BD分别交AB、CD于E、F.
(1)求证:四边形BEDF是菱形.
(2)若BC=3,CD=5,求S菱形BEDF.
18.如图,正方形ABCD中,AB=6,点E在CD边上运动(不与点C、D重合).过点B作AE的平行线交DC的延长线于点F,过点D作AE的垂线DN分别交于AE,BF于点M、N.
(1)求证:四边形ABFE是平行四边形;
(2)若,求线段MN的长;
(3)点E在CD边上运动过程中,∠CND的大小是否改变?若不变,求出该值,若改变请说明理由.
参考答案
一、选择题
1-7:DCBAC DB
二、填空题
8.【解答】解:如图:
∵四边形ABCD为平行四边形,有两个内角的度数比为1:4,
∴AD∥BC,∠A=4∠B,
∴∠A+∠B=180°,
∴4∠B+∠B=180°,
∴∠B=36°,
∴∠A=144°,
∴平行四边形ABCD中较小内角的度数为36°,
故答案为:36°.
9.【解答】解:过D作DE⊥AB于E,
在Rt△ADE中,∵∠A=30°,AD=2,
∴DEAD,AEAD=3,
在Rt△BDE中,
∵BD=2,
∴BE2,
如图1,∴AB=4,
∴平行四边形ABCD的面积=AB DE=4;
如图2,AB=2,
∴平行四边形ABCD的面积=AB DE=2.
故答案为:2或4.
10.【解答】解:∵四边形ABCD是正方形,AC是对角线,
∴AD=CD,∠ADC=90°,
∴,
在△ADF和△CDF中,
,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF,
∵EC=EF,
∴∠ECF=∠EFC,
∴∠AED=2∠ECF,则∠AED=2∠EAD,
在Rt△ADE中,∠EAD+∠AED=90°,
∴∠EAD+2∠EAD=90°,
解得∠EAD=30°;
在Rt△ADE中,,
∴AE=2DE,
由勾股定理得:AE2=AD2+DE2,即,
解得DE=3(负值舍去),
∴AE=6,,
∴;
故答案为:30°;.
11.【解答】解:(Ⅰ)∵正方形EFGH的对角线.
∴EF2,
故答案为:2;
(Ⅱ)连接HM并延长至点P,使MP=MH,作PQ⊥CD于点Q,连接PC、FH、PD,
∵M是线段CF的中点,
∴MF=MC,
在△FHM和△CPM中,
∴△FHM≌△CPM(SAS),
∴FH=PC=2,∠HFM=∠PCM,
∵FG∥BC,
∴∠GFM=∠BCM,
∴∠HFG=∠PCB=45°
∴∠PCQ=45°,
∴PQ=QC=2,
∴DQ=CD+CQ=8,
∴,
∵线段HP的中点为M,DH的中点为N,
∴.
故答案为:.
12.【解答】解:连接OP,过点D作DH⊥AC于点H,如图所示:
∵四边形ABCD为矩形,且AB=6,AD=8,
∴CD=AB=6,OA=OC=OD=OB,∠ADC=90°,
在Rt△ACD中,由勾股定理得:AC10,
∴OA=OC=OD=1/2AC=5,
∵PE⊥AC,PF⊥BD,
∴S△OAPOA PEPE,S△ODPOD PFPF,S△OADOA DHDH,
∵S△OAP+S△ODP=S△OAD,
∴PEPFDH,
∴PE+PF=DH,
∵∠ADC=90°,DH⊥AC,
∴由三角形的面积公式得:S△ACDAC DHAD CD,
∴DH4.8,
∴PE+PF=4.8.
故答案为:4.8.
三、解答题
13.解:(1)证明:延长BD交AC于E,
∵AD⊥BD,
∴∠ADB=∠ADE=90°,
∵AD为∠BAC的平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中,
,
∴△BAD≌△EAD(ASA),
∴AB=AE,BD=DE,
∵M为BC的中点,
∴DMCE(AC﹣AB);
(2)∵在Rt△ADB中,∠ADB=90°,AD=6,BD=8,
∴由勾股定理得:AE=AB10,
∵DM=2,DMCE,
∴CE=4,
∴AC=10+4=14.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADB=∠CBD.
∴∠ADE=∠CBF.
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
∴AE=CF,∠AED=∠CBF.
∴AE∥CF,
∴四边形AFCE是平行四边形;
(2)解:∵BD⊥AD,AB=5,BC=AD=3,
∴BD4,
连接AC交EF于O,如图,
∴DO=OBBD=2,
∵四边形AECF是平行四边形,
∴EO=OFEF,
∴DE=BF,
设DE=BF=x,
∴EF=2x+4,
∵EF﹣AF=2,
∴AF=2x+2,
∵AF2=AD2+DF2,
∴(2x+2)2=32+(4+x)2,
∴x(负值舍去),
∴DE的长为.
15.【解答】解:(1)由勾股定理得,AB,AC,BC,
∴AB=AC,AB2+AC2=BC2,
∴∠BAC=90°,
∴△ABC为等腰直角三角形.
故答案为:等腰直角三角形.
(2)如图,△A1B1C1即为所求.
这个变化过程中△ABC扫过的面积为.
(3)如图,△CA2B2即为所求.
16.【解答】(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∵BD∥CE,
∴CE⊥AC,
又∵BE⊥EC,
∴∠BOC=∠OCE=∠CEB=90°,
∴四边形OBEC是矩形;
(2)解:∵四边形OBEC的周长为18,四边形OBEC是矩形,
∴OC+OB=9,
∵菱形ABCD的面积为33,
∴AC BD=33,
即2OB×2OC=33,
∴2OB OC=33,
∵OC+OB=9,
∴(OC+OB)2=81,
∴OC2+2OB OC+OB2=81,
∴OC2+OB2=48,
∴BC4,
∵四边形ABCD是菱形,
∴AB=BC=4,
设平行线AB与DC间的距离为x,
则AB x=33,
即4x=33,
解得x,
即平行线AB与DC间的距离为.
17.【解答】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,OB=OD,
∴∠EBD=∠FDB,
在△EBO和△FDO中,
,
∴△EBO≌△FDO(ASA),
∴OE=OF,
∵OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠BCD=90°,
∵四边形BEDF是菱形,
∴BF=DF,
∵BC=3,CD=5,
∴FC=CD﹣DF=5﹣BF,
在Rt△BCF中,根据勾股定理得:
BF2=BC2+FC2,
∴BF2=32+(5﹣BF)2,
∴BF=,
∴S菱形BEDF=DF BC=BF BC=×3=.
18.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB∥DC,
∵AE∥BF,
∴四边形ABFE是平行四边形;
(2)解:在正方形ABCD中,AB=6,
∴BC=CD=AD=AB=6,∠ADC=∠BCD=90°,
∵,
∴DE=2,CE=4,
∴AE=2,
对于△AED,∠ADE=90°,DM⊥AE,
∴AD DE=AE DM,
解得DM=.
连接BD,
∵AE∥BF,
∴DN⊥BF,
∴∠DNF=90°.
∴BC DF=BF DN,
由(1)知,四边形ABFE是平行四边形,
∴EF=AB=6,BF=AE=2,
∴DF=8,
∴6×8=2 DN,
∴DN=.
∴MN=DN﹣DM=.
(3)不变,∠CND=45°,理由如下:
如图,在DN上取点G,使DG=BN,连接CG,CN,
∵∠NDF+∠F=∠CBF+∠F=90°,
∴∠NDF=∠CBF,
∵DC=BC,DG=BN,
∴△CDG≌△CBN(SAS),
∴CG=CN,∠DCG=∠BCN,
∵∠DCG+∠BCG=90°,
∴∠BCN+∠BCG=90°,即∠GCN=90°.
∴∠CNG=45°,即∠CND=45°.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
