第三次月考数学模拟试卷试卷(含答案)
文档属性
| 名称 | 第三次月考数学模拟试卷试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 476.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 20:51:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三次月考数学模拟试卷试卷人教版2024—2025学年九年级下册
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题
1.下列图形中,是轴对称图形但不是中心对称图形的是( )
A. B. C.D.
2.若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6 B.12 C.16 D.18
3.使二次根式有意义的x的取值范围是( )
A.x≥2 B.x>2 C.x≥﹣2 D.x>﹣2
4.若式子x2+2(m﹣3)x+16是完全平方式,则m的值可能是( )
A.﹣1或7 B.0或6 C.1或5 D.2或4
5.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )
A.x(x+1)=1035 B.x(x+1)=1035
C.x(x﹣1)=1035 D.x(x﹣1)=1035
6.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
7.将抛物线y=(x﹣1)2+2向左平移1个单位,再向上平移5个单位后所得抛物线的解析式为( )
A.y=(x﹣2)2+7 B.y=(x﹣2)2+3 C.y=x2+7 D.y=x2+3
8.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为( )
A.1 B. C.1 D.
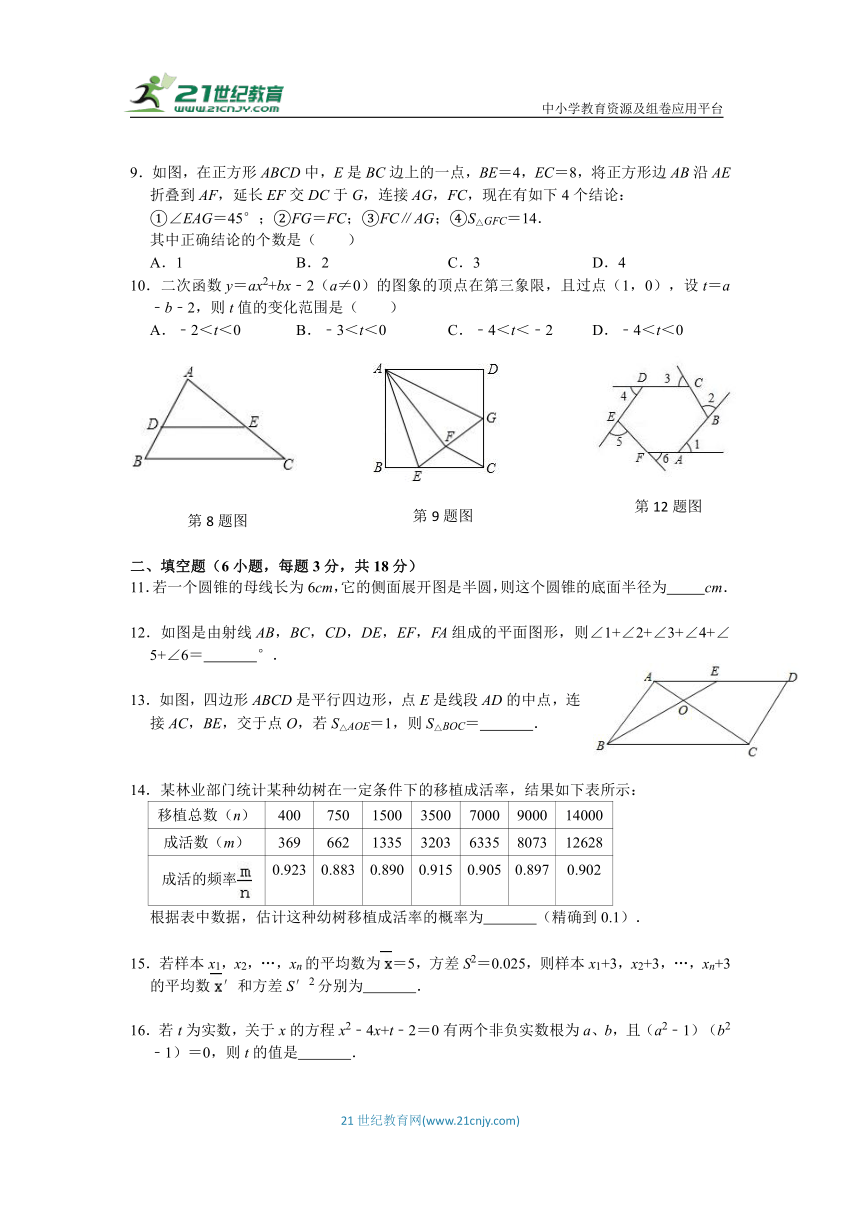
9.如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG,FC,现在有如下4个结论:
①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.二次函数y=ax2+bx﹣2(a≠0)的图象的顶点在第三象限,且过点(1,0),设t=a﹣b﹣2,则t值的变化范围是( )
A.﹣2<t<0 B.﹣3<t<0 C.﹣4<t<﹣2 D.﹣4<t<0
二、填空题(6小题,每题3分,共18分)
11.若一个圆锥的母线长为6cm,它的侧面展开图是半圆,则这个圆锥的底面半径为 cm.
12.如图是由射线AB,BC,CD,DE,EF,FA组成的平面图形,则∠1+∠2+∠3+∠4+∠5+∠6= °.
13.如图,四边形ABCD是平行四边形,点E是线段AD的中点,连接AC,BE,交于点O,若S△AOE=1,则S△BOC= .
14.某林业部门统计某种幼树在一定条件下的移植成活率,结果如下表所示:
移植总数(n) 400 750 1500 3500 7000 9000 14000
成活数(m) 369 662 1335 3203 6335 8073 12628
成活的频率 0.923 0.883 0.890 0.915 0.905 0.897 0.902
根据表中数据,估计这种幼树移植成活率的概率为 (精确到0.1).
15.若样本x1,x2,…,xn的平均数为=5,方差S2=0.025,则样本x1+3,x2+3,…,xn+3的平均数′和方差S′2分别为 .
16.若t为实数,关于x的方程x2﹣4x+t﹣2=0有两个非负实数根为a、b,且(a2﹣1)(b2﹣1)=0,则t的值是 .
第II卷
第八次月考数学模拟试卷试卷人教版2024—2025学年九年级下册
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
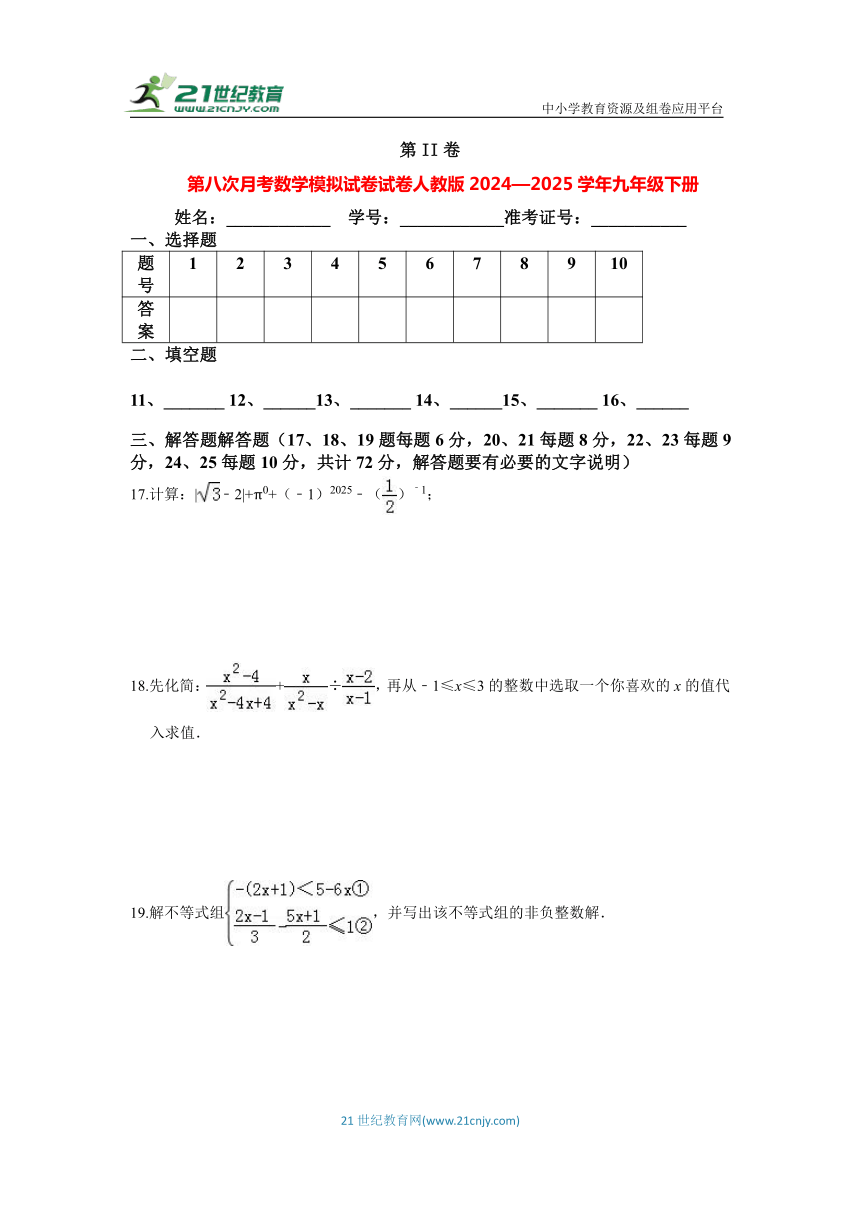
17.计算:|﹣2|+π0+(﹣1)2025﹣()﹣1;
18.先化简:+÷,再从﹣1≤x≤3的整数中选取一个你喜欢的x的值代入求值.
19.解不等式组,并写出该不等式组的非负整数解.
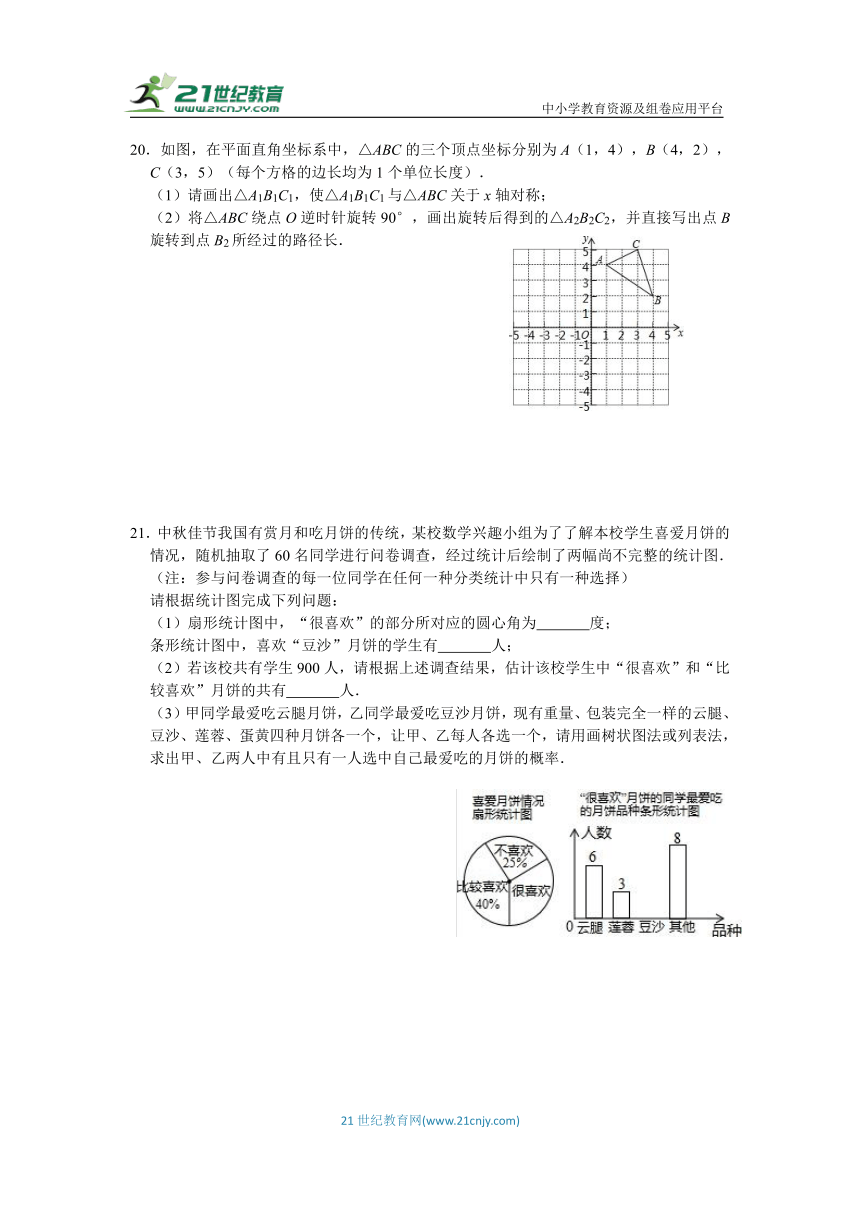
20.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
21.中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.
(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为 度;
条形统计图中,喜欢“豆沙”月饼的学生有 人;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”月饼的共有 人.
(3)甲同学最爱吃云腿月饼,乙同学最爱吃豆沙月饼,现有重量、包装完全一样的云腿、豆沙、莲蓉、蛋黄四种月饼各一个,让甲、乙每人各选一个,请用画树状图法或列表法,求出甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率.
22.某文体商店计划购进一批同种型号的篮球和同种型号的排球,每一个排球的进价是每一个篮球的进价的90%,用3600元购买排球的个数要比用3600元购买篮球的个数多10个.
(1)问每一个篮球、排球的进价各是多少元?
(2)该文体商店计划购进篮球和排球共100个,且排球个数不低于篮球个数的3倍,篮球的售价定为每一个100元,排球的售价定为每一个90元.若该批篮球、排球都能卖完,问该文体商店应购进篮球、排球各多少个才能获得最大利润?最大利润是多少?
23.如图,CD是⊙O的直径,AB是⊙O的一条弦,=,AO的延长线交⊙O于点F、交DB的延长线于点P,连接PC且恰好PC∥AB,连接DF交AB于点G,延长DF交CP于点E,连接BF.
(1)求证:PC是⊙O的切线;
(2)求证:CE=PE;
(3)当BF=2时,求tan∠APD的值.
24.我们定义:点P在一次函数y=ax+b上,点Q在反比例函数上,若存在P、Q两点关于y轴对称,我们称二次函数y=ax2+bx+c为一次函数和y=ax+b反比例函数的“向光函数”,点P称为“幸福点”.例如:点P(﹣1,﹣2)在y=x﹣1上,点Q(1,﹣2)在上,P、Q两点关于y轴对称,此时二次函数y=x2﹣x﹣2为一次函数y=x﹣1和反比例函数的“向光函数”,点P(﹣1,﹣2)是“幸福点”.
(1)判断一次函数y=x+1和反比例函数是否存在“向光函数”,若存在,请求出“幸福点”坐标;若不存在,请说明理由;
(2)若一次函数y=x﹣k与反比例函数只有一个“幸福点”,求其“向光函数”的解析式;
(3)已知一次函数y=ax+b与反比例函数有两个“幸福点”A、B(A在B左侧),其“向光函数”y=ax2+bx+c与轴x交于C、D两点(C在D左侧),若有以下条件:
①a+b+c=0②“向光函数”经过点(﹣3,4),③a>b>0,记四边形ACBD的面积为S,求的取值范围.
25.如图,已知抛物线与x轴交于A,B两点,交y轴于点C,以AB为直径作⊙O′,⊙O′经过点C,连接AC,BC.
(1)求⊙O'的圆心O′的坐标;
(2)如图1,点E是AC延长线上的一点,∠BCE的平分线CD交⊙O'于点D,连接BD,求直线BD的解析式.
(3)如图2,在(2)的条件下,F是⊙O'上一动点(不与B点重合),连接BF,M是BF中点,连接DM,求DM的最大值.
参考答案
选择题
1-10:ABBAC CCCBD
二、填空题
11.解:设圆锥底面半径为rcm,
那么圆锥底面圆周长为2πrcm,
所以侧面展开图的弧长为2πrcm,
S圆锥侧面积=×2πr×6=,
解得:r=3,
故答案为:3.
12.解:由多边形的外角和等于360°可知,
∠1+∠2+∠3+∠4+∠5+∠6=360°,
故答案为:360.
13.解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E是线段AD的中点,
∴AE=AD=BC,
∵AD∥BC,
∴△AEO∽△CBO,
∴=()2=,
∴S△BOC=4×1=4,
故答案为:4.
14.解:由表格数据可得,随着样本数量不等增加,这种幼树移植成活率稳定的0.9左右,
故这种幼树移植成活率的概率约为0.9.
故本题答案为:0.9.
15.解:∵样本x1,x2,…,xn的平均数为5,
∴样本x1+3,x2+3,…,xn+3的平均数是5+3=8;
∵样本x1,x2,…,xn的方差为0.025,
∴样本x1+3,x2+3,…,xn+3的方差是0.025;
故答案为:8,0.025.
16.解:由根的判别式可知:△=16﹣4(t﹣2)=24﹣4t≥0,
∴t≤6,
由根与系数的关系可知:a+b=4,ab=t﹣2,
由于关于x的方程x2﹣4x+t﹣2=0有两个非负实数根为a、b,
∴t﹣2≥0,
∴2≤t≤6,
∵关于x的方程x2﹣4x+t﹣2=0有两个非负实数根为a、b,
∴a2﹣4a+t﹣2=0,b2﹣4b+t﹣2=0,
∴两式相加可得:a2+b2﹣4(a+b)+2(t﹣2)=0,
∴a2+b2=4(a+b)﹣2(t﹣2)=16﹣2(t﹣2)=20﹣2t,
∵(a2﹣1)(b2﹣1)=0,
∴a2b2﹣(a2+b2)+1=0,
∴(t﹣2)2﹣(20﹣2t)+1=0,
∴t2﹣2t﹣15=0,
∴t=5或t=﹣3(舍去)
∴t=5
故答案为:5.
三、解答题
17.解:(1)|﹣2|+π0+(﹣1)2025﹣()﹣1
=2﹣+1+(﹣1)﹣2
=﹣;
18.解:(1)+÷
=
=
=,
当x=3时,原式==6;
19.解(2),
由不等式①,得
x<,
由不等式②,得
x≥﹣1,
故原不等式组的解集是﹣1≤x<,
∴该不等式组的非负整数解是0,1.
20.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
点B旋转到点B2所经过的路径长为:=π.
故点B旋转到点B2所经过的路径长是π.
21.解:(1)∵“很喜欢”的部分占的百分比为:1﹣25%﹣40%=35%,
∴扇形统计图中,“很喜欢”的部分所对应的圆心角为:360°×35%=126°;
∵“很喜欢”月饼的同学数:60×35%=21,
∴条形统计图中,喜欢“豆沙”月饼的学生数:21﹣6﹣3﹣8=4,
故答案分别为126°,4.
(2)900名学生中“很喜欢”的有900×35%=315人,
900名学生中“比较喜欢”的有900×40%=360人,
∴估计该校学生中“很喜欢”和“比较喜欢”月饼的共有675人.
故答案为675.
(3)为了表示方便,记云腿、豆沙、莲蓉、蛋黄四种月饼分别为A、B、C、D.画出的树状图如图所示,
∴甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率==
22.解:(1)设每一个篮球的进价是x元,则每一个排球的进价是90%x元,依题意有
+10=,
解得x=40,
经检验,x=40是原方程的解,
90%x=90%×40=36.
故每一个篮球的进价是40元,每一个排球的进价是36元;
(2)设文体商店计划购进篮球m个,总利润y元,则
y=(100﹣40)m+(90﹣36)(100﹣m)=6m+5400,
依题意有,
解得0<m≤25且m为整数,
∵m为整数,
∴y随m的增大而增大,
∴m=25时,y最大,这时y=6×25+5400=5550,
100﹣25=75(个).
故该文体商店应购进篮球25个、排球75个才能获得最大利润,最大利润是5550元.
23.(1)证明:∵CD是⊙O的直径,
∴CD⊥AB,
又∵PC∥AB,
∴PC⊥CD,
∴PC为⊙O的切线; ……(3分)
(2)∵PC∥AB,
∴∠EPF=∠PAB,
∠FDB=∠PAB,
∴∠EPF=∠FDB,
∵∠PEF=∠DEP,
∴△FEP∽△PED,
∴,
∴PE2=EF ED,
连接CF,
同理得:△ECF∽△EDC,
∴,即EC2=EF ED,
∴CE2=PE2,
∴CE=PE; ……(7分)
(3)∵PC∥AB,
∴,,
∴,
由(2)知:CE=PE,
∴GH=BG,
∴∠HGD=∠BGF,∠DHG=∠FBG=90°,
∴△DHG≌△FBG(ASA),
∴DH=BF=2,
又AO=OF,AH=HB,
∴OH=BF=1,
∴OD=3,CD=6,
连接OB,过点O作OM⊥DB,则OB=OD=3,
∴,
∴,,
∴,
又PC∥AB,
∴,
∴,
∴,
∴MP=5,
在Rt△POM中,tan∠APD===……(10分)
24.解:(1)一次函数y=x+1和反比例函数存在“向光函数”,理由如下:
点P在一次函数y=ax+b上,点Q在反比例函数上,若存在P、Q两点关于y轴对称,我们称二次函数y=ax2+bx+c为一次函数和y=ax+b反比例函数的“向光函数”,点P称为“幸福点”.设“幸福点”坐标为P(m,n),则Q(﹣m,n),
∴,
解并检验得:,,
∴一次函数y=x+2和反比例函数是存在“向光函数”,“幸福点”坐标为(1,2),(﹣2,﹣1);
(2)∵一次函数y=x﹣k关于y轴对称的直线函数解析式为y=﹣x﹣k,而且一次函数y=x﹣k与反比例函数只有一个“幸福点”,
所以y=﹣x﹣k与反比例函数只有一个交点,
∴y=﹣x﹣k③,,
整理得:x2+kx+(k+3)=0,
Δ=k2﹣4(k+3)=0,
解得:k1=﹣2,k2=6,
当k=﹣2时,则一次函数y=x+2与反比例函数只有一个“幸福点”,向光函数”的解析式为:y=x2+2x+1,
当k=6时,则一次函数y=x﹣6与反比例函数只有一个“幸福点”,向光函数”的解析式为:y=x2﹣6x+9,
∴“向光函数”的解析式为:y=x2+2x+1或y=x2﹣6x+9.
(3)已知一次函数y=ax+b与反比例函数有两个“幸福点”A、B(A在B左侧),其“向光函数”y=ax2+bx+c与轴x交于C、D两点(C在D左侧),
∴A、B关于y轴对称的点A′、B′一定在y=﹣ax+b上,且是y=﹣ax+b与的交点坐标,
∴,
整理得:ax2﹣bx+c=0,
由①②得,,
∴,
即“向光函数”为y=ax2+(2a﹣1)x+(1﹣3a),
又∵a>b>0,
∴,
∴,
∵ax2﹣(2a﹣1)x+(1﹣3a)=0,
∴x1=﹣1,,
∴xB′=﹣1,,
∴xB=1,,
∴B(1,3a﹣1),,
令“向光函数”y=ax2+bx+c中,y=0得0=ax2+bx+c即0=ax2+(2a﹣1)x+(1﹣3a),
解得x1=1,,
∴xD=1,,
∴,
∴,
∵,
∴,
∴,
∴,
∴的取值范围是:.
25.解:(1),令y=0,
解得:x=﹣1或4,
故点A、B的坐标分别为:(﹣1,0)、(4,0),
∵AB是⊙O'的直径,故O′为AB的中点,
∴点O′的坐标为;
(2)连接O′D,如图1,
∵AB是直径,
∴∠ACB=90°,
∴∠BCE=90°,
∵∠BCE的平分线为CD,
∴∠BCD=45°,
∴∠DO′B=90°,即O′D⊥AB,
∴圆的半径为,
故点D的坐标为,
又∵B(4,0),
设直线BD的表达式为:y=kx+b,
则,
解得:,
∴直线BD的表达式为:y=x﹣4;
(3)连接O′M,如图2,
∵M是BF的中点,
由垂径定理可得,∠O′MB=90°,
取O'B中点K,则M在以K为圆心,O′K为半径的圆上运动.
∴当M运动到如图G点位置时(即DG经过圆心K时),DM最长.
在Rt△O′DK中,,由勾股定理可得,,
∴.
21世纪教育网(www.21cnjy.com)
第三次月考数学模拟试卷试卷人教版2024—2025学年九年级下册
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题
1.下列图形中,是轴对称图形但不是中心对称图形的是( )
A. B. C.D.
2.若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6 B.12 C.16 D.18
3.使二次根式有意义的x的取值范围是( )
A.x≥2 B.x>2 C.x≥﹣2 D.x>﹣2
4.若式子x2+2(m﹣3)x+16是完全平方式,则m的值可能是( )
A.﹣1或7 B.0或6 C.1或5 D.2或4
5.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )
A.x(x+1)=1035 B.x(x+1)=1035
C.x(x﹣1)=1035 D.x(x﹣1)=1035
6.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
7.将抛物线y=(x﹣1)2+2向左平移1个单位,再向上平移5个单位后所得抛物线的解析式为( )
A.y=(x﹣2)2+7 B.y=(x﹣2)2+3 C.y=x2+7 D.y=x2+3
8.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为( )
A.1 B. C.1 D.
9.如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG,FC,现在有如下4个结论:
①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.二次函数y=ax2+bx﹣2(a≠0)的图象的顶点在第三象限,且过点(1,0),设t=a﹣b﹣2,则t值的变化范围是( )
A.﹣2<t<0 B.﹣3<t<0 C.﹣4<t<﹣2 D.﹣4<t<0
二、填空题(6小题,每题3分,共18分)
11.若一个圆锥的母线长为6cm,它的侧面展开图是半圆,则这个圆锥的底面半径为 cm.
12.如图是由射线AB,BC,CD,DE,EF,FA组成的平面图形,则∠1+∠2+∠3+∠4+∠5+∠6= °.
13.如图,四边形ABCD是平行四边形,点E是线段AD的中点,连接AC,BE,交于点O,若S△AOE=1,则S△BOC= .
14.某林业部门统计某种幼树在一定条件下的移植成活率,结果如下表所示:
移植总数(n) 400 750 1500 3500 7000 9000 14000
成活数(m) 369 662 1335 3203 6335 8073 12628
成活的频率 0.923 0.883 0.890 0.915 0.905 0.897 0.902
根据表中数据,估计这种幼树移植成活率的概率为 (精确到0.1).
15.若样本x1,x2,…,xn的平均数为=5,方差S2=0.025,则样本x1+3,x2+3,…,xn+3的平均数′和方差S′2分别为 .
16.若t为实数,关于x的方程x2﹣4x+t﹣2=0有两个非负实数根为a、b,且(a2﹣1)(b2﹣1)=0,则t的值是 .
第II卷
第八次月考数学模拟试卷试卷人教版2024—2025学年九年级下册
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:|﹣2|+π0+(﹣1)2025﹣()﹣1;
18.先化简:+÷,再从﹣1≤x≤3的整数中选取一个你喜欢的x的值代入求值.
19.解不等式组,并写出该不等式组的非负整数解.
20.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
21.中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.
(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为 度;
条形统计图中,喜欢“豆沙”月饼的学生有 人;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”月饼的共有 人.
(3)甲同学最爱吃云腿月饼,乙同学最爱吃豆沙月饼,现有重量、包装完全一样的云腿、豆沙、莲蓉、蛋黄四种月饼各一个,让甲、乙每人各选一个,请用画树状图法或列表法,求出甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率.
22.某文体商店计划购进一批同种型号的篮球和同种型号的排球,每一个排球的进价是每一个篮球的进价的90%,用3600元购买排球的个数要比用3600元购买篮球的个数多10个.
(1)问每一个篮球、排球的进价各是多少元?
(2)该文体商店计划购进篮球和排球共100个,且排球个数不低于篮球个数的3倍,篮球的售价定为每一个100元,排球的售价定为每一个90元.若该批篮球、排球都能卖完,问该文体商店应购进篮球、排球各多少个才能获得最大利润?最大利润是多少?
23.如图,CD是⊙O的直径,AB是⊙O的一条弦,=,AO的延长线交⊙O于点F、交DB的延长线于点P,连接PC且恰好PC∥AB,连接DF交AB于点G,延长DF交CP于点E,连接BF.
(1)求证:PC是⊙O的切线;
(2)求证:CE=PE;
(3)当BF=2时,求tan∠APD的值.
24.我们定义:点P在一次函数y=ax+b上,点Q在反比例函数上,若存在P、Q两点关于y轴对称,我们称二次函数y=ax2+bx+c为一次函数和y=ax+b反比例函数的“向光函数”,点P称为“幸福点”.例如:点P(﹣1,﹣2)在y=x﹣1上,点Q(1,﹣2)在上,P、Q两点关于y轴对称,此时二次函数y=x2﹣x﹣2为一次函数y=x﹣1和反比例函数的“向光函数”,点P(﹣1,﹣2)是“幸福点”.
(1)判断一次函数y=x+1和反比例函数是否存在“向光函数”,若存在,请求出“幸福点”坐标;若不存在,请说明理由;
(2)若一次函数y=x﹣k与反比例函数只有一个“幸福点”,求其“向光函数”的解析式;
(3)已知一次函数y=ax+b与反比例函数有两个“幸福点”A、B(A在B左侧),其“向光函数”y=ax2+bx+c与轴x交于C、D两点(C在D左侧),若有以下条件:
①a+b+c=0②“向光函数”经过点(﹣3,4),③a>b>0,记四边形ACBD的面积为S,求的取值范围.
25.如图,已知抛物线与x轴交于A,B两点,交y轴于点C,以AB为直径作⊙O′,⊙O′经过点C,连接AC,BC.
(1)求⊙O'的圆心O′的坐标;
(2)如图1,点E是AC延长线上的一点,∠BCE的平分线CD交⊙O'于点D,连接BD,求直线BD的解析式.
(3)如图2,在(2)的条件下,F是⊙O'上一动点(不与B点重合),连接BF,M是BF中点,连接DM,求DM的最大值.
参考答案
选择题
1-10:ABBAC CCCBD
二、填空题
11.解:设圆锥底面半径为rcm,
那么圆锥底面圆周长为2πrcm,
所以侧面展开图的弧长为2πrcm,
S圆锥侧面积=×2πr×6=,
解得:r=3,
故答案为:3.
12.解:由多边形的外角和等于360°可知,
∠1+∠2+∠3+∠4+∠5+∠6=360°,
故答案为:360.
13.解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E是线段AD的中点,
∴AE=AD=BC,
∵AD∥BC,
∴△AEO∽△CBO,
∴=()2=,
∴S△BOC=4×1=4,
故答案为:4.
14.解:由表格数据可得,随着样本数量不等增加,这种幼树移植成活率稳定的0.9左右,
故这种幼树移植成活率的概率约为0.9.
故本题答案为:0.9.
15.解:∵样本x1,x2,…,xn的平均数为5,
∴样本x1+3,x2+3,…,xn+3的平均数是5+3=8;
∵样本x1,x2,…,xn的方差为0.025,
∴样本x1+3,x2+3,…,xn+3的方差是0.025;
故答案为:8,0.025.
16.解:由根的判别式可知:△=16﹣4(t﹣2)=24﹣4t≥0,
∴t≤6,
由根与系数的关系可知:a+b=4,ab=t﹣2,
由于关于x的方程x2﹣4x+t﹣2=0有两个非负实数根为a、b,
∴t﹣2≥0,
∴2≤t≤6,
∵关于x的方程x2﹣4x+t﹣2=0有两个非负实数根为a、b,
∴a2﹣4a+t﹣2=0,b2﹣4b+t﹣2=0,
∴两式相加可得:a2+b2﹣4(a+b)+2(t﹣2)=0,
∴a2+b2=4(a+b)﹣2(t﹣2)=16﹣2(t﹣2)=20﹣2t,
∵(a2﹣1)(b2﹣1)=0,
∴a2b2﹣(a2+b2)+1=0,
∴(t﹣2)2﹣(20﹣2t)+1=0,
∴t2﹣2t﹣15=0,
∴t=5或t=﹣3(舍去)
∴t=5
故答案为:5.
三、解答题
17.解:(1)|﹣2|+π0+(﹣1)2025﹣()﹣1
=2﹣+1+(﹣1)﹣2
=﹣;
18.解:(1)+÷
=
=
=,
当x=3时,原式==6;
19.解(2),
由不等式①,得
x<,
由不等式②,得
x≥﹣1,
故原不等式组的解集是﹣1≤x<,
∴该不等式组的非负整数解是0,1.
20.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
点B旋转到点B2所经过的路径长为:=π.
故点B旋转到点B2所经过的路径长是π.
21.解:(1)∵“很喜欢”的部分占的百分比为:1﹣25%﹣40%=35%,
∴扇形统计图中,“很喜欢”的部分所对应的圆心角为:360°×35%=126°;
∵“很喜欢”月饼的同学数:60×35%=21,
∴条形统计图中,喜欢“豆沙”月饼的学生数:21﹣6﹣3﹣8=4,
故答案分别为126°,4.
(2)900名学生中“很喜欢”的有900×35%=315人,
900名学生中“比较喜欢”的有900×40%=360人,
∴估计该校学生中“很喜欢”和“比较喜欢”月饼的共有675人.
故答案为675.
(3)为了表示方便,记云腿、豆沙、莲蓉、蛋黄四种月饼分别为A、B、C、D.画出的树状图如图所示,
∴甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率==
22.解:(1)设每一个篮球的进价是x元,则每一个排球的进价是90%x元,依题意有
+10=,
解得x=40,
经检验,x=40是原方程的解,
90%x=90%×40=36.
故每一个篮球的进价是40元,每一个排球的进价是36元;
(2)设文体商店计划购进篮球m个,总利润y元,则
y=(100﹣40)m+(90﹣36)(100﹣m)=6m+5400,
依题意有,
解得0<m≤25且m为整数,
∵m为整数,
∴y随m的增大而增大,
∴m=25时,y最大,这时y=6×25+5400=5550,
100﹣25=75(个).
故该文体商店应购进篮球25个、排球75个才能获得最大利润,最大利润是5550元.
23.(1)证明:∵CD是⊙O的直径,
∴CD⊥AB,
又∵PC∥AB,
∴PC⊥CD,
∴PC为⊙O的切线; ……(3分)
(2)∵PC∥AB,
∴∠EPF=∠PAB,
∠FDB=∠PAB,
∴∠EPF=∠FDB,
∵∠PEF=∠DEP,
∴△FEP∽△PED,
∴,
∴PE2=EF ED,
连接CF,
同理得:△ECF∽△EDC,
∴,即EC2=EF ED,
∴CE2=PE2,
∴CE=PE; ……(7分)
(3)∵PC∥AB,
∴,,
∴,
由(2)知:CE=PE,
∴GH=BG,
∴∠HGD=∠BGF,∠DHG=∠FBG=90°,
∴△DHG≌△FBG(ASA),
∴DH=BF=2,
又AO=OF,AH=HB,
∴OH=BF=1,
∴OD=3,CD=6,
连接OB,过点O作OM⊥DB,则OB=OD=3,
∴,
∴,,
∴,
又PC∥AB,
∴,
∴,
∴,
∴MP=5,
在Rt△POM中,tan∠APD===……(10分)
24.解:(1)一次函数y=x+1和反比例函数存在“向光函数”,理由如下:
点P在一次函数y=ax+b上,点Q在反比例函数上,若存在P、Q两点关于y轴对称,我们称二次函数y=ax2+bx+c为一次函数和y=ax+b反比例函数的“向光函数”,点P称为“幸福点”.设“幸福点”坐标为P(m,n),则Q(﹣m,n),
∴,
解并检验得:,,
∴一次函数y=x+2和反比例函数是存在“向光函数”,“幸福点”坐标为(1,2),(﹣2,﹣1);
(2)∵一次函数y=x﹣k关于y轴对称的直线函数解析式为y=﹣x﹣k,而且一次函数y=x﹣k与反比例函数只有一个“幸福点”,
所以y=﹣x﹣k与反比例函数只有一个交点,
∴y=﹣x﹣k③,,
整理得:x2+kx+(k+3)=0,
Δ=k2﹣4(k+3)=0,
解得:k1=﹣2,k2=6,
当k=﹣2时,则一次函数y=x+2与反比例函数只有一个“幸福点”,向光函数”的解析式为:y=x2+2x+1,
当k=6时,则一次函数y=x﹣6与反比例函数只有一个“幸福点”,向光函数”的解析式为:y=x2﹣6x+9,
∴“向光函数”的解析式为:y=x2+2x+1或y=x2﹣6x+9.
(3)已知一次函数y=ax+b与反比例函数有两个“幸福点”A、B(A在B左侧),其“向光函数”y=ax2+bx+c与轴x交于C、D两点(C在D左侧),
∴A、B关于y轴对称的点A′、B′一定在y=﹣ax+b上,且是y=﹣ax+b与的交点坐标,
∴,
整理得:ax2﹣bx+c=0,
由①②得,,
∴,
即“向光函数”为y=ax2+(2a﹣1)x+(1﹣3a),
又∵a>b>0,
∴,
∴,
∵ax2﹣(2a﹣1)x+(1﹣3a)=0,
∴x1=﹣1,,
∴xB′=﹣1,,
∴xB=1,,
∴B(1,3a﹣1),,
令“向光函数”y=ax2+bx+c中,y=0得0=ax2+bx+c即0=ax2+(2a﹣1)x+(1﹣3a),
解得x1=1,,
∴xD=1,,
∴,
∴,
∵,
∴,
∴,
∴,
∴的取值范围是:.
25.解:(1),令y=0,
解得:x=﹣1或4,
故点A、B的坐标分别为:(﹣1,0)、(4,0),
∵AB是⊙O'的直径,故O′为AB的中点,
∴点O′的坐标为;
(2)连接O′D,如图1,
∵AB是直径,
∴∠ACB=90°,
∴∠BCE=90°,
∵∠BCE的平分线为CD,
∴∠BCD=45°,
∴∠DO′B=90°,即O′D⊥AB,
∴圆的半径为,
故点D的坐标为,
又∵B(4,0),
设直线BD的表达式为:y=kx+b,
则,
解得:,
∴直线BD的表达式为:y=x﹣4;
(3)连接O′M,如图2,
∵M是BF的中点,
由垂径定理可得,∠O′MB=90°,
取O'B中点K,则M在以K为圆心,O′K为半径的圆上运动.
∴当M运动到如图G点位置时(即DG经过圆心K时),DM最长.
在Rt△O′DK中,,由勾股定理可得,,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
