第十八章平行四边形期中章节复习(二)(含答案)
文档属性
| 名称 | 第十八章平行四边形期中章节复习(二)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 752.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十八章平行四边形期中章节复习(二)人教版2024—2025学年八年级下册
一、选择题
1.观察图,根据所标注的数据能判断其一定是平行四边形的是( )
A.只有③ B.只有② C.①② D.①②③
2.下列关于平行四边形的说法中错误的是( )
A.平行四边形的对角相等,邻角互补
B.一组对边相等,一组对角相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
3.如图,△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AB=4,AC=6,则MD等于( )
A.4 B.3 C.2 D.1
4.已知 ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使得 ABCD是矩形的条件是( )
A.①②③ B.②③④ C.①②④ D.①③④
5.如图,D是△ABC内部一点,AC⊥BD,且,依次取AB,BC,CD,AD的中点,并顺次连接得到四边形MNPQ,则四边形MNPQ的面积是( )
A.6 B.12 C.24 D.48
6.如图,在菱形ABCD中,AB=10,AC=16,AC交BD于点O,DE⊥BC于点E,连接OE,则OE的长为( )
A.6 B.5 C.4 D.3
二、填空题
7.如图,菱形ABCD的对角线AC,BD相交于点O,E为AD中点,OE=4,则菱形ABCD的周长为 .
8.如图,在正方形ABCD中,点O是对角线AC,BD交点,过点O作射线OM,ON分别交BC,CD于点E,F,且∠EOF=90°,OC,EF交于点G.有下列结论:
(1)△DOF≌△COE;
(2)CF=BE;
(3)四边形CEOF的面积为正方形ABCD面积的;
(4)OF2+OE2=EF2.其中正确的是 .
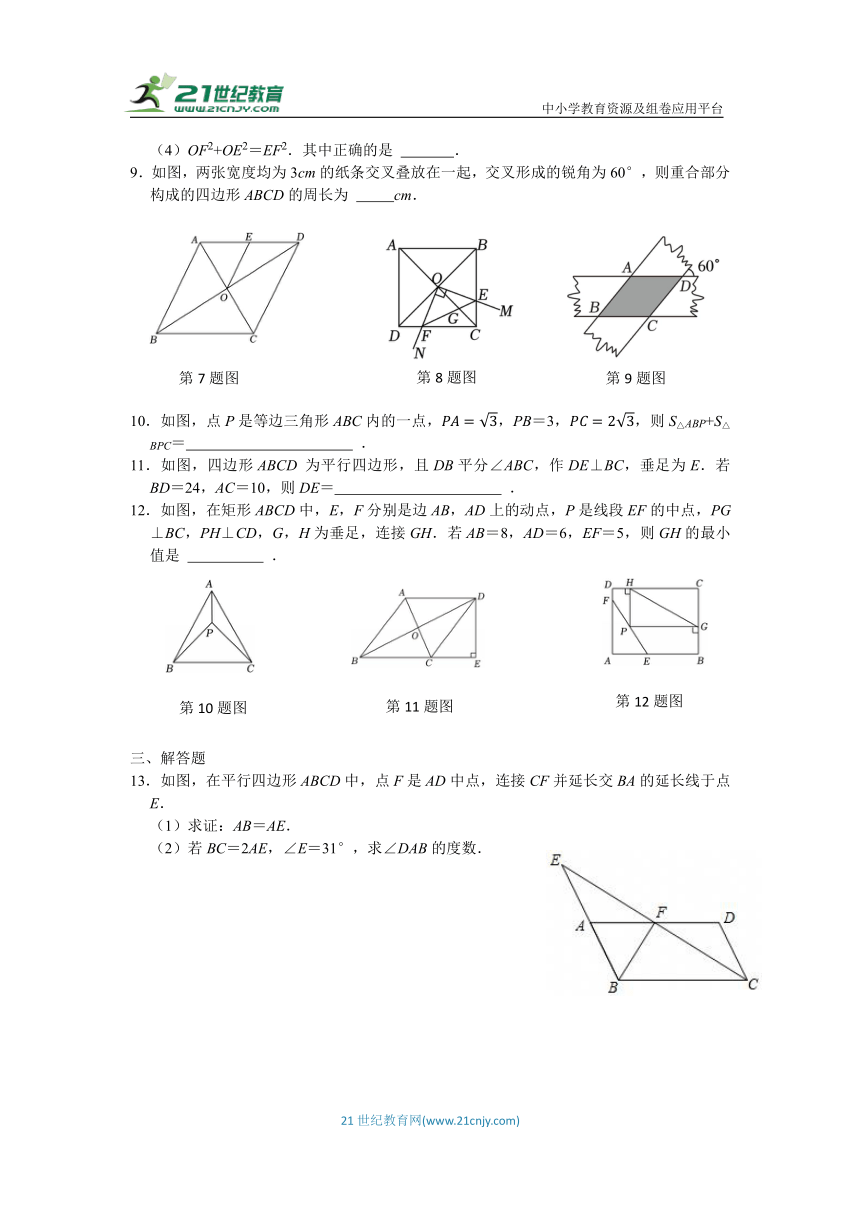
9.如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形ABCD的周长为 cm.
10.如图,点P是等边三角形ABC内的一点,,PB=3,,则S△ABP+S△BPC= .
11.如图,四边形ABCD 为平行四边形,且DB平分∠ABC,作DE⊥BC,垂足为E.若BD=24,AC=10,则DE= .
12.如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=5,则GH的最小值是 .
三、解答题
13.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
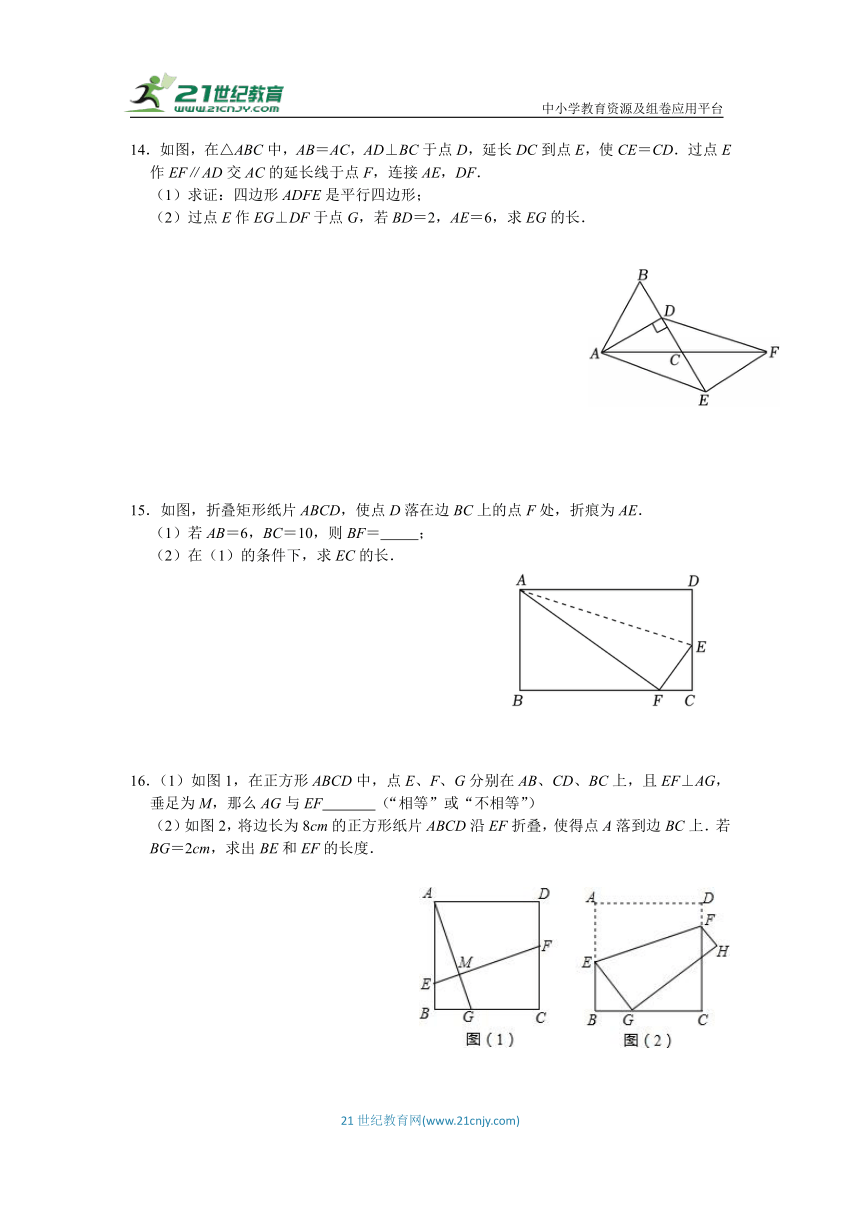
14.如图,在△ABC中,AB=AC,AD⊥BC于点D,延长DC到点E,使CE=CD.过点E作EF∥AD交AC的延长线于点F,连接AE,DF.
(1)求证:四边形ADFE是平行四边形;
(2)过点E作EG⊥DF于点G,若BD=2,AE=6,求EG的长.
15.如图,折叠矩形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.
(1)若AB=6,BC=10,则BF= ;
(2)在(1)的条件下,求EC的长.
16.(1)如图1,在正方形ABCD中,点E、F、G分别在AB、CD、BC上,且EF⊥AG,垂足为M,那么AG与EF (“相等”或“不相等”)
(2)如图2,将边长为8cm的正方形纸片ABCD沿EF折叠,使得点A落到边BC上.若BG=2cm,求出BE和EF的长度.
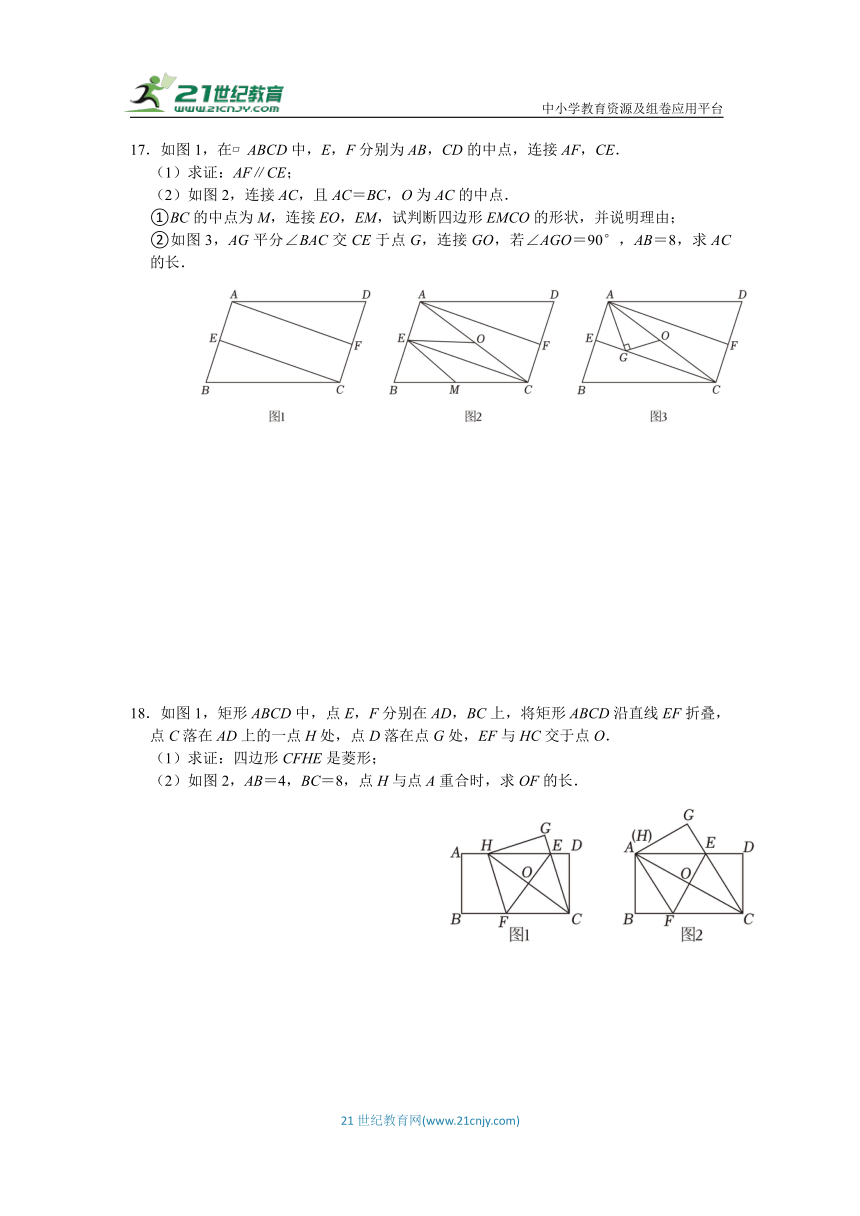
17.如图1,在 ABCD中,E,F分别为AB,CD的中点,连接AF,CE.
(1)求证:AF∥CE;
(2)如图2,连接AC,且AC=BC,O为AC的中点.
①BC的中点为M,连接EO,EM,试判断四边形EMCO的形状,并说明理由;
②如图3,AG平分∠BAC交CE于点G,连接GO,若∠AGO=90°,AB=8,求AC的长.
18.如图1,矩形ABCD中,点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,EF与HC交于点O.
(1)求证:四边形CFHE是菱形;
(2)如图2,AB=4,BC=8,点H与点A重合时,求OF的长.
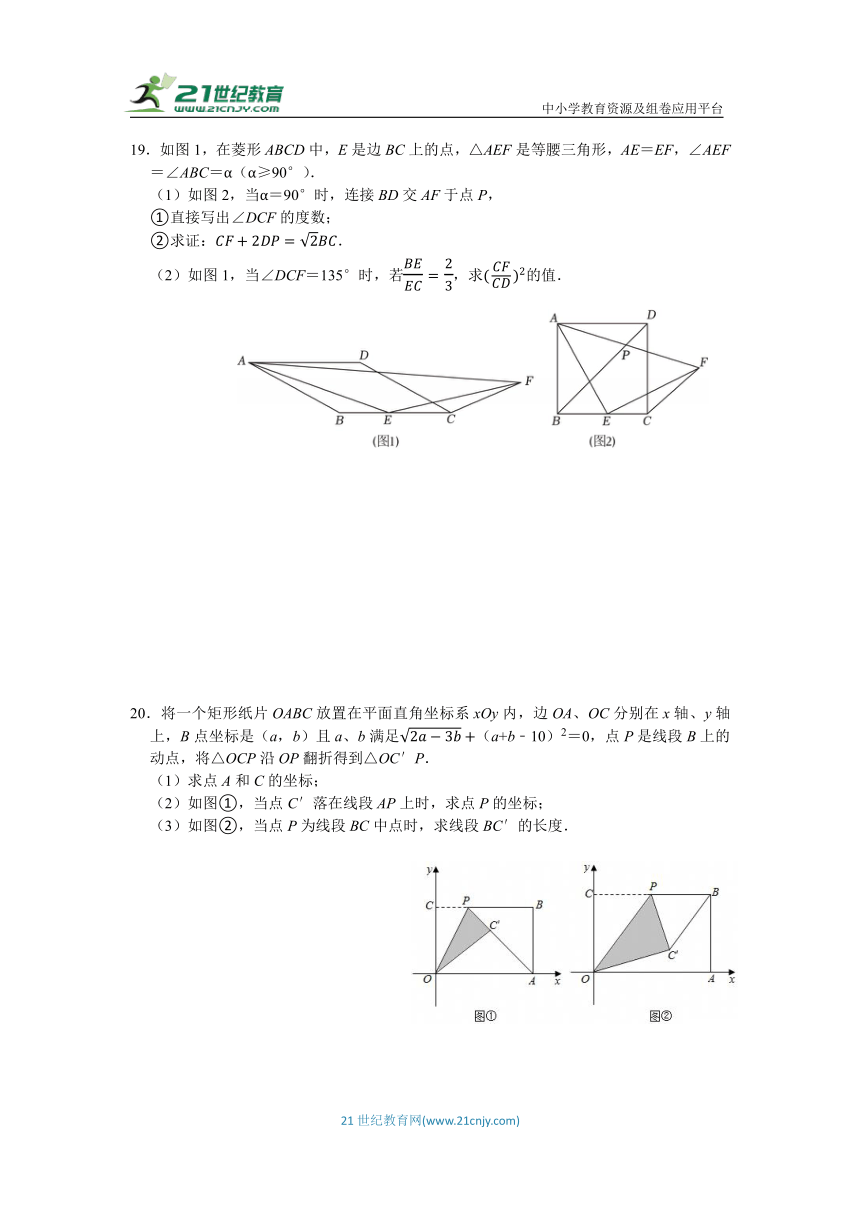
19.如图1,在菱形ABCD中,E是边BC上的点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°).
(1)如图2,当α=90°时,连接BD交AF于点P,
①直接写出∠DCF的度数;
②求证:.
(2)如图1,当∠DCF=135°时,若,求的值.
20.将一个矩形纸片OABC放置在平面直角坐标系xOy内,边OA、OC分别在x轴、y轴上,B点坐标是(a,b)且a、b满足(a+b﹣10)2=0,点P是线段B上的动点,将△OCP沿OP翻折得到△OC′P.
(1)求点A和C的坐标;
(2)如图①,当点C′落在线段AP上时,求点P的坐标;
(3)如图②,当点P为线段BC中点时,求线段BC′的长度.
参考答案
一、选择题
1-6:ABDDBA
二、填空题
7.【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△AOD为直角三角形.
∵OE=4,且点E为线段AD的中点,
∴AD=2OE=8.
∴C菱形ABCD=4AD=4×8=32.
故答案为:32.
8.【解答】解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE+∠EOF=∠COF+∠DOF=90°,
∴∠COE=∠DOF,
在△COE和△DOF中,
,
∴△COE≌△DOF(ASA),故①正确;
②∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,故②正确;
③由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的 ,故③正确;
④在Rt△ECF中,∠EOF=90°,根据勾股定理,得:OE2+OF2=EF2,故④正确;
综上所述,正确的是①②③④,
故答案为:①②③④.
9.【解答】解:答案为:.
10.【解答】解:将△APC绕点A旋转60°得到△AEB,过点B作BF⊥AP于点F,
∴AE=AP,BE=PC=3,∠PAE=60°,
∴△AEP是等边三角形,
∴EP=AP,∠APE=60°,
∵BE2=12,PB2+PE2=9+3=12,
∴BE2=PE2+PB2,
∴∠BPE=90°,
∴∠APB=150°,
∴∠BPF=30°,
∴BFPB,
∵BE=2PE,∠BPE=90°,
∴∠EBP=30°,
∴∠BEP=90°﹣30°=60°,
∵∠AEP=60°,
∴∠APC=∠AEB=120°,
∴∠BPC=360°﹣150°﹣120°=90°,
∴S△APB+S△PBC3×2.
故答案为:.
11.【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵DB平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴OBBD=4,OCAC=5,AC⊥BD,
∴∠BOC=90°,
∴BC13,
∵DE⊥BC,
∴菱形ABCD的面积=BC DEAC BD,
即13DE10×24,
解得:DE,
故答案为:.
12.【解答】解:连接AC、AP、CP,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,∠BAD=∠B=∠C=90°,
∴AC10,
∵P是线段EF的中点,
∴APEF=2.5,
∵PG⊥BC,PH⊥CD,
∴∠PGC=∠PHC=90°,
∴四边形PGCH是矩形,
∴GH=CP,
当A、P、C三点共线时,CP最小=AC﹣AP=10﹣2.5=7.5,
∴GH的最小值是7.5,
故答案为:7.5.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
14.【解答】(1)证明:∵EF∥AD,
∴∠FEC=∠ADC,
又∵CE=CD,∠FCE=∠ACD,
∴△FCE≌△ACD(ASA),
∴EF=AD,
∴四边形ADFE是平行四边形;
(2)解:如图,
由(1)可知,四边形ADFE是平行四边形,
∴DF=AE=6,
∵AB=AC,AD⊥BC,
∴CD=BD=2,
∴CE=CD=2,
∴DE=2CD=4,
∵EF∥AD,
∴EF⊥BC,
∴∠DEF=90°,
∴EF2,
∵EG⊥DF,
∴S△DEFDF EG EF,
∴EG,
即EG的长为.
15.【解答】解:(1)∵四边形ABCD是长方形,
∴AD=BC=10,CD=AB=6,
∵长方形纸片沿AE折叠,点D落在BC边的点F处,
∴AF=AD=10,EF=DE,
在Rt△ABF中,;
(2)由(1)知BF=8,
∴FC=BC﹣BF=10﹣8=2,
设DE=x,则EC=CD﹣DE=6﹣x,
在Rt△CEF中,EC2+FC2=EF2,
即(6﹣x)2+22=x2,
解得,
∴.
16.【解答】解:(1)如图(1)所示,过点E作EH∥AD,交CD于H;则四边形AEHD为矩形;
∴EH=AD=AB;
∵AG⊥EF,EH∥AD,
∴∠BAG+∠AEF=90°,∠AEF+∠FEH=90°,
∴∠BAG=∠FEH;在△ABG与△EHF中,
∵,∴△ABG≌△EHF(ASA)
∴AG=EF.
故答案为相等;
(2)如图(2),连接AG;
设BE=x,则AE=8﹣x;由对称原理得:EG=EA=8﹣x,∠AEF=∠GEF,
∴EF⊥AG;由问题(1)知:EF=AG;
∵四边形ABCD为正方形,∴∠EBG=90°;
由勾股定理得:AG2=82+22,AG=;
(8﹣x)2=x2+22,解得x=,
∴BE=(cm),EF=(cm).
17.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵E,F分别为AB,CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF∥CE;
(2)解:①四边形EMCO为菱形.理由:
∵O为AC的中点,E为AB的中点,
∴OE为△ABC的中位线,
∴OE∥BC,OE=BC.
∵E为AB的中点,BC的中点为M,
∴EM∥AC,EM=AC,
∴四边形EMCO为平行四边形.
∵AC=BC,
∴EO=EM,
∴四边形EMCO为菱形.
②过点O作OH⊥EC于点H,过点G作GM⊥AC于点M,如图,
∵AC=BC,E为AB的中点,
∴CE⊥AB,AE=AB=4.
∵AG平分∠BAC交CE于点G,
∴∠GAE=∠GAC,
∵GM⊥AC,GE⊥AB,
∴GE=GM.
在Rt△AEG和Rt△AMG中,
,
∴Rt△AEG≌Rt△AMG(HL),
∴AE=AM=4.
∵CE⊥AE,OH⊥EC,
∴OH∥AE,
∵O为AC的中点,
∴OH=AE=2.
∵∠AGO=90°,
∴∠AGE+∠OGC=90°,∠AGM+∠OGM=90°,
∵Rt△AEG≌Rt△AMG,
∴∠AGE=∠AGM,
∴∠OGM=∠OGH,
∵OM⊥GM,OH⊥GH,
∴OM=OH=2,
∴OA=AM+OM=6,
∵O为AC的中点,
∴AC=2OA=12.
18.【解答】(1)证明:在矩形ABCD中,AD∥BC,
即HE∥CF,
∴∠HEF=∠EFC,
由翻折可知:∠EFC=∠HFE,
∴∠HEF=∠HFE,
∴HE=HF,
∵FC=FH,
∴HE=CF,
∵EH∥CF,
∴四边形CFHE是平行四边形,
∵CF=FH,
∴四边形CFHE是菱形;
(2)解:点H与点A重合时,设BF=x,则AF=FC=BC﹣BF=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8﹣x)2,
解得x=3,
∴CE=AF=8﹣x=5,
∵CD=AB=4,
∴DE===3,
如图,过点F作FM⊥AD于M,得矩形ABFM,矩形CDMF,
∴AM=BF,DM=CF,MF=AB=4,
∴ME=8﹣3﹣3=2,
由勾股定理得,EF===2,
∴OF=EF=.
19.【解答】解:(1)①∠DCF的度数是45°,
理由:如图2,作FN⊥CD于点N,FM⊥BC交BC的延长线于点M,则∠M=90°,
∵四边形ABCD是菱形,∠AEF=∠ABC=α=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCD=90°,
∴∠ABE=∠M,∠BAE=∠MEF=90°﹣∠AEB,∠MCN=90°,
在△ABE和△EMF中,
,
∴△ABE≌△EMF(AAS),
∴AB=EM=BC,BE=MF,
∵BE=BC﹣CE=EM﹣CE=CM,
∴CM=MF,
∴∠MCF=∠MFC=45°,
∴∠DCF=90°﹣∠MCF=45°,
∴∠DCF的度数是45°.
②证明:如图2,连接AC交BD于点Q,连接CP,则AQ=CQ,DQ=BQ,
∵BD垂直平分AC,
∴AP=CP,
∴∠PCA=∠PAC,
∵AD=CD,∠ADC=90°,
∴∠DCA=∠DAC=45°,
∴∠ACF=∠DCA+∠DCF=90°,
∴∠PCF=90°﹣∠PCA=90°﹣∠PAC=∠PFC,
∴FP=CP,
∴AP=FP,
∴CF=2QP,
∴CF+2DP=2QP+2DP=2DQ=BD,
∵BC=CD,∠BCD=90°,
∴BDBC,
∴CF+2DPBC.
(2)如图1,作FL⊥BC交BC的延长线于点L,在CL上取一点H,使CH=BE,连接FH,
∵四边形ABCD是菱形,∠AEF=∠ABC=α,
∴AB=BC=BE+CE=CH+CE=EH,∠BAE=∠HEF=180°﹣α﹣∠AEB,
在△ABE和△EHF中,
,
∴△ABE≌△EHF(SAS),
∴BE=HF,∠B=∠EHF,
∴CH=HF,
∴∠HCF=∠HFC,
∴∠FHL=∠HCF+∠HFC=2∠HCF,
∵AB∥CD,∠DCF=135°,
∴∠B=∠DCH,
∴∠EHF=∠DCH=135°+∠HCF,
∴135°+∠HCF+2∠HCF=180°,
∴∠HCF=15°,
∴∠FHL=30°,
设FL=m,
∵∠L=90°,
∴CH=HF=2FL=2m,
∴HLm,
∴CF2=(2mm)2+m2=(8+4)m2,
∵,
∴ECCH2m=3m,
∴CD=BC=EH=3m+2m=5m,
∴CD2=(5m)2=25m2,
∴,
∴的值为.
20.解:(1)∵(a+b﹣10)2=0,
∴.
解得:,
∴B(6,4),
又∵四边形OABC为矩形,
∴A(6,0),C(0,4);
(2)由(1)可知:AO=BC=6,CO=BA=4,
∵AO∥BC,
∴∠CPO=∠AOP,
由折叠易知:∠CPO=∠C'PO,
∴∠AOP=∠C'PO,
∴AO=AP=6,
在Rt△ABP中,PB.
∴CP=BC﹣PB=6﹣2,
∴点P坐标为:(6﹣2,4);
(3)连接CC',交PO于点D,如图所示:
在Rt△PCO中,OC=4,PC3,
∴OP,
由折叠易知:OP垂直平分线段CC',即D为CC'的中点,
∴S△PCO,
∴CD,
在Rt△PDC中,PD,
又∵D为CC'的中点,P为BC中点,
∴PD为△CC'B的中位线,
∴BC'=2PD=2.
21世纪教育网(www.21cnjy.com)
第十八章平行四边形期中章节复习(二)人教版2024—2025学年八年级下册
一、选择题
1.观察图,根据所标注的数据能判断其一定是平行四边形的是( )
A.只有③ B.只有② C.①② D.①②③
2.下列关于平行四边形的说法中错误的是( )
A.平行四边形的对角相等,邻角互补
B.一组对边相等,一组对角相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
3.如图,△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AB=4,AC=6,则MD等于( )
A.4 B.3 C.2 D.1
4.已知 ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使得 ABCD是矩形的条件是( )
A.①②③ B.②③④ C.①②④ D.①③④
5.如图,D是△ABC内部一点,AC⊥BD,且,依次取AB,BC,CD,AD的中点,并顺次连接得到四边形MNPQ,则四边形MNPQ的面积是( )
A.6 B.12 C.24 D.48
6.如图,在菱形ABCD中,AB=10,AC=16,AC交BD于点O,DE⊥BC于点E,连接OE,则OE的长为( )
A.6 B.5 C.4 D.3
二、填空题
7.如图,菱形ABCD的对角线AC,BD相交于点O,E为AD中点,OE=4,则菱形ABCD的周长为 .
8.如图,在正方形ABCD中,点O是对角线AC,BD交点,过点O作射线OM,ON分别交BC,CD于点E,F,且∠EOF=90°,OC,EF交于点G.有下列结论:
(1)△DOF≌△COE;
(2)CF=BE;
(3)四边形CEOF的面积为正方形ABCD面积的;
(4)OF2+OE2=EF2.其中正确的是 .
9.如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形ABCD的周长为 cm.
10.如图,点P是等边三角形ABC内的一点,,PB=3,,则S△ABP+S△BPC= .
11.如图,四边形ABCD 为平行四边形,且DB平分∠ABC,作DE⊥BC,垂足为E.若BD=24,AC=10,则DE= .
12.如图,在矩形ABCD中,E,F分别是边AB,AD上的动点,P是线段EF的中点,PG⊥BC,PH⊥CD,G,H为垂足,连接GH.若AB=8,AD=6,EF=5,则GH的最小值是 .
三、解答题
13.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
14.如图,在△ABC中,AB=AC,AD⊥BC于点D,延长DC到点E,使CE=CD.过点E作EF∥AD交AC的延长线于点F,连接AE,DF.
(1)求证:四边形ADFE是平行四边形;
(2)过点E作EG⊥DF于点G,若BD=2,AE=6,求EG的长.
15.如图,折叠矩形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.
(1)若AB=6,BC=10,则BF= ;
(2)在(1)的条件下,求EC的长.
16.(1)如图1,在正方形ABCD中,点E、F、G分别在AB、CD、BC上,且EF⊥AG,垂足为M,那么AG与EF (“相等”或“不相等”)
(2)如图2,将边长为8cm的正方形纸片ABCD沿EF折叠,使得点A落到边BC上.若BG=2cm,求出BE和EF的长度.
17.如图1,在 ABCD中,E,F分别为AB,CD的中点,连接AF,CE.
(1)求证:AF∥CE;
(2)如图2,连接AC,且AC=BC,O为AC的中点.
①BC的中点为M,连接EO,EM,试判断四边形EMCO的形状,并说明理由;
②如图3,AG平分∠BAC交CE于点G,连接GO,若∠AGO=90°,AB=8,求AC的长.
18.如图1,矩形ABCD中,点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,EF与HC交于点O.
(1)求证:四边形CFHE是菱形;
(2)如图2,AB=4,BC=8,点H与点A重合时,求OF的长.
19.如图1,在菱形ABCD中,E是边BC上的点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°).
(1)如图2,当α=90°时,连接BD交AF于点P,
①直接写出∠DCF的度数;
②求证:.
(2)如图1,当∠DCF=135°时,若,求的值.
20.将一个矩形纸片OABC放置在平面直角坐标系xOy内,边OA、OC分别在x轴、y轴上,B点坐标是(a,b)且a、b满足(a+b﹣10)2=0,点P是线段B上的动点,将△OCP沿OP翻折得到△OC′P.
(1)求点A和C的坐标;
(2)如图①,当点C′落在线段AP上时,求点P的坐标;
(3)如图②,当点P为线段BC中点时,求线段BC′的长度.
参考答案
一、选择题
1-6:ABDDBA
二、填空题
7.【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△AOD为直角三角形.
∵OE=4,且点E为线段AD的中点,
∴AD=2OE=8.
∴C菱形ABCD=4AD=4×8=32.
故答案为:32.
8.【解答】解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE+∠EOF=∠COF+∠DOF=90°,
∴∠COE=∠DOF,
在△COE和△DOF中,
,
∴△COE≌△DOF(ASA),故①正确;
②∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,故②正确;
③由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的 ,故③正确;
④在Rt△ECF中,∠EOF=90°,根据勾股定理,得:OE2+OF2=EF2,故④正确;
综上所述,正确的是①②③④,
故答案为:①②③④.
9.【解答】解:答案为:.
10.【解答】解:将△APC绕点A旋转60°得到△AEB,过点B作BF⊥AP于点F,
∴AE=AP,BE=PC=3,∠PAE=60°,
∴△AEP是等边三角形,
∴EP=AP,∠APE=60°,
∵BE2=12,PB2+PE2=9+3=12,
∴BE2=PE2+PB2,
∴∠BPE=90°,
∴∠APB=150°,
∴∠BPF=30°,
∴BFPB,
∵BE=2PE,∠BPE=90°,
∴∠EBP=30°,
∴∠BEP=90°﹣30°=60°,
∵∠AEP=60°,
∴∠APC=∠AEB=120°,
∴∠BPC=360°﹣150°﹣120°=90°,
∴S△APB+S△PBC3×2.
故答案为:.
11.【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵DB平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴OBBD=4,OCAC=5,AC⊥BD,
∴∠BOC=90°,
∴BC13,
∵DE⊥BC,
∴菱形ABCD的面积=BC DEAC BD,
即13DE10×24,
解得:DE,
故答案为:.
12.【解答】解:连接AC、AP、CP,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,∠BAD=∠B=∠C=90°,
∴AC10,
∵P是线段EF的中点,
∴APEF=2.5,
∵PG⊥BC,PH⊥CD,
∴∠PGC=∠PHC=90°,
∴四边形PGCH是矩形,
∴GH=CP,
当A、P、C三点共线时,CP最小=AC﹣AP=10﹣2.5=7.5,
∴GH的最小值是7.5,
故答案为:7.5.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
14.【解答】(1)证明:∵EF∥AD,
∴∠FEC=∠ADC,
又∵CE=CD,∠FCE=∠ACD,
∴△FCE≌△ACD(ASA),
∴EF=AD,
∴四边形ADFE是平行四边形;
(2)解:如图,
由(1)可知,四边形ADFE是平行四边形,
∴DF=AE=6,
∵AB=AC,AD⊥BC,
∴CD=BD=2,
∴CE=CD=2,
∴DE=2CD=4,
∵EF∥AD,
∴EF⊥BC,
∴∠DEF=90°,
∴EF2,
∵EG⊥DF,
∴S△DEFDF EG EF,
∴EG,
即EG的长为.
15.【解答】解:(1)∵四边形ABCD是长方形,
∴AD=BC=10,CD=AB=6,
∵长方形纸片沿AE折叠,点D落在BC边的点F处,
∴AF=AD=10,EF=DE,
在Rt△ABF中,;
(2)由(1)知BF=8,
∴FC=BC﹣BF=10﹣8=2,
设DE=x,则EC=CD﹣DE=6﹣x,
在Rt△CEF中,EC2+FC2=EF2,
即(6﹣x)2+22=x2,
解得,
∴.
16.【解答】解:(1)如图(1)所示,过点E作EH∥AD,交CD于H;则四边形AEHD为矩形;
∴EH=AD=AB;
∵AG⊥EF,EH∥AD,
∴∠BAG+∠AEF=90°,∠AEF+∠FEH=90°,
∴∠BAG=∠FEH;在△ABG与△EHF中,
∵,∴△ABG≌△EHF(ASA)
∴AG=EF.
故答案为相等;
(2)如图(2),连接AG;
设BE=x,则AE=8﹣x;由对称原理得:EG=EA=8﹣x,∠AEF=∠GEF,
∴EF⊥AG;由问题(1)知:EF=AG;
∵四边形ABCD为正方形,∴∠EBG=90°;
由勾股定理得:AG2=82+22,AG=;
(8﹣x)2=x2+22,解得x=,
∴BE=(cm),EF=(cm).
17.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵E,F分别为AB,CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF∥CE;
(2)解:①四边形EMCO为菱形.理由:
∵O为AC的中点,E为AB的中点,
∴OE为△ABC的中位线,
∴OE∥BC,OE=BC.
∵E为AB的中点,BC的中点为M,
∴EM∥AC,EM=AC,
∴四边形EMCO为平行四边形.
∵AC=BC,
∴EO=EM,
∴四边形EMCO为菱形.
②过点O作OH⊥EC于点H,过点G作GM⊥AC于点M,如图,
∵AC=BC,E为AB的中点,
∴CE⊥AB,AE=AB=4.
∵AG平分∠BAC交CE于点G,
∴∠GAE=∠GAC,
∵GM⊥AC,GE⊥AB,
∴GE=GM.
在Rt△AEG和Rt△AMG中,
,
∴Rt△AEG≌Rt△AMG(HL),
∴AE=AM=4.
∵CE⊥AE,OH⊥EC,
∴OH∥AE,
∵O为AC的中点,
∴OH=AE=2.
∵∠AGO=90°,
∴∠AGE+∠OGC=90°,∠AGM+∠OGM=90°,
∵Rt△AEG≌Rt△AMG,
∴∠AGE=∠AGM,
∴∠OGM=∠OGH,
∵OM⊥GM,OH⊥GH,
∴OM=OH=2,
∴OA=AM+OM=6,
∵O为AC的中点,
∴AC=2OA=12.
18.【解答】(1)证明:在矩形ABCD中,AD∥BC,
即HE∥CF,
∴∠HEF=∠EFC,
由翻折可知:∠EFC=∠HFE,
∴∠HEF=∠HFE,
∴HE=HF,
∵FC=FH,
∴HE=CF,
∵EH∥CF,
∴四边形CFHE是平行四边形,
∵CF=FH,
∴四边形CFHE是菱形;
(2)解:点H与点A重合时,设BF=x,则AF=FC=BC﹣BF=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8﹣x)2,
解得x=3,
∴CE=AF=8﹣x=5,
∵CD=AB=4,
∴DE===3,
如图,过点F作FM⊥AD于M,得矩形ABFM,矩形CDMF,
∴AM=BF,DM=CF,MF=AB=4,
∴ME=8﹣3﹣3=2,
由勾股定理得,EF===2,
∴OF=EF=.
19.【解答】解:(1)①∠DCF的度数是45°,
理由:如图2,作FN⊥CD于点N,FM⊥BC交BC的延长线于点M,则∠M=90°,
∵四边形ABCD是菱形,∠AEF=∠ABC=α=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCD=90°,
∴∠ABE=∠M,∠BAE=∠MEF=90°﹣∠AEB,∠MCN=90°,
在△ABE和△EMF中,
,
∴△ABE≌△EMF(AAS),
∴AB=EM=BC,BE=MF,
∵BE=BC﹣CE=EM﹣CE=CM,
∴CM=MF,
∴∠MCF=∠MFC=45°,
∴∠DCF=90°﹣∠MCF=45°,
∴∠DCF的度数是45°.
②证明:如图2,连接AC交BD于点Q,连接CP,则AQ=CQ,DQ=BQ,
∵BD垂直平分AC,
∴AP=CP,
∴∠PCA=∠PAC,
∵AD=CD,∠ADC=90°,
∴∠DCA=∠DAC=45°,
∴∠ACF=∠DCA+∠DCF=90°,
∴∠PCF=90°﹣∠PCA=90°﹣∠PAC=∠PFC,
∴FP=CP,
∴AP=FP,
∴CF=2QP,
∴CF+2DP=2QP+2DP=2DQ=BD,
∵BC=CD,∠BCD=90°,
∴BDBC,
∴CF+2DPBC.
(2)如图1,作FL⊥BC交BC的延长线于点L,在CL上取一点H,使CH=BE,连接FH,
∵四边形ABCD是菱形,∠AEF=∠ABC=α,
∴AB=BC=BE+CE=CH+CE=EH,∠BAE=∠HEF=180°﹣α﹣∠AEB,
在△ABE和△EHF中,
,
∴△ABE≌△EHF(SAS),
∴BE=HF,∠B=∠EHF,
∴CH=HF,
∴∠HCF=∠HFC,
∴∠FHL=∠HCF+∠HFC=2∠HCF,
∵AB∥CD,∠DCF=135°,
∴∠B=∠DCH,
∴∠EHF=∠DCH=135°+∠HCF,
∴135°+∠HCF+2∠HCF=180°,
∴∠HCF=15°,
∴∠FHL=30°,
设FL=m,
∵∠L=90°,
∴CH=HF=2FL=2m,
∴HLm,
∴CF2=(2mm)2+m2=(8+4)m2,
∵,
∴ECCH2m=3m,
∴CD=BC=EH=3m+2m=5m,
∴CD2=(5m)2=25m2,
∴,
∴的值为.
20.解:(1)∵(a+b﹣10)2=0,
∴.
解得:,
∴B(6,4),
又∵四边形OABC为矩形,
∴A(6,0),C(0,4);
(2)由(1)可知:AO=BC=6,CO=BA=4,
∵AO∥BC,
∴∠CPO=∠AOP,
由折叠易知:∠CPO=∠C'PO,
∴∠AOP=∠C'PO,
∴AO=AP=6,
在Rt△ABP中,PB.
∴CP=BC﹣PB=6﹣2,
∴点P坐标为:(6﹣2,4);
(3)连接CC',交PO于点D,如图所示:
在Rt△PCO中,OC=4,PC3,
∴OP,
由折叠易知:OP垂直平分线段CC',即D为CC'的中点,
∴S△PCO,
∴CD,
在Rt△PDC中,PD,
又∵D为CC'的中点,P为BC中点,
∴PD为△CC'B的中位线,
∴BC'=2PD=2.
21世纪教育网(www.21cnjy.com)
