山西省百师联盟2024-2025学年高二下学期3月联考数学试题(含详解)
文档属性
| 名称 | 山西省百师联盟2024-2025学年高二下学期3月联考数学试题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 389.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:23:29 | ||
图片预览



文档简介
山西省百师联盟2024 2025学年高二下学期3月联考数学试题
一、单选题(本大题共8小题)
1.书架上有10 本不同的自然科学图书和9本不同的社会科学图书,甲同学想从中选出1本阅读,则不同的选法共有( )
A.9种 B.10种 C.19种 D.90种
2.现有3名同学站成一排,再将甲、乙2名同学加入排列,保持原来3名同学顺序不变,不同的方法共有( )
A.12种 B.20种 C.6种 D.8种
3.用数字0,1,2,3,4,5组成的没有重复数字的三位数中,偶数的个数为( )
A.60 B.52 C.32 D.20
4.在的展开式中,的系数为( )
A. B.12 C. D.80
5.某冷饮店有种瓶装饮品可供选择,现有位同学到店,每人购买一瓶,则恰好购买了种饮料的购买方法有( )
A.种 B.种 C.种 D.种
6.在展开式中,含的项的系数是,则( )
A. B. C.3 D.6
7.若函数在区间上单调递减,则实数的取值范围是( )
A. B.
C. D.
8.设集合,那么集合中满足的元素的个数为( )
A.232 B.144 C.184 D.252
二、多选题(本大题共3小题)
9.已知圆的半径为2,则下列说法正确的是( )
A.
B.点在圆的外部
C.圆与圆外切
D.当直线平分圆的周长时,
10.下列说法正确的是( )
A.空间中的三个向量,若有两个向量共线,则这三个向量一定共面
B.直线的方向向量,平面的法向量,则
C.已知直线经过点,,则到的距离为
D.若,则为钝角
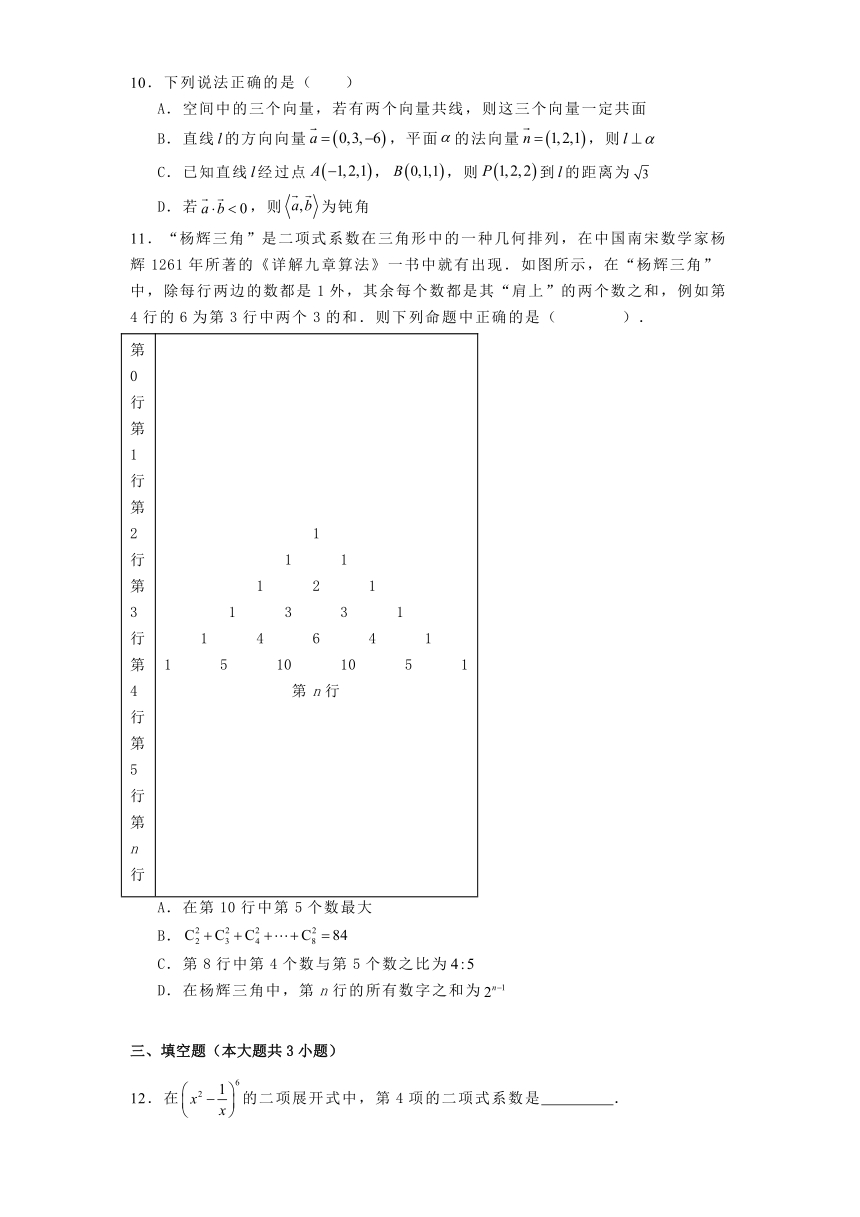
11.“杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.如图所示,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数之和,例如第4行的6为第3行中两个3的和.则下列命题中正确的是( ).
第0行 第1行 第2行 第3行 第4行 第5行 第n行 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 第n行
A.在第10行中第5个数最大
B.
C.第8行中第4个数与第5个数之比为
D.在杨辉三角中,第n行的所有数字之和为
三、填空题(本大题共3小题)
12.在的二项展开式中,第4项的二项式系数是 .
13.在的二项展开式中,所有二项式系数之和为128,则展开式共有 项.
14.我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,,记作数列,则 ;若数列的前项和为,则 .
四、解答题(本大题共5小题)
15.在平面直角坐标系内,已知曲线方程.
(1)若方程表示圆,则圆有多少个?
(2)若方程表示椭圆,则椭圆有多少个?
16.现有甲、乙、丙、丁、戊五类不同的书,放入四个窗格的书架中.
(1)每个窗格从五类书中选一类放入(书的本数不限),共有多少种放法?
(2)若甲、乙两类书必须放在同一窗格,丙、丁、戊分别放到剩余三个窗格内,共有多少种放法?
17.已知(其中)的展开式中第9项与第11项的二项式系数之和是第10项的二项式系数的2倍.
(1)求n的值;
(2)写出该二项式的展开式中所有的有理项.
18.从7名男生和5名女生中选取3人依次进行面试.
(1)若参加面试的人全是女生,则有多少种不同的面试方法?
(2)若参加面试的人中,恰好有1名女生,则有多少种不同的面试方法?
19.现有大小相同的8个球,其中2个标号不同的红球,3个标号不同的白球,3个标号不同的黑球.(结果用数字作答)
(1)将这8个球排成一列且相同颜色的球必须排在一起,有多少种排法?
(2)将这8个球排成一列,黑球不相邻且不排两端,有多少种排法?
(3)若从8个球中任取4个球,且各种颜色的球都被取到,有多少种取法?
参考答案
1.【答案】C
【详解】由分类加法计数原理知,不同的选法种数为.
故选 C.
2.【答案】B
【详解】原来名同学站成一排,有个空位可以插入甲同学,所以甲同学有种不同的排法.
当甲同学插入后,此时包括原来名同学和甲同学一共有个人,
这个人形成了个空位,所以乙同学有种不同的排法.
故完成将甲、乙名同学加入排列这件事,分两步:
第一步甲同学有种排法,第二步乙同学有种排法,
那么根据分步乘法计数原理,不同的方法共有(种).
故选B.
3.【答案】B
【详解】末位是0的有, 末位不是0的有:,共有20+32=52个.
故选B.
4.【答案】C
【详解】的二项展开式的通项为:
,
令,解得,
故的系数为,
故选C.
5.【答案】A
【详解】先指定购买的种饮料,共种,要求这位同学只能购买这种饮料,
利用间接法,每位同学共有种选择,共种购买方法,
除去位同学所买的饮料都是同一种,共种情况,
由分步乘法计数原理可知,恰好购买了种饮料的购买方法种数为种.
故选A.
6.【答案】D
【详解】由题可得含的项为,
所以,解得.
故选D.
7.【答案】A
【详解】函数,.
则,
因为在区间上单调递减,
则在区间上恒成立,即,
所以在区间上恒成立,
所以,解得,
故选A.
8.【答案】A
【详解】由题意可得或或,
下面分三种情况讨论:
(1),此时中有一项为,其余均为,
且的情况为一个,或一个,
故此时集合中元素的个数为;
(2),此时中有两项为,其余均为,
且的情况为两个,或者两个,或者一个和一个,
故此时集合中元素的个数为;
(3),此时中有三项为,其余均为,
且的情况为三个,或者两个和一个,或者一个和两个,或者三个,
故此时集合中元素的个数为;
综上可得集合中的元素的个数为.
故选A.
9.【答案】ABC
【详解】根据题意得,解得,A正确.
由选项A可知,圆,圆心为,半径为2.因为,所以点在圆的外部,B正确.
圆的圆心为,半径为8,因为,
所以圆与圆外切,C正确.
若直线平分圆的周长,则直线过圆心,则,解得,D错误.
故选ABC.
10.【答案】AC
【详解】A:对于空间向量,若,
空间中任意两个向量均是共面的,即、均共面,
所以一定共面,故A对;
B:因为,,所以与不平行,
故不成立,故B错;
C:由题设,,
则直线上的单位方向向量为,
故,
所以到直线的距离,故C对;
D:当反向共线时,也有,但此时不是钝角,故D错.
故选AC.
11.【答案】BC
【详解】对于A:第10行是二项式的展开式的系数,
所以第10行中第个数最大,故A错误;
对于B:
,故B正确;
对于C:第8行是二项式的展开式的系数,又展开式的通项为,
所以第4个数为,第5个数为,
所以第4个数与第5个数之比为,故C正确;
对于D:第n行是二项式的展开式的系数,故第n行的所有数字之和为,故D错误.
故选BC.
12.【答案】20
【详解】在的二项展开式中,第4项的二项式系数为.
13.【答案】8
【详解】在的二项展开式中,所有二项式系数之和为,
解得,则二项展开式共有8项.
14.【答案】
【详解】由题意可知是第5行第4个数,所以;
使得每行的序数与该行的项数相等,则第行最后项在数列中的项数为:
设位于第行,则:,解得:
且第行最后一项在数列中的项数为:,
位于杨辉三角数阵的第行第个
而第一行各项和为,第二行各项和为,第三行各项的和为
依此类推,第行各项的和为
.
15.【答案】(1)5
(2)20
【详解】(1)因为方程表示圆,所以.
因为,所以共有5种情况,
即圆有5个.
(2)因为方程表示椭圆,所以.
因为,所以当焦点在轴上时,,
当时,没有对应的值,有0个椭圆;
当时,,有1个椭圆;
当时,,有2个椭圆;
当时,,有3个椭圆;
当时,,有4个椭圆.
由分类加法计数原理知,焦点在轴上的椭圆有个.
焦点在轴上的椭圆与焦点在轴上的椭圆个数相同,有10个.
综上所述,满足题意的椭圆共有个
16.【答案】(1)625
(2)24
【详解】(1)第1个窗格,从五类书中任选一类,有5种选法,
同理,第2,3,4个窗格也分别有5种选法,
由分步乘法计数原理可得,共有种放法.
(2)先放甲、乙,有4种放法;
再放丙,有3种放法;
然后放丁,有2种放法;
最后放戊,剩1种放法.
由分步乘法计数原理可得,共计种放法.
17.【答案】(1)
(2)答案见解析
【详解】(1)(其中)的展开式中第9项,第10项,第11项的二项式系数分别是,,.
依题意得,,
即,
化简得,
即,解得或.
因为,所以.
(2)由(1)知,,
故二项式的展开式的通项,
当且仅当是6的倍数时,展开式中的项是有理项,
又,,
所以展开式中的有理项共3项,分别是
当时,;
当时,;
当时,.
18.【答案】(1)60
(2)630
【详解】(1)由题意从5名女生中选取3人依次进行面试,结合排列数的意义可知相当于从5名女生中选取3人依次进行排列,
此时对应有种不同的面试方法.
(2)安排满足题意的面试顺序一共需要分以下两大步:
一方面:由题意先抽取符合题意的组合,这里可以分为两小步:
第一步从5名女生中选取1名女生;第二步从7名男生中选取名男生;
由分步乘法计数原理可得符合题意的组合有种.
另一方面:注意到3名面试者是依次进行面试的,即再对刚刚组合好的3名面试者进行一次排列,
有种排列方法.结合以上两方面且由分步乘法计数原理可知满足题意的不同的面试方法有
种.
19.【答案】(1)432
(2)2880
(3)45
【详解】(1)把相同颜色的球看成一个整体,故3种不同的颜色球有种排法.
2个不同标号的红球的位置可以变换,有种排法;同理,3个不同标号的白球之间有种排法,3个不同标号的黑球之间有种排法.
故不同的排法的种数为.
(2)先把除黑球外的5个球全排列,共有种排法,
再把3个黑球插入上述5个球中间的4个空当,有种排法,
故共有种排法.
(3)从8个球中任取4个球,且各种颜色的球都被取到,则必有一种颜色的球取2个球,其余颜色的球各取1个,
故不同的取法总数为
一、单选题(本大题共8小题)
1.书架上有10 本不同的自然科学图书和9本不同的社会科学图书,甲同学想从中选出1本阅读,则不同的选法共有( )
A.9种 B.10种 C.19种 D.90种
2.现有3名同学站成一排,再将甲、乙2名同学加入排列,保持原来3名同学顺序不变,不同的方法共有( )
A.12种 B.20种 C.6种 D.8种
3.用数字0,1,2,3,4,5组成的没有重复数字的三位数中,偶数的个数为( )
A.60 B.52 C.32 D.20
4.在的展开式中,的系数为( )
A. B.12 C. D.80
5.某冷饮店有种瓶装饮品可供选择,现有位同学到店,每人购买一瓶,则恰好购买了种饮料的购买方法有( )
A.种 B.种 C.种 D.种
6.在展开式中,含的项的系数是,则( )
A. B. C.3 D.6
7.若函数在区间上单调递减,则实数的取值范围是( )
A. B.
C. D.
8.设集合,那么集合中满足的元素的个数为( )
A.232 B.144 C.184 D.252
二、多选题(本大题共3小题)
9.已知圆的半径为2,则下列说法正确的是( )
A.
B.点在圆的外部
C.圆与圆外切
D.当直线平分圆的周长时,
10.下列说法正确的是( )
A.空间中的三个向量,若有两个向量共线,则这三个向量一定共面
B.直线的方向向量,平面的法向量,则
C.已知直线经过点,,则到的距离为
D.若,则为钝角
11.“杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.如图所示,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数之和,例如第4行的6为第3行中两个3的和.则下列命题中正确的是( ).
第0行 第1行 第2行 第3行 第4行 第5行 第n行 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 第n行
A.在第10行中第5个数最大
B.
C.第8行中第4个数与第5个数之比为
D.在杨辉三角中,第n行的所有数字之和为
三、填空题(本大题共3小题)
12.在的二项展开式中,第4项的二项式系数是 .
13.在的二项展开式中,所有二项式系数之和为128,则展开式共有 项.
14.我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,,记作数列,则 ;若数列的前项和为,则 .
四、解答题(本大题共5小题)
15.在平面直角坐标系内,已知曲线方程.
(1)若方程表示圆,则圆有多少个?
(2)若方程表示椭圆,则椭圆有多少个?
16.现有甲、乙、丙、丁、戊五类不同的书,放入四个窗格的书架中.
(1)每个窗格从五类书中选一类放入(书的本数不限),共有多少种放法?
(2)若甲、乙两类书必须放在同一窗格,丙、丁、戊分别放到剩余三个窗格内,共有多少种放法?
17.已知(其中)的展开式中第9项与第11项的二项式系数之和是第10项的二项式系数的2倍.
(1)求n的值;
(2)写出该二项式的展开式中所有的有理项.
18.从7名男生和5名女生中选取3人依次进行面试.
(1)若参加面试的人全是女生,则有多少种不同的面试方法?
(2)若参加面试的人中,恰好有1名女生,则有多少种不同的面试方法?
19.现有大小相同的8个球,其中2个标号不同的红球,3个标号不同的白球,3个标号不同的黑球.(结果用数字作答)
(1)将这8个球排成一列且相同颜色的球必须排在一起,有多少种排法?
(2)将这8个球排成一列,黑球不相邻且不排两端,有多少种排法?
(3)若从8个球中任取4个球,且各种颜色的球都被取到,有多少种取法?
参考答案
1.【答案】C
【详解】由分类加法计数原理知,不同的选法种数为.
故选 C.
2.【答案】B
【详解】原来名同学站成一排,有个空位可以插入甲同学,所以甲同学有种不同的排法.
当甲同学插入后,此时包括原来名同学和甲同学一共有个人,
这个人形成了个空位,所以乙同学有种不同的排法.
故完成将甲、乙名同学加入排列这件事,分两步:
第一步甲同学有种排法,第二步乙同学有种排法,
那么根据分步乘法计数原理,不同的方法共有(种).
故选B.
3.【答案】B
【详解】末位是0的有, 末位不是0的有:,共有20+32=52个.
故选B.
4.【答案】C
【详解】的二项展开式的通项为:
,
令,解得,
故的系数为,
故选C.
5.【答案】A
【详解】先指定购买的种饮料,共种,要求这位同学只能购买这种饮料,
利用间接法,每位同学共有种选择,共种购买方法,
除去位同学所买的饮料都是同一种,共种情况,
由分步乘法计数原理可知,恰好购买了种饮料的购买方法种数为种.
故选A.
6.【答案】D
【详解】由题可得含的项为,
所以,解得.
故选D.
7.【答案】A
【详解】函数,.
则,
因为在区间上单调递减,
则在区间上恒成立,即,
所以在区间上恒成立,
所以,解得,
故选A.
8.【答案】A
【详解】由题意可得或或,
下面分三种情况讨论:
(1),此时中有一项为,其余均为,
且的情况为一个,或一个,
故此时集合中元素的个数为;
(2),此时中有两项为,其余均为,
且的情况为两个,或者两个,或者一个和一个,
故此时集合中元素的个数为;
(3),此时中有三项为,其余均为,
且的情况为三个,或者两个和一个,或者一个和两个,或者三个,
故此时集合中元素的个数为;
综上可得集合中的元素的个数为.
故选A.
9.【答案】ABC
【详解】根据题意得,解得,A正确.
由选项A可知,圆,圆心为,半径为2.因为,所以点在圆的外部,B正确.
圆的圆心为,半径为8,因为,
所以圆与圆外切,C正确.
若直线平分圆的周长,则直线过圆心,则,解得,D错误.
故选ABC.
10.【答案】AC
【详解】A:对于空间向量,若,
空间中任意两个向量均是共面的,即、均共面,
所以一定共面,故A对;
B:因为,,所以与不平行,
故不成立,故B错;
C:由题设,,
则直线上的单位方向向量为,
故,
所以到直线的距离,故C对;
D:当反向共线时,也有,但此时不是钝角,故D错.
故选AC.
11.【答案】BC
【详解】对于A:第10行是二项式的展开式的系数,
所以第10行中第个数最大,故A错误;
对于B:
,故B正确;
对于C:第8行是二项式的展开式的系数,又展开式的通项为,
所以第4个数为,第5个数为,
所以第4个数与第5个数之比为,故C正确;
对于D:第n行是二项式的展开式的系数,故第n行的所有数字之和为,故D错误.
故选BC.
12.【答案】20
【详解】在的二项展开式中,第4项的二项式系数为.
13.【答案】8
【详解】在的二项展开式中,所有二项式系数之和为,
解得,则二项展开式共有8项.
14.【答案】
【详解】由题意可知是第5行第4个数,所以;
使得每行的序数与该行的项数相等,则第行最后项在数列中的项数为:
设位于第行,则:,解得:
且第行最后一项在数列中的项数为:,
位于杨辉三角数阵的第行第个
而第一行各项和为,第二行各项和为,第三行各项的和为
依此类推,第行各项的和为
.
15.【答案】(1)5
(2)20
【详解】(1)因为方程表示圆,所以.
因为,所以共有5种情况,
即圆有5个.
(2)因为方程表示椭圆,所以.
因为,所以当焦点在轴上时,,
当时,没有对应的值,有0个椭圆;
当时,,有1个椭圆;
当时,,有2个椭圆;
当时,,有3个椭圆;
当时,,有4个椭圆.
由分类加法计数原理知,焦点在轴上的椭圆有个.
焦点在轴上的椭圆与焦点在轴上的椭圆个数相同,有10个.
综上所述,满足题意的椭圆共有个
16.【答案】(1)625
(2)24
【详解】(1)第1个窗格,从五类书中任选一类,有5种选法,
同理,第2,3,4个窗格也分别有5种选法,
由分步乘法计数原理可得,共有种放法.
(2)先放甲、乙,有4种放法;
再放丙,有3种放法;
然后放丁,有2种放法;
最后放戊,剩1种放法.
由分步乘法计数原理可得,共计种放法.
17.【答案】(1)
(2)答案见解析
【详解】(1)(其中)的展开式中第9项,第10项,第11项的二项式系数分别是,,.
依题意得,,
即,
化简得,
即,解得或.
因为,所以.
(2)由(1)知,,
故二项式的展开式的通项,
当且仅当是6的倍数时,展开式中的项是有理项,
又,,
所以展开式中的有理项共3项,分别是
当时,;
当时,;
当时,.
18.【答案】(1)60
(2)630
【详解】(1)由题意从5名女生中选取3人依次进行面试,结合排列数的意义可知相当于从5名女生中选取3人依次进行排列,
此时对应有种不同的面试方法.
(2)安排满足题意的面试顺序一共需要分以下两大步:
一方面:由题意先抽取符合题意的组合,这里可以分为两小步:
第一步从5名女生中选取1名女生;第二步从7名男生中选取名男生;
由分步乘法计数原理可得符合题意的组合有种.
另一方面:注意到3名面试者是依次进行面试的,即再对刚刚组合好的3名面试者进行一次排列,
有种排列方法.结合以上两方面且由分步乘法计数原理可知满足题意的不同的面试方法有
种.
19.【答案】(1)432
(2)2880
(3)45
【详解】(1)把相同颜色的球看成一个整体,故3种不同的颜色球有种排法.
2个不同标号的红球的位置可以变换,有种排法;同理,3个不同标号的白球之间有种排法,3个不同标号的黑球之间有种排法.
故不同的排法的种数为.
(2)先把除黑球外的5个球全排列,共有种排法,
再把3个黑球插入上述5个球中间的4个空当,有种排法,
故共有种排法.
(3)从8个球中任取4个球,且各种颜色的球都被取到,则必有一种颜色的球取2个球,其余颜色的球各取1个,
故不同的取法总数为
同课章节目录
