第 5 讲 半角模型 (含答案)2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第 5 讲 半角模型 (含答案)2025年中考数学几何模型方法巩固练习 |  | |
| 格式 | docx | ||
| 文件大小 | 763.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:23:57 | ||
图片预览


文档简介
第 5 讲 半角模型
模块1 本 质 原 理
由特殊到一般的分析
定义 从∠AOB 的顶点引出夹角为∠EOF 的两条射线,由于两射线的夹角是原角度的一半,故称半角模型.
模型分析
如图5.1所示,已知
连接 FB,将△FOB 绕着点O 顺时针旋转,使得OB 与OA 重合,易证△OEF≌△OEF′.
其实半角模型和手拉手模型的原理一致,均属于“等线段、共顶点、用旋转”,通过旋转实现边和角的转移,构造出新的特殊图形,再利用特殊图形的性质得证结论.
常见图形归纳
已知:如图5.2所示,四边形 ABCD 为正方形,∠PAQ=45°.
结论:①△AQP≌△AQ'P;② AP 平分∠DPQ,AQ 平分∠B(
已知:如图5.3所示,四边形 ABCD 为正方形,∠PAQ=45°.
结论:①△APQ≌△AP'Q;② PD+PQ= BQ.
已知:如图5.4所示,△ABD 为等腰直角三角形,∠MAN=45°.
结论:(1)全等形:①△AN'M≌△ANM;② BN +DM = MN ;③ BN +DN =N'N
(2) 相似形:△ABM∽△NDA.
【分析】 由∠AND=∠B+∠NAB=45°+∠NAB,∠MAB=45°+∠NAB,得∠AND=∠MAB.又∠D=∠B=45°,得证△ABM∽△NDA.
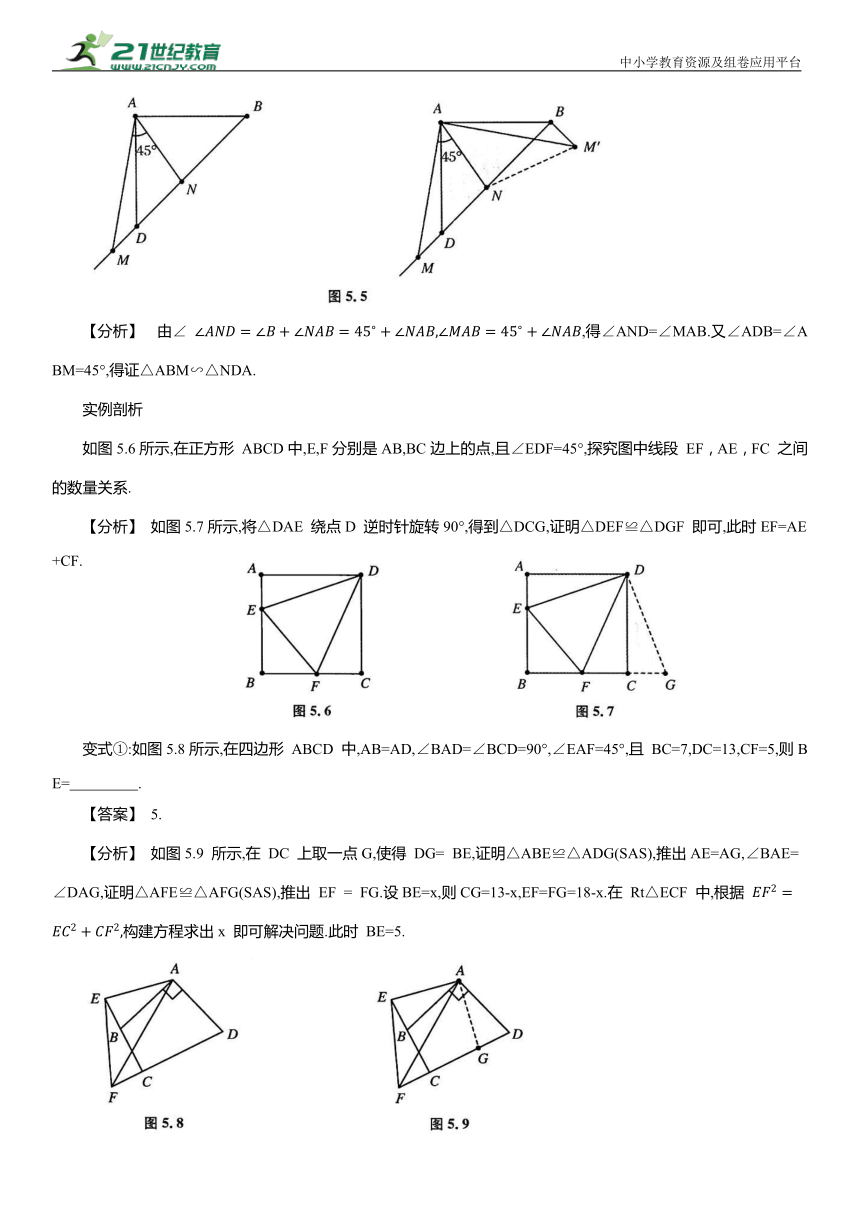
已知:如图5.5所示,△ABD 为等腰直角三角形,∠MAN=45°.
结论:(1) 全等形:①△AMN≌△AM'N;② BN +DM = MN .
(2) 相似形:△ABM∽△NDA.
【分析】 由∠ ,得∠AND=∠MAB.又∠ADB=∠ABM=45°,得证△ABM∽△NDA.
实例剖析
如图5.6所示,在正方形 ABCD中,E,F分别是AB,BC边上的点,且∠EDF=45°,探究图中线段 EF,AE,FC 之间的数量关系.
【分析】 如图5.7所示,将△DAE 绕点D 逆时针旋转90°,得到△DCG,证明△DEF≌△DGF 即可,此时EF=AE+CF.
变式①:如图5.8所示,在四边形 ABCD 中,AB=AD,∠BAD=∠BCD=90°,∠EAF=45°,且 BC=7,DC=13,CF=5,则BE= .
【答案】 5.
【分析】 如图5.9 所示,在 DC 上取一点G,使得 DG= BE,证明△ABE≌△ADG(SAS),推出AE=AG,∠BAE=∠DAG,证明△AFE≌△AFG(SAS),推出 EF = FG.设BE=x,则CG=13-x,EF=FG=18-x.在 Rt△ECF 中,根据 构建方程求出x 即可解决问题.此时 BE=5.
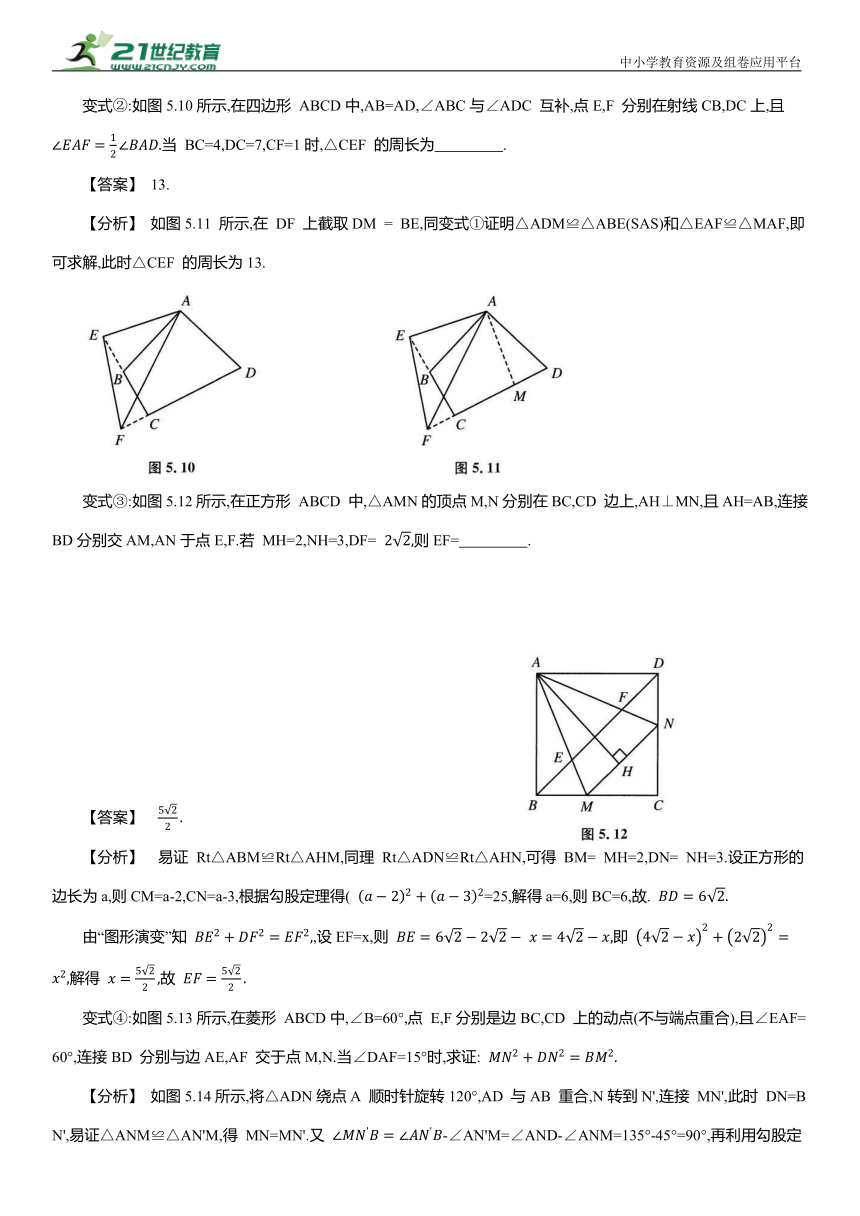
变式②:如图5.10所示,在四边形 ABCD中,AB=AD,∠ABC与∠ADC 互补,点E,F 分别在射线CB,DC上,且 当 BC=4,DC=7,CF=1时,△CEF 的周长为 .
【答案】 13.
【分析】 如图5.11 所示,在 DF 上截取DM = BE,同变式①证明△ADM≌△ABE(SAS)和△EAF≌△MAF,即可求解,此时△CEF 的周长为13.
变式③:如图5.12所示,在正方形 ABCD 中,△AMN的顶点M,N分别在BC,CD 边上,AH⊥MN,且AH=AB,连接BD分别交AM,AN于点E,F.若 MH=2,NH=3,DF= 则EF= .
【答案】
【分析】 易证 Rt△ABM≌Rt△AHM,同理 Rt△ADN≌Rt△AHN,可得 BM= MH=2,DN= NH=3.设正方形的边长为a,则CM=a-2,CN=a-3,根据勾股定理得( =25,解得a=6,则BC=6,故.
由“图形演变”知 ,设EF=x,则 即 解得 故
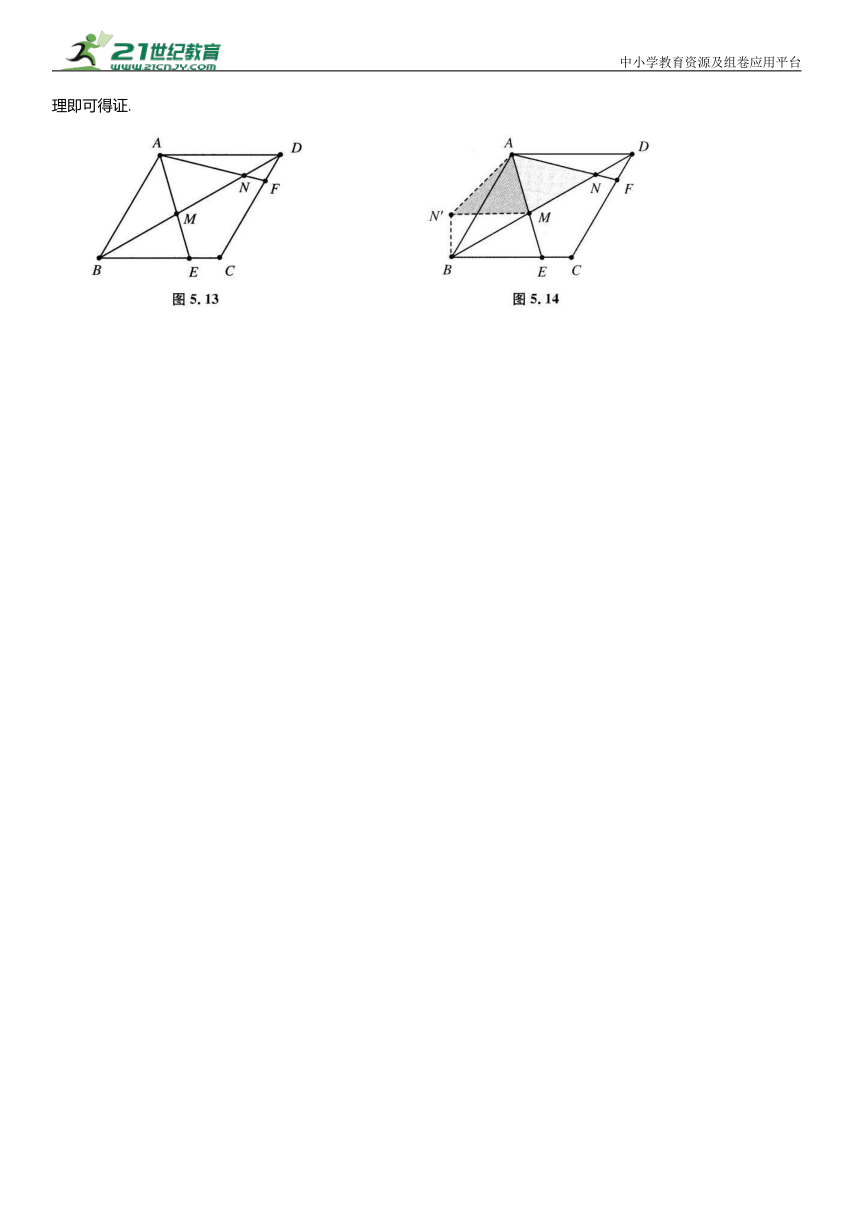
变式④:如图5.13所示,在菱形 ABCD中,∠B=60°,点 E,F分别是边BC,CD 上的动点(不与端点重合),且∠EAF=60°,连接BD 分别与边AE,AF 交于点M,N.当∠DAF=15°时,求证:
【分析】 如图5.14所示,将△ADN绕点A 顺时针旋转120°,AD 与AB 重合,N转到N',连接 MN',此时 DN=BN',易证△ANM≌△AN'M,得 MN=MN'.又 -∠AN'M=∠AND-∠ANM=135°-45°=90°,再利用勾股定理即可得证.
中小学教育资源及组卷应用平台
模块2 场 景 演 练
模型的识别:全等形
类型1:旋转后拼角互补
1. 如图5.15 所示,在四边形 ABCD 中, . E,F分别是BC,CD 上的点,且 则 EF,BE,DF 的关系为 .
2. 如图5.16所示, 是正三角形, 是等腰三角形, 以D 为顶点作一个( 角,角的两边分别交 AB,AC 边于点M,N,连接MN.若 的边长为2,则 的周长为 .
3.如图5.17所示,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西; 的A 处,舰艇乙在指挥中心南偏东 的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东 的方向以80海里/小时的速度前进,2小时后,甲、乙两舰艇分别到达E,F处,此时在指挥中心观测到两舰艇之间的夹角为 ,此时两舰艇之间的距离为 .
类型2:旋转后拼角非互补(特殊角)
4.如图5.18所示,在等边 中,点 P,Q在BC 边上,且 若 则
5. 如图5.19所示,在⊙O中, ,DF,AB 为直径,求证:
类型3:半角模型综合应用
6. 如图5.20所示,正方形 ABCD 的边长为3,点 E,F 分别在AD,CD 上, ,经过E,D,F的圆交BF 于点G,连接DG,则(
模型的识别:相似形
7. 如图5.21所示,在 中, ,E,F 为线段AB 上两动点,且 ,过点 E,F 分别作BC,AC 的垂线相交于点M,垂足分别为点 H,G,则
8. 如图5.22所示,在 中, ,E,F为直线AB 上两动点,且 过点 E,F分别作直线BC,AC的垂线相交于点M,垂足分别为点H,G,则
模型的构造
9. 如图5.23 所示,在四边形 ABCD 中, E为 CD上一点,且 若 则 的面积为 .
10. 如图5.24所示,已知在 中, 于点D.若 BD=3,CD 则
11.如图5.25所示,将正方形ABCD 折叠,使顶点 A 与CD 边上的一点H 重合(H不与端点C,D重合),折痕交AD 于点E,交 BC 于点F,边 AB 折叠后与边BC交于点G.设正方形 ABCD 的周长为m,△CHG 的周长为n,则
半角模型的深入探究
12. 如图5.26所示,在正方形 ABCD中,E,F分别在线段BC,CD上,且 AE,AF 分别交BD 于M,N两点,补充完整下列结论:
(1) BE+DF= .
EA 平分 ,FA 平分
(3)若AB=2,点 E 是BC 中点,则 DF= .
(7) △AMN 与△AFE .
(9) △AMN与 , 成8字相似.
(12) 连接 MF,NE,则△ANE,△AMF为 三角形.
.
13.如图5.27所示,正方形 ABCD 的边长为2,BM,DN分别是正方形的两个外角的平分线,点P,Q分别是平分线BM,DN 上的点,且满足 连接 PQ,PC,CQ.则下列结论:
②∠QAD=∠APB;
③∠PCQ=135°;
其中正确的有 .
模型的综合应用:遇见中考
14.【教材呈现】 (1)如图5.28 所示,在同一平面内,将两个全等的等腰 Rt△ABC 和Rt△AFG 摆放在一起,点 A 为公共顶点,∠BAC=∠G=90°,若△ABC 固定不动,将△AFG 绕点A 旋转,边 AF,AG 与边BC 分别交于点D,E(点 D 不与点B 重合,点 E 不与点C 重合),则结论 BE·CD=AB 是否成立 (填“成立”或“不成立”).
【类比引申】 (2)如图5.29 所示,在正方形 ABCD 中,∠EAF 为∠BAD 内的一个动角,两边分别与 BD,BC 交于点E,F,且满足∠EAF=∠ADB,求证:△ADE∽△ACF.
【拓展延伸】 (3)如图5.30所示,菱形 ABCD 的边长为12cm,∠BAD=120°,∠EAF的两边分别与BD,BC 相交于点E,F,且满足∠EAF=∠ADB,若 BF=9cm,则线段 DE 的长为 cm.
番外篇:由半角 引发的思考
15. 由“45°+⊥”引发的思考:如图5.31所示,已知∠
联想①:如图5.31所示,若 则
联想②:如图5.31所示,若CD=3,BD=2,则AD= .
联想③:如图5.32所示,若EF=5,BE=15,AF=FC,则.
番外篇:遇见中考
16. 如图5.33 所示,已知在 中, D为AB 的中点, 于点F,交 BC于点E,连接 BF,若 则
17. 如图5.34所示,已知 是直角三角形, 5, 连接CE,以 CE 为底作 且 F 是AE 边上的一点,连接BD 和BF,且 ,则 AF长为 .
第5讲 半 角 模 型
1. EF=BE+DF.
提示:如图J5.1所示,延长 FD 到点G,使DG= BE,连接AG,先证△ABE≌△ADG,再证△AEF≌△GAF 即可.
2. 4.
△AMN的周长=AM+MN+AN=(AM+BM)+(NC+AN)=2+2=4.
3. 280海里.
如图J5.2所示,连接EF,延长AE,BF 相交于点G.
因为 0°,所以
又 °,所以EF=AE+BF,即 EF=2×(60+80)=280(海里).
如图J5.3所示,在△ABC 外侧作∠BAD=∠CAQ,在射线 AD 上截取AD=AQ,连接PD,BD,过点 D 作 DE⊥BC 交CB 的延长线于点 E,易得△AQC≌△ADB,所以BD=QC=3,∠ABD=∠C=60°.
在△DBP 中,∠DBP =120°,则 60°,易得 故
在Rt△DPE中,
由△APQ≌△APD,得 故
5. 由∠DAN=90°,∠MAC=45°,可考虑半角模型.
如图 J5.4 所示,△ANC≌△ADC',∠ANC =∠ADC'=135°,∠MDC'=∠ADC'- 则△ACM≌△AC'M,易证 等量代换得
设 -a)
连接EG,此时∠EGF=90°,则△BEG为等腰直角三角形,过点 G 作MN⊥AD.
如图J5.5所示,易证△EMG≌△GNB.设 MD=x,则.ME=NG=2-x,MG=BN=3-x,所以 MG+NG=3-x+2-x=3,解得x=1.在 Rt△MDG 中,
如图J5.6所示,作AF⊥CB交CB的延长线于点F,在 CF 的延长线上取一点G,使得FG=DE.
易证△AFG≌△ADE,△BAE≌△BAG,所以BE=BG=BF+GF=BF+DE.
设BC=a,则AB=4+a,BF=4-a.
在 Rt△ABF 中, 解得a=1,所以BC=1,BF=3.
设DE=b,则 BE=b+3,CE=4-b.
在Rt△BCE中, 解得 则
故
10. 15.
如图J5.7所示,将△ABD 沿AB 所在的直线折叠,使点 D 落在点E 处;将△ACD 沿AC 所在的直线折叠,使点 D 落在点F 处,分别延长 EB,FC使其交于点M.
易得四边形 AEMF 是正方形,设正方形 AEMF 的边长是x,则 BM=x-3,CM=x-2.
在 Rt△BMC中,由勾股定理得 即( 解得x=6,则AE=AD=6,故
如图J5.8所示,连接AH,AG,作 于点M.
由∠1=∠HAB=∠AHD,∠D=∠AMH=90°,AH = AH,得△AHD≌△AHM,则DH=HM,AD=AM.
因为AM=AB,AG=AG,所以Rt△AGM≌Rt△AGB,则GM=GB,故△GCH 的周长=n=CH+HM+MG+CG=CH+DH+CG+GB=2BC.
因为四边形 ABCD 的周长=m=4BC,所以
12.(1) EF.
(2)2AB,∠BEF,∠DFE.
提示:设 DF=x,则 即 解得
(4) MN .
(5)2AM .
提示:旋转△ABM,使AB与AD 重合,再利用勾股定理求解即可.
2AN .
提示:旋转△ADN,使AD 与AB 重合,再利用勾股定理求解即可.
提示:连接AC,证明△ADN∽△ACE,△AFC∽△AMB 即可.
(7) 相似.
提示:∠ANM=∠MEB=∠AEF.
(8) ,AN·AF.
提示: 再由△AMN∽△AFE 可得.
(9)△BME,△DFN.
(10) BM·MN,MN·ND.
提示:由(9)可得.
(11) MN·MD,NB·NM.
提示:由△AMN∽△DMA,△ANM∽△BNA 可得.
(12) 等腰直角.
提示:由A,M,F,D,以及A,N,E,B四点共圆倒角可得.
提示:由A,M,F,D,以及A,N,E,B四点共圆后,通过“等线(AN= NE 或AM=MF)、共点(点 N 或M)、旋转(△BNE 或△MFD)”可得.
13. ②③④.
由题意可得∠BAP+∠APB=45°,∠QAD+∠BAP=45°,则∠QAD=∠APB,故②正确;根据△ABP∽△QDA,得 可知①错误;再根据△PBC∽△CDQ,得∠BCP=∠DQC,可知③正确;将△AQD 绕点A 顺时针旋转90°得△ABG,连接 GP 交AB 的延长线于点H,利用SAS证明△AGP≌△APQ,得GP=QP,再说明∠GBP=90°,利用勾股定理可判断④正确.
14. (1) 成立.
理由:因为∠DAC=∠CAE+45°,∠AEB=∠CAE+45°,所以∠DAC=∠AEB.
又∠B=∠C,则△BEA∽△CAD,于是 即 AB·AC=BE·CD.
因为AC=AB,所以BE·CD=AB .
(2) 因为四边形 ABCD 是正方形,所以∠CAD=∠ACB=∠ADB=45°.
又∠EAF=∠ADB,则∠EAF=∠CAD=45°,即∠CAF+∠CAE=∠DAE+∠CAE,故∠CAF=∠DAE.
因为∠ACB=∠ADB,所以△ADE∽△ACF.
如图J5.9 所示,在 DE 上取一点M,使∠MAD =30°,过点 M 作MN⊥AD 于点N.
同(2)的证法可得△ACF∽△AME,则 即 亦即 则 故.
15. 联想①
如图 J5.10 所示,易证△CBP≌△AQP,所以(
联想②:6.
解法1 如图J5.11 所示,设 ( 则 AD·BC = AB·CL
解法2 如图J5.12所示,利用补形,将 和 各翻折一次,设 MN=MO=x.
在 Rt△MCB 中,
解法3 如图J5.13所示,利用补形,补成一线三等角模型(也可以内部补型,如图J5.14所示).设 则
解法4* 利用“和角公式”,设 AD = x,∠BAD =α,∠CAD =β,则 tan(α+β)= 即 解得 AD=6.
联想③:24.
如图J5.15所示,设 BD=3CG=3GD=3a.
在 Rt△FGB中, .
如图J5.16所示,过点 B 作BG⊥AE 交AE 的延长线于点G.
因为 AE⊥CD,∠BFE=45°,所以△BFG 为等腰直角三角形,设
又 AG⊥DF,AG⊥BG,D 为AB 边的中点,则 DF 为 的中位线,即 AG=2a,所以
在 Rt△ABC 中,CD 为AB 边上的中线,则
又CF∥GB,则△CFE∽△BGE,故
如图J5.17所示,利用∠DBF=45°,构造等腰 Rt△BDM,连接 ME.
因为△BDM,△CDE 为等腰直角三角形,易证△EDM≌△CDB(SAS),所以. =5,∠MED=∠DCB=∠CDE=90°,可得到 ME∥DC∥AB,则 解得
模块1 本 质 原 理
由特殊到一般的分析
定义 从∠AOB 的顶点引出夹角为∠EOF 的两条射线,由于两射线的夹角是原角度的一半,故称半角模型.
模型分析
如图5.1所示,已知
连接 FB,将△FOB 绕着点O 顺时针旋转,使得OB 与OA 重合,易证△OEF≌△OEF′.
其实半角模型和手拉手模型的原理一致,均属于“等线段、共顶点、用旋转”,通过旋转实现边和角的转移,构造出新的特殊图形,再利用特殊图形的性质得证结论.
常见图形归纳
已知:如图5.2所示,四边形 ABCD 为正方形,∠PAQ=45°.
结论:①△AQP≌△AQ'P;② AP 平分∠DPQ,AQ 平分∠B(
已知:如图5.3所示,四边形 ABCD 为正方形,∠PAQ=45°.
结论:①△APQ≌△AP'Q;② PD+PQ= BQ.
已知:如图5.4所示,△ABD 为等腰直角三角形,∠MAN=45°.
结论:(1)全等形:①△AN'M≌△ANM;② BN +DM = MN ;③ BN +DN =N'N
(2) 相似形:△ABM∽△NDA.
【分析】 由∠AND=∠B+∠NAB=45°+∠NAB,∠MAB=45°+∠NAB,得∠AND=∠MAB.又∠D=∠B=45°,得证△ABM∽△NDA.
已知:如图5.5所示,△ABD 为等腰直角三角形,∠MAN=45°.
结论:(1) 全等形:①△AMN≌△AM'N;② BN +DM = MN .
(2) 相似形:△ABM∽△NDA.
【分析】 由∠ ,得∠AND=∠MAB.又∠ADB=∠ABM=45°,得证△ABM∽△NDA.
实例剖析
如图5.6所示,在正方形 ABCD中,E,F分别是AB,BC边上的点,且∠EDF=45°,探究图中线段 EF,AE,FC 之间的数量关系.
【分析】 如图5.7所示,将△DAE 绕点D 逆时针旋转90°,得到△DCG,证明△DEF≌△DGF 即可,此时EF=AE+CF.
变式①:如图5.8所示,在四边形 ABCD 中,AB=AD,∠BAD=∠BCD=90°,∠EAF=45°,且 BC=7,DC=13,CF=5,则BE= .
【答案】 5.
【分析】 如图5.9 所示,在 DC 上取一点G,使得 DG= BE,证明△ABE≌△ADG(SAS),推出AE=AG,∠BAE=∠DAG,证明△AFE≌△AFG(SAS),推出 EF = FG.设BE=x,则CG=13-x,EF=FG=18-x.在 Rt△ECF 中,根据 构建方程求出x 即可解决问题.此时 BE=5.
变式②:如图5.10所示,在四边形 ABCD中,AB=AD,∠ABC与∠ADC 互补,点E,F 分别在射线CB,DC上,且 当 BC=4,DC=7,CF=1时,△CEF 的周长为 .
【答案】 13.
【分析】 如图5.11 所示,在 DF 上截取DM = BE,同变式①证明△ADM≌△ABE(SAS)和△EAF≌△MAF,即可求解,此时△CEF 的周长为13.
变式③:如图5.12所示,在正方形 ABCD 中,△AMN的顶点M,N分别在BC,CD 边上,AH⊥MN,且AH=AB,连接BD分别交AM,AN于点E,F.若 MH=2,NH=3,DF= 则EF= .
【答案】
【分析】 易证 Rt△ABM≌Rt△AHM,同理 Rt△ADN≌Rt△AHN,可得 BM= MH=2,DN= NH=3.设正方形的边长为a,则CM=a-2,CN=a-3,根据勾股定理得( =25,解得a=6,则BC=6,故.
由“图形演变”知 ,设EF=x,则 即 解得 故
变式④:如图5.13所示,在菱形 ABCD中,∠B=60°,点 E,F分别是边BC,CD 上的动点(不与端点重合),且∠EAF=60°,连接BD 分别与边AE,AF 交于点M,N.当∠DAF=15°时,求证:
【分析】 如图5.14所示,将△ADN绕点A 顺时针旋转120°,AD 与AB 重合,N转到N',连接 MN',此时 DN=BN',易证△ANM≌△AN'M,得 MN=MN'.又 -∠AN'M=∠AND-∠ANM=135°-45°=90°,再利用勾股定理即可得证.
中小学教育资源及组卷应用平台
模块2 场 景 演 练
模型的识别:全等形
类型1:旋转后拼角互补
1. 如图5.15 所示,在四边形 ABCD 中, . E,F分别是BC,CD 上的点,且 则 EF,BE,DF 的关系为 .
2. 如图5.16所示, 是正三角形, 是等腰三角形, 以D 为顶点作一个( 角,角的两边分别交 AB,AC 边于点M,N,连接MN.若 的边长为2,则 的周长为 .
3.如图5.17所示,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西; 的A 处,舰艇乙在指挥中心南偏东 的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东 的方向以80海里/小时的速度前进,2小时后,甲、乙两舰艇分别到达E,F处,此时在指挥中心观测到两舰艇之间的夹角为 ,此时两舰艇之间的距离为 .
类型2:旋转后拼角非互补(特殊角)
4.如图5.18所示,在等边 中,点 P,Q在BC 边上,且 若 则
5. 如图5.19所示,在⊙O中, ,DF,AB 为直径,求证:
类型3:半角模型综合应用
6. 如图5.20所示,正方形 ABCD 的边长为3,点 E,F 分别在AD,CD 上, ,经过E,D,F的圆交BF 于点G,连接DG,则(
模型的识别:相似形
7. 如图5.21所示,在 中, ,E,F 为线段AB 上两动点,且 ,过点 E,F 分别作BC,AC 的垂线相交于点M,垂足分别为点 H,G,则
8. 如图5.22所示,在 中, ,E,F为直线AB 上两动点,且 过点 E,F分别作直线BC,AC的垂线相交于点M,垂足分别为点H,G,则
模型的构造
9. 如图5.23 所示,在四边形 ABCD 中, E为 CD上一点,且 若 则 的面积为 .
10. 如图5.24所示,已知在 中, 于点D.若 BD=3,CD 则
11.如图5.25所示,将正方形ABCD 折叠,使顶点 A 与CD 边上的一点H 重合(H不与端点C,D重合),折痕交AD 于点E,交 BC 于点F,边 AB 折叠后与边BC交于点G.设正方形 ABCD 的周长为m,△CHG 的周长为n,则
半角模型的深入探究
12. 如图5.26所示,在正方形 ABCD中,E,F分别在线段BC,CD上,且 AE,AF 分别交BD 于M,N两点,补充完整下列结论:
(1) BE+DF= .
EA 平分 ,FA 平分
(3)若AB=2,点 E 是BC 中点,则 DF= .
(7) △AMN 与△AFE .
(9) △AMN与 , 成8字相似.
(12) 连接 MF,NE,则△ANE,△AMF为 三角形.
.
13.如图5.27所示,正方形 ABCD 的边长为2,BM,DN分别是正方形的两个外角的平分线,点P,Q分别是平分线BM,DN 上的点,且满足 连接 PQ,PC,CQ.则下列结论:
②∠QAD=∠APB;
③∠PCQ=135°;
其中正确的有 .
模型的综合应用:遇见中考
14.【教材呈现】 (1)如图5.28 所示,在同一平面内,将两个全等的等腰 Rt△ABC 和Rt△AFG 摆放在一起,点 A 为公共顶点,∠BAC=∠G=90°,若△ABC 固定不动,将△AFG 绕点A 旋转,边 AF,AG 与边BC 分别交于点D,E(点 D 不与点B 重合,点 E 不与点C 重合),则结论 BE·CD=AB 是否成立 (填“成立”或“不成立”).
【类比引申】 (2)如图5.29 所示,在正方形 ABCD 中,∠EAF 为∠BAD 内的一个动角,两边分别与 BD,BC 交于点E,F,且满足∠EAF=∠ADB,求证:△ADE∽△ACF.
【拓展延伸】 (3)如图5.30所示,菱形 ABCD 的边长为12cm,∠BAD=120°,∠EAF的两边分别与BD,BC 相交于点E,F,且满足∠EAF=∠ADB,若 BF=9cm,则线段 DE 的长为 cm.
番外篇:由半角 引发的思考
15. 由“45°+⊥”引发的思考:如图5.31所示,已知∠
联想①:如图5.31所示,若 则
联想②:如图5.31所示,若CD=3,BD=2,则AD= .
联想③:如图5.32所示,若EF=5,BE=15,AF=FC,则.
番外篇:遇见中考
16. 如图5.33 所示,已知在 中, D为AB 的中点, 于点F,交 BC于点E,连接 BF,若 则
17. 如图5.34所示,已知 是直角三角形, 5, 连接CE,以 CE 为底作 且 F 是AE 边上的一点,连接BD 和BF,且 ,则 AF长为 .
第5讲 半 角 模 型
1. EF=BE+DF.
提示:如图J5.1所示,延长 FD 到点G,使DG= BE,连接AG,先证△ABE≌△ADG,再证△AEF≌△GAF 即可.
2. 4.
△AMN的周长=AM+MN+AN=(AM+BM)+(NC+AN)=2+2=4.
3. 280海里.
如图J5.2所示,连接EF,延长AE,BF 相交于点G.
因为 0°,所以
又 °,所以EF=AE+BF,即 EF=2×(60+80)=280(海里).
如图J5.3所示,在△ABC 外侧作∠BAD=∠CAQ,在射线 AD 上截取AD=AQ,连接PD,BD,过点 D 作 DE⊥BC 交CB 的延长线于点 E,易得△AQC≌△ADB,所以BD=QC=3,∠ABD=∠C=60°.
在△DBP 中,∠DBP =120°,则 60°,易得 故
在Rt△DPE中,
由△APQ≌△APD,得 故
5. 由∠DAN=90°,∠MAC=45°,可考虑半角模型.
如图 J5.4 所示,△ANC≌△ADC',∠ANC =∠ADC'=135°,∠MDC'=∠ADC'- 则△ACM≌△AC'M,易证 等量代换得
设 -a)
连接EG,此时∠EGF=90°,则△BEG为等腰直角三角形,过点 G 作MN⊥AD.
如图J5.5所示,易证△EMG≌△GNB.设 MD=x,则.ME=NG=2-x,MG=BN=3-x,所以 MG+NG=3-x+2-x=3,解得x=1.在 Rt△MDG 中,
如图J5.6所示,作AF⊥CB交CB的延长线于点F,在 CF 的延长线上取一点G,使得FG=DE.
易证△AFG≌△ADE,△BAE≌△BAG,所以BE=BG=BF+GF=BF+DE.
设BC=a,则AB=4+a,BF=4-a.
在 Rt△ABF 中, 解得a=1,所以BC=1,BF=3.
设DE=b,则 BE=b+3,CE=4-b.
在Rt△BCE中, 解得 则
故
10. 15.
如图J5.7所示,将△ABD 沿AB 所在的直线折叠,使点 D 落在点E 处;将△ACD 沿AC 所在的直线折叠,使点 D 落在点F 处,分别延长 EB,FC使其交于点M.
易得四边形 AEMF 是正方形,设正方形 AEMF 的边长是x,则 BM=x-3,CM=x-2.
在 Rt△BMC中,由勾股定理得 即( 解得x=6,则AE=AD=6,故
如图J5.8所示,连接AH,AG,作 于点M.
由∠1=∠HAB=∠AHD,∠D=∠AMH=90°,AH = AH,得△AHD≌△AHM,则DH=HM,AD=AM.
因为AM=AB,AG=AG,所以Rt△AGM≌Rt△AGB,则GM=GB,故△GCH 的周长=n=CH+HM+MG+CG=CH+DH+CG+GB=2BC.
因为四边形 ABCD 的周长=m=4BC,所以
12.(1) EF.
(2)2AB,∠BEF,∠DFE.
提示:设 DF=x,则 即 解得
(4) MN .
(5)2AM .
提示:旋转△ABM,使AB与AD 重合,再利用勾股定理求解即可.
2AN .
提示:旋转△ADN,使AD 与AB 重合,再利用勾股定理求解即可.
提示:连接AC,证明△ADN∽△ACE,△AFC∽△AMB 即可.
(7) 相似.
提示:∠ANM=∠MEB=∠AEF.
(8) ,AN·AF.
提示: 再由△AMN∽△AFE 可得.
(9)△BME,△DFN.
(10) BM·MN,MN·ND.
提示:由(9)可得.
(11) MN·MD,NB·NM.
提示:由△AMN∽△DMA,△ANM∽△BNA 可得.
(12) 等腰直角.
提示:由A,M,F,D,以及A,N,E,B四点共圆倒角可得.
提示:由A,M,F,D,以及A,N,E,B四点共圆后,通过“等线(AN= NE 或AM=MF)、共点(点 N 或M)、旋转(△BNE 或△MFD)”可得.
13. ②③④.
由题意可得∠BAP+∠APB=45°,∠QAD+∠BAP=45°,则∠QAD=∠APB,故②正确;根据△ABP∽△QDA,得 可知①错误;再根据△PBC∽△CDQ,得∠BCP=∠DQC,可知③正确;将△AQD 绕点A 顺时针旋转90°得△ABG,连接 GP 交AB 的延长线于点H,利用SAS证明△AGP≌△APQ,得GP=QP,再说明∠GBP=90°,利用勾股定理可判断④正确.
14. (1) 成立.
理由:因为∠DAC=∠CAE+45°,∠AEB=∠CAE+45°,所以∠DAC=∠AEB.
又∠B=∠C,则△BEA∽△CAD,于是 即 AB·AC=BE·CD.
因为AC=AB,所以BE·CD=AB .
(2) 因为四边形 ABCD 是正方形,所以∠CAD=∠ACB=∠ADB=45°.
又∠EAF=∠ADB,则∠EAF=∠CAD=45°,即∠CAF+∠CAE=∠DAE+∠CAE,故∠CAF=∠DAE.
因为∠ACB=∠ADB,所以△ADE∽△ACF.
如图J5.9 所示,在 DE 上取一点M,使∠MAD =30°,过点 M 作MN⊥AD 于点N.
同(2)的证法可得△ACF∽△AME,则 即 亦即 则 故.
15. 联想①
如图 J5.10 所示,易证△CBP≌△AQP,所以(
联想②:6.
解法1 如图J5.11 所示,设 ( 则 AD·BC = AB·CL
解法2 如图J5.12所示,利用补形,将 和 各翻折一次,设 MN=MO=x.
在 Rt△MCB 中,
解法3 如图J5.13所示,利用补形,补成一线三等角模型(也可以内部补型,如图J5.14所示).设 则
解法4* 利用“和角公式”,设 AD = x,∠BAD =α,∠CAD =β,则 tan(α+β)= 即 解得 AD=6.
联想③:24.
如图J5.15所示,设 BD=3CG=3GD=3a.
在 Rt△FGB中, .
如图J5.16所示,过点 B 作BG⊥AE 交AE 的延长线于点G.
因为 AE⊥CD,∠BFE=45°,所以△BFG 为等腰直角三角形,设
又 AG⊥DF,AG⊥BG,D 为AB 边的中点,则 DF 为 的中位线,即 AG=2a,所以
在 Rt△ABC 中,CD 为AB 边上的中线,则
又CF∥GB,则△CFE∽△BGE,故
如图J5.17所示,利用∠DBF=45°,构造等腰 Rt△BDM,连接 ME.
因为△BDM,△CDE 为等腰直角三角形,易证△EDM≌△CDB(SAS),所以. =5,∠MED=∠DCB=∠CDE=90°,可得到 ME∥DC∥AB,则 解得
同课章节目录
