第 7 讲 十字模型(含答案)2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第 7 讲 十字模型(含答案)2025年中考数学几何模型方法巩固练习 |  | |
| 格式 | docx | ||
| 文件大小 | 445.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:26:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第 7 讲 十 字 模 型
模块1 本 质 原 理
常见十字模型见表7.1.
表7.1
已知:△ABC 为等边三角形,AD 与BE 的夹角为60°则:AD= BE 已知:△ABC 为等边三角形,BD=CE 则:AD 与BE 的夹角为60° 已知:ABCD 为正方形,EF 与MN 的夹角为90°则:MN=EF 已知:ABCD 为矩形,EF 与MN 的夹角为90°则:EF/BC
十字模型的本质原理就是利用同角(或等角)的“等量代换”证明全等三角形或者相似三角形
实例剖析:全等形
场景①:如图7.1所示,在等边△ABC 中,M,N分别是AC,AB上的点,BM 与CN相交于点O,若∠BON=60°,求证:BM=CN.
【分析】 因为△ABC 是正三角形,所以 BC=CA,∠BCM=∠CAN=60°.
又∠BON=60°,则∠CBM+∠BCN=60°.
因为∠BCN+∠ACN=60°,所以∠CBM=∠ACN.
故△BCM≌△CAN(ASA),则 BM=CN.
场景②:如图7.2所示,在正方形 ABCD 中,M,N分别是CD,AD 上的点,BM 与CN相交于点O,若∠BON=90°,求证:BM=CN.
【分析】 因为四边形 ABCD 是正方形,所以 BC=CD,∠BCM=∠CDN=90°.
又∠BON=90°,则∠CBM+∠BCN=90°.
因为∠BCN+∠DCN=90°,所以∠CBM=∠DCN.
故△BCM≌△CDN(ASA),则 BM=CN.
场景③:如图7.3所示,在正五边形 ABCDE 中,M,N分别是CD,DE 上的点,BM与CN 相交于点O,若∠BON=108°,求证:BM=CN.
【分析】 因为五边形 ABCDE 是正五边形,所以 BC=CD,∠BCM=∠CDN=108°.
又∠BON=108°,则∠CBM+∠BCN=108°.
因为∠BCN+∠DCN=108°,所以∠CBM=∠DCN.
故△BCM≌△CDN(ASA),则 BM=CN.
场景④:如图7.4所示,在正 n(n>3)边形 ABCDEF…中,M,N分别是CD,DE 上的点,BM与CN 相交于点O,当∠BON= 时,结论BM=CN成立.
【分析】 当 时,结论成立.
易知 因为 所以
又 则∠CBM=∠DCN.
故△BCM≌△CDN(ASA),则 BM=CN.
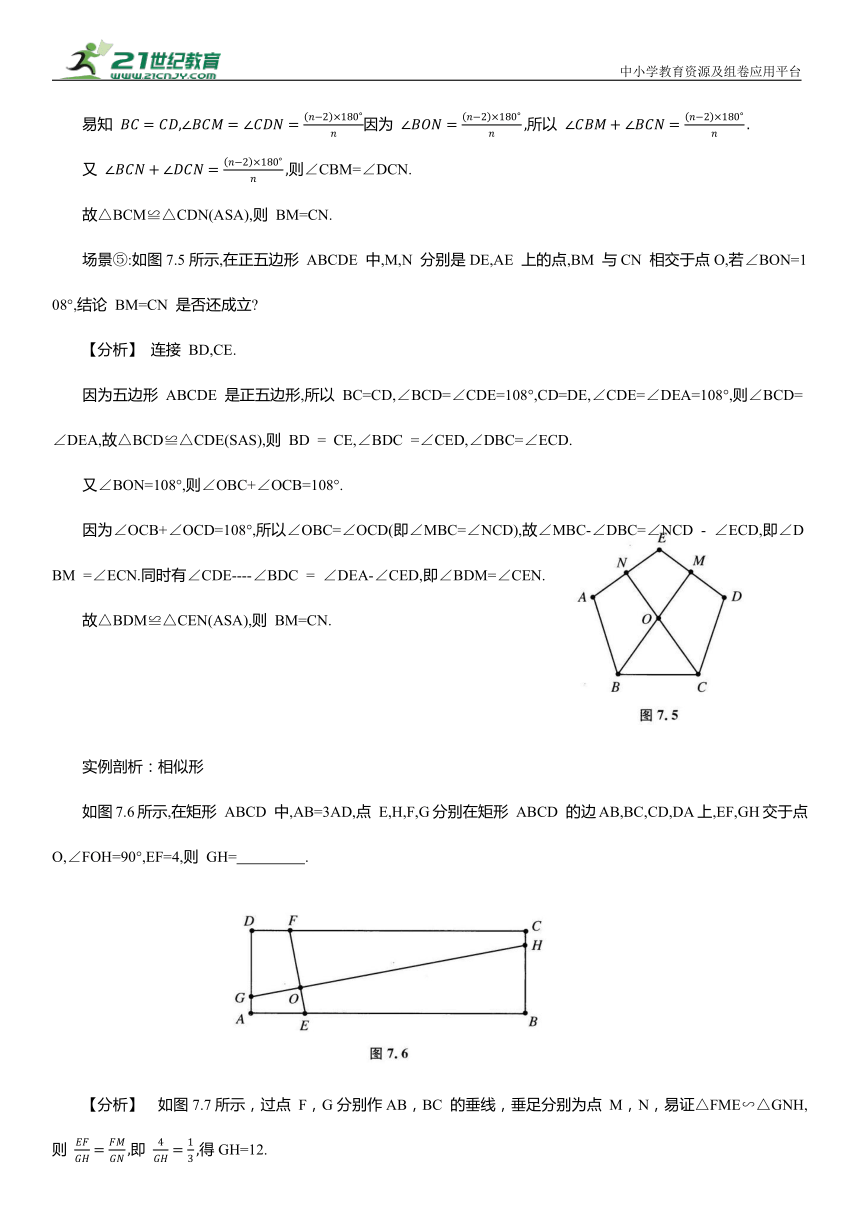
场景⑤:如图7.5所示,在正五边形 ABCDE 中,M,N 分别是DE,AE 上的点,BM 与CN 相交于点O,若∠BON=108°,结论 BM=CN 是否还成立
【分析】 连接 BD,CE.
因为五边形 ABCDE 是正五边形,所以 BC=CD,∠BCD=∠CDE=108°,CD=DE,∠CDE=∠DEA=108°,则∠BCD=∠DEA,故△BCD≌△CDE(SAS),则 BD = CE,∠BDC =∠CED,∠DBC=∠ECD.
又∠BON=108°,则∠OBC+∠OCB=108°.
因为∠OCB+∠OCD=108°,所以∠OBC=∠OCD(即∠MBC=∠NCD),故∠MBC-∠DBC=∠NCD - ∠ECD,即∠DBM =∠ECN.同时有∠CDE----∠BDC = ∠DEA-∠CED,即∠BDM=∠CEN.
故△BDM≌△CEN(ASA),则 BM=CN.
实例剖析:相似形
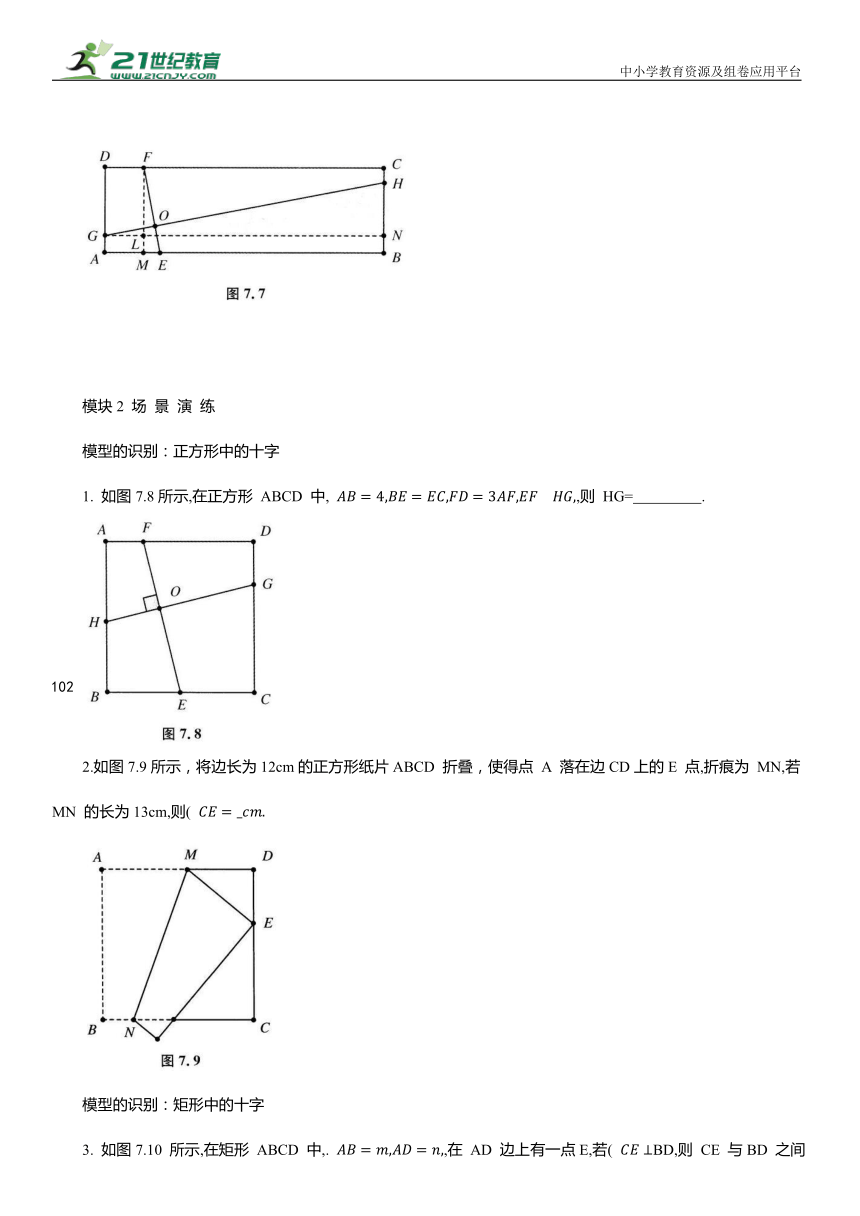
如图7.6所示,在矩形 ABCD 中,AB=3AD,点 E,H,F,G分别在矩形 ABCD 的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4,则 GH= .
【分析】 如图7.7所示,过点 F,G分别作AB,BC 的垂线,垂足分别为点 M,N,易证△FME∽△GNH,则 即 得GH=12.
模块2 场 景 演 练
模型的识别:正方形中的十字
1. 如图7.8所示,在正方形 ABCD 中, ,则 HG= .
2.如图7.9所示,将边长为12cm的正方形纸片ABCD 折叠,使得点 A 落在边CD上的E 点,折痕为 MN,若 MN 的长为13cm,则(
模型的识别:矩形中的十字
3. 如图7.10 所示,在矩形 ABCD 中,. ,在 AD 边上有一点E,若( BD,则 CE 与BD 之间的数量关系为 .
4. 如图7.11 所示,在矩形 ABCD 中, ,将矩形对折,使点 A 和点C 重合,则折痕
5. 如图7.12所示,在矩形 ABCD 中, ,将矩形沿着 EC 折叠,使点 B 落在边AD上的F点处,则折痕(
6. 如图7.13 所示,在矩形 ABCD 中,若 则
7.如图7.14 所示,在正方形 ABCD中,点 E 是边BC 上的一点,点F 在边CD 的延长线上,且 过点 A 作 垂足为点 M,交边CD 于点N.若 则线段 AN 的长为 .
8. 如图7.15 所示,在四边形 ABCD 中,. 点 E,F 分别在线段AB,AD上,且 则
模型的构造:矩形中的十字
9.如图7.16所示,把边长为 且 的平行四边形ABCD 对折,使点 B 和D 重合,则折痕.
10. 如图7.17所示,在四边形 ABCD 中,点 M,N 分别在边BC,AB 上, 则
11.如图7.18所示,已知直线 分别与x轴、y轴交于点B,A,将 沿着AB 折叠,使点 O 与点D 重合.当反比例函数 的图像经过点D 时,
模型的构造:三角形中的十字
12. 如图7.19所示,在 中, ,D 为BC 边的中点, AD 于点E,交 AC 于点F,则 AF:FC 的值为 .
13. 如图7.20所示,在 中, D 为BC 边的中点, 于点E,交 AC 于点F,若 则
模型的综合应用:遇见中考
14.某数学兴趣小组在数学课外活动中,对四边形内两条互相垂直的线段做了如下探究:
【观察与猜想】 (1) 如图7.21所示,在矩形ABCD中,AD=7,CD=4,点E 是AD上的一点,连接CE,BD,且CE⊥BD,则
【类比探究】 (2)如图7.22所示,若 BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,则
【拓展延伸】 (3)如图7.23所示,在 Rt△ABD 中, 将△ABD 沿BD 翻折,点 A 落在点C 处得△CBD,点E,F 分别在边AB,AD 上,连接DE,CF,DE⊥CF.
的值为 ;
② 连接 BF,若 ,则BF 的长度为 .
第7讲 十 字 模 型
如图 J7.1 所示,先证明△FME≌△HNG,则
2. 7.
如图J7.2所示,连接 AE,此时 AE⊥MN,则(
证明△CDE∽△BCD 即可.
根据十字模型可得
易得 则 因为 所以
用两次十字模型.
设BC=x,则CE=x-5,DN=x-8,CF=x+5.
易证△ADN∽△FCE,则 即 解得x=20.
在 Rt△ADN中,
如图J7.3所示,过点 C 作CM⊥AB 于点M.设CE 交BF 于点O.
因为 CM⊥AB,所以∠CME=90°,即∠1+∠2=90°.
又 CE⊥BF,则∠BOE=90°,即∠2+∠3=90°,则∠1=∠3,故△CME∽△BAF,则
因为 AB=BC,∠ABC=60°,所以
如图J7.4所示,过点 B 作BE⊥AD 的延长线于点E,过点 M 作MF⊥BC,连接 BD.
所以MF=BE=2,则
易证△MNF∽△DBE,则 即 故
过点 D 作平行于AB 的直线,交过点 A 且平行于BC 的直线于点R,交BC 的延长线于点S,如图J7.5所示,则四边形 ABSR 是平行四边形.易得
连接 AC,易证△ADC≌△ABC(SSS),则. 进而易得 ∽△DSC.
设SC=x,DR=2x,则 DS=10-2x,于是. 解得 故
如图J7.6 所示,四边形 OBEF 为矩形,可得
利用十字模型得 可得
在 Rt△DFA 中,根据勾股定理得 所以 则
12. 2.
如图J7.7所示,过点A作AM∥BC,过点C作CM∥AB,两线相交于点M,延长BF 交CM 于点G.
所以四边形 ABCM 是正方形,则 AB=BC=CM.
易得△ABD≌△BCG,则CG=BD.
再证△AFB∽△CFG,故
如图J7.8所示,过点 A 作AN∥BC,过点 C 作( ,两线相交于点 N,延长 BF 交CN 于点P.
所以四边形 ABCN 是矩形.
易证△ABD∽△BCP,则 即 故
再证△CFP∽△AFB,则 则 故
得到△DEC∽△ABD 即可,则
如图J7.9所示,过点 C作CM⊥AB 交AB 的延长线于点M,过点 D 作DN⊥MN交MC 的延长线于点N,连接 BD.
易证△BAD≌△BCD(SSS),则.
再证△CMB∽△DNC(一线三垂直),相似比为3∶4.
设 BM = x,则 故 DN = 解得
利用(1)得
(3)①
如图J7.10所示,过点C作CG⊥AD 于点G,连接AC 交BD 于点H,CG 与DE 相交于点O.
因为CF⊥DE,GC⊥AD,所以∠FCG+∠CFG=∠CFG+∠ADE=90°,因此∠FCG=∠ADE,∠BAD=∠CGF=90°,故△DEA∽△CFG,则
在 Rt△ABD 中, 所以AB=3.
在 Rt△ADH 中, 所以
设AH=a,则DH=3a.
因为 所以 则 负值已舍去),于是AH= 故
又 则 解得 CG 故
因为 所 以
由①得△DEA∽△CFG,则
又 则 故 =
第 7 讲 十 字 模 型
模块1 本 质 原 理
常见十字模型见表7.1.
表7.1
已知:△ABC 为等边三角形,AD 与BE 的夹角为60°则:AD= BE 已知:△ABC 为等边三角形,BD=CE 则:AD 与BE 的夹角为60° 已知:ABCD 为正方形,EF 与MN 的夹角为90°则:MN=EF 已知:ABCD 为矩形,EF 与MN 的夹角为90°则:EF/BC
十字模型的本质原理就是利用同角(或等角)的“等量代换”证明全等三角形或者相似三角形
实例剖析:全等形
场景①:如图7.1所示,在等边△ABC 中,M,N分别是AC,AB上的点,BM 与CN相交于点O,若∠BON=60°,求证:BM=CN.
【分析】 因为△ABC 是正三角形,所以 BC=CA,∠BCM=∠CAN=60°.
又∠BON=60°,则∠CBM+∠BCN=60°.
因为∠BCN+∠ACN=60°,所以∠CBM=∠ACN.
故△BCM≌△CAN(ASA),则 BM=CN.
场景②:如图7.2所示,在正方形 ABCD 中,M,N分别是CD,AD 上的点,BM 与CN相交于点O,若∠BON=90°,求证:BM=CN.
【分析】 因为四边形 ABCD 是正方形,所以 BC=CD,∠BCM=∠CDN=90°.
又∠BON=90°,则∠CBM+∠BCN=90°.
因为∠BCN+∠DCN=90°,所以∠CBM=∠DCN.
故△BCM≌△CDN(ASA),则 BM=CN.
场景③:如图7.3所示,在正五边形 ABCDE 中,M,N分别是CD,DE 上的点,BM与CN 相交于点O,若∠BON=108°,求证:BM=CN.
【分析】 因为五边形 ABCDE 是正五边形,所以 BC=CD,∠BCM=∠CDN=108°.
又∠BON=108°,则∠CBM+∠BCN=108°.
因为∠BCN+∠DCN=108°,所以∠CBM=∠DCN.
故△BCM≌△CDN(ASA),则 BM=CN.
场景④:如图7.4所示,在正 n(n>3)边形 ABCDEF…中,M,N分别是CD,DE 上的点,BM与CN 相交于点O,当∠BON= 时,结论BM=CN成立.
【分析】 当 时,结论成立.
易知 因为 所以
又 则∠CBM=∠DCN.
故△BCM≌△CDN(ASA),则 BM=CN.
场景⑤:如图7.5所示,在正五边形 ABCDE 中,M,N 分别是DE,AE 上的点,BM 与CN 相交于点O,若∠BON=108°,结论 BM=CN 是否还成立
【分析】 连接 BD,CE.
因为五边形 ABCDE 是正五边形,所以 BC=CD,∠BCD=∠CDE=108°,CD=DE,∠CDE=∠DEA=108°,则∠BCD=∠DEA,故△BCD≌△CDE(SAS),则 BD = CE,∠BDC =∠CED,∠DBC=∠ECD.
又∠BON=108°,则∠OBC+∠OCB=108°.
因为∠OCB+∠OCD=108°,所以∠OBC=∠OCD(即∠MBC=∠NCD),故∠MBC-∠DBC=∠NCD - ∠ECD,即∠DBM =∠ECN.同时有∠CDE----∠BDC = ∠DEA-∠CED,即∠BDM=∠CEN.
故△BDM≌△CEN(ASA),则 BM=CN.
实例剖析:相似形
如图7.6所示,在矩形 ABCD 中,AB=3AD,点 E,H,F,G分别在矩形 ABCD 的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4,则 GH= .
【分析】 如图7.7所示,过点 F,G分别作AB,BC 的垂线,垂足分别为点 M,N,易证△FME∽△GNH,则 即 得GH=12.
模块2 场 景 演 练
模型的识别:正方形中的十字
1. 如图7.8所示,在正方形 ABCD 中, ,则 HG= .
2.如图7.9所示,将边长为12cm的正方形纸片ABCD 折叠,使得点 A 落在边CD上的E 点,折痕为 MN,若 MN 的长为13cm,则(
模型的识别:矩形中的十字
3. 如图7.10 所示,在矩形 ABCD 中,. ,在 AD 边上有一点E,若( BD,则 CE 与BD 之间的数量关系为 .
4. 如图7.11 所示,在矩形 ABCD 中, ,将矩形对折,使点 A 和点C 重合,则折痕
5. 如图7.12所示,在矩形 ABCD 中, ,将矩形沿着 EC 折叠,使点 B 落在边AD上的F点处,则折痕(
6. 如图7.13 所示,在矩形 ABCD 中,若 则
7.如图7.14 所示,在正方形 ABCD中,点 E 是边BC 上的一点,点F 在边CD 的延长线上,且 过点 A 作 垂足为点 M,交边CD 于点N.若 则线段 AN 的长为 .
8. 如图7.15 所示,在四边形 ABCD 中,. 点 E,F 分别在线段AB,AD上,且 则
模型的构造:矩形中的十字
9.如图7.16所示,把边长为 且 的平行四边形ABCD 对折,使点 B 和D 重合,则折痕.
10. 如图7.17所示,在四边形 ABCD 中,点 M,N 分别在边BC,AB 上, 则
11.如图7.18所示,已知直线 分别与x轴、y轴交于点B,A,将 沿着AB 折叠,使点 O 与点D 重合.当反比例函数 的图像经过点D 时,
模型的构造:三角形中的十字
12. 如图7.19所示,在 中, ,D 为BC 边的中点, AD 于点E,交 AC 于点F,则 AF:FC 的值为 .
13. 如图7.20所示,在 中, D 为BC 边的中点, 于点E,交 AC 于点F,若 则
模型的综合应用:遇见中考
14.某数学兴趣小组在数学课外活动中,对四边形内两条互相垂直的线段做了如下探究:
【观察与猜想】 (1) 如图7.21所示,在矩形ABCD中,AD=7,CD=4,点E 是AD上的一点,连接CE,BD,且CE⊥BD,则
【类比探究】 (2)如图7.22所示,若 BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,则
【拓展延伸】 (3)如图7.23所示,在 Rt△ABD 中, 将△ABD 沿BD 翻折,点 A 落在点C 处得△CBD,点E,F 分别在边AB,AD 上,连接DE,CF,DE⊥CF.
的值为 ;
② 连接 BF,若 ,则BF 的长度为 .
第7讲 十 字 模 型
如图 J7.1 所示,先证明△FME≌△HNG,则
2. 7.
如图J7.2所示,连接 AE,此时 AE⊥MN,则(
证明△CDE∽△BCD 即可.
根据十字模型可得
易得 则 因为 所以
用两次十字模型.
设BC=x,则CE=x-5,DN=x-8,CF=x+5.
易证△ADN∽△FCE,则 即 解得x=20.
在 Rt△ADN中,
如图J7.3所示,过点 C 作CM⊥AB 于点M.设CE 交BF 于点O.
因为 CM⊥AB,所以∠CME=90°,即∠1+∠2=90°.
又 CE⊥BF,则∠BOE=90°,即∠2+∠3=90°,则∠1=∠3,故△CME∽△BAF,则
因为 AB=BC,∠ABC=60°,所以
如图J7.4所示,过点 B 作BE⊥AD 的延长线于点E,过点 M 作MF⊥BC,连接 BD.
所以MF=BE=2,则
易证△MNF∽△DBE,则 即 故
过点 D 作平行于AB 的直线,交过点 A 且平行于BC 的直线于点R,交BC 的延长线于点S,如图J7.5所示,则四边形 ABSR 是平行四边形.易得
连接 AC,易证△ADC≌△ABC(SSS),则. 进而易得 ∽△DSC.
设SC=x,DR=2x,则 DS=10-2x,于是. 解得 故
如图J7.6 所示,四边形 OBEF 为矩形,可得
利用十字模型得 可得
在 Rt△DFA 中,根据勾股定理得 所以 则
12. 2.
如图J7.7所示,过点A作AM∥BC,过点C作CM∥AB,两线相交于点M,延长BF 交CM 于点G.
所以四边形 ABCM 是正方形,则 AB=BC=CM.
易得△ABD≌△BCG,则CG=BD.
再证△AFB∽△CFG,故
如图J7.8所示,过点 A 作AN∥BC,过点 C 作( ,两线相交于点 N,延长 BF 交CN 于点P.
所以四边形 ABCN 是矩形.
易证△ABD∽△BCP,则 即 故
再证△CFP∽△AFB,则 则 故
得到△DEC∽△ABD 即可,则
如图J7.9所示,过点 C作CM⊥AB 交AB 的延长线于点M,过点 D 作DN⊥MN交MC 的延长线于点N,连接 BD.
易证△BAD≌△BCD(SSS),则.
再证△CMB∽△DNC(一线三垂直),相似比为3∶4.
设 BM = x,则 故 DN = 解得
利用(1)得
(3)①
如图J7.10所示,过点C作CG⊥AD 于点G,连接AC 交BD 于点H,CG 与DE 相交于点O.
因为CF⊥DE,GC⊥AD,所以∠FCG+∠CFG=∠CFG+∠ADE=90°,因此∠FCG=∠ADE,∠BAD=∠CGF=90°,故△DEA∽△CFG,则
在 Rt△ABD 中, 所以AB=3.
在 Rt△ADH 中, 所以
设AH=a,则DH=3a.
因为 所以 则 负值已舍去),于是AH= 故
又 则 解得 CG 故
因为 所 以
由①得△DEA∽△CFG,则
又 则 故 =
同课章节目录
