第1讲 中点的联想 (含答案)2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第1讲 中点的联想 (含答案)2025年中考数学几何模型方法巩固练习 |  | |
| 格式 | docx | ||
| 文件大小 | 662.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:26:52 | ||
图片预览

文档简介
第1讲 中点的联想
模块1 本 质 原 理
提到中点,在整个初中的概念中有:三角形中线、斜边中线、中位线、中垂线、圆中弦、倍长中线、中点坐标公式等;如果具体到应用场景里面,实际上只有5类:等腰三角形中,三线合一;直角三角形中,斜边中线;双中点,中位线;转移边角,倍长中线;计算辅助,中点坐标公式.
下面让我们一个一个来看(表1.1).
表1.1
类 型 图 示
三线合一
斜边中线
中位线
中小学教育资源及组卷应用平台
续表
类 型 图 示
倍长中线
中点坐标公式 已知 A(x ,y ),B(x ,y ), 则中点c(x +2x ,y +y )
模块2 场景演练
模型的识别:三线合一
表1.2
已 知 辅助线图示 核心结论
AB= AC ① DC=DB,AD⊥BC,∠CAD=∠BAD;② AB=AC,DC= DB,AD⊥BC,∠CAD=∠BAD,以上四个条件:知二推二.(尝试自己推导下)
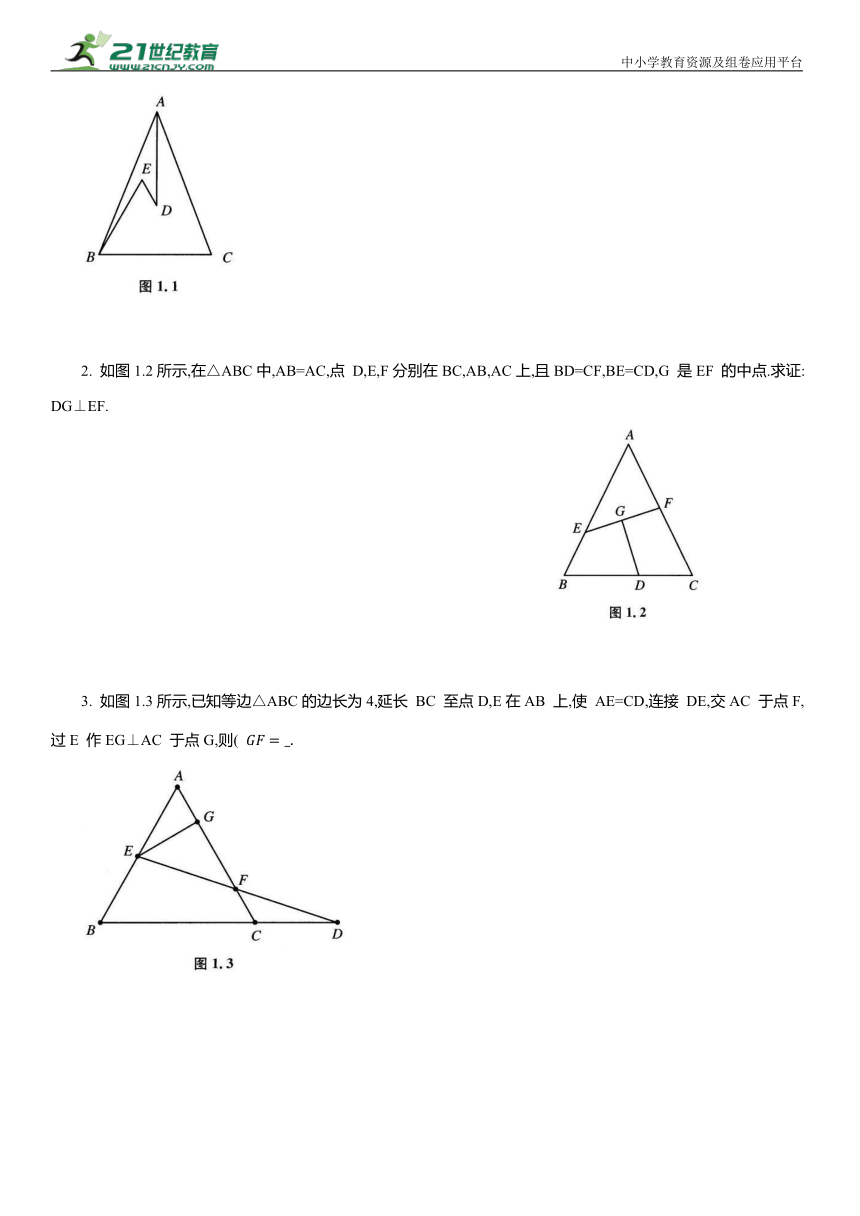
1. 如图1.1所示,在△ABC 中,AB=AC,D,E 是△ABC 内两点,AD 平分∠BAC,∠EBC=∠E=60°,若 BE=6cm,DE=2cm,则 BC= cm.
2. 如图1.2所示,在△ABC中,AB=AC,点 D,E,F分别在BC,AB,AC上,且BD=CF,BE=CD,G 是EF 的中点.求证:DG⊥EF.
3. 如图1.3所示,已知等边△ABC的边长为4,延长 BC 至点D,E在AB 上,使 AE=CD,连接 DE,交AC 于点F,过E 作EG⊥AC 于点G,则(
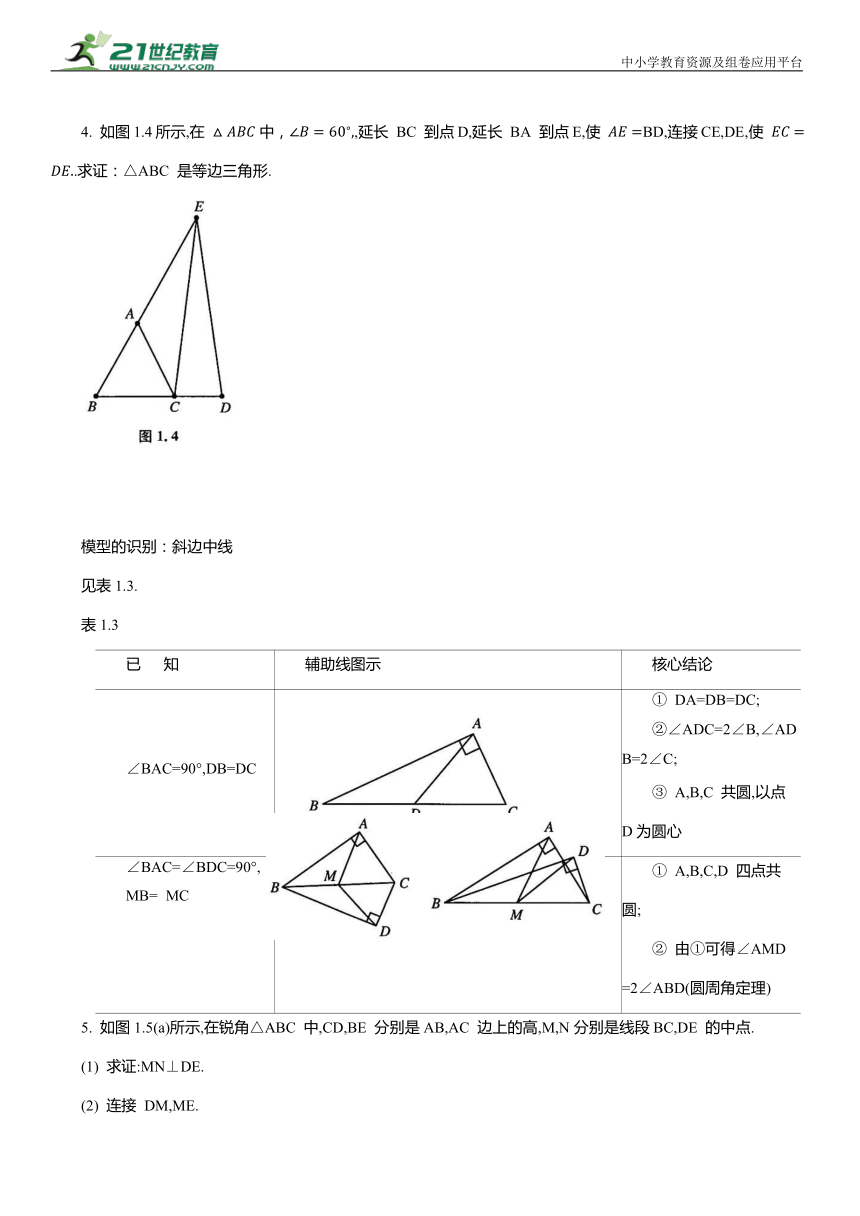
4. 如图1.4所示,在 中, ,延长 BC 到点D,延长 BA 到点E,使 BD,连接CE,DE,使 .求证:△ABC 是等边三角形.
模型的识别:斜边中线
见表1.3.
表1.3
已 知 辅助线图示 核心结论
∠BAC=90°,DB=DC ① DA=DB=DC; ②∠ADC=2∠B,∠ADB=2∠C; ③ A,B,C 共圆,以点 D为圆心
∠BAC=∠BDC=90°, MB= MC ① A,B,C,D 四点共圆; ② 由①可得∠AMD =2∠ABD(圆周角定理)
5. 如图1.5(a)所示,在锐角△ABC 中,CD,BE 分别是AB,AC 边上的高,M,N分别是线段BC,DE 的中点.
(1) 求证:MN⊥DE.
(2) 连接 DM,ME.
① 猜想∠DME 与∠ABE 之间的关系: ;
② 猜想∠BAC 与∠DME 之间的关系: .
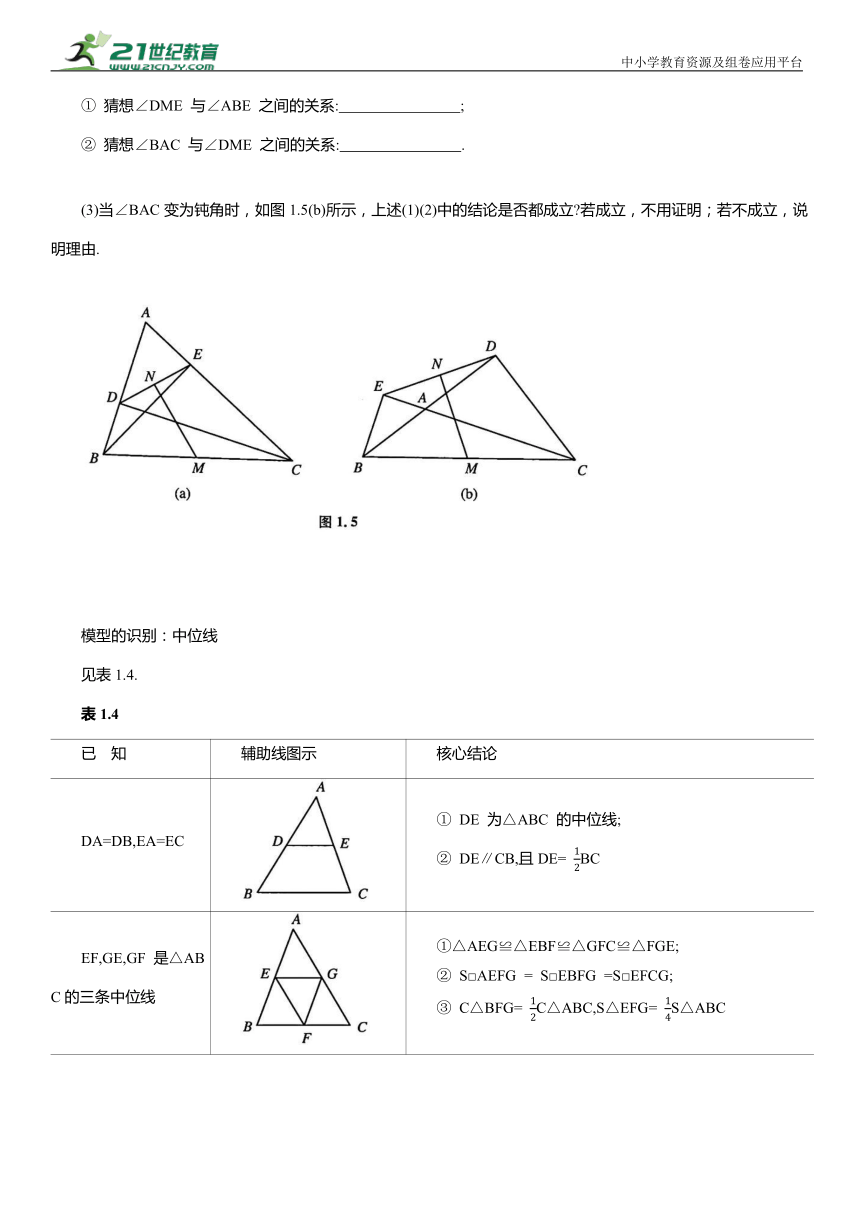
(3)当∠BAC变为钝角时,如图1.5(b)所示,上述(1)(2)中的结论是否都成立 若成立,不用证明;若不成立,说明理由.
模型的识别:中位线
见表1.4.
表1.4
已 知 辅助线图示 核心结论
DA=DB,EA=EC ① DE 为△ABC 的中位线; ② DE∥CB,且DE= BC
EF,GE,GF 是△ABC的三条中位线 ①△AEG≌△EBF≌△GFC≌△FGE; ② S□AEFG = S□EBFG =S□EFCG; ③ C△BFG= C△ABC,S△EFG= S△ABC
在四边形 ABCD 中,AB=CD,点 E,F 分别为AD,BC 的中点 结论:△EFG 为等腰三角形. 证明:连接 BD,取 BD 的中点G,连接 EF,EG,GF,所以EG = AB,GF= CD,I即GE= GF,故△EFG 为等腰三角形
辅助线图示 核心结论
点 E,F,G,H 分别为四边形ABCD 的边AB,BC,CD,DA 的中点 结论:四边形 EFGH 为平行四边形. 证明:连接AC,BD,由题意得 EF∥AC,EF= AC,GH∥AC,GH= AC,所以 EF ∥GH,EF = GH,故四边形 EFGH 为平行四边形
类型1:中位线的性质
6.如图1.6所示,在四边形 ABCD 中,点 P 是对角线BD 的中点,点 E,F分别是AB,CD 的中点,AD=BC,∠CBD=30°,∠ADB=100°,则
7. 如图1.7所示,点 D 是 内一点, 点E,F,G,H 分别是AB,AC,CD,BD的中点,则四边形 EFGH 的周长是 .
8. 如图1.8所示,在四边形 ABCD 中, 点M,N分别为线段BC,AB 上的动点(含端点,但点 M 不与点B 重合),点 E,F分别为DM,MN 的中点,则 EF长度的最大值为 .
9. 如图1.9所示,点 E,F,G,H 分别为四边形ABCD 的边AB,BC,CD,DA 的中点.
(1) 对角线 AC 与DB 满足 时,四边形 EFGH 是菱形.
(2) 对角线 AC与DB 满足 时,四边形 EFGH 是矩形.
(3)对角线 AC 与DB 满足 时,四边形 EFGH 是正方形.
类型2:中位线的构造
10. 如图1.10所示,在 中, D 是边AB 的中点,E 是边BC上一点.若DE 平分 的周长,则DE 的长是 .
11. 如图1.11所示,在 中, 点 E,F 分别在CA,CB 上,且 点 M,N 分别为AF,BE 的中点,则 MN 的长为 .
12.(1)如图1.12(a)所示,在四边形 ABCD 中,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD 的延长线交于点M,N,∠BME=∠CNE.求证:AB=CD.
(2)如图1.12(b)所示,在△ABC 中,O是BC 边的中点,D 是AC边上一点,E 是AD的中点,直线 OE 交BA 的延长线于点G.若AB=DC=5,∠OEC=60°,则OE= .
模型的识别:倍长中线
表1.5
已 知 辅助线图示 核心结论
类型1:倍长中线(倍长三角形中线) BD=CD 延长 AD 至点E,使 DE = AD,则: ①△BDE≌△CDA. ② AC∥BE. 本质:通过构造一对旋转型全等三角形,实现边和角的转移
已 知 辅助线图示 核心结论
策略2: 延长 DC,GE 交于点F,可得“8字形”全等,即△BEG≌△CEF(ASA). 优点:D,C,F 天然共线
类型1:单次全等的倍长中线
13. 如图1.13所示,在△ABC中,D为BC的中点,若AB=5,AC=3,则AD 的取值范围是 .
14. 如图1.14所示,在 中,AD 是BC 边上的中线,E 是AD 上一点,延长 BE 交AC 于点F,. 求证:
类型2:单次全等的类倍长中线
15. 如图1.15 所示,在正方形 ABCD 中, E 为AB边的中点,G,F 分别为AD,BC 边上的点,且 ,则 GF 的长为 .
16. 如图1.16 所示,已知 C 为 BE 的中点, 求证:
类型3:双次全等的倍长中线
17. 如图1.17所示,在 中, ,CE 是 AB 边上的中线,延长 AB 到点D,使 .求证:
18. 如图1.18所示,在 中,分别以 AB,AC 为边长,向三角形的外侧作正方形ABDE 和正方形ACFG,M 为BC 的中点.求证:
19. 如图1.19 所示, ,M 是BE 的中点, 求证:
20. 如图1.20所示, 垂足为点 B, ,垂足为点 A, ,点 E 是CD 的中点,则.
21. 如图1.21所示,在 中, 若 1,则 BC 的长为 .
22. 如图1.22所示, 均为等腰直角三角形,连接 AE,F为AE 的中点,连接 BF,FD.求证: 且
第1讲 中点的联想
1. 8.
如图J1.1所示,延长ED 交BC 于点M,延长 AD 交BC 于点N.
因为 AB=AC,AD 平分∠BAC,所以 AN⊥BC,BN=CN.
又 ,因此△BEM 为等边三角形.
因为 BE=6,DE=2,所以 DM=4.
因为△BEM 为等边三角形,所以∠EMB = 60°,又 AN⊥BC,即. 则 ,所以 NM=2,BN=4,故 BC=2BN=8.
2. 如图J1.2所示,连接ED,DF.
因为AB=AC,所以∠B=∠C,易证 所以DE=DF.
又 G 是EF的中点,所以 DG⊥EF.
3. 2.
如图J1.3所示,过点 E 作EH∥BC交AC 于点H,易证 则 又 为等边三角形且EG⊥AC,所以AG=GH,故
4. 如图J1.4 所示,作 EF⊥CD 交CD 于点F.
设CF=FD=a,BC=b,所以AE=2a+b.
在 Rt△EBF 中,∠B=60°,所以.
因为BF=a+b,所以BE=2a+2b,又AE=2a+b,则AB=b.
因为 AB=BC=b,∠B=60°,所以△ABC 为等边三角形.
5. (1) 如图J1.5(a)所示,连接DM,ME.
因为 CD,BE 分别是AB,AC边上的高,M是BC 的中点,所以 又因为 N 为DE 的中点,所以 MN⊥DE.
(2) ①因为 MD=MB=ME=MC,所以B,D,E,C四点共圆,故∠DME=2∠ABE.
② 在 Rt△ABE 中,∠BAC+∠ABE=90°,所以 即∠DME=180°-2∠BAC.
(3)(2)中结论②不成立,其余均成立.理由如下:
如图J1.5(b)所示,连接 DM,ME.
因为 MD=MB=ME=MC,所以 B,D,E,C 四点共圆,故∠DME=2∠ABE.
对于 Rt△ABE,利用外角性质可得∠BAC=∠ABE+90°,所以 90°,即∠DME=2∠BAC-180°.
6. 35°.
易得 PE 是△ABD 的中位线,所以 则∠EPD=180°-∠ADB=
80°,同理可得 所以 故 ∠FPD=110°.
因为AD= BC,所以 PE=PF,故
7. 21.
利用勾股定理求出 BC=10,再根据三角形的中位线性质求出 然后代入数据计算即可.
8. 5.
连接 DN,2
9.(1)当AC=DB 时,EF=EH,所以四边形 EFGH 为菱形.
(2) 当 AC⊥BD时,EF⊥EH,所以四边形 EFGH 为矩形.
(3)当AC=DB,AC⊥BD 时,EF=EH,EF⊥EH,所以四边形 EFGH 为正方形.
如图J1.6所示,延长BC 至点M,使CM=CA,连接AM,作 CN⊥AM 于点N.
因为 DE 平分△ABC 的周长,AD= DB,所以 ME=EB,则
因为∠ACB=60°,所以∠ACM=120°.
因为 CM=CA,所以∠ACN=60°,AN = MN,则 因此 AM 故
如图J1.7所示,取 AB 的中点D,连接 MD,ND,
因为点 M,N分别为AF,BE 的中点,所以 DM 为 的中位线,DN 为 的中位线,则
又 AE⊥BF,则 DM⊥DN,因此. 为等腰直角三角形,故
12.(1) 如图J1.8(a)所示,连接 BD,取 DB 的中点H,连接 EH,FH.
因为 E,F分别是AD,BC的中点,所以 则∠BME=∠HEF,∠CNE=∠HFE.
又∠BME=∠CNE,则 HE=HF,故AB=CD.
(2)如图J1.8(b)所示,连接BD,取 DB的中点H,连接EH,OH.
因为AB=CD,O是BC边的中点,所以HO=HE,∠HOE=∠OEC.
又∠OEC=60°,则∠HOE=∠OEC=60°,因此△OEH 是等边三角形.
因为 AB=DC=5,所以
13. 1如图J1.9所示,延长 AD 至点E,使 DE=AD.
因为 D 为BC 的中点,所以 DB=CD,易证 则
在△ABE 中,因为AB+BE>AE,所以AB+AC>2AD,又AB=5,AC=3,则5+3>2AD,即 AD<4.
由 AB--BE1,故114. 如图J1.10所示,延长AD 到点G,使 DG=AD,连接BG.
因为 BD=CD,∠BDG=∠CDA,AD=GD,所以△ADC≌△GDB,则AC=GB,∠G=∠CAD.
又AF=EF,所以∠CAD=∠AEF=∠BED,则∠G=∠BED,因此 BE = BG,故 AC= BE.
15. 3.
延长GE与FB 的延长线交于点H,易证△AEG≌△BEH,从而得证△FGE≌△FHE,所以GF=FH=FB+BH=FB+GA=3.
16. 延长AC交EF 的延长线于点H,易证△ACB≌△HCE,所以AB=EH,∠A=∠H=∠CDF,则△DFH 为等腰三角形,故 EH=AB=EF+FH=EF+FD.
17. 如图J1.11所示,延长 CE 到点F,使 EF=CE,连接 BF.
因为 CE 是AB 边上的中线,所以 AE=EB.
又因为∠AEC =∠BEF,CE = FE,所以△EBF≌△EAC(SAS),则 BF = AC = BD,∠EBF=∠A,于是∠FBC=∠FBE +∠EBC =∠A +∠ACB =∠DBC,因此△FBC≌△DBC(SAS),故CD=CF=2CE.
18. 如图J1.12 所示,延长 AM 到点N,使 MN=MA,连接NC.
因为∠AMB=∠NMC,BM=CM,所以△ABM≌△NCM(SAS),则 CN= AB= AE,∠ABM=∠NCM,于是 AB∥NC,从而∠ACN+∠BAC=180°.又因为∠EAG+∠BAC=180°,所以∠EAG=∠ACN.再由 AG = CA,可得△EAG≌△NCA(SAS),故 EG = NA=2AM.
19. 如图J1.13 所示,延长 AM 交 DC 于点H,要证明 AM⊥CD,实际上就是证明∠AHD=90°.根据 BM=ME,可以倍长中线 AM 到点F,连接 BF 交AD 于点N,交 CD 于点O.
易证△AME≌△FMB,则AE=FB,∠EAF=∠F,从而 AE∥FB,∠ANF=90°.
而 故 从而 △ABF,故∠D=∠F.
而 ,所以∠AHD=90°,即 AM⊥CD.
思路1 倍长中线+勾股定理.
如图J1.14所示,延长 AE 交BC 于点F.
因为点 E 是CD 的中点,所以 DE=CE.
又AB⊥BC,AB⊥AD,则 AD∥BC,因此∠ADE =∠BCE 且l ∠CEF,故△AED≌△FEC(ASA),则AD=FC=5,AE=EF,可得 BF=BC--FC=5.
在 Rt△ABF中, 故
思路2 中位线+勾股定理.
如图J1.15所示,延长DA 至点F,使AF=AD,连接 FC,过点 F 作FG⊥BC 于点G.
因为点 E 是CD 的中点,所以
因为 BC=10,AF=AD=BG=5,所以CG=5.
在 Rt△CFG 中, 故
思路3 利用线段比1:2构造相似三角形+勾股定理.
如图J1.16所示,连接 BD.
因为 所以△ADE∽△BCD,则
在 Rt△ABD 中, 故
21.
思路1 中点+中点,构造中位线.
如图J1.17所示,过点 D,B分别作DF⊥AE,BE⊥AE 于点F,E.
设CF=EF=x,BE=2DF=2y,则AF=x+1,AE=2x+1.
因为sin∠BAC=tan∠DAC,所以 即 解得 则AE=2.
在 Rt△ABE 中,
在 Rt△BCE 中,
思路2 倍长中线+勾股定理.
如图J1.18所示,延长AD 至点E,使 ED=AD,连接EB,过点 A 作AF⊥EB 延长线于点 F,过点 A 作AG∥BC 交EF 于点G.
设FG=x,AF=y.
因为 AD=DE,DB=DC,∠ADC=∠BDE,所以△ADC≌△EDB(SAS),则AC=BE=1,∠CAD=∠E,故AC∥EF.
因为∠BAC=∠ABF,sin∠BAC=tan∠DAC,所以 即3=2+x,解得. 则 BF=2.
在 Rt△ABF 中,
在 Rt△AGF 中,
22.思路1 倍长中线+二次全等.
如图J1.19所示,延长 DF 至点G,使 连接AG,BG,BD.因为AF=FE,FD=FG,∠AFG=∠EFD,所以 则
AG = DE = CD, ∠GAF = ∠FED = ∠1+∠CED = ∠1+45°,
故∠BAG =∠1+45°+∠2 +45°= 180°-∠ACE +90°= 270°-∠ACE.因为∠BCD=360°-∠ACB-∠ECD--∠ACE=270°-∠ACE,所以∠BAG=∠BCD.
又AG=CD,AB=BC,则△BAG≌△BCD(SAS),因此 BG=BD,∠ABG=∠CBD.
因为 FD=FG,所以 BF⊥FD.
又∠ABG=∠CBD,∠ABG+∠GBC=90°,则∠CBD+∠GBC=90°,即∠DBG=90°,故
思路2 三线合一+一次全等.
如图J1.20所示,分别过点 B,D作AC,CE 的垂线,垂足为点 P,Q,连接 PF,FQ.
因为 AP=PC,AF=FE,QE=QC,所以 则 FQ∥PC,PF∥CE,即 PFQC 为平行四边形,所以∠FPC=∠FQC,则∠FPB=∠FQD =90°+∠FPC,故△BPF≌△FQD(SAS),于是 BF= DF,∠1=∠2,故
∠BFD= ∠PFQ-∠1-∠3
= ∠PFQ-∠2-∠3
= ∠PFQ-(180°-∠BPF)
= ∠PFQ-(180°-90°-∠FPC)
= ∠PFQ+∠FPC-90°
= 90°,即 BF⊥FD.
思路3 构造手拉手模型+中位线性质.
如图J1.21所示,过点 C 作AC,CE 的垂线,分别交 AB,ED 的延长线于点M,N,连接AN,ME,交于点J,CN,ME 交于点K.
因为AC=CM,∠ACN=∠MCE,CN= CE,所以△ACN≌△MCE(SAS),则 AN=ME,∠1=∠2.
又∠CKE=∠NKJ,则∠EJN=∠ECN=90°,即 AN⊥ME.
因为 AB=BM,AF= FE,ED= DN,所以 且 BF∥ME,FD∥AN.
又 AN=ME,AN⊥ME,则 BF=FD,BF⊥FD.
模块1 本 质 原 理
提到中点,在整个初中的概念中有:三角形中线、斜边中线、中位线、中垂线、圆中弦、倍长中线、中点坐标公式等;如果具体到应用场景里面,实际上只有5类:等腰三角形中,三线合一;直角三角形中,斜边中线;双中点,中位线;转移边角,倍长中线;计算辅助,中点坐标公式.
下面让我们一个一个来看(表1.1).
表1.1
类 型 图 示
三线合一
斜边中线
中位线
中小学教育资源及组卷应用平台
续表
类 型 图 示
倍长中线
中点坐标公式 已知 A(x ,y ),B(x ,y ), 则中点c(x +2x ,y +y )
模块2 场景演练
模型的识别:三线合一
表1.2
已 知 辅助线图示 核心结论
AB= AC ① DC=DB,AD⊥BC,∠CAD=∠BAD;② AB=AC,DC= DB,AD⊥BC,∠CAD=∠BAD,以上四个条件:知二推二.(尝试自己推导下)
1. 如图1.1所示,在△ABC 中,AB=AC,D,E 是△ABC 内两点,AD 平分∠BAC,∠EBC=∠E=60°,若 BE=6cm,DE=2cm,则 BC= cm.
2. 如图1.2所示,在△ABC中,AB=AC,点 D,E,F分别在BC,AB,AC上,且BD=CF,BE=CD,G 是EF 的中点.求证:DG⊥EF.
3. 如图1.3所示,已知等边△ABC的边长为4,延长 BC 至点D,E在AB 上,使 AE=CD,连接 DE,交AC 于点F,过E 作EG⊥AC 于点G,则(
4. 如图1.4所示,在 中, ,延长 BC 到点D,延长 BA 到点E,使 BD,连接CE,DE,使 .求证:△ABC 是等边三角形.
模型的识别:斜边中线
见表1.3.
表1.3
已 知 辅助线图示 核心结论
∠BAC=90°,DB=DC ① DA=DB=DC; ②∠ADC=2∠B,∠ADB=2∠C; ③ A,B,C 共圆,以点 D为圆心
∠BAC=∠BDC=90°, MB= MC ① A,B,C,D 四点共圆; ② 由①可得∠AMD =2∠ABD(圆周角定理)
5. 如图1.5(a)所示,在锐角△ABC 中,CD,BE 分别是AB,AC 边上的高,M,N分别是线段BC,DE 的中点.
(1) 求证:MN⊥DE.
(2) 连接 DM,ME.
① 猜想∠DME 与∠ABE 之间的关系: ;
② 猜想∠BAC 与∠DME 之间的关系: .
(3)当∠BAC变为钝角时,如图1.5(b)所示,上述(1)(2)中的结论是否都成立 若成立,不用证明;若不成立,说明理由.
模型的识别:中位线
见表1.4.
表1.4
已 知 辅助线图示 核心结论
DA=DB,EA=EC ① DE 为△ABC 的中位线; ② DE∥CB,且DE= BC
EF,GE,GF 是△ABC的三条中位线 ①△AEG≌△EBF≌△GFC≌△FGE; ② S□AEFG = S□EBFG =S□EFCG; ③ C△BFG= C△ABC,S△EFG= S△ABC
在四边形 ABCD 中,AB=CD,点 E,F 分别为AD,BC 的中点 结论:△EFG 为等腰三角形. 证明:连接 BD,取 BD 的中点G,连接 EF,EG,GF,所以EG = AB,GF= CD,I即GE= GF,故△EFG 为等腰三角形
辅助线图示 核心结论
点 E,F,G,H 分别为四边形ABCD 的边AB,BC,CD,DA 的中点 结论:四边形 EFGH 为平行四边形. 证明:连接AC,BD,由题意得 EF∥AC,EF= AC,GH∥AC,GH= AC,所以 EF ∥GH,EF = GH,故四边形 EFGH 为平行四边形
类型1:中位线的性质
6.如图1.6所示,在四边形 ABCD 中,点 P 是对角线BD 的中点,点 E,F分别是AB,CD 的中点,AD=BC,∠CBD=30°,∠ADB=100°,则
7. 如图1.7所示,点 D 是 内一点, 点E,F,G,H 分别是AB,AC,CD,BD的中点,则四边形 EFGH 的周长是 .
8. 如图1.8所示,在四边形 ABCD 中, 点M,N分别为线段BC,AB 上的动点(含端点,但点 M 不与点B 重合),点 E,F分别为DM,MN 的中点,则 EF长度的最大值为 .
9. 如图1.9所示,点 E,F,G,H 分别为四边形ABCD 的边AB,BC,CD,DA 的中点.
(1) 对角线 AC 与DB 满足 时,四边形 EFGH 是菱形.
(2) 对角线 AC与DB 满足 时,四边形 EFGH 是矩形.
(3)对角线 AC 与DB 满足 时,四边形 EFGH 是正方形.
类型2:中位线的构造
10. 如图1.10所示,在 中, D 是边AB 的中点,E 是边BC上一点.若DE 平分 的周长,则DE 的长是 .
11. 如图1.11所示,在 中, 点 E,F 分别在CA,CB 上,且 点 M,N 分别为AF,BE 的中点,则 MN 的长为 .
12.(1)如图1.12(a)所示,在四边形 ABCD 中,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD 的延长线交于点M,N,∠BME=∠CNE.求证:AB=CD.
(2)如图1.12(b)所示,在△ABC 中,O是BC 边的中点,D 是AC边上一点,E 是AD的中点,直线 OE 交BA 的延长线于点G.若AB=DC=5,∠OEC=60°,则OE= .
模型的识别:倍长中线
表1.5
已 知 辅助线图示 核心结论
类型1:倍长中线(倍长三角形中线) BD=CD 延长 AD 至点E,使 DE = AD,则: ①△BDE≌△CDA. ② AC∥BE. 本质:通过构造一对旋转型全等三角形,实现边和角的转移
已 知 辅助线图示 核心结论
策略2: 延长 DC,GE 交于点F,可得“8字形”全等,即△BEG≌△CEF(ASA). 优点:D,C,F 天然共线
类型1:单次全等的倍长中线
13. 如图1.13所示,在△ABC中,D为BC的中点,若AB=5,AC=3,则AD 的取值范围是 .
14. 如图1.14所示,在 中,AD 是BC 边上的中线,E 是AD 上一点,延长 BE 交AC 于点F,. 求证:
类型2:单次全等的类倍长中线
15. 如图1.15 所示,在正方形 ABCD 中, E 为AB边的中点,G,F 分别为AD,BC 边上的点,且 ,则 GF 的长为 .
16. 如图1.16 所示,已知 C 为 BE 的中点, 求证:
类型3:双次全等的倍长中线
17. 如图1.17所示,在 中, ,CE 是 AB 边上的中线,延长 AB 到点D,使 .求证:
18. 如图1.18所示,在 中,分别以 AB,AC 为边长,向三角形的外侧作正方形ABDE 和正方形ACFG,M 为BC 的中点.求证:
19. 如图1.19 所示, ,M 是BE 的中点, 求证:
20. 如图1.20所示, 垂足为点 B, ,垂足为点 A, ,点 E 是CD 的中点,则.
21. 如图1.21所示,在 中, 若 1,则 BC 的长为 .
22. 如图1.22所示, 均为等腰直角三角形,连接 AE,F为AE 的中点,连接 BF,FD.求证: 且
第1讲 中点的联想
1. 8.
如图J1.1所示,延长ED 交BC 于点M,延长 AD 交BC 于点N.
因为 AB=AC,AD 平分∠BAC,所以 AN⊥BC,BN=CN.
又 ,因此△BEM 为等边三角形.
因为 BE=6,DE=2,所以 DM=4.
因为△BEM 为等边三角形,所以∠EMB = 60°,又 AN⊥BC,即. 则 ,所以 NM=2,BN=4,故 BC=2BN=8.
2. 如图J1.2所示,连接ED,DF.
因为AB=AC,所以∠B=∠C,易证 所以DE=DF.
又 G 是EF的中点,所以 DG⊥EF.
3. 2.
如图J1.3所示,过点 E 作EH∥BC交AC 于点H,易证 则 又 为等边三角形且EG⊥AC,所以AG=GH,故
4. 如图J1.4 所示,作 EF⊥CD 交CD 于点F.
设CF=FD=a,BC=b,所以AE=2a+b.
在 Rt△EBF 中,∠B=60°,所以.
因为BF=a+b,所以BE=2a+2b,又AE=2a+b,则AB=b.
因为 AB=BC=b,∠B=60°,所以△ABC 为等边三角形.
5. (1) 如图J1.5(a)所示,连接DM,ME.
因为 CD,BE 分别是AB,AC边上的高,M是BC 的中点,所以 又因为 N 为DE 的中点,所以 MN⊥DE.
(2) ①因为 MD=MB=ME=MC,所以B,D,E,C四点共圆,故∠DME=2∠ABE.
② 在 Rt△ABE 中,∠BAC+∠ABE=90°,所以 即∠DME=180°-2∠BAC.
(3)(2)中结论②不成立,其余均成立.理由如下:
如图J1.5(b)所示,连接 DM,ME.
因为 MD=MB=ME=MC,所以 B,D,E,C 四点共圆,故∠DME=2∠ABE.
对于 Rt△ABE,利用外角性质可得∠BAC=∠ABE+90°,所以 90°,即∠DME=2∠BAC-180°.
6. 35°.
易得 PE 是△ABD 的中位线,所以 则∠EPD=180°-∠ADB=
80°,同理可得 所以 故 ∠FPD=110°.
因为AD= BC,所以 PE=PF,故
7. 21.
利用勾股定理求出 BC=10,再根据三角形的中位线性质求出 然后代入数据计算即可.
8. 5.
连接 DN,2
9.(1)当AC=DB 时,EF=EH,所以四边形 EFGH 为菱形.
(2) 当 AC⊥BD时,EF⊥EH,所以四边形 EFGH 为矩形.
(3)当AC=DB,AC⊥BD 时,EF=EH,EF⊥EH,所以四边形 EFGH 为正方形.
如图J1.6所示,延长BC 至点M,使CM=CA,连接AM,作 CN⊥AM 于点N.
因为 DE 平分△ABC 的周长,AD= DB,所以 ME=EB,则
因为∠ACB=60°,所以∠ACM=120°.
因为 CM=CA,所以∠ACN=60°,AN = MN,则 因此 AM 故
如图J1.7所示,取 AB 的中点D,连接 MD,ND,
因为点 M,N分别为AF,BE 的中点,所以 DM 为 的中位线,DN 为 的中位线,则
又 AE⊥BF,则 DM⊥DN,因此. 为等腰直角三角形,故
12.(1) 如图J1.8(a)所示,连接 BD,取 DB 的中点H,连接 EH,FH.
因为 E,F分别是AD,BC的中点,所以 则∠BME=∠HEF,∠CNE=∠HFE.
又∠BME=∠CNE,则 HE=HF,故AB=CD.
(2)如图J1.8(b)所示,连接BD,取 DB的中点H,连接EH,OH.
因为AB=CD,O是BC边的中点,所以HO=HE,∠HOE=∠OEC.
又∠OEC=60°,则∠HOE=∠OEC=60°,因此△OEH 是等边三角形.
因为 AB=DC=5,所以
13. 1
因为 D 为BC 的中点,所以 DB=CD,易证 则
在△ABE 中,因为AB+BE>AE,所以AB+AC>2AD,又AB=5,AC=3,则5+3>2AD,即 AD<4.
由 AB--BE
因为 BD=CD,∠BDG=∠CDA,AD=GD,所以△ADC≌△GDB,则AC=GB,∠G=∠CAD.
又AF=EF,所以∠CAD=∠AEF=∠BED,则∠G=∠BED,因此 BE = BG,故 AC= BE.
15. 3.
延长GE与FB 的延长线交于点H,易证△AEG≌△BEH,从而得证△FGE≌△FHE,所以GF=FH=FB+BH=FB+GA=3.
16. 延长AC交EF 的延长线于点H,易证△ACB≌△HCE,所以AB=EH,∠A=∠H=∠CDF,则△DFH 为等腰三角形,故 EH=AB=EF+FH=EF+FD.
17. 如图J1.11所示,延长 CE 到点F,使 EF=CE,连接 BF.
因为 CE 是AB 边上的中线,所以 AE=EB.
又因为∠AEC =∠BEF,CE = FE,所以△EBF≌△EAC(SAS),则 BF = AC = BD,∠EBF=∠A,于是∠FBC=∠FBE +∠EBC =∠A +∠ACB =∠DBC,因此△FBC≌△DBC(SAS),故CD=CF=2CE.
18. 如图J1.12 所示,延长 AM 到点N,使 MN=MA,连接NC.
因为∠AMB=∠NMC,BM=CM,所以△ABM≌△NCM(SAS),则 CN= AB= AE,∠ABM=∠NCM,于是 AB∥NC,从而∠ACN+∠BAC=180°.又因为∠EAG+∠BAC=180°,所以∠EAG=∠ACN.再由 AG = CA,可得△EAG≌△NCA(SAS),故 EG = NA=2AM.
19. 如图J1.13 所示,延长 AM 交 DC 于点H,要证明 AM⊥CD,实际上就是证明∠AHD=90°.根据 BM=ME,可以倍长中线 AM 到点F,连接 BF 交AD 于点N,交 CD 于点O.
易证△AME≌△FMB,则AE=FB,∠EAF=∠F,从而 AE∥FB,∠ANF=90°.
而 故 从而 △ABF,故∠D=∠F.
而 ,所以∠AHD=90°,即 AM⊥CD.
思路1 倍长中线+勾股定理.
如图J1.14所示,延长 AE 交BC 于点F.
因为点 E 是CD 的中点,所以 DE=CE.
又AB⊥BC,AB⊥AD,则 AD∥BC,因此∠ADE =∠BCE 且l ∠CEF,故△AED≌△FEC(ASA),则AD=FC=5,AE=EF,可得 BF=BC--FC=5.
在 Rt△ABF中, 故
思路2 中位线+勾股定理.
如图J1.15所示,延长DA 至点F,使AF=AD,连接 FC,过点 F 作FG⊥BC 于点G.
因为点 E 是CD 的中点,所以
因为 BC=10,AF=AD=BG=5,所以CG=5.
在 Rt△CFG 中, 故
思路3 利用线段比1:2构造相似三角形+勾股定理.
如图J1.16所示,连接 BD.
因为 所以△ADE∽△BCD,则
在 Rt△ABD 中, 故
21.
思路1 中点+中点,构造中位线.
如图J1.17所示,过点 D,B分别作DF⊥AE,BE⊥AE 于点F,E.
设CF=EF=x,BE=2DF=2y,则AF=x+1,AE=2x+1.
因为sin∠BAC=tan∠DAC,所以 即 解得 则AE=2.
在 Rt△ABE 中,
在 Rt△BCE 中,
思路2 倍长中线+勾股定理.
如图J1.18所示,延长AD 至点E,使 ED=AD,连接EB,过点 A 作AF⊥EB 延长线于点 F,过点 A 作AG∥BC 交EF 于点G.
设FG=x,AF=y.
因为 AD=DE,DB=DC,∠ADC=∠BDE,所以△ADC≌△EDB(SAS),则AC=BE=1,∠CAD=∠E,故AC∥EF.
因为∠BAC=∠ABF,sin∠BAC=tan∠DAC,所以 即3=2+x,解得. 则 BF=2.
在 Rt△ABF 中,
在 Rt△AGF 中,
22.思路1 倍长中线+二次全等.
如图J1.19所示,延长 DF 至点G,使 连接AG,BG,BD.因为AF=FE,FD=FG,∠AFG=∠EFD,所以 则
AG = DE = CD, ∠GAF = ∠FED = ∠1+∠CED = ∠1+45°,
故∠BAG =∠1+45°+∠2 +45°= 180°-∠ACE +90°= 270°-∠ACE.因为∠BCD=360°-∠ACB-∠ECD--∠ACE=270°-∠ACE,所以∠BAG=∠BCD.
又AG=CD,AB=BC,则△BAG≌△BCD(SAS),因此 BG=BD,∠ABG=∠CBD.
因为 FD=FG,所以 BF⊥FD.
又∠ABG=∠CBD,∠ABG+∠GBC=90°,则∠CBD+∠GBC=90°,即∠DBG=90°,故
思路2 三线合一+一次全等.
如图J1.20所示,分别过点 B,D作AC,CE 的垂线,垂足为点 P,Q,连接 PF,FQ.
因为 AP=PC,AF=FE,QE=QC,所以 则 FQ∥PC,PF∥CE,即 PFQC 为平行四边形,所以∠FPC=∠FQC,则∠FPB=∠FQD =90°+∠FPC,故△BPF≌△FQD(SAS),于是 BF= DF,∠1=∠2,故
∠BFD= ∠PFQ-∠1-∠3
= ∠PFQ-∠2-∠3
= ∠PFQ-(180°-∠BPF)
= ∠PFQ-(180°-90°-∠FPC)
= ∠PFQ+∠FPC-90°
= 90°,即 BF⊥FD.
思路3 构造手拉手模型+中位线性质.
如图J1.21所示,过点 C 作AC,CE 的垂线,分别交 AB,ED 的延长线于点M,N,连接AN,ME,交于点J,CN,ME 交于点K.
因为AC=CM,∠ACN=∠MCE,CN= CE,所以△ACN≌△MCE(SAS),则 AN=ME,∠1=∠2.
又∠CKE=∠NKJ,则∠EJN=∠ECN=90°,即 AN⊥ME.
因为 AB=BM,AF= FE,ED= DN,所以 且 BF∥ME,FD∥AN.
又 AN=ME,AN⊥ME,则 BF=FD,BF⊥FD.
同课章节目录
