第 3 讲 辅助圆的妙用 (含答案)2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第 3 讲 辅助圆的妙用 (含答案)2025年中考数学几何模型方法巩固练习 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:27:38 | ||
图片预览


文档简介
第 3 讲 辅助圆的妙用
模块1 本质原理
很多题目中没有出现圆,但是如果利用圆的特征添加圆,能让题目解起来变得十分简单.因此,辅助圆思想是我们解题中非常重要的工具.
表3.1中是几种较为常见的辅助圆的情景.
辅助圆图示 辅助圆结论
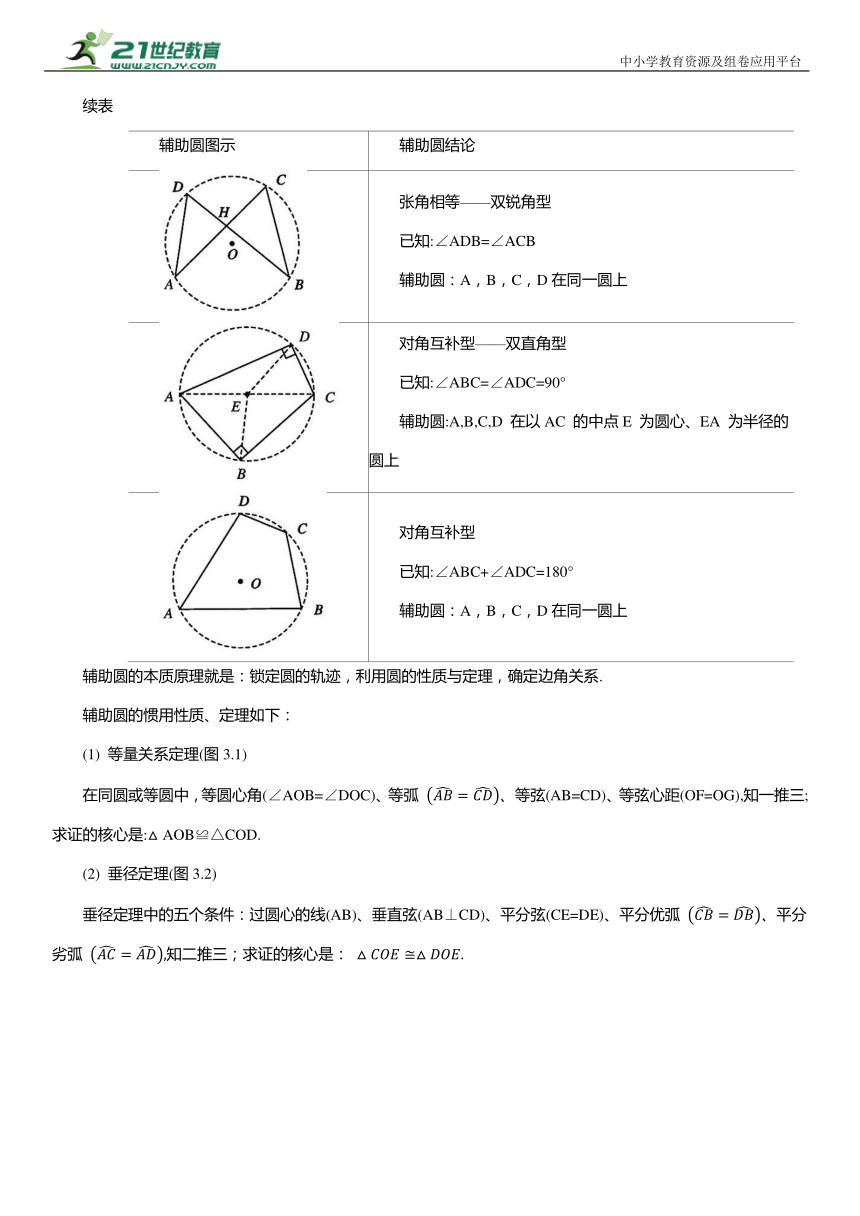
已知:OA=OB=OC 辅助圆:A,B,C在以点O为圆心、OA 为半径的圆上
已知:OC=OD,∠COD=2∠CAD 辅助圆:A,C,D在以点O 为圆心、OC 为半径的圆上
张角相等——双直角型 已知:∠ABD=∠ACD=90° 辅助圆:A,B,C,D 在以AD 的中点E 为圆心、EA 为半径的圆上
中小学教育资源及组卷应用平台
续表
辅助圆图示 辅助圆结论
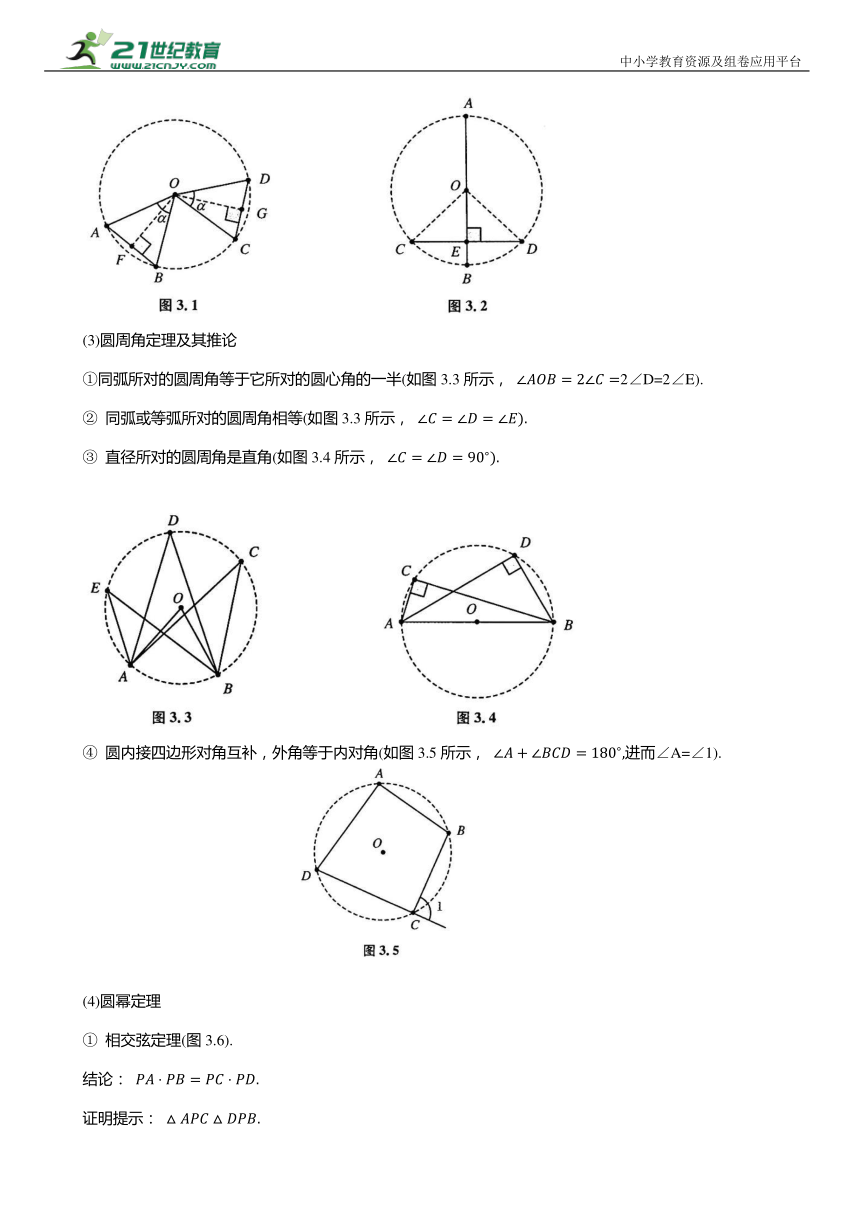
张角相等——双锐角型 已知:∠ADB=∠ACB 辅助圆:A,B,C,D在同一圆上
对角互补型——双直角型 已知:∠ABC=∠ADC=90° 辅助圆:A,B,C,D 在以AC 的中点E 为圆心、EA 为半径的圆上
对角互补型 已知:∠ABC+∠ADC=180° 辅助圆:A,B,C,D在同一圆上
辅助圆的本质原理就是:锁定圆的轨迹,利用圆的性质与定理,确定边角关系.
辅助圆的惯用性质、定理如下:
(1) 等量关系定理(图3.1)
在同圆或等圆中,等圆心角(∠AOB=∠DOC)、等弧 等弦(AB=CD)、等弦心距(OF=OG),知一推三;求证的核心是:△AOB≌△COD.
(2) 垂径定理(图3.2)
垂径定理中的五个条件:过圆心的线(AB)、垂直弦(AB⊥CD)、平分弦(CE=DE)、平分优弧 平分劣弧 知二推三;求证的核心是:
(3)圆周角定理及其推论
①同弧所对的圆周角等于它所对的圆心角的一半(如图3.3所示, 2∠D=2∠E).
② 同弧或等弧所对的圆周角相等(如图3.3所示,
③ 直径所对的圆周角是直角(如图3.4所示,
④ 圆内接四边形对角互补,外角等于内对角(如图3.5所示, 进而∠A=∠1).
(4)圆幂定理
① 相交弦定理(图3.6).
结论:
证明提示:
② 切割线定理(PA 为切线)(图3.7).
结论:
证明提示:△PAC∽△PDA.
③割线定理(图3.8).
结论:PA·PB=PC·PD.
证明提示:△PBC∽△PDA.
模块2 场 景 演 练
四点共圆的判定
类型1:双垂直型
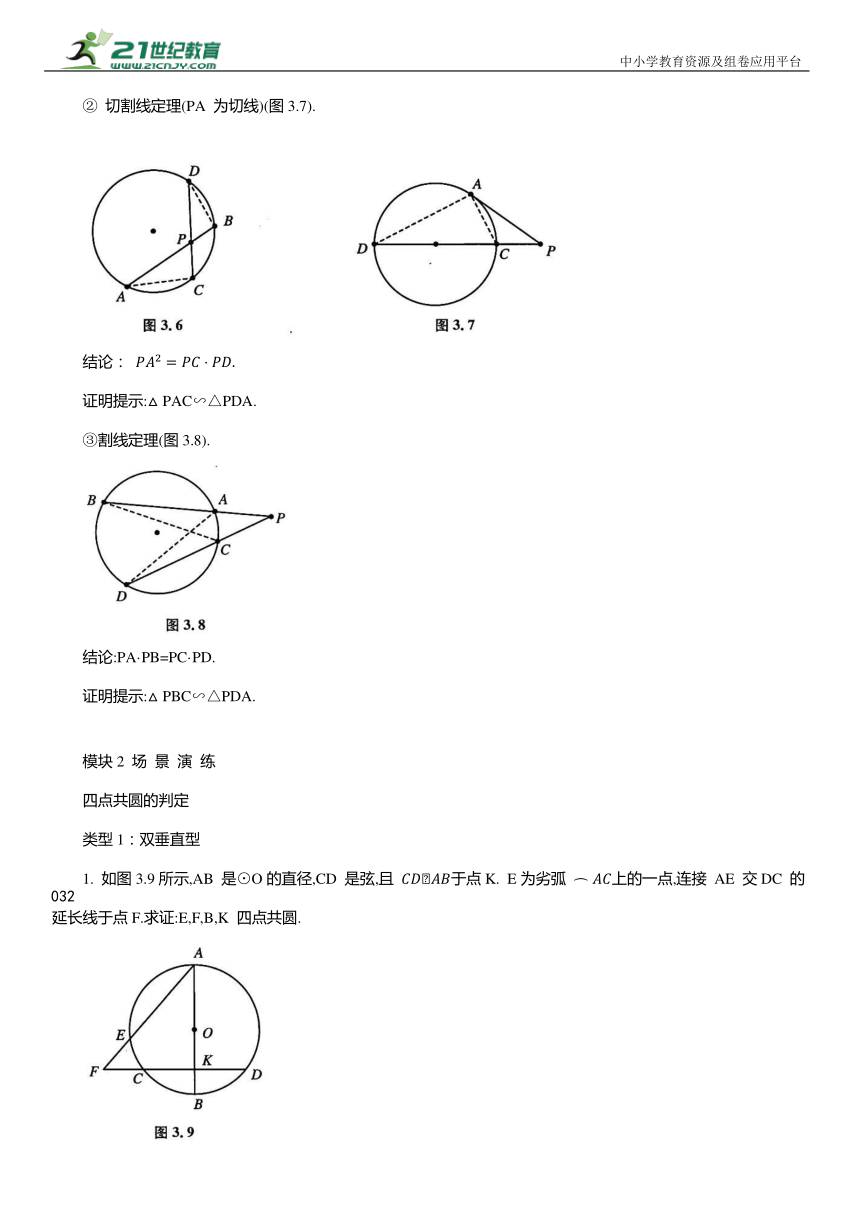
1. 如图3.9所示,AB 是⊙O的直径,CD 是弦,且 于点K. E为劣弧 上的一点,连接 AE 交DC 的延长线于点F.求证:E,F,B,K 四点共圆.
类型2:双锐角型
2. 如图3.10所示,四边形 ABCD 内接于⊙O,P,Q,R 分别是AB,BC,AD的中点.连接QP 与DA 的延长线交于点S,连接RP 与CB 的延长线交于点T.求证:S,T,Q,R 四点共圆.
类型3:对角互补型
3. 如图3.11所示,P为 内一点,D,E,F分别在BC,CA,AB边上,已知 P,D,C,E四点共圆,P,E,A,F四点共圆.求证:B,D,P,F也四点共圆.
辅助圆的应用:计算与证明
4. 如图3.12 所示,在四边形 ABCD 中,, 若 则
5.如图3.13 所示,正方形 ABCD 的中心为O,面积为 ,P为正方形内一点,且 则
6. 如图3.14所示,平面上有四个点 A,O,B,C,其中∠AOB=120°,∠ACB=60°,AO 则
7. 如图3.15所示,在 中, 点 P 为 外一点(P与C在直线AB 异侧),且 .设点 P 关于AB 的对称点为E,连接 PE,CE,线段 AB与CE 的数量关系为 .
8. 如图3.16所示,已知四边形 ABCD, 且 b,则
9. 如图3.17所示,四边形 ABCD 是正方形,M 是BC 上一点, 交 的外角平分线于点E.求证:
10. 如图3.18所示,已知 是等腰三角形, 点 D 在BC 上(不与BC 的中点重合),连接AD.作点C 关于AD 的对称点E,连接EB并延长交AD的延长线于点 F,连接AE,DE.
(1) 证明:A,D,B,E四点共圆.
(2)AD·AF的值是否会发生变化 若不变化,求出其值;若变化,请说明理由.
辅助圆的应用:定弦定角
如图3.19所示,在△ABC中,AB 的长为定值(即 AB=a),∠C 的角度为定值(即∠C=α),该图形为定弦定角模型.
情景 1 如图3.20所示,当∠C<90°时,点 C 在△ABC 外接圆⊙O 的优弧 上运动(不与点 A,B重合).此时,OA=OB=OC,∠AOB=2∠ACB.
情 景 2 如图3.21所示,当∠C=90°时,点 C 在△ABC 外接圆⊙O 上运动(不与点A,B重合).此时,OA=OB=OC.
情景 3 如图3.22所示,当∠C>90°时,点 C 在△ABC 外接圆⊙O 的劣孤 上运动(不与点 A,B重合).此时,
模型的识别:定弦定角
11. 如图3.23 所示,已知 点 P 是矩形ABCD 内一点,且 则 面积的最大值为 .
12. 如图3.24所示,在 Rt△ACB中, 两顶点 B,C分别在x轴的正半轴和y轴的正半轴上运动,则顶点 A 到原点O 的最大距离为 .
13. 如图3.25所示, 点A,B 分别在射线OM,ON 上运动,以 AB 为斜边在其右侧作等腰 ,则点 O 与点C 的最大距离为 .
14. 如图3.26所示, 点A,B 分别在射线OM,ON上运动,在运动中, 面积的最大值为 .
15.如图3.27所示,已知抛物线 与x轴交于A,B两点(点 A在点B 的左侧),与y轴交于点C,在抛物线对称轴上找到一点 Q,使 此时点 Q 的坐标为 .
16.如图3.28所示,已知抛物线 交x轴于A(-3,0),B(4,0)两点,交y轴于点C,连接 AC,BC,在抛物线的对称轴上找到一点 Q,使得 此时点 Q 的坐标为 .
17. 如图3.29所示,在 中,AC=4,BC=6,∠ACB=30°,D 是. 内一动点,⊙O为 的外接圆,⊙O 交直线BD于点P,交边 BC 于点E,若 则 AD的最小值为 .
18.如图3.30所示,顶点为 M 的抛物线 与 x轴交于A,B 两点,与 y轴交于点C,若在第一象限的抛物线下方有一动点 D,满足 ,过点 D 作. 轴于点G,设 的内心为I,则CI 的最小值为 .
19. 如图3.31所示,在正方形 ABCD中, ,点 E 在边AD 上,点 F 在边BE 上,且 ,则DF 的最小值为 .
遇见中考:定弦定角
20.(2022·通辽)如图3.32所示,⊙O 是 的外接圆,AC 为直径,若 点P 从B 点出发,在 内运动且始终保持 当C,P两点距离最小时,动点 P 的运动路径长为 .
辅助圆的应用:定角定高
如图3.33所示,在△ABC中,AD⊥BC于点D,其中∠BAC=α为定角度,AD= h为定值,该图形为定角定高模型.
情景 ① 如图3.34所示,当∠BAC=90°时,探究 BC 的最小值.
先:作△ABC的外接圆⊙O;
再:连接OA;
后:由图知 AO≥AD,当AO=AD(或h)时,BC取得最小值.
情景 2 如图3.35所示,当∠BAC<90°时,探究 BC 的最小值.
先:作△ABC 的外接圆⊙O;
再:连接OA,OB,OC,过点 O作OE⊥BC 于点E;
后:由图知AO+OE≥AD,当AO+OE=AD时,BC取得最小值.
【分析】 因为∠BAC=α,所以∠BOE=α,则 BE=rsinα,故
BC = 2rsinα. ①
又 r+OE≥AD,则 r+rcosα≥AD,即
②
由式①②可得
当点A,O,E共线时,即AO+OE=AD,BC取最小值,此时BD=DC.
针对情景1与情景2的解题点睛 ① 当 BC 取最小值时,S△ABC也取最小值;② 当 BC取最小值时,BD=DC.
模型的识别:定角定高
类型1:模型直接用
21. 如图3.36所示,在 中,点B,C在直线l上运动,且 D是BC边上一点,且 则 BC 边的最小值为 ;△ABC面积的最小值为
22. 如图3.37所示,在菱形 ABCD 中, AC 与BD 相交于点O,点E,F 是对角线BD 上的两点,且 当 EF 取得最小值时,AE 的长为 .
23.如图3.38所示,有块边长为4m的正方形营地 ABCD,在它的中心O处架设了一盏可以自由旋转的探照灯,已知探照灯照射的角 始终是 ,设在探照灯旋转过程中某时刻营地被照明部分的面积为S,则S 的最小值为 .
24. 如图3.39 所示,正方形 ABCD 的边长为4,E,F分别是边BC,CD 上的动点,则 面积的最小值为 .
25.如图3.40所示,点 A,B分别在y轴、x轴的正半轴上. 的两条外角平分线交于点P,点P 在反比例函数 的图像上. PA 的延长线交x轴于点C,PB的延长线交y轴于点D,连接 CD.
(1) ∠P 的度数为 ,点 P 的坐标为 .
(2)△AOB 面积的最大值为 .
类型2:构造相似
26.图3.41是某市街道的一部分,因自来水抢修,需在 的矩形ABCD 平面开挖一个 的工作面,其中E,F分别在直线BC、直线 CD 上,且 为了减少对该路段的拥堵影响,要求 的面积最小,那么 面积的最小值为 m .
27.图3.42是某座城市街道的一部分,因自来水抢修需在 的矩形ABCD 区域内开挖一个 的工作面,其中 E,F分别在BC,CD 边上(不与B,C,D重合),且 ,为了减少对该路段的拥堵影响,要求 面积最小,此时 的面积为 m .
辅助圆的应用:米勒圆
如图3.43所示,两定点 A,B在 的一条边上,另有一动点 P 在 的另一条边上,连接 AP,BP,则点 P 在何处时∠APB 最大
解题方法:如图3.44所示,过A,B两点且和 的另一边相切作⊙O,当点 P 运动到切点P'处时, 最大.
理论依据:同弧所对圆周角相等( ,圆外角小于圆周角( ∠APB).
此类问题叫作米勒圆,也叫作最大张角问题.
模型的识别:米勒圆
28. 如图3.45所示,在正方形 ABCD 中, ,点 E 是AD 边上一点,连接 BE,CE,过点 B 作 于点F,当 最小时,BF 的长为 .
29. 如图3.46所示,点A 的坐标为(0,2),点 C的坐标为(4,6),点 P 在x轴正半轴上运动,当 取得最大值时,点P 的坐标为 .
30. 如图3.47所示,A(0,8),B(0,2),点E 为x轴正半轴上一动点,设 则 m 的取值范围是 .
31. 如图3.48所示,在矩形 ABCD 中, ,点 E,F 分别是边CD,BC 上的动点,且 当DE 取 时, 最大.
图3.49为矩形足球场的示意图,宽 球门 且 点P,Q分别为 BC,AD上的点, 一位左前锋球员从点 P 处带球,沿PQ方向跑动,球员在 PQ 上的何处才能使射门角度( 最大 此时 PM 的长度为 m.
遇见中考:米勒圆
33.(2022·桂林)如图3.50所示,某雕塑 MN 位于河段OA 上,游客 P 在步道上由点O 出发沿OB方向行走.已知 ,当观景视角 最大时,游客 P 行走的距离OP 是 m.
第3讲 辅助圆的妙用
1. 如图J3.1所示,连接 BE,BF.
因为 AB 是⊙O 的直径,所以∠AEB=∠BEF=90°.
又CD⊥AB,则∠FKB=90°,因此∠FKB=∠FEB=90°,故E,F,B,K 四点共圆.
2. 如图J3.2所示,连接AC,BD.
因为 P,Q,R都是中点,所以 ,则 =∠ADB.
又∠ADB=∠ACB,则∠PRA=∠PQB,故S,T,Q,R 四点共圆.
3. 如图J3.3所示,连接 PE,PF,PD.
因为A,E,P,F四点共圆,所以∠AFP=∠CEP.
又C,D,P,E四点共圆,则∠BDP=∠CEP,即∠AFP=∠BDP,于是∠BFP+∠BDP=180°,故 B,D,P,F四点共圆.
4. 38°,26°.
以点 A 为圆心、AB 为半径作辅助圆,则点 C,D均在⊙A 上,所以 =38°,∠BAC=2∠BDC=26°.
5. 2cm.
如图J3.4所示,连接OA,OB.
因为 ABCD 是正方形,所以∠AOB=90°,∠OAB=45°.
又∠OPB=45°,则A,B,O,P 四点共圆,于是∠APB=∠AOB=90°.
在 Rt△ABP 中, .设 PA=k,PB=2k,则 解得 k=1,故PB=2cm.
6. 2.
因为∠AOB=120°,∠ACB=60°,AO=BO,所以点 A,B,C在以点O 为圆心、OA 为半径的圆周上.
又 故
如图J3.5所示,连接AE.
因为点 P、点 E 关于AB 对称,所以∠APB=∠AEB=45°.
又∠ACB=90°,AC=BC,则点 A,B,E在以点C为圆心的圆上,于是 CA=CB= CE.因为 所以
如图J3.6所示,以点 A 为圆心、a为半径作圆,则点 B,C,D 都在圆上.延长 BA 交⊙A 于点E,连接 ED.
因为 AB∥CD,所以∠CAB=∠DCA,∠DAE=∠CDA.
又AC=AD,则∠DCA=∠CDA,于是∠DAE=∠CAB,故△CAB≌△DAE,则ED=BC=b.
因为 BE 是直径,所以∠EDB=90°.由勾股定理得 故
9. 如图J3.7所示,连接AC,AE.
因为四边形 ABCD 是正方形,所以∠ACD=45°.
又CE 是外角平分线,则∠DCE =45°,于是∠ACE=90°.由∠AME=90°可知 A,M,C,E 四点共圆,所以∠AEM=∠ACB=45°,则∠EAM=45°,故 AM=EM.
10.(1) 因为 AB=AC,所以∠ABC=∠ACB.
又点 E 与点C 关于AD 对称,则AE=AC,DE=DC,于是∠AEC=∠ACE,∠DEC=∠DCE,即∠AED=∠ACB,则∠AED=∠ABC,故A,D,B,E四点共圆.
(2) AD·AF 的值不会发生变化,恒为8.
证明如下:如图J3.8所示,连接 CF.
因为点 E 与点C 关于AD 对称,所以 FE= FC,则∠FEC=∠FCE.
又∠DEC=∠DCE,则∠FED=∠FCD.
因为A,D,B,E四点共圆,所以∠FED=∠BAF,于是∠BAF=∠FCD,则A,B,F,C四点共圆,故∠AFB=∠ACB=∠ABC.
又因为∠BAD=∠FAB,所以△ABD∽△AFB,则 故
11. 4.
如图J3.9所示,由∠PBC=∠PCD得∠P=90°.以 BC的中点O为圆心、OB长为半径画圆,作 PE⊥BC,则
如图J3.10所示,因为∠COB=90°,所以点O在以BC的中点D 为圆心、OD 长为半径的圆上运动,此问题就转化为点 A 到⊙D上的距离,故点 A 到原点O 的最大距离为
如图J3.11所示,作△AOB 的外接圆⊙I,连接CI并延长,分别交⊙I和AB 于点( 和点D.
当O运动到O'时,OC 最大,此时△AOB 是等边三角形,则 故
如图J3.12 所示,作△AOB 的外接圆⊙I,则由∠AOB =45°,得∠AIB =90°,所以△AIB 为等腰直角三角形,故
当 OI⊥AB时,△AOB的面积最大,直线 OI 交AB 于点C,此时 所以
15. (1,2)或(1,-2).
易证∠ACB=90°,如图J3.13所示,作Rt△ABC 的外接圆⊙E,则∠ACB=∠AQB=90°,此时△AQB 为等腰直角三角形,所以 EQ = AE = BE = 2.故点 Q 的坐标为(1,2)或(1,-2).
或
设 因为∠AQC=∠CBA=45°,所以C,Q,B,A 四点共圆,此时圆心在直线 与线段 BC 的中垂线y=x的交点处,则 解得 q= 或 故点 Q 的坐标为 或
如图J3.14所示,因为 所以∠ACB=∠CDP=30°,则. 150°,因此点 D 在以BC 为弦、∠BDC=150°的圆弧上运动.
如图J3.14所示,设点 D 运动的圆弧圆心为点M,当 A,D,M三点共线时,AD 最小,取优弧 上一点N,连接 MB,MC,NB,NC,AM,MD,则. 所以∠BMC=60°.
因为 BM=CM,所以△BMC 为等边三角形,则∠MCB=60°,MC=BC=6.
又 则 于是
此时,
如图J3.15所示,连接 IO,ID,IA.
因为I是 的内心,所以易得. ,由双内模型可得,
又 OA 为定线段,∠OIA 恒等于135°,则点I在以OA 为弦、所含的圆周角等于135°的圆弧上.
当点I在线段CE 上时,CI 的值最小,则
CI 的最小值
如图J3.16所示,由
因此
△BAF∽△BEA ∠BAE = ∠AFB = 90°,
所以点 F 在以AB 为直径的圆弧上,当点 F 在线段DG 上时,DF 的值最小,故
DF 的最小值
如图J3.17所示,取AB的中点J.
因为 AC 是直径,所以∠ABC =90°,则∠ABP +∠PBC
又∠BAP=∠PBC,则. 因此∠APB=90°,故点 P 在以AB 为直径的⊙J 上运动,当点 J,P,C共线时,PC 的值最小.
在 Rt△CBJ 中, 则 即∠BJC=60°,故当 C,P 两点距离最小时,动点 P 的运动路径长为
当 BC 取最小值时,BD=DC,∠BAD=30°,所以 即 故
当 EF 取最小值时,EO= FO,∠EAO=30°,所以 即 AE=
如图J3.18所示,当S 取最小值时,GM=GN,此时
tan22.5°可通过图J3.19 所示求解, 则 即 故
如图J3.20所示,
以EF 为斜边,作等腰 ,则点 A 在以点O 为圆心、OE 为半径的圆上.
设OH=a,则 由半角模型知
因为 AO+OH≥AG=4,所以 解得 故 当然,依然还可以直接用EG=GF 搭建勾股求解.
25. (1) 45°,(3,3).
如图J3.21所示,作 PM⊥OA 于点M,PN⊥OB 于点N,PH⊥AB于点H.
易证△PAM≌△PAH,同理可证△BPN≌△BPH,所以
因为 PM=PN,所以可以假设 P(m,m).
又P(m,m)在 上,则m=3,故 P(3,3).
如图J3.22所示,当 S△ABP最小时,S△AOB最大.以AB 为斜边,作等腰 Rt△ARB,则点 P在以点 R 为圆心、AR 为半径的圆上.
设RV=a,则
因为PR+RV≥PW=3,所以 解得 因此 故
26. 6.
如图J3.23所示,把△ADF 绕点A 顺时针旋转90°并把边长缩小为原来的 得到△ABG,则 过点 E 作 EN⊥AF 于点 N,此时 ·EN.
因为 所以
即 又 根据“定角定高”模型可得 故
如图J3.24所示,把△ADF 绕点A 顺时针旋转90°并把边长缩小为原来的 得到△ABG,则 过点 E 作EN⊥AF 于点N,此时 因为 所以
即 同26题可得 故
当∠EBF 最小时,∠BEF 最大.
如图J3.25所示,过点 B,C作⊙O与AD 相切于点E,此时∠BEF 最大.连接 EO 并延长交BC 于点G,则 EG 垂直平分BC,即 CG=4,则 故 即 解得
当∠EBF 最小时,BF 的长为
如图J3.26 所示,过点 A,C 作⊙Q 与x轴正半轴相切于点 P,连接 QA,QP,此时∠APC 最大, 作AC 的中垂线,交 AC 于点B,交⊙Q 于点D,E.
因为A(0,2),C(4,6),所以B(2,4),直线 AC 的解析式为y=x+2.
又DE⊥AC,则设直线DE 的解析式为y=-x+b,将B(2,4)代入得4=-2+b,解得b=6,所以直线 DE 的解析式为y=-x+6.
因为圆心 Q在直线DE 上,所以设Q(x,-x+6),则P(x,0),因此. 即 解得 (舍去),故点 P 的坐标为
如图J3.27所示,过A,B,E 三点的圆O'与x轴相切时,∠AEB 最大.
作O'D⊥AB于点D,则
因为OA=8,所以OD=O'E=5,即⊙O'的半径为5.在 Rt△O'AD 中,由勾股定理得
因为∠AEB=∠AO'D,所以 则m的最大值为
又m>0,则
如图J3.28所示,取 AE 的中点O,连接OD,OF.
因为 (对角互补),所以 A,D,E,F四点共圆,则 =∠AFD.
当⊙O 与BC 相切时,∠AFD 的值最大,易知 BF=CF=4.
因为△ABF∽△FCE,所以 即 解得 则 DE=DC-CE=6-
当 时,∠AED 的值最大.
如图J3.29所示,过点 E,F作圆,与 PQ 相切于点. ,圆心为点 O,连接 此时∠FM'E 的度数最大.
作线段 EF 的中垂线l,l经过圆心O,且交 EF 于点N,交 PQ于点K,过点 K 作 BC 于点H.设⊙O 的半径为r,则(
因为∠BPQ=135°,所以∠KPH=45°,则△PHK 是等腰直角三角形,于是 PH=KH= 则 BH=KN=33+7=40(m).
在等腰Rt△OKM'中,( 所以
在Rt△ONE 中, 解得 (舍去),所以
当射门角度最大时,PM 的长度为(
如图J3.30所示,取 MN的中点F,过点 F 作FE⊥OB 于点E,以直径 MN 作⊙F.
因为 ,点 F 是MN的中点,所以.
又∠AOB=30°,EF⊥OB,则 故EF=MF.
因为 EF⊥OB,所以 OB 是⊙F 的切线,切点为 E,故当点 P 与点E 重合时,观景视角∠MPN 最大,此时
模块1 本质原理
很多题目中没有出现圆,但是如果利用圆的特征添加圆,能让题目解起来变得十分简单.因此,辅助圆思想是我们解题中非常重要的工具.
表3.1中是几种较为常见的辅助圆的情景.
辅助圆图示 辅助圆结论
已知:OA=OB=OC 辅助圆:A,B,C在以点O为圆心、OA 为半径的圆上
已知:OC=OD,∠COD=2∠CAD 辅助圆:A,C,D在以点O 为圆心、OC 为半径的圆上
张角相等——双直角型 已知:∠ABD=∠ACD=90° 辅助圆:A,B,C,D 在以AD 的中点E 为圆心、EA 为半径的圆上
中小学教育资源及组卷应用平台
续表
辅助圆图示 辅助圆结论
张角相等——双锐角型 已知:∠ADB=∠ACB 辅助圆:A,B,C,D在同一圆上
对角互补型——双直角型 已知:∠ABC=∠ADC=90° 辅助圆:A,B,C,D 在以AC 的中点E 为圆心、EA 为半径的圆上
对角互补型 已知:∠ABC+∠ADC=180° 辅助圆:A,B,C,D在同一圆上
辅助圆的本质原理就是:锁定圆的轨迹,利用圆的性质与定理,确定边角关系.
辅助圆的惯用性质、定理如下:
(1) 等量关系定理(图3.1)
在同圆或等圆中,等圆心角(∠AOB=∠DOC)、等弧 等弦(AB=CD)、等弦心距(OF=OG),知一推三;求证的核心是:△AOB≌△COD.
(2) 垂径定理(图3.2)
垂径定理中的五个条件:过圆心的线(AB)、垂直弦(AB⊥CD)、平分弦(CE=DE)、平分优弧 平分劣弧 知二推三;求证的核心是:
(3)圆周角定理及其推论
①同弧所对的圆周角等于它所对的圆心角的一半(如图3.3所示, 2∠D=2∠E).
② 同弧或等弧所对的圆周角相等(如图3.3所示,
③ 直径所对的圆周角是直角(如图3.4所示,
④ 圆内接四边形对角互补,外角等于内对角(如图3.5所示, 进而∠A=∠1).
(4)圆幂定理
① 相交弦定理(图3.6).
结论:
证明提示:
② 切割线定理(PA 为切线)(图3.7).
结论:
证明提示:△PAC∽△PDA.
③割线定理(图3.8).
结论:PA·PB=PC·PD.
证明提示:△PBC∽△PDA.
模块2 场 景 演 练
四点共圆的判定
类型1:双垂直型
1. 如图3.9所示,AB 是⊙O的直径,CD 是弦,且 于点K. E为劣弧 上的一点,连接 AE 交DC 的延长线于点F.求证:E,F,B,K 四点共圆.
类型2:双锐角型
2. 如图3.10所示,四边形 ABCD 内接于⊙O,P,Q,R 分别是AB,BC,AD的中点.连接QP 与DA 的延长线交于点S,连接RP 与CB 的延长线交于点T.求证:S,T,Q,R 四点共圆.
类型3:对角互补型
3. 如图3.11所示,P为 内一点,D,E,F分别在BC,CA,AB边上,已知 P,D,C,E四点共圆,P,E,A,F四点共圆.求证:B,D,P,F也四点共圆.
辅助圆的应用:计算与证明
4. 如图3.12 所示,在四边形 ABCD 中,, 若 则
5.如图3.13 所示,正方形 ABCD 的中心为O,面积为 ,P为正方形内一点,且 则
6. 如图3.14所示,平面上有四个点 A,O,B,C,其中∠AOB=120°,∠ACB=60°,AO 则
7. 如图3.15所示,在 中, 点 P 为 外一点(P与C在直线AB 异侧),且 .设点 P 关于AB 的对称点为E,连接 PE,CE,线段 AB与CE 的数量关系为 .
8. 如图3.16所示,已知四边形 ABCD, 且 b,则
9. 如图3.17所示,四边形 ABCD 是正方形,M 是BC 上一点, 交 的外角平分线于点E.求证:
10. 如图3.18所示,已知 是等腰三角形, 点 D 在BC 上(不与BC 的中点重合),连接AD.作点C 关于AD 的对称点E,连接EB并延长交AD的延长线于点 F,连接AE,DE.
(1) 证明:A,D,B,E四点共圆.
(2)AD·AF的值是否会发生变化 若不变化,求出其值;若变化,请说明理由.
辅助圆的应用:定弦定角
如图3.19所示,在△ABC中,AB 的长为定值(即 AB=a),∠C 的角度为定值(即∠C=α),该图形为定弦定角模型.
情景 1 如图3.20所示,当∠C<90°时,点 C 在△ABC 外接圆⊙O 的优弧 上运动(不与点 A,B重合).此时,OA=OB=OC,∠AOB=2∠ACB.
情 景 2 如图3.21所示,当∠C=90°时,点 C 在△ABC 外接圆⊙O 上运动(不与点A,B重合).此时,OA=OB=OC.
情景 3 如图3.22所示,当∠C>90°时,点 C 在△ABC 外接圆⊙O 的劣孤 上运动(不与点 A,B重合).此时,
模型的识别:定弦定角
11. 如图3.23 所示,已知 点 P 是矩形ABCD 内一点,且 则 面积的最大值为 .
12. 如图3.24所示,在 Rt△ACB中, 两顶点 B,C分别在x轴的正半轴和y轴的正半轴上运动,则顶点 A 到原点O 的最大距离为 .
13. 如图3.25所示, 点A,B 分别在射线OM,ON 上运动,以 AB 为斜边在其右侧作等腰 ,则点 O 与点C 的最大距离为 .
14. 如图3.26所示, 点A,B 分别在射线OM,ON上运动,在运动中, 面积的最大值为 .
15.如图3.27所示,已知抛物线 与x轴交于A,B两点(点 A在点B 的左侧),与y轴交于点C,在抛物线对称轴上找到一点 Q,使 此时点 Q 的坐标为 .
16.如图3.28所示,已知抛物线 交x轴于A(-3,0),B(4,0)两点,交y轴于点C,连接 AC,BC,在抛物线的对称轴上找到一点 Q,使得 此时点 Q 的坐标为 .
17. 如图3.29所示,在 中,AC=4,BC=6,∠ACB=30°,D 是. 内一动点,⊙O为 的外接圆,⊙O 交直线BD于点P,交边 BC 于点E,若 则 AD的最小值为 .
18.如图3.30所示,顶点为 M 的抛物线 与 x轴交于A,B 两点,与 y轴交于点C,若在第一象限的抛物线下方有一动点 D,满足 ,过点 D 作. 轴于点G,设 的内心为I,则CI 的最小值为 .
19. 如图3.31所示,在正方形 ABCD中, ,点 E 在边AD 上,点 F 在边BE 上,且 ,则DF 的最小值为 .
遇见中考:定弦定角
20.(2022·通辽)如图3.32所示,⊙O 是 的外接圆,AC 为直径,若 点P 从B 点出发,在 内运动且始终保持 当C,P两点距离最小时,动点 P 的运动路径长为 .
辅助圆的应用:定角定高
如图3.33所示,在△ABC中,AD⊥BC于点D,其中∠BAC=α为定角度,AD= h为定值,该图形为定角定高模型.
情景 ① 如图3.34所示,当∠BAC=90°时,探究 BC 的最小值.
先:作△ABC的外接圆⊙O;
再:连接OA;
后:由图知 AO≥AD,当AO=AD(或h)时,BC取得最小值.
情景 2 如图3.35所示,当∠BAC<90°时,探究 BC 的最小值.
先:作△ABC 的外接圆⊙O;
再:连接OA,OB,OC,过点 O作OE⊥BC 于点E;
后:由图知AO+OE≥AD,当AO+OE=AD时,BC取得最小值.
【分析】 因为∠BAC=α,所以∠BOE=α,则 BE=rsinα,故
BC = 2rsinα. ①
又 r+OE≥AD,则 r+rcosα≥AD,即
②
由式①②可得
当点A,O,E共线时,即AO+OE=AD,BC取最小值,此时BD=DC.
针对情景1与情景2的解题点睛 ① 当 BC 取最小值时,S△ABC也取最小值;② 当 BC取最小值时,BD=DC.
模型的识别:定角定高
类型1:模型直接用
21. 如图3.36所示,在 中,点B,C在直线l上运动,且 D是BC边上一点,且 则 BC 边的最小值为 ;△ABC面积的最小值为
22. 如图3.37所示,在菱形 ABCD 中, AC 与BD 相交于点O,点E,F 是对角线BD 上的两点,且 当 EF 取得最小值时,AE 的长为 .
23.如图3.38所示,有块边长为4m的正方形营地 ABCD,在它的中心O处架设了一盏可以自由旋转的探照灯,已知探照灯照射的角 始终是 ,设在探照灯旋转过程中某时刻营地被照明部分的面积为S,则S 的最小值为 .
24. 如图3.39 所示,正方形 ABCD 的边长为4,E,F分别是边BC,CD 上的动点,则 面积的最小值为 .
25.如图3.40所示,点 A,B分别在y轴、x轴的正半轴上. 的两条外角平分线交于点P,点P 在反比例函数 的图像上. PA 的延长线交x轴于点C,PB的延长线交y轴于点D,连接 CD.
(1) ∠P 的度数为 ,点 P 的坐标为 .
(2)△AOB 面积的最大值为 .
类型2:构造相似
26.图3.41是某市街道的一部分,因自来水抢修,需在 的矩形ABCD 平面开挖一个 的工作面,其中E,F分别在直线BC、直线 CD 上,且 为了减少对该路段的拥堵影响,要求 的面积最小,那么 面积的最小值为 m .
27.图3.42是某座城市街道的一部分,因自来水抢修需在 的矩形ABCD 区域内开挖一个 的工作面,其中 E,F分别在BC,CD 边上(不与B,C,D重合),且 ,为了减少对该路段的拥堵影响,要求 面积最小,此时 的面积为 m .
辅助圆的应用:米勒圆
如图3.43所示,两定点 A,B在 的一条边上,另有一动点 P 在 的另一条边上,连接 AP,BP,则点 P 在何处时∠APB 最大
解题方法:如图3.44所示,过A,B两点且和 的另一边相切作⊙O,当点 P 运动到切点P'处时, 最大.
理论依据:同弧所对圆周角相等( ,圆外角小于圆周角( ∠APB).
此类问题叫作米勒圆,也叫作最大张角问题.
模型的识别:米勒圆
28. 如图3.45所示,在正方形 ABCD 中, ,点 E 是AD 边上一点,连接 BE,CE,过点 B 作 于点F,当 最小时,BF 的长为 .
29. 如图3.46所示,点A 的坐标为(0,2),点 C的坐标为(4,6),点 P 在x轴正半轴上运动,当 取得最大值时,点P 的坐标为 .
30. 如图3.47所示,A(0,8),B(0,2),点E 为x轴正半轴上一动点,设 则 m 的取值范围是 .
31. 如图3.48所示,在矩形 ABCD 中, ,点 E,F 分别是边CD,BC 上的动点,且 当DE 取 时, 最大.
图3.49为矩形足球场的示意图,宽 球门 且 点P,Q分别为 BC,AD上的点, 一位左前锋球员从点 P 处带球,沿PQ方向跑动,球员在 PQ 上的何处才能使射门角度( 最大 此时 PM 的长度为 m.
遇见中考:米勒圆
33.(2022·桂林)如图3.50所示,某雕塑 MN 位于河段OA 上,游客 P 在步道上由点O 出发沿OB方向行走.已知 ,当观景视角 最大时,游客 P 行走的距离OP 是 m.
第3讲 辅助圆的妙用
1. 如图J3.1所示,连接 BE,BF.
因为 AB 是⊙O 的直径,所以∠AEB=∠BEF=90°.
又CD⊥AB,则∠FKB=90°,因此∠FKB=∠FEB=90°,故E,F,B,K 四点共圆.
2. 如图J3.2所示,连接AC,BD.
因为 P,Q,R都是中点,所以 ,则 =∠ADB.
又∠ADB=∠ACB,则∠PRA=∠PQB,故S,T,Q,R 四点共圆.
3. 如图J3.3所示,连接 PE,PF,PD.
因为A,E,P,F四点共圆,所以∠AFP=∠CEP.
又C,D,P,E四点共圆,则∠BDP=∠CEP,即∠AFP=∠BDP,于是∠BFP+∠BDP=180°,故 B,D,P,F四点共圆.
4. 38°,26°.
以点 A 为圆心、AB 为半径作辅助圆,则点 C,D均在⊙A 上,所以 =38°,∠BAC=2∠BDC=26°.
5. 2cm.
如图J3.4所示,连接OA,OB.
因为 ABCD 是正方形,所以∠AOB=90°,∠OAB=45°.
又∠OPB=45°,则A,B,O,P 四点共圆,于是∠APB=∠AOB=90°.
在 Rt△ABP 中, .设 PA=k,PB=2k,则 解得 k=1,故PB=2cm.
6. 2.
因为∠AOB=120°,∠ACB=60°,AO=BO,所以点 A,B,C在以点O 为圆心、OA 为半径的圆周上.
又 故
如图J3.5所示,连接AE.
因为点 P、点 E 关于AB 对称,所以∠APB=∠AEB=45°.
又∠ACB=90°,AC=BC,则点 A,B,E在以点C为圆心的圆上,于是 CA=CB= CE.因为 所以
如图J3.6所示,以点 A 为圆心、a为半径作圆,则点 B,C,D 都在圆上.延长 BA 交⊙A 于点E,连接 ED.
因为 AB∥CD,所以∠CAB=∠DCA,∠DAE=∠CDA.
又AC=AD,则∠DCA=∠CDA,于是∠DAE=∠CAB,故△CAB≌△DAE,则ED=BC=b.
因为 BE 是直径,所以∠EDB=90°.由勾股定理得 故
9. 如图J3.7所示,连接AC,AE.
因为四边形 ABCD 是正方形,所以∠ACD=45°.
又CE 是外角平分线,则∠DCE =45°,于是∠ACE=90°.由∠AME=90°可知 A,M,C,E 四点共圆,所以∠AEM=∠ACB=45°,则∠EAM=45°,故 AM=EM.
10.(1) 因为 AB=AC,所以∠ABC=∠ACB.
又点 E 与点C 关于AD 对称,则AE=AC,DE=DC,于是∠AEC=∠ACE,∠DEC=∠DCE,即∠AED=∠ACB,则∠AED=∠ABC,故A,D,B,E四点共圆.
(2) AD·AF 的值不会发生变化,恒为8.
证明如下:如图J3.8所示,连接 CF.
因为点 E 与点C 关于AD 对称,所以 FE= FC,则∠FEC=∠FCE.
又∠DEC=∠DCE,则∠FED=∠FCD.
因为A,D,B,E四点共圆,所以∠FED=∠BAF,于是∠BAF=∠FCD,则A,B,F,C四点共圆,故∠AFB=∠ACB=∠ABC.
又因为∠BAD=∠FAB,所以△ABD∽△AFB,则 故
11. 4.
如图J3.9所示,由∠PBC=∠PCD得∠P=90°.以 BC的中点O为圆心、OB长为半径画圆,作 PE⊥BC,则
如图J3.10所示,因为∠COB=90°,所以点O在以BC的中点D 为圆心、OD 长为半径的圆上运动,此问题就转化为点 A 到⊙D上的距离,故点 A 到原点O 的最大距离为
如图J3.11所示,作△AOB 的外接圆⊙I,连接CI并延长,分别交⊙I和AB 于点( 和点D.
当O运动到O'时,OC 最大,此时△AOB 是等边三角形,则 故
如图J3.12 所示,作△AOB 的外接圆⊙I,则由∠AOB =45°,得∠AIB =90°,所以△AIB 为等腰直角三角形,故
当 OI⊥AB时,△AOB的面积最大,直线 OI 交AB 于点C,此时 所以
15. (1,2)或(1,-2).
易证∠ACB=90°,如图J3.13所示,作Rt△ABC 的外接圆⊙E,则∠ACB=∠AQB=90°,此时△AQB 为等腰直角三角形,所以 EQ = AE = BE = 2.故点 Q 的坐标为(1,2)或(1,-2).
或
设 因为∠AQC=∠CBA=45°,所以C,Q,B,A 四点共圆,此时圆心在直线 与线段 BC 的中垂线y=x的交点处,则 解得 q= 或 故点 Q 的坐标为 或
如图J3.14所示,因为 所以∠ACB=∠CDP=30°,则. 150°,因此点 D 在以BC 为弦、∠BDC=150°的圆弧上运动.
如图J3.14所示,设点 D 运动的圆弧圆心为点M,当 A,D,M三点共线时,AD 最小,取优弧 上一点N,连接 MB,MC,NB,NC,AM,MD,则. 所以∠BMC=60°.
因为 BM=CM,所以△BMC 为等边三角形,则∠MCB=60°,MC=BC=6.
又 则 于是
此时,
如图J3.15所示,连接 IO,ID,IA.
因为I是 的内心,所以易得. ,由双内模型可得,
又 OA 为定线段,∠OIA 恒等于135°,则点I在以OA 为弦、所含的圆周角等于135°的圆弧上.
当点I在线段CE 上时,CI 的值最小,则
CI 的最小值
如图J3.16所示,由
因此
△BAF∽△BEA ∠BAE = ∠AFB = 90°,
所以点 F 在以AB 为直径的圆弧上,当点 F 在线段DG 上时,DF 的值最小,故
DF 的最小值
如图J3.17所示,取AB的中点J.
因为 AC 是直径,所以∠ABC =90°,则∠ABP +∠PBC
又∠BAP=∠PBC,则. 因此∠APB=90°,故点 P 在以AB 为直径的⊙J 上运动,当点 J,P,C共线时,PC 的值最小.
在 Rt△CBJ 中, 则 即∠BJC=60°,故当 C,P 两点距离最小时,动点 P 的运动路径长为
当 BC 取最小值时,BD=DC,∠BAD=30°,所以 即 故
当 EF 取最小值时,EO= FO,∠EAO=30°,所以 即 AE=
如图J3.18所示,当S 取最小值时,GM=GN,此时
tan22.5°可通过图J3.19 所示求解, 则 即 故
如图J3.20所示,
以EF 为斜边,作等腰 ,则点 A 在以点O 为圆心、OE 为半径的圆上.
设OH=a,则 由半角模型知
因为 AO+OH≥AG=4,所以 解得 故 当然,依然还可以直接用EG=GF 搭建勾股求解.
25. (1) 45°,(3,3).
如图J3.21所示,作 PM⊥OA 于点M,PN⊥OB 于点N,PH⊥AB于点H.
易证△PAM≌△PAH,同理可证△BPN≌△BPH,所以
因为 PM=PN,所以可以假设 P(m,m).
又P(m,m)在 上,则m=3,故 P(3,3).
如图J3.22所示,当 S△ABP最小时,S△AOB最大.以AB 为斜边,作等腰 Rt△ARB,则点 P在以点 R 为圆心、AR 为半径的圆上.
设RV=a,则
因为PR+RV≥PW=3,所以 解得 因此 故
26. 6.
如图J3.23所示,把△ADF 绕点A 顺时针旋转90°并把边长缩小为原来的 得到△ABG,则 过点 E 作 EN⊥AF 于点 N,此时 ·EN.
因为 所以
即 又 根据“定角定高”模型可得 故
如图J3.24所示,把△ADF 绕点A 顺时针旋转90°并把边长缩小为原来的 得到△ABG,则 过点 E 作EN⊥AF 于点N,此时 因为 所以
即 同26题可得 故
当∠EBF 最小时,∠BEF 最大.
如图J3.25所示,过点 B,C作⊙O与AD 相切于点E,此时∠BEF 最大.连接 EO 并延长交BC 于点G,则 EG 垂直平分BC,即 CG=4,则 故 即 解得
当∠EBF 最小时,BF 的长为
如图J3.26 所示,过点 A,C 作⊙Q 与x轴正半轴相切于点 P,连接 QA,QP,此时∠APC 最大, 作AC 的中垂线,交 AC 于点B,交⊙Q 于点D,E.
因为A(0,2),C(4,6),所以B(2,4),直线 AC 的解析式为y=x+2.
又DE⊥AC,则设直线DE 的解析式为y=-x+b,将B(2,4)代入得4=-2+b,解得b=6,所以直线 DE 的解析式为y=-x+6.
因为圆心 Q在直线DE 上,所以设Q(x,-x+6),则P(x,0),因此. 即 解得 (舍去),故点 P 的坐标为
如图J3.27所示,过A,B,E 三点的圆O'与x轴相切时,∠AEB 最大.
作O'D⊥AB于点D,则
因为OA=8,所以OD=O'E=5,即⊙O'的半径为5.在 Rt△O'AD 中,由勾股定理得
因为∠AEB=∠AO'D,所以 则m的最大值为
又m>0,则
如图J3.28所示,取 AE 的中点O,连接OD,OF.
因为 (对角互补),所以 A,D,E,F四点共圆,则 =∠AFD.
当⊙O 与BC 相切时,∠AFD 的值最大,易知 BF=CF=4.
因为△ABF∽△FCE,所以 即 解得 则 DE=DC-CE=6-
当 时,∠AED 的值最大.
如图J3.29所示,过点 E,F作圆,与 PQ 相切于点. ,圆心为点 O,连接 此时∠FM'E 的度数最大.
作线段 EF 的中垂线l,l经过圆心O,且交 EF 于点N,交 PQ于点K,过点 K 作 BC 于点H.设⊙O 的半径为r,则(
因为∠BPQ=135°,所以∠KPH=45°,则△PHK 是等腰直角三角形,于是 PH=KH= 则 BH=KN=33+7=40(m).
在等腰Rt△OKM'中,( 所以
在Rt△ONE 中, 解得 (舍去),所以
当射门角度最大时,PM 的长度为(
如图J3.30所示,取 MN的中点F,过点 F 作FE⊥OB 于点E,以直径 MN 作⊙F.
因为 ,点 F 是MN的中点,所以.
又∠AOB=30°,EF⊥OB,则 故EF=MF.
因为 EF⊥OB,所以 OB 是⊙F 的切线,切点为 E,故当点 P 与点E 重合时,观景视角∠MPN 最大,此时
同课章节目录
