第15讲 阿氏圆最值(含答案) 2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第15讲 阿氏圆最值(含答案) 2025年中考数学几何模型方法巩固练习 |
|
|
| 格式 | docx | ||
| 文件大小 | 417.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览




文档简介
阿氏圆最值
由来:这个问题是由古希腊数学家阿波罗尼斯提出的有关圆的问题,在平面内,到两个定点距离之比等于定值(不为1)的所有点的轨迹是圆,简称阿氏圆.
如图10.93所示,已知平面上两定点 A,B,一动点P 此时所有满足条件的点 P 的轨迹是一个圆.
证明:如图10.94所示,已知 作∠APB 的平分线交AB 于点M,则 作∠APB 的外角平分线交直线AB 于点N,则 此时∠NPM=90°,故点 P 在以 MN 为直径的圆上运动(图10.95).
思考:如图10.96所示,点 Q 是⊙O外一定点,求 的最小值.
【分析】 解决阿氏圆问题,首先要熟练掌握“共边共角型”相似三角形的性质和构造方法.
如图10.95所示,连接OP.因为OP=OM,所以∠OPM=∠OMP.
又∠OBP=∠OMP+α,∠OPA=∠OPM+α,则∠OBP=∠OPA.
又因为∠POB=∠POA,所以△OPB∽△OAP,则
①
故 QP+kPA=QP+PB≥QB.此时我们需要锁定点 B 的位置,可是点 B 的位置我们不是知道吗 但实际上点 B 的位置往往我们不知道,要利用式①中的 锁定点B的位置.
解题步骤:连半径、定比例、构相似.
实例剖析
如图10.97所示,已知∠ACB=90°,CB=4,CA=6,⊙C的半径为2,P为圆上一动点.
的最小值为 .
的最小值为 .
【答案】 (1)
【分析】 (1)第1步:连半径.连接CP,如图10.98所示.
第2步:定比例.从问题中发现,我们需要构造 BP,所以相似比为 ,而此时
第3步:构相似.构造以半径 CP 为共边且PB 参与的“共边共角型相似”,相似比为 如图10.99 所示,此时 则 即 解得CE=1,故
中小学教育资源及组卷应用平台
(2)第1步:连半径.连接CP.
第2步:定比例.从问题中发现,我们需要构造- ,所以相似比为- ,而此时
第3步:构相似.构造以半径 CP 为共边且AP 参与的“共边共角型相似”,相似比为 如图10.100所示,此时 则 即 解得 CF= 故
类①:构造“分边”
1.(1) 如图 10.101 所示,已知正方形 ABCD 的边长为4,圆 B 的半径为2,点 P 是圆B 上的一个动点,则 的最小值为 ,. 的最大值为 .
(2)如图10.102所示,已知正方形 ABCD的边长为9,圆B 的半径为6,点 P 是圆B上的一个动点,那么 的最小值为 , 的最大值为 .
(3)如图10.103所示,已知菱形 ABCD 的边长为4,∠B=60°,圆 B 的半径为2,点 P是圆B上的一个动点,那么 的最小值为 , 的最大值为
2. 如图10.104所示,在直角坐标系中,已知点 A(4,0),B(0,3),点E 在以原点O为圆心、半径为2的圆上运动.
的最小值为 .
的最小值为 .
3. 如图10.105所示,已知抛物线 与x轴交于A,C两点,与 y轴交于点B,点 将线段OM 绕原点O 顺时针旋转得到线段ON(旋转角度在 90°之间).
(1)线段 OB 上是否存在定点P,使得在旋转过程中, 的值不变 若存在,求出点 P的坐标;若不存在,说明理由.
(2)在旋转过程中, 的最小值为 .
类②:构造“倍边”
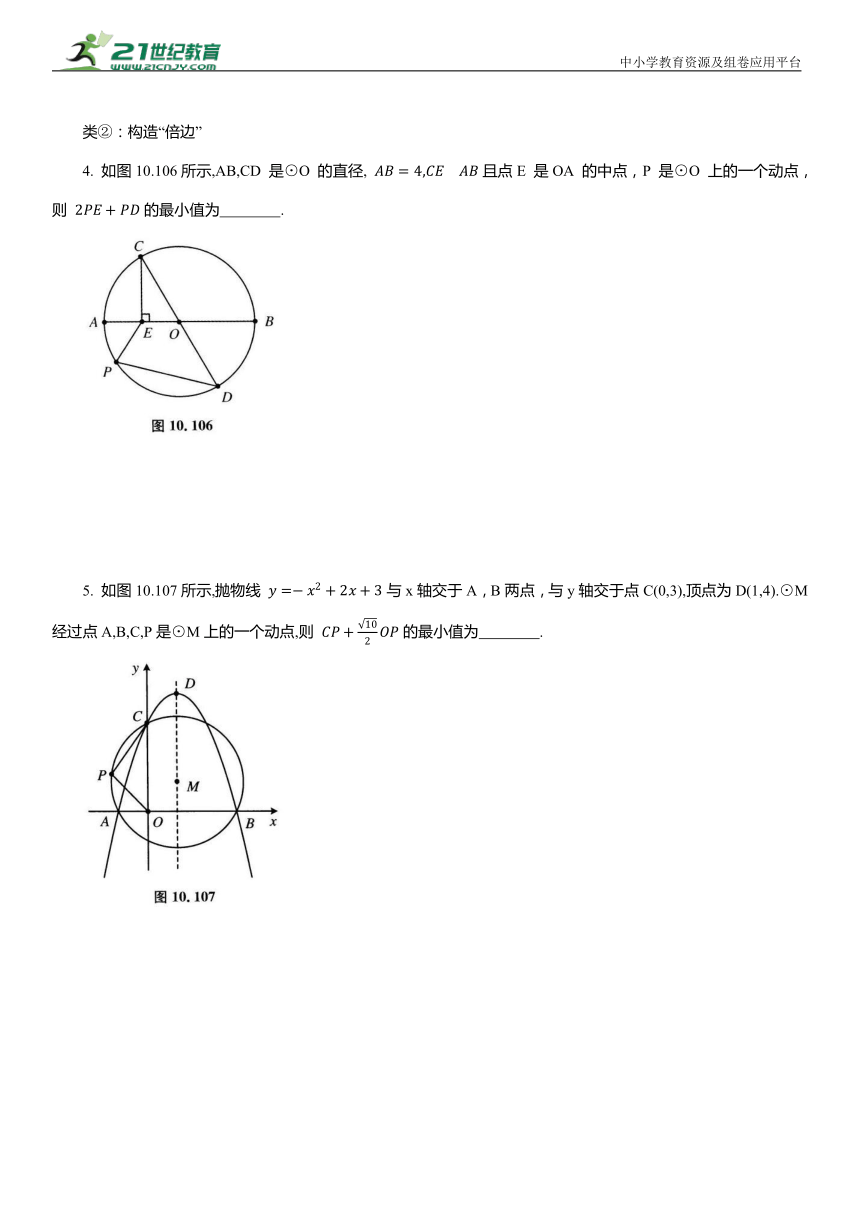
4. 如图10.106所示,AB,CD 是⊙O 的直径, 且点E 是OA 的中点,P 是⊙O 上的一个动点,则 的最小值为 .
5. 如图10.107所示,抛物线 与x轴交于A,B两点,与y轴交于点C(0,3),顶点为D(1,4).⊙M经过点A,B,C,P是⊙M上的一个动点,则 的最小值为 .
类型5:全等变换
6. 如图10.108所示,已知直线AB: 分别交x轴、y轴于B,A 两点,C(3,0),D,E 分别为线段AO 和线段AC上一动点,BE 交y轴于点H,且. 当 BD 的值最小时,点H 的坐标为 .
7. 如图10.109所示,在 中, 点 D,E 分别在AB,AC边上,且. 则 CD+BE 的最小值为 .
8. 如图10.110 所示,在菱形 ABCD中, 点 E 为边AB 上一动点,点 F 在对角线AC 上,且 则 的最小值为 ,此时 AE 的长为
1. (1)5,5.
如图J10.70所示,在 BC 上取一点G,使得 BG=1.
因为 所以 又∠PBG=∠PBC,故△PBG∽△CBP,于是 即 故
因为 DP+PG>DG,所以当点 D,G,P 共线时, 的值最小,最小值为 DG
因为 所以当点 P 在DG 的延长线上时, 的值最大(图J10.71),最大值为 DG=5.
如图J10.72 所示,在 BC 上取一点G,使得 BG=4.
因为 所以 又∠PBG =∠PBC,则△PBG∽△CBP,于是 即 故
因为 DP+PG>DG,所以当点 D,G,P 共线时, 的值最小,最小值为 DG
因为 所以当点 P 在DG 的延长线上时, 的值最大,最大值为
如图J10.73所示,在 BC上取一点G,使得 BG=1,作 DF⊥BC 于点F.
因为 所以 又∠PBG=∠PBC,则△PBG∽△CBP,于是 即 故
因为 DP+PG>DG,所以当点 D,G,P共线时, 的值最小,最小值为 DG.
在 Rt△CDF 中,∠DCF=60°,CD=4,则
在 Rt△GDF 中,
因为 所以当点 P 在DG 的延长线上时, 的值最大,最大值为
2. (1)
如图J10.74所示,取点 M(1,0),连接OE,EM.
因为 所以△OME∽△OEA,则 故 ≥BM.
当 B,E,M 三点共线时, 取得最小值为
取点 连接OE,EM.
因为 所以△OME∽△OEB,则 故 AE
当A,E,M三点共线时, 取得最小值为
3.易得点A(-6,0),B(0, )
(1)存在,点 P 的坐标为(0,3).
如图J10.75所示,因为 所以△OPN∽△ONB,则 为定值,得证.
已知 由(1)得 恒成立,则 NP≥AP.
当A,N,P 三点共线时, 取得最小值, 故4NA+3NB 的最小值为 4
如图J10.76所示,延长 OA 至点M,使得 连接OP,MP.
因为 所以 则 即MP=2PE,故
当 D,P,M三点共线时,2PE+PD 取得最小值,
由题意得点 A(-1,0),B(3,0).
设点 M(1,m),则 因此 解得m=1,故点 M(1,1),半径
如图 J10.77 所示,取点 连接 PQ,MO,OQ.
易证M,O,Q三点共线,
因为 所以△MQP∽△MPO,则 即 故 CP +
当C,P,Q三点共线时, 取得最小值,即
6. (0,4).
由题意得点 A(0, ),B(-3,0),C(3,0),则AB=AC=8.
如图J10.78所示,过点 C作CF⊥x轴于点C,使得 CF=AB,连接 CF,EF,BF,易证△ECF≌△DAB,则 BD=EF,即BD+BE=BE+EF≥BF,故当点 B,E,F 共线时, BE 的值最小.
因为直线 BF 的解析式为 所以 H(0,4),故当 BD+BE 的值最小时,点 H的坐标为(0,4).
7
因为 CE = AD,如图 J10.79 所示,构造, 使得 所以 0,解得
8.
如图J10.80所示,因为 CF = AE,构造 所以
6,
此时 AE=CF'.在△CDF'中, 解三角形得
由来:这个问题是由古希腊数学家阿波罗尼斯提出的有关圆的问题,在平面内,到两个定点距离之比等于定值(不为1)的所有点的轨迹是圆,简称阿氏圆.
如图10.93所示,已知平面上两定点 A,B,一动点P 此时所有满足条件的点 P 的轨迹是一个圆.
证明:如图10.94所示,已知 作∠APB 的平分线交AB 于点M,则 作∠APB 的外角平分线交直线AB 于点N,则 此时∠NPM=90°,故点 P 在以 MN 为直径的圆上运动(图10.95).
思考:如图10.96所示,点 Q 是⊙O外一定点,求 的最小值.
【分析】 解决阿氏圆问题,首先要熟练掌握“共边共角型”相似三角形的性质和构造方法.
如图10.95所示,连接OP.因为OP=OM,所以∠OPM=∠OMP.
又∠OBP=∠OMP+α,∠OPA=∠OPM+α,则∠OBP=∠OPA.
又因为∠POB=∠POA,所以△OPB∽△OAP,则
①
故 QP+kPA=QP+PB≥QB.此时我们需要锁定点 B 的位置,可是点 B 的位置我们不是知道吗 但实际上点 B 的位置往往我们不知道,要利用式①中的 锁定点B的位置.
解题步骤:连半径、定比例、构相似.
实例剖析
如图10.97所示,已知∠ACB=90°,CB=4,CA=6,⊙C的半径为2,P为圆上一动点.
的最小值为 .
的最小值为 .
【答案】 (1)
【分析】 (1)第1步:连半径.连接CP,如图10.98所示.
第2步:定比例.从问题中发现,我们需要构造 BP,所以相似比为 ,而此时
第3步:构相似.构造以半径 CP 为共边且PB 参与的“共边共角型相似”,相似比为 如图10.99 所示,此时 则 即 解得CE=1,故
中小学教育资源及组卷应用平台
(2)第1步:连半径.连接CP.
第2步:定比例.从问题中发现,我们需要构造- ,所以相似比为- ,而此时
第3步:构相似.构造以半径 CP 为共边且AP 参与的“共边共角型相似”,相似比为 如图10.100所示,此时 则 即 解得 CF= 故
类①:构造“分边”
1.(1) 如图 10.101 所示,已知正方形 ABCD 的边长为4,圆 B 的半径为2,点 P 是圆B 上的一个动点,则 的最小值为 ,. 的最大值为 .
(2)如图10.102所示,已知正方形 ABCD的边长为9,圆B 的半径为6,点 P 是圆B上的一个动点,那么 的最小值为 , 的最大值为 .
(3)如图10.103所示,已知菱形 ABCD 的边长为4,∠B=60°,圆 B 的半径为2,点 P是圆B上的一个动点,那么 的最小值为 , 的最大值为
2. 如图10.104所示,在直角坐标系中,已知点 A(4,0),B(0,3),点E 在以原点O为圆心、半径为2的圆上运动.
的最小值为 .
的最小值为 .
3. 如图10.105所示,已知抛物线 与x轴交于A,C两点,与 y轴交于点B,点 将线段OM 绕原点O 顺时针旋转得到线段ON(旋转角度在 90°之间).
(1)线段 OB 上是否存在定点P,使得在旋转过程中, 的值不变 若存在,求出点 P的坐标;若不存在,说明理由.
(2)在旋转过程中, 的最小值为 .
类②:构造“倍边”
4. 如图10.106所示,AB,CD 是⊙O 的直径, 且点E 是OA 的中点,P 是⊙O 上的一个动点,则 的最小值为 .
5. 如图10.107所示,抛物线 与x轴交于A,B两点,与y轴交于点C(0,3),顶点为D(1,4).⊙M经过点A,B,C,P是⊙M上的一个动点,则 的最小值为 .
类型5:全等变换
6. 如图10.108所示,已知直线AB: 分别交x轴、y轴于B,A 两点,C(3,0),D,E 分别为线段AO 和线段AC上一动点,BE 交y轴于点H,且. 当 BD 的值最小时,点H 的坐标为 .
7. 如图10.109所示,在 中, 点 D,E 分别在AB,AC边上,且. 则 CD+BE 的最小值为 .
8. 如图10.110 所示,在菱形 ABCD中, 点 E 为边AB 上一动点,点 F 在对角线AC 上,且 则 的最小值为 ,此时 AE 的长为
1. (1)5,5.
如图J10.70所示,在 BC 上取一点G,使得 BG=1.
因为 所以 又∠PBG=∠PBC,故△PBG∽△CBP,于是 即 故
因为 DP+PG>DG,所以当点 D,G,P 共线时, 的值最小,最小值为 DG
因为 所以当点 P 在DG 的延长线上时, 的值最大(图J10.71),最大值为 DG=5.
如图J10.72 所示,在 BC 上取一点G,使得 BG=4.
因为 所以 又∠PBG =∠PBC,则△PBG∽△CBP,于是 即 故
因为 DP+PG>DG,所以当点 D,G,P 共线时, 的值最小,最小值为 DG
因为 所以当点 P 在DG 的延长线上时, 的值最大,最大值为
如图J10.73所示,在 BC上取一点G,使得 BG=1,作 DF⊥BC 于点F.
因为 所以 又∠PBG=∠PBC,则△PBG∽△CBP,于是 即 故
因为 DP+PG>DG,所以当点 D,G,P共线时, 的值最小,最小值为 DG.
在 Rt△CDF 中,∠DCF=60°,CD=4,则
在 Rt△GDF 中,
因为 所以当点 P 在DG 的延长线上时, 的值最大,最大值为
2. (1)
如图J10.74所示,取点 M(1,0),连接OE,EM.
因为 所以△OME∽△OEA,则 故 ≥BM.
当 B,E,M 三点共线时, 取得最小值为
取点 连接OE,EM.
因为 所以△OME∽△OEB,则 故 AE
当A,E,M三点共线时, 取得最小值为
3.易得点A(-6,0),B(0, )
(1)存在,点 P 的坐标为(0,3).
如图J10.75所示,因为 所以△OPN∽△ONB,则 为定值,得证.
已知 由(1)得 恒成立,则 NP≥AP.
当A,N,P 三点共线时, 取得最小值, 故4NA+3NB 的最小值为 4
如图J10.76所示,延长 OA 至点M,使得 连接OP,MP.
因为 所以 则 即MP=2PE,故
当 D,P,M三点共线时,2PE+PD 取得最小值,
由题意得点 A(-1,0),B(3,0).
设点 M(1,m),则 因此 解得m=1,故点 M(1,1),半径
如图 J10.77 所示,取点 连接 PQ,MO,OQ.
易证M,O,Q三点共线,
因为 所以△MQP∽△MPO,则 即 故 CP +
当C,P,Q三点共线时, 取得最小值,即
6. (0,4).
由题意得点 A(0, ),B(-3,0),C(3,0),则AB=AC=8.
如图J10.78所示,过点 C作CF⊥x轴于点C,使得 CF=AB,连接 CF,EF,BF,易证△ECF≌△DAB,则 BD=EF,即BD+BE=BE+EF≥BF,故当点 B,E,F 共线时, BE 的值最小.
因为直线 BF 的解析式为 所以 H(0,4),故当 BD+BE 的值最小时,点 H的坐标为(0,4).
7
因为 CE = AD,如图 J10.79 所示,构造, 使得 所以 0,解得
8.
如图J10.80所示,因为 CF = AE,构造 所以
6,
此时 AE=CF'.在△CDF'中, 解三角形得
同课章节目录
