第 16 讲 定值问题(含答案) 2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第 16 讲 定值问题(含答案) 2025年中考数学几何模型方法巩固练习 |

|
|
| 格式 | docx | ||
| 文件大小 | 648.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:29:51 | ||
图片预览


文档简介
第 16 讲 定值问题
模块1 本质原理
1.代数定值
多变量中,消元导致系数为零,进而带动产生一系列的定值.
2.几何定值
位置不变、几何量不变、数量关系不变,具体见表11.1.
表11.1
几何定值分类 求解工具
角为定值 ① 利用三角形的性质及定理倒角; ② 利用平行线的性质倒角; ③ 利用圆的性质及定理倒角
边为定值 ①利用特殊三角形(等腰三角形、等边三角形)的性质; ② 利用特殊四边形(平行四边形、矩形、菱形、正方形)的性质; ③ 利用圆的性质及定理; ④ 利用特殊角的三角函数
线段和或差为定值 (或和差关系式) ① 利用等面积法; ② 利用截长补短法
线段乘积或比值为定值 (常见于函数中) ① 构造相似法; ② 含参计算法
面积为定值 (常见于函数中) ① 定义法(s△= 底×高,,S梯形= ×(上底+下底)×高); ② 割补法(利用“水平宽、铅垂高”); ③ 等积变形法(平行线内的同底等高)
模块2 场景演练
模型的识别:代数中的定值
1.若一次函数 y=2mx+m+3的图像经过一个定点,则这个定点的坐标为 .
变式①:不论 k 取什么样的实数,直线. 总经过一定点,则这个定点的坐标为 .
变式②:已知二次函数 当 m 取不同的值时,抛物线都会经过一个定点,此定点的坐标为 .
模型的识别:几何中的定值
类型1:角为定值
2. 如图11.1所示,菱形 ABCD 的边长为1, 点 E 是边AB 上任意一点(端点除外),线段CE 的垂直平分线分别交BD,CE 于点F,G.
(1)求证:
(2)当点 E 在AB上运动时,∠CEF 的大小不变,其度数为 .
3. 如图11.2所示,函数 的图像上有一点P(a,b),由点 P分别向x轴、y轴作垂线 PM,PN,垂足为点 M,N,直线 AB: 分别交PM,PN于点E,F,则 与 的关系为 ;∠EOF =_.
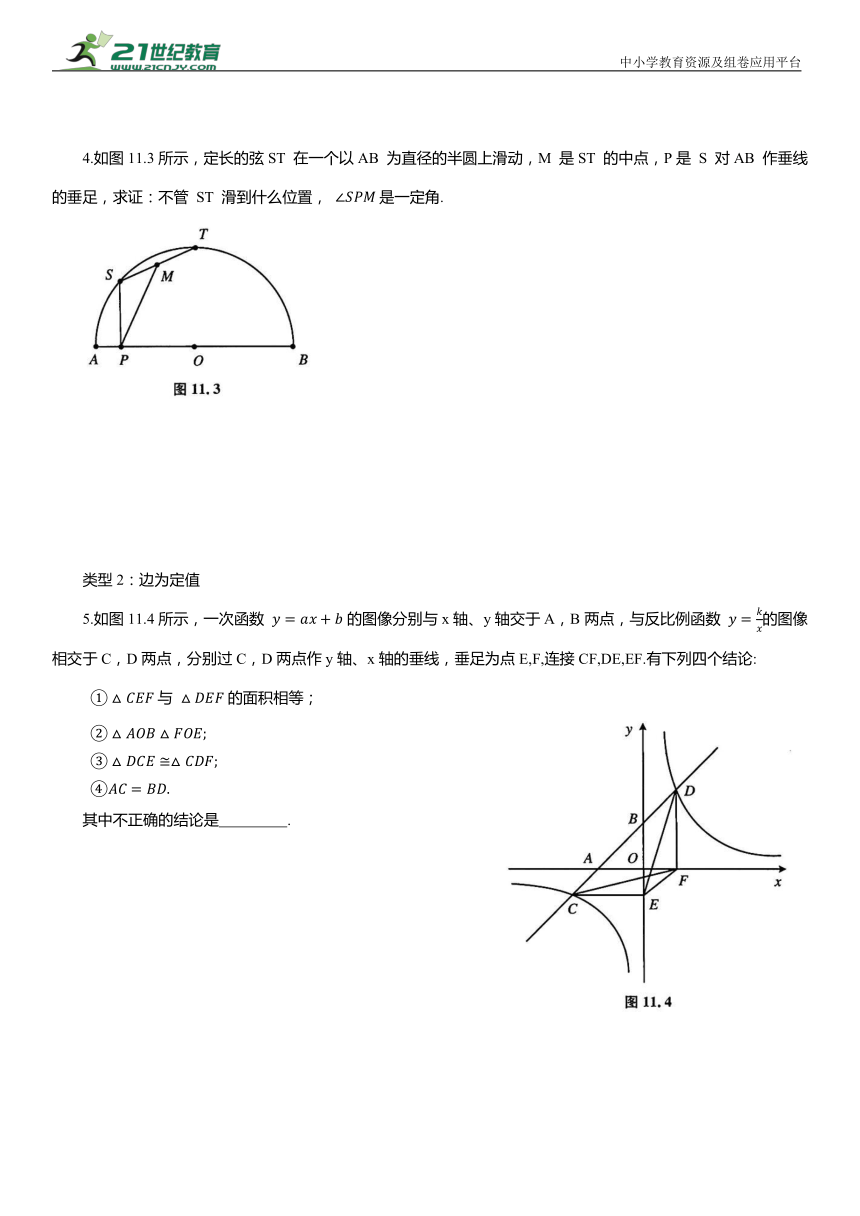
4.如图11.3所示,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P是 S 对AB 作垂线的垂足,求证:不管 ST 滑到什么位置, 是一定角.
类型2:边为定值
5.如图11.4所示,一次函数 的图像分别与x轴、y轴交于A,B两点,与反比例函数 的图像相交于C,D两点,分别过C,D两点作y轴、x轴的垂线,垂足为点E,F,连接CF,DE,EF.有下列四个结论:
与 的面积相等;
其中不正确的结论是 .
类型3:线段和或差为定值(或和差关系式)
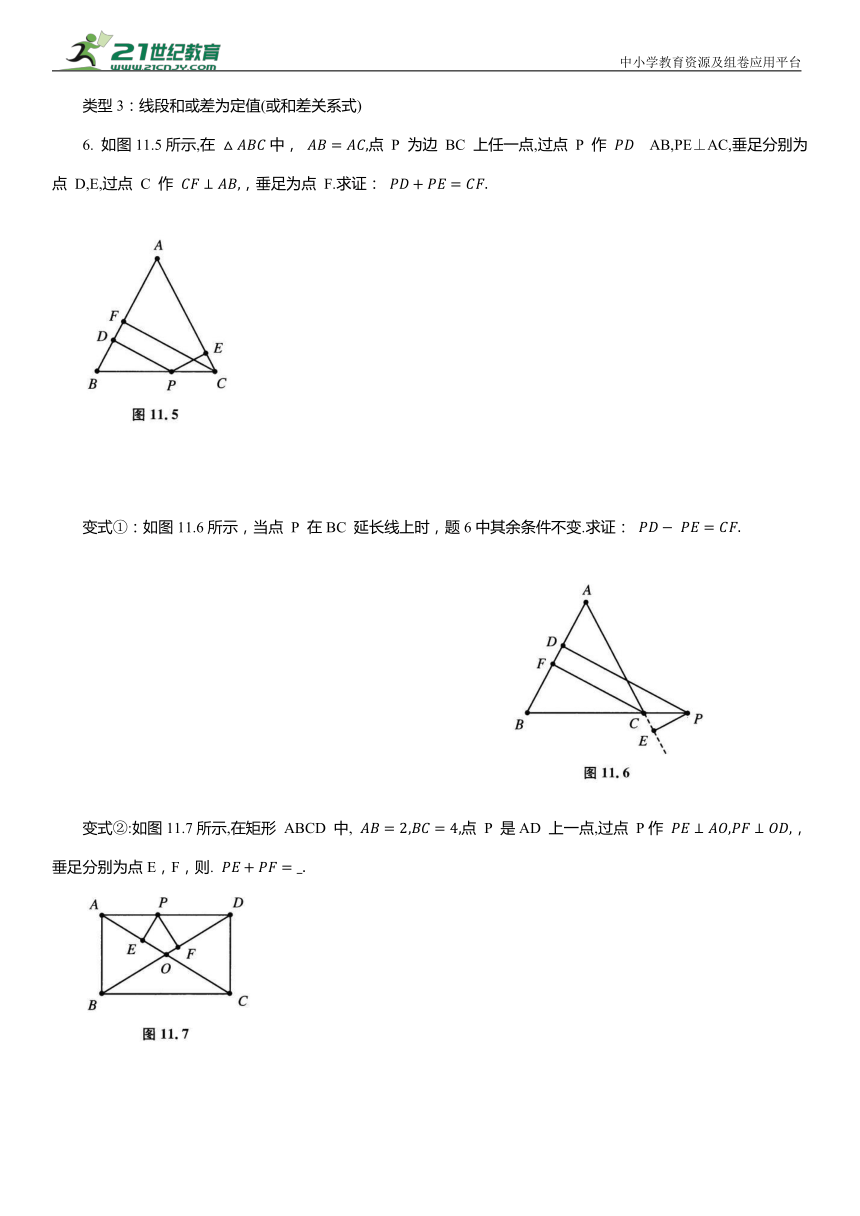
6. 如图11.5所示,在 中, 点 P 为边 BC 上任一点,过点 P 作 AB,PE⊥AC,垂足分别为点 D,E,过点 C 作 ,垂足为点 F.求证:
变式①:如图11.6所示,当点 P 在BC 延长线上时,题6中其余条件不变.求证:
变式②:如图11.7所示,在矩形 ABCD 中, 点 P 是AD 上一点,过点 P作 ,垂足分别为点E,F,则.
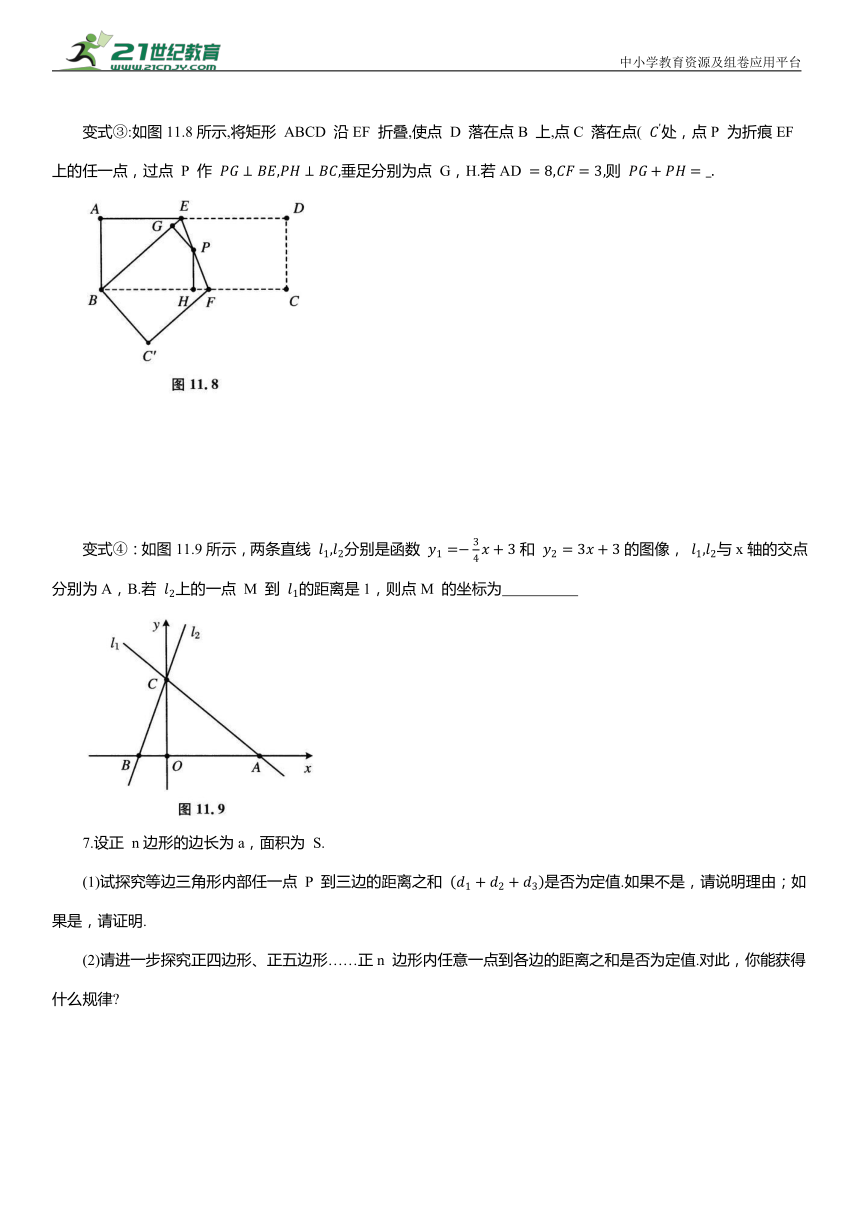
变式③:如图11.8所示,将矩形 ABCD 沿EF 折叠,使点 D 落在点B 上,点C 落在点( 处,点P 为折痕EF 上的任一点,过点 P 作 垂足分别为点 G,H.若AD 则
变式④:如图11.9所示,两条直线 分别是函数 和 的图像, 与x轴的交点分别为A,B.若 上的一点 M 到 的距离是1,则点M 的坐标为
7.设正 n边形的边长为a,面积为 S.
(1)试探究等边三角形内部任一点 P 到三边的距离之和 是否为定值.如果不是,请说明理由;如果是,请证明.
(2)请进一步探究正四边形、正五边形……正n 边形内任意一点到各边的距离之和是否为定值.对此,你能获得什么规律
变式:如图11.10所示,等边 外一点P 到三边的距离分别为 且 其中 则 的面积= .
8.如图11.11 所示,已知 P 为正方形ABCD 的外接圆的劣弧 上任意一点,则
9. 如图11.12所示,已知矩形 AEFG 和矩形ABCD,将矩形 AEFG 绕点A 按顺时针方向旋转, 连接DE,BG,在旋转过程中, 的值是定值,此定值为 .
中小学教育资源及组卷应用平台
10. 如图11.13 所示,抛物线 交x轴于A,B 两点,与 y轴交于点C,抛物线的顶点坐标为 D,过点 D 作直线 轴交x轴于点E,点P 是抛物线上B,D两点间的一个动点(点 P 不与B,D 两点重合),直线 PA,PB 与直线DE 分别交于点F,G.当点P 运动时,
类型4:线段乘积或比值为定值
11. 如图11.14所示,等边 内接于圆,在劣弧 上取异于A,B的点M,设直线CA 与BM 相交于点K,直线CB 与AM 相交于点N.证明:线段AK 和BN的乘积与点M的选择无关.
12. 如图11.15所示,在 中, O是BA上一点,以点 O 为圆心、OB为半径的圆与AB 交于点P,与AC 相切于点D.已知. ⊙O 的半径为r,存在一个常数 m,不论半径r如何变化,. 的值始终是一个定值,此定值为 .
13. 如图11.16所示,在等腰 中,O为底边BC的中点,以点 O 为圆心作半圆与AB,AC 相切,切点分别为 D,E,过半圆上一点 F 作半圆的切线,分别交 AB,AC 于点M,N,则
14.如图11.17所示,P 为反比例函数 在第一象限内图像上的一点,过点P 分别作x轴、y轴的垂线交一次函数. 的图像于点 A,B.若 AO,BO 分别平分 ,则k 的值为 .
类型5:面积为定值
15.如图11.18所示,点 A 是反比例函数 图像上的任意一点, 轴交反比例函数 的图像于点 B,以AB 为边作 其中点 C,D 在x轴上,则S□ABCD为 .
16. 如图11.19所示,在 中,已知 D是AB 的中点,点E,F分别在AC,BC 边上运动(点 E 不与点A,C 重合),且保持 连接 DE,DF,EF.在此运动变化的过程中,求证:四边形 CEDF 的面积是定值.
17. 如图11.20 所示,P 为定角 平分线上的一个定点,且 与 互补, 在绕点P转动的过程中,其两边分别与 OA,OB 相交于M,N两点.求证:四边形 PMON 的面积是定值.
18. 如图11.21所示,已知A,B,C是函数 图像上的动点,且三点的横坐标依次为 .小生同学用软件 GeoGebra 对 的几何特征进行了探究,发现 的面积是个定值,则这个定值为 .
19. 如图11.22 所示,抛物线 与 y轴交于点A,与x 轴交于点B(6,0).设点 P 是抛物线上的动点,若在此抛物线上有且只有三个点 P 使得 的面积是定值S,则此定值 S为 .
整理得y=2mx+m+3=m(2x+1)+3,当 时,正好消掉参数m,此时y=3.
变式①:(2010,2009).
整理得y= kx+(2009-2010k)=k(x-2010)+2009,当x=2010时,y=2009.
变式②:(-4,-1).
整理得y=x +(m+1)x+4m-13=m(x+4)+x +x-13,当x=-4时,y=-1.
2.(1)连接CF,根据垂直平分线的性质和菱形的对称性得到 和CF=AF 即可得证.
(2) 30°.
如图J11.1所示,延长 EF,交 DC 于点H,连接 CF,由 AF= CF =EF,得到∠AEF =∠EAF=α,∠FEC=∠FCE=β,利用外角的性质得∠AFC=2(α+β),从而推断出∠AFD=α+β=α+∠ABF=α+30°,故∠CEF=β=30°.
3.△AOF∽△BEO;45°.
因为O ,所以 又∠OBE=∠OAF=45°,则△AOF∽△BEO,故∠AFO=∠BOE.
因为∠AFO =∠BOF +∠FBO =∠BOF +45°,而. 所以∠EOF=∠FBO=45°.
4. 连接OS,OT,OM.
因为 M 是ST 的中点,所以OM⊥ST.
又SP⊥AB,则∠SPO=∠SMO=90°,所以S,P,O,M 四点共圆,故∠SPM=∠SOM.
因为OS=OT,OM⊥ST,所以 即
故不管 ST 滑到什么位置,∠SPM 是一定角.
5. ③.
由 同理可得 即S△DEF = S△CEF.故①正确.
若两个三角形以EF为底,则 EF 边上的高相等,所以CD∥EF,则△AOB∽△FOE.故②正确.
条件不足,无法得到判定两三角形全等的条件.故③错误.
因为CD∥EF,DF∥BE,所以四边形 DBEF,ACEF 均是平行四边形,则 BD = EF =AC.故④正确.
6. 连接AP,由△ABP 与△ACP 面积之和等于△ABC的面积可以证得PD+PE=CF.
变式①:连接 AP,易得S△ABC = S△ABP - S△ACP,即 ·PE.
因为 AB=AC,所以 CF=PD-PE.
变式②:
连接 PO,因为S△APO + S△DPO = S△AOD,所以 即 解得
变式③:4.
过点 E 作EQ⊥BC.
因为∠BEF=∠DEF,∠DEF=∠EFB,所以∠BEF=∠EFB,则 BE= BF.
又CF=3,AD=8,则BF=8-3=5.
在 Rt△BFC'中, 则 易得 EQ=4.
变式(④ 或
过点 M 分别作MP⊥x轴,MQ⊥AC,垂足分别为点 P,Q.
①如图J11.2所示,当点 M 在线段BC 上时,易得点 A(4,0),C(0,3),B(-1,0),则AB=AC=5.
因为l 上的一点 M到 的距离是1,所以 易得 即 2,亦即点 M 的纵坐标为2.
当y=2时, 故点 M 的坐标为(
② 如图J11.3所示,当点 M 在线段AC 外时,易得 或MP=MQ-OC=3-1=2,即点M 的纵坐标为4或-2,分别代入 可求得 或x= (舍去,因为它到 l 的距离不是1),故点 M 的坐标为(
7.(1)是定值.
证明如下:如图J11.4所示,△ABC 是等边三角形,点P 是等边三角形内部任一点.
因为 所以
即 亦即 为定值.故 为定值.
(2)同(1)中证法,正四边形、正五边形……正n 边形内任意一点到各边的距离之和均为定值,规律为
变式:
连接 PA,PB,PC,如图J11.5所示.设△ABC 的边长为x.
因为 所以 即 故
8.
如图J11.6所示,延长 PA 到点E,使 AE=PC,连接 BE.
因为∠BAE+∠BAP=180°,∠BAP+∠PCB=180°,所以∠BAE=∠PCB.
又四边形 ABCD 是正方形,则 AB= BC,∠ABC=90°,易证△ABE≌△CBP(SAS),则∠ABE=∠CBP,BE=BP,所以∠ABE+∠ABP=∠ABP+∠CBP=90°,故△BEP 是等腰直角三角形,则 即
9. 260.
设 BE 与DG 交于点Q,连接EG,BD.由手拉手全等,知BE⊥DG.
由勾股定理可得
E )
10. 8.
如图J11.7所示,过点 P 作PQ∥y轴交x轴于点Q.
设 则PQ=﹣t ﹣2t+3,AQ=t+3,QB=1﹣t.
因为 PQ∥EF,所以△AEF∽△AQP,则 即
).
又 PQ∥EG,则△BEG∽△BQP,所以 即
故EF+EG=2(1-t)+2(t+3)=8.
11. 因为△ABC是等边三角形,所以∠C=∠BAC=∠ABC=60°,则. =120°.由120°=∠ABN=∠ABM+∠MBN,120°=∠AMB=∠N+∠MBN,得∠ABM=∠N,所以△ABK∽△BNA,则 即 AK·BN=AB .
故线段 AK 和BN 的乘积与点M 的选择无关.
12. 64.
连接OD,易证△ADO∽△ABC,则 即 AD·CB=AB·OD.
因为CB=CD,所以AD·CD=AB·OD=8r,则
AD·CD-mOA = 8r--m(8--r)= (m+8)r-8m,故m=-8时,其定值为64.
13.
如图J11.8所示,连接OD,OM,OF,ON,OE.
设∠B=∠C =α,则. .又易得 则 ,故∠MON=∠B=∠C=α.
由一线三等角模型易得△BOM∽△CNO,则 即 BM·CN = BO·CO= 故
14. 8.
如图J11.9所示,设点 P 坐标为(a,b).
因为 AO,BO 分别平分∠BAP,∠ABP,所以 (角平分线的内内模型),因此∠3+∠4=45°,易得OM=ON=4,则∠2+∠4=45°,即∠2=∠3,同理∠4=∠1,于是△BMO∽△ONA,则 OM·ON=BM·AN,即
,
故16=2ab,即k= ab=8.
15. 5.
提示:
16. 连接CD,易证△AED≌△CFD,则 S△AED=S△CFD,故
17. 如图J11.10所示,作 PE⊥OA 于点E,PF⊥OB 于点F,设∠POF=∠POE=α.利用对角互补模型,易证△PEM≌△PFN,则S△PEM=S△PNF,故
则四边形 PMON 的面积是定值.
18. 1.
作 AD⊥x轴于点D,BE⊥x轴于点E,CF⊥x轴于点F.
因为A,B,C三点的横坐标依次为( 所以 故
S△ABC = S梯形ADFC - S梯形ADEB - S梯形BEFC
= 1.
因为点 A(0,6),点 B(6,0),所以直线 AB的解析式为y=-x+6.当 时, 故点 D(2,4),点 D 为对称轴与AB 的交点.
如图J11.11所示,设AB 上方的抛物线上有点P,过点 P 作AB 的平行线交对称轴于点C,当与抛物线只有一个交点时,满足题意.
设直线 PC 的解析式为y=-x+b,则 且只有一个交点,所以 解得 故直线 PC 的解析式为
因为 解得x=3,所以点 当x=3时,代入直线AB 的解析式,解得 y=3,i故
模块1 本质原理
1.代数定值
多变量中,消元导致系数为零,进而带动产生一系列的定值.
2.几何定值
位置不变、几何量不变、数量关系不变,具体见表11.1.
表11.1
几何定值分类 求解工具
角为定值 ① 利用三角形的性质及定理倒角; ② 利用平行线的性质倒角; ③ 利用圆的性质及定理倒角
边为定值 ①利用特殊三角形(等腰三角形、等边三角形)的性质; ② 利用特殊四边形(平行四边形、矩形、菱形、正方形)的性质; ③ 利用圆的性质及定理; ④ 利用特殊角的三角函数
线段和或差为定值 (或和差关系式) ① 利用等面积法; ② 利用截长补短法
线段乘积或比值为定值 (常见于函数中) ① 构造相似法; ② 含参计算法
面积为定值 (常见于函数中) ① 定义法(s△= 底×高,,S梯形= ×(上底+下底)×高); ② 割补法(利用“水平宽、铅垂高”); ③ 等积变形法(平行线内的同底等高)
模块2 场景演练
模型的识别:代数中的定值
1.若一次函数 y=2mx+m+3的图像经过一个定点,则这个定点的坐标为 .
变式①:不论 k 取什么样的实数,直线. 总经过一定点,则这个定点的坐标为 .
变式②:已知二次函数 当 m 取不同的值时,抛物线都会经过一个定点,此定点的坐标为 .
模型的识别:几何中的定值
类型1:角为定值
2. 如图11.1所示,菱形 ABCD 的边长为1, 点 E 是边AB 上任意一点(端点除外),线段CE 的垂直平分线分别交BD,CE 于点F,G.
(1)求证:
(2)当点 E 在AB上运动时,∠CEF 的大小不变,其度数为 .
3. 如图11.2所示,函数 的图像上有一点P(a,b),由点 P分别向x轴、y轴作垂线 PM,PN,垂足为点 M,N,直线 AB: 分别交PM,PN于点E,F,则 与 的关系为 ;∠EOF =_.
4.如图11.3所示,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P是 S 对AB 作垂线的垂足,求证:不管 ST 滑到什么位置, 是一定角.
类型2:边为定值
5.如图11.4所示,一次函数 的图像分别与x轴、y轴交于A,B两点,与反比例函数 的图像相交于C,D两点,分别过C,D两点作y轴、x轴的垂线,垂足为点E,F,连接CF,DE,EF.有下列四个结论:
与 的面积相等;
其中不正确的结论是 .
类型3:线段和或差为定值(或和差关系式)
6. 如图11.5所示,在 中, 点 P 为边 BC 上任一点,过点 P 作 AB,PE⊥AC,垂足分别为点 D,E,过点 C 作 ,垂足为点 F.求证:
变式①:如图11.6所示,当点 P 在BC 延长线上时,题6中其余条件不变.求证:
变式②:如图11.7所示,在矩形 ABCD 中, 点 P 是AD 上一点,过点 P作 ,垂足分别为点E,F,则.
变式③:如图11.8所示,将矩形 ABCD 沿EF 折叠,使点 D 落在点B 上,点C 落在点( 处,点P 为折痕EF 上的任一点,过点 P 作 垂足分别为点 G,H.若AD 则
变式④:如图11.9所示,两条直线 分别是函数 和 的图像, 与x轴的交点分别为A,B.若 上的一点 M 到 的距离是1,则点M 的坐标为
7.设正 n边形的边长为a,面积为 S.
(1)试探究等边三角形内部任一点 P 到三边的距离之和 是否为定值.如果不是,请说明理由;如果是,请证明.
(2)请进一步探究正四边形、正五边形……正n 边形内任意一点到各边的距离之和是否为定值.对此,你能获得什么规律
变式:如图11.10所示,等边 外一点P 到三边的距离分别为 且 其中 则 的面积= .
8.如图11.11 所示,已知 P 为正方形ABCD 的外接圆的劣弧 上任意一点,则
9. 如图11.12所示,已知矩形 AEFG 和矩形ABCD,将矩形 AEFG 绕点A 按顺时针方向旋转, 连接DE,BG,在旋转过程中, 的值是定值,此定值为 .
中小学教育资源及组卷应用平台
10. 如图11.13 所示,抛物线 交x轴于A,B 两点,与 y轴交于点C,抛物线的顶点坐标为 D,过点 D 作直线 轴交x轴于点E,点P 是抛物线上B,D两点间的一个动点(点 P 不与B,D 两点重合),直线 PA,PB 与直线DE 分别交于点F,G.当点P 运动时,
类型4:线段乘积或比值为定值
11. 如图11.14所示,等边 内接于圆,在劣弧 上取异于A,B的点M,设直线CA 与BM 相交于点K,直线CB 与AM 相交于点N.证明:线段AK 和BN的乘积与点M的选择无关.
12. 如图11.15所示,在 中, O是BA上一点,以点 O 为圆心、OB为半径的圆与AB 交于点P,与AC 相切于点D.已知. ⊙O 的半径为r,存在一个常数 m,不论半径r如何变化,. 的值始终是一个定值,此定值为 .
13. 如图11.16所示,在等腰 中,O为底边BC的中点,以点 O 为圆心作半圆与AB,AC 相切,切点分别为 D,E,过半圆上一点 F 作半圆的切线,分别交 AB,AC 于点M,N,则
14.如图11.17所示,P 为反比例函数 在第一象限内图像上的一点,过点P 分别作x轴、y轴的垂线交一次函数. 的图像于点 A,B.若 AO,BO 分别平分 ,则k 的值为 .
类型5:面积为定值
15.如图11.18所示,点 A 是反比例函数 图像上的任意一点, 轴交反比例函数 的图像于点 B,以AB 为边作 其中点 C,D 在x轴上,则S□ABCD为 .
16. 如图11.19所示,在 中,已知 D是AB 的中点,点E,F分别在AC,BC 边上运动(点 E 不与点A,C 重合),且保持 连接 DE,DF,EF.在此运动变化的过程中,求证:四边形 CEDF 的面积是定值.
17. 如图11.20 所示,P 为定角 平分线上的一个定点,且 与 互补, 在绕点P转动的过程中,其两边分别与 OA,OB 相交于M,N两点.求证:四边形 PMON 的面积是定值.
18. 如图11.21所示,已知A,B,C是函数 图像上的动点,且三点的横坐标依次为 .小生同学用软件 GeoGebra 对 的几何特征进行了探究,发现 的面积是个定值,则这个定值为 .
19. 如图11.22 所示,抛物线 与 y轴交于点A,与x 轴交于点B(6,0).设点 P 是抛物线上的动点,若在此抛物线上有且只有三个点 P 使得 的面积是定值S,则此定值 S为 .
整理得y=2mx+m+3=m(2x+1)+3,当 时,正好消掉参数m,此时y=3.
变式①:(2010,2009).
整理得y= kx+(2009-2010k)=k(x-2010)+2009,当x=2010时,y=2009.
变式②:(-4,-1).
整理得y=x +(m+1)x+4m-13=m(x+4)+x +x-13,当x=-4时,y=-1.
2.(1)连接CF,根据垂直平分线的性质和菱形的对称性得到 和CF=AF 即可得证.
(2) 30°.
如图J11.1所示,延长 EF,交 DC 于点H,连接 CF,由 AF= CF =EF,得到∠AEF =∠EAF=α,∠FEC=∠FCE=β,利用外角的性质得∠AFC=2(α+β),从而推断出∠AFD=α+β=α+∠ABF=α+30°,故∠CEF=β=30°.
3.△AOF∽△BEO;45°.
因为O ,所以 又∠OBE=∠OAF=45°,则△AOF∽△BEO,故∠AFO=∠BOE.
因为∠AFO =∠BOF +∠FBO =∠BOF +45°,而. 所以∠EOF=∠FBO=45°.
4. 连接OS,OT,OM.
因为 M 是ST 的中点,所以OM⊥ST.
又SP⊥AB,则∠SPO=∠SMO=90°,所以S,P,O,M 四点共圆,故∠SPM=∠SOM.
因为OS=OT,OM⊥ST,所以 即
故不管 ST 滑到什么位置,∠SPM 是一定角.
5. ③.
由 同理可得 即S△DEF = S△CEF.故①正确.
若两个三角形以EF为底,则 EF 边上的高相等,所以CD∥EF,则△AOB∽△FOE.故②正确.
条件不足,无法得到判定两三角形全等的条件.故③错误.
因为CD∥EF,DF∥BE,所以四边形 DBEF,ACEF 均是平行四边形,则 BD = EF =AC.故④正确.
6. 连接AP,由△ABP 与△ACP 面积之和等于△ABC的面积可以证得PD+PE=CF.
变式①:连接 AP,易得S△ABC = S△ABP - S△ACP,即 ·PE.
因为 AB=AC,所以 CF=PD-PE.
变式②:
连接 PO,因为S△APO + S△DPO = S△AOD,所以 即 解得
变式③:4.
过点 E 作EQ⊥BC.
因为∠BEF=∠DEF,∠DEF=∠EFB,所以∠BEF=∠EFB,则 BE= BF.
又CF=3,AD=8,则BF=8-3=5.
在 Rt△BFC'中, 则 易得 EQ=4.
变式(④ 或
过点 M 分别作MP⊥x轴,MQ⊥AC,垂足分别为点 P,Q.
①如图J11.2所示,当点 M 在线段BC 上时,易得点 A(4,0),C(0,3),B(-1,0),则AB=AC=5.
因为l 上的一点 M到 的距离是1,所以 易得 即 2,亦即点 M 的纵坐标为2.
当y=2时, 故点 M 的坐标为(
② 如图J11.3所示,当点 M 在线段AC 外时,易得 或MP=MQ-OC=3-1=2,即点M 的纵坐标为4或-2,分别代入 可求得 或x= (舍去,因为它到 l 的距离不是1),故点 M 的坐标为(
7.(1)是定值.
证明如下:如图J11.4所示,△ABC 是等边三角形,点P 是等边三角形内部任一点.
因为 所以
即 亦即 为定值.故 为定值.
(2)同(1)中证法,正四边形、正五边形……正n 边形内任意一点到各边的距离之和均为定值,规律为
变式:
连接 PA,PB,PC,如图J11.5所示.设△ABC 的边长为x.
因为 所以 即 故
8.
如图J11.6所示,延长 PA 到点E,使 AE=PC,连接 BE.
因为∠BAE+∠BAP=180°,∠BAP+∠PCB=180°,所以∠BAE=∠PCB.
又四边形 ABCD 是正方形,则 AB= BC,∠ABC=90°,易证△ABE≌△CBP(SAS),则∠ABE=∠CBP,BE=BP,所以∠ABE+∠ABP=∠ABP+∠CBP=90°,故△BEP 是等腰直角三角形,则 即
9. 260.
设 BE 与DG 交于点Q,连接EG,BD.由手拉手全等,知BE⊥DG.
由勾股定理可得
E )
10. 8.
如图J11.7所示,过点 P 作PQ∥y轴交x轴于点Q.
设 则PQ=﹣t ﹣2t+3,AQ=t+3,QB=1﹣t.
因为 PQ∥EF,所以△AEF∽△AQP,则 即
).
又 PQ∥EG,则△BEG∽△BQP,所以 即
故EF+EG=2(1-t)+2(t+3)=8.
11. 因为△ABC是等边三角形,所以∠C=∠BAC=∠ABC=60°,则. =120°.由120°=∠ABN=∠ABM+∠MBN,120°=∠AMB=∠N+∠MBN,得∠ABM=∠N,所以△ABK∽△BNA,则 即 AK·BN=AB .
故线段 AK 和BN 的乘积与点M 的选择无关.
12. 64.
连接OD,易证△ADO∽△ABC,则 即 AD·CB=AB·OD.
因为CB=CD,所以AD·CD=AB·OD=8r,则
AD·CD-mOA = 8r--m(8--r)= (m+8)r-8m,故m=-8时,其定值为64.
13.
如图J11.8所示,连接OD,OM,OF,ON,OE.
设∠B=∠C =α,则. .又易得 则 ,故∠MON=∠B=∠C=α.
由一线三等角模型易得△BOM∽△CNO,则 即 BM·CN = BO·CO= 故
14. 8.
如图J11.9所示,设点 P 坐标为(a,b).
因为 AO,BO 分别平分∠BAP,∠ABP,所以 (角平分线的内内模型),因此∠3+∠4=45°,易得OM=ON=4,则∠2+∠4=45°,即∠2=∠3,同理∠4=∠1,于是△BMO∽△ONA,则 OM·ON=BM·AN,即
,
故16=2ab,即k= ab=8.
15. 5.
提示:
16. 连接CD,易证△AED≌△CFD,则 S△AED=S△CFD,故
17. 如图J11.10所示,作 PE⊥OA 于点E,PF⊥OB 于点F,设∠POF=∠POE=α.利用对角互补模型,易证△PEM≌△PFN,则S△PEM=S△PNF,故
则四边形 PMON 的面积是定值.
18. 1.
作 AD⊥x轴于点D,BE⊥x轴于点E,CF⊥x轴于点F.
因为A,B,C三点的横坐标依次为( 所以 故
S△ABC = S梯形ADFC - S梯形ADEB - S梯形BEFC
= 1.
因为点 A(0,6),点 B(6,0),所以直线 AB的解析式为y=-x+6.当 时, 故点 D(2,4),点 D 为对称轴与AB 的交点.
如图J11.11所示,设AB 上方的抛物线上有点P,过点 P 作AB 的平行线交对称轴于点C,当与抛物线只有一个交点时,满足题意.
设直线 PC 的解析式为y=-x+b,则 且只有一个交点,所以 解得 故直线 PC 的解析式为
因为 解得x=3,所以点 当x=3时,代入直线AB 的解析式,解得 y=3,i故
同课章节目录
