第17 讲 一题多解、一题多变与多题归一(含答案) 2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第17 讲 一题多解、一题多变与多题归一(含答案) 2025年中考数学几何模型方法巩固练习 |
|
|
| 格式 | docx | ||
| 文件大小 | 546.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:30:21 | ||
图片预览


文档简介
第17 讲 一题多解、一题多变与多题归一
实例剖析
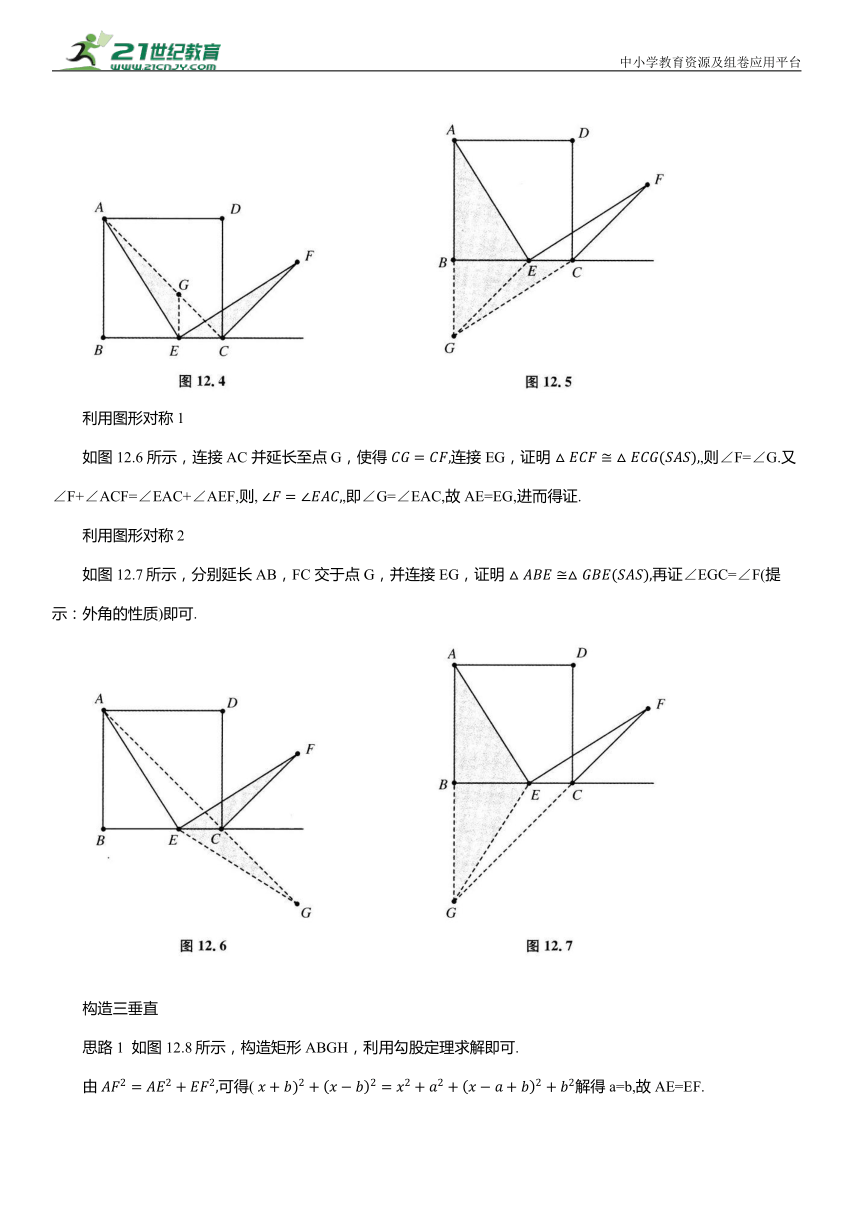
母题:如图12.1所示,四边形 ABCD 是正方形,点 E 是边BC 上一点,∠AEF=90°,EF交正方形外角平分线CF 于点F.求证:AE=EF.
12.1 一 题 多 解
利用图形旋转1
如图12.2所示,在 AB上取一点G 使得AG=CE,易得△BGE 为等腰直角三角形,再证明△AGE≌△ECF(ASA)即可.
利用图形旋转2
如图12.3所示,连接AC,过点 E 作EG⊥BC交FC 的延长线于点G,证明△AEC≌△FEG(ASA)即可.
利用图形旋转3
如图12.4所示,连接 AC,过点 E 作EG⊥BC 交AC 于点G,证明. (ASA)即可.
利用图形旋转4
如图12.5 所示,延长 AB 至点G,使得 BG = BE,并连接 EG,CG,证明. △CBG(SAS),再证明四边形 EGCF 为平行四边形即可(两组对边分别平行).
利用图形对称1
如图12.6 所示,连接 AC 并延长至点G,使得 连接 EG,证明 ,则∠F=∠G.又∠F+∠ACF=∠EAC+∠AEF,则, ,即∠G=∠EAC,故 AE=EG,进而得证.
利用图形对称2
如图12.7所示,分别延长AB,FC 交于点G,并连接EG,证明 再证∠EGC=∠F(提示:外角的性质)即可.
构造三垂直
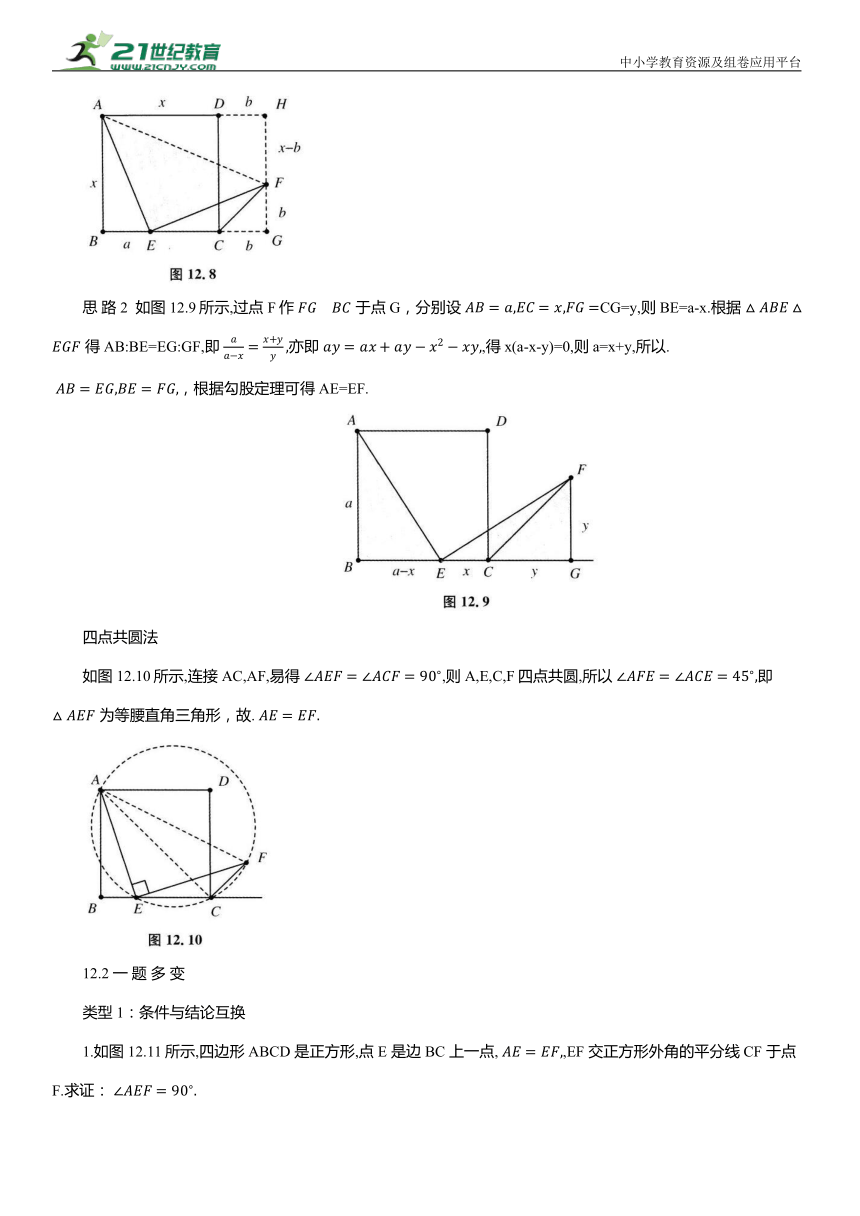
思路 1 如图12.8所示,构造矩形 ABGH,利用勾股定理求解即可.
由 可得( 解得a=b,故 AE=EF.
思 路 2 如图12.9所示,过点 F作 于点G,分别设 CG=y,则BE=a-x.根据 得AB:BE=EG:GF,即 亦即 ,得x(a-x-y)=0,则a=x+y,所以. ,根据勾股定理可得AE=EF.
四点共圆法
如图12.10所示,连接AC,AF,易得 ,则A,E,C,F四点共圆,所以 即 为等腰直角三角形,故.
12.2 一 题 多 变
类型1:条件与结论互换
1.如图12.11所示,四边形 ABCD 是正方形,点 E 是边BC 上一点, ,EF 交正方形外角的平分线CF 于点F.求证:
2.四边形 ABCD 是正方形,点 E 是边BC 上一点, .求证:CF 为正方形的外角平分线.
类型2:位置拓展
3.四边形 ABCD 是正方形,点E 是BC 延长线上一点(或BC 反向延长线上一点), EF 交正方形外角平分线所在直线CF 于点F,AE 与EF 是否还相等
类型3:背景变换
4. 如图 12.12 所示,在正. 中,点E 是边BC上一点, EF 交正 的外角平分线CF 于点F,此时AE 与EF 是否还相等
中小学教育资源及组卷应用平台
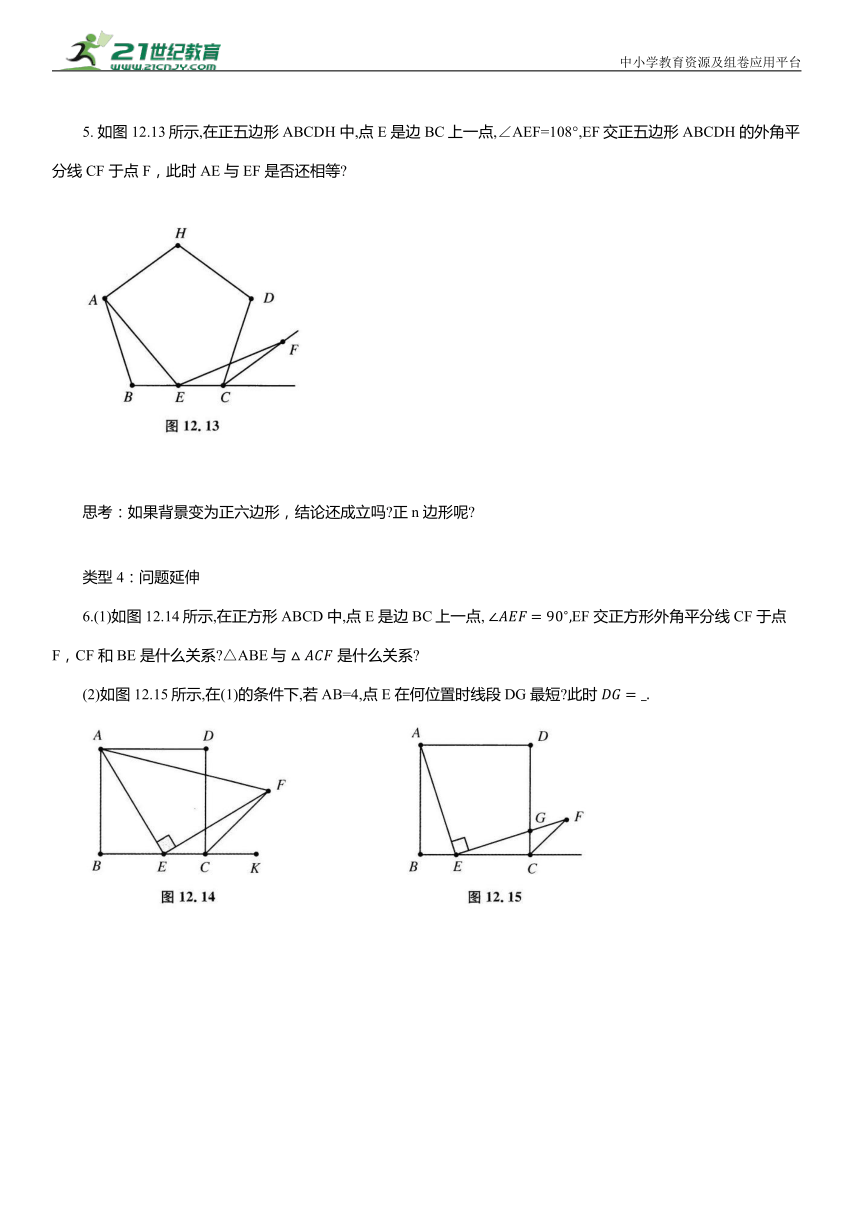
5. 如图12.13所示,在正五边形 ABCDH 中,点 E 是边BC上一点,∠AEF=108°,EF交正五边形ABCDH 的外角平分线CF 于点F,此时 AE 与EF 是否还相等
思考:如果背景变为正六边形,结论还成立吗 正n 边形呢
类型4:问题延伸
6.(1)如图12.14所示,在正方形ABCD 中,点 E 是边BC上一点, EF 交正方形外角平分线 CF 于点F,CF 和BE 是什么关系 △ABE与 是什么关系
(2)如图12.15所示,在(1)的条件下,若AB=4,点E 在何位置时线段DG 最短 此时
类型5:化特殊为一般
7. 如图12.16所示,四边形 ABCD 是矩形, 点 E 是边BC 上的任意一点(不与点 B,C重合), 且 ,连接CF,则 的值为 .
8.如图12.17 所示,当四边形 ABCD 为矩形时,已知 .证明:A,E,C,F四点共圆.
9. 如图12.18 所示,当四边形 ABCD 为平行四边形时,已知 BC = nAB,∠AEF =∠ACF=∠B,则 AE 与EF 是什么关系
由题9可得,此问题的基本图形可抽象为如图12.19所示,其本质是由∠AEF=∠ACF=∠B,得到A,E,C,F四点共圆,连接 AF,由此可得∠ACB=∠AFE,再得到△ABC∽△AEF,进而得到 反之,也可由 BC=nAB,EF= nAE,∠AEF=∠B,得到△ABC∽△AEF,由“一转成双”可得△ABE∽△ACF,所以∠AEF=∠ACF,故 A,E,C,F四点共圆.
12.4 类 比 变 式
10. 如图12.20所示,在正方形 ABCD中,P 是对角线AC上一点,连接PD,过点 P 作PE⊥PD,交边 CB 于点E,写出 PE 与PD 的数量关系,并加以证明.
思考:还有其他方法吗 提示:利用 ,过点 P 作 AD 的垂线,可构造三垂直模型的全等.
类型1:以正方形为背景的动态变式
变式①:如图12.21 所示,四边形 ABCD 是正方形,点 P 在线段AC 上(不含端点), ,交射线 BC 于点E,试写出 PE 与PD 的数量关系,并说明理由.
变式②:如图12.22 所示,当点 P 在线段AC 的延长线上时,试写出 PE与PD 的数量关系,并说明理由.
变式③:如图12.23所示,点 P 在线段AC 的延长线上,当 时,线段 DE的长为 .
变式④:如图12.24所示,四边形 ABCD 是正方形,点 P 在线段AC上(不含端点),点 E在射线 BC上,连接PD,PE, 试写出 的度数,并说明理由.
变式⑤:如图12.25所示, ,连接 BD 交 PE 于点 M,连接 DE 交 AC 于点 H,给出下列三个结论:① AP=BE;②S△DPM= S△MBE;(;③ CP=AP+ CE.正确的结论是
类型2:以矩形为背景的动态变式
11.变式①:如图12.26所示,把正方形变为矩形,点 P 在线段AC上(不含端点),点 E在边BC上, C=2AB,试写出 的值,并说明理由.
变式②:如图12.27所示,点 E 在射线BC 上, AB=2BC,试写出 的值,并说明理由.
变式③:如图 12.28所示,点 P 在射线AC 上, 2AB,试写出 的值,并说明理由.
变式④:如图12.29所示,点 P 在线段AC 上(不含端点),点 E 在边 BC 上, 试写出 的度数,并说明理由.
思考:在“类比变式”中,所有问题的“多题归一”的通法是什么 你还可以设计哪些延伸的问题 请总结下.
第12讲 一题多解、一题多变与多题归一
1.如图J12.1所示,在AB上截取BG,使得 BG=BE,构造三垂直模型,先证得 ≌△CEI,再证得 Rt△AEH≌Rt△EFI(HL)即可.
2. 如图J12.2所示,在 AB 上截取BG,使得 BG=BE,构造旋转型全等,证得△AGE≌△ECF(SAS)即可.
3. 如图J12.3所示,连接AC,易得∠AEF=∠ACF=90°,则 A,E,F,C 四点共圆,所以∠ACE=∠ECF=45°,即 AE=EF(圆内圆周角相等所对的弦也相等).
如图J12.4所示,连接AC,AF,易得∠AEF=∠ACF=90°,则A,C,E,F四点共圆,所以∠FAE=∠FCE=45°,即△EAF 为等腰直角三角形,故AE=EF.
4. 易得∠2=∠3=60°,则 A,E,C,F 四点共圆,所以 ,故 AE=EF.
5. 连接 AC,易得∠AEF =∠ACF =108°,则 A,E,C,F 四点共圆,所以∠AFE =∠ACE=36°,即△EAF 为等腰三角形,故 AE=EF.
提示:连接 AC,证明△ABE∽△ACF 即可.
(2) 3.
设BE=x,则CE=4-x.
由“三垂直模型”易得△ABE∽△ECG,则 即 所以 GC= 故
当x=2,即 E 为BC 的中点时,线段 DG 最短,
7.
思路1 三垂直模型.
如图J12.5所示,作 FM⊥CG 于点M,易证△EAB∽△FEM,则
因为AE=2EF,所以AB=2EM,BE=2FM.
又AB=2AD,则EM=AD.
因为AD= BC,所以EM=BC,则BE=CM,即CM=2FM,故
思路2 四点共圆.
如图J12.6所示,连接AC.由 可证△ABC∽△AEF.由第4讲的“一转成双”可得△ABE∽△ACF,则∠B=∠ACF=90°.
因为∠AEF =∠ACF = 90°,所以 A,E,C,F 四点共圆,则∠FCG =∠EAF,故
8. 如图 J12.7 所示,连接 AC,由 可证 △AEF.由第4讲的“一转成双”可得△ABE∽△ACF,则 故A,E,C,F 四点共圆.
9. 如图J12.8所示,连接AF.
因为 所以A,E,C,F四点共圆,则∠AFE=∠ACB.
又 则 故 即 EF= nAE.
10. 连接DE,因为∠DPE=∠DCE =90°,所以 D,P,E,C 四点共圆,则∠PCD=∠DEP=45°,即△DPE 为等腰直角三角形,故 PE=PD.
变式①:连接DE.因为∠DPE=∠DCE=90°,所以 D,P,C,E 四点共圆,则∠PCD=∠DEP=45°,即△DPE 为等腰直角三角形,故 PE=PD.
变式②:连接DE.因为∠DPE=∠DCE=90°,所以 D,C,P,E 四点共圆,则∠PCE =∠PDE=45°,即△DPE 为等腰直角三角形,故 PE=PD.
变式③:
连接 DE.因为 PE=PD,∠DPE=90°,所以, 在△CDP 中,( 3,∠DCP=135°,解三角形可得. 故
变式④:如图J12.9所示,过点 P 作MN⊥AD 交AD 于点M,交 BC 于点N,易得AM=MP= BN,则MD=NC=PN.又PD=PE,所以Rt△DMP≌Rt△PNE(HL),故∠1=∠E.
因为∠E+∠EPN=90°,所以∠1+∠EPN=90°,故∠DPE=90°.
变式⑤:①③.
如图J12.10所示,连接BP,作 PN⊥BC 于点N,作 PT⊥AB 于点T,可得 BN =PT= 由对称性易得 PB=PD,则 PB=PE,所以 .故①正确.(也可以通过证△ADP∽△BDE 得证.)
当点 P 逐渐向点A 运动时,△DPM 的面积逐渐增大,而△MBE 的面积逐渐减小,趋近于0.故②不正确.
作 EK⊥BC 交AC 于点K,则 .因为 KE∥PN∥AB,N是BE 的中点,所以AP:PK=BN: NE=1:1,则 故③正确.
11. 变式①:连接 DE.因为∠DPE =∠DCE =90°,所以 D,P,E,C 四点共圆,则∠PCD=∠DEP,故
变式②:连接 DE.因为∠DPE=∠DCE=90°,所以 D,P,C,E 四点共圆,则 ∠DEP,故
变式③:连接DE.因为∠DPE=∠DCE=90°,所以 D,C,P,E 四点共圆,则. ∠PDE,故 即
变式④:如图J12.11所示,过点 P作MN⊥AD,交AD 于点M,交 BC 于点N.设 2PE=2a,AM=2MP=2b,BC=2AB=2m,则, .根据勾股定理可得 则
于是 所以△DMP∽△PNE,故∠MDP=∠NPE.
因为 所以 故
实例剖析
母题:如图12.1所示,四边形 ABCD 是正方形,点 E 是边BC 上一点,∠AEF=90°,EF交正方形外角平分线CF 于点F.求证:AE=EF.
12.1 一 题 多 解
利用图形旋转1
如图12.2所示,在 AB上取一点G 使得AG=CE,易得△BGE 为等腰直角三角形,再证明△AGE≌△ECF(ASA)即可.
利用图形旋转2
如图12.3所示,连接AC,过点 E 作EG⊥BC交FC 的延长线于点G,证明△AEC≌△FEG(ASA)即可.
利用图形旋转3
如图12.4所示,连接 AC,过点 E 作EG⊥BC 交AC 于点G,证明. (ASA)即可.
利用图形旋转4
如图12.5 所示,延长 AB 至点G,使得 BG = BE,并连接 EG,CG,证明. △CBG(SAS),再证明四边形 EGCF 为平行四边形即可(两组对边分别平行).
利用图形对称1
如图12.6 所示,连接 AC 并延长至点G,使得 连接 EG,证明 ,则∠F=∠G.又∠F+∠ACF=∠EAC+∠AEF,则, ,即∠G=∠EAC,故 AE=EG,进而得证.
利用图形对称2
如图12.7所示,分别延长AB,FC 交于点G,并连接EG,证明 再证∠EGC=∠F(提示:外角的性质)即可.
构造三垂直
思路 1 如图12.8所示,构造矩形 ABGH,利用勾股定理求解即可.
由 可得( 解得a=b,故 AE=EF.
思 路 2 如图12.9所示,过点 F作 于点G,分别设 CG=y,则BE=a-x.根据 得AB:BE=EG:GF,即 亦即 ,得x(a-x-y)=0,则a=x+y,所以. ,根据勾股定理可得AE=EF.
四点共圆法
如图12.10所示,连接AC,AF,易得 ,则A,E,C,F四点共圆,所以 即 为等腰直角三角形,故.
12.2 一 题 多 变
类型1:条件与结论互换
1.如图12.11所示,四边形 ABCD 是正方形,点 E 是边BC 上一点, ,EF 交正方形外角的平分线CF 于点F.求证:
2.四边形 ABCD 是正方形,点 E 是边BC 上一点, .求证:CF 为正方形的外角平分线.
类型2:位置拓展
3.四边形 ABCD 是正方形,点E 是BC 延长线上一点(或BC 反向延长线上一点), EF 交正方形外角平分线所在直线CF 于点F,AE 与EF 是否还相等
类型3:背景变换
4. 如图 12.12 所示,在正. 中,点E 是边BC上一点, EF 交正 的外角平分线CF 于点F,此时AE 与EF 是否还相等
中小学教育资源及组卷应用平台
5. 如图12.13所示,在正五边形 ABCDH 中,点 E 是边BC上一点,∠AEF=108°,EF交正五边形ABCDH 的外角平分线CF 于点F,此时 AE 与EF 是否还相等
思考:如果背景变为正六边形,结论还成立吗 正n 边形呢
类型4:问题延伸
6.(1)如图12.14所示,在正方形ABCD 中,点 E 是边BC上一点, EF 交正方形外角平分线 CF 于点F,CF 和BE 是什么关系 △ABE与 是什么关系
(2)如图12.15所示,在(1)的条件下,若AB=4,点E 在何位置时线段DG 最短 此时
类型5:化特殊为一般
7. 如图12.16所示,四边形 ABCD 是矩形, 点 E 是边BC 上的任意一点(不与点 B,C重合), 且 ,连接CF,则 的值为 .
8.如图12.17 所示,当四边形 ABCD 为矩形时,已知 .证明:A,E,C,F四点共圆.
9. 如图12.18 所示,当四边形 ABCD 为平行四边形时,已知 BC = nAB,∠AEF =∠ACF=∠B,则 AE 与EF 是什么关系
由题9可得,此问题的基本图形可抽象为如图12.19所示,其本质是由∠AEF=∠ACF=∠B,得到A,E,C,F四点共圆,连接 AF,由此可得∠ACB=∠AFE,再得到△ABC∽△AEF,进而得到 反之,也可由 BC=nAB,EF= nAE,∠AEF=∠B,得到△ABC∽△AEF,由“一转成双”可得△ABE∽△ACF,所以∠AEF=∠ACF,故 A,E,C,F四点共圆.
12.4 类 比 变 式
10. 如图12.20所示,在正方形 ABCD中,P 是对角线AC上一点,连接PD,过点 P 作PE⊥PD,交边 CB 于点E,写出 PE 与PD 的数量关系,并加以证明.
思考:还有其他方法吗 提示:利用 ,过点 P 作 AD 的垂线,可构造三垂直模型的全等.
类型1:以正方形为背景的动态变式
变式①:如图12.21 所示,四边形 ABCD 是正方形,点 P 在线段AC 上(不含端点), ,交射线 BC 于点E,试写出 PE 与PD 的数量关系,并说明理由.
变式②:如图12.22 所示,当点 P 在线段AC 的延长线上时,试写出 PE与PD 的数量关系,并说明理由.
变式③:如图12.23所示,点 P 在线段AC 的延长线上,当 时,线段 DE的长为 .
变式④:如图12.24所示,四边形 ABCD 是正方形,点 P 在线段AC上(不含端点),点 E在射线 BC上,连接PD,PE, 试写出 的度数,并说明理由.
变式⑤:如图12.25所示, ,连接 BD 交 PE 于点 M,连接 DE 交 AC 于点 H,给出下列三个结论:① AP=BE;②S△DPM= S△MBE;(;③ CP=AP+ CE.正确的结论是
类型2:以矩形为背景的动态变式
11.变式①:如图12.26所示,把正方形变为矩形,点 P 在线段AC上(不含端点),点 E在边BC上, C=2AB,试写出 的值,并说明理由.
变式②:如图12.27所示,点 E 在射线BC 上, AB=2BC,试写出 的值,并说明理由.
变式③:如图 12.28所示,点 P 在射线AC 上, 2AB,试写出 的值,并说明理由.
变式④:如图12.29所示,点 P 在线段AC 上(不含端点),点 E 在边 BC 上, 试写出 的度数,并说明理由.
思考:在“类比变式”中,所有问题的“多题归一”的通法是什么 你还可以设计哪些延伸的问题 请总结下.
第12讲 一题多解、一题多变与多题归一
1.如图J12.1所示,在AB上截取BG,使得 BG=BE,构造三垂直模型,先证得 ≌△CEI,再证得 Rt△AEH≌Rt△EFI(HL)即可.
2. 如图J12.2所示,在 AB 上截取BG,使得 BG=BE,构造旋转型全等,证得△AGE≌△ECF(SAS)即可.
3. 如图J12.3所示,连接AC,易得∠AEF=∠ACF=90°,则 A,E,F,C 四点共圆,所以∠ACE=∠ECF=45°,即 AE=EF(圆内圆周角相等所对的弦也相等).
如图J12.4所示,连接AC,AF,易得∠AEF=∠ACF=90°,则A,C,E,F四点共圆,所以∠FAE=∠FCE=45°,即△EAF 为等腰直角三角形,故AE=EF.
4. 易得∠2=∠3=60°,则 A,E,C,F 四点共圆,所以 ,故 AE=EF.
5. 连接 AC,易得∠AEF =∠ACF =108°,则 A,E,C,F 四点共圆,所以∠AFE =∠ACE=36°,即△EAF 为等腰三角形,故 AE=EF.
提示:连接 AC,证明△ABE∽△ACF 即可.
(2) 3.
设BE=x,则CE=4-x.
由“三垂直模型”易得△ABE∽△ECG,则 即 所以 GC= 故
当x=2,即 E 为BC 的中点时,线段 DG 最短,
7.
思路1 三垂直模型.
如图J12.5所示,作 FM⊥CG 于点M,易证△EAB∽△FEM,则
因为AE=2EF,所以AB=2EM,BE=2FM.
又AB=2AD,则EM=AD.
因为AD= BC,所以EM=BC,则BE=CM,即CM=2FM,故
思路2 四点共圆.
如图J12.6所示,连接AC.由 可证△ABC∽△AEF.由第4讲的“一转成双”可得△ABE∽△ACF,则∠B=∠ACF=90°.
因为∠AEF =∠ACF = 90°,所以 A,E,C,F 四点共圆,则∠FCG =∠EAF,故
8. 如图 J12.7 所示,连接 AC,由 可证 △AEF.由第4讲的“一转成双”可得△ABE∽△ACF,则 故A,E,C,F 四点共圆.
9. 如图J12.8所示,连接AF.
因为 所以A,E,C,F四点共圆,则∠AFE=∠ACB.
又 则 故 即 EF= nAE.
10. 连接DE,因为∠DPE=∠DCE =90°,所以 D,P,E,C 四点共圆,则∠PCD=∠DEP=45°,即△DPE 为等腰直角三角形,故 PE=PD.
变式①:连接DE.因为∠DPE=∠DCE=90°,所以 D,P,C,E 四点共圆,则∠PCD=∠DEP=45°,即△DPE 为等腰直角三角形,故 PE=PD.
变式②:连接DE.因为∠DPE=∠DCE=90°,所以 D,C,P,E 四点共圆,则∠PCE =∠PDE=45°,即△DPE 为等腰直角三角形,故 PE=PD.
变式③:
连接 DE.因为 PE=PD,∠DPE=90°,所以, 在△CDP 中,( 3,∠DCP=135°,解三角形可得. 故
变式④:如图J12.9所示,过点 P 作MN⊥AD 交AD 于点M,交 BC 于点N,易得AM=MP= BN,则MD=NC=PN.又PD=PE,所以Rt△DMP≌Rt△PNE(HL),故∠1=∠E.
因为∠E+∠EPN=90°,所以∠1+∠EPN=90°,故∠DPE=90°.
变式⑤:①③.
如图J12.10所示,连接BP,作 PN⊥BC 于点N,作 PT⊥AB 于点T,可得 BN =PT= 由对称性易得 PB=PD,则 PB=PE,所以 .故①正确.(也可以通过证△ADP∽△BDE 得证.)
当点 P 逐渐向点A 运动时,△DPM 的面积逐渐增大,而△MBE 的面积逐渐减小,趋近于0.故②不正确.
作 EK⊥BC 交AC 于点K,则 .因为 KE∥PN∥AB,N是BE 的中点,所以AP:PK=BN: NE=1:1,则 故③正确.
11. 变式①:连接 DE.因为∠DPE =∠DCE =90°,所以 D,P,E,C 四点共圆,则∠PCD=∠DEP,故
变式②:连接 DE.因为∠DPE=∠DCE=90°,所以 D,P,C,E 四点共圆,则 ∠DEP,故
变式③:连接DE.因为∠DPE=∠DCE=90°,所以 D,C,P,E 四点共圆,则. ∠PDE,故 即
变式④:如图J12.11所示,过点 P作MN⊥AD,交AD 于点M,交 BC 于点N.设 2PE=2a,AM=2MP=2b,BC=2AB=2m,则, .根据勾股定理可得 则
于是 所以△DMP∽△PNE,故∠MDP=∠NPE.
因为 所以 故
同课章节目录
