第8讲 一线三等角模型 (含答案)2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第8讲 一线三等角模型 (含答案)2025年中考数学几何模型方法巩固练习 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览


文档简介
第8讲 一线三等角模型
模块1 本 质 原 理
1.概念
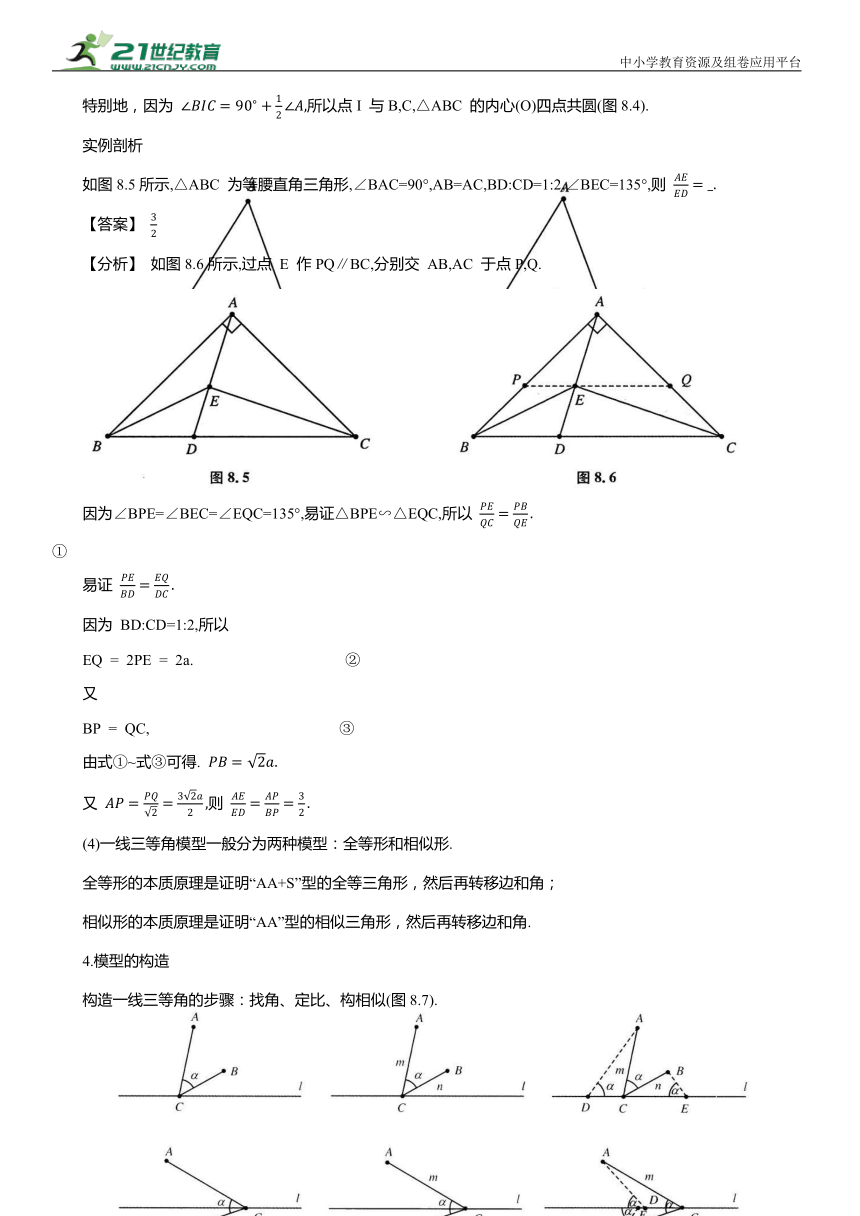
由三个等角的顶点在同一条直线上构成的相似图形(可以是直角、锐角或钝角),称此模型为一线三等角模型.
2.常见图形演变
同侧型:如图8.1所示,已知∠B=∠ACE=∠D.
异侧型:如图8.2所示,已知∠ACE=∠ABD=∠EDF.
3.模型的性质
(1)在上面的6个图中均可得到
(2)在图8.1中,当点 C 为BD的中点时,△ABC∽△CDE∽△ACE.
简证:因为△ABC∽△CDE,所以 又 BC=CD,则 即
因为∠B=∠ACE,所以△ABC∽△ACE,即可得证.
思考:若△ABC∽△CDE∽△ACE,点 C 是BD 的中点吗
(3) 如图8.3所示,当 时,有△BDI∽△IEC.证明如下:
设∠ADE=∠AED=α,则∠BDI=∠CEI=180°-α,∠A=180°-2α,∠BIC=180°-α,此时∠BDI=∠CEI=∠BIC=180°-α,易证△BDI∽△IEC.
特别地,因为 所以点I 与B,C,△ABC 的内心(O)四点共圆(图8.4).
实例剖析
如图8.5所示,△ABC 为等腰直角三角形,∠BAC=90°,AB=AC,BD:CD=1:2,∠BEC=135°,则
【答案】
【分析】 如图8.6所示,过点 E 作PQ∥BC,分别交 AB,AC 于点P,Q.
因为∠BPE=∠BEC=∠EQC=135°,易证△BPE∽△EQC,所以 ①
易证
因为 BD:CD=1:2,所以
EQ = 2PE = 2a. ②
又
BP = QC, ③
由式①~式③可得.
又 则
(4)一线三等角模型一般分为两种模型:全等形和相似形.
全等形的本质原理是证明“AA+S”型的全等三角形,然后再转移边和角;
相似形的本质原理是证明“AA”型的相似三角形,然后再转移边和角.
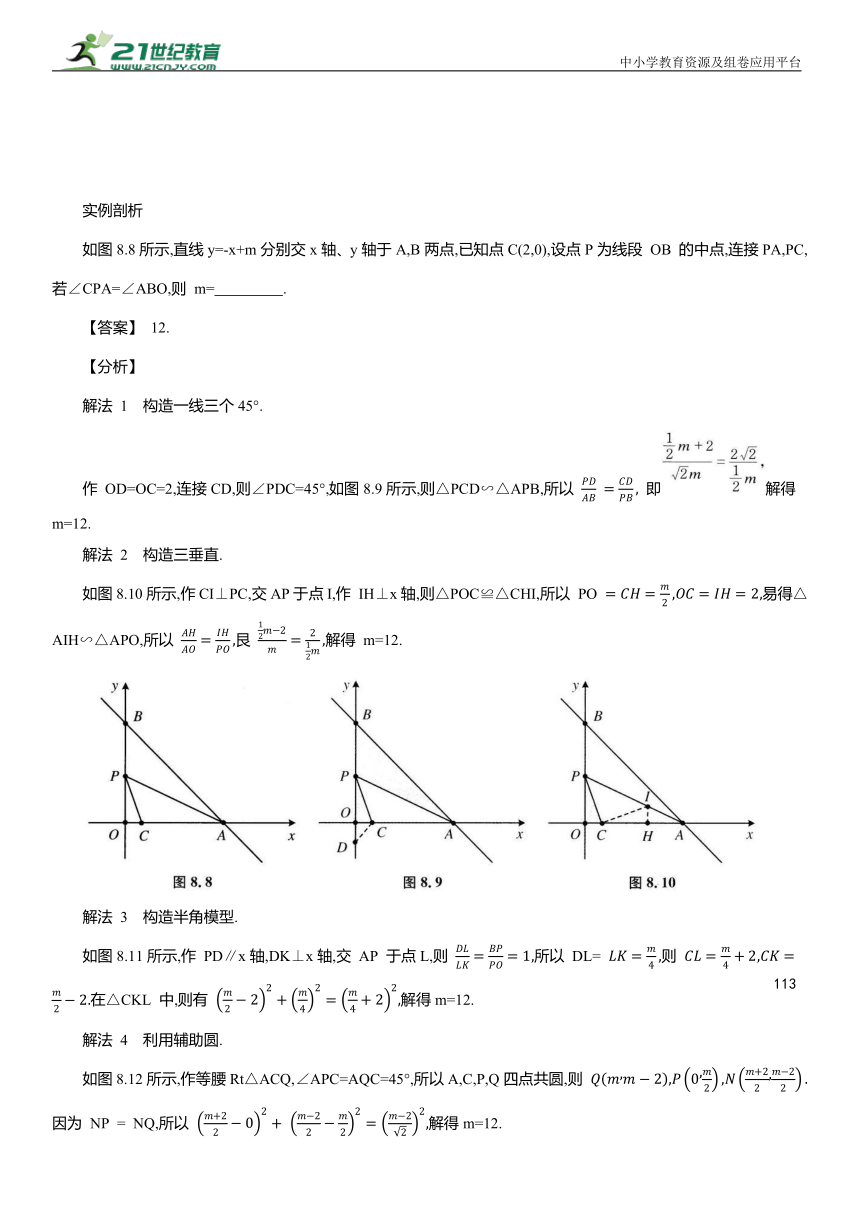
4.模型的构造
构造一线三等角的步骤:找角、定比、构相似(图8.7).
实例剖析
如图8.8所示,直线y=-x+m分别交x轴、y轴于A,B两点,已知点C(2,0),设点P为线段 OB 的中点,连接PA,PC,若∠CPA=∠ABO,则 m= .
【答案】 12.
【分析】
解法 1 构造一线三个45°.
作 OD=OC=2,连接CD,则∠PDC=45°,如图8.9所示,则△PCD∽△APB,所以 即解得 m=12.
解法 2 构造三垂直.
如图8.10所示,作CI⊥PC,交AP于点I,作 IH⊥x轴,则△POC≌△CHI,所以 PO 易得△AIH∽△APO,所以 艮 解得 m=12.
解法 3 构造半角模型.
如图8.11所示,作 PD∥x轴,DK⊥x轴,交 AP 于点L,则 所以 DL= 则 在△CKL 中,则有 解得m=12.
解法 4 利用辅助圆.
如图8.12所示,作等腰Rt△ACQ,∠APC=AQC=45°,所以A,C,P,Q四点共圆,则 因为 NP = NQ,所以 解得m=12.
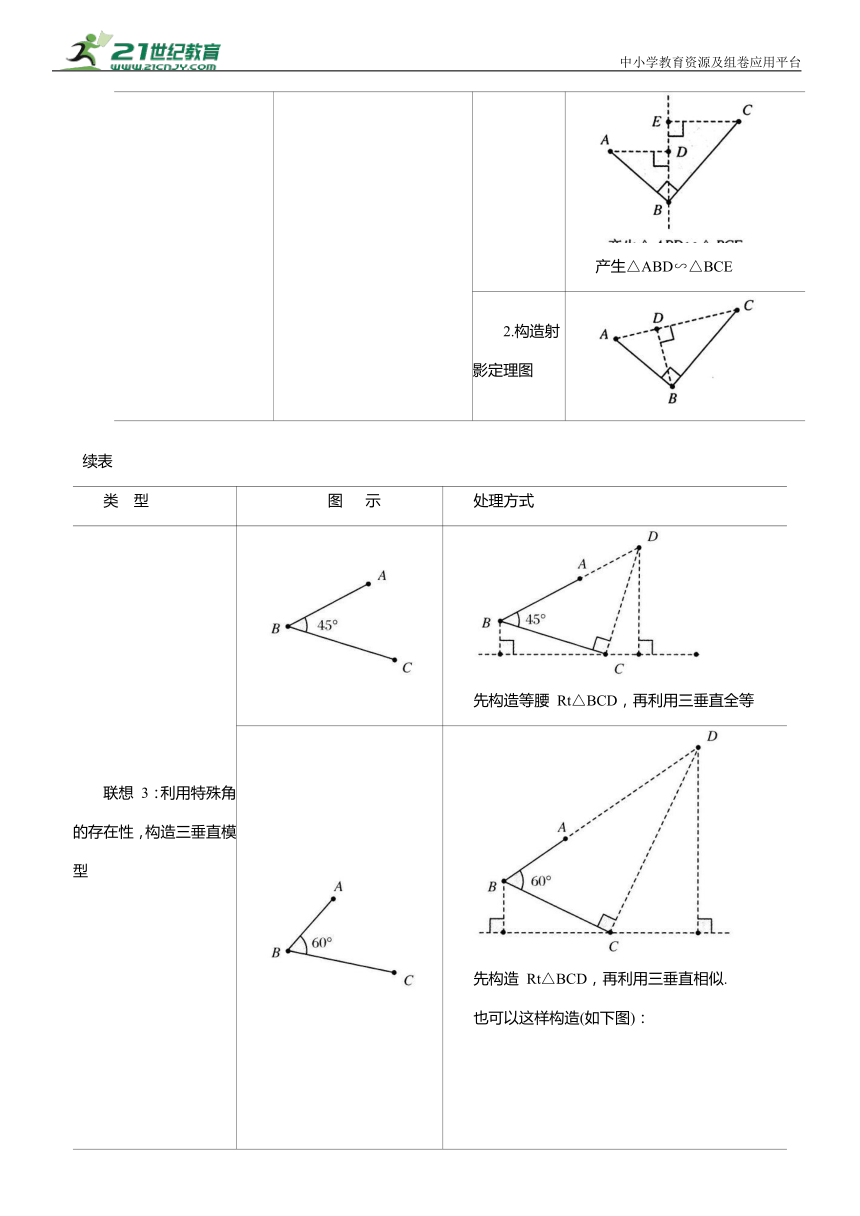
5.应用总结:垂直的联想(见表8.1)
表8.1
类 型 图 示 处理方式
联想1:线垂直 (AB⊥CD) C 1.代数法:kAB·kcD=-1. 2.几何法:补成矩形后,利用十字模型,搭建相似比例
联想2:直角 (AB⊥BC) 1.构造三垂直模型 产生△ABD∽△BCE
延长 BA后,使得△BC'D≌△CBE
产生△ABD∽△BCE
2.构造射影定理图
续表
类 型 图 示 处理方式
联想 3:利用特殊角的存在性,构造三垂直模型 先构造等腰 Rt△BCD,再利用三垂直全等
先构造 Rt△BCD,再利用三垂直相似. 也可以这样构造(如下图):
已知:tanα= 先构造 Rt△BCD,再利用三垂直相似. 也可以这样构造(如下图): 先构造一线三等角,再利用相似求解
续表
类 型 图 示 处理方式
联想4:隐形垂直
6.利用三垂直模型证明“12345模型”
12345模型: 这三个条件知二推一,因含有数字“12345”,故叫作12345模型.
证明如下:如图8.13所示网格,每个正方形的边长均为1,线段AB,AC 的端点均在格点上,此时 连接 BC,利用三垂直和全等易证△ABC 为等腰直角三角形,此时∠BAC=45°.
实例剖析1
如图8.14所示,网格是正方形网格,则∠PAB+∠PBA= (点 A,B,P 是网格线交点).
【答案】 45°.
【分析】 则∠PAB+∠PBA=45°.
实例剖析2
如图8.15所示,在正方形 ABCD中,AB=6,G是BC 的中点.将△ABG 沿AG 对折至△AFG,延长 GF 交DC 于点E,则 DE= .
【答案】 2.
【分析】 如图8.16所示,连接AE.因为 AE=AE,AF=AD,所以 Rt△AFE≌Rt△ADE(HL),则EF=DE,因此α+β=45°.又 则 即 DE=2.
模块2 场 景 演 练
模型的识别
1. 如图8.17所示,在 中, 点D,E 分别在边BC,AC 上, 求证:
2. 如图8.18所示,在正方形 ABCD 中, ,点 E 是DC 延长线上一点,连接 BE,过点 E 作 与 AD 的延长线交于点F.若 CE=2,则
3.如图8.19所示,将等边 折叠,使得点 C 落在AB边上的点D 处,折痕为 EF,点 E,F 分别在AC 和BC 边上.若 则 的周长为 ,
4. 如图8.20 所示,点 E 是矩形ABCD 中 DC 边上一点,将 沿BE 折叠得到 点C 的对应点F恰好落在AD 上.若 则
5. 如图8.21 所示,在 中, 点 D,E,F 分别在边AB,BC,AC 上, 当点 E 是BC 的中点时,求证:EF 平分.
模型的构造:全等形
类型1:已知直角,构造三垂直模型
6. 如图8.22所示,直线 一等腰 的三个顶点A,B,C分别在 上,AC交 于点 D, 已知 与 的距离为2, 与 的距离为6,则
7.如图8.23所示,在等腰 中, 顶点 O 为坐标原点,顶点 A,B在某反比例函数的图像上,点A 的横坐标为2,则
8. 如图8.24所示,正方形 ABCD 的边长为5,点 A 的坐标为(4,0),点 B 在y轴上,若反比例函数 的图像过点 C,则k 的值为 .
9.如图8.25所示,反比例函数 的图像与反比例函数 的图像关于x轴对称.若有一等腰 顶点 O 为坐标原点,点A 在. 图像上,点B 在. 图像上,其中点 A 的横坐标为4,则点 B 的横坐标为 .
10. 如图8.26所示,正方形 的顶点 在反比例函数 的图像上,顶点 分别在x轴和y轴的正半轴上,再在其右侧作正方形 顶点 在 x轴的正半轴上,则点. 的坐标为 .
类型2:利用 构造三垂直模型
11. 如图8.27所示,已知点 A(2,3)和点 B(0,2),点 A 在反比例函数 的图像上,作射线 AB,再将射线 AB 绕点A 按逆时针方向旋转 交反比例函数图像于点 C,则点 C的坐标为 .
12.在平面直角坐标系内,一次函数. 的图像分别交x,y轴于点A,B,将直线AB 绕点B 旋转 交x轴于点C,则直线 BC的函数表达式是 .
13. 如图8.28所示,在 中, 点 D 在 AC 上,点 E在BC 上, ,分别连接 BD,AE交于点F.若 则
类型3:利用 构造一线三等角
14. 如图8.29 所示, 是等边三角形,点A 与点D 的坐标分别是A(4,0),D(10,0).点 C 从点O 沿y轴向下移动,过点 B作 轴,垂足为点 Q.当点 C 的坐标为 时,
类型4:等腰直角三角形存在性问题
15. 如图8.30所示,在矩形 ABCO 中,点 B 的坐标为(8,6),点 A,C分别在坐标轴上,点 P 是线段 BC上的动点.已知点 D 在第一象限,且是直线 上的一点,若 是不以A 为直角顶点的等腰直角三角形,请直接写出所有符合条件的点 D 的坐标: .
模型的构造:相似形
类型1:利用直角,直接构造三垂直模型
16. 如图8.31所示,在Rt△AOB 中,O 为坐标原点, 如果点 A 在反比例函数 的图像上运动,那么点 B 在函数 (填函数解析式)的图像上运动.
17.如图8.32所示,已知 A 是双曲线 在第一象限上的一个动点,连接 AO 并延长交另一分支于点B,以AB 为边作等边 点C 在第四象限.已知点 C 的位置始终在一函数图像上运动,则这个函数解析式为 .
中小学教育资源及组卷应用平台
18.如图8.33 所示,半圆O 的直径 点 D 在 上, 点 P 是半径OC 上的一个动点,连接 DP,过点 P 作 ,交直径 AB 于点E.当点 P 与点C 重合时,(
19. 如图8.34所示,在等腰△ABC 中, 点 D 为边 AC 上的一个动点(不与点 C 重合),作 DE⊥BD 于点D,使得 连接CE,则 的面积的最大值为 .
类型2:建直角,构造三垂直模型
20. 如图8.35所示,函数 的图像上有一点 A(4,3),将射线 OA 绕着原点O 逆时针旋转角α,交图像于点 B,且 则点 B 的坐标为 .
21. 如图8.36所示, 是等边三角形,顶点 C 在y轴的负半轴上,点 点 B 在第一象限,经过点 A 的反比例函数 的图像恰好经过顶点 B,则. 的边长为 .
类型3:隐形的一线三等角模型
22. 如图8.37所示, 为等边三角形, =60°,BM=FN=5,则 CF= .
模型的综合应用:遇见中考
23.在△ABC 中,∠ABC=90°.
(1)如图8.38所示,分别过A,C两点作经过点B 的直线的垂线,垂足分别为点 M,N,求证:△ABM∽△BCN.
(2) 如图8.39 所示,P 是边 BC 上一点, 求 tan C的值.
(3)如图8.40所示,D 是边CA 延长线上一点,AE=AB,∠DEB=90°,sin∠BAC= 则tan∠CEB= .
第8讲 一线三等角模型
1. 易证△ABD≌△DCE,则AB=DC=AC,利用等腰三角形的性质即可证得.
2. 3.
提示:易证△CBE∽△DEF,则 即 解得 DF=3.
3. 10,
提示:因为△AED∽△BDF,所以CE:CF=(AE+DE+AD):(DF+BF+BD).
提示:易证△DFE∽△ABF,设 DE=2a,则 利用折叠的性质可得出 EC=EF,进而可得出 AB=DC=5a,利用相似三角形的性质可得出 又 代入数值即可得证.
5. 易证△CEF∽△BDE,则 因为 E 为BC 的中点,所以 又∠DEF=∠C,则△DEF∽△ECF,故∠DFE=∠CFE,即 EF 平分∠DFC.
如图J8.1所示,作BF⊥l ,AE⊥l .易证△ACE≌△CBF,进而 所以 即 故
如图J8.2所示,过点 B 作BM⊥y轴于点M,过点 A 作AN⊥x轴于点N,并延长 MB,NA 交于一点W.
易证△AON≌△BAW.
设点 A(2,m),则点 B(2-m,2+m),)所以( 解得
故
8. - 3.
过点 C作CE⊥y轴于点E,易证△ABO≌△BCE,所以OA=BE=4,CE=OB=3,则OE=BE-OB=4-3=1,故点 C 的坐标为(-3,1).
因为反比例函数 的图像过点 C,所以k= xy=-3×1=-3.
如图J8.3所示,过点 B 作x轴的平行线EB,过点 A 作AF⊥EB 的延长线于点F,AF 交x轴于点D.
易证△OEB≌△BFA,则 EO= BF,BE=AF.
设BE= x,则 OE = BF =4--x,AD =x--(4--x)=2x-4,故 A(4,2x-4),B(x,x-4).
因为两函数图像关于 x 轴对称,所以 即4(2x-4)+x(x-4)=0,解得 (不合题意舍去), 则点 B 的横坐标为
如图J8.4所示,作 轴于点C, 轴于点D, 轴于点E, 于点F.
易证
设 则 所以点 的坐标为 把 代入 得 解得 (舍去), 故
设点 P 的坐标为 易证 则 因此 即 解得 舍去),( 故点P 的坐标为
11. (-1,-6).
如图J8.5所示,过点 B 作BF⊥AC 于点F,过点 F 作 轴于点D,过点A 作 DF 的延长线于点E,则△ABF 为等腰直角三角形,易得
设 BD=a,则EF=a.
因为点 A(2,3)和点 B(0,2),所以.
又AE+OD=3,即2-a+2-a=3,解得 故
设直线 AF 的解析式为 则 解得 所以 y=3x-3.解方程组 可得 或 故 C(-1,-6).
或y=-3x-1.
解法1 利用三垂直模型.
分两种情况:
①点C在x轴正半轴上时,如图J8.6所示,过点 D 作DE⊥AC 于点E,由三垂直模型易证△AOB≌△DEA,得出 又B(0,-1),则
②点C在x轴负半轴上时,如图J8.7所示,过点 A 作AP⊥AB 于点P,作PI⊥AI 于点I,由三垂直模型易证△AOB≌△PIA,得出 又 B(0,-1),则yBC = - 3x-1.
解法2 利用12345模型.
①点 C在x轴正半轴上时,如图J8.6所示,易得∠ABO+∠OCB=45°.又tan∠ABO 则 于是OC=3,故
②点C在x轴负半轴上时,如图J8.7所示,易得∠ABO+∠OBC=45°.又 tan∠ABO 则 于是 故yBc=-3x-1.
13.
如图J8.8所示,过点 D 作AE 的平行线DI,过点 B 作DI 的垂线,交于点 I,再利用三垂直模型设边求解.
设CG= BH = GI=x,则 IH= DG=x+2=8-x,解得x=3,所以 tan∠EAC = 故 得
解法1 构造一线三等角(图J8.9).
构造△AEC≌△BFA,其中∠AEC=∠AFB=60°,求得 故
解法2 构造一线三垂直(图J8.10).
有△AFE∽△EGB,其中 由“三线合一”可得 E 为AC 的中点,所以 EF 为△AOC 的中位线,则 ,故 tan∠ODB
15.(4,2)或 或
如图J8.11 所示,当 时,AD=PD,则点 D 的坐标为(4,2).
如图J8.12 所示,当∠ADP=90°时,AD=PD,同理可求得点 D 的坐标为
如图J8.13所示,当∠APD=90°时,AP=PD,设点 P 的坐标为(8,m),则点 D 的坐标为(14-m,8+m).由8+m=2(14-m)-6,得 所以点 D 的坐标为
如图J8.14所示,分别过点 A,B 作 轴于点C, 轴于点D.设A(a,b).易证△OAC∽△BOD,则 故点 B 在函数 的图像上运动.
连接OC, 解法同题16.
作 DF⊥OC 于点F.由三垂直模型易证 则 即 故
如图J8.15所示,构造三垂直模型,易证△DEG∽△BDF,则
因为 所以CF=16.
设CD=a,则 FD=16-a,于是 故
则
如图J8.16所示,构造出三垂直模型,易证△OAC∽△AED,则 所以 故yOB=2x.由可得
解法1 如图J8.17 所示,延长 AB 到点D,使得 AB=BD,连接CD,作 AH⊥y轴于点H,DE⊥y轴于点E.设C(0,c).
因为 BA= BC=BD,所以△ACD 是直角三角形,因此 ,易证△ACH∽△CDE,则
因为 所以 则EC= 故
又 BA=BD,利用中点坐标公式得 代入 得 整理得 解得 或 (舍去),则 故
解法2 如图J8.18所示,构造三垂直模型,易证△ADE∽△EFC,则
设 根据中点坐标公式得 所以
因为CF=xE,所以 解得 或m=5.
当 时,点C在y轴的正半轴上,不符合题意,舍去,则m=5,因此 AB
解法3 如图J8.19所示,也可以构造一线三等角模型,请同学们自己试一试吧.
22. 1.
如图J8.20所示,过点 P 作GH∥BC,分别交 AB,AC 于点G,H.
第1步:因为∠MGP=∠MPN=∠NHP=60°,易证 所以 又∠BGP=∠BPF=∠PHF =120°,易证△BGP∽△PHF,如图J8.21 所示,则 故GM·NH = GB·HF. ①
第2步:易证△DGP∽△DBE,则 解得
MG = 2. ②
第3步:由式①、式②得2·NH=3·(5-NH),解得 NH=3,故HF=2,FC=HC-HF=3-2=1.
利用等边三角形的形式,构造二次“三等角”型相似,利用边比求解即可.
23.(1) 因为 AM⊥MN,所以∠MAB+∠MBA =90°.又∠ABC =90°,则∠CBN+∠MBA=90°,因此∠MAB=∠NBC.因为∠M=∠N=90°,所以△ABM∽△BCN.
如图J8.22所示,过点 P 作PD⊥AC 于点D,作 PM⊥AP交AC 于点M.
因为 PM⊥PA,PD⊥AM,所以易证△PDM∽△APM.
又 设DM=2a,则 由勾股定理得 =3a.
因为∠B=∠APM=90°,易得∠1=∠2=∠3,所以CD=DM+CM=DM+PM=5a,故
如图J8.23所示,过点 A 作AG⊥BE 于点G,过点 C 作CH⊥BE 交EB 的延长线于点H.
因为∠DEB=90°,所以 CH∥AG∥DE,故
由(1)可知,△ABG∽△BCH,则
设 BG=4m,则CH=3m,EG=4m,于是 即 GH=10m,故tan∠CEB
模块1 本 质 原 理
1.概念
由三个等角的顶点在同一条直线上构成的相似图形(可以是直角、锐角或钝角),称此模型为一线三等角模型.
2.常见图形演变
同侧型:如图8.1所示,已知∠B=∠ACE=∠D.
异侧型:如图8.2所示,已知∠ACE=∠ABD=∠EDF.
3.模型的性质
(1)在上面的6个图中均可得到
(2)在图8.1中,当点 C 为BD的中点时,△ABC∽△CDE∽△ACE.
简证:因为△ABC∽△CDE,所以 又 BC=CD,则 即
因为∠B=∠ACE,所以△ABC∽△ACE,即可得证.
思考:若△ABC∽△CDE∽△ACE,点 C 是BD 的中点吗
(3) 如图8.3所示,当 时,有△BDI∽△IEC.证明如下:
设∠ADE=∠AED=α,则∠BDI=∠CEI=180°-α,∠A=180°-2α,∠BIC=180°-α,此时∠BDI=∠CEI=∠BIC=180°-α,易证△BDI∽△IEC.
特别地,因为 所以点I 与B,C,△ABC 的内心(O)四点共圆(图8.4).
实例剖析
如图8.5所示,△ABC 为等腰直角三角形,∠BAC=90°,AB=AC,BD:CD=1:2,∠BEC=135°,则
【答案】
【分析】 如图8.6所示,过点 E 作PQ∥BC,分别交 AB,AC 于点P,Q.
因为∠BPE=∠BEC=∠EQC=135°,易证△BPE∽△EQC,所以 ①
易证
因为 BD:CD=1:2,所以
EQ = 2PE = 2a. ②
又
BP = QC, ③
由式①~式③可得.
又 则
(4)一线三等角模型一般分为两种模型:全等形和相似形.
全等形的本质原理是证明“AA+S”型的全等三角形,然后再转移边和角;
相似形的本质原理是证明“AA”型的相似三角形,然后再转移边和角.
4.模型的构造
构造一线三等角的步骤:找角、定比、构相似(图8.7).
实例剖析
如图8.8所示,直线y=-x+m分别交x轴、y轴于A,B两点,已知点C(2,0),设点P为线段 OB 的中点,连接PA,PC,若∠CPA=∠ABO,则 m= .
【答案】 12.
【分析】
解法 1 构造一线三个45°.
作 OD=OC=2,连接CD,则∠PDC=45°,如图8.9所示,则△PCD∽△APB,所以 即解得 m=12.
解法 2 构造三垂直.
如图8.10所示,作CI⊥PC,交AP于点I,作 IH⊥x轴,则△POC≌△CHI,所以 PO 易得△AIH∽△APO,所以 艮 解得 m=12.
解法 3 构造半角模型.
如图8.11所示,作 PD∥x轴,DK⊥x轴,交 AP 于点L,则 所以 DL= 则 在△CKL 中,则有 解得m=12.
解法 4 利用辅助圆.
如图8.12所示,作等腰Rt△ACQ,∠APC=AQC=45°,所以A,C,P,Q四点共圆,则 因为 NP = NQ,所以 解得m=12.
5.应用总结:垂直的联想(见表8.1)
表8.1
类 型 图 示 处理方式
联想1:线垂直 (AB⊥CD) C 1.代数法:kAB·kcD=-1. 2.几何法:补成矩形后,利用十字模型,搭建相似比例
联想2:直角 (AB⊥BC) 1.构造三垂直模型 产生△ABD∽△BCE
延长 BA后,使得△BC'D≌△CBE
产生△ABD∽△BCE
2.构造射影定理图
续表
类 型 图 示 处理方式
联想 3:利用特殊角的存在性,构造三垂直模型 先构造等腰 Rt△BCD,再利用三垂直全等
先构造 Rt△BCD,再利用三垂直相似. 也可以这样构造(如下图):
已知:tanα= 先构造 Rt△BCD,再利用三垂直相似. 也可以这样构造(如下图): 先构造一线三等角,再利用相似求解
续表
类 型 图 示 处理方式
联想4:隐形垂直
6.利用三垂直模型证明“12345模型”
12345模型: 这三个条件知二推一,因含有数字“12345”,故叫作12345模型.
证明如下:如图8.13所示网格,每个正方形的边长均为1,线段AB,AC 的端点均在格点上,此时 连接 BC,利用三垂直和全等易证△ABC 为等腰直角三角形,此时∠BAC=45°.
实例剖析1
如图8.14所示,网格是正方形网格,则∠PAB+∠PBA= (点 A,B,P 是网格线交点).
【答案】 45°.
【分析】 则∠PAB+∠PBA=45°.
实例剖析2
如图8.15所示,在正方形 ABCD中,AB=6,G是BC 的中点.将△ABG 沿AG 对折至△AFG,延长 GF 交DC 于点E,则 DE= .
【答案】 2.
【分析】 如图8.16所示,连接AE.因为 AE=AE,AF=AD,所以 Rt△AFE≌Rt△ADE(HL),则EF=DE,因此α+β=45°.又 则 即 DE=2.
模块2 场 景 演 练
模型的识别
1. 如图8.17所示,在 中, 点D,E 分别在边BC,AC 上, 求证:
2. 如图8.18所示,在正方形 ABCD 中, ,点 E 是DC 延长线上一点,连接 BE,过点 E 作 与 AD 的延长线交于点F.若 CE=2,则
3.如图8.19所示,将等边 折叠,使得点 C 落在AB边上的点D 处,折痕为 EF,点 E,F 分别在AC 和BC 边上.若 则 的周长为 ,
4. 如图8.20 所示,点 E 是矩形ABCD 中 DC 边上一点,将 沿BE 折叠得到 点C 的对应点F恰好落在AD 上.若 则
5. 如图8.21 所示,在 中, 点 D,E,F 分别在边AB,BC,AC 上, 当点 E 是BC 的中点时,求证:EF 平分.
模型的构造:全等形
类型1:已知直角,构造三垂直模型
6. 如图8.22所示,直线 一等腰 的三个顶点A,B,C分别在 上,AC交 于点 D, 已知 与 的距离为2, 与 的距离为6,则
7.如图8.23所示,在等腰 中, 顶点 O 为坐标原点,顶点 A,B在某反比例函数的图像上,点A 的横坐标为2,则
8. 如图8.24所示,正方形 ABCD 的边长为5,点 A 的坐标为(4,0),点 B 在y轴上,若反比例函数 的图像过点 C,则k 的值为 .
9.如图8.25所示,反比例函数 的图像与反比例函数 的图像关于x轴对称.若有一等腰 顶点 O 为坐标原点,点A 在. 图像上,点B 在. 图像上,其中点 A 的横坐标为4,则点 B 的横坐标为 .
10. 如图8.26所示,正方形 的顶点 在反比例函数 的图像上,顶点 分别在x轴和y轴的正半轴上,再在其右侧作正方形 顶点 在 x轴的正半轴上,则点. 的坐标为 .
类型2:利用 构造三垂直模型
11. 如图8.27所示,已知点 A(2,3)和点 B(0,2),点 A 在反比例函数 的图像上,作射线 AB,再将射线 AB 绕点A 按逆时针方向旋转 交反比例函数图像于点 C,则点 C的坐标为 .
12.在平面直角坐标系内,一次函数. 的图像分别交x,y轴于点A,B,将直线AB 绕点B 旋转 交x轴于点C,则直线 BC的函数表达式是 .
13. 如图8.28所示,在 中, 点 D 在 AC 上,点 E在BC 上, ,分别连接 BD,AE交于点F.若 则
类型3:利用 构造一线三等角
14. 如图8.29 所示, 是等边三角形,点A 与点D 的坐标分别是A(4,0),D(10,0).点 C 从点O 沿y轴向下移动,过点 B作 轴,垂足为点 Q.当点 C 的坐标为 时,
类型4:等腰直角三角形存在性问题
15. 如图8.30所示,在矩形 ABCO 中,点 B 的坐标为(8,6),点 A,C分别在坐标轴上,点 P 是线段 BC上的动点.已知点 D 在第一象限,且是直线 上的一点,若 是不以A 为直角顶点的等腰直角三角形,请直接写出所有符合条件的点 D 的坐标: .
模型的构造:相似形
类型1:利用直角,直接构造三垂直模型
16. 如图8.31所示,在Rt△AOB 中,O 为坐标原点, 如果点 A 在反比例函数 的图像上运动,那么点 B 在函数 (填函数解析式)的图像上运动.
17.如图8.32所示,已知 A 是双曲线 在第一象限上的一个动点,连接 AO 并延长交另一分支于点B,以AB 为边作等边 点C 在第四象限.已知点 C 的位置始终在一函数图像上运动,则这个函数解析式为 .
中小学教育资源及组卷应用平台
18.如图8.33 所示,半圆O 的直径 点 D 在 上, 点 P 是半径OC 上的一个动点,连接 DP,过点 P 作 ,交直径 AB 于点E.当点 P 与点C 重合时,(
19. 如图8.34所示,在等腰△ABC 中, 点 D 为边 AC 上的一个动点(不与点 C 重合),作 DE⊥BD 于点D,使得 连接CE,则 的面积的最大值为 .
类型2:建直角,构造三垂直模型
20. 如图8.35所示,函数 的图像上有一点 A(4,3),将射线 OA 绕着原点O 逆时针旋转角α,交图像于点 B,且 则点 B 的坐标为 .
21. 如图8.36所示, 是等边三角形,顶点 C 在y轴的负半轴上,点 点 B 在第一象限,经过点 A 的反比例函数 的图像恰好经过顶点 B,则. 的边长为 .
类型3:隐形的一线三等角模型
22. 如图8.37所示, 为等边三角形, =60°,BM=FN=5,则 CF= .
模型的综合应用:遇见中考
23.在△ABC 中,∠ABC=90°.
(1)如图8.38所示,分别过A,C两点作经过点B 的直线的垂线,垂足分别为点 M,N,求证:△ABM∽△BCN.
(2) 如图8.39 所示,P 是边 BC 上一点, 求 tan C的值.
(3)如图8.40所示,D 是边CA 延长线上一点,AE=AB,∠DEB=90°,sin∠BAC= 则tan∠CEB= .
第8讲 一线三等角模型
1. 易证△ABD≌△DCE,则AB=DC=AC,利用等腰三角形的性质即可证得.
2. 3.
提示:易证△CBE∽△DEF,则 即 解得 DF=3.
3. 10,
提示:因为△AED∽△BDF,所以CE:CF=(AE+DE+AD):(DF+BF+BD).
提示:易证△DFE∽△ABF,设 DE=2a,则 利用折叠的性质可得出 EC=EF,进而可得出 AB=DC=5a,利用相似三角形的性质可得出 又 代入数值即可得证.
5. 易证△CEF∽△BDE,则 因为 E 为BC 的中点,所以 又∠DEF=∠C,则△DEF∽△ECF,故∠DFE=∠CFE,即 EF 平分∠DFC.
如图J8.1所示,作BF⊥l ,AE⊥l .易证△ACE≌△CBF,进而 所以 即 故
如图J8.2所示,过点 B 作BM⊥y轴于点M,过点 A 作AN⊥x轴于点N,并延长 MB,NA 交于一点W.
易证△AON≌△BAW.
设点 A(2,m),则点 B(2-m,2+m),)所以( 解得
故
8. - 3.
过点 C作CE⊥y轴于点E,易证△ABO≌△BCE,所以OA=BE=4,CE=OB=3,则OE=BE-OB=4-3=1,故点 C 的坐标为(-3,1).
因为反比例函数 的图像过点 C,所以k= xy=-3×1=-3.
如图J8.3所示,过点 B 作x轴的平行线EB,过点 A 作AF⊥EB 的延长线于点F,AF 交x轴于点D.
易证△OEB≌△BFA,则 EO= BF,BE=AF.
设BE= x,则 OE = BF =4--x,AD =x--(4--x)=2x-4,故 A(4,2x-4),B(x,x-4).
因为两函数图像关于 x 轴对称,所以 即4(2x-4)+x(x-4)=0,解得 (不合题意舍去), 则点 B 的横坐标为
如图J8.4所示,作 轴于点C, 轴于点D, 轴于点E, 于点F.
易证
设 则 所以点 的坐标为 把 代入 得 解得 (舍去), 故
设点 P 的坐标为 易证 则 因此 即 解得 舍去),( 故点P 的坐标为
11. (-1,-6).
如图J8.5所示,过点 B 作BF⊥AC 于点F,过点 F 作 轴于点D,过点A 作 DF 的延长线于点E,则△ABF 为等腰直角三角形,易得
设 BD=a,则EF=a.
因为点 A(2,3)和点 B(0,2),所以.
又AE+OD=3,即2-a+2-a=3,解得 故
设直线 AF 的解析式为 则 解得 所以 y=3x-3.解方程组 可得 或 故 C(-1,-6).
或y=-3x-1.
解法1 利用三垂直模型.
分两种情况:
①点C在x轴正半轴上时,如图J8.6所示,过点 D 作DE⊥AC 于点E,由三垂直模型易证△AOB≌△DEA,得出 又B(0,-1),则
②点C在x轴负半轴上时,如图J8.7所示,过点 A 作AP⊥AB 于点P,作PI⊥AI 于点I,由三垂直模型易证△AOB≌△PIA,得出 又 B(0,-1),则yBC = - 3x-1.
解法2 利用12345模型.
①点 C在x轴正半轴上时,如图J8.6所示,易得∠ABO+∠OCB=45°.又tan∠ABO 则 于是OC=3,故
②点C在x轴负半轴上时,如图J8.7所示,易得∠ABO+∠OBC=45°.又 tan∠ABO 则 于是 故yBc=-3x-1.
13.
如图J8.8所示,过点 D 作AE 的平行线DI,过点 B 作DI 的垂线,交于点 I,再利用三垂直模型设边求解.
设CG= BH = GI=x,则 IH= DG=x+2=8-x,解得x=3,所以 tan∠EAC = 故 得
解法1 构造一线三等角(图J8.9).
构造△AEC≌△BFA,其中∠AEC=∠AFB=60°,求得 故
解法2 构造一线三垂直(图J8.10).
有△AFE∽△EGB,其中 由“三线合一”可得 E 为AC 的中点,所以 EF 为△AOC 的中位线,则 ,故 tan∠ODB
15.(4,2)或 或
如图J8.11 所示,当 时,AD=PD,则点 D 的坐标为(4,2).
如图J8.12 所示,当∠ADP=90°时,AD=PD,同理可求得点 D 的坐标为
如图J8.13所示,当∠APD=90°时,AP=PD,设点 P 的坐标为(8,m),则点 D 的坐标为(14-m,8+m).由8+m=2(14-m)-6,得 所以点 D 的坐标为
如图J8.14所示,分别过点 A,B 作 轴于点C, 轴于点D.设A(a,b).易证△OAC∽△BOD,则 故点 B 在函数 的图像上运动.
连接OC, 解法同题16.
作 DF⊥OC 于点F.由三垂直模型易证 则 即 故
如图J8.15所示,构造三垂直模型,易证△DEG∽△BDF,则
因为 所以CF=16.
设CD=a,则 FD=16-a,于是 故
则
如图J8.16所示,构造出三垂直模型,易证△OAC∽△AED,则 所以 故yOB=2x.由可得
解法1 如图J8.17 所示,延长 AB 到点D,使得 AB=BD,连接CD,作 AH⊥y轴于点H,DE⊥y轴于点E.设C(0,c).
因为 BA= BC=BD,所以△ACD 是直角三角形,因此 ,易证△ACH∽△CDE,则
因为 所以 则EC= 故
又 BA=BD,利用中点坐标公式得 代入 得 整理得 解得 或 (舍去),则 故
解法2 如图J8.18所示,构造三垂直模型,易证△ADE∽△EFC,则
设 根据中点坐标公式得 所以
因为CF=xE,所以 解得 或m=5.
当 时,点C在y轴的正半轴上,不符合题意,舍去,则m=5,因此 AB
解法3 如图J8.19所示,也可以构造一线三等角模型,请同学们自己试一试吧.
22. 1.
如图J8.20所示,过点 P 作GH∥BC,分别交 AB,AC 于点G,H.
第1步:因为∠MGP=∠MPN=∠NHP=60°,易证 所以 又∠BGP=∠BPF=∠PHF =120°,易证△BGP∽△PHF,如图J8.21 所示,则 故GM·NH = GB·HF. ①
第2步:易证△DGP∽△DBE,则 解得
MG = 2. ②
第3步:由式①、式②得2·NH=3·(5-NH),解得 NH=3,故HF=2,FC=HC-HF=3-2=1.
利用等边三角形的形式,构造二次“三等角”型相似,利用边比求解即可.
23.(1) 因为 AM⊥MN,所以∠MAB+∠MBA =90°.又∠ABC =90°,则∠CBN+∠MBA=90°,因此∠MAB=∠NBC.因为∠M=∠N=90°,所以△ABM∽△BCN.
如图J8.22所示,过点 P 作PD⊥AC 于点D,作 PM⊥AP交AC 于点M.
因为 PM⊥PA,PD⊥AM,所以易证△PDM∽△APM.
又 设DM=2a,则 由勾股定理得 =3a.
因为∠B=∠APM=90°,易得∠1=∠2=∠3,所以CD=DM+CM=DM+PM=5a,故
如图J8.23所示,过点 A 作AG⊥BE 于点G,过点 C 作CH⊥BE 交EB 的延长线于点H.
因为∠DEB=90°,所以 CH∥AG∥DE,故
由(1)可知,△ABG∽△BCH,则
设 BG=4m,则CH=3m,EG=4m,于是 即 GH=10m,故tan∠CEB
同课章节目录
