苏教版数学六年级上册第一单元长方体和正方体的表面积同步练习
文档属性
| 名称 | 苏教版数学六年级上册第一单元长方体和正方体的表面积同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 73.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-13 00:00:00 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
苏教版数学六年级上册第一单元长方体和正方体的表面积同步练习
一、填空题
1. 正方体是由 个完全相同的 围成的立体图形,正方体有 条棱,它们的长度都 ,正方体有 个顶点。
答案:6|正方形|12|相等|8
解析:解答:正方体是由 6 个完全相同的 正方形 围成的立体图形,正方体有 12 条棱,它们的长度都 相等 ,正方体有 8 个顶点。
分析: 根据正方体的特征可知:正方体有6个面,每个面都是相同的正方形;正方体有12条棱,长度相等;正方体有8个顶点;即可解答。
2.长方体或者正方体 叫做它的表面积。
答案:6个面的总面积
解析:解答:长方体或者正方体 6个面的总面积 叫做它的表面积。
分析: 根据表面积的词义,即物体表面的面积,所以长方体或者正方体 6个面的总面积 叫做它的表面积。
3. 一个长方体的长、宽、高都扩大2倍,它的表面积就 。
答案:扩大4倍
解析:解答:设原来的长、宽、高分别为a、b、c,
则原来的表面积:(ab+ac+cb)×2
现在的表面积:(4ab+4ac+4bc)×2=(ab+ac+bc) ×8
现在的表面积是原来的:[(ab+ac+bc) ×8]÷[(ab+ac+cb) ×2]=4(倍)
分析: 设出原来的长、宽、高,利用长方体的表面积公式表示出其表面积,再用现在的长、宽、高,得出现在的表面积,用现在的表面积除以原来的表面积,就是表面积扩大的倍数。
4. 一个长方体最多可以有 个面是正方形,最多可以有 条棱长度相等。
答案:2|8
解析:解答:如图:一个长方体最多可以有 2 个面是正方形,最多可以有 8 条棱长度相等。
分析: 有2个面是正方形的长方体,也是比较特殊的,最多可以有8条棱长度相等。
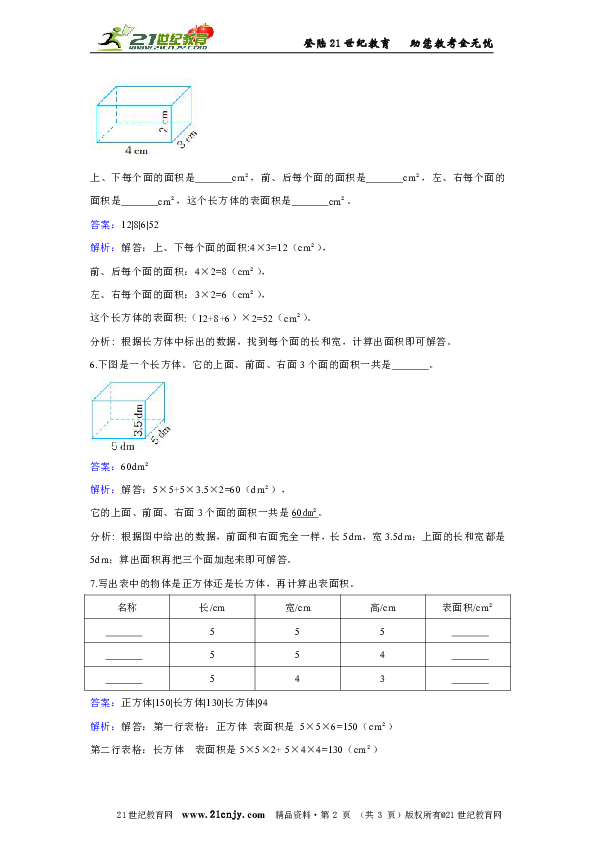
5. 一个长方体如右图。
上、下每个面的面积是 cm ,前、后每个面的面积是 cm ,左、右每个面的面积是 cm ,这个长方体的表面积是 cm 。
答案:12|8|6|52
解析:解答:上、下每个面的面积:4×3=12(cm ),
前、后每个面的面积:4×2=8(cm ),
左、右每个面的面积:3×2=6(cm ),
这个长方体的表面积:(12+8+6)×2=52(cm )。
分析: 根据长方体中标出的数据,找到每个面的长和宽,计算出面积即可解答。
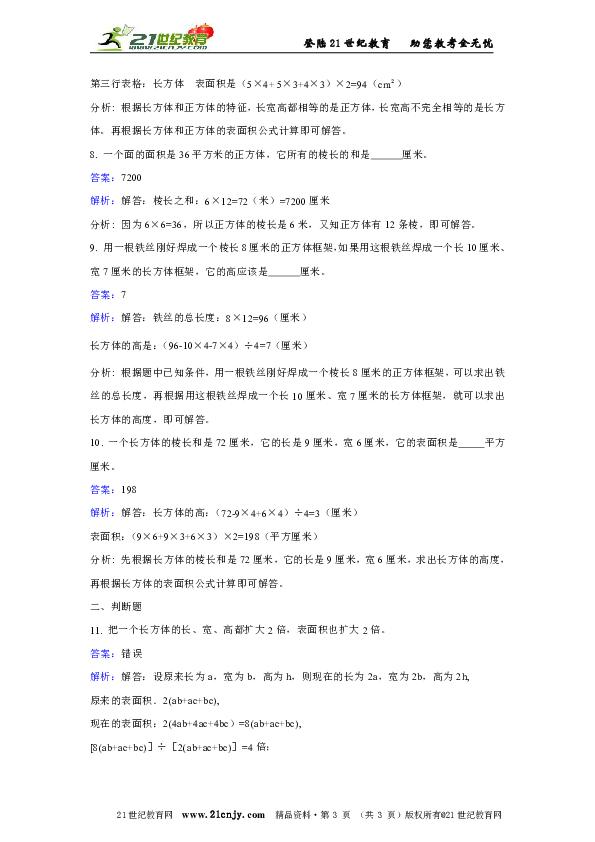
6.下图是一个长方体。它的上面、前面、右面3个面的面积一共是 。
答案:60dm
解析:解答:5×5+5×3.5×2=60(dm ),
它的上面、前面、右面3个面的面积一共是60dm 。
分析: 根据图中给出的数据,前面和右面完全一样,长5dm,宽3.5dm;上面的长和宽都是5dm;算出面积再把三个面加起来即可解答。
7.写出表中的物体是正方体还是长方体,再计算出表面积。
名称 长/cm 宽/cm 高/cm 表面积/cm
5 5 5
5 5 4
5 4 3
答案:正方体|150|长方体|130|长方体|94
解析:解答:第一行表格:正方体 表面积是 5×5×6=150(cm )
第二行表格:长方体 表面积是5×5×2+ 5×4×4=130(cm )
第三行表格:长方体 表面积是(5×4+ 5×3+4×3)×2=94(cm )
分析: 根据长方体和正方体的特征,长宽高都相等的是正方体,长宽高不完全相等的是长方体。再根据长方体和正方体的表面积公式计算即可解答。
8. 一个面的面积是36平方米的正方体,它所有的棱长的和是 厘米。
答案:7200
解析:解答:棱长之和:6×12=72(米)=7200厘米
分析: 因为6×6=36,所以正方体的棱长是6米,又知正方体有12条棱,即可解答。
9. 用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是 厘米。
答案:7
解析:解答:铁丝的总长度:8×12=96(厘米)
长方体的高是:(96-10×4-7×4)÷4=7(厘米)
分析: 根据题中已知条件,用一根铁丝刚好焊成一个棱长8厘米的正方体框架,可以求出铁丝的总长度,再根据用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,就可以求出长方体的高度,即可解答。
10. 一个长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,它的表面积是 平方厘米。
答案:198
解析:解答:长方体的高:(72-9×4+6×4)÷4=3(厘米)
表面积:(9×6+9×3+6×3)×2=198(平方厘米)
分析: 先根据长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,求出长方体的高度,再根据长方体的表面积公式计算即可解答。
二、判断题
11. 把一个长方体的长、宽、高都扩大2倍,表面积也扩大2倍。
答案:错误
解析:解答:设原来长为a,宽为b,高为h,则现在的长为2a,宽为2b,高为2h,
原来的表面积.2(ab+ac+bc),
现在的表面积:2(4ab+4ac+4bc)=8(ab+ac+bc),
[8(ab+ac+bc)]÷[2(ab+ac+bc)]=4倍;
答:表面积扩大4倍。
所以原题说法错误。
分析: 解答此题可设原来长、宽、高分别为a、b、h,那么现在就分别为2a、2b、2h,分别表示出原来的表面积与现在的表面积,即可得出答案。
12.因为正方体的长、宽、高都相等,所以正方体是特殊的长方体。
答案:正确
解析:解答:因为正方体的长、宽、高都相等,所以正方体是特殊的长方体,说法正确。
分析: 因为正方体的长、宽、高都相等,所以正方体是特殊的长方体,即可判断。
13. 求长方体的表面积必须知道长方体的长和宽。
答案:错误
解析:解答:求长方体的表面积必须知道长方体的长、宽、高,原题说法错误。
分析: 求长方体的表面积,即6个面的总面积,必须知道长方体的长、宽、高才能计算。
14. 正方体的棱长扩大3倍,它的表面积就扩大9倍。
答案:正确
解析:解答:设正方体的棱长为a,原来的表面积是6a ,棱长扩大3倍后,表面积变为6(3a) =6×9 a ,所以正方体的棱长扩大3倍,它的表面积就扩大9倍,说法正确。
分析: 先表示出原来的正方体的表面积,再表示出棱长扩大3倍后的正方体的表面积,即可比较出结果。
15. 一个长方体有四个面的面积相等,则其余两个面是长方形。
答案:错误
解析:解答:一个长方体有四个面的面积相等,则其余两个面是正方形,原题说法错误。
分析: 一个长方体有四个面的面积相等,说明这个长方体有8条棱长度相等,则其余两个面是正方形,即可判断。
三、选择题
16. 一个长方体的长、宽、高都扩大到原来的5倍,表面积就扩大到原来的( )倍。
A.25 B.15 C.5
答案:A
解析:解答:一个长方体的长、宽、高分别扩大到原来的5倍,表面积就扩大5×5=25倍,
答:表面积就扩大到原来的25倍。故选A。
分析: 根据长方体的表面积公式:s=〔ab+ah+bh)×2,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此解答。
17. 一个棱长是1分米的正方体木块,横截成三个体积相等的小长方体后,表面积增加( )。
A.2平方分米 B.4平方分米 C.6平方分米
答案:B
解析:解答:一个棱长是1分米的正方体木块,横截成三个体积相等的小长方体后,多出了4个小正方形面,表面积增加了4平方分米,故选B。
分析: 一个棱长是1分米的正方体木块,横截成三个体积相等的小长方体后,多出了4个小正方形面,所以表面积增加了4平方分米,即可解答。
18. 一个正方体的棱长是0.5分米,它的表面积是( )平方分米。
A.1平方分米 B.1.5平方分米 C.2平方分米
答案:B
解析:解答:0.5×0.5×6=1.5(平方分米)答:它的表面积是1.5平方分米。故选B。
分析: 根据正方体的表面积公式,先求出一个面的面积,再×6即可解答。
19. 一个长4分米、宽2分米、高2分米的长方体,它占地面积最大是( )。
A.4平方分米 B.8平方分米 C.16平方分米
答案:B
解析:解答:4×2=8(平方分米),答:它的占地面积最大是8平方分米。故选B。
分析: 求占地面积最大是多少,必须用最长的两条棱长相乘,即可解答。
20. 做20个棱长为30厘米的小正方体纸箱,至少需要( )平方米硬纸。
A.9平方米 B.54平方米 C.10.8平方米
答案:C
解析:解答:30×30×6×20=108000(平方厘米)=10.8平方米
答:至少需要10.8平方米。
故选C。
分析: 先求出一个小正方体的表面积,再求出20个的总面积即可解答。
四、应用题
21. 一只无盖的长方形鱼缸,长0.4米,宽0.25米,深0.3米,做这只鱼缸至少要用玻璃多少平方米?
答案:0.4×0.25+(0.4×0.3+0.25×0.3)×2
=0.1+0.39
=0.49(平方米)
答:做这只鱼缸至少要用玻璃0.49平方米。
解析:解答:0.4×0.25+(0.4×0.3+0.25×0.3)×2
=0.1+0.39
=0.49(平方米)
答:做这只鱼缸至少要用玻璃0.49平方米。
分析: 无盖的长方体鱼缸,即1个底面,2个侧面,2个前后面,加起来就是鱼缸的表面积,即可解答。
22. 用36厘米的铁丝折一个正方体框架,这个正方体棱长是多少?如果用纸糊满框架的表面,至少需要纸多少平方厘米?
答案:棱长:36÷12=3(厘米)
表面积:3×3×6=54(平方厘米)
答:至少需要纸54平方厘米。
解析:解答:棱长:36÷12=3(厘米)
表面积:3×3×6=54(平方厘米)
答:至少需要纸54平方厘米。
分析:①正方体有12条棱,所以求棱长用36除以12即可;②求表面积,先求出一个面的面积,再乘以6即可。
23. 张大爷制作了一种卖苹果用的长方体木箱(无盖),它的长是60厘米,宽40厘米,高30厘米。做这种箱子至少用木板多少平方米?
答案:60×40+(60×30+40×30)×2=8400(平方厘米)=0.84(平方米)
答:做这种箱子至少用木板0.84平方米。
解析:解答:60×40+(60×30+40×30)×2=8400(平方厘米)=0.84(平方米)
答:做这种箱子至少用木板0.84平方米。
分析: 无盖的长方体木箱,即1个底面,2个侧面,2个前后面,加起来就是木箱的表面积,即可解答。
24. 水泥厂要制作10根长方体铁皮通风管,管口是边长30厘米的正方形,管子长2米。共需多少平方米铁皮?
答案:30厘米=0.3米
0.3×2×4=2.4(平方米)
2.4×10=24(平方米)
答:共需24平方米铁皮。
解析:解答:30厘米=0.3米
0.3×2×4=2.4(平方米)
2.4×10=24(平方米)
答:共需24平方米铁皮。
分析: 由题干可知,长方体铁皮通风管只有4个面,一根通风管所用的铁皮求出4个面的面积即可,再乘10,即可解答。
25. 一间教室长8米、宽6米,高3米,现在要用涂料粉刷它的四壁和顶棚。如果扣除门、窗和黑板24平方米,求要粉刷的面积有多大?如果每平方米用涂料0.15千克,一共需要多少千克涂料?
答案:①粉刷面积:8×6+(8×3+6×3)×2-24=108(平方米)②108×0.15=16.2(千克)
答:要粉刷的面积有108平方米,一共需要16.2千克涂料。
解析:解答:①粉刷面积:8×6+(8×3+6×3)×2-24=108(平方米)
②108×0.15=16.2(千克)
答:要粉刷的面积有108平方米,一共需要16.2千克涂料。
分析: ①粉刷教室除去地面,只需要粉刷房顶和四壁的面积,再除去门、窗和黑板的面积就是粉刷的面积。②如果每平方米用涂料0.15千克,一共需要多少千克涂料?用求出的面积乘0.15即可解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 7 页)版权所有@21世纪教育网
苏教版数学六年级上册第一单元长方体和正方体的表面积同步练习
一、填空题
1. 正方体是由 个完全相同的 围成的立体图形,正方体有 条棱,它们的长度都 ,正方体有 个顶点。
答案:6|正方形|12|相等|8
解析:解答:正方体是由 6 个完全相同的 正方形 围成的立体图形,正方体有 12 条棱,它们的长度都 相等 ,正方体有 8 个顶点。
分析: 根据正方体的特征可知:正方体有6个面,每个面都是相同的正方形;正方体有12条棱,长度相等;正方体有8个顶点;即可解答。
2.长方体或者正方体 叫做它的表面积。
答案:6个面的总面积
解析:解答:长方体或者正方体 6个面的总面积 叫做它的表面积。
分析: 根据表面积的词义,即物体表面的面积,所以长方体或者正方体 6个面的总面积 叫做它的表面积。
3. 一个长方体的长、宽、高都扩大2倍,它的表面积就 。
答案:扩大4倍
解析:解答:设原来的长、宽、高分别为a、b、c,
则原来的表面积:(ab+ac+cb)×2
现在的表面积:(4ab+4ac+4bc)×2=(ab+ac+bc) ×8
现在的表面积是原来的:[(ab+ac+bc) ×8]÷[(ab+ac+cb) ×2]=4(倍)
分析: 设出原来的长、宽、高,利用长方体的表面积公式表示出其表面积,再用现在的长、宽、高,得出现在的表面积,用现在的表面积除以原来的表面积,就是表面积扩大的倍数。
4. 一个长方体最多可以有 个面是正方形,最多可以有 条棱长度相等。
答案:2|8
解析:解答:如图:一个长方体最多可以有 2 个面是正方形,最多可以有 8 条棱长度相等。
分析: 有2个面是正方形的长方体,也是比较特殊的,最多可以有8条棱长度相等。
5. 一个长方体如右图。
上、下每个面的面积是 cm ,前、后每个面的面积是 cm ,左、右每个面的面积是 cm ,这个长方体的表面积是 cm 。
答案:12|8|6|52
解析:解答:上、下每个面的面积:4×3=12(cm ),
前、后每个面的面积:4×2=8(cm ),
左、右每个面的面积:3×2=6(cm ),
这个长方体的表面积:(12+8+6)×2=52(cm )。
分析: 根据长方体中标出的数据,找到每个面的长和宽,计算出面积即可解答。
6.下图是一个长方体。它的上面、前面、右面3个面的面积一共是 。
答案:60dm
解析:解答:5×5+5×3.5×2=60(dm ),
它的上面、前面、右面3个面的面积一共是60dm 。
分析: 根据图中给出的数据,前面和右面完全一样,长5dm,宽3.5dm;上面的长和宽都是5dm;算出面积再把三个面加起来即可解答。
7.写出表中的物体是正方体还是长方体,再计算出表面积。
名称 长/cm 宽/cm 高/cm 表面积/cm
5 5 5
5 5 4
5 4 3
答案:正方体|150|长方体|130|长方体|94
解析:解答:第一行表格:正方体 表面积是 5×5×6=150(cm )
第二行表格:长方体 表面积是5×5×2+ 5×4×4=130(cm )
第三行表格:长方体 表面积是(5×4+ 5×3+4×3)×2=94(cm )
分析: 根据长方体和正方体的特征,长宽高都相等的是正方体,长宽高不完全相等的是长方体。再根据长方体和正方体的表面积公式计算即可解答。
8. 一个面的面积是36平方米的正方体,它所有的棱长的和是 厘米。
答案:7200
解析:解答:棱长之和:6×12=72(米)=7200厘米
分析: 因为6×6=36,所以正方体的棱长是6米,又知正方体有12条棱,即可解答。
9. 用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是 厘米。
答案:7
解析:解答:铁丝的总长度:8×12=96(厘米)
长方体的高是:(96-10×4-7×4)÷4=7(厘米)
分析: 根据题中已知条件,用一根铁丝刚好焊成一个棱长8厘米的正方体框架,可以求出铁丝的总长度,再根据用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,就可以求出长方体的高度,即可解答。
10. 一个长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,它的表面积是 平方厘米。
答案:198
解析:解答:长方体的高:(72-9×4+6×4)÷4=3(厘米)
表面积:(9×6+9×3+6×3)×2=198(平方厘米)
分析: 先根据长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,求出长方体的高度,再根据长方体的表面积公式计算即可解答。
二、判断题
11. 把一个长方体的长、宽、高都扩大2倍,表面积也扩大2倍。
答案:错误
解析:解答:设原来长为a,宽为b,高为h,则现在的长为2a,宽为2b,高为2h,
原来的表面积.2(ab+ac+bc),
现在的表面积:2(4ab+4ac+4bc)=8(ab+ac+bc),
[8(ab+ac+bc)]÷[2(ab+ac+bc)]=4倍;
答:表面积扩大4倍。
所以原题说法错误。
分析: 解答此题可设原来长、宽、高分别为a、b、h,那么现在就分别为2a、2b、2h,分别表示出原来的表面积与现在的表面积,即可得出答案。
12.因为正方体的长、宽、高都相等,所以正方体是特殊的长方体。
答案:正确
解析:解答:因为正方体的长、宽、高都相等,所以正方体是特殊的长方体,说法正确。
分析: 因为正方体的长、宽、高都相等,所以正方体是特殊的长方体,即可判断。
13. 求长方体的表面积必须知道长方体的长和宽。
答案:错误
解析:解答:求长方体的表面积必须知道长方体的长、宽、高,原题说法错误。
分析: 求长方体的表面积,即6个面的总面积,必须知道长方体的长、宽、高才能计算。
14. 正方体的棱长扩大3倍,它的表面积就扩大9倍。
答案:正确
解析:解答:设正方体的棱长为a,原来的表面积是6a ,棱长扩大3倍后,表面积变为6(3a) =6×9 a ,所以正方体的棱长扩大3倍,它的表面积就扩大9倍,说法正确。
分析: 先表示出原来的正方体的表面积,再表示出棱长扩大3倍后的正方体的表面积,即可比较出结果。
15. 一个长方体有四个面的面积相等,则其余两个面是长方形。
答案:错误
解析:解答:一个长方体有四个面的面积相等,则其余两个面是正方形,原题说法错误。
分析: 一个长方体有四个面的面积相等,说明这个长方体有8条棱长度相等,则其余两个面是正方形,即可判断。
三、选择题
16. 一个长方体的长、宽、高都扩大到原来的5倍,表面积就扩大到原来的( )倍。
A.25 B.15 C.5
答案:A
解析:解答:一个长方体的长、宽、高分别扩大到原来的5倍,表面积就扩大5×5=25倍,
答:表面积就扩大到原来的25倍。故选A。
分析: 根据长方体的表面积公式:s=〔ab+ah+bh)×2,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此解答。
17. 一个棱长是1分米的正方体木块,横截成三个体积相等的小长方体后,表面积增加( )。
A.2平方分米 B.4平方分米 C.6平方分米
答案:B
解析:解答:一个棱长是1分米的正方体木块,横截成三个体积相等的小长方体后,多出了4个小正方形面,表面积增加了4平方分米,故选B。
分析: 一个棱长是1分米的正方体木块,横截成三个体积相等的小长方体后,多出了4个小正方形面,所以表面积增加了4平方分米,即可解答。
18. 一个正方体的棱长是0.5分米,它的表面积是( )平方分米。
A.1平方分米 B.1.5平方分米 C.2平方分米
答案:B
解析:解答:0.5×0.5×6=1.5(平方分米)答:它的表面积是1.5平方分米。故选B。
分析: 根据正方体的表面积公式,先求出一个面的面积,再×6即可解答。
19. 一个长4分米、宽2分米、高2分米的长方体,它占地面积最大是( )。
A.4平方分米 B.8平方分米 C.16平方分米
答案:B
解析:解答:4×2=8(平方分米),答:它的占地面积最大是8平方分米。故选B。
分析: 求占地面积最大是多少,必须用最长的两条棱长相乘,即可解答。
20. 做20个棱长为30厘米的小正方体纸箱,至少需要( )平方米硬纸。
A.9平方米 B.54平方米 C.10.8平方米
答案:C
解析:解答:30×30×6×20=108000(平方厘米)=10.8平方米
答:至少需要10.8平方米。
故选C。
分析: 先求出一个小正方体的表面积,再求出20个的总面积即可解答。
四、应用题
21. 一只无盖的长方形鱼缸,长0.4米,宽0.25米,深0.3米,做这只鱼缸至少要用玻璃多少平方米?
答案:0.4×0.25+(0.4×0.3+0.25×0.3)×2
=0.1+0.39
=0.49(平方米)
答:做这只鱼缸至少要用玻璃0.49平方米。
解析:解答:0.4×0.25+(0.4×0.3+0.25×0.3)×2
=0.1+0.39
=0.49(平方米)
答:做这只鱼缸至少要用玻璃0.49平方米。
分析: 无盖的长方体鱼缸,即1个底面,2个侧面,2个前后面,加起来就是鱼缸的表面积,即可解答。
22. 用36厘米的铁丝折一个正方体框架,这个正方体棱长是多少?如果用纸糊满框架的表面,至少需要纸多少平方厘米?
答案:棱长:36÷12=3(厘米)
表面积:3×3×6=54(平方厘米)
答:至少需要纸54平方厘米。
解析:解答:棱长:36÷12=3(厘米)
表面积:3×3×6=54(平方厘米)
答:至少需要纸54平方厘米。
分析:①正方体有12条棱,所以求棱长用36除以12即可;②求表面积,先求出一个面的面积,再乘以6即可。
23. 张大爷制作了一种卖苹果用的长方体木箱(无盖),它的长是60厘米,宽40厘米,高30厘米。做这种箱子至少用木板多少平方米?
答案:60×40+(60×30+40×30)×2=8400(平方厘米)=0.84(平方米)
答:做这种箱子至少用木板0.84平方米。
解析:解答:60×40+(60×30+40×30)×2=8400(平方厘米)=0.84(平方米)
答:做这种箱子至少用木板0.84平方米。
分析: 无盖的长方体木箱,即1个底面,2个侧面,2个前后面,加起来就是木箱的表面积,即可解答。
24. 水泥厂要制作10根长方体铁皮通风管,管口是边长30厘米的正方形,管子长2米。共需多少平方米铁皮?
答案:30厘米=0.3米
0.3×2×4=2.4(平方米)
2.4×10=24(平方米)
答:共需24平方米铁皮。
解析:解答:30厘米=0.3米
0.3×2×4=2.4(平方米)
2.4×10=24(平方米)
答:共需24平方米铁皮。
分析: 由题干可知,长方体铁皮通风管只有4个面,一根通风管所用的铁皮求出4个面的面积即可,再乘10,即可解答。
25. 一间教室长8米、宽6米,高3米,现在要用涂料粉刷它的四壁和顶棚。如果扣除门、窗和黑板24平方米,求要粉刷的面积有多大?如果每平方米用涂料0.15千克,一共需要多少千克涂料?
答案:①粉刷面积:8×6+(8×3+6×3)×2-24=108(平方米)②108×0.15=16.2(千克)
答:要粉刷的面积有108平方米,一共需要16.2千克涂料。
解析:解答:①粉刷面积:8×6+(8×3+6×3)×2-24=108(平方米)
②108×0.15=16.2(千克)
答:要粉刷的面积有108平方米,一共需要16.2千克涂料。
分析: ①粉刷教室除去地面,只需要粉刷房顶和四壁的面积,再除去门、窗和黑板的面积就是粉刷的面积。②如果每平方米用涂料0.15千克,一共需要多少千克涂料?用求出的面积乘0.15即可解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 7 页)版权所有@21世纪教育网
