第10讲 单线段最值问题 (含答案)2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第10讲 单线段最值问题 (含答案)2025年中考数学几何模型方法巩固练习 |
|
|
| 格式 | docx | ||
| 文件大小 | 914.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览

文档简介
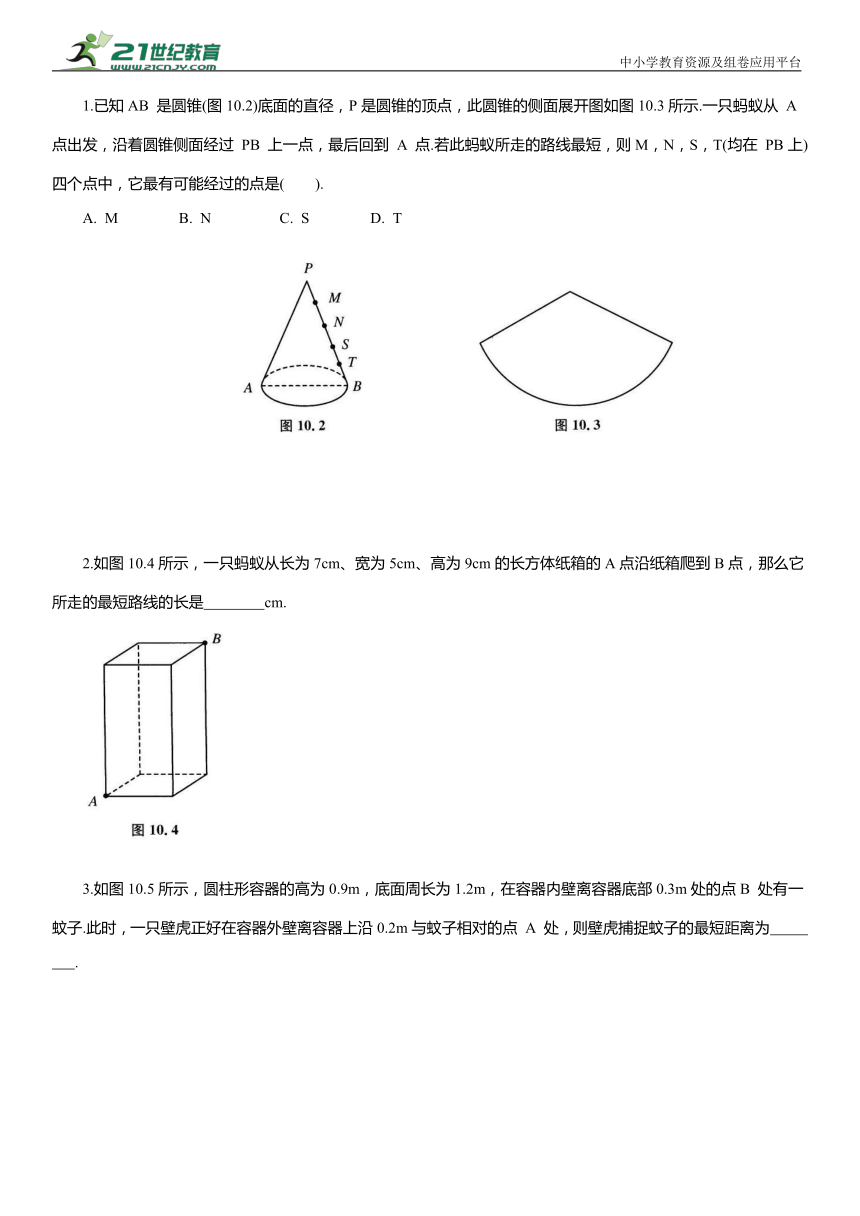
第10讲 单线段最值问题
表10.1
最值类型 图 示 原理(及结论)
点到点 A B 两点之间线段最短
点到线 垂线段最短
线到线 平行线间垂线段最短
点到圆 最小值:AP=OA-r 最大值:AQ=OA+r
线到圆 最小值:AC=OA-r 最大值:AB=OA+r
圆到圆 最小值:BC=OO'-r -r 最大值:AD=OO'+r +r
模块2 场 景 演 练
模型的识别:单线段最值
类型1:点到点
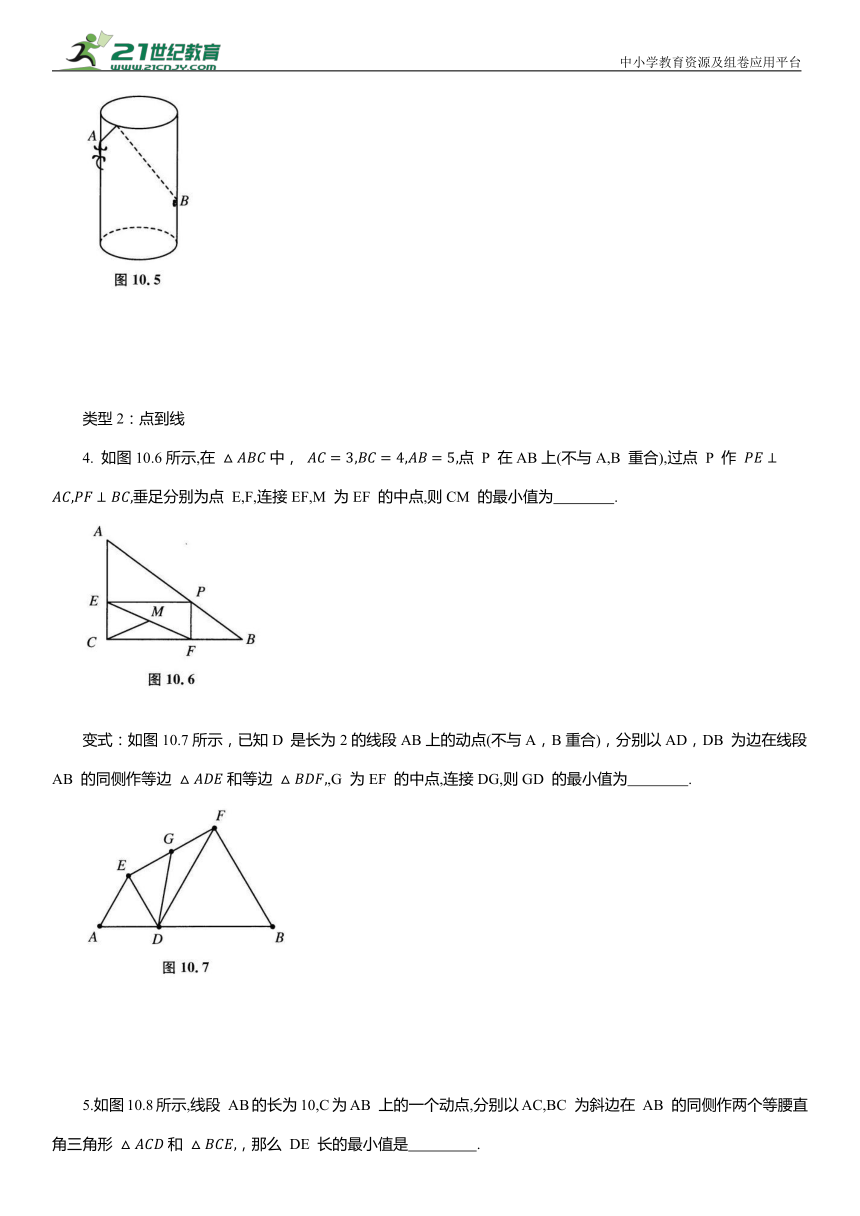
1.已知AB 是圆锥(图10.2)底面的直径,P是圆锥的顶点,此圆锥的侧面展开图如图10.3所示.一只蚂蚁从 A 点出发,沿着圆锥侧面经过 PB 上一点,最后回到 A 点.若此蚂蚁所走的路线最短,则M,N,S,T(均在 PB上)四个点中,它最有可能经过的点是( ).
A. M B. N C. S D. T
2.如图10.4所示,一只蚂蚁从长为7cm、宽为5cm、高为9cm的长方体纸箱的A点沿纸箱爬到B点,那么它所走的最短路线的长是 cm.
3.如图10.5所示,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B 处有一蚊子.此时,一只壁虎正好在容器外壁离容器上沿0.2m与蚊子相对的点 A 处,则壁虎捕捉蚊子的最短距离为 .
类型2:点到线
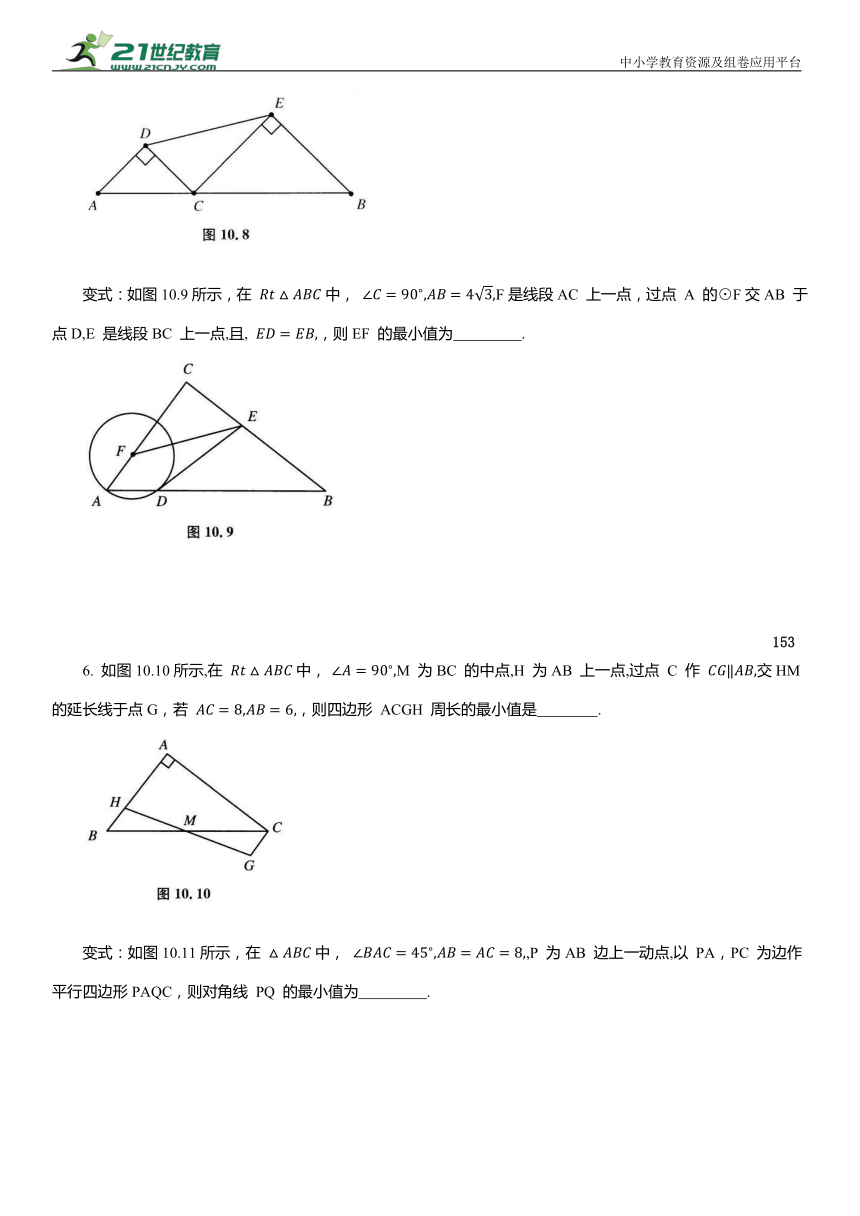
4. 如图10.6所示,在 中, 点 P 在AB上(不与A,B 重合),过点 P 作 垂足分别为点 E,F,连接EF,M 为EF 的中点,则CM 的最小值为 .
变式:如图10.7所示,已知D 是长为2的线段AB上的动点(不与A,B重合),分别以AD,DB 为边在线段AB 的同侧作等边 和等边 ,G 为EF 的中点,连接DG,则GD 的最小值为 .
5.如图10.8所示,线段 AB的长为10,C为AB 上的一个动点,分别以AC,BC 为斜边在 AB 的同侧作两个等腰直角三角形 和 ,那么 DE 长的最小值是 .
变式:如图10.9所示,在 中, F是线段AC 上一点,过点 A 的⊙F交AB 于点D,E 是线段BC 上一点,且, ,则EF 的最小值为 .
6. 如图10.10所示,在 中, M 为BC 的中点,H 为AB 上一点,过点 C 作 交HM 的延长线于点G,若 ,则四边形 ACGH 周长的最小值是 .
变式:如图10.11所示,在 中, ,P 为AB 边上一动点,以 PA,PC 为边作平行四边形PAQC,则对角线 PQ 的最小值为 .
模型的识别:拔高特训
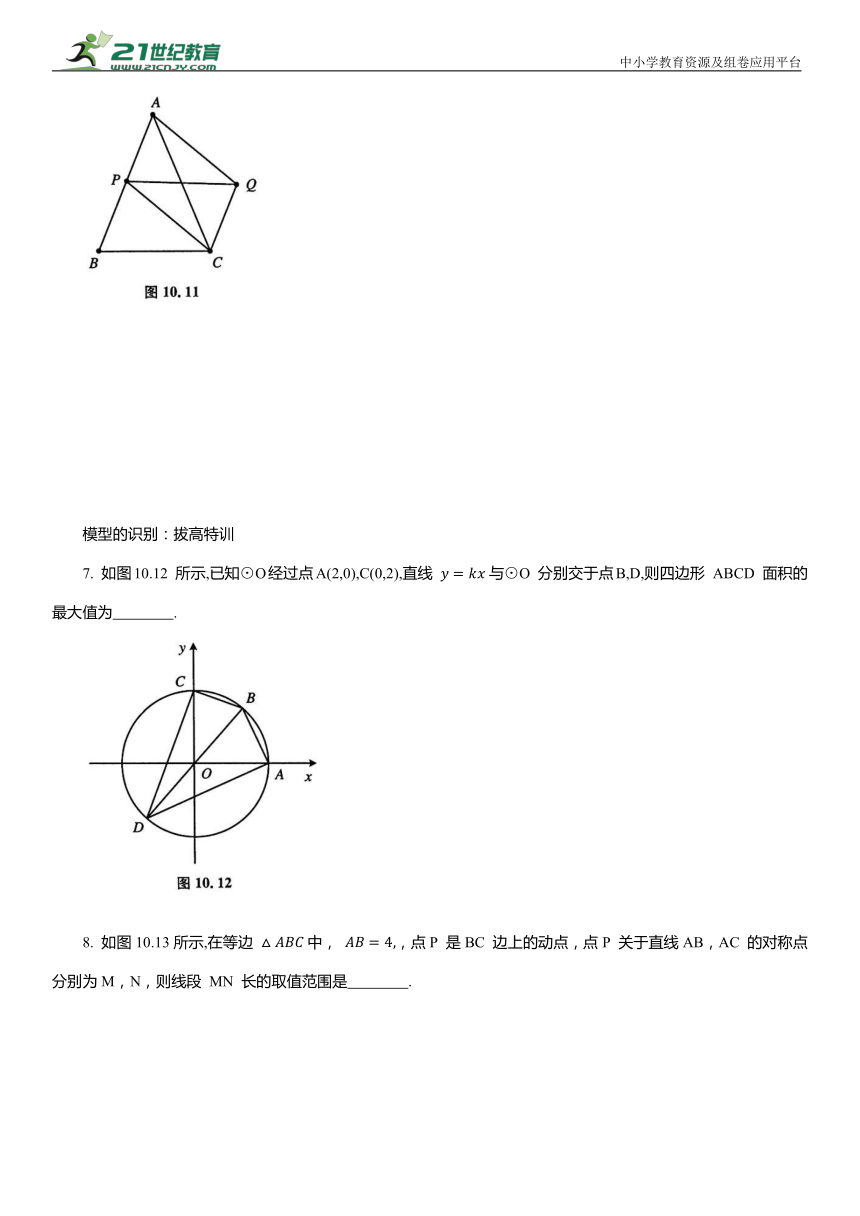
7. 如图10.12 所示,已知⊙O经过点A(2,0),C(0,2),直线 与⊙O 分别交于点B,D,则四边形 ABCD 面积的最大值为 .
8. 如图10.13所示,在等边 中, ,点P 是BC 边上的动点,点P 关于直线AB,AC 的对称点分别为M,N,则线段 MN 长的取值范围是 .
9. 如图10.14所示,在 中, D 是线段BC上的一个动点,以AD 为直径作⊙O 分别交AB,AC于点E,F,连接EF,则线段 EF 长度的最小值为 .
10. 如图10.15所示,在 中, D,E分别是AC,BC上的一点,且. .若以 DE 为直径的圆与斜边AB 相交于点M,N,则MN 的最大值为
11. 如图10.16所示,在 中, 点 D 是 BC 边上的动点,连接AD,过点 D 作 ,交 AB 于点E,则线段 AE 的最小值为 .
中小学教育资源及组卷应用平台
类型3:点、线到圆(圆已知)
类①:线到圆
12. 如图10.17所示,在 中, ,以边 AB 中点O 为圆心,作半圆与AC 相切,点P,Q分别是边BC 和半圆上的动点,连接PQ,则PQ长的最小值是 ;PQ 长的最大值是 .
13. 如图10.18所示,已知直线 与x轴、y轴分别交于A,B两点,P是以点C(0,1)为圆心、1为半径的圆上一动点,连接 PA,PB,则 面积的最大值是 .
类②:点到圆
14. 如图10.19所示,在 中, ,以BC 为直径的半圆交 AB 于点D,P 是 上的一个动点,连接 AP,则AP 的最小值是 .
15. 如图10.20所示,已知点 A(1,0),. 点 P 在以点D(4,4)为圆心、1为半径的圆上运动,且始终满足 则a 的最大值是 .
16. 如图10.21所示,一次函数 与反比例函数 的图像交于 A,B两点,点 P 在以点C(-2,0)为圆心、1为半径的⊙C上,Q是AP 的中点.已知OQ长的最大值为 ,则k 的值为 .
类型4:点、线到圆(辅助圆)
17. 如图10.22所示,正方形 ABCD 的边长为10,点 G 是边CD 的中点,点 E 是边AD上一动点,连接 BE,将. 沿BE翻折得到 连接 GF,则 GF 的最小值为
18. 如图10.23所示,四边形 ABCD 为矩形, 点P 是线段BC 上一动点,点 M 为线段AP 上一点, ,则BM 的最小值为 .
19. 如图10.24所示,在正方形 ABCD中, ,动点 E 从点 A 出发向点D 运动,同时动点 F 从点D 出发向点C运动,点E,F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段 AF,BE 相交于点P,则线段 DP 的最小值为 .
20. 如图10.25 所示,在矩形 ABCD 中, ,E 为边 BC 上一动点,F 为AE的中点,G为DE 上一点, ,则CG 的最小值为 .
21.如图10.26所示,线段 BC 的两个端点分别在x轴与直线 上(点 B,C 均与原点O 不重合)滑动,且 分别作 轴,CP⊥直线 经探究,在整个滑动过程中,P,O两点间的距离为定值 .
.如图10.27所示,A(-2,0),B(0,2),⊙O的半径为1,点 C 为⊙O上一动点,过点 B 作BP⊥直线 AC,垂足为点 P,则点 P 纵坐标的最大值为 .
1. B.
如图J10.1所示,根据圆锥侧面展开图,要使此蚂蚁所走的路线最短,四个点中,它最有可能经过的点是 N.
2. 15.
当展开前面和右面时,最短路线长是
) ;
当展开前面和上面时,最短路线长是
当展开左面和上面时,最短路线长是
,
因为 所以它所走的最短路线的长是15cm.
3. 1m.
如图J10.2所示,将容器侧面展开,作A 关于EF 的对称点A',连接. 则 即为最短距离,
4. 1.2.
如图J10.3所示,连接CP,因为四边形 EPFC 为矩形,所以
当CP⊥AB时,CP 最短,此时, 则 即CM 的最小值为1.2.
变式:
如图J10.4所示,分别延长 AE,BF 交于点C,连接CD,易得四边形 CEDF 为平行四边形,则CD,EF 互相平分.
因为点 G 是EF 的中点,所以点 G 是CD 的中点,则
当CD⊥AB时,CD 最短.
因为△ABC 为等边三角形,CD⊥AB,所以 故 GD的最小值为
5. 5.
解法1 如图J10.5所示,延长AD,BE 交于点F,易证四边形 DCEF 为矩形,DE 最小即CF 最小.
当CF⊥AB时,CF 最小,此时
解法2 设AM=MC=x,CN=NB=y,如图J10.6所示,作 DM⊥AC,EN⊥BC,DF⊥EN.在 Rt△DEF 中,DE≥DF,而 故 DE 的最小值为5.
变式:
如图J10.7所示,连接FD,作 FG⊥AB于点G,EH⊥AB 于点H,FM⊥EH 于点M,则四边形 FGHM 是矩形,△AFD,△DEB 为等腰三角形,所以 FG∥EH.
因为 EF>FM,所以 EF 的最小值为2
6. 22.
易证△BMH≌△CMG,则 BH=CG,所以四边形 ACGH 的周长 GH=AC+AB+GH=14+GH,当 GH 最小,即 MH⊥AB 时,四边形 ACGH 的周长最小,此时GH=AC=8,故四边形 ACGH 周长的最小值为14+8=22.
变式:
如图J10.8所示,因为 AB∥CQ,所以当 PQ⊥AB 时,PQ 最小,而. 在等腰Rt△AFC 中, 故 PQ 的最小值为
如图J10.9所示,连接AC,交 BD 于点K.易知当 BD⊥AC时,四边形 ABCD 的面积最大,此时
如图J10.10 所示,∠MAN =120°,易得. 为等腰三角形,此时
当 AP⊥BC时,MN 最小,当 AP=AB 时,MN 最大,故
如图J10.11 所示,连接 OE,OF,过点 O 作 垂足为点 H,此时∠EOF =2∠BAC=120°.又 OE=OF,则
当 AD⊥BC 时,AD 最小,此时 即 r=1,故
如图J10.12所示,取 DE 的中点O,过点O 作OG⊥AB 于点G,连接OC.
又 则只有点C,O,G共线时,点G 到圆心O的距离最小,此时 OG 达到最小,在△OMG 中,MG 最大,所以 MN 达到最大.
作CF⊥AB 于点 F,易得 所以 则 MG= 故
11.
如图J10.13所示,取AE 的中点F,连接 FD,过点 F 作FG⊥BC,垂足为点 G.
根据直角三角形斜边中线性质,易得 FD = AF = FE,设 FD = AF = FE = x,则 FB =4--x.
因为∠B=30°,所以 又 FG≤FD,即 解得 故 AE 的最小值为
12. 1;8.
如图J10.14所示,设⊙O与AC 相切于点E,连接 OE,作( 垂足为点 P 且交⊙O 于点 Q ,此时垂线段 OP 最短,
因为AB=10,AC=8,BC=6,所以 故
如图J10.14所示,当点 Q 在AB 边上,P 与 B 重合时,P Q 经过圆心,经过圆心的弦最长,故
如图J10.15所示,过点 C 作CM⊥AB 于点M,连接 AC.
由等面积法可得 即5×CM=(3+1)×4,解得
圆C上的点到直线 的最大距离为 故△PAB 面积的最大值为
如图J10.16所示,找到 BC 的中点E,连接AE,交半圆于点 P ,在半圆上取点, 连接AP ,EP ,可见. ,即 AP 是 AP 的最小值.
因为 所以
15. 6.
因为A(1,0),B(1-a,0),C(1+a,0)(a>0),所以AB=1-(1-a)=a,CA=a+1-1=a,即AB=AC.
又∠BPC=90°,则 PA=AB=AC=a.
如图J10.17所示,延长 AD 交⊙D 于点P',此时 AP'最大.
因为A(1,0),D(4,4),所以 AD=5,则 故 a 的最大值为6.
如图J10.18所示,连接 BP,由对称性得 OA=OB.
因为Q是AP 的中点,所以
又 OQ长的最大值为 ,则BP 长的最大值为
如图J10.18所示,当 BP 过圆心C时,BP 最长,过点 B 作BD⊥x轴于点D.
因为CP=1,所以 BC=2.
又点 B在直线y=2x上,设B(t,2t),则CD=t-(-2)=t+2,BD=-2t.
在Rt△BCD中,由勾股定理得 即 解得 t=0(舍去)或 故
因为点 B 在反比例函数 的图像上,所以
易得点 F 在以点B为圆心、10为半径的圆上运动,所以当G,F,B三点共线时,GF 最小,由勾股定理得 故
易得∠AMD=90°,如图J10.19所示,取 AD 的中点O,点 M 在以AD 为直径的⊙O上,当点 O,M,B共线时,BM 最小,故
如图J10.20所示,易证△ABE≌△DAF,则∠ABE=∠DAF.
因为∠ABE+∠BEA=90°,所以∠FAD+∠BEA=90°,则∠APB=90°,故点 P 的路径是一段以AB 为直径的弧.
设 AB 的中点为G,连接DG 交弧于点P,此时DP 的长度最小,故
如图J10.21所示,连接AG.由题可知 则A,B,E,G四点共圆,因此∠AGE=∠AGD=90°,故点 G 在以AD 为直径的圆上运动,取AD 的中点O,连接OG.
当O,G,C 三点共线时,CG 的值最小,故
21. 4.
O,B,P,C四点共圆,OP 为直径.如图J10.22所示,设圆心为 D,分别连接CD 和BD.△BCD 是顶角为120°的等腰三角形,三边比为 DB :DC ∶CB=1∶1∶
因为 所以 BD=2,故 OP=2BD=4.
因为∠APB=∠AOB=90°,所以A,O,P,B 四点共圆,以 AB 为直径.
要使点 P 的纵坐标最大,需要∠PAO 最大,如图J10.23 所示,当 PA 与⊙O 相切时,∠PAO 最大,直线 AC交y轴于点D,连接OC,作CH⊥x轴于点H,PM⊥x轴于点M,DN⊥PM 于点N.
当AC与⊙O 相切于点C时,点 P 的纵坐标取最大值,如图J10.23所示.
在 Rt△AOD 中,因为∠DAO=30°,所以
在Rt△BDP 中,因为∠BDP=∠ADO=60°,所以
在 Rt△DPN 中,因为∠PDN=30°,所以 而 故 即点 P 纵坐标的最大值为
表10.1
最值类型 图 示 原理(及结论)
点到点 A B 两点之间线段最短
点到线 垂线段最短
线到线 平行线间垂线段最短
点到圆 最小值:AP=OA-r 最大值:AQ=OA+r
线到圆 最小值:AC=OA-r 最大值:AB=OA+r
圆到圆 最小值:BC=OO'-r -r 最大值:AD=OO'+r +r
模块2 场 景 演 练
模型的识别:单线段最值
类型1:点到点
1.已知AB 是圆锥(图10.2)底面的直径,P是圆锥的顶点,此圆锥的侧面展开图如图10.3所示.一只蚂蚁从 A 点出发,沿着圆锥侧面经过 PB 上一点,最后回到 A 点.若此蚂蚁所走的路线最短,则M,N,S,T(均在 PB上)四个点中,它最有可能经过的点是( ).
A. M B. N C. S D. T
2.如图10.4所示,一只蚂蚁从长为7cm、宽为5cm、高为9cm的长方体纸箱的A点沿纸箱爬到B点,那么它所走的最短路线的长是 cm.
3.如图10.5所示,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B 处有一蚊子.此时,一只壁虎正好在容器外壁离容器上沿0.2m与蚊子相对的点 A 处,则壁虎捕捉蚊子的最短距离为 .
类型2:点到线
4. 如图10.6所示,在 中, 点 P 在AB上(不与A,B 重合),过点 P 作 垂足分别为点 E,F,连接EF,M 为EF 的中点,则CM 的最小值为 .
变式:如图10.7所示,已知D 是长为2的线段AB上的动点(不与A,B重合),分别以AD,DB 为边在线段AB 的同侧作等边 和等边 ,G 为EF 的中点,连接DG,则GD 的最小值为 .
5.如图10.8所示,线段 AB的长为10,C为AB 上的一个动点,分别以AC,BC 为斜边在 AB 的同侧作两个等腰直角三角形 和 ,那么 DE 长的最小值是 .
变式:如图10.9所示,在 中, F是线段AC 上一点,过点 A 的⊙F交AB 于点D,E 是线段BC 上一点,且, ,则EF 的最小值为 .
6. 如图10.10所示,在 中, M 为BC 的中点,H 为AB 上一点,过点 C 作 交HM 的延长线于点G,若 ,则四边形 ACGH 周长的最小值是 .
变式:如图10.11所示,在 中, ,P 为AB 边上一动点,以 PA,PC 为边作平行四边形PAQC,则对角线 PQ 的最小值为 .
模型的识别:拔高特训
7. 如图10.12 所示,已知⊙O经过点A(2,0),C(0,2),直线 与⊙O 分别交于点B,D,则四边形 ABCD 面积的最大值为 .
8. 如图10.13所示,在等边 中, ,点P 是BC 边上的动点,点P 关于直线AB,AC 的对称点分别为M,N,则线段 MN 长的取值范围是 .
9. 如图10.14所示,在 中, D 是线段BC上的一个动点,以AD 为直径作⊙O 分别交AB,AC于点E,F,连接EF,则线段 EF 长度的最小值为 .
10. 如图10.15所示,在 中, D,E分别是AC,BC上的一点,且. .若以 DE 为直径的圆与斜边AB 相交于点M,N,则MN 的最大值为
11. 如图10.16所示,在 中, 点 D 是 BC 边上的动点,连接AD,过点 D 作 ,交 AB 于点E,则线段 AE 的最小值为 .
中小学教育资源及组卷应用平台
类型3:点、线到圆(圆已知)
类①:线到圆
12. 如图10.17所示,在 中, ,以边 AB 中点O 为圆心,作半圆与AC 相切,点P,Q分别是边BC 和半圆上的动点,连接PQ,则PQ长的最小值是 ;PQ 长的最大值是 .
13. 如图10.18所示,已知直线 与x轴、y轴分别交于A,B两点,P是以点C(0,1)为圆心、1为半径的圆上一动点,连接 PA,PB,则 面积的最大值是 .
类②:点到圆
14. 如图10.19所示,在 中, ,以BC 为直径的半圆交 AB 于点D,P 是 上的一个动点,连接 AP,则AP 的最小值是 .
15. 如图10.20所示,已知点 A(1,0),. 点 P 在以点D(4,4)为圆心、1为半径的圆上运动,且始终满足 则a 的最大值是 .
16. 如图10.21所示,一次函数 与反比例函数 的图像交于 A,B两点,点 P 在以点C(-2,0)为圆心、1为半径的⊙C上,Q是AP 的中点.已知OQ长的最大值为 ,则k 的值为 .
类型4:点、线到圆(辅助圆)
17. 如图10.22所示,正方形 ABCD 的边长为10,点 G 是边CD 的中点,点 E 是边AD上一动点,连接 BE,将. 沿BE翻折得到 连接 GF,则 GF 的最小值为
18. 如图10.23所示,四边形 ABCD 为矩形, 点P 是线段BC 上一动点,点 M 为线段AP 上一点, ,则BM 的最小值为 .
19. 如图10.24所示,在正方形 ABCD中, ,动点 E 从点 A 出发向点D 运动,同时动点 F 从点D 出发向点C运动,点E,F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段 AF,BE 相交于点P,则线段 DP 的最小值为 .
20. 如图10.25 所示,在矩形 ABCD 中, ,E 为边 BC 上一动点,F 为AE的中点,G为DE 上一点, ,则CG 的最小值为 .
21.如图10.26所示,线段 BC 的两个端点分别在x轴与直线 上(点 B,C 均与原点O 不重合)滑动,且 分别作 轴,CP⊥直线 经探究,在整个滑动过程中,P,O两点间的距离为定值 .
.如图10.27所示,A(-2,0),B(0,2),⊙O的半径为1,点 C 为⊙O上一动点,过点 B 作BP⊥直线 AC,垂足为点 P,则点 P 纵坐标的最大值为 .
1. B.
如图J10.1所示,根据圆锥侧面展开图,要使此蚂蚁所走的路线最短,四个点中,它最有可能经过的点是 N.
2. 15.
当展开前面和右面时,最短路线长是
) ;
当展开前面和上面时,最短路线长是
当展开左面和上面时,最短路线长是
,
因为 所以它所走的最短路线的长是15cm.
3. 1m.
如图J10.2所示,将容器侧面展开,作A 关于EF 的对称点A',连接. 则 即为最短距离,
4. 1.2.
如图J10.3所示,连接CP,因为四边形 EPFC 为矩形,所以
当CP⊥AB时,CP 最短,此时, 则 即CM 的最小值为1.2.
变式:
如图J10.4所示,分别延长 AE,BF 交于点C,连接CD,易得四边形 CEDF 为平行四边形,则CD,EF 互相平分.
因为点 G 是EF 的中点,所以点 G 是CD 的中点,则
当CD⊥AB时,CD 最短.
因为△ABC 为等边三角形,CD⊥AB,所以 故 GD的最小值为
5. 5.
解法1 如图J10.5所示,延长AD,BE 交于点F,易证四边形 DCEF 为矩形,DE 最小即CF 最小.
当CF⊥AB时,CF 最小,此时
解法2 设AM=MC=x,CN=NB=y,如图J10.6所示,作 DM⊥AC,EN⊥BC,DF⊥EN.在 Rt△DEF 中,DE≥DF,而 故 DE 的最小值为5.
变式:
如图J10.7所示,连接FD,作 FG⊥AB于点G,EH⊥AB 于点H,FM⊥EH 于点M,则四边形 FGHM 是矩形,△AFD,△DEB 为等腰三角形,所以 FG∥EH.
因为 EF>FM,所以 EF 的最小值为2
6. 22.
易证△BMH≌△CMG,则 BH=CG,所以四边形 ACGH 的周长 GH=AC+AB+GH=14+GH,当 GH 最小,即 MH⊥AB 时,四边形 ACGH 的周长最小,此时GH=AC=8,故四边形 ACGH 周长的最小值为14+8=22.
变式:
如图J10.8所示,因为 AB∥CQ,所以当 PQ⊥AB 时,PQ 最小,而. 在等腰Rt△AFC 中, 故 PQ 的最小值为
如图J10.9所示,连接AC,交 BD 于点K.易知当 BD⊥AC时,四边形 ABCD 的面积最大,此时
如图J10.10 所示,∠MAN =120°,易得. 为等腰三角形,此时
当 AP⊥BC时,MN 最小,当 AP=AB 时,MN 最大,故
如图J10.11 所示,连接 OE,OF,过点 O 作 垂足为点 H,此时∠EOF =2∠BAC=120°.又 OE=OF,则
当 AD⊥BC 时,AD 最小,此时 即 r=1,故
如图J10.12所示,取 DE 的中点O,过点O 作OG⊥AB 于点G,连接OC.
又 则只有点C,O,G共线时,点G 到圆心O的距离最小,此时 OG 达到最小,在△OMG 中,MG 最大,所以 MN 达到最大.
作CF⊥AB 于点 F,易得 所以 则 MG= 故
11.
如图J10.13所示,取AE 的中点F,连接 FD,过点 F 作FG⊥BC,垂足为点 G.
根据直角三角形斜边中线性质,易得 FD = AF = FE,设 FD = AF = FE = x,则 FB =4--x.
因为∠B=30°,所以 又 FG≤FD,即 解得 故 AE 的最小值为
12. 1;8.
如图J10.14所示,设⊙O与AC 相切于点E,连接 OE,作( 垂足为点 P 且交⊙O 于点 Q ,此时垂线段 OP 最短,
因为AB=10,AC=8,BC=6,所以 故
如图J10.14所示,当点 Q 在AB 边上,P 与 B 重合时,P Q 经过圆心,经过圆心的弦最长,故
如图J10.15所示,过点 C 作CM⊥AB 于点M,连接 AC.
由等面积法可得 即5×CM=(3+1)×4,解得
圆C上的点到直线 的最大距离为 故△PAB 面积的最大值为
如图J10.16所示,找到 BC 的中点E,连接AE,交半圆于点 P ,在半圆上取点, 连接AP ,EP ,可见. ,即 AP 是 AP 的最小值.
因为 所以
15. 6.
因为A(1,0),B(1-a,0),C(1+a,0)(a>0),所以AB=1-(1-a)=a,CA=a+1-1=a,即AB=AC.
又∠BPC=90°,则 PA=AB=AC=a.
如图J10.17所示,延长 AD 交⊙D 于点P',此时 AP'最大.
因为A(1,0),D(4,4),所以 AD=5,则 故 a 的最大值为6.
如图J10.18所示,连接 BP,由对称性得 OA=OB.
因为Q是AP 的中点,所以
又 OQ长的最大值为 ,则BP 长的最大值为
如图J10.18所示,当 BP 过圆心C时,BP 最长,过点 B 作BD⊥x轴于点D.
因为CP=1,所以 BC=2.
又点 B在直线y=2x上,设B(t,2t),则CD=t-(-2)=t+2,BD=-2t.
在Rt△BCD中,由勾股定理得 即 解得 t=0(舍去)或 故
因为点 B 在反比例函数 的图像上,所以
易得点 F 在以点B为圆心、10为半径的圆上运动,所以当G,F,B三点共线时,GF 最小,由勾股定理得 故
易得∠AMD=90°,如图J10.19所示,取 AD 的中点O,点 M 在以AD 为直径的⊙O上,当点 O,M,B共线时,BM 最小,故
如图J10.20所示,易证△ABE≌△DAF,则∠ABE=∠DAF.
因为∠ABE+∠BEA=90°,所以∠FAD+∠BEA=90°,则∠APB=90°,故点 P 的路径是一段以AB 为直径的弧.
设 AB 的中点为G,连接DG 交弧于点P,此时DP 的长度最小,故
如图J10.21所示,连接AG.由题可知 则A,B,E,G四点共圆,因此∠AGE=∠AGD=90°,故点 G 在以AD 为直径的圆上运动,取AD 的中点O,连接OG.
当O,G,C 三点共线时,CG 的值最小,故
21. 4.
O,B,P,C四点共圆,OP 为直径.如图J10.22所示,设圆心为 D,分别连接CD 和BD.△BCD 是顶角为120°的等腰三角形,三边比为 DB :DC ∶CB=1∶1∶
因为 所以 BD=2,故 OP=2BD=4.
因为∠APB=∠AOB=90°,所以A,O,P,B 四点共圆,以 AB 为直径.
要使点 P 的纵坐标最大,需要∠PAO 最大,如图J10.23 所示,当 PA 与⊙O 相切时,∠PAO 最大,直线 AC交y轴于点D,连接OC,作CH⊥x轴于点H,PM⊥x轴于点M,DN⊥PM 于点N.
当AC与⊙O 相切于点C时,点 P 的纵坐标取最大值,如图J10.23所示.
在 Rt△AOD 中,因为∠DAO=30°,所以
在Rt△BDP 中,因为∠BDP=∠ADO=60°,所以
在 Rt△DPN 中,因为∠PDN=30°,所以 而 故 即点 P 纵坐标的最大值为
同课章节目录
