第9讲 图形对称之折叠 (含答案)2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第9讲 图形对称之折叠 (含答案)2025年中考数学几何模型方法巩固练习 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:37:33 | ||
图片预览

文档简介
第9讲 图形对称之折叠
模块1 本 质 原 理
在折叠问题中,其本质原理会产生以下6种情景:
(1)产生全等:折叠前后会有全等产生,所以会有等边和等角;
(2)产生角平分线:如遇平行线,那么翻折后会有等腰三角形出现;
(3)产生中垂线:折痕是对称点连线的垂直平分线;
(4)求边长:利用设元勾股求边长,一般情况下,求什么设什么;
(5)折叠后图不定:可能是等腰三角形或直角三角形等,需要分类讨论;
(6)最值问题:如折痕过某一定点,此时往往用辅助圆来解决问题.
1.折对角线
如图9.1所示,已知四边形 ABCD 为矩形.
①△ABE≌△C'DE;
②△BED 为等腰三角形;
实例剖析
如图9.2所示,在矩形 ABCD中,AB=4,BC=3.将矩形 ABCD 沿对角线AC 折叠,点B 的对称点为B',连接 DB',则
【答案】
【分析】 设 AB'与CD 交于点F,易得 则△DAF≌△B'CF(AAS),故
在矩形 ABCD中,AB=4,BC=3,∠B=90°,则.
设 则FC=4-x.
在 Rt△DFA 中,依据勾股定理得 解得 故 易得△FAC∽△FB'D,则 即 解得
2.点折到点
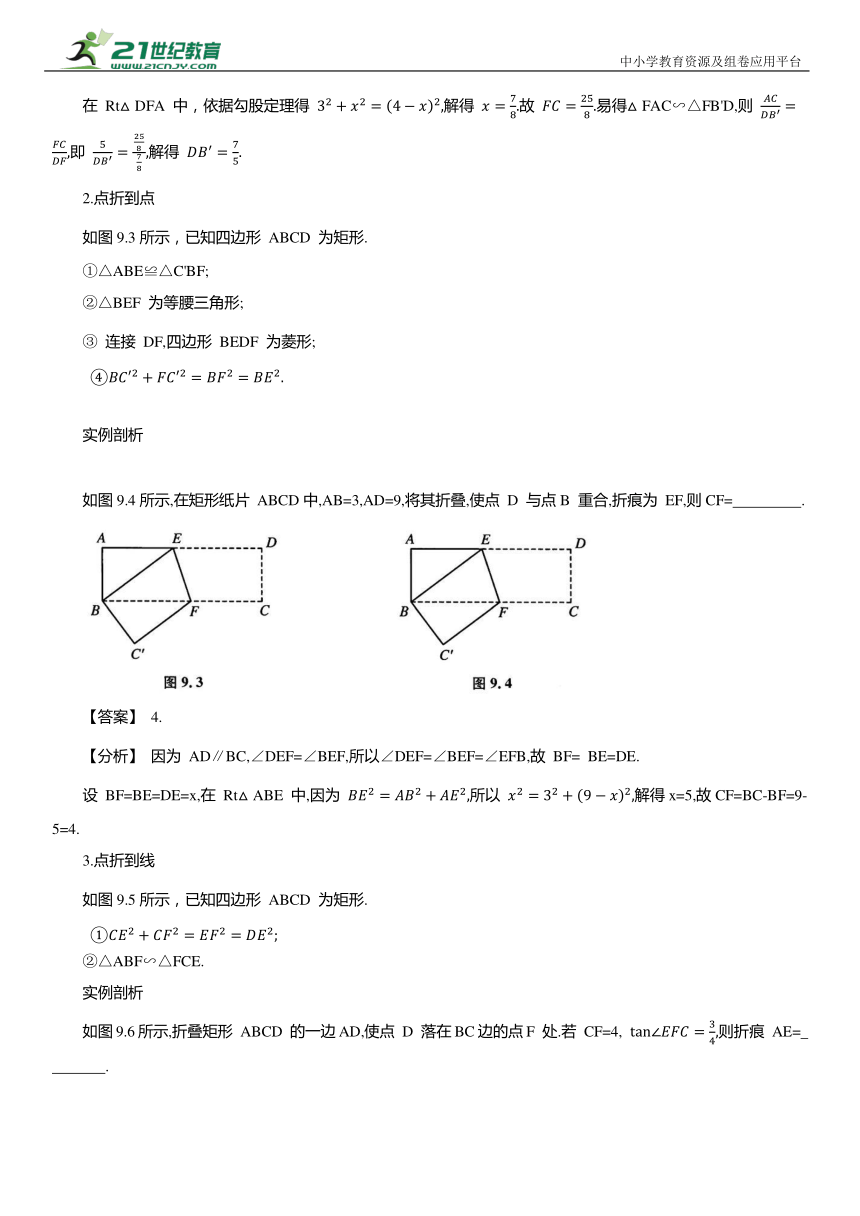
如图9.3所示,已知四边形 ABCD 为矩形.
①△ABE≌△C'BF;
②△BEF 为等腰三角形;
③ 连接 DF,四边形 BEDF 为菱形;
实例剖析
如图9.4所示,在矩形纸片 ABCD中,AB=3,AD=9,将其折叠,使点 D 与点B 重合,折痕为 EF,则CF= .
【答案】 4.
【分析】 因为 AD∥BC,∠DEF=∠BEF,所以∠DEF=∠BEF=∠EFB,故 BF= BE=DE.
设 BF=BE=DE=x,在 Rt△ABE 中,因为 所以 解得x=5,故CF=BC-BF=9-5=4.
3.点折到线
如图9.5所示,已知四边形 ABCD 为矩形.
②△ABF∽△FCE.
实例剖析
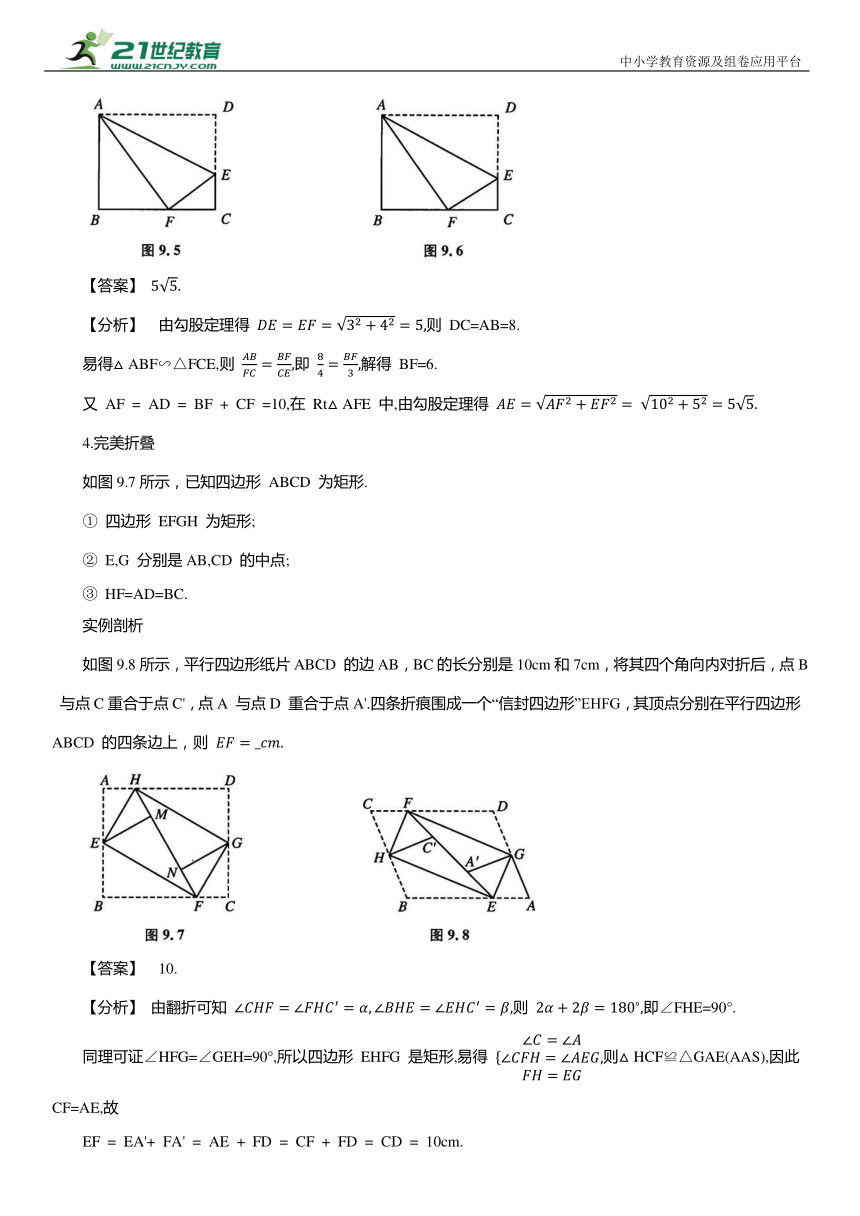
如图9.6所示,折叠矩形 ABCD 的一边AD,使点 D 落在BC边的点F 处.若 CF=4, 则折痕 AE= .
【答案】
【分析】 由勾股定理得 则 DC=AB=8.
易得△ABF∽△FCE,则 即 解得 BF=6.
又 AF = AD = BF + CF =10,在 Rt△AFE 中,由勾股定理得
4.完美折叠
如图9.7所示,已知四边形 ABCD 为矩形.
① 四边形 EFGH 为矩形;
② E,G 分别是AB,CD 的中点;
③ HF=AD=BC.
实例剖析
如图9.8所示,平行四边形纸片ABCD 的边AB,BC的长分别是10cm和7cm,将其四个角向内对折后,点B 与点C重合于点C',点A 与点D 重合于点A'.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形 ABCD 的四条边上,则
【答案】 10.
【分析】 由翻折可知 则 即∠FHE=90°.
同理可证∠HFG=∠GEH=90°,所以四边形 EHFG 是矩形,易得 则△HCF≌△GAE(AAS),因此 CF=AE,故
EF = EA'+ FA' = AE + FD = CF + FD = CD = 10cm.
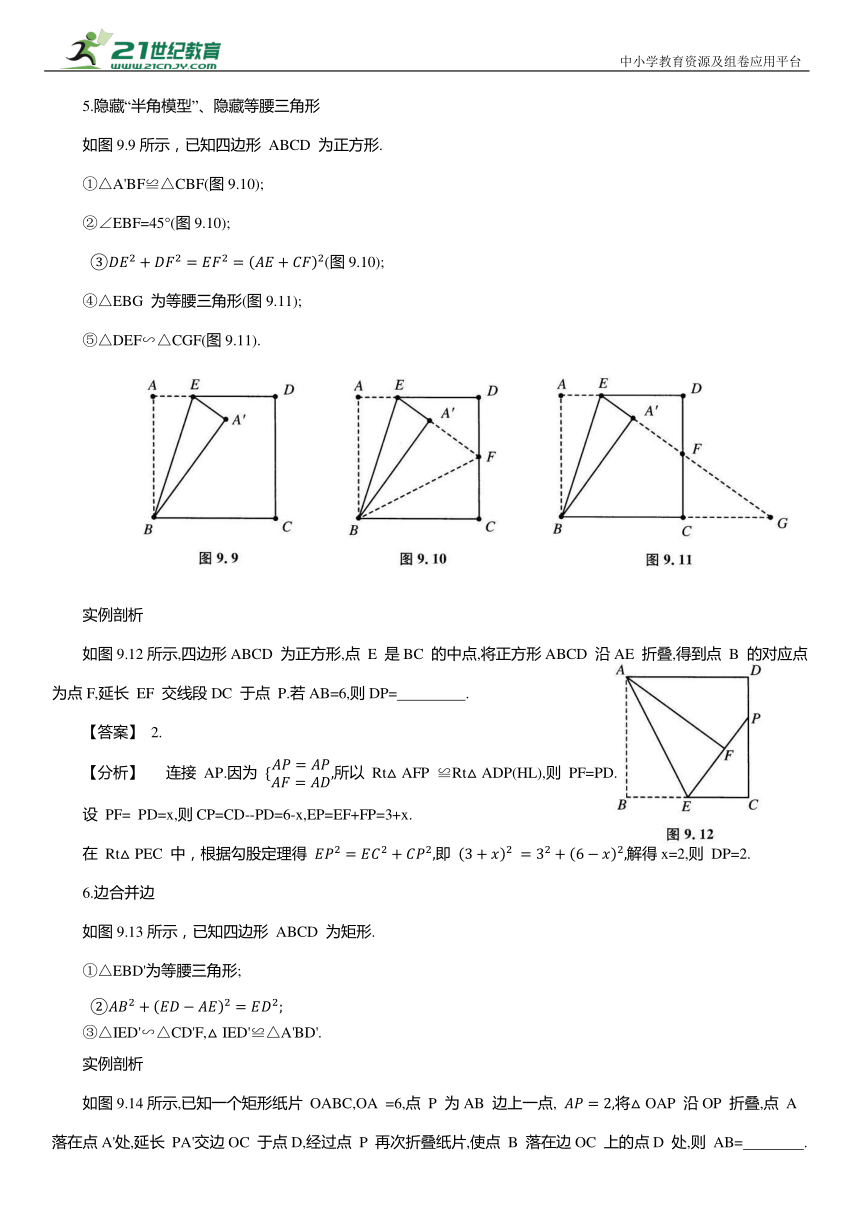
5.隐藏“半角模型”、隐藏等腰三角形
如图9.9所示,已知四边形 ABCD 为正方形.
①△A'BF≌△CBF(图9.10);
②∠EBF=45°(图9.10);
(图9.10);
④△EBG 为等腰三角形(图9.11);
⑤△DEF∽△CGF(图9.11).
实例剖析
如图9.12所示,四边形ABCD 为正方形,点 E 是BC 的中点,将正方形ABCD 沿AE 折叠,得到点 B 的对应点为点F,延长 EF 交线段DC 于点 P.若AB=6,则DP= .
【答案】 2.
【分析】 连接 AP.因为 所以 Rt△AFP ≌Rt△ADP(HL),则 PF=PD.
设 PF= PD=x,则CP=CD--PD=6-x,EP=EF+FP=3+x.
在 Rt△PEC 中,根据勾股定理得 即 解得x=2,则 DP=2.
6.边合并边
如图9.13所示,已知四边形 ABCD 为矩形.
①△EBD'为等腰三角形;
③△IED'∽△CD'F,△IED'≌△A'BD'.
实例剖析
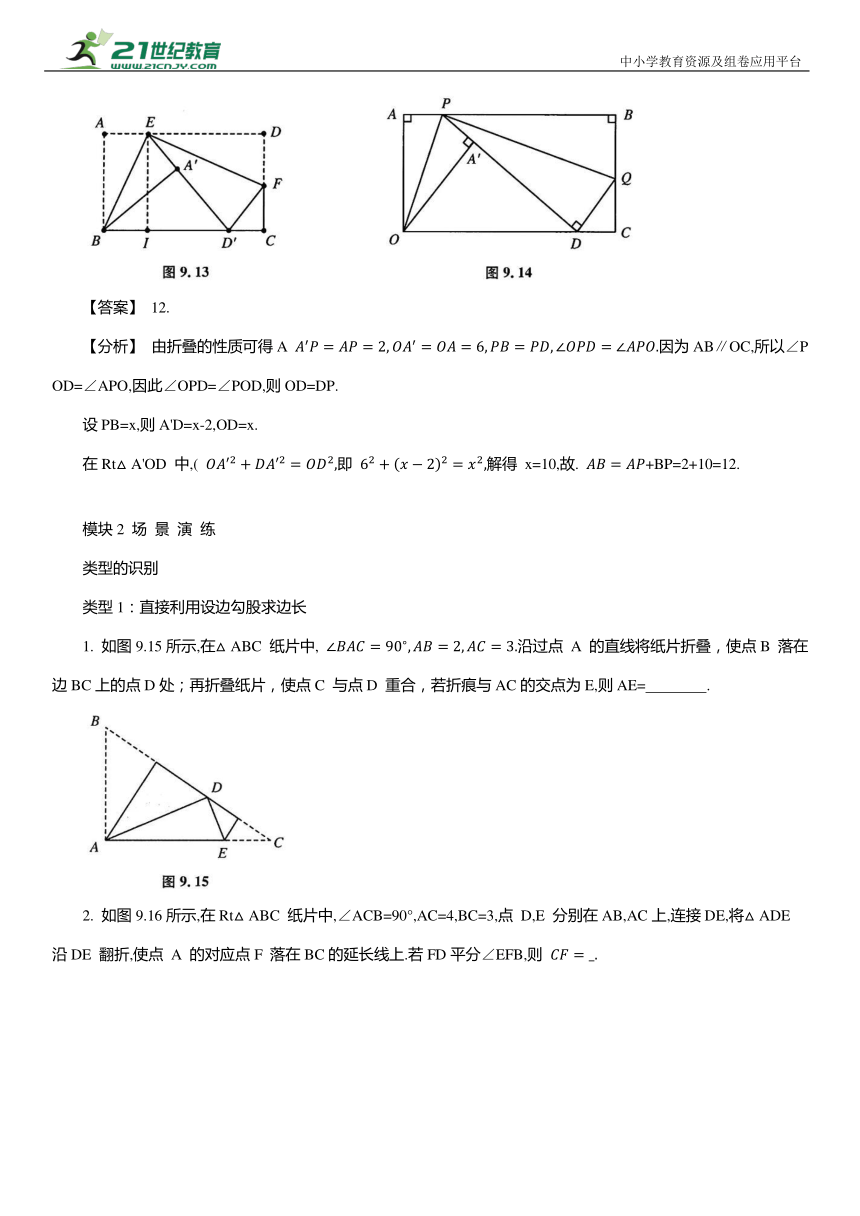
如图9.14所示,已知一个矩形纸片 OABC,OA =6,点 P 为AB 边上一点, 将△OAP 沿OP 折叠,点 A 落在点A'处,延长 PA'交边OC 于点D,经过点 P 再次折叠纸片,使点 B 落在边OC 上的点D 处,则 AB= .
【答案】 12.
【分析】 由折叠的性质可得A 因为AB∥OC,所以∠POD=∠APO,因此∠OPD=∠POD,则OD=DP.
设PB=x,则A'D=x-2,OD=x.
在Rt△A'OD 中,( 即 解得 x=10,故. +BP=2+10=12.
模块2 场 景 演 练
类型的识别
类型1:直接利用设边勾股求边长
1. 如图9.15所示,在△ABC 纸片中, 沿过点 A 的直线将纸片折叠,使点B 落在边BC上的点D处;再折叠纸片,使点C 与点D 重合,若折痕与AC的交点为E,则AE= .
2. 如图9.16所示,在Rt△ABC 纸片中,∠ACB=90°,AC=4,BC=3,点 D,E 分别在AB,AC上,连接DE,将△ADE 沿DE 翻折,使点 A 的对应点F 落在BC的延长线上.若FD平分∠EFB,则
3. 如图9.17所示,在矩形 ABCD 中,AB=4,AD=6,点E 为BC上一点,将△ABE 沿AE 折叠得到△AEF,点 H 为CD 上一点,将△CEH 沿EH 折叠得到△EHG,且点 F 落在线段EG 上.当GF=GH 时,
4. 如图9.18所示,在 中,点 E,F分别在边AB,AD 上,将 沿EF 折叠,点 A 恰好落在BC 边上的点G 处.若 则
类型2:平行线+角平分线 等腰三角形
5. 如图9.19所示,在长方形纸片 ABCD 中, 把纸片沿直线 AC 折叠,点B落在点E 处,AE 交DC 于点O,若 ,则 CD 的长为 .
6.如图9.20所示,将矩形纸片 ABCD 沿EF,GN折叠,使点 A 和点C 重合于点M,点D与点H 重合,点 B 落在边AD 上的点P 处,且 MN 经过点P.已知 则
类型3:对称点的连线,巧用十字模型
7.如图9.21所示,点 E 和点F 分别在正方形纸片ABCD的边CD 和AD上,连接AE,BF,沿BF 所在直线折叠该纸片,点A 恰好落在线段AE 上点G 处.若正方形纸片边长为12,DE=5,则(
8. 如图9.22所示,在矩形纸片 ABCD 中,E 为BC 的中点,连接AE,将 沿AE折叠得到 连接CF.若 则
9.如图9.23所示,将矩形 ABCD 沿着DE 所在的直线折叠,点 A 的对应点是点 连接 并延长交CD 于点F.若E 是AB 的中点,AB=2,AD=3,则
类型4:直角的翻折,巧用三垂直模型
10.如图9.24所示,在平面直角坐标系中,已知矩形 OABC,O为原点,点 A,C分别在x轴、y轴上,点 B 的坐标为(1,2),连接OB,将 沿直线OB 翻折,点A 落在点D 的位置,则 的值是 .
11.如图9.25所示,小红用一张长方形纸片 ABCD 进行折纸,使得顶点 D 落在边 BC上的点F处(折痕为 AE).已知AB为8cm,BC为10cm,则 EC 的长度为 .
中小学教育资源及组卷应用平台
12. 如图9.26所示,在矩形纸片 ABCD中,点 E,F 分别在矩形的边AB,AD 上,将矩形纸片沿CE,CF 折叠,点 B 落在点H 处,点 D 落在点G 处,点 C,H,G 恰好在同一直线上.若 ,则
类型5:等边三角形的翻折,巧用一线三等角模型
13. 如图9.27所示,在等边 中,D是BC边上的一点,把 折叠,使点 A 落在 BC 边上的点D 处,折痕与边 AB,AC 分别交于点M,N.若 ,则边 BC长为 .
类型6:无长度数据的特殊角度型
14.如图9.28所示,先将正方形纸片ABCD 对折,折痕为直线 EF,把正方形 ABCD 展平.点H在FC上,将纸片沿直线 DH 折叠,点 C 恰好落在直线EF 上的点G处,连接AG.下列结论:
① 直线 EF 垂直平分线段AD;
与 关于直线DH 成轴对称;
是等边三角形;
其中正确的结论为 .
15.如图9.29所示,将四边形纸片 ABCD 沿过点A 的直线折叠,使得点 B 落在CD上的点Q处,折痕为 AP.再将 分别沿PQ,AQ 折叠,此时点 C,D 落在AP 上的同一点R 处.当. 时,
类型7:定长翻折,巧用辅助圆
16. 如图9.30所示,在矩形 ABCD 中, ,点 E 是AD 边的中点,点 F 是射线AB 上的一动点,将 沿EF 所在的直线翻折得到, 连接 则 的最小值为 .
17. 如图9.31所示,在边长为8的菱形 ABCD 中, M是边AD的中点,N是AB 上一点,将 沿MN所在的直线翻折得到 连接 则 的取值范围为 .
18. 如图9.32所示,在菱形 ABCD中, 折叠该菱形,使点 A 落在边BC 上的点M处,折痕分别与边 AB,AD 交于点E,F.当点 M 的位置变化时,DF 长的最大值为 .
类型8:折叠后图形不确定,分类讨论问题
在矩形 ABCD 中,将边AB 翻折到对角线BD 上,点A 落在点M 处,折痕BE 交AD于点 E.将边 CD 翻折到对角线BD 上,点 C 落在点N 处,折痕 DF 交BC 于点F. 则
20. 如图9.33所示,正方形 ABCD 的边长是8,点 E 在边AB 上, 点F 是边BC上不与点 B,C重合的一个动点,把 沿EF 折叠,点 B 落在 处.若 恰为等腰三角形,则 的长为 .
21. 如图9.34所示,在 中, 点 E,F 分别为AB,AC 上一个动点,连接 EF,以 EF 为轴将 折叠得到 使点 D 落在BC 上.当 为直角三角形时,BE 的值为 .
综合应用:遇见中考
22.如图9.35所示,在正方形 ABCD 中, ,将 BC 沿CE 翻折,使点B对应点刚好落在对角线AC上的点G,将AD 沿AF 翻折,使点 D 对应点刚好落在对角线AC 上的点H,则.
23.如图9.36所示,在矩形 ABCD 中,点 M 在AB边上,把 沿直线CM 折叠,使点 B落在AD边上的点E 处,连接EC,过点 B 作 ,垂足为点 F.若 ,则线段
24.如图9.37所示,在 中, 将边 BC 沿CN折叠,使点 B 落在AB 上的点. 处,再将边 AC 沿CM 折叠,使点 A 落在( 的延长线上的点 处,两条折痕与斜边 AB 分别交于点N,M,则线段
25如图9.38所示,在矩形纸片 ABCD 中, ,M 是BC上的点,且 将矩形纸片 ABCD 沿过点M 的直线折叠,使点 D 落在AB 上的点P 处,点C落在点 处,折痕为 MN,则线段.
26. 如图9.39 所示,在 中,D,E 分别为BC,AC 上的点,将 沿DE 折叠,得到 连接BF,CF, 若 10,则 AE 的长为 .
27.如图9.40所示,在矩形纸片 ABCD 中, .把 沿对角线BD 折叠,使点 C 落在点( 处, 交AD 于点G;E,F分别是C'D 和BD 上的点,线段 EF 交AD 于点H,把 沿EF 折叠,使点 D 落在点A 处,则.
28.(2022·深圳)(1)发现:如图9.41所示,在正方形 ABCD 中,E为AD边上一点.将 沿BE 翻折到 处,延长 EF 交CD 边于点G.求证:
(2)探究:如图9.42所示,在矩形 ABCD中,E 为AD 边上一点,且. 将△AEB 沿BE 翻折到 处,延长EF交BC 边于点G,延长BF 交CD 边于点H,且 FH=CH,求 AE 的长.
(3)拓展:如图9.43所示,在菱形 ABCD 中,E为CD 边上的三等分点,( 60°.将△ADE 沿AE 翻折得到 ,直线 EF 交直线BC 于点P,则
第9讲 图形对称之折叠
1.
在 Rt△ADE 中, ,设AE=x,则CE=DE=3-x,即 x ,解得 故
2.
因为将△ADE 沿DE 翻折得到△DEF,所以∠A=∠DFE=∠DFB,则∠B+∠DFB=90°,于是
设BD=m,则AD=DF=5-m,因为 所以 则 故CF= BF
3. 2.
由折叠可得 进而得出在 Rt△AEH 中,.
设BE=x,则EF=x,CE=6-x=EG,FG=GH=HC=6-2x,DH=4-(6-2x)=2x-2,再根据勾股定理,可得 即 解得x=2,即可得到 BE 的长为2.
如图J9.1所示,过点 B 作BM⊥AD 于点M,过点 F 作FH⊥BC 于点H,过点 E 作EN⊥CB 的延长线于点 N,得到矩形 BHFM.
在 Rt△GEN中,根据勾股定理,得 即 解得GN=7.
设MF=BH=x,则GH=GN-BN-BH=7-1-x=6-x,GF=AF=AM+FM=6+x.
在 Rt△GFH 中,根据勾股定理,得( 即 解得 故
5. 8cm.
由折叠的性质可得∠BAC=∠EAC=∠ACD,则AO=CO=5cm.在Rt△ADO 中,根据勾股定理得 故CD=DO+CO=3+5=8(cm).
作 PR⊥BC于点R.因为∠PFE=∠BFE,AD∥BC,所以∠PFE=∠PEF=∠BFE,则PE= PF.
同理可得 PN=PG,则
设PF=4a,PN=3a,则FN=5a,即5a=10,亦即a=2,故PF=4a=8,PN=3a=6.
因为 所以 故 AB= PR
设 BF 与AE 的交点为H,由折叠及轴对称的性质可知△ABF≌△GBF,BF 垂直平分AG,易得△ABF≌△DAE(ASA),则 AE=BF=13.
因为 所以12×5=13AH,即 故AG=2AH
又 AE=BF=13,则
如图J9.2所示,连接 BF,交 AE 于点O.将△ABE 沿AE 折叠得到△AFE,AE 垂直平分BF.
因为 BE=CE=EF=3,所以∠BFC=90°.
在 Rt△ABE 中,由勾股定理得 所以 故
在Rt△BCF中,由勾股定理得
如图J9.3所示,连接 AA′,则 AA′⊥ED.
将矩形 ABCD 沿着DE 所在的直线折叠,则.
因为 E 为AB 的中点,所以 AE = BE = EA′,因此. ∠EA'A=β,则. 即AA′⊥BF,故 DE∥BF.
又因为 BE∥DF,所以四边形 EBFD 是平行四边形,则 DE=BF.
因为AE=1,AD=3,所以 故
如图J9.4所示,构造一线三垂直,易证△BED∽△DFO,相似比为OD:BD=1∶2.
设 OF = CE = x,则 DE = 2x,DF =2-2x,即 解得 故
11. 3cm.
易证△ABF∽△FCE,设CE=x,则 DE=EF=8-x,所以 解得x=3(cm).
12. 2.
如图J9.5所示,延长EH 交CF 于点P,过点 P 作MN⊥CD 于点N.
将矩形纸片沿CE,CF 折叠,点 B 落在点H 处,点 D 落在点G 处,则 BC=CH =4,∠DCF=∠GCF,BE=EH=2,∠B=∠CHE=90°,易得△CPH≌△CPN(AAS),故 NP=PH,CH=CN=4.
又 CN=CB=4,则四边形 BCNM 是正方形.
在Rt△EPM中, 即( 解得
因为 所以 故 DF=2.
设BD=x,DC=y.由△BMD∽△CDN,可得(BM+MD+BD):(DN+NC+CD)=DM:DN=2:3,推出(2x+y):(x+2y)=2:3,即y=4x,则AB=BC=AC=5x,MB=5x-2,CN=5x-3.再根据 构建方程 解得 故 BC=5x
14. ①②③.
因为是将正方形纸片 ABCD 对折,得折痕为直线 EF,把正方形 ABCD 展平,得 AE=DE,∠AEF=∠DEF=90°,所以直线 EF 垂直平分线段AD,故①正确;
因为△DGH 是△DCH 沿DH 折叠得到的,所以△DGH 与△DCH 关于直线DH 成轴对称,故②正确;
由①得GA=GD,由②得GD=CD,因为 CD=AD,所以△ADG 是等边三角形,故③正确;
因为∠ADG=60°,所以 故④不正确.
因为∠QRA+∠QRP=180°,所以∠D+∠C=180°,AD∥BC,又AD=CP,则四边形APCD 是平行四边形.
因为∠DQR+∠CQR =180°,所以∠DQA+∠CQP=90°,则∠AQP=90°,因此 AD=CP=AR = PR =QR =a,CD=AP=2QR =2a,由折叠的性质可得∠CPQ=∠QPR =∠APB,故∠QPA=60°.
在 Rt△AQP 中, 则 故
如图J9.6 所示,根据点 F 是射线AB 上的一动点,将△AEF 沿EF 所在的直线翻折得到△A'EF,可得点 A'的运动路径为以点E 为圆心、AE 长为半径的半圆,再根据两点之间线段最短,即可得出当点 A',C,E三点共线时,A'C的长最小,最后根据勾股定理进行计算即可.
如图J9.7所示,连接 BM,BD.依据 M 是边AD 的中点, 沿 MN 所在的直线翻折得到 即可得到点 A'的轨迹为以AD 为直径的半圆M.依据, 即可得出
当点 N 与点A 或点D 重合时,A'B的最大值为8,即可得到 的取值范围.
如图J9.8 所示,当 FM 最小时,FD 最大,此时 在 中, sin C = 解得
19. 12或
① 当点 M 在线段BN 上时,如图J9.9所示.
由折叠性质得 AB=BM=DC=DN=5,则 BD= BM+MN+DN=13.
因为 所以
② 当点 M 在线段DN 上时,如图J9.10所示.
由折叠性质得 AB = BM= DC = DN=5,则 DM=5+2=7.
因为∠C=90°,所以
或8.
① 如图J9.11所示.当. 时,过点 B'作GH∥AD,则∠B'GE=90°.
此时,
由 得 由翻折的性质,得 则 EG=AG-AE= 所以. ,故
②如图J9.12所示.当 时,
③当 时,因为EB=EB',CB=CB',点 E,C在BB'的垂直平分线上,故 EC垂直平分BB'.
由折叠可知点 F 与点C 重合,不符合题意,舍去.
综上所述,DB'的长为 或8.
或
①如图J9.13所示,当∠EDB=90°时,设BE=x,则AE=ED=10-x.
因为 DE∥AC,所以 即 解得
②如图J9.14所示,当∠DEB=90°时,设 BE=x,则AE=ED=10-x.
因为 所以 解得
综上所述,满足条件的 BE 的值为 或
22.
如图J9.15所示,作 FM⊥AB 于点M.
因为 EG=EB=AG=1,∠EGC=∠B=90°,所以 进而可设 FD=FH=CH=a,CF= a,则. 解得a =1,因此 AM=FD=1,EM= 故
因为 BC=CE,∠EDC=∠CFB=90°,∠DEC=∠BCF,所以△EDC≌△CFB(AAS),则 D AD,故 AE = AD - DE =
24.
由两次翻折知∠MCN=45°.因为 CN·AB=AC·BC,所以 CN·10=8×6=48,即 故
又 代入数值得 故
25. 5.
连接 PM,MD.如图J9.16所示,由折叠性质得 则 Rt△PBM≌Rt△MCD(HL),故 PB=CM=2,PA=AB--PB=5.
如图J9.17所示,延长ED 交FC 于点G,延长 BA,DE 交于点H.
由折叠可得 EG⊥CF,又∠BFC=90°,则 BF∥EG.
因为AB∥EF,所以四边形 BFEH 是平行四边形,故BH=EF=10,AH=BH---AB=10
因为AB∥EF,则∠H=∠1,又∠2=∠1=∠3,则∠H=∠3,故.
由翻折得到∠C'DB=∠BDC.因为 EF⊥AD,CD⊥AD,所以 EF∥CD,∠EFD =∠BDC,故∠EFD=∠EDF,ED=EF.
设ED=x,则EH=x-3.在 Rt△EHD中, 即 解得 故
28.(1)利用HL 型全等即可得证.
(2) 如图J9.18所示,连接GH,易证△FHG≌△CHG(HL),故 FG=CG.
设 FG=CG=x,则 BG=8-x.
因为∠1=∠2,∠1=∠EBC,所以∠2=∠EBG,故EG=BG=8-x.在Rt△BFG 中, 解得 故
或
思路 1 同第(1)(2)问的方法类比可得.
①当 时:
如图J9.19所示,连接AC,AP,易得∠PFA=∠PCA=120°,AF=AC=6.
连接CF,∠AFC=∠ACF,则∠PFC=∠PCF,PC=PF=2x.
作 PH⊥CD,在 Rt△PCH 中,∠PCH=60°,则(
在 Rt△PHE中,( 解得 故
② 当 时:
如图J9.20所示,同①得CP=PF,所以PC=PF=m,则EP=4-m.
在△PCE 中,∠ECP=120°,解三角形可得 故
综上所述, 或
思路2 角平分线+平行线 等腰三角形.
①当 时:
如图J9.21所示,延长PE,BA 交于点M,由于折叠,∠DEA=∠FEA,因此∠1=∠2.因为DC∥AB,所以∠2=∠EAM,则∠1=∠EAM,即 MA=ME.
设MA=ME=n,在△MAF 中,∠AFM=60°,AF=6,AM=n,MF=n+2,解三角形可得 n=14.
由 可得
②当 时:
如图J9.22所示,延长EF,AB 交于点R,同①可得△AER 为等腰三角形,则RE=RA.
设BR=c,则AR=c+6,FR=c+2.在△FAR 中, ,解三角形可得c=8.
由 可得
思路3 通过二次相似转化.
①当 时:
如图J9.23所示,可得△EFG∽△ECP,则
设FG=a,则AG=6-a,PC=2a.连接AC,又易得△EFG∽△ACG,则 即GC=3a,因此EG=4-3a,则 解得 故
②当 时:
如图J9.24所示,延长 DC,AF 交于点G,可得 则 设 FG=2b,则AG=6+2b,PC=b,连接AC,又易得 则 即GC=3b,因此EG=2+3b,则 解得 故
模块1 本 质 原 理
在折叠问题中,其本质原理会产生以下6种情景:
(1)产生全等:折叠前后会有全等产生,所以会有等边和等角;
(2)产生角平分线:如遇平行线,那么翻折后会有等腰三角形出现;
(3)产生中垂线:折痕是对称点连线的垂直平分线;
(4)求边长:利用设元勾股求边长,一般情况下,求什么设什么;
(5)折叠后图不定:可能是等腰三角形或直角三角形等,需要分类讨论;
(6)最值问题:如折痕过某一定点,此时往往用辅助圆来解决问题.
1.折对角线
如图9.1所示,已知四边形 ABCD 为矩形.
①△ABE≌△C'DE;
②△BED 为等腰三角形;
实例剖析
如图9.2所示,在矩形 ABCD中,AB=4,BC=3.将矩形 ABCD 沿对角线AC 折叠,点B 的对称点为B',连接 DB',则
【答案】
【分析】 设 AB'与CD 交于点F,易得 则△DAF≌△B'CF(AAS),故
在矩形 ABCD中,AB=4,BC=3,∠B=90°,则.
设 则FC=4-x.
在 Rt△DFA 中,依据勾股定理得 解得 故 易得△FAC∽△FB'D,则 即 解得
2.点折到点
如图9.3所示,已知四边形 ABCD 为矩形.
①△ABE≌△C'BF;
②△BEF 为等腰三角形;
③ 连接 DF,四边形 BEDF 为菱形;
实例剖析
如图9.4所示,在矩形纸片 ABCD中,AB=3,AD=9,将其折叠,使点 D 与点B 重合,折痕为 EF,则CF= .
【答案】 4.
【分析】 因为 AD∥BC,∠DEF=∠BEF,所以∠DEF=∠BEF=∠EFB,故 BF= BE=DE.
设 BF=BE=DE=x,在 Rt△ABE 中,因为 所以 解得x=5,故CF=BC-BF=9-5=4.
3.点折到线
如图9.5所示,已知四边形 ABCD 为矩形.
②△ABF∽△FCE.
实例剖析
如图9.6所示,折叠矩形 ABCD 的一边AD,使点 D 落在BC边的点F 处.若 CF=4, 则折痕 AE= .
【答案】
【分析】 由勾股定理得 则 DC=AB=8.
易得△ABF∽△FCE,则 即 解得 BF=6.
又 AF = AD = BF + CF =10,在 Rt△AFE 中,由勾股定理得
4.完美折叠
如图9.7所示,已知四边形 ABCD 为矩形.
① 四边形 EFGH 为矩形;
② E,G 分别是AB,CD 的中点;
③ HF=AD=BC.
实例剖析
如图9.8所示,平行四边形纸片ABCD 的边AB,BC的长分别是10cm和7cm,将其四个角向内对折后,点B 与点C重合于点C',点A 与点D 重合于点A'.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形 ABCD 的四条边上,则
【答案】 10.
【分析】 由翻折可知 则 即∠FHE=90°.
同理可证∠HFG=∠GEH=90°,所以四边形 EHFG 是矩形,易得 则△HCF≌△GAE(AAS),因此 CF=AE,故
EF = EA'+ FA' = AE + FD = CF + FD = CD = 10cm.
5.隐藏“半角模型”、隐藏等腰三角形
如图9.9所示,已知四边形 ABCD 为正方形.
①△A'BF≌△CBF(图9.10);
②∠EBF=45°(图9.10);
(图9.10);
④△EBG 为等腰三角形(图9.11);
⑤△DEF∽△CGF(图9.11).
实例剖析
如图9.12所示,四边形ABCD 为正方形,点 E 是BC 的中点,将正方形ABCD 沿AE 折叠,得到点 B 的对应点为点F,延长 EF 交线段DC 于点 P.若AB=6,则DP= .
【答案】 2.
【分析】 连接 AP.因为 所以 Rt△AFP ≌Rt△ADP(HL),则 PF=PD.
设 PF= PD=x,则CP=CD--PD=6-x,EP=EF+FP=3+x.
在 Rt△PEC 中,根据勾股定理得 即 解得x=2,则 DP=2.
6.边合并边
如图9.13所示,已知四边形 ABCD 为矩形.
①△EBD'为等腰三角形;
③△IED'∽△CD'F,△IED'≌△A'BD'.
实例剖析
如图9.14所示,已知一个矩形纸片 OABC,OA =6,点 P 为AB 边上一点, 将△OAP 沿OP 折叠,点 A 落在点A'处,延长 PA'交边OC 于点D,经过点 P 再次折叠纸片,使点 B 落在边OC 上的点D 处,则 AB= .
【答案】 12.
【分析】 由折叠的性质可得A 因为AB∥OC,所以∠POD=∠APO,因此∠OPD=∠POD,则OD=DP.
设PB=x,则A'D=x-2,OD=x.
在Rt△A'OD 中,( 即 解得 x=10,故. +BP=2+10=12.
模块2 场 景 演 练
类型的识别
类型1:直接利用设边勾股求边长
1. 如图9.15所示,在△ABC 纸片中, 沿过点 A 的直线将纸片折叠,使点B 落在边BC上的点D处;再折叠纸片,使点C 与点D 重合,若折痕与AC的交点为E,则AE= .
2. 如图9.16所示,在Rt△ABC 纸片中,∠ACB=90°,AC=4,BC=3,点 D,E 分别在AB,AC上,连接DE,将△ADE 沿DE 翻折,使点 A 的对应点F 落在BC的延长线上.若FD平分∠EFB,则
3. 如图9.17所示,在矩形 ABCD 中,AB=4,AD=6,点E 为BC上一点,将△ABE 沿AE 折叠得到△AEF,点 H 为CD 上一点,将△CEH 沿EH 折叠得到△EHG,且点 F 落在线段EG 上.当GF=GH 时,
4. 如图9.18所示,在 中,点 E,F分别在边AB,AD 上,将 沿EF 折叠,点 A 恰好落在BC 边上的点G 处.若 则
类型2:平行线+角平分线 等腰三角形
5. 如图9.19所示,在长方形纸片 ABCD 中, 把纸片沿直线 AC 折叠,点B落在点E 处,AE 交DC 于点O,若 ,则 CD 的长为 .
6.如图9.20所示,将矩形纸片 ABCD 沿EF,GN折叠,使点 A 和点C 重合于点M,点D与点H 重合,点 B 落在边AD 上的点P 处,且 MN 经过点P.已知 则
类型3:对称点的连线,巧用十字模型
7.如图9.21所示,点 E 和点F 分别在正方形纸片ABCD的边CD 和AD上,连接AE,BF,沿BF 所在直线折叠该纸片,点A 恰好落在线段AE 上点G 处.若正方形纸片边长为12,DE=5,则(
8. 如图9.22所示,在矩形纸片 ABCD 中,E 为BC 的中点,连接AE,将 沿AE折叠得到 连接CF.若 则
9.如图9.23所示,将矩形 ABCD 沿着DE 所在的直线折叠,点 A 的对应点是点 连接 并延长交CD 于点F.若E 是AB 的中点,AB=2,AD=3,则
类型4:直角的翻折,巧用三垂直模型
10.如图9.24所示,在平面直角坐标系中,已知矩形 OABC,O为原点,点 A,C分别在x轴、y轴上,点 B 的坐标为(1,2),连接OB,将 沿直线OB 翻折,点A 落在点D 的位置,则 的值是 .
11.如图9.25所示,小红用一张长方形纸片 ABCD 进行折纸,使得顶点 D 落在边 BC上的点F处(折痕为 AE).已知AB为8cm,BC为10cm,则 EC 的长度为 .
中小学教育资源及组卷应用平台
12. 如图9.26所示,在矩形纸片 ABCD中,点 E,F 分别在矩形的边AB,AD 上,将矩形纸片沿CE,CF 折叠,点 B 落在点H 处,点 D 落在点G 处,点 C,H,G 恰好在同一直线上.若 ,则
类型5:等边三角形的翻折,巧用一线三等角模型
13. 如图9.27所示,在等边 中,D是BC边上的一点,把 折叠,使点 A 落在 BC 边上的点D 处,折痕与边 AB,AC 分别交于点M,N.若 ,则边 BC长为 .
类型6:无长度数据的特殊角度型
14.如图9.28所示,先将正方形纸片ABCD 对折,折痕为直线 EF,把正方形 ABCD 展平.点H在FC上,将纸片沿直线 DH 折叠,点 C 恰好落在直线EF 上的点G处,连接AG.下列结论:
① 直线 EF 垂直平分线段AD;
与 关于直线DH 成轴对称;
是等边三角形;
其中正确的结论为 .
15.如图9.29所示,将四边形纸片 ABCD 沿过点A 的直线折叠,使得点 B 落在CD上的点Q处,折痕为 AP.再将 分别沿PQ,AQ 折叠,此时点 C,D 落在AP 上的同一点R 处.当. 时,
类型7:定长翻折,巧用辅助圆
16. 如图9.30所示,在矩形 ABCD 中, ,点 E 是AD 边的中点,点 F 是射线AB 上的一动点,将 沿EF 所在的直线翻折得到, 连接 则 的最小值为 .
17. 如图9.31所示,在边长为8的菱形 ABCD 中, M是边AD的中点,N是AB 上一点,将 沿MN所在的直线翻折得到 连接 则 的取值范围为 .
18. 如图9.32所示,在菱形 ABCD中, 折叠该菱形,使点 A 落在边BC 上的点M处,折痕分别与边 AB,AD 交于点E,F.当点 M 的位置变化时,DF 长的最大值为 .
类型8:折叠后图形不确定,分类讨论问题
在矩形 ABCD 中,将边AB 翻折到对角线BD 上,点A 落在点M 处,折痕BE 交AD于点 E.将边 CD 翻折到对角线BD 上,点 C 落在点N 处,折痕 DF 交BC 于点F. 则
20. 如图9.33所示,正方形 ABCD 的边长是8,点 E 在边AB 上, 点F 是边BC上不与点 B,C重合的一个动点,把 沿EF 折叠,点 B 落在 处.若 恰为等腰三角形,则 的长为 .
21. 如图9.34所示,在 中, 点 E,F 分别为AB,AC 上一个动点,连接 EF,以 EF 为轴将 折叠得到 使点 D 落在BC 上.当 为直角三角形时,BE 的值为 .
综合应用:遇见中考
22.如图9.35所示,在正方形 ABCD 中, ,将 BC 沿CE 翻折,使点B对应点刚好落在对角线AC上的点G,将AD 沿AF 翻折,使点 D 对应点刚好落在对角线AC 上的点H,则.
23.如图9.36所示,在矩形 ABCD 中,点 M 在AB边上,把 沿直线CM 折叠,使点 B落在AD边上的点E 处,连接EC,过点 B 作 ,垂足为点 F.若 ,则线段
24.如图9.37所示,在 中, 将边 BC 沿CN折叠,使点 B 落在AB 上的点. 处,再将边 AC 沿CM 折叠,使点 A 落在( 的延长线上的点 处,两条折痕与斜边 AB 分别交于点N,M,则线段
25如图9.38所示,在矩形纸片 ABCD 中, ,M 是BC上的点,且 将矩形纸片 ABCD 沿过点M 的直线折叠,使点 D 落在AB 上的点P 处,点C落在点 处,折痕为 MN,则线段.
26. 如图9.39 所示,在 中,D,E 分别为BC,AC 上的点,将 沿DE 折叠,得到 连接BF,CF, 若 10,则 AE 的长为 .
27.如图9.40所示,在矩形纸片 ABCD 中, .把 沿对角线BD 折叠,使点 C 落在点( 处, 交AD 于点G;E,F分别是C'D 和BD 上的点,线段 EF 交AD 于点H,把 沿EF 折叠,使点 D 落在点A 处,则.
28.(2022·深圳)(1)发现:如图9.41所示,在正方形 ABCD 中,E为AD边上一点.将 沿BE 翻折到 处,延长 EF 交CD 边于点G.求证:
(2)探究:如图9.42所示,在矩形 ABCD中,E 为AD 边上一点,且. 将△AEB 沿BE 翻折到 处,延长EF交BC 边于点G,延长BF 交CD 边于点H,且 FH=CH,求 AE 的长.
(3)拓展:如图9.43所示,在菱形 ABCD 中,E为CD 边上的三等分点,( 60°.将△ADE 沿AE 翻折得到 ,直线 EF 交直线BC 于点P,则
第9讲 图形对称之折叠
1.
在 Rt△ADE 中, ,设AE=x,则CE=DE=3-x,即 x ,解得 故
2.
因为将△ADE 沿DE 翻折得到△DEF,所以∠A=∠DFE=∠DFB,则∠B+∠DFB=90°,于是
设BD=m,则AD=DF=5-m,因为 所以 则 故CF= BF
3. 2.
由折叠可得 进而得出在 Rt△AEH 中,.
设BE=x,则EF=x,CE=6-x=EG,FG=GH=HC=6-2x,DH=4-(6-2x)=2x-2,再根据勾股定理,可得 即 解得x=2,即可得到 BE 的长为2.
如图J9.1所示,过点 B 作BM⊥AD 于点M,过点 F 作FH⊥BC 于点H,过点 E 作EN⊥CB 的延长线于点 N,得到矩形 BHFM.
在 Rt△GEN中,根据勾股定理,得 即 解得GN=7.
设MF=BH=x,则GH=GN-BN-BH=7-1-x=6-x,GF=AF=AM+FM=6+x.
在 Rt△GFH 中,根据勾股定理,得( 即 解得 故
5. 8cm.
由折叠的性质可得∠BAC=∠EAC=∠ACD,则AO=CO=5cm.在Rt△ADO 中,根据勾股定理得 故CD=DO+CO=3+5=8(cm).
作 PR⊥BC于点R.因为∠PFE=∠BFE,AD∥BC,所以∠PFE=∠PEF=∠BFE,则PE= PF.
同理可得 PN=PG,则
设PF=4a,PN=3a,则FN=5a,即5a=10,亦即a=2,故PF=4a=8,PN=3a=6.
因为 所以 故 AB= PR
设 BF 与AE 的交点为H,由折叠及轴对称的性质可知△ABF≌△GBF,BF 垂直平分AG,易得△ABF≌△DAE(ASA),则 AE=BF=13.
因为 所以12×5=13AH,即 故AG=2AH
又 AE=BF=13,则
如图J9.2所示,连接 BF,交 AE 于点O.将△ABE 沿AE 折叠得到△AFE,AE 垂直平分BF.
因为 BE=CE=EF=3,所以∠BFC=90°.
在 Rt△ABE 中,由勾股定理得 所以 故
在Rt△BCF中,由勾股定理得
如图J9.3所示,连接 AA′,则 AA′⊥ED.
将矩形 ABCD 沿着DE 所在的直线折叠,则.
因为 E 为AB 的中点,所以 AE = BE = EA′,因此. ∠EA'A=β,则. 即AA′⊥BF,故 DE∥BF.
又因为 BE∥DF,所以四边形 EBFD 是平行四边形,则 DE=BF.
因为AE=1,AD=3,所以 故
如图J9.4所示,构造一线三垂直,易证△BED∽△DFO,相似比为OD:BD=1∶2.
设 OF = CE = x,则 DE = 2x,DF =2-2x,即 解得 故
11. 3cm.
易证△ABF∽△FCE,设CE=x,则 DE=EF=8-x,所以 解得x=3(cm).
12. 2.
如图J9.5所示,延长EH 交CF 于点P,过点 P 作MN⊥CD 于点N.
将矩形纸片沿CE,CF 折叠,点 B 落在点H 处,点 D 落在点G 处,则 BC=CH =4,∠DCF=∠GCF,BE=EH=2,∠B=∠CHE=90°,易得△CPH≌△CPN(AAS),故 NP=PH,CH=CN=4.
又 CN=CB=4,则四边形 BCNM 是正方形.
在Rt△EPM中, 即( 解得
因为 所以 故 DF=2.
设BD=x,DC=y.由△BMD∽△CDN,可得(BM+MD+BD):(DN+NC+CD)=DM:DN=2:3,推出(2x+y):(x+2y)=2:3,即y=4x,则AB=BC=AC=5x,MB=5x-2,CN=5x-3.再根据 构建方程 解得 故 BC=5x
14. ①②③.
因为是将正方形纸片 ABCD 对折,得折痕为直线 EF,把正方形 ABCD 展平,得 AE=DE,∠AEF=∠DEF=90°,所以直线 EF 垂直平分线段AD,故①正确;
因为△DGH 是△DCH 沿DH 折叠得到的,所以△DGH 与△DCH 关于直线DH 成轴对称,故②正确;
由①得GA=GD,由②得GD=CD,因为 CD=AD,所以△ADG 是等边三角形,故③正确;
因为∠ADG=60°,所以 故④不正确.
因为∠QRA+∠QRP=180°,所以∠D+∠C=180°,AD∥BC,又AD=CP,则四边形APCD 是平行四边形.
因为∠DQR+∠CQR =180°,所以∠DQA+∠CQP=90°,则∠AQP=90°,因此 AD=CP=AR = PR =QR =a,CD=AP=2QR =2a,由折叠的性质可得∠CPQ=∠QPR =∠APB,故∠QPA=60°.
在 Rt△AQP 中, 则 故
如图J9.6 所示,根据点 F 是射线AB 上的一动点,将△AEF 沿EF 所在的直线翻折得到△A'EF,可得点 A'的运动路径为以点E 为圆心、AE 长为半径的半圆,再根据两点之间线段最短,即可得出当点 A',C,E三点共线时,A'C的长最小,最后根据勾股定理进行计算即可.
如图J9.7所示,连接 BM,BD.依据 M 是边AD 的中点, 沿 MN 所在的直线翻折得到 即可得到点 A'的轨迹为以AD 为直径的半圆M.依据, 即可得出
当点 N 与点A 或点D 重合时,A'B的最大值为8,即可得到 的取值范围.
如图J9.8 所示,当 FM 最小时,FD 最大,此时 在 中, sin C = 解得
19. 12或
① 当点 M 在线段BN 上时,如图J9.9所示.
由折叠性质得 AB=BM=DC=DN=5,则 BD= BM+MN+DN=13.
因为 所以
② 当点 M 在线段DN 上时,如图J9.10所示.
由折叠性质得 AB = BM= DC = DN=5,则 DM=5+2=7.
因为∠C=90°,所以
或8.
① 如图J9.11所示.当. 时,过点 B'作GH∥AD,则∠B'GE=90°.
此时,
由 得 由翻折的性质,得 则 EG=AG-AE= 所以. ,故
②如图J9.12所示.当 时,
③当 时,因为EB=EB',CB=CB',点 E,C在BB'的垂直平分线上,故 EC垂直平分BB'.
由折叠可知点 F 与点C 重合,不符合题意,舍去.
综上所述,DB'的长为 或8.
或
①如图J9.13所示,当∠EDB=90°时,设BE=x,则AE=ED=10-x.
因为 DE∥AC,所以 即 解得
②如图J9.14所示,当∠DEB=90°时,设 BE=x,则AE=ED=10-x.
因为 所以 解得
综上所述,满足条件的 BE 的值为 或
22.
如图J9.15所示,作 FM⊥AB 于点M.
因为 EG=EB=AG=1,∠EGC=∠B=90°,所以 进而可设 FD=FH=CH=a,CF= a,则. 解得a =1,因此 AM=FD=1,EM= 故
因为 BC=CE,∠EDC=∠CFB=90°,∠DEC=∠BCF,所以△EDC≌△CFB(AAS),则 D AD,故 AE = AD - DE =
24.
由两次翻折知∠MCN=45°.因为 CN·AB=AC·BC,所以 CN·10=8×6=48,即 故
又 代入数值得 故
25. 5.
连接 PM,MD.如图J9.16所示,由折叠性质得 则 Rt△PBM≌Rt△MCD(HL),故 PB=CM=2,PA=AB--PB=5.
如图J9.17所示,延长ED 交FC 于点G,延长 BA,DE 交于点H.
由折叠可得 EG⊥CF,又∠BFC=90°,则 BF∥EG.
因为AB∥EF,所以四边形 BFEH 是平行四边形,故BH=EF=10,AH=BH---AB=10
因为AB∥EF,则∠H=∠1,又∠2=∠1=∠3,则∠H=∠3,故.
由翻折得到∠C'DB=∠BDC.因为 EF⊥AD,CD⊥AD,所以 EF∥CD,∠EFD =∠BDC,故∠EFD=∠EDF,ED=EF.
设ED=x,则EH=x-3.在 Rt△EHD中, 即 解得 故
28.(1)利用HL 型全等即可得证.
(2) 如图J9.18所示,连接GH,易证△FHG≌△CHG(HL),故 FG=CG.
设 FG=CG=x,则 BG=8-x.
因为∠1=∠2,∠1=∠EBC,所以∠2=∠EBG,故EG=BG=8-x.在Rt△BFG 中, 解得 故
或
思路 1 同第(1)(2)问的方法类比可得.
①当 时:
如图J9.19所示,连接AC,AP,易得∠PFA=∠PCA=120°,AF=AC=6.
连接CF,∠AFC=∠ACF,则∠PFC=∠PCF,PC=PF=2x.
作 PH⊥CD,在 Rt△PCH 中,∠PCH=60°,则(
在 Rt△PHE中,( 解得 故
② 当 时:
如图J9.20所示,同①得CP=PF,所以PC=PF=m,则EP=4-m.
在△PCE 中,∠ECP=120°,解三角形可得 故
综上所述, 或
思路2 角平分线+平行线 等腰三角形.
①当 时:
如图J9.21所示,延长PE,BA 交于点M,由于折叠,∠DEA=∠FEA,因此∠1=∠2.因为DC∥AB,所以∠2=∠EAM,则∠1=∠EAM,即 MA=ME.
设MA=ME=n,在△MAF 中,∠AFM=60°,AF=6,AM=n,MF=n+2,解三角形可得 n=14.
由 可得
②当 时:
如图J9.22所示,延长EF,AB 交于点R,同①可得△AER 为等腰三角形,则RE=RA.
设BR=c,则AR=c+6,FR=c+2.在△FAR 中, ,解三角形可得c=8.
由 可得
思路3 通过二次相似转化.
①当 时:
如图J9.23所示,可得△EFG∽△ECP,则
设FG=a,则AG=6-a,PC=2a.连接AC,又易得△EFG∽△ACG,则 即GC=3a,因此EG=4-3a,则 解得 故
②当 时:
如图J9.24所示,延长 DC,AF 交于点G,可得 则 设 FG=2b,则AG=6+2b,PC=b,连接AC,又易得 则 即GC=3b,因此EG=2+3b,则 解得 故
同课章节目录
