第11讲 瓜豆原理最值问题(含答案) 2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第11讲 瓜豆原理最值问题(含答案) 2025年中考数学几何模型方法巩固练习 |  | |
| 格式 | docx | ||
| 文件大小 | 610.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:39:46 | ||
图片预览

文档简介
瓜豆原理最值问题
类型1:瓜豆原理(直线形路径)
模型说明 图 示 结论及证明方法
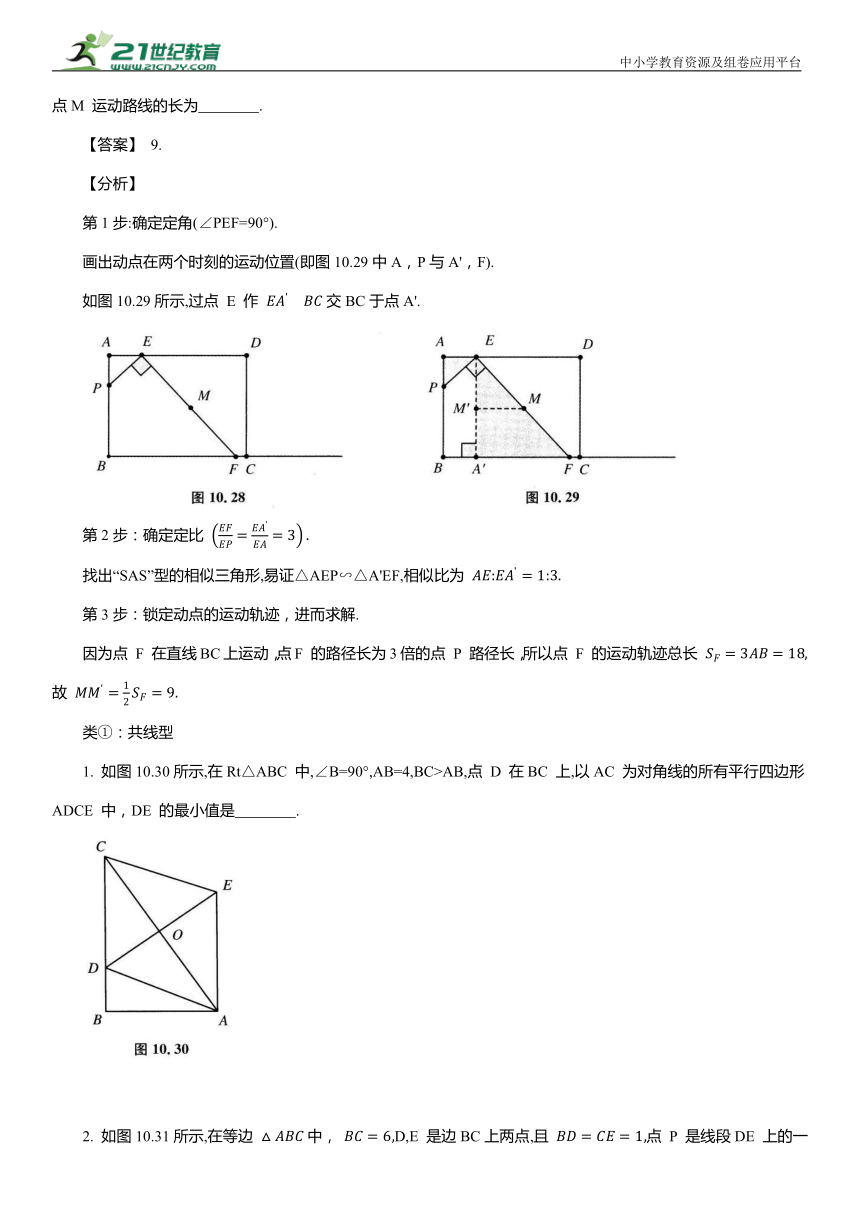
类①:共线型 点 P 在直线l上运动,点O是定点, 0P=k,点 P 叫作主动点,点Q 叫作从动点 在运动过程中,点Q 的运动轨迹也是直线. 证明:由 p= 0=k,i可得△OQ'Q∽△OP'P,则∠OQ'Q=∠OP'P,故得证
模型说明 图 示 结论及证明方法
类②:折角型 点 P 在直线l 上运动,点O是定点, φ=k,∠O=a,点 P 叫作主动点,点Q 叫作从动点 在运动过程中,点Q 的运动轨迹也是直线且P,Q两点运动轨迹的夹角为α. 证明:由 z = =k,∠POP'=∠QOQ',可得△OQ'Q∽△OP'P,则00/ pp=k,旋转角为α,故得证
解题步骤 (1)先画出动点在两个时刻的运动位置; (2)再找出“SAS”型的相似三角形; (3)后锁定动点的运动轨迹,进而求解
实例剖析
如图10.28所示,在矩形 ABCD中,AB=6,AD=8,点 E 在边AD 上,且 AE :ED=1:3.动点 P 从点A 出发,沿AB 运动到点B 停止.过点 E 作EF⊥PE 交射线BC 于点F,设M 是线段EF 的中点,则在点 P 运动的整个过程中,点M 运动路线的长为 .
【答案】 9.
【分析】
第1步:确定定角(∠PEF=90°).
画出动点在两个时刻的运动位置(即图10.29中A,P与A',F).
如图10.29所示,过点 E 作 交BC于点A'.
第2步:确定定比
找出“SAS”型的相似三角形,易证△AEP∽△A'EF,相似比为
第3步:锁定动点的运动轨迹,进而求解.
因为点 F 在直线BC上运动,点F 的路径长为3倍的点 P 路径长,所以点 F 的运动轨迹总长 故
类①:共线型
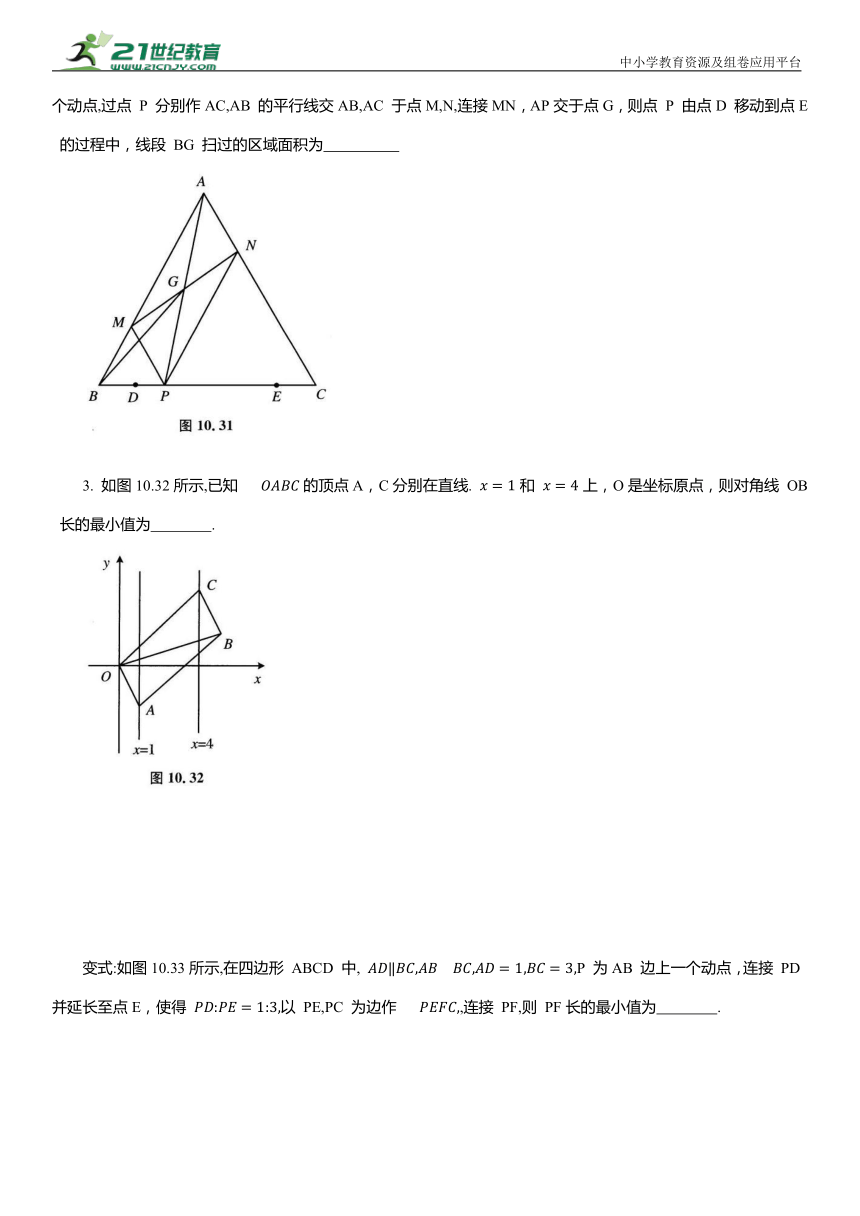
1. 如图10.30所示,在Rt△ABC 中,∠B=90°,AB=4,BC>AB,点 D 在BC 上,以AC 为对角线的所有平行四边形ADCE 中,DE 的最小值是 .
2. 如图10.31所示,在等边 中, D,E 是边BC上两点,且 点 P 是线段DE 上的一个动点,过点 P 分别作AC,AB 的平行线交AB,AC 于点M,N,连接MN,AP交于点G,则点 P 由点D 移动到点E 的过程中,线段 BG 扫过的区域面积为
3. 如图10.32所示,已知 的顶点A,C分别在直线. 和 上,O是坐标原点,则对角线 OB 长的最小值为 .
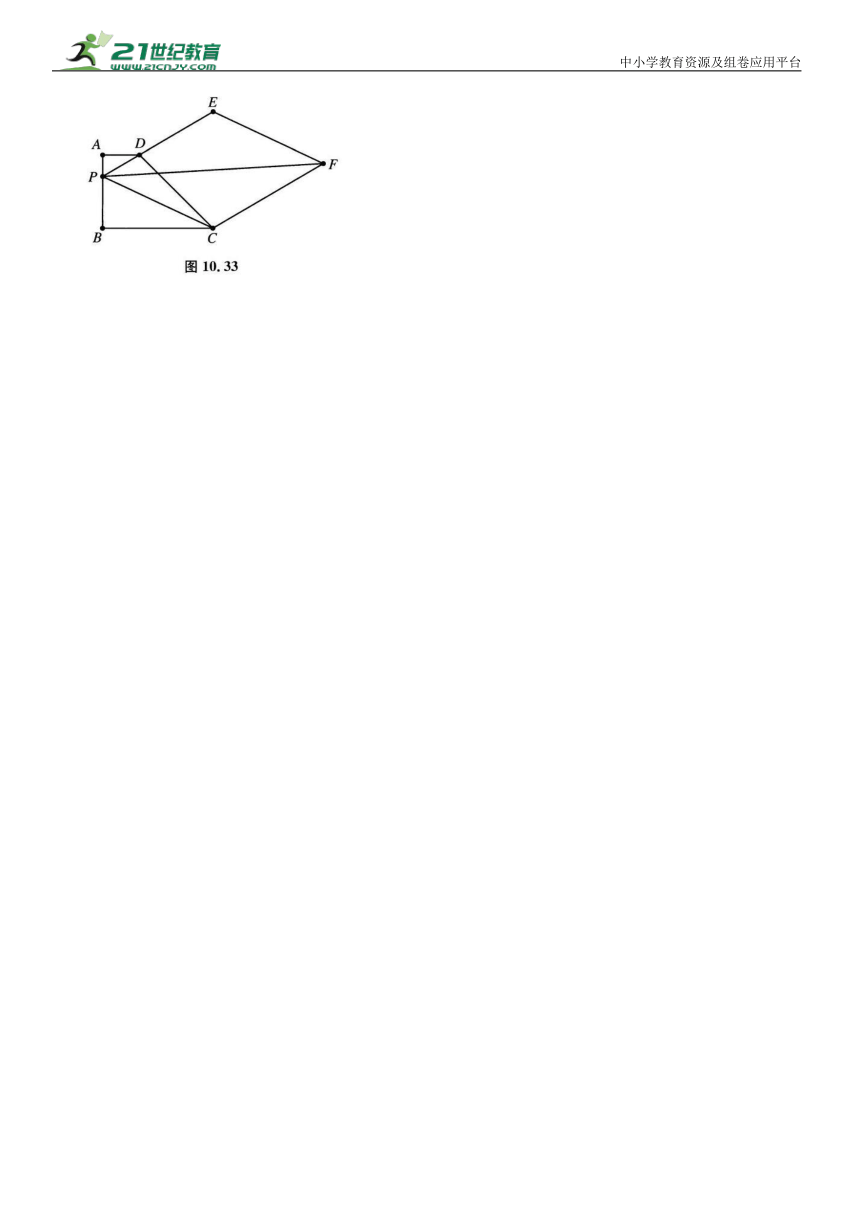
变式:如图10.33所示,在四边形 ABCD 中, P 为AB 边上一个动点,连接 PD 并延长至点E,使得 以 PE,PC 为边作 ,连接 PF,则 PF长的最小值为 .
类②:折角型
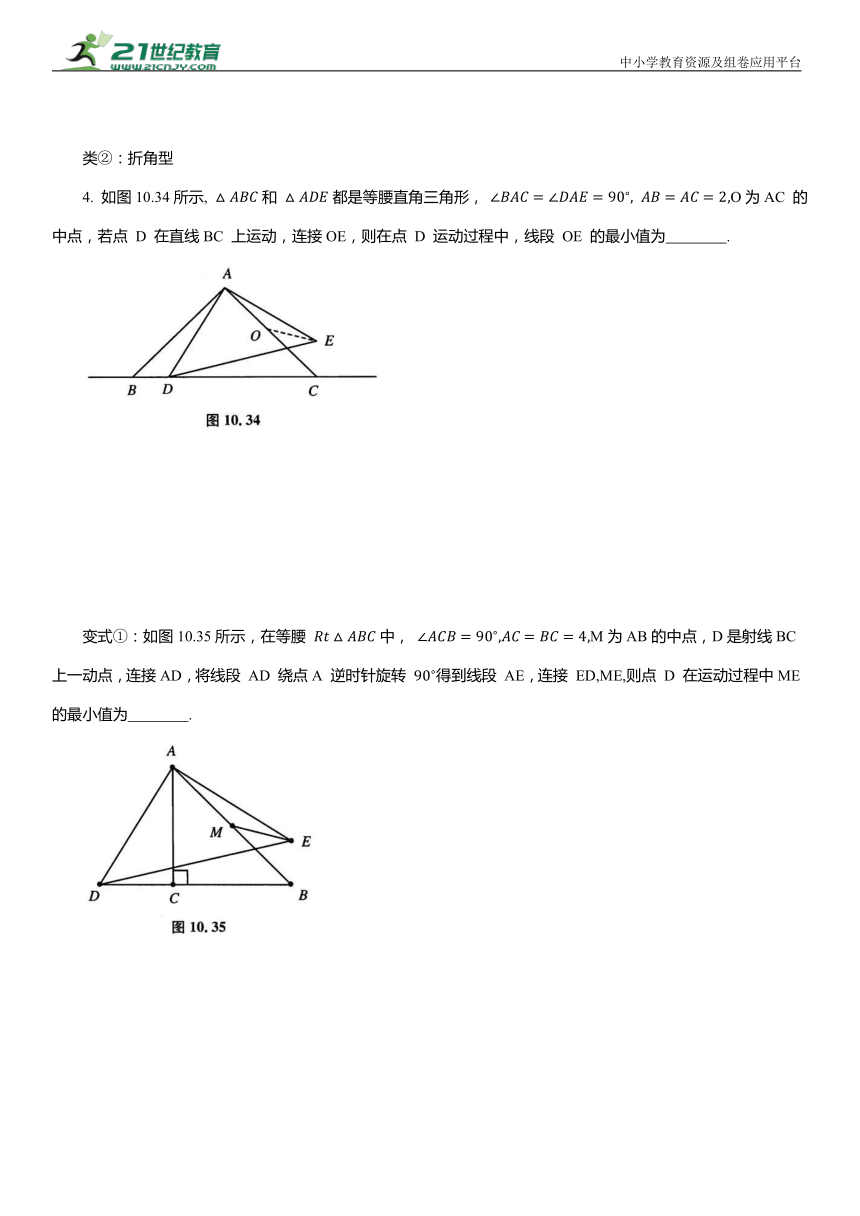
4. 如图10.34所示, 和 都是等腰直角三角形, O为AC 的中点,若点 D 在直线BC 上运动,连接OE,则在点 D 运动过程中,线段 OE 的最小值为 .
变式①:如图10.35所示,在等腰 中, M为AB的中点,D是射线BC上一动点,连接AD,将线段 AD 绕点A 逆时针旋转 得到线段 AE,连接 ED,ME,则点 D 在运动过程中ME 的最小值为 .
变式②:如图10.36所示,已知点 A 是第一象限内横坐标为 的一个定点,射线 AM⊥x轴于点M,交直线. 于点N,点P 是线段ON 上的一个动点, PA,当点 P 从点O 运动到点N时,点B 运动的路径长为 .
5.如图10.37所示,在边长为2a 的等边 中,M是高CH 所在直线上的一个动点,连接 BM,将线段 BM 绕点B 逆时针旋转( 0°得到 BN,连接 HN,则在点 M 运动的过程中,线段 HN长度的最小值为 .
变式①:如图10.38所示,在 中, ,线段 BC 上一动点P 从点C 开始运动,到点 B 停止,以AP 为边在AC 的右侧作等边 则点 Q 运动的路径长为 cm.
变式②:如图10.39所示,点 A 的坐标为(0,4),P 是x轴上一动点,把线段 PA 绕点P顺时针旋转( 得到线段 PF,连接 OF,则线段 OF 长的最小值是 .
类型6:瓜豆原理(圆形路径)
见表10.3.
表10.3
模型说明 图 示 结论及证明方法
类①:共线型 点 P 在⊙M 上运动, 点O 是定点,OP= k,点P 叫作主动点,点 Q 叫作从动点 点 Q 的运动轨迹是⊙N(如上图) 证明:连接OM,PM,在OM 上取一点N,满足 =π/ k=k,连接 NQ,∠QON = ∠POM,因而△OQN∽△OPM,相似比为 k
类②:折角型 点 P 在⊙M 上运动, 点 O 是定点, = k,∠O =α,点 P 叫 作主动点,点Q 叫作 从动点 点 Q 的运动轨迹是⊙N(如上图) 证明:连接OM 并旋转α角和ON 重合,使得ON/ =k,此时09=08=π/k=k,∠QON=∠POM,因而△OQN∽△OPM(旋转型),相似比为 k
中小学教育资源及组卷应用平台
类①:共线型
6. 如图10.40所示,在 中, 点 D 是平面内的一个动点,且. ,M为BD 的中点,在点 D 运动过程中,线段 CM 长度的取值范围是
7.一大一小两个三角板按照图10.41所示的方式摆放,其中 G 为DC 的中点,则在, 绕着点B 旋转的过程中,点 G 到直线AB 的距离的最大值是 .
8. 如图10.42 所示,在 中,/ ,点O 是 的重心,将线段 AO 绕点A 逆时针旋转至点( 点 D 为线段 的中点,连接 BD,则BD 的最大值为
类②:折角型
9. 如图10.43所示,在正方形 ABCD中, O 是BC 边的中点,点E 是正方形内一动点, ,连接 DE,将线段 DE 绕点 D 逆时针旋转! 得 DF,连接 AE,CF,则线段OF 长的最小值为 .
10. 如图10.44所示,在 中, 点E 为平面内一点,且 连接 AE,将 AE 绕着点A 顺时针旋转 得到线段 AF,连接EF,CF,则 CF的最小值为 .
11. 如图10.45所示,点 O 为等腰] 的斜边AB的中点, 2,连接 BE,作等腰 其中 连接 AF,则 的面积的最大值为
.如图10.46所示,在 中,AD 是中线,分别以 AB,AC 为边向外作正方形ABEF,ACGH,连接FH,在 FH 上取一点P,使 若 则点 P 到BC的距离的最大值为 .
1. 4.
提示:由∠BCA =∠CAE 可得AE∥CD,所以点 E 的轨迹在直线AE 上,故 DEmin=AB.
如图J10.24所示,因为 ,所以四边形 AMPN 是平行四边形,则G是AP 的中点,故点 G 的运动路线是△APP'的中位线.
又 BC=6,BD=CE=1,则
因为 BC=6,所以△BGG'的底边GG'上的高 故线段 BG 扫过的区域面积
3. 5.
提示:利用中点坐标公式 可得xB=5,则点 B 的轨迹是直线x=5,故
变式:6.
以B为原点建立坐标系,由 可得.xF=6,则点 F 的轨迹是直线x=6,故
4
连接CE,易证△ABD≌△ACE,则点 E 的轨迹在直线CE上,故
变式①:2.
如图J10.25所示,因为 AD转角为90°,所以先追踪 AC 旋转后的位置AC',从而构造出旋转型全等:△ADC≌△AEC',则点 E 的轨迹在直线EC'上,故 =2.
变式②:3
如图J10.26所示,过点 A 作AN'⊥AN,使 连接 BN'.
由 且∠PAN=∠BAN',得△PAN∽△BAN',则
当 时, 故点 B 运动的路径长为3
连接 AN,易证△ABN≌△CBM,则∠BAN=∠BCM=30°,故点 N 的轨迹在直线AN上,当HN⊥AN时,HN有最小值,利用三角函数求解即可.
变式①:2
如图J10.27所示,因为 AP 转角为60°,所以先追踪 AC 旋转后的位置AC',再构造全等:△ACP≌△AC'Q,故CB与B'C'的夹角为60°,点 Q 在直线C'Q上运动,以 AB 为边长构造等边△ABB',易知当点 P 与点B 重合时,点Q 与点B'重合,点Q 运动的路径长等于
变式②:2.
如图J10.28 所示,构造 为等边三角形,易证 则∠AFE=∠APO,A,P,E,F 四点共圆,, ,故点 F 一直在直线EF 上运动, .连接 AE,易证△AOE≌△AF'E,则. .又OA=4,则 在 Rt△OEG中,OG=2,故
连接 AD,取 AB 的中点N,连接 MN,则点 M 的轨迹就在以点N 为圆心、 为半径的圆上,再根据“点到圆”的最值关系求解即可.
如图J10.29所示,点 O 为BC 的中点,过点 O 作( 于点K.
点G 在以点O为圆心、 为半径的圆上,其中
根据“线到圆”的最值关系,点G 到直线AB 的距离的最大值为
8
如图J10.30所示,取 AC 的中点A',连接. ,则点 D 在以点. 为圆心、 为半径的圆上运动.当点 B,A′,D 共线时,BD 最大.
因为 AB=AC=10,BC=16,点 O 是△ABC 的重心,所以 BC,则 ,故 则
9
本题为折角90°问题.如图J10.31 所示,点 E 的轨迹是以点O 为圆心、OE 为半径的圆,点 F 的轨迹也一定是圆,先追踪定点和圆心距离 OD 的位置,使其逆时针旋转 即和 重合,从而得出 故点 F 在以点 为圆心、 为半径的圆上运动,当点O,F,O'共线时,OF 最小,即
10
本题为折角120°问题,如图J10.32所示,点 E 的轨迹是以点C 为圆心、CE 为半径的圆,点F 的轨迹也一定是圆,先追踪定点和圆心距离AC 的位置,使其顺时针旋转 即和AB 重合,从而得出△ACE≌△ABF,故点 F 的轨迹就是以点B 为圆心、 为半径的圆,当点 C,F,B共线时,
11
本题为折角45°问题.如图J10.33所示,先追踪圆心O 的初始位置( ,使BO 顺时针旋转45°,使得 ,从而易得△BOE∽△BO'F,相似比为 则点 F 的轨迹就是以点O'为圆心. 为半径的圆,故
本题的入手点是经典的“瓜豆原理”,点A 为主动点,点F,H为从动点,为折角 问题,故产生以下步骤:
第1步:如图 J10.34 所示,倍长 AD 至点N,因为, ∠ABN,所以 则 故
第2步:如图J10.35所示,连接 BF,以 BD 为直角边作等腰直角三角形,易得 △BDM,相似比为 ,所以△BDA∽△BMF(一转成双).因为 AD=6,所以
第3步:如图J10.36所示,连接 CH,以 CD 为直角边作等腰直角三角形,易得△ACD∽△HCM,相似比为 因为AD=6,所以
第4步:如图J10.37所示,因为 ,所以△FMH 为等腰直角三角形,连接MP,作 MK⊥FH,易得 MK=6,PK=2,则 故点 P 在以点M 为圆心、 为半径(r)的圆上运动,于是点 P 到BC 的距离的最大值为r+
类型1:瓜豆原理(直线形路径)
模型说明 图 示 结论及证明方法
类①:共线型 点 P 在直线l上运动,点O是定点, 0P=k,点 P 叫作主动点,点Q 叫作从动点 在运动过程中,点Q 的运动轨迹也是直线. 证明:由 p= 0=k,i可得△OQ'Q∽△OP'P,则∠OQ'Q=∠OP'P,故得证
模型说明 图 示 结论及证明方法
类②:折角型 点 P 在直线l 上运动,点O是定点, φ=k,∠O=a,点 P 叫作主动点,点Q 叫作从动点 在运动过程中,点Q 的运动轨迹也是直线且P,Q两点运动轨迹的夹角为α. 证明:由 z = =k,∠POP'=∠QOQ',可得△OQ'Q∽△OP'P,则00/ pp=k,旋转角为α,故得证
解题步骤 (1)先画出动点在两个时刻的运动位置; (2)再找出“SAS”型的相似三角形; (3)后锁定动点的运动轨迹,进而求解
实例剖析
如图10.28所示,在矩形 ABCD中,AB=6,AD=8,点 E 在边AD 上,且 AE :ED=1:3.动点 P 从点A 出发,沿AB 运动到点B 停止.过点 E 作EF⊥PE 交射线BC 于点F,设M 是线段EF 的中点,则在点 P 运动的整个过程中,点M 运动路线的长为 .
【答案】 9.
【分析】
第1步:确定定角(∠PEF=90°).
画出动点在两个时刻的运动位置(即图10.29中A,P与A',F).
如图10.29所示,过点 E 作 交BC于点A'.
第2步:确定定比
找出“SAS”型的相似三角形,易证△AEP∽△A'EF,相似比为
第3步:锁定动点的运动轨迹,进而求解.
因为点 F 在直线BC上运动,点F 的路径长为3倍的点 P 路径长,所以点 F 的运动轨迹总长 故
类①:共线型
1. 如图10.30所示,在Rt△ABC 中,∠B=90°,AB=4,BC>AB,点 D 在BC 上,以AC 为对角线的所有平行四边形ADCE 中,DE 的最小值是 .
2. 如图10.31所示,在等边 中, D,E 是边BC上两点,且 点 P 是线段DE 上的一个动点,过点 P 分别作AC,AB 的平行线交AB,AC 于点M,N,连接MN,AP交于点G,则点 P 由点D 移动到点E 的过程中,线段 BG 扫过的区域面积为
3. 如图10.32所示,已知 的顶点A,C分别在直线. 和 上,O是坐标原点,则对角线 OB 长的最小值为 .
变式:如图10.33所示,在四边形 ABCD 中, P 为AB 边上一个动点,连接 PD 并延长至点E,使得 以 PE,PC 为边作 ,连接 PF,则 PF长的最小值为 .
类②:折角型
4. 如图10.34所示, 和 都是等腰直角三角形, O为AC 的中点,若点 D 在直线BC 上运动,连接OE,则在点 D 运动过程中,线段 OE 的最小值为 .
变式①:如图10.35所示,在等腰 中, M为AB的中点,D是射线BC上一动点,连接AD,将线段 AD 绕点A 逆时针旋转 得到线段 AE,连接 ED,ME,则点 D 在运动过程中ME 的最小值为 .
变式②:如图10.36所示,已知点 A 是第一象限内横坐标为 的一个定点,射线 AM⊥x轴于点M,交直线. 于点N,点P 是线段ON 上的一个动点, PA,当点 P 从点O 运动到点N时,点B 运动的路径长为 .
5.如图10.37所示,在边长为2a 的等边 中,M是高CH 所在直线上的一个动点,连接 BM,将线段 BM 绕点B 逆时针旋转( 0°得到 BN,连接 HN,则在点 M 运动的过程中,线段 HN长度的最小值为 .
变式①:如图10.38所示,在 中, ,线段 BC 上一动点P 从点C 开始运动,到点 B 停止,以AP 为边在AC 的右侧作等边 则点 Q 运动的路径长为 cm.
变式②:如图10.39所示,点 A 的坐标为(0,4),P 是x轴上一动点,把线段 PA 绕点P顺时针旋转( 得到线段 PF,连接 OF,则线段 OF 长的最小值是 .
类型6:瓜豆原理(圆形路径)
见表10.3.
表10.3
模型说明 图 示 结论及证明方法
类①:共线型 点 P 在⊙M 上运动, 点O 是定点,OP= k,点P 叫作主动点,点 Q 叫作从动点 点 Q 的运动轨迹是⊙N(如上图) 证明:连接OM,PM,在OM 上取一点N,满足 =π/ k=k,连接 NQ,∠QON = ∠POM,因而△OQN∽△OPM,相似比为 k
类②:折角型 点 P 在⊙M 上运动, 点 O 是定点, = k,∠O =α,点 P 叫 作主动点,点Q 叫作 从动点 点 Q 的运动轨迹是⊙N(如上图) 证明:连接OM 并旋转α角和ON 重合,使得ON/ =k,此时09=08=π/k=k,∠QON=∠POM,因而△OQN∽△OPM(旋转型),相似比为 k
中小学教育资源及组卷应用平台
类①:共线型
6. 如图10.40所示,在 中, 点 D 是平面内的一个动点,且. ,M为BD 的中点,在点 D 运动过程中,线段 CM 长度的取值范围是
7.一大一小两个三角板按照图10.41所示的方式摆放,其中 G 为DC 的中点,则在, 绕着点B 旋转的过程中,点 G 到直线AB 的距离的最大值是 .
8. 如图10.42 所示,在 中,/ ,点O 是 的重心,将线段 AO 绕点A 逆时针旋转至点( 点 D 为线段 的中点,连接 BD,则BD 的最大值为
类②:折角型
9. 如图10.43所示,在正方形 ABCD中, O 是BC 边的中点,点E 是正方形内一动点, ,连接 DE,将线段 DE 绕点 D 逆时针旋转! 得 DF,连接 AE,CF,则线段OF 长的最小值为 .
10. 如图10.44所示,在 中, 点E 为平面内一点,且 连接 AE,将 AE 绕着点A 顺时针旋转 得到线段 AF,连接EF,CF,则 CF的最小值为 .
11. 如图10.45所示,点 O 为等腰] 的斜边AB的中点, 2,连接 BE,作等腰 其中 连接 AF,则 的面积的最大值为
.如图10.46所示,在 中,AD 是中线,分别以 AB,AC 为边向外作正方形ABEF,ACGH,连接FH,在 FH 上取一点P,使 若 则点 P 到BC的距离的最大值为 .
1. 4.
提示:由∠BCA =∠CAE 可得AE∥CD,所以点 E 的轨迹在直线AE 上,故 DEmin=AB.
如图J10.24所示,因为 ,所以四边形 AMPN 是平行四边形,则G是AP 的中点,故点 G 的运动路线是△APP'的中位线.
又 BC=6,BD=CE=1,则
因为 BC=6,所以△BGG'的底边GG'上的高 故线段 BG 扫过的区域面积
3. 5.
提示:利用中点坐标公式 可得xB=5,则点 B 的轨迹是直线x=5,故
变式:6.
以B为原点建立坐标系,由 可得.xF=6,则点 F 的轨迹是直线x=6,故
4
连接CE,易证△ABD≌△ACE,则点 E 的轨迹在直线CE上,故
变式①:2.
如图J10.25所示,因为 AD转角为90°,所以先追踪 AC 旋转后的位置AC',从而构造出旋转型全等:△ADC≌△AEC',则点 E 的轨迹在直线EC'上,故 =2.
变式②:3
如图J10.26所示,过点 A 作AN'⊥AN,使 连接 BN'.
由 且∠PAN=∠BAN',得△PAN∽△BAN',则
当 时, 故点 B 运动的路径长为3
连接 AN,易证△ABN≌△CBM,则∠BAN=∠BCM=30°,故点 N 的轨迹在直线AN上,当HN⊥AN时,HN有最小值,利用三角函数求解即可.
变式①:2
如图J10.27所示,因为 AP 转角为60°,所以先追踪 AC 旋转后的位置AC',再构造全等:△ACP≌△AC'Q,故CB与B'C'的夹角为60°,点 Q 在直线C'Q上运动,以 AB 为边长构造等边△ABB',易知当点 P 与点B 重合时,点Q 与点B'重合,点Q 运动的路径长等于
变式②:2.
如图J10.28 所示,构造 为等边三角形,易证 则∠AFE=∠APO,A,P,E,F 四点共圆,, ,故点 F 一直在直线EF 上运动, .连接 AE,易证△AOE≌△AF'E,则. .又OA=4,则 在 Rt△OEG中,OG=2,故
连接 AD,取 AB 的中点N,连接 MN,则点 M 的轨迹就在以点N 为圆心、 为半径的圆上,再根据“点到圆”的最值关系求解即可.
如图J10.29所示,点 O 为BC 的中点,过点 O 作( 于点K.
点G 在以点O为圆心、 为半径的圆上,其中
根据“线到圆”的最值关系,点G 到直线AB 的距离的最大值为
8
如图J10.30所示,取 AC 的中点A',连接. ,则点 D 在以点. 为圆心、 为半径的圆上运动.当点 B,A′,D 共线时,BD 最大.
因为 AB=AC=10,BC=16,点 O 是△ABC 的重心,所以 BC,则 ,故 则
9
本题为折角90°问题.如图J10.31 所示,点 E 的轨迹是以点O 为圆心、OE 为半径的圆,点 F 的轨迹也一定是圆,先追踪定点和圆心距离 OD 的位置,使其逆时针旋转 即和 重合,从而得出 故点 F 在以点 为圆心、 为半径的圆上运动,当点O,F,O'共线时,OF 最小,即
10
本题为折角120°问题,如图J10.32所示,点 E 的轨迹是以点C 为圆心、CE 为半径的圆,点F 的轨迹也一定是圆,先追踪定点和圆心距离AC 的位置,使其顺时针旋转 即和AB 重合,从而得出△ACE≌△ABF,故点 F 的轨迹就是以点B 为圆心、 为半径的圆,当点 C,F,B共线时,
11
本题为折角45°问题.如图J10.33所示,先追踪圆心O 的初始位置( ,使BO 顺时针旋转45°,使得 ,从而易得△BOE∽△BO'F,相似比为 则点 F 的轨迹就是以点O'为圆心. 为半径的圆,故
本题的入手点是经典的“瓜豆原理”,点A 为主动点,点F,H为从动点,为折角 问题,故产生以下步骤:
第1步:如图 J10.34 所示,倍长 AD 至点N,因为, ∠ABN,所以 则 故
第2步:如图J10.35所示,连接 BF,以 BD 为直角边作等腰直角三角形,易得 △BDM,相似比为 ,所以△BDA∽△BMF(一转成双).因为 AD=6,所以
第3步:如图J10.36所示,连接 CH,以 CD 为直角边作等腰直角三角形,易得△ACD∽△HCM,相似比为 因为AD=6,所以
第4步:如图J10.37所示,因为 ,所以△FMH 为等腰直角三角形,连接MP,作 MK⊥FH,易得 MK=6,PK=2,则 故点 P 在以点M 为圆心、 为半径(r)的圆上运动,于是点 P 到BC 的距离的最大值为r+
同课章节目录
