第13讲 费马点最值(含答案) 2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第13讲 费马点最值(含答案) 2025年中考数学几何模型方法巩固练习 |  | |
| 格式 | docx | ||
| 文件大小 | 297.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:43:07 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
费马点
问 题 作 法 图 形 原 理
平面内有一点 P,点P 到△ABC(三个内角均小于 120°)三个顶点的距离和何时最小 将△PBC 绕着点 B 逆时针旋转60°,连接PP',AC'.故(AP+BP +CP) min = (AP + PP'+ CP') min =AC',此时 A,P,P',C'共线,且∠APB=∠APC =∠CPB = 120°,满足条件的点 P 叫作费马点 两点之间线 段最短 核心思想: 手拉手模型 的构造
注:若三角形有一个内角大于或等于120°,那么这个顶点就是费马点.
实例剖析
如图10.75所示,在Rt△ABC 中,∠C=90°,AC=1,∠ABC=30°,点 P 为 Rt△ABC的费马点,连接AP,BP,CP,则 PA+PB+PC 的值为 .
【答案】
【分析】 如图10.76所示,将△APB 绕点B 顺时针旋转60°至△A'P'B 处,连接 PP',则A'B=AB=2,BP=BP',A'P'=AP,于是△BPP'是等边三角形,故. ∠BP'P=60°.
因为 ,所以 ,故C,P,A',P'四点共线.
在Rt△A'BC 中, 故
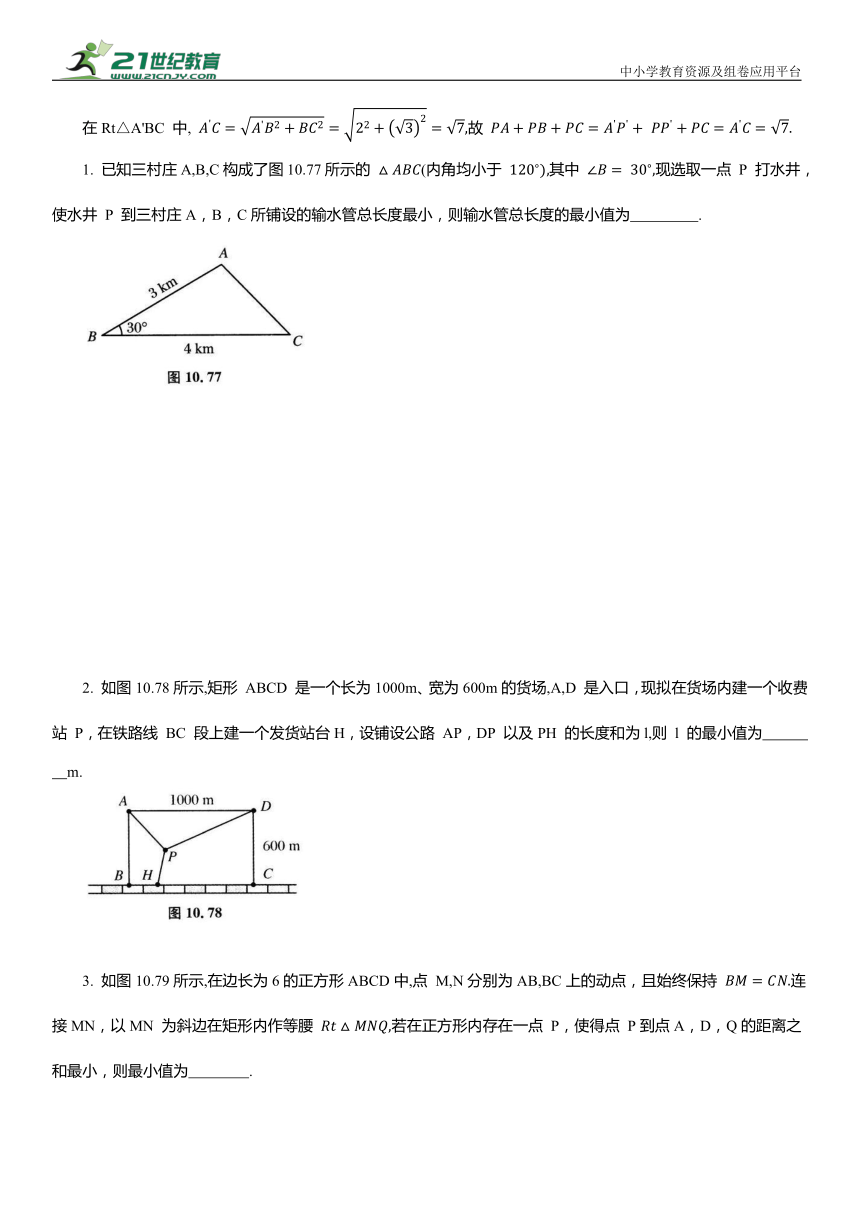
1. 已知三村庄A,B,C构成了图10.77所示的 (内角均小于 其中 现选取一点 P 打水井,使水井 P 到三村庄A,B,C所铺设的输水管总长度最小,则输水管总长度的最小值为 .
2. 如图10.78所示,矩形 ABCD 是一个长为1000m、宽为600m的货场,A,D 是入口,现拟在货场内建一个收费站 P,在铁路线 BC 段上建一个发货站台H,设铺设公路 AP,DP 以及PH 的长度和为l,则 l 的最小值为 m.
3. 如图10.79所示,在边长为6的正方形ABCD中,点 M,N分别为AB,BC上的动点,且始终保持 连接MN,以MN 为斜边在矩形内作等腰 若在正方形内存在一点 P,使得点 P到点A,D,Q的距离之和最小,则最小值为 .
4. 如图10.80所示,在 中, P为 的费马点,且满足 则 的面积为 .
1. 5km.
如图J10.59所示,以 BC为边在△ABC 的外部作等边△BCD,连接AD,则 AD 的长就是△ABC 的费马距离,可得∠ABD=90°,故.
2
提示:如图J10.60所示,将 绕着点D 顺时针旋转过点 作 于点E,线段 A E 即为最短.
3
如图J10.61所示,易得 Q,M,B,N 四点共圆,且 ,利用“邻等对补模型”易得 ,此时 为等腰直角三角形,点Q 刚好在正方形对角线的交点处,过点 Q作 于点E.
因为 PA+PD+PQ最小,所以点 P 是△ADQ 的费马点,则∠APD=∠APQ=∠DPQ=120°,而 解得 故 则PA+PD+PQ=
4
如图J10.62所示,延长 BP 交AC 于点D.
因为∠BAC=∠PBA=45°,所以∠ADB=90°,AD=BD.
又 P 为△ABC 的费马点,则∠APB=∠CPA=120°,故.
在 Rt△PAD 中,因为 PA=4,所以
又∠APC=120°,则.
在 Rt△PDC 中,因为∠PCD=30°,所以( 故. 4 ,则
费马点
问 题 作 法 图 形 原 理
平面内有一点 P,点P 到△ABC(三个内角均小于 120°)三个顶点的距离和何时最小 将△PBC 绕着点 B 逆时针旋转60°,连接PP',AC'.故(AP+BP +CP) min = (AP + PP'+ CP') min =AC',此时 A,P,P',C'共线,且∠APB=∠APC =∠CPB = 120°,满足条件的点 P 叫作费马点 两点之间线 段最短 核心思想: 手拉手模型 的构造
注:若三角形有一个内角大于或等于120°,那么这个顶点就是费马点.
实例剖析
如图10.75所示,在Rt△ABC 中,∠C=90°,AC=1,∠ABC=30°,点 P 为 Rt△ABC的费马点,连接AP,BP,CP,则 PA+PB+PC 的值为 .
【答案】
【分析】 如图10.76所示,将△APB 绕点B 顺时针旋转60°至△A'P'B 处,连接 PP',则A'B=AB=2,BP=BP',A'P'=AP,于是△BPP'是等边三角形,故. ∠BP'P=60°.
因为 ,所以 ,故C,P,A',P'四点共线.
在Rt△A'BC 中, 故
1. 已知三村庄A,B,C构成了图10.77所示的 (内角均小于 其中 现选取一点 P 打水井,使水井 P 到三村庄A,B,C所铺设的输水管总长度最小,则输水管总长度的最小值为 .
2. 如图10.78所示,矩形 ABCD 是一个长为1000m、宽为600m的货场,A,D 是入口,现拟在货场内建一个收费站 P,在铁路线 BC 段上建一个发货站台H,设铺设公路 AP,DP 以及PH 的长度和为l,则 l 的最小值为 m.
3. 如图10.79所示,在边长为6的正方形ABCD中,点 M,N分别为AB,BC上的动点,且始终保持 连接MN,以MN 为斜边在矩形内作等腰 若在正方形内存在一点 P,使得点 P到点A,D,Q的距离之和最小,则最小值为 .
4. 如图10.80所示,在 中, P为 的费马点,且满足 则 的面积为 .
1. 5km.
如图J10.59所示,以 BC为边在△ABC 的外部作等边△BCD,连接AD,则 AD 的长就是△ABC 的费马距离,可得∠ABD=90°,故.
2
提示:如图J10.60所示,将 绕着点D 顺时针旋转过点 作 于点E,线段 A E 即为最短.
3
如图J10.61所示,易得 Q,M,B,N 四点共圆,且 ,利用“邻等对补模型”易得 ,此时 为等腰直角三角形,点Q 刚好在正方形对角线的交点处,过点 Q作 于点E.
因为 PA+PD+PQ最小,所以点 P 是△ADQ 的费马点,则∠APD=∠APQ=∠DPQ=120°,而 解得 故 则PA+PD+PQ=
4
如图J10.62所示,延长 BP 交AC 于点D.
因为∠BAC=∠PBA=45°,所以∠ADB=90°,AD=BD.
又 P 为△ABC 的费马点,则∠APB=∠CPA=120°,故.
在 Rt△PAD 中,因为 PA=4,所以
又∠APC=120°,则.
在 Rt△PDC 中,因为∠PCD=30°,所以( 故. 4 ,则
同课章节目录
