第14讲 胡不归最值(含答案) 2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第14讲 胡不归最值(含答案) 2025年中考数学几何模型方法巩固练习 |
|
|
| 格式 | docx | ||
| 文件大小 | 245.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览

文档简介
胡不归最值
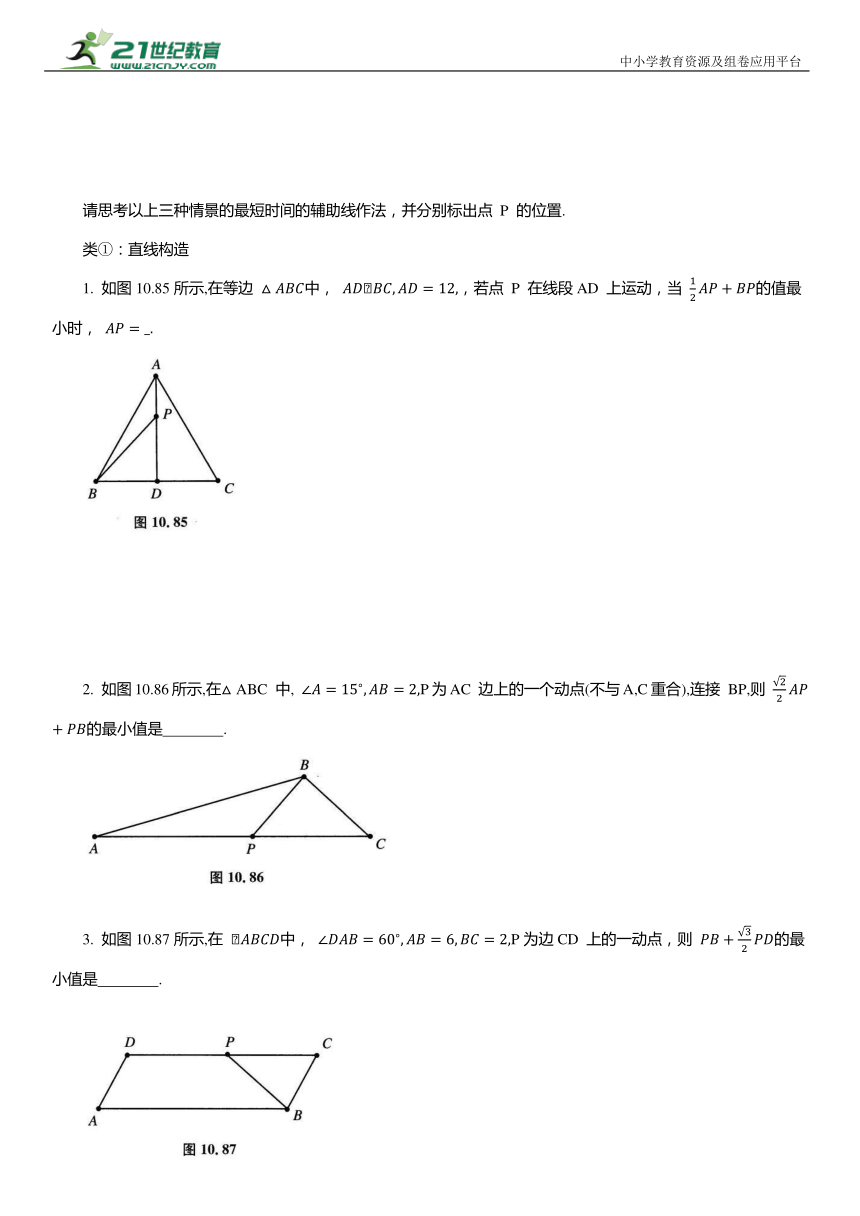
问题背景:传说从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.途中他要先坐高铁再坐汽车(图10.81),但是到家老人就去世了,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归 胡不归 ”.
问题1:如图10.82所示,若公路的速度 ,高铁的速度 则小伙子回家需要的时间为 .
问题2:如图10.83所示,若公路的速度 高铁的速度 则小伙子回家需要的时间为 .
问题3:如图10.84所示,若公路的速度 高铁的速度 则小伙子回家需要的时间为 .
请思考以上三种情景的最短时间的辅助线作法,并分别标出点 P 的位置.
类①:直线构造
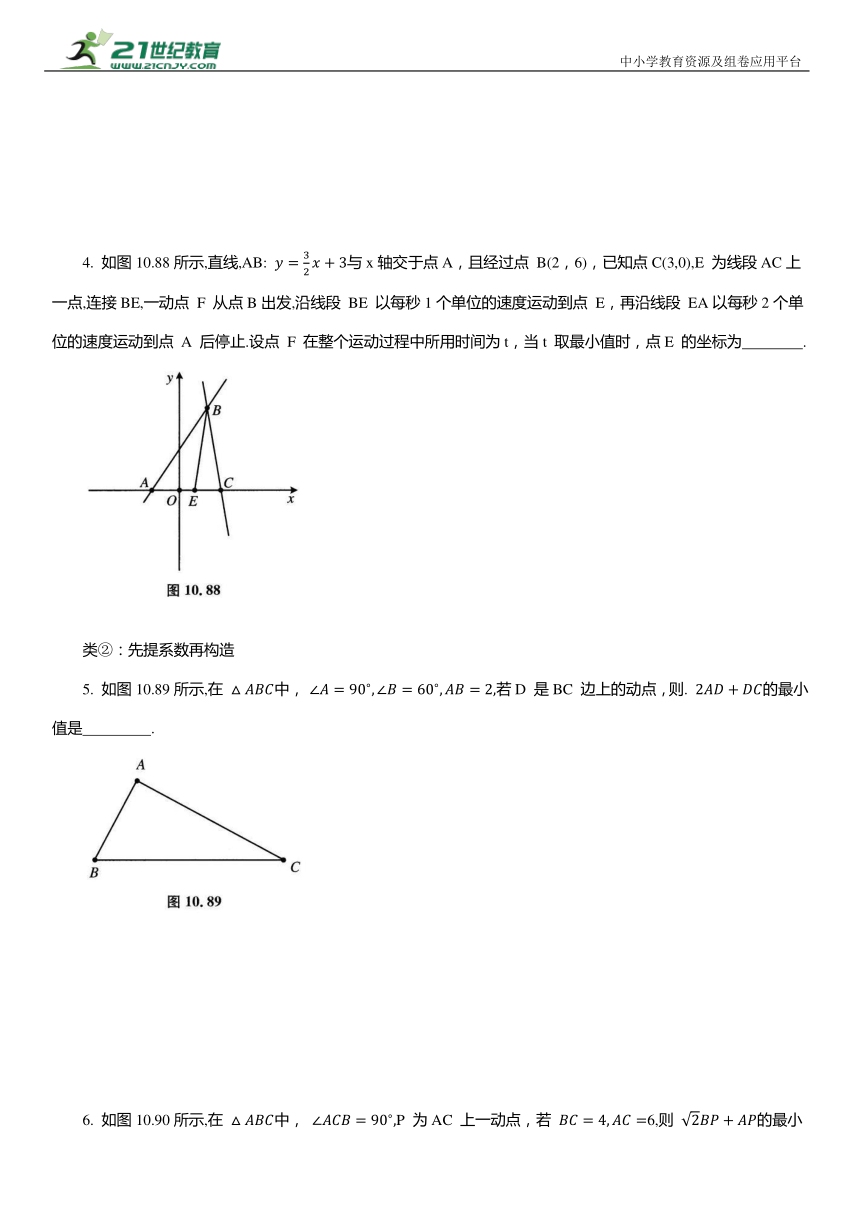
1. 如图10.85所示,在等边 中, ,若点 P 在线段AD 上运动,当 的值最小时,
2. 如图10.86所示,在△ABC 中, P为AC 边上的一个动点(不与A,C重合),连接 BP,则 的最小值是 .
3. 如图10.87所示,在 中, P为边CD 上的一动点,则 的最小值是 .
4. 如图10.88所示,直线,AB: 与x轴交于点A,且经过点 B(2,6),已知点C(3,0),E 为线段AC上一点,连接BE,一动点 F 从点B出发,沿线段 BE 以每秒1个单位的速度运动到点 E,再沿线段 EA以每秒2个单位的速度运动到点 A 后停止.设点 F 在整个运动过程中所用时间为t,当t 取最小值时,点E 的坐标为 .
类②:先提系数再构造
5. 如图10.89所示,在 中, 若D 是BC 边上的动点,则. 的最小值是 .
6. 如图10.90所示,在 中, P 为AC 上一动点,若 6,则 的最小值为 .
类③:非特殊角
7. 如图10.91所示,在 中, P 为BC 上一动点,则 的最小值是 .
8. 如图10.92 所示, 在直角坐标系中,AB=AC,A(0,2 ),C(1,0),D为射线AO上一点,一动点 P从A 出发,运动路径为A→D→C,点 P在AD 上的运动速度是在CD 上的3倍,要使整个运动时间最少,则点 D 的坐标应为 .
中小学教育资源及组卷应用平台
1. 8.
如图J10.63所示,AP'的长度即为所求.
2
提示:如图J10.64所示,构造 此时 的长度即为所求.
提示:如图J10.65所示,构造∠QDC=60°,即延长 AD,此时 BQ'的长度即为所求.
4
如图J10.66所示,过点 B作BM⊥x轴于点M,过点 A 作直线AH 使 过点 B 作 于点H',交x轴于点E',则点 E'为所求点.
因为 (对顶角),所以. 因为BM=6,所以 又OM=2,所以 故点 E'的坐标为(
5. 6.
提示: 求 的最小值即可,如图J10.67所示,AP'即为所求,因为 所以2AD+DC=6.
6. 10.
提示: 求 的最小值即可,如图J10.68所示,BD 即为所求.因为 所以
提示:如图 J10.69 所示, 结合 AP + PJ>AK,由等面积法可得 AK·BH= BC·AH,代入数值可得 故
假设点 P 在AD 上的速度为3V,在CD 上的速度为V,则总时间 要使 t 最小,就要 最小.
因为AB=AC=3,过点 B 作BH⊥AC交AC 于点H,交 OA 于点D,易证△ADH∽△ACO,所以 即
因为△ABC 是等腰三角形,所以 BD =CD,要使 最小,就要 DH+BD 最小,即 B,D,H三点共线就行了.
因为△AOC∽△BOD,所以 即 亦即 故点 D 的坐标应为
问题背景:传说从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.途中他要先坐高铁再坐汽车(图10.81),但是到家老人就去世了,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归 胡不归 ”.
问题1:如图10.82所示,若公路的速度 ,高铁的速度 则小伙子回家需要的时间为 .
问题2:如图10.83所示,若公路的速度 高铁的速度 则小伙子回家需要的时间为 .
问题3:如图10.84所示,若公路的速度 高铁的速度 则小伙子回家需要的时间为 .
请思考以上三种情景的最短时间的辅助线作法,并分别标出点 P 的位置.
类①:直线构造
1. 如图10.85所示,在等边 中, ,若点 P 在线段AD 上运动,当 的值最小时,
2. 如图10.86所示,在△ABC 中, P为AC 边上的一个动点(不与A,C重合),连接 BP,则 的最小值是 .
3. 如图10.87所示,在 中, P为边CD 上的一动点,则 的最小值是 .
4. 如图10.88所示,直线,AB: 与x轴交于点A,且经过点 B(2,6),已知点C(3,0),E 为线段AC上一点,连接BE,一动点 F 从点B出发,沿线段 BE 以每秒1个单位的速度运动到点 E,再沿线段 EA以每秒2个单位的速度运动到点 A 后停止.设点 F 在整个运动过程中所用时间为t,当t 取最小值时,点E 的坐标为 .
类②:先提系数再构造
5. 如图10.89所示,在 中, 若D 是BC 边上的动点,则. 的最小值是 .
6. 如图10.90所示,在 中, P 为AC 上一动点,若 6,则 的最小值为 .
类③:非特殊角
7. 如图10.91所示,在 中, P 为BC 上一动点,则 的最小值是 .
8. 如图10.92 所示, 在直角坐标系中,AB=AC,A(0,2 ),C(1,0),D为射线AO上一点,一动点 P从A 出发,运动路径为A→D→C,点 P在AD 上的运动速度是在CD 上的3倍,要使整个运动时间最少,则点 D 的坐标应为 .
中小学教育资源及组卷应用平台
1. 8.
如图J10.63所示,AP'的长度即为所求.
2
提示:如图J10.64所示,构造 此时 的长度即为所求.
提示:如图J10.65所示,构造∠QDC=60°,即延长 AD,此时 BQ'的长度即为所求.
4
如图J10.66所示,过点 B作BM⊥x轴于点M,过点 A 作直线AH 使 过点 B 作 于点H',交x轴于点E',则点 E'为所求点.
因为 (对顶角),所以. 因为BM=6,所以 又OM=2,所以 故点 E'的坐标为(
5. 6.
提示: 求 的最小值即可,如图J10.67所示,AP'即为所求,因为 所以2AD+DC=6.
6. 10.
提示: 求 的最小值即可,如图J10.68所示,BD 即为所求.因为 所以
提示:如图 J10.69 所示, 结合 AP + PJ>AK,由等面积法可得 AK·BH= BC·AH,代入数值可得 故
假设点 P 在AD 上的速度为3V,在CD 上的速度为V,则总时间 要使 t 最小,就要 最小.
因为AB=AC=3,过点 B 作BH⊥AC交AC 于点H,交 OA 于点D,易证△ADH∽△ACO,所以 即
因为△ABC 是等腰三角形,所以 BD =CD,要使 最小,就要 DH+BD 最小,即 B,D,H三点共线就行了.
因为△AOC∽△BOD,所以 即 亦即 故点 D 的坐标应为
同课章节目录
