第4讲 手拉手模型 (含答案)2025年中考数学几何模型方法巩固练习
文档属性
| 名称 | 第4讲 手拉手模型 (含答案)2025年中考数学几何模型方法巩固练习 |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:43:56 | ||
图片预览



文档简介
第4讲 手拉手模型
模块1 本 质 原 理
观察图4.1,已知 ,A,E拉手,B,D 拉手(即连接AE,BD),则 ,此模型称为手拉手模型,这也是手拉手模型的雏形.
特别地,当 ,且 B,C,D 三点共线时,如图4.2所示,连接 AD,BE,则
我们再连接 AB,DE,如图4.3所示,我们就可以证明出如下5组常用结论:
说明:
中小学教育资源及组卷应用平台
结论3:三组平行线(如图4.6所示),即
结论4:三个特殊60°(如图4.7所示),即
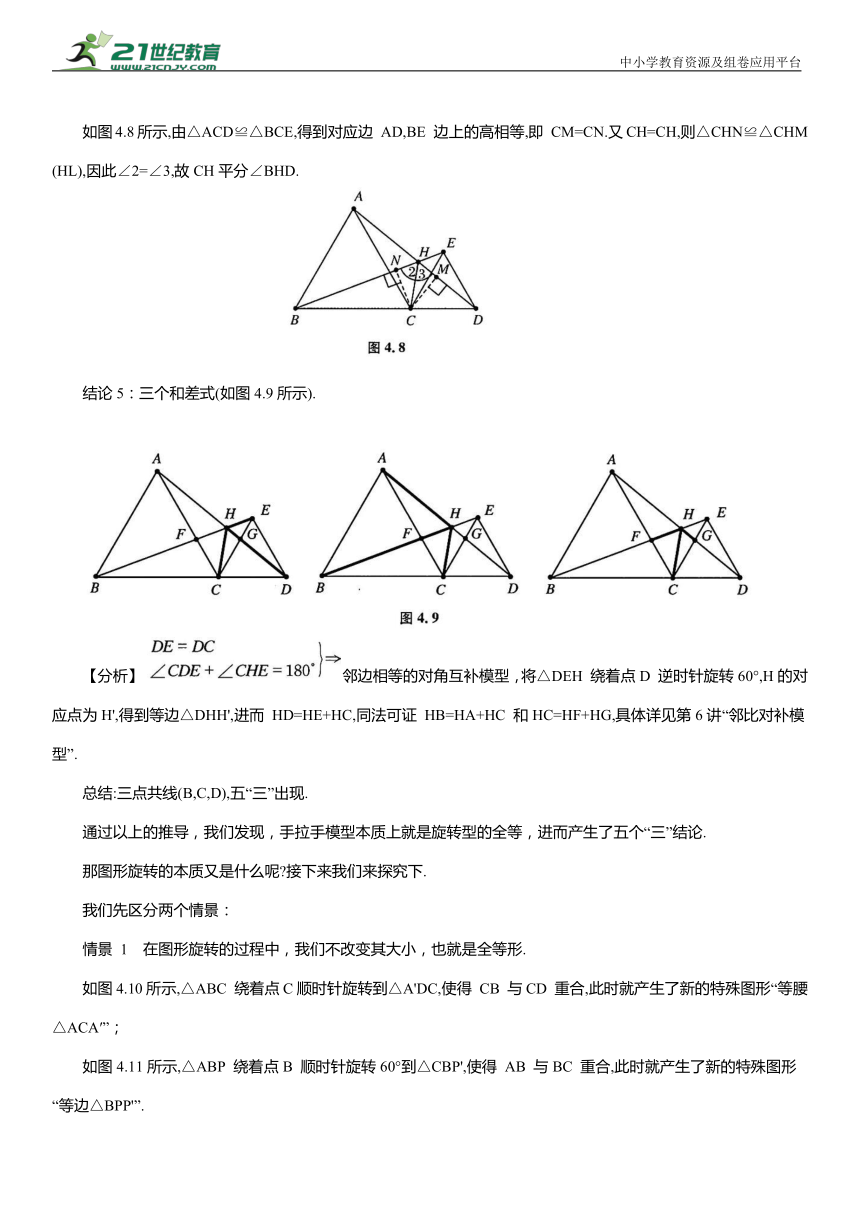
【分析】 如图4.7所示,由△ACD≌△BCE,可得∠HAF=∠CBF,易得在△AFH 和△BCF中,∠1=∠FCB=60°.
如图4.8所示,由△ACD≌△BCE,得到对应边 AD,BE 边上的高相等,即 CM=CN.又CH=CH,则△CHN≌△CHM(HL),因此∠2=∠3,故CH平分∠BHD.
结论5:三个和差式(如图4.9所示).
【分析】 邻边相等的对角互补模型,将△DEH 绕着点D 逆时针旋转60°,H的对应点为H',得到等边△DHH',进而 HD=HE+HC,同法可证 HB=HA+HC 和HC=HF+HG,具体详见第6讲“邻比对补模型”.
总结:三点共线(B,C,D),五“三”出现.
通过以上的推导,我们发现,手拉手模型本质上就是旋转型的全等,进而产生了五个“三”结论.
那图形旋转的本质又是什么呢 接下来我们来探究下.
我们先区分两个情景:
情景 1 在图形旋转的过程中,我们不改变其大小,也就是全等形.
如图4.10所示,△ABC 绕着点C顺时针旋转到△A'DC,使得 CB 与CD 重合,此时就产生了新的特殊图形“等腰△ACA′”;
如图4.11所示,△ABP 绕着点B 顺时针旋转60°到△CBP',使得 AB 与BC 重合,此时就产生了新的特殊图形“等边△BPP'”.
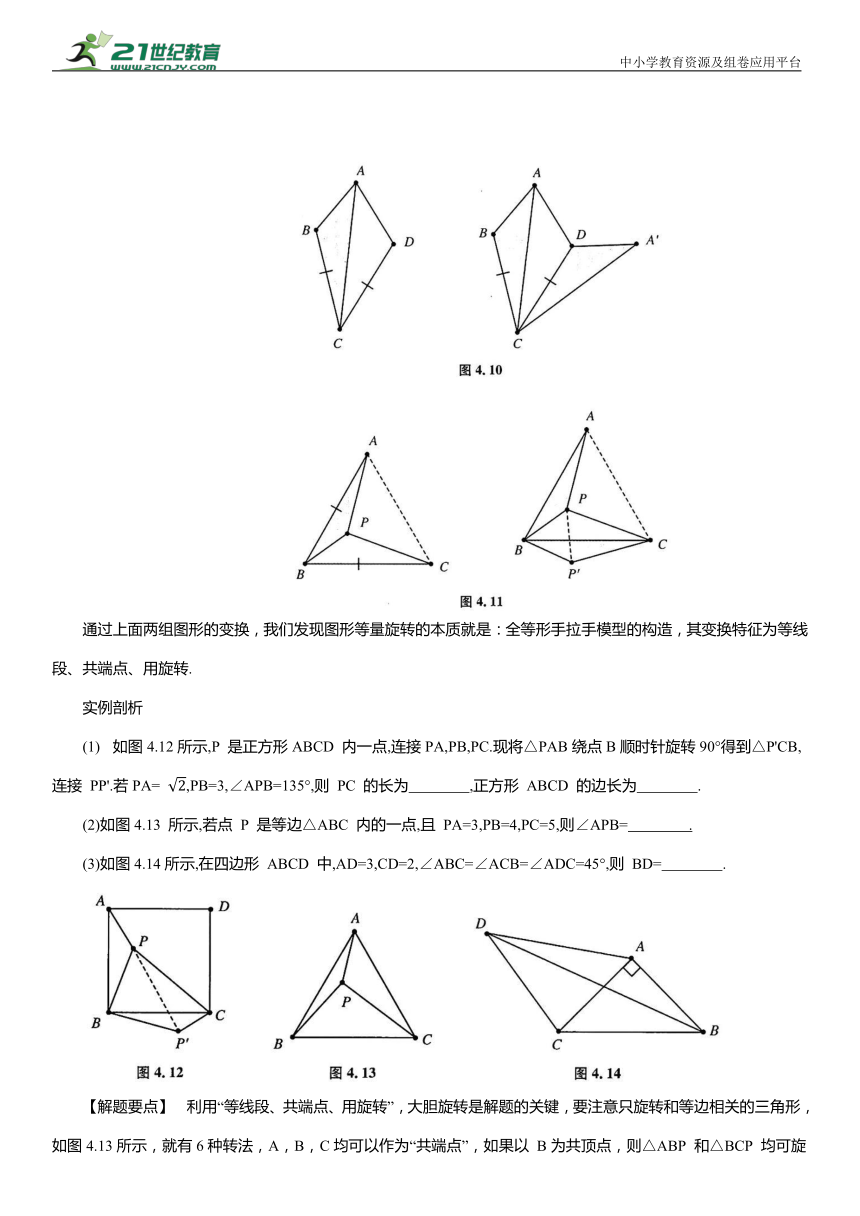
通过上面两组图形的变换,我们发现图形等量旋转的本质就是:全等形手拉手模型的构造,其变换特征为等线段、共端点、用旋转.
实例剖析
如图4.12所示,P 是正方形ABCD 内一点,连接PA,PB,PC.现将△PAB绕点B顺时针旋转90°得到△P'CB,连接 PP'.若PA= ,PB=3,∠APB=135°,则 PC 的长为 ,正方形 ABCD 的边长为 .
(2)如图4.13 所示,若点 P 是等边△ABC 内的一点,且 PA=3,PB=4,PC=5,则∠APB= .
(3)如图4.14所示,在四边形 ABCD 中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则 BD= .
【解题要点】 利用“等线段、共端点、用旋转”,大胆旋转是解题的关键,要注意只旋转和等边相关的三角形,如图4.13所示,就有6种转法,A,B,C均可以作为“共端点”,如果以 B为共顶点,则△ABP 和△BCP 均可旋转,目的只有一个,就是使等边重合,即AB,BC重合.
【答案】
【分析】 (1) 由. 知△BPP'为等腰直角三角形,又∠BP'C =∠APB=135°,所以. 故
在 Rt△PP'C 中,
过点 A 作AE⊥BP 交 BP 的延长线于点E,在 Rt△AEB 中,由勾股定理得 AB =
(2) 如图4.15 所示,将△BPC 绕点B 逆时针旋转60°得到△BP'A,连接 PP',易得△BPP'是等边三角形,则.
在△APP'中,. 则 故
(3)等线段(AB=AC),共端点(点 A),用旋转(可旋转△ABD或△ACD).
如图4.16所示,将△ABD 绕点A 顺时针旋转90°得到△ACK,连接DK.
由旋转的性质得△ABD≌△ACK,则 AK = AD =3,CK = BD,∠KAD =90°,所以△DAK 是等腰直角三角形,则 ,故∠CDK =∠ADC +
在 Rt△CDK 中,( 则
情 景 2 在图形旋转的过程中,我们改变其大小,将其进行缩放,也就是相似形.
如图4.17所示,将∠ABC 绕点A 按逆时针方向旋转一定角度后,得到△AB'C',其中相似比为. 则 即
又 ,连接 BB',CC',如图4.18所示,可得△BAB'∽△CAC'.
由此我们可以得到,只要三角形产生了旋转,就会有两组相似三角形产生,记忆口诀就是:一转成双.
我们发现图形等量旋转的本质就是:相似形手拉手模型的构造,其变换特征为比线段、共端点、用旋转.
实例剖析
【问题背景】 如图4.19所示,已知△ABC∽△ADE,求证:△ABD∽△ACE.
【尝试应用】 如图4.20所示,在△ABC 和△ADE 中,∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE 相交于点F,点 D 在BC 边上, 则
【拓展创新】 如图4.21所示,D 是△ABC 内一点,∠BAD=∠CBD=30°,∠BDC=90°,AB=4,AC=2 ,则AD= .
【答案】
【分析】
【问题背景】 因为△ABC∽△ADE,所以 则∠BAD= 故△ABD∽△ACE.
【尝试应用】 连接 EC.因为∠BAC =∠DAE =90°,∠ABC =∠ADE = 30°,所以△ABC∽△ADE.
由“问题背景”知△ABD∽△ACE,则 在图4.20中,∠B=∠ACE=30°.
设EC=a,则
因为∠ADF=∠ACE=30°,∠AFD=∠EFC,所以△ADF∽△ECF,则 =3.
【拓展创新】 比线段( 共端点(点 D),用旋转(可旋转△ADC 或△ADB或△CDB).
如图4.22 所示,将∠ADC 绕点D 按顺时针方向旋转90°,得到△BDM,相似比为1: ,连接AM,此时
设AD=x,则. 在 Rt△ADM 中,AM=2x,则 即∠DAM=60°,所以∠BAM=∠BAD+∠DAM=90°.
在Rt△BAM中, 即 解得 舍去),故
情 景 3 这个情景比较特殊,如图4.23所示,△AMN 和△APQ 均为等腰直角三角形,如果顶点 N 和顶点Q 重合,很明显是要构造手拉手模型了,但是它偏偏是锐角顶点 A重合在了一起,说好的手拉手一起走呢
这还没完,它居然连接了 MP,又取 MP 的中点G,最后连接了 NG,QG,完啦,全乱了……
不过先别急,既然有了中点就要有“中点四联想”(中位线、直角三角形斜边中线、三线合一、倍长中线).
但是怎么用呢 难道真的没有手拉手了吗
真相马上揭晓,如图4.24所示,我们分别把△AMN 和△APQ 补成以A 为直角顶点的等腰直角三角形△AMB 和△APC
.
眼快的同学应该已经看出来了,没错,手拉手又出现了,只不过我们需要连接MC,BP,如图4.25所示.
于是我们得到了△MAC≌△BAP,所以 此时 NG,GQ 分别为 和 的中位线,故 又 MC,则 ,其实它的本质就是一个隐藏型的手拉手模型的应用.为了方便记忆,我们姑且把它叫作“脚拉脚模型”吧,其实我们在第1讲就研究过它,本讲后面我们还会深入研究它.
无论是情景1、情景2还是情景3,其实都在构造手拉手模型.同学们需要先做的就是学会识图和构图,让我们开始吧.
模块2 场 景 演 练
模型的识别
1. 如图4.26所示,已知△ABC 和△ECD 都是等边三角形,且B,C,D 在一条直线上,连接BE,AD 相交于点O,点 M,N分别是线段BE,AD 上的两点,且 .给出下列结论:
① BE= AD;② △BCM≌△ACN;③ ∠BOD=100°;④△CMN 是等边三角形;⑤ BC=ND.
其中正确的结论是 .(填序号)
2. 如图4.27所示,点 E 在 的边DB上,点 A 在 内部, 给出下列结论:
① BD⊥CE;②∠DCB-∠ABD=45°;③CE-BE= AD;④BE +CD =2(AD +
其中正确的结论是 .(填序号)
3. 如图4.28所示,在 和 中, 连接AC,BD交于点M,连接OM.给出下列结论:
① AC=BD;②∠AMB=40°;③ OM平分∠AOD;④ MO平分
其中正确的结论是 .(填序号)
模型的构造:全等形手拉手
4. 如图4.29 所示,点 P 是等边. 外一点, 则
5. 如图4.30所示,在 中, ,点 D 是线段AC 上一点,连接 BD.以BD 为直角边作等腰直角. ,连接AE,点 F 为AE 的中点.若 则
6. 如图4.31所示, 是边长为4的等边三角形,点D 是 外一点, 点 E 是BD 上一点,点 F 是CD 上一点,且( 连接FE,FB.若 则
7. 如图4.32 所示,在四边形 ABCD 中,. 则四边形 ABCD 的面积为 .
8. 如图4.33所示,在正六边形 ABCDEF 内有一点P,且. 则 ,正六边形的边长为 .
9. 如图4.34所示, ,以 AB 为一边作正方形ABCD,使 P,D 两点落在直线AB 的两侧,则,
10. 如图4.35所示,在 中, .点 P 在直线AB 上方且 若 则
11*. 如图4.36所示,在 中, ,以BC 为边向外作等腰, 连接 AD,AD 的最大值为 .
全等形:遇见中考
12.如图4.37所示,在正方形 ABCD 中,AC为对角线,点 P 在线段AC 上运动,以 DP 为边向右作正方形DPFE,连接CE.
【初步探究】
(1) AP 与CE 的数量关系是 ,AP 与CE 的夹角度数为 .
【探索发现】
(2)点 P 在线段AC 及其延长线上运动时,如图4.38所示,线段 DC,PC 和CE 三者之间的数量关系为 .
【拓展延伸】
(3)点 P 在对角线AC 的延长线上时,如图4.39 所示,连接AE,若 ,则四边形 DCPE 的面积为 .
模型的构造:相似形手拉手
13. 如图 4.40 所示,在矩形 ABCD 中, ,则
14. 如图4.41所示,在 中, ,点 D 在线段AC 上,连接BD,将 DB 绕点D 逆时针旋转 ,得到线段 DE,连接 BE,CE,则
15.如图4.42所示,两个大小不同的三角板放在同一平面内,直角顶点重合于点 C,点D在AB 上, AC 与 DE 交于点 F,若 则
16. 如图4.43所示,在矩形 ABCD 中,将 绕点A 按逆时针方向旋转一定角度后,BC 的对应边 交CD 边于点G.连接 若 则
17. 如图4.44所示,四边形 ABCD为正方形,对角线AC,BD 交于点O, 为等腰直角三角形, ,连接CE,H 为CE 的中点,连接OH,BH,BF,HF.证明: 为等腰直角三角形.
证明:在凸四边形 ABCD 中,如图4.45 所示,总有 AC·BD.
模型的综合应用:遇见中考
19.【问题背景】 如图4.46所示,∠ACB=∠ADE=90°,AC=BC,AD=DE.求证:BE=
【变式迁移】 如图4.47 所示,E 为正方形ABCD 外一点,∠E=45°,过点 D 作DF⊥BE,垂足为点 F,连接CF,则
【拓展创新】 如图4.48所示,A 是△BEF 内一点,BE = BF,AF =2,∠EAB=90°,∠FEA=∠BFA,AE=2AB,则AB= .
模型的构造:脚拉脚模型
20.已知两个等腰 有公共顶点C, 连接AF,M是AF 的中点.如图4.49 所示,连接MB,ME,当 时,求证:BM= ME 且BM⊥ME.
21.在任意 中,分别以AB 和AC为斜边,向. 的内侧作等腰直角三角形,如图4.50所示,M 是BC的中点,连接 MD 和ME,试判断 的形状,并说明理由.
番外篇:脚拉脚模型的深入探究
实例剖析
母题:如图4.51所示,以△ABC的边AB 和AC 分别为一边,向形内作正方形 ABMN,ACPQ,求证:BQ=CN且BQ⊥CN.
【分析】 如图4.52所示,易证 则 ,故 A,Q,R,C四点共圆,即 得 即
变式①:如图 4.53 所示,以. 的边AB和 AC 分别为一边,向形外作正方形ABMN,ACPQ.
结论(1):BQ与CN垂直且相等(如图4.54所示,手拉手模型).
结论(2):NC,BQ,MP 三条直线交于一点(如图4.55所示).
【分析】 因为 所以A,G,C,Q四点共圆,则 45°,∠AGC=135°,∠APC=45°,∠AGP=∠ACP=90°.
同理可得
故得证.
结论(3):AG⊥MP(结论(2)中已证).
结论(4):如图4.56所示.
①若RN=RQ,则RW⊥BC.
提示:利用倍长中线,如图4.57所示,延长AR 至点J,使得 AR =RJ,易证△AQR≌△JNR,所以 NJ = AQ,∠AQR =∠JNR,则 NJ∥AQ,于是∠JNA +∠NAQ=180°.又∠BAC+∠NAQ=180°,所以∠JNA =∠BAC.因为 NJ = AC,AN= AB,所以△NJA≌△ACB,则∠NAJ=∠ABC.又∠NAJ+∠BAW =90°,则∠ABC+∠BAW=90°,即RW⊥BC.
②若RW⊥BC,则
提示:利用三垂直模型,如图 4.58 所示,作I ,易证△QAL≌△ACW,△KNA≌△WAB,所以NK=AW=QL,进而△NKR≌△QLR,得到 RN=RQ,由①得
变式②:如图4.59所示,点 R,D,E,F分别为NQ,AM,BC,AP 的中点,求证:DEFR是正方形.
【分析】 如图4.60所示,连接 BN,CN,BQ,CQ,则
因为 BQ与CN 相等且垂直,所以 EF与ED 相等且垂直.
同理可得证.
结论(1):
提示:如图4.61所示,利用中位线易证.
结论(2):G 为MP 的中点,则 为等腰直角三角形.
提示:如图4.62所示,利用本质原理中的推导易证.
图形归一(第一类)
如图4.63所示, 均为等腰直角三角形,连接 PM,取PM 的中点G,连接 NG,QG,求证: 且
证法 1 构造手拉手法,如图4.64所示(证法请参考第1讲中第22题).
证法 2 三线合一法,如图4.65所示(证法请参考第1讲中第22题).
图形归一(第二类)
如图4.66所示, 均为等腰直角三角形,连接 PM,取PM 的中点G,连接 BG,CG,求证:BG=CG 且BG⊥CG.
证法① 构造手拉手法,如图4.67所示(证法请参考第1讲中第22题).
证法 2 三线合一法,如图4.68所示(证法请参考第1讲中第22题).
番外篇:遇见中考
22.(2022·深圳模拟)如图4.69 所示,四边形 ABCD 和BEFG 都是正方形,BH⊥AE于点H,延长 HB交CG 于点M,证明发现 CM=MG.小生同学想到了这样的证明方法:过点C作CN⊥BM,交 BM 的延长线于点N.他已经证明了△ABH≌△BCN,但接下来的证明过程,他有些迷茫了.
(1)请同学们帮小生同学将剩余的证明过程补充完整.
(2)深入研究:若将原题中的“正方形”改为“矩形”(如图4.70所示),且 (其中 k>0),请直接写出线段CM,MG 的数量关系: .
(3) 拓展应用:如图4.71所示,在 Rt△ABC 和 Rt△ADE 中, ∠ACB=∠AED = 30°,连接 BD,CE,F 为 BD 的中点,则 AF 与CE 的数量关系为
第4 讲 手拉手模型
1. ①②④.
∠BOD=∠BAC+∠CBE+∠OBA=∠BAC+∠ABC=120°≠100°,故③错误;先证△MCE≌△NCD(SSS),则 ME= ND,故⑤错误.
2. ①③④.
因为△ABD≌△ACE,所以∠ABD=∠ACE,显然∠ABD≠∠ACD,故②错误;
BE 2) - -CD ,故④正确.
3. ①②④.
4. 30°.
提示:因为 AB=AC=BC,且互为共端点,所以每一个端点都可以进行两种旋转.
如图J4.1所示,连接CE,延长 AB,CE 交于点T.
利用手拉手模型易得 所以 ,则 为等腰直角三角形,因此 BC=BT=AB.
因为点 F 是AE 的中点,所以 BF 是 的中位线,则 故
6. 16.
解题要点:利用CF = BE,∠ABE=∠ACF,连接 AE,AF 构造手拉手模型是此题的关键.
如图J4.2 所示,连接 AE,AF,易证△ABE≌△ACF(SAS),可得∠AFB=∠AFE + 故.
如图J4.3所示,连接 BD.因为 AD=CD,所以可将△BCD 绕点D 顺时针方向旋转60°,得到△B'AD.连接 BB',延长 BA,作 B'E⊥BA 于点E,则 ∠CBD=∠AB'D,此时S四边形ABCD = S凹四边形BDB'A,△BDB'是等边三角形.
因为∠ABC=75°,∠ADC=60°,所以. 则
因为 所以 则.
设等边△BB'D的高为h,则由勾股定理得 故
提示:因为 AB=AF,所以可把△ABP 或△APF 绕点A 旋转120°,使AB 和AF 重合,再利用勾股定理求解即可.
提示:因为 AB=AD,所以可把△ABP 或△APD 绕点A 旋转90°,使 AB 和AD 重合,再利用勾股定理求解即可.
提示:因为 AB=AC,所以可把△ABP 或△APC 绕点A 旋转120°,使 AB 和AC 重合,
再利用勾股定理求解即可.
如图J4.4所示,以点 D 为旋转中心,将 绕点D 顺时针旋转 得到 连接 AF,则. ,故当 A,B,F 三点共线时,AF 最大,此时AD 最大.
因为AB=4,AC=8,所以AF=AB+BF=AB+AC=12,则. 故AD 的最大值为
12. (1) AP=CE,90°.
因为四边形 ABCD 是正方形,所以 AD=DC,∠ACD=∠DAC=45°,∠ADC=90°.
又四边形 DPFE 是正方形,则 DP=DE,∠PDE=∠ADC=90°,于是∠ADP=∠CDE,故△ADP≌△CDE(SAS),有AP=CE,∠DAC=∠DCE=45°,故∠ACE=90°.
或(
如图4.37所示,由(1)可得 AP=CE,则
如图4.38所示,因为四边形 ABCD 是正方形,所以 AD=DC,∠ACD=∠DAC=45°,
又四边形 DPFE 是正方形,则 DP= DE,∠PDE=∠ADC=90°,∠ADP=∠CDE,故△ADP≌△CDE(SAS),有 AP=CE,∠DAC=∠DCE=45°,故
(3)12.
如图J4.5所示,连接CE.
因为△ADP≌△CDE,所以∠DCE=∠DAP=45°,故∠ACE=∠ACD+∠DCE=90°.
因为 所以( 则
又 AP=CE=6,则 PC=6-4=2,于是 故 则
13. 150°.
比线段 ,共端点(点 B),用旋转(可旋转△BCP 或
解法1 如图J4.6 所示,将△ABP 绕点B 顺时针旋转90°,构造 连接PP',易得 因为 根据勾股逆定理可得 =90°,故
解法2 如图J4.7 所示,将△BCP 绕点B 逆时针旋转90°,构造 连接PP',下面的解法同解法1.
利用一转成双,由△ABC∽△DBE 得△ABD∽△CBE,故
连接AE.因为△ABC∽△EDC,可得△BCD∽△ACE,所以 则 AE =
又BD=2,BC=5,∠B=60°,可得 故
如图J4.8所示,连接 AC,AG,AC′.
利用一转成双,由△ABC∽△AB'C'得△ABB'∽△ACC',则
因为 ,所以△AB′G 是等腰直角三角形,则 AG=
设 则
在 Rt△ADG 中, 即 解得 (舍去),故 AB=5.
在 Rt△ABC中, 故
17.由正方形的性质得 O为AC 的中点.
因为 H 为CE 的中点,所以
又△AEF 是等腰直角三角形,则. 故
如图J4.9 所示,因为 OH∥AE,所以∠COH =∠CAE,则∠BOH =∠BAF,因此△BOH∽△BAF,则 故∠HBF =∠HBO+∠DBF =∠DBA =45°,即△BHF 为等腰直角三角形.
18*.本题为广义的托勒密定理,证明过程如下:
如图 J4.10 所示,作∠BAE = ∠DAC,且使 进而得到△ABE∽△ACD(图J4.11),所以
AB·CD = BE·AC. ①
又∠CAD =∠BAE,则∠EAD =∠BAC,因为 所以△AED∽△ABC(图J4.12),则
AD·BC = DE·AC. ②
①+②,有AB·CD +AD·BC = BE·AC + DE·AC,
即 AB·CD+AD·BC=AC(BE+DE).
因为 BE+DE≥BD,所以 AB·CD+AD·BC≥AC·BD.
19.【问题背景】 因为∠ACB =∠ADE =90°,AC = BC,AD = DE,所以∠DAE =∠CAB,且. ,则∠DAC=∠EAB,于是△ABE∽△ACD,则 即
【变式迁移】
如图J4.13所示,连接 BD.
因为∠E=45°,DF⊥BE,所以∠EDF=∠E=45°.
在正方形 ABCD 中,∠BDC=45°,则. 所以△EDB∽△FDC,故
【拓展创新】
如图J4.14所示,过点 A 作AH⊥AF,交 EF 于点H,连接BH.
因为 BE= BF,所以∠BEF=∠BFE.
又∠FEA=∠BFA,则∠AFE=∠BEA,即 tan∠AFE= tan∠BEA,于是 即 故
由一转成双易得△FAE∽△HAB,则∠AHB=∠AFE=∠AEB,A,H,E,B四点共圆,所以∠BHE=∠BAE=90°,则
因为AE=2AB,所以 故
20. 如图J4.15 所示,分别把△ABC 和△CEF 补成以C为直角顶点的等腰 Rt△ACP和Rt△HCF,然后再连接AH,PF,利用手拉手全等证明△CAH≌△CPF,易得AH=PF且AH⊥PF.因为 BM,ME 分别为△APF 和△AHF 的中位线,所以 BM∥PF,ME∥AH,故 BM=ME 且BM⊥ME.
21. 如图J4.16所示,分别把△ACE 和△ABD 补成等腰Rt△ACF 和 Rt△ABG,然后再连接BF,CG,利用手拉手全等易证△AFB≌△ACG,易得 BF=CG 且BF⊥CG.因为EM,MD 分别为△CFB 和△BCG 的中位线,所以 )∥CG,故 ME=MD 且ME⊥MD,即△MED 是等腰直角三角形.
22.(1)如图J4.17所示,过点 G 作GT⊥NH 于点T.
因为△ABH≌△BCN,所以 BH=CN.
同法可证△EHB≌BTG,所以 BH=TG,则 CN=GT.
因为CN⊥NH,GT⊥NH,所以∠N=∠GTM=90°.
又∠CMN=∠GMT,则△CMN≌△GMT(AAS),故CM=GM.
证明如下:如图J4.18所示,过点C作CN⊥MH 于点N,过点 G 作GT⊥NM交HM 的延长线于点 T.
因为四边形 ABCD 是矩形,所以∠ABC=∠AHB=∠CNB=90°,则∠ABH+∠CBN=90°,∠CBN+∠BCN=90°,于是∠ABH=∠BCN,则△AHB∽△BNC,故 即
同法可证△EHB∽△BTG,所以 即 TG=kBH.
又∠T=∠CNM=90°,∠CMN=∠GMT,则△CNM∽△GTM,于是
证明如下:如图J4.19 所示,延长 AF 到点T,使得 AF=FT,连接 BT,DT.
因为 AF=FT,BF=FD,所以四边形 ABTD 是平行四边形,则AD=BT,AD∥BT,于是∠ABT+∠BAD=180°.
又∠CAB=∠DAE=90°,则∠BAD +∠CAE=180°,于是∠ABT=∠CAE.
因为∠ACB =∠AED =30°,所以. 则 于是△CAE∽△ABT,则 即 故
模块1 本 质 原 理
观察图4.1,已知 ,A,E拉手,B,D 拉手(即连接AE,BD),则 ,此模型称为手拉手模型,这也是手拉手模型的雏形.
特别地,当 ,且 B,C,D 三点共线时,如图4.2所示,连接 AD,BE,则
我们再连接 AB,DE,如图4.3所示,我们就可以证明出如下5组常用结论:
说明:
中小学教育资源及组卷应用平台
结论3:三组平行线(如图4.6所示),即
结论4:三个特殊60°(如图4.7所示),即
【分析】 如图4.7所示,由△ACD≌△BCE,可得∠HAF=∠CBF,易得在△AFH 和△BCF中,∠1=∠FCB=60°.
如图4.8所示,由△ACD≌△BCE,得到对应边 AD,BE 边上的高相等,即 CM=CN.又CH=CH,则△CHN≌△CHM(HL),因此∠2=∠3,故CH平分∠BHD.
结论5:三个和差式(如图4.9所示).
【分析】 邻边相等的对角互补模型,将△DEH 绕着点D 逆时针旋转60°,H的对应点为H',得到等边△DHH',进而 HD=HE+HC,同法可证 HB=HA+HC 和HC=HF+HG,具体详见第6讲“邻比对补模型”.
总结:三点共线(B,C,D),五“三”出现.
通过以上的推导,我们发现,手拉手模型本质上就是旋转型的全等,进而产生了五个“三”结论.
那图形旋转的本质又是什么呢 接下来我们来探究下.
我们先区分两个情景:
情景 1 在图形旋转的过程中,我们不改变其大小,也就是全等形.
如图4.10所示,△ABC 绕着点C顺时针旋转到△A'DC,使得 CB 与CD 重合,此时就产生了新的特殊图形“等腰△ACA′”;
如图4.11所示,△ABP 绕着点B 顺时针旋转60°到△CBP',使得 AB 与BC 重合,此时就产生了新的特殊图形“等边△BPP'”.
通过上面两组图形的变换,我们发现图形等量旋转的本质就是:全等形手拉手模型的构造,其变换特征为等线段、共端点、用旋转.
实例剖析
如图4.12所示,P 是正方形ABCD 内一点,连接PA,PB,PC.现将△PAB绕点B顺时针旋转90°得到△P'CB,连接 PP'.若PA= ,PB=3,∠APB=135°,则 PC 的长为 ,正方形 ABCD 的边长为 .
(2)如图4.13 所示,若点 P 是等边△ABC 内的一点,且 PA=3,PB=4,PC=5,则∠APB= .
(3)如图4.14所示,在四边形 ABCD 中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则 BD= .
【解题要点】 利用“等线段、共端点、用旋转”,大胆旋转是解题的关键,要注意只旋转和等边相关的三角形,如图4.13所示,就有6种转法,A,B,C均可以作为“共端点”,如果以 B为共顶点,则△ABP 和△BCP 均可旋转,目的只有一个,就是使等边重合,即AB,BC重合.
【答案】
【分析】 (1) 由. 知△BPP'为等腰直角三角形,又∠BP'C =∠APB=135°,所以. 故
在 Rt△PP'C 中,
过点 A 作AE⊥BP 交 BP 的延长线于点E,在 Rt△AEB 中,由勾股定理得 AB =
(2) 如图4.15 所示,将△BPC 绕点B 逆时针旋转60°得到△BP'A,连接 PP',易得△BPP'是等边三角形,则.
在△APP'中,. 则 故
(3)等线段(AB=AC),共端点(点 A),用旋转(可旋转△ABD或△ACD).
如图4.16所示,将△ABD 绕点A 顺时针旋转90°得到△ACK,连接DK.
由旋转的性质得△ABD≌△ACK,则 AK = AD =3,CK = BD,∠KAD =90°,所以△DAK 是等腰直角三角形,则 ,故∠CDK =∠ADC +
在 Rt△CDK 中,( 则
情 景 2 在图形旋转的过程中,我们改变其大小,将其进行缩放,也就是相似形.
如图4.17所示,将∠ABC 绕点A 按逆时针方向旋转一定角度后,得到△AB'C',其中相似比为. 则 即
又 ,连接 BB',CC',如图4.18所示,可得△BAB'∽△CAC'.
由此我们可以得到,只要三角形产生了旋转,就会有两组相似三角形产生,记忆口诀就是:一转成双.
我们发现图形等量旋转的本质就是:相似形手拉手模型的构造,其变换特征为比线段、共端点、用旋转.
实例剖析
【问题背景】 如图4.19所示,已知△ABC∽△ADE,求证:△ABD∽△ACE.
【尝试应用】 如图4.20所示,在△ABC 和△ADE 中,∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE 相交于点F,点 D 在BC 边上, 则
【拓展创新】 如图4.21所示,D 是△ABC 内一点,∠BAD=∠CBD=30°,∠BDC=90°,AB=4,AC=2 ,则AD= .
【答案】
【分析】
【问题背景】 因为△ABC∽△ADE,所以 则∠BAD= 故△ABD∽△ACE.
【尝试应用】 连接 EC.因为∠BAC =∠DAE =90°,∠ABC =∠ADE = 30°,所以△ABC∽△ADE.
由“问题背景”知△ABD∽△ACE,则 在图4.20中,∠B=∠ACE=30°.
设EC=a,则
因为∠ADF=∠ACE=30°,∠AFD=∠EFC,所以△ADF∽△ECF,则 =3.
【拓展创新】 比线段( 共端点(点 D),用旋转(可旋转△ADC 或△ADB或△CDB).
如图4.22 所示,将∠ADC 绕点D 按顺时针方向旋转90°,得到△BDM,相似比为1: ,连接AM,此时
设AD=x,则. 在 Rt△ADM 中,AM=2x,则 即∠DAM=60°,所以∠BAM=∠BAD+∠DAM=90°.
在Rt△BAM中, 即 解得 舍去),故
情 景 3 这个情景比较特殊,如图4.23所示,△AMN 和△APQ 均为等腰直角三角形,如果顶点 N 和顶点Q 重合,很明显是要构造手拉手模型了,但是它偏偏是锐角顶点 A重合在了一起,说好的手拉手一起走呢
这还没完,它居然连接了 MP,又取 MP 的中点G,最后连接了 NG,QG,完啦,全乱了……
不过先别急,既然有了中点就要有“中点四联想”(中位线、直角三角形斜边中线、三线合一、倍长中线).
但是怎么用呢 难道真的没有手拉手了吗
真相马上揭晓,如图4.24所示,我们分别把△AMN 和△APQ 补成以A 为直角顶点的等腰直角三角形△AMB 和△APC
.
眼快的同学应该已经看出来了,没错,手拉手又出现了,只不过我们需要连接MC,BP,如图4.25所示.
于是我们得到了△MAC≌△BAP,所以 此时 NG,GQ 分别为 和 的中位线,故 又 MC,则 ,其实它的本质就是一个隐藏型的手拉手模型的应用.为了方便记忆,我们姑且把它叫作“脚拉脚模型”吧,其实我们在第1讲就研究过它,本讲后面我们还会深入研究它.
无论是情景1、情景2还是情景3,其实都在构造手拉手模型.同学们需要先做的就是学会识图和构图,让我们开始吧.
模块2 场 景 演 练
模型的识别
1. 如图4.26所示,已知△ABC 和△ECD 都是等边三角形,且B,C,D 在一条直线上,连接BE,AD 相交于点O,点 M,N分别是线段BE,AD 上的两点,且 .给出下列结论:
① BE= AD;② △BCM≌△ACN;③ ∠BOD=100°;④△CMN 是等边三角形;⑤ BC=ND.
其中正确的结论是 .(填序号)
2. 如图4.27所示,点 E 在 的边DB上,点 A 在 内部, 给出下列结论:
① BD⊥CE;②∠DCB-∠ABD=45°;③CE-BE= AD;④BE +CD =2(AD +
其中正确的结论是 .(填序号)
3. 如图4.28所示,在 和 中, 连接AC,BD交于点M,连接OM.给出下列结论:
① AC=BD;②∠AMB=40°;③ OM平分∠AOD;④ MO平分
其中正确的结论是 .(填序号)
模型的构造:全等形手拉手
4. 如图4.29 所示,点 P 是等边. 外一点, 则
5. 如图4.30所示,在 中, ,点 D 是线段AC 上一点,连接 BD.以BD 为直角边作等腰直角. ,连接AE,点 F 为AE 的中点.若 则
6. 如图4.31所示, 是边长为4的等边三角形,点D 是 外一点, 点 E 是BD 上一点,点 F 是CD 上一点,且( 连接FE,FB.若 则
7. 如图4.32 所示,在四边形 ABCD 中,. 则四边形 ABCD 的面积为 .
8. 如图4.33所示,在正六边形 ABCDEF 内有一点P,且. 则 ,正六边形的边长为 .
9. 如图4.34所示, ,以 AB 为一边作正方形ABCD,使 P,D 两点落在直线AB 的两侧,则,
10. 如图4.35所示,在 中, .点 P 在直线AB 上方且 若 则
11*. 如图4.36所示,在 中, ,以BC 为边向外作等腰, 连接 AD,AD 的最大值为 .
全等形:遇见中考
12.如图4.37所示,在正方形 ABCD 中,AC为对角线,点 P 在线段AC 上运动,以 DP 为边向右作正方形DPFE,连接CE.
【初步探究】
(1) AP 与CE 的数量关系是 ,AP 与CE 的夹角度数为 .
【探索发现】
(2)点 P 在线段AC 及其延长线上运动时,如图4.38所示,线段 DC,PC 和CE 三者之间的数量关系为 .
【拓展延伸】
(3)点 P 在对角线AC 的延长线上时,如图4.39 所示,连接AE,若 ,则四边形 DCPE 的面积为 .
模型的构造:相似形手拉手
13. 如图 4.40 所示,在矩形 ABCD 中, ,则
14. 如图4.41所示,在 中, ,点 D 在线段AC 上,连接BD,将 DB 绕点D 逆时针旋转 ,得到线段 DE,连接 BE,CE,则
15.如图4.42所示,两个大小不同的三角板放在同一平面内,直角顶点重合于点 C,点D在AB 上, AC 与 DE 交于点 F,若 则
16. 如图4.43所示,在矩形 ABCD 中,将 绕点A 按逆时针方向旋转一定角度后,BC 的对应边 交CD 边于点G.连接 若 则
17. 如图4.44所示,四边形 ABCD为正方形,对角线AC,BD 交于点O, 为等腰直角三角形, ,连接CE,H 为CE 的中点,连接OH,BH,BF,HF.证明: 为等腰直角三角形.
证明:在凸四边形 ABCD 中,如图4.45 所示,总有 AC·BD.
模型的综合应用:遇见中考
19.【问题背景】 如图4.46所示,∠ACB=∠ADE=90°,AC=BC,AD=DE.求证:BE=
【变式迁移】 如图4.47 所示,E 为正方形ABCD 外一点,∠E=45°,过点 D 作DF⊥BE,垂足为点 F,连接CF,则
【拓展创新】 如图4.48所示,A 是△BEF 内一点,BE = BF,AF =2,∠EAB=90°,∠FEA=∠BFA,AE=2AB,则AB= .
模型的构造:脚拉脚模型
20.已知两个等腰 有公共顶点C, 连接AF,M是AF 的中点.如图4.49 所示,连接MB,ME,当 时,求证:BM= ME 且BM⊥ME.
21.在任意 中,分别以AB 和AC为斜边,向. 的内侧作等腰直角三角形,如图4.50所示,M 是BC的中点,连接 MD 和ME,试判断 的形状,并说明理由.
番外篇:脚拉脚模型的深入探究
实例剖析
母题:如图4.51所示,以△ABC的边AB 和AC 分别为一边,向形内作正方形 ABMN,ACPQ,求证:BQ=CN且BQ⊥CN.
【分析】 如图4.52所示,易证 则 ,故 A,Q,R,C四点共圆,即 得 即
变式①:如图 4.53 所示,以. 的边AB和 AC 分别为一边,向形外作正方形ABMN,ACPQ.
结论(1):BQ与CN垂直且相等(如图4.54所示,手拉手模型).
结论(2):NC,BQ,MP 三条直线交于一点(如图4.55所示).
【分析】 因为 所以A,G,C,Q四点共圆,则 45°,∠AGC=135°,∠APC=45°,∠AGP=∠ACP=90°.
同理可得
故得证.
结论(3):AG⊥MP(结论(2)中已证).
结论(4):如图4.56所示.
①若RN=RQ,则RW⊥BC.
提示:利用倍长中线,如图4.57所示,延长AR 至点J,使得 AR =RJ,易证△AQR≌△JNR,所以 NJ = AQ,∠AQR =∠JNR,则 NJ∥AQ,于是∠JNA +∠NAQ=180°.又∠BAC+∠NAQ=180°,所以∠JNA =∠BAC.因为 NJ = AC,AN= AB,所以△NJA≌△ACB,则∠NAJ=∠ABC.又∠NAJ+∠BAW =90°,则∠ABC+∠BAW=90°,即RW⊥BC.
②若RW⊥BC,则
提示:利用三垂直模型,如图 4.58 所示,作I ,易证△QAL≌△ACW,△KNA≌△WAB,所以NK=AW=QL,进而△NKR≌△QLR,得到 RN=RQ,由①得
变式②:如图4.59所示,点 R,D,E,F分别为NQ,AM,BC,AP 的中点,求证:DEFR是正方形.
【分析】 如图4.60所示,连接 BN,CN,BQ,CQ,则
因为 BQ与CN 相等且垂直,所以 EF与ED 相等且垂直.
同理可得证.
结论(1):
提示:如图4.61所示,利用中位线易证.
结论(2):G 为MP 的中点,则 为等腰直角三角形.
提示:如图4.62所示,利用本质原理中的推导易证.
图形归一(第一类)
如图4.63所示, 均为等腰直角三角形,连接 PM,取PM 的中点G,连接 NG,QG,求证: 且
证法 1 构造手拉手法,如图4.64所示(证法请参考第1讲中第22题).
证法 2 三线合一法,如图4.65所示(证法请参考第1讲中第22题).
图形归一(第二类)
如图4.66所示, 均为等腰直角三角形,连接 PM,取PM 的中点G,连接 BG,CG,求证:BG=CG 且BG⊥CG.
证法① 构造手拉手法,如图4.67所示(证法请参考第1讲中第22题).
证法 2 三线合一法,如图4.68所示(证法请参考第1讲中第22题).
番外篇:遇见中考
22.(2022·深圳模拟)如图4.69 所示,四边形 ABCD 和BEFG 都是正方形,BH⊥AE于点H,延长 HB交CG 于点M,证明发现 CM=MG.小生同学想到了这样的证明方法:过点C作CN⊥BM,交 BM 的延长线于点N.他已经证明了△ABH≌△BCN,但接下来的证明过程,他有些迷茫了.
(1)请同学们帮小生同学将剩余的证明过程补充完整.
(2)深入研究:若将原题中的“正方形”改为“矩形”(如图4.70所示),且 (其中 k>0),请直接写出线段CM,MG 的数量关系: .
(3) 拓展应用:如图4.71所示,在 Rt△ABC 和 Rt△ADE 中, ∠ACB=∠AED = 30°,连接 BD,CE,F 为 BD 的中点,则 AF 与CE 的数量关系为
第4 讲 手拉手模型
1. ①②④.
∠BOD=∠BAC+∠CBE+∠OBA=∠BAC+∠ABC=120°≠100°,故③错误;先证△MCE≌△NCD(SSS),则 ME= ND,故⑤错误.
2. ①③④.
因为△ABD≌△ACE,所以∠ABD=∠ACE,显然∠ABD≠∠ACD,故②错误;
BE 2) - -CD ,故④正确.
3. ①②④.
4. 30°.
提示:因为 AB=AC=BC,且互为共端点,所以每一个端点都可以进行两种旋转.
如图J4.1所示,连接CE,延长 AB,CE 交于点T.
利用手拉手模型易得 所以 ,则 为等腰直角三角形,因此 BC=BT=AB.
因为点 F 是AE 的中点,所以 BF 是 的中位线,则 故
6. 16.
解题要点:利用CF = BE,∠ABE=∠ACF,连接 AE,AF 构造手拉手模型是此题的关键.
如图J4.2 所示,连接 AE,AF,易证△ABE≌△ACF(SAS),可得∠AFB=∠AFE + 故.
如图J4.3所示,连接 BD.因为 AD=CD,所以可将△BCD 绕点D 顺时针方向旋转60°,得到△B'AD.连接 BB',延长 BA,作 B'E⊥BA 于点E,则 ∠CBD=∠AB'D,此时S四边形ABCD = S凹四边形BDB'A,△BDB'是等边三角形.
因为∠ABC=75°,∠ADC=60°,所以. 则
因为 所以 则.
设等边△BB'D的高为h,则由勾股定理得 故
提示:因为 AB=AF,所以可把△ABP 或△APF 绕点A 旋转120°,使AB 和AF 重合,再利用勾股定理求解即可.
提示:因为 AB=AD,所以可把△ABP 或△APD 绕点A 旋转90°,使 AB 和AD 重合,再利用勾股定理求解即可.
提示:因为 AB=AC,所以可把△ABP 或△APC 绕点A 旋转120°,使 AB 和AC 重合,
再利用勾股定理求解即可.
如图J4.4所示,以点 D 为旋转中心,将 绕点D 顺时针旋转 得到 连接 AF,则. ,故当 A,B,F 三点共线时,AF 最大,此时AD 最大.
因为AB=4,AC=8,所以AF=AB+BF=AB+AC=12,则. 故AD 的最大值为
12. (1) AP=CE,90°.
因为四边形 ABCD 是正方形,所以 AD=DC,∠ACD=∠DAC=45°,∠ADC=90°.
又四边形 DPFE 是正方形,则 DP=DE,∠PDE=∠ADC=90°,于是∠ADP=∠CDE,故△ADP≌△CDE(SAS),有AP=CE,∠DAC=∠DCE=45°,故∠ACE=90°.
或(
如图4.37所示,由(1)可得 AP=CE,则
如图4.38所示,因为四边形 ABCD 是正方形,所以 AD=DC,∠ACD=∠DAC=45°,
又四边形 DPFE 是正方形,则 DP= DE,∠PDE=∠ADC=90°,∠ADP=∠CDE,故△ADP≌△CDE(SAS),有 AP=CE,∠DAC=∠DCE=45°,故
(3)12.
如图J4.5所示,连接CE.
因为△ADP≌△CDE,所以∠DCE=∠DAP=45°,故∠ACE=∠ACD+∠DCE=90°.
因为 所以( 则
又 AP=CE=6,则 PC=6-4=2,于是 故 则
13. 150°.
比线段 ,共端点(点 B),用旋转(可旋转△BCP 或
解法1 如图J4.6 所示,将△ABP 绕点B 顺时针旋转90°,构造 连接PP',易得 因为 根据勾股逆定理可得 =90°,故
解法2 如图J4.7 所示,将△BCP 绕点B 逆时针旋转90°,构造 连接PP',下面的解法同解法1.
利用一转成双,由△ABC∽△DBE 得△ABD∽△CBE,故
连接AE.因为△ABC∽△EDC,可得△BCD∽△ACE,所以 则 AE =
又BD=2,BC=5,∠B=60°,可得 故
如图J4.8所示,连接 AC,AG,AC′.
利用一转成双,由△ABC∽△AB'C'得△ABB'∽△ACC',则
因为 ,所以△AB′G 是等腰直角三角形,则 AG=
设 则
在 Rt△ADG 中, 即 解得 (舍去),故 AB=5.
在 Rt△ABC中, 故
17.由正方形的性质得 O为AC 的中点.
因为 H 为CE 的中点,所以
又△AEF 是等腰直角三角形,则. 故
如图J4.9 所示,因为 OH∥AE,所以∠COH =∠CAE,则∠BOH =∠BAF,因此△BOH∽△BAF,则 故∠HBF =∠HBO+∠DBF =∠DBA =45°,即△BHF 为等腰直角三角形.
18*.本题为广义的托勒密定理,证明过程如下:
如图 J4.10 所示,作∠BAE = ∠DAC,且使 进而得到△ABE∽△ACD(图J4.11),所以
AB·CD = BE·AC. ①
又∠CAD =∠BAE,则∠EAD =∠BAC,因为 所以△AED∽△ABC(图J4.12),则
AD·BC = DE·AC. ②
①+②,有AB·CD +AD·BC = BE·AC + DE·AC,
即 AB·CD+AD·BC=AC(BE+DE).
因为 BE+DE≥BD,所以 AB·CD+AD·BC≥AC·BD.
19.【问题背景】 因为∠ACB =∠ADE =90°,AC = BC,AD = DE,所以∠DAE =∠CAB,且. ,则∠DAC=∠EAB,于是△ABE∽△ACD,则 即
【变式迁移】
如图J4.13所示,连接 BD.
因为∠E=45°,DF⊥BE,所以∠EDF=∠E=45°.
在正方形 ABCD 中,∠BDC=45°,则. 所以△EDB∽△FDC,故
【拓展创新】
如图J4.14所示,过点 A 作AH⊥AF,交 EF 于点H,连接BH.
因为 BE= BF,所以∠BEF=∠BFE.
又∠FEA=∠BFA,则∠AFE=∠BEA,即 tan∠AFE= tan∠BEA,于是 即 故
由一转成双易得△FAE∽△HAB,则∠AHB=∠AFE=∠AEB,A,H,E,B四点共圆,所以∠BHE=∠BAE=90°,则
因为AE=2AB,所以 故
20. 如图J4.15 所示,分别把△ABC 和△CEF 补成以C为直角顶点的等腰 Rt△ACP和Rt△HCF,然后再连接AH,PF,利用手拉手全等证明△CAH≌△CPF,易得AH=PF且AH⊥PF.因为 BM,ME 分别为△APF 和△AHF 的中位线,所以 BM∥PF,ME∥AH,故 BM=ME 且BM⊥ME.
21. 如图J4.16所示,分别把△ACE 和△ABD 补成等腰Rt△ACF 和 Rt△ABG,然后再连接BF,CG,利用手拉手全等易证△AFB≌△ACG,易得 BF=CG 且BF⊥CG.因为EM,MD 分别为△CFB 和△BCG 的中位线,所以 )∥CG,故 ME=MD 且ME⊥MD,即△MED 是等腰直角三角形.
22.(1)如图J4.17所示,过点 G 作GT⊥NH 于点T.
因为△ABH≌△BCN,所以 BH=CN.
同法可证△EHB≌BTG,所以 BH=TG,则 CN=GT.
因为CN⊥NH,GT⊥NH,所以∠N=∠GTM=90°.
又∠CMN=∠GMT,则△CMN≌△GMT(AAS),故CM=GM.
证明如下:如图J4.18所示,过点C作CN⊥MH 于点N,过点 G 作GT⊥NM交HM 的延长线于点 T.
因为四边形 ABCD 是矩形,所以∠ABC=∠AHB=∠CNB=90°,则∠ABH+∠CBN=90°,∠CBN+∠BCN=90°,于是∠ABH=∠BCN,则△AHB∽△BNC,故 即
同法可证△EHB∽△BTG,所以 即 TG=kBH.
又∠T=∠CNM=90°,∠CMN=∠GMT,则△CNM∽△GTM,于是
证明如下:如图J4.19 所示,延长 AF 到点T,使得 AF=FT,连接 BT,DT.
因为 AF=FT,BF=FD,所以四边形 ABTD 是平行四边形,则AD=BT,AD∥BT,于是∠ABT+∠BAD=180°.
又∠CAB=∠DAE=90°,则∠BAD +∠CAE=180°,于是∠ABT=∠CAE.
因为∠ACB =∠AED =30°,所以. 则 于是△CAE∽△ABT,则 即 故
同课章节目录
