第4单元 比例高频易错培优讲练测(讲义)-2024-2025学年六年级下册数学人教版
文档属性
| 名称 | 第4单元 比例高频易错培优讲练测(讲义)-2024-2025学年六年级下册数学人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 699.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 07:35:45 | ||
图片预览





文档简介
【思维导图+知识精讲+典型例题+高频真题+答案解析】
例题1:在比例尺是的图纸上,画一个边长是4厘米的正方形草坪,草坪的实际周长是多少米?实际面积是多少公顷?
【答案】见试题解答内容
【分析】先依据“图上距离÷比例尺=实际距离”求出正方形的边长的实际长度,进而依据正方形的周长=边长×4和面积=边长×边长即可得解,注意单位换算.
【解答】解:420000(cm)
20000cm=200 m
周长为200×4=800 (m)
面积为 200×200=40000(m2)
40000m2=4公顷
答:草坪的实际周长是800米,实际面积是4公顷.
【点评】此题主要考查图上距离、实际距离和比例尺的关系,以及正方形的周长面积的计算方法.
例题2:一个房间,用边长5dm的方砖铺地,需要128块,如果改成用边长8dm的方砖铺地,需要多少块?
【答案】50块。
【分析】房间的面积一定,方砖的面积与块数成反比例,解决此题,首先根据方砖的边长得求出方砖的面积。据此列出比例解答即可。
【解答】解:设需要x块。
82x=52×128
64x÷64=3200÷64
x=50
答:需要50块。
【点评】根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解。
例题3:一个长方形的篮球场,长40米,宽30米,请你用的比例尺画出篮球场的平面图.(先计算,再画图)
【答案】见试题解答内容
【分析】篮球场的长和宽的实际长度以及比例尺已知,依据“图上距离=实际距离×比例尺”即可求出篮球场长和宽的图上距离,进而就可以画出篮球场的平面图.
【解答】解:40米=4000厘米,30米=3000厘米
40002(厘米)
30001.5(厘米)
【点评】此题主要考查图上距离、实际距离和比例尺的关系.
例题4:世界上最长的跨海大桥﹣﹣杭州湾跨海大桥,在比例尺1:400000的地图上量得它的长度是9cm.杭州湾跨海大桥的实际长度是多少千米?
【答案】见试题解答内容
【分析】要求杭州湾跨海大桥的实际长度是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可.
【解答】解:93600000(厘米)
3600000厘米=36千米.
答:杭州湾跨海大桥的实际长度是36千米.
【点评】此题有计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论.
例题5:在一幅地图上,量得广州到东莞的图上距离是4厘米,广州到东莞的实际距离大约是50千米.求这幅地图的比例尺是多少?
【答案】见试题解答内容
【分析】已知图上距离、实际距离,求比例尺,用比例尺=图上距离:实际距离,统一单位代入即可解决问题.
【解答】解:4厘米:50千米
=4厘米:5000000厘米
=1:1250000
答:这幅地图的比例尺是1:1250000.
【点评】本题考查了考查了比例尺的概念,图上距离、实际距离、比例尺三者之间的关系.
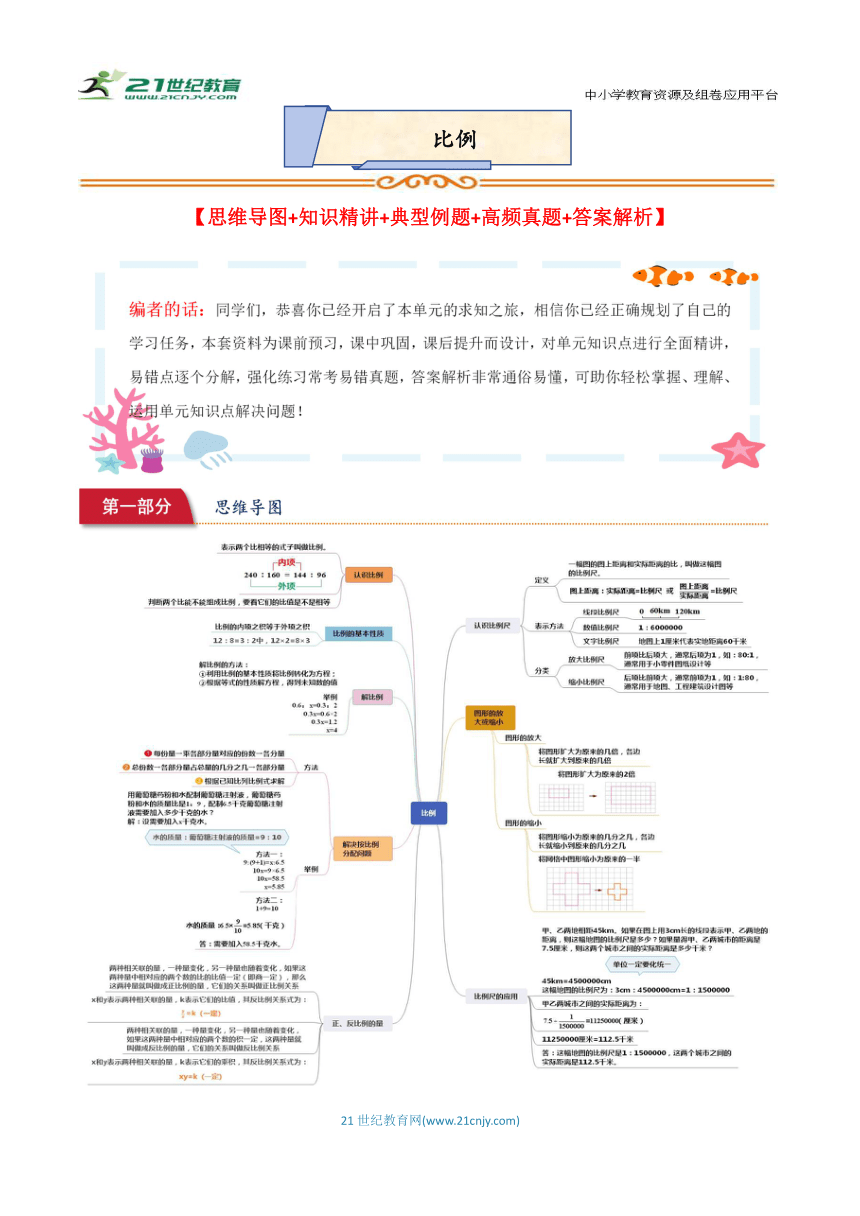
1.比例的意义和基本性质 【知识点归纳】 比例的意义:表示两个比相等的式子,叫做比例. 组成比例的四个数,叫做比例的项. 组成比例两端的两项叫做外项,中间的两项叫做内项. 比例的性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质. 如:4:5=16:20 4×20=5×16 2.正比例和反比例的意义 【知识点归纳】 1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为:k(一定). 2.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的乘积(一定),反比例的关系可以表示为:xy=k(一定). 3.辨识成正比例的量与成反比例的量 【知识点归纳】 1.成正比例的量: (1)“变化方向”相同,一种量扩大或缩小,另一种量也扩大或缩小. (2)相对应的两个数的比值(商)一定. (3)关系式:k(一定). 2.成反比例的量: (1)“变化方向”相反,一种量扩大或缩小,另一种量反而缩小或扩大. (2)相对应的两个数的乘积一定. (3)关系式:xy=k(一定). 3.判断方法:关键是看着两种相关量中相对应的两个数是商一定还是积一定,如果商一定,就成正比例;如果积一定,就成反比例. 4.解比例 【知识点归纳】 根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项.求比例中的未知项,叫做解比例. 一般来说,求比例的未知项有以下两种情况: (1)求未知外项 (2)求未知内项 5.比例的应用 【知识点归纳】 根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解. 6.比例尺 【知识点归纳】 1.比例尺: 表示图上距离比实地距离缩小的程度,因此也叫缩尺.图上距离和实际距离的比,叫做这幅图的比例尺. 即:图上距离:实际距离=图上距离÷比例尺 比例尺分类: 比例尺一般分为数值比例尺和线段比例尺: (1)数值比例尺:例如一幅图的比例尺是1:20000或.为了方便,通常把比例尺写成前项(或后项)是1的比. (2)线段比例尺是在图上附上一条标有数量的线段,用来表示实际相对应的距离. 2.比例尺表示方法: 用公式表示为:实际距离=图上距离÷比例尺.比例尺通常有三种表示方法. (1)数字式,用数字的比例式或分数式表示比例尺的大小.例如地图上1厘米代表实地距离500千米,可写成:1:50000000或写成:. (2)线段式,在地图上画一条线段,并注明地图上1厘米所代表的实际距离. (3)文字式,在地图上用文字直接写出地图上1厘米代表实地距离多少千米,如:图上1厘米相当于地面距离500千米,或五千万分之一. 3.比例尺公式: 图上距离=实际距离×比例尺 实际距离=图上距离÷比例尺 比例尺=图上距离÷实际距离.
1.车队向武汉灾区运送一批救援物资,去时每小时行50千米,6.4小时到达武汉;按原路返回,每小时行80千米,返回时间是多少?(用比例解)
2.身高1.8米的大卫在公园里观赏一尊雕像时,想知道雕像的高度。他灵机一动,站到雕像旁边拍了一张合影,然后量得照片上的他高3厘米,雕像高8厘米。因此很快算出了雕像的高度。你知道雕像的实际高度是多少米吗?
3.在比例尺1:2500000的的地图上量得A、B两地相距4.8厘米。甲骑自行车以每小时12km的速度从A地骑往B地,同时乙开车以每小时36km的速度从B开往A地。两人几小时后相遇?
4.如图,少年宫到市民广场的实际距离是1200米.这幅平面图的比例尺是多少?图书馆到市民广场的实际距离是多少米?
5.六一班有男生30人,女生18人,又转来一部分女生,这时,女生的人数与男生人数的比是2:3,又转来了多少名女生?
6.北京到广州的实际距离是2400千米,在某幅地图上量得北京到广州的图上距离是2.4厘米。求这幅地图的比例尺,并用线段比例尺表示出来。
7.一个手机零件长3mm,在一幅设计图上量得长9cm,这幅设计图的比例尺是多少?
8.一块梯形地的上底是40m,下底是60m,高是50m,如果将它画在比例尺为1:2000的图纸上,这块地在图纸上的面积是多少平方厘米?
9.在比例尺1:6000000的地图上,量得南京到北京的距离为15厘米.一列动车以每小时300千米的速度从南京开往北京,几小时能到达?
10.把线段比例尺改写成数值比例尺是多少?
11.修一条6400米的公路,修了20天后,还剩下4800米,照这样计算,剩下的路还要修多少天?(用比例解)
12.一辆汽车从甲地到乙地,平均每小时行80千米,12小时到达。回来时空车原路返回,10小时返回原地。返程时汽车的速度是多少?(用比例解)
13.一个零件在图纸上的宽度是9cm,已知这个零件的实际宽度是3mm,你能算出图纸的比例尺吗?
14.一块正方形地的边长是60米,如果把它的边长缩小到它的画在一张图纸上,图上的正方形边长应是多少厘米?
15.加工一批零件,第一天加工了总数的,第二天比第一天多加工5个,这时已加工的与未加工的零件个数比是7:5,这批零件共多少个?
16.一幅中国地图的比例尺是1:4000000.在这幅地图上,量得北京到上海的高铁路线长33厘米.一列高铁平均速度是每时300千米,它从北京到上海需要多长时间?
17.给客厅铺砖,如果用边长3分米的地砖需要400块。因为装饰需要改用面积是6平方分米的地砖,需要多少块?
18.希望小学教学楼的地基是长方形,长72米,宽24米,用1:1200的比例尺把它画在图纸上,图上长方形的面积是多少平方厘米?
19.“神舟”十二号是中国航天工程发射的第十二艘飞船,“神舟”十二号在太空球飞行10圈需用14小时,它飞行15圈要用多少小时?(用比例解答)
20.某校五年级只有两个班,全年级的男生人数与女生人数之比为8:7,已知一班男生有51人,女生有48人,二班的男生人数与女生人数之比为5:4,那么二班男生有多少人?女生有多少人?
21.在一幅比例尺是1:3000000的地图上,量得甲乙两地相距40cm,在另一幅地图上,量得甲乙两地相距20cm。另一幅地图的比例尺是多少?
22.大宝和小宝一起喝汤圆,本来大宝碗里的和小宝碗里的个数之比为2:3,后来大宝想要减肥,又夹了4个汤圆到小宝碗里,此时大小宝碗里汤圆之比为1:2,求两人一共有多少个汤圆?
23.王阿姨买了一辆电瓶车,七五折优惠付了1500元.这辆车比原来便宜了多少钱?先在线段图上补上缺少的信息和问题,再列式计算.
24.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
25.把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后,得到的卡片的面积是多少平方厘米?
26.甲、乙两人从A、B两地同时出发同向而行,甲、乙的速度之比为3:2,当甲追上乙时,甲比乙多走了500米,此时甲共走了多少米?
27.一种精密零件长5毫米,画在纸上长10厘米,这幅图纸的比例尺是多少?
28.在一幅比例尺是1:500000的地图上,量得甲、乙两地的距离是6.8厘米。如果把比例尺改为1:250000,画在新图上时甲、乙两地的距离是多少厘米?(列比例式解)
29.某地为便于残障人士的轮椅通行,发布了一项关于建筑物前斜坡高度的规定:每高1米的斜坡,至少需要12米的水平长度。某建筑物前的空地水平长度为18米,那么此处的斜坡高度最高为多少米?
30.计算机的CPU是计算机的心脏,将一个长30毫米的CPU零件画在图纸上,长为18厘米。这张图纸的比例尺是多少?
31.装订一批书籍,计划每天装订90本,20天装订完。实际提前5天完成任务,实际每天装订多少本?(用比例解)
32.一只瓢虫的实际长度是4毫米。画在图纸上的长度是2.4厘米,这幅图纸的比例尺是多少?
33.爸爸买一堆同样的铁钉。先数100根称了称是50克,又称了全部的质量是600克,这堆铁钉有多少根?(用比例解)
34.在一幅比例尺是1:2000000的地图上,量得A、B两地之间的距离是8.5cm,在另一幅比例尺是1:5000000的地图上,这两地之间的距离是多少厘米?
35.如图是乐乐绘制的校园平面图。
(1)图上1cm表示实际距离 。
(2)在平面图中,教学楼的长是2.5cm,宽是0.5cm,教学楼实际长 m,宽 m,教学楼实际占地面积是 m2。
(3)先量一量,再算一算校园的实际占地面积是 m2。
(4)王老师在黑板上画该校园的平面图,他用50cm表示校园的长。黑板上的平面图的比例尺是多少?
36.小明为准备学校读书竞赛,他要看完3本课外书,其中一本书共360页,他3天看了全书的25%。照这样的速度,看完这本书一共需要多少天?(用比例解)
37.学校组织同学们参观科技博物馆,如果每辆车坐35人,需要12辆车;如果每辆车坐28人,需要多少辆车?(用比例解)
38.某小区要修建一个长方体水池,在比例尺是1:200的设计图上,水池的长为14cm,宽为10cm,深为3cm.按图施工,这个水池的长、宽、深各应挖多少米?
39.李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
40.把下面左边的平行四边形按比例缩小后得到右边的平行四边形,那么缩小后的平行四边形的高是多少?
41.聪聪读一本《数学大王》,如果每天读20页,15天可以读完。聪聪想10天读完,那么平均每天要读多少页?(用比例的知识解)
42.一个精密零件,画在比例尺是25:1的图纸上,图上距离是12厘米,该零件的实际长度是多少?
43.一个飞机模型长15厘米,它的实际长度是60米,这个飞机模型的比例尺是多少?
44.在一幅比例尺是1:34000000的地图上,量得北京到上海的距离是3厘米.两地之间的实际距离是多少千米?
45.小明和小华吃鹤鹑蛋,原来小明和小华吃的鹤鹑蛋的个数比为2:3,后来小明又吃了4个,小华又吃了3个,此时小明和小华吃的鹤鹑蛋的个数比为3:4。原来两人各吃了多少个鹤鹑蛋?(用比例解)
46.2022年第24届冬季奥运会将在北京和张家口联合举办,北京至张家口的距离约为165km,在一幅冬奥会宣传图上,两地间的图上距离是55cm.
(1)这幅宣传图的比例尺是多少?
(2)北京至张家口将建设京张高铁,在宣传图上京张高铁全线长58cm,那么京张高铁全长多少千米?
47.一间房子要用方砖铺地,若用边长为4分米的方砖,需要72块,如果改用边长为6分米的方砖,需要多少块?(用比例解答)
48.强子的实际身高为1.6米,在照片上的身高为5厘米,照片的比例尺是多少?
49.把一个9毫米长的机器零件画在一张图纸上,量得零件的长是18厘米。这张图纸的比例尺是多少?
50.一种稀释消毒液,用药液和水按1:200配制而成。要配制这种稀释消毒液603千克,需要药液多少千克?(用比例知识解答)
参考答案与试题解析
1.车队向武汉灾区运送一批救援物资,去时每小时行50千米,6.4小时到达武汉;按原路返回,每小时行80千米,返回时间是多少?(用比例解)
【答案】4小时。
【分析】路程一定,速度和时间成反比例关系;去时速度×去时时间=回来时速度×回来时时间,据此列比例解答即可。
【解答】解:返回时间是x小时。
80x=50×6.4
80x=320
x=4
答:返回时间是4小时。
【点评】找出题中数量之间的比例关系,列出等量关系式,根据等量关系式列比例解答。
2.身高1.8米的大卫在公园里观赏一尊雕像时,想知道雕像的高度。他灵机一动,站到雕像旁边拍了一张合影,然后量得照片上的他高3厘米,雕像高8厘米。因此很快算出了雕像的高度。你知道雕像的实际高度是多少米吗?
【答案】4.8米。
【分析】设雕像的实际高度是x米,因为大卫和雕像在一张照片上,所以大卫的身高:照片上他的高度=雕像的实际高度:照片上雕像高度,列出比例解答即可。
【解答】解:设雕像的实际高度是x米。
1.8:3=x:8
3x=1.8×8
3x=14.4
x=4.8
答:雕像的实际高度是4.8米。
【点评】解答此题的关键是,判断实际高度与照片上高度成正比例,由此列出比例解决问题。
3.在比例尺1:2500000的的地图上量得A、B两地相距4.8厘米。甲骑自行车以每小时12km的速度从A地骑往B地,同时乙开车以每小时36km的速度从B开往A地。两人几小时后相遇?
【答案】2.5小时。
【分析】根据实际距离=图上距离÷比例尺,求出A,B两地的实际距离,再根据相遇时间=总路程÷速度和。
【解答】解:4.812000000(厘米)
12000000厘米=120千米
120÷(12+36)
=120÷48
=2.5(小时)
答:两人2.5小时后相遇。
【点评】此题考查了比例尺、图上距离和实际距离的关系以及时间、速度和路程的关系。
4.如图,少年宫到市民广场的实际距离是1200米.这幅平面图的比例尺是多少?图书馆到市民广场的实际距离是多少米?
【答案】见试题解答内容
【分析】(1)用直尺测量出少年宫到市民广场的图上距离是2厘米,根据图上距离:实际距离=比例尺,列式解答即可;
(2)用直尺测量出超图书馆到市民广场的图上距离;再根据实际距离=图上距离÷比例尺,据此解答.
【解答】解:(1)少年宫到市民广场的图上距离是2厘米;
1200米=120000厘米
2:120000=1:60000;
答:这幅平面图的比例尺是1:60000.
(2)图书馆到市民广场的图上距离1厘米
所以1×60000=60000(厘米)=600(米)
答:图书馆到市民广场的实际距离是600米.
【点评】本题主要考查了比例尺,图上距离与实际距离的关系.
5.六一班有男生30人,女生18人,又转来一部分女生,这时,女生的人数与男生人数的比是2:3,又转来了多少名女生?
【答案】2名。
【分析】设后来转来x个女生,这时女生的人数与男生人数的比是2:3,根据等量关系:(原有女生人数+后来转来女生人数):男生人数=2:3,列方程解答即可。
【解答】解:设又转来了x名女生。
(18+x):30=2:3
54+3x=60
3x=6
x=2
答:又转来了2名女生。
【点评】本题考查了比的应用,关键是根据等量关系:男生人数:(原有女生人数+后来转来女生人数):男生人数=2:3,列方程。
6.北京到广州的实际距离是2400千米,在某幅地图上量得北京到广州的图上距离是2.4厘米。求这幅地图的比例尺,并用线段比例尺表示出来。
【答案】1:100000000,。
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这幅图的比例尺。
【解答】解:2400千米=240000000厘米
2.4:240000000=1:100000000
100000000厘米=1000千米
答:这幅地图的比例尺是1:100000000,用线段比例尺表示出来是。
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算。
7.一个手机零件长3mm,在一幅设计图上量得长9cm,这幅设计图的比例尺是多少?
【答案】见试题解答内容
【分析】图上距离和实际距离已知,依据比例尺=图上距离:实际距离,即可求得这幅设计图的比例尺.
【解答】解:9cm=90mm
90:3=30:1
答:这幅设计图的比例尺为30:1.
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算.
8.一块梯形地的上底是40m,下底是60m,高是50m,如果将它画在比例尺为1:2000的图纸上,这块地在图纸上的面积是多少平方厘米?
【答案】见试题解答内容
【分析】根据图上距离=实际距离×比例尺,分别求出这个梯形画在图上的图上距离,再根据梯形的面积公式:S=(a+b)h÷2可求出图上的面积是多少.据此解答.
【解答】解:40m=4000厘米,60m=6000厘米,50m=5000厘米
40002(厘米)
60003(厘米)
50002.5(厘米)
(2+3)×2.5÷2
=5×1.25
=6.25(平方厘米)
答:这块地在图纸上的面积是6.25平方厘米.
【点评】本题的关键是根据图上距离=实际距离×比例尺,求出图上距离,再根据梯形的面积公式进行解答.
9.在比例尺1:6000000的地图上,量得南京到北京的距离为15厘米.一列动车以每小时300千米的速度从南京开往北京,几小时能到达?
【答案】见试题解答内容
【分析】这道题是已知比例尺、图上距离,求实际距离,根据图上距离÷比例尺=实际距离列式求得实际距离,再根据时间=路程÷速度即可解答.
【解答】解:1590000000(厘米)
90000000厘米=900(千米)
900÷300=3(小时)
答:3小时到达.
【点评】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,灵活变形列式解决问题.
10.把线段比例尺改写成数值比例尺是多少?
【答案】见试题解答内容
【分析】已知图上距离1cm、实际距离20km,求比例尺,用比例尺=图上距离:实际距离,统一单位代入数据即可解决问题.
【解答】解:1厘米:20千米
=1厘米:2000000厘米
=1:2000000
答:改写成数值比例尺为1:2000000.
【点评】本题考查了比例尺的意义,即比例尺=图上距离:实际距离,注意单位的统一.
11.修一条6400米的公路,修了20天后,还剩下4800米,照这样计算,剩下的路还要修多少天?(用比例解)
【答案】60天。
【分析】照这样计算,说明平均每天修路的米数是一定的,那么一共修的米数与修的天数的比值一定,即两种量成正比例,由此设出未知数,列比例解答问题。
【解答】解:设剩下的路还要修x天,由题意得:
(6400﹣4800):20=4800:x
1600x=20×4800
1600x=96000
x=60
答:剩下的路还要修60天。
【点评】此题主要考查对正比例意义的运用,解决此题关键是先用6400减去4800米求出余下的没修的米数,进而列比例解答。
12.一辆汽车从甲地到乙地,平均每小时行80千米,12小时到达。回来时空车原路返回,10小时返回原地。返程时汽车的速度是多少?(用比例解)
【答案】96米/时。
【分析】根据题意总路程不变,速度和时间成反比例,由此列式解答即可。
【解答】解:设返程时汽车的速度是x千米/时,
10x=80×12
10x=960
x=96
答:返程时汽车的速度是96千米/时。
【点评】解答此题的关键是弄清题意,找出相关联的量成什么比例,找准对应量,列式解答即可。
13.一个零件在图纸上的宽度是9cm,已知这个零件的实际宽度是3mm,你能算出图纸的比例尺吗?
【答案】见试题解答内容
【分析】根据比例尺=图上距离÷实际距离,代入数据解答即可.
【解答】解:9cm=90mm
90:3=30:1
答:图纸的比例尺是30:1.
【点评】解答此题的关键是掌握比例尺=图上距离÷实际距离这个公式及其变形.
14.一块正方形地的边长是60米,如果把它的边长缩小到它的画在一张图纸上,图上的正方形边长应是多少厘米?
【答案】见试题解答内容
【分析】实际距离和比例尺已知,依据“图上距离=实际距离×比例尺”即可求出图上的边长.
【解答】解:60米=6000厘米
60006(厘米)
答:图上的正方形边长应是6厘米.
【点评】此题主要考查图上距离、实际距离和比例尺的关系.
15.加工一批零件,第一天加工了总数的,第二天比第一天多加工5个,这时已加工的与未加工的零件个数比是7:5,这批零件共多少个?
【答案】420个。
【分析】这时已加工的与未加工的个数比是7:5,即此时已加工的占全部的,又第一天加工了总数的,所以第二天加工了全部的(),第二天比第一天多加工总数的(),根据分数除法的意义,用除法计算即可得这批零件一共的个数。
【解答】解:5÷()
=5÷[()]
=5÷[]
=5
=420(个)
答:这批零件共420个。
【点评】本题考查了比的应用,首先根据两天后已加工的与未加工的个数比求出此时已加工的占全部的分率是完成本题的关键。
16.一幅中国地图的比例尺是1:4000000.在这幅地图上,量得北京到上海的高铁路线长33厘米.一列高铁平均速度是每时300千米,它从北京到上海需要多长时间?
【答案】见试题解答内容
【分析】根据图上距离÷比例尺=实际距离列式求得北京到上海的实际距离,再根据路程、速度与时间的关系,列式即可解答.
【解答】解:33132000000(厘米)
132000000厘米=1320千米
1320÷300=4.4(小时)
答:它从北京到上海4.4小时.
【点评】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,以及时间=路程÷速度的实际应用.
17.给客厅铺砖,如果用边长3分米的地砖需要400块。因为装饰需要改用面积是6平方分米的地砖,需要多少块?
【答案】600块。
【分析】根据题意可知,每块地砖的面积×块数=铺地的面积(一定),所以每块地砖的面积和需要的块数成反比例,设需要x块,据此列方程解答。
【解答】解:设需要x块。
6×x=3×3×400
6x=9×400
x=600
答:需要600块。
【点评】此题主要考查正方形面积公式的灵活运用,反比例的意义及应用,注意:是每块地砖的面积和块成反比例,不是每块地砖的边长和块数成反比例。
18.希望小学教学楼的地基是长方形,长72米,宽24米,用1:1200的比例尺把它画在图纸上,图上长方形的面积是多少平方厘米?
【答案】见试题解答内容
【分析】根据比例尺的定义,图上距离=实际距离×比例尺,即可得到图形上的长和宽,再用长乘上宽即得面积.
【解答】解:因为72米=7200厘米,24米=2400厘米,
长:72006(厘米)
宽:24002(厘米)
面积:6×2=12(平方厘米)
答:图上长方形的面积是12平方厘米.
【点评】关键是理解比例尺的意义,注意单位的转换.
19.“神舟”十二号是中国航天工程发射的第十二艘飞船,“神舟”十二号在太空球飞行10圈需用14小时,它飞行15圈要用多少小时?(用比例解答)
【答案】21小时。
【分析】根据题意知道速度一定,路程和时间成正比例,据此列式解答即可。
【解答】解:设飞行15圈要用x小时,
10:14=15:x
10x=14×15
x=14×15÷10
x=21
答:它飞行15圈要用21小时。
【点评】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,再列出方程进行解答。
20.某校五年级只有两个班,全年级的男生人数与女生人数之比为8:7,已知一班男生有51人,女生有48人,二班的男生人数与女生人数之比为5:4,那么二班男生有多少人?女生有多少人?
【答案】二班男生有45人,女生有36人。
【分析】二班的男生人数与女生人数之比为5:4,设二班男生5x人,女生4x人,根据等量关系:(一班男生人数+二班男生人数):(一班女生人数+二班女生人数)=8:7,列方程解答即可。
【解答】解:设二班男生5x人,女生4x人,
(51+5x):(48+4x)=8:7
357+35x=384+32x
3x=27
x=9
9×5=45(人)
9×4=36(人)
答:二班男生有45人,女生有36人。
【点评】本题主要考查了比例的应用,关键是根据等量关系:(一班男生人数+二班男生人数):(一班女生人数+二班女生人数)=8:7,列方程。
21.在一幅比例尺是1:3000000的地图上,量得甲乙两地相距40cm,在另一幅地图上,量得甲乙两地相距20cm。另一幅地图的比例尺是多少?
【答案】1:6000000。
【分析】先根据“图上距离÷比例尺=实际距离”,求出甲乙两地间实际距离,求另一幅地图的比例尺,依据“比例尺=图上距离:实际距离”解答。
【解答】解:40120000000(厘米)
20:120000000=1:6000000
答:另一幅地图的比例尺是1:6000000。
【点评】此题考查的目的是理解掌握比例尺的意义及应用。根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可。
22.大宝和小宝一起喝汤圆,本来大宝碗里的和小宝碗里的个数之比为2:3,后来大宝想要减肥,又夹了4个汤圆到小宝碗里,此时大小宝碗里汤圆之比为1:2,求两人一共有多少个汤圆?
【答案】60个。
【分析】设两人一共有x个汤圆,则本来大宝碗里有x个,小宝碗里有x个,根据等量关系:(大宝碗里汤圆个数﹣4个):(小宝碗里汤圆个数+4个)=1:2,列方程解答即可。
【解答】解:设两人一共有x个汤圆,
(x﹣4):(x+4)=1:2
x+4x﹣8
x=12
x=60
答:两人一共有60个汤圆。
【点评】本题主要考查了比例的应用,关键是根据等量关系:(大宝碗里汤圆个数﹣4个):(小宝碗里汤圆个数+4个)=1:2,列方程。
23.王阿姨买了一辆电瓶车,七五折优惠付了1500元.这辆车比原来便宜了多少钱?先在线段图上补上缺少的信息和问题,再列式计算.
【答案】见试题解答内容
【分析】七五折是指现价是原价的75%,把原价看成单位“1”,它的75%对应的数量是现价1500元,根据已知一个数的百分之几是多少,用除法计算,求出原价,再用原价减去现价即可得出结论.
【解答】解
1500÷75%﹣1500
=2000﹣1500
=500(元)
答:这辆车比原来便宜了500元.
【点评】本题关键是理解打折的含义:打几几折,现价就是原价的百分之几十几.
24.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出甲车行驶的路程与行驶时间同时扩大或缩小的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)由图象可知:行驶150千米的路程甲车用的时间少,所以速度较快;据此解答即可.
【解答】解:(1)两辆车子所行的路程和时间成比例,因为是一条直线,所以成正比例;
(2)由图象可知:甲行驶150km,用4.2小时,乙行驶150km,用4.4小时,
4.2<4.4,
路程相同,用的时间越少,速度较快,即甲汽车的行驶速度快些;
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的比值一定,这两种量成正比例.
25.把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后,得到的卡片的面积是多少平方厘米?
【答案】见试题解答内容
【分析】一个长7厘米、宽5厘米的长方形按3:1放大,即将这个长方形的长和宽同时扩大3倍,根据长方形的面积公式可知得到的图形的面积是:(7×3)×(5×3)=315(平方厘米).
【解答】解:(7×3)×(5×3)
=21×15
=315(平方厘米)
答:得到的卡片的面积是315平方厘米.
【点评】本题主要考查图形的放大或缩小,关键根据长方形的面积公式完成本题.
26.甲、乙两人从A、B两地同时出发同向而行,甲、乙的速度之比为3:2,当甲追上乙时,甲比乙多走了500米,此时甲共走了多少米?
【答案】1500米。
【分析】甲、乙的速度之比为3:2,因为走的时间相同,所以甲与乙走的路程比也为3:2,甲比乙多走的占甲走的,是500米,用除法计算即可得甲共走了多少米。
【解答】解:500
=500
=1500(米)
答:此时甲共走了1500米。
【点评】本题主要考查了比例的应用,已知一个数的几分之几是多少,求这个数,用除法计算。
27.一种精密零件长5毫米,画在纸上长10厘米,这幅图纸的比例尺是多少?
【答案】20:1。
【分析】依据比例尺的意义,即图上距离与实际距离的比即为比例尺,即可求解。
【解答】解:10厘米:5毫米
=100毫米:5毫米
=100:5
=20:1
答:这幅图纸的比例尺是20:1。
【点评】此题主要考查比例尺的意义,解答时要注意单位的换算。
28.在一幅比例尺是1:500000的地图上,量得甲、乙两地的距离是6.8厘米。如果把比例尺改为1:250000,画在新图上时甲、乙两地的距离是多少厘米?(列比例式解)
【答案】13.6厘米。
【分析】设画在新图上时甲、乙两地的距离是x厘米,根据图上距离÷比例尺=实际距离列比例式解答即可。
【解答】解:设画在新图上时甲、乙两地的距离是x厘米,
6.8:x:
x=6.8
x=13.6
答:设画在新图上时甲、乙两地的距离是13.6厘米。
【点评】解答此题应明确图上距离、比例尺和实际距离三者的关系。
29.某地为便于残障人士的轮椅通行,发布了一项关于建筑物前斜坡高度的规定:每高1米的斜坡,至少需要12米的水平长度。某建筑物前的空地水平长度为18米,那么此处的斜坡高度最高为多少米?
【答案】1.5米。
【分析】因为每1米高度的斜坡,至少需要12米的水平长度,也就是水平长度与斜坡的高度的比值是一定的,设此处斜坡最高x米,根据水平高度斜坡的高度的比值是一定的列出方程。
【解答】解:设此处斜坡最高x米。
12:1=18:x
12x=18
x=1.5
答:此处斜坡最高1.5米。
【点评】解答此题的关键是根据比例列方程。
30.计算机的CPU是计算机的心脏,将一个长30毫米的CPU零件画在图纸上,长为18厘米。这张图纸的比例尺是多少?
【答案】6:1。
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这张图纸的比例尺。
【解答】解:30毫米=3厘米
18厘米:3厘米=6:1
答:这张图纸的比例尺是6:1。
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算。
31.装订一批书籍,计划每天装订90本,20天装订完。实际提前5天完成任务,实际每天装订多少本?(用比例解)
【答案】120本。
【分析】每天装订的本数×天数=总本数(一定),每天装订的本数和天数成反比例关系。据此用比例求出实际每天装订多少本。
【解答】解:设实际每天装订x本。
90×20=(20﹣5)×x
15x=1800
x=120
答:实际每天装订120本。
【点评】如果相关的两个量的比值一定,这两个量成正比例关系,如果相关的两个量的乘积一定,这两个量成反比例关系。
32.一只瓢虫的实际长度是4毫米。画在图纸上的长度是2.4厘米,这幅图纸的比例尺是多少?
【答案】6:1。
【分析】比例尺=图上距离:实际距离,根据题意代入数据可直接得出这张地图的比例尺。
【解答】解:2.4厘米=24毫米
这幅地图的比例尺为24:4=6:1。
【点评】本题考查了比例尺的概念,掌握比例尺的计算方法,注意在求比的过程中,单位要统一。
33.爸爸买一堆同样的铁钉。先数100根称了称是50克,又称了全部的质量是600克,这堆铁钉有多少根?(用比例解)
【答案】1200根。
【分析】根据题意可知,每一根的质量是一定的,铁钉的根数与质量成正比例,依此列出比例解答。
【解答】解:设这堆铁钉有x根。
50x=100×600
50x÷50=60000÷50
x=1200
答:这堆铁钉有1200根。
【点评】根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解。
34.在一幅比例尺是1:2000000的地图上,量得A、B两地之间的距离是8.5cm,在另一幅比例尺是1:5000000的地图上,这两地之间的距离是多少厘米?
【答案】见试题解答内容
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出甲乙两地的实际距离,再据“图上距离=实际距离×比例尺”即可求出在另一幅图上的图上距离.
【解答】解:8.5
=17000000
=3.4(厘米)
答:在另一幅比例尺是1:5000000的地图上,这两地之间的距离是3.4厘米.
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算.
35.如图是乐乐绘制的校园平面图。
(1)图上1cm表示实际距离 25m 。
(2)在平面图中,教学楼的长是2.5cm,宽是0.5cm,教学楼实际长 62.5 m,宽 12.5 m,教学楼实际占地面积是 781.25 m2。
(3)先量一量,再算一算校园的实际占地面积是 11250 m2。
(4)王老师在黑板上画该校园的平面图,他用50cm表示校园的长。黑板上的平面图的比例尺是多少?
【答案】(1)25;(2)62.5,12.5,781.25;(3)11250;(4)1:300。
【分析】(1)因为比例尺1:2500表示图上距离1厘米代表实际距离2500厘米,又因2500厘米=25米,所以比例尺1:2500表示地图上1厘米的距离相当于地面上25米的实际距离。
(2)依据“实际距离=图上距离÷比例尺”即可求出长和宽的实际长度,进而依据长方形的面积公式即可求解。
(3)先量出校园的图上的长和宽,根据“实际距离=图上距离÷比例尺”即可求出长和宽的实际长度,进而依据长方形的面积公式即可求解。
(4)根据“比例尺=图上距离÷实际距离”计算即可。
【解答】解:(1)图上1cm表示实际距离25m。
(2)2.56250(cm)=62.5(m)
0.51250(cm)=12.5(m)
62.5×12.5=781.25(m2)
答:教学楼实际长62.5m,宽12.5m,教学楼实际占地面积是781.25m2。
(3)量得校园的长为6cm,宽为3cm,
615000(cm)=150(m)
37500(cm)=75(m)
150×75=11250(m2)
答:校园的实际占地面积是11250m2。
(4)150m=15000cm
50÷15000=1:300
答:黑板上的平面图的比例尺是1:300。
故答案为:25;62.5,12.5,781.25;11250。
【点评】此题是一道综合性的题目,涉及到了比例尺的应用,长方形得面积公式,要求学生要细心审题,仔细作答。
36.小明为准备学校读书竞赛,他要看完3本课外书,其中一本书共360页,他3天看了全书的25%。照这样的速度,看完这本书一共需要多少天?(用比例解)
【答案】12天。
【分析】根据每天看书的页数一定,书的页数和看此页数所需的天数成正比例,由此列比例解答即可。
【解答】解:设看完这本书一共需要x天,
3:25%=x:1
25%x=3×1
25%x÷25%=3÷25%
x=12
答:看完这本书一共需要12天。
【点评】根据题意,判断哪两种相关联的量成何种比例,由此列比例式解答即可。
37.学校组织同学们参观科技博物馆,如果每辆车坐35人,需要12辆车;如果每辆车坐28人,需要多少辆车?(用比例解)
【答案】15辆。
【分析】设需要x辆车,因为每辆车坐的人数×车的辆数=总人数(一定),所以每辆车坐的人数与车的辆数成反比例,列式解答即可。
【解答】解:设需要x辆车,
28x=35×12
28x=420
x=15
答:需要15辆车。
【点评】本题主要考查了比例的应用,关键是得出每辆车坐的人数与车的辆数成反比例。
38.某小区要修建一个长方体水池,在比例尺是1:200的设计图上,水池的长为14cm,宽为10cm,深为3cm.按图施工,这个水池的长、宽、深各应挖多少米?
【答案】见试题解答内容
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可分别求出水池的长、宽、深的实际长度.
【解答】解:142800(厘米)
2800厘米=28米
102000(厘米)
2000厘米=20米
3600(厘米)
600厘米=6米
答:按图施工,这个水池的长应挖28米,宽应挖20米,深应挖6米.
【点评】此题主要考查图上距离、实际距离和比例尺的关系的运用.
39.李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
【答案】9厘米。
【分析】由题意可知:放大前后的长及放大前后的宽的比是一定的,即放大前后的对应的边成正比例,由此列出比例解决问题。
【解答】解:设放大后照片的宽应是x厘米,
6:13.5=4:x
6x=54
x=9
答:宽是9厘米。
【点评】解答此题关键是明确按比例放大长与长的比等于宽与宽的比。
40.把下面左边的平行四边形按比例缩小后得到右边的平行四边形,那么缩小后的平行四边形的高是多少?
【答案】见试题解答内容
【分析】由题意可知:平行四边形各边缩小的倍数一定,则缩小后的边和高的长度与原来边与高的长度成正比,据此即可列比例求解.
【解答】解:设缩小后的平行四边形的高是xcm,根据题意可得:
24:36=x:24
36x=24×24
36x÷36=24×24÷36
x=16
答:缩小后的平行四边形的高是16厘米.
【点评】解答此题的关键是明白:平行四边形各边缩小的倍数一定,则缩小后的边和高的长度与原来边与高的长度成正比.
41.聪聪读一本《数学大王》,如果每天读20页,15天可以读完。聪聪想10天读完,那么平均每天要读多少页?(用比例的知识解)
【答案】30
【分析】根据题意可知:每天读的页×读的天数=这本书的页数(一定),所以每天读的页和读的天数成反比例,设平均每天要读x页,据此列比例解答。
【解答】解:设平均每天要读x页
10x=20×15
x=300÷10
x=30
答:平均每天要读30页。
故答案为:30
【点评】本题主要考查比例在日常生活中的应用,要正确判断哪两种量成反比例是解答关键。
42.一个精密零件,画在比例尺是25:1的图纸上,图上距离是12厘米,该零件的实际长度是多少?
【答案】见试题解答内容
【分析】根据实际距离=图上距离÷比例尺,代入数据解答即可.
【解答】解:12÷25=0.48(厘米)
答:该零件的实际长度是0.48厘米.
【点评】解答此题的关键是掌握比例尺=图上距离÷实际距离这个公式及其变形.
43.一个飞机模型长15厘米,它的实际长度是60米,这个飞机模型的比例尺是多少?
【答案】1:400。
【分析】根据比例尺的意义,图上距离:实际距离=比例尺,据此解答。
【解答】解:15厘米:60米
=15厘米:6000厘米
=1:400
答:这个飞机模型的比例尺是1:400。
【点评】此题考查的目的是理解掌握比例尺的意义,要熟练掌握。
44.在一幅比例尺是1:34000000的地图上,量得北京到上海的距离是3厘米.两地之间的实际距离是多少千米?
【答案】见试题解答内容
【分析】要求实际距离,根据“图上距离÷比例尺=实际距离”,代入数据,即可解决问题.
【解答】解:3102000000(厘米)
102000000厘米=1020千米;
答:这两地之间的实际距离是1020千米.
【点评】此题解题的关键是根据图上距离、实际距离和比例尺的三者之间的关系,进行列式解答即可得出结论.
45.小明和小华吃鹤鹑蛋,原来小明和小华吃的鹤鹑蛋的个数比为2:3,后来小明又吃了4个,小华又吃了3个,此时小明和小华吃的鹤鹑蛋的个数比为3:4。原来两人各吃了多少个鹤鹑蛋?(用比例解)
【答案】14个;21个。
【分析】设原来小明吃了2x个鹌鹑蛋,小华吃了3x个鹌鹑蛋,根据等量关系:(原来小明吃的个数+4个):(原来小华吃的个数+3个)=3:4,列方程解答即可。
【解答】解:设原来小明吃了2x个鹌鹑蛋,小华吃了3x个鹌鹑蛋。
(2x+4):(3x+3)=3:4
(3x+3)×3=(2x+4)×4
9x+9=8x+16
x=7
7×2=14(个)
7×3=21(个)
答:原来小明吃了14个鹌鹑蛋,小华吃了21个鹌鹑蛋。
【点评】本题主要考查了比例的应用,关键是根据等量关系:(原来小明吃的个数+4个):(原来小华吃的个数+3个)=3:4,列方程。
46.2022年第24届冬季奥运会将在北京和张家口联合举办,北京至张家口的距离约为165km,在一幅冬奥会宣传图上,两地间的图上距离是55cm.
(1)这幅宣传图的比例尺是多少?
(2)北京至张家口将建设京张高铁,在宣传图上京张高铁全线长58cm,那么京张高铁全长多少千米?
【答案】见试题解答内容
【分析】(1)根据比例尺=图上距离÷实际距离,代入数据解答即可.
(2)根据实际距离=图上距离÷比例尺,代入数据解答即可.
【解答】解:(1)165km=16500000cm
55:16500000=1:300000
答:这幅宣传图的比例尺是1:300000.
(2)5817400000(cm)
17400000cm=174km
答:京张高铁全长174千米.
【点评】解答此题的关键是掌握比例尺=图上距离÷实际距离这个公式及其变形.
47.一间房子要用方砖铺地,若用边长为4分米的方砖,需要72块,如果改用边长为6分米的方砖,需要多少块?(用比例解答)
【答案】32块。
【分析】根据题意知道,一间教室的地面的面积一定,一块方砖的面积×方砖的块数=一间教室的面积(一定),由此判断一块方砖的面积与方砖的块数成反比例,设出未知数,列比例解答即可
【解答】解:设需要x块,
6×6x=4×4×72
36x=1152
x=1152÷36
x=32
答:需要32块。
【点评】关键是判断出一块方砖的面积与方砖的块数成反比例,注意6分米与4分米是方砖的边长,不是方砖的面积。
48.强子的实际身高为1.6米,在照片上的身高为5厘米,照片的比例尺是多少?
【答案】1:32。
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】解:1.6米=160厘米
5:160
=(5÷5):(160÷5)
=1:32
答:照片的比例尺是1:32。
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
49.把一个9毫米长的机器零件画在一张图纸上,量得零件的长是18厘米。这张图纸的比例尺是多少?
【答案】20:1。
【分析】根据比例尺图上距离:实际距离,即可解答。
【解答】解:18厘米=180毫米
180:9=20:1
答:这张图纸的比例尺是20:1。
【点评】本题考查的是比例尺应用题,掌握比例尺图上距离:实际距离是解答关键。
50.一种稀释消毒液,用药液和水按1:200配制而成。要配制这种稀释消毒液603千克,需要药液多少千克?(用比例知识解答)
【答案】3千克。
【分析】由“用药液和水按照1:200配制而成”可以看出,农药的浓度一定,那么药液和农药的质量的比值一定,所以药液和农药的质量成正比例,设需要药液x千克,利用药液和农药的比,列出比例解答即可。
【解答】解:设需要药液x千克,
x:(603﹣x)=1:200
200x=603﹣x
201x=603
x=3
答:需要药液3千克。
【点评】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
21世纪教育网(www.21cnjy.com)
例题1:在比例尺是的图纸上,画一个边长是4厘米的正方形草坪,草坪的实际周长是多少米?实际面积是多少公顷?
【答案】见试题解答内容
【分析】先依据“图上距离÷比例尺=实际距离”求出正方形的边长的实际长度,进而依据正方形的周长=边长×4和面积=边长×边长即可得解,注意单位换算.
【解答】解:420000(cm)
20000cm=200 m
周长为200×4=800 (m)
面积为 200×200=40000(m2)
40000m2=4公顷
答:草坪的实际周长是800米,实际面积是4公顷.
【点评】此题主要考查图上距离、实际距离和比例尺的关系,以及正方形的周长面积的计算方法.
例题2:一个房间,用边长5dm的方砖铺地,需要128块,如果改成用边长8dm的方砖铺地,需要多少块?
【答案】50块。
【分析】房间的面积一定,方砖的面积与块数成反比例,解决此题,首先根据方砖的边长得求出方砖的面积。据此列出比例解答即可。
【解答】解:设需要x块。
82x=52×128
64x÷64=3200÷64
x=50
答:需要50块。
【点评】根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解。
例题3:一个长方形的篮球场,长40米,宽30米,请你用的比例尺画出篮球场的平面图.(先计算,再画图)
【答案】见试题解答内容
【分析】篮球场的长和宽的实际长度以及比例尺已知,依据“图上距离=实际距离×比例尺”即可求出篮球场长和宽的图上距离,进而就可以画出篮球场的平面图.
【解答】解:40米=4000厘米,30米=3000厘米
40002(厘米)
30001.5(厘米)
【点评】此题主要考查图上距离、实际距离和比例尺的关系.
例题4:世界上最长的跨海大桥﹣﹣杭州湾跨海大桥,在比例尺1:400000的地图上量得它的长度是9cm.杭州湾跨海大桥的实际长度是多少千米?
【答案】见试题解答内容
【分析】要求杭州湾跨海大桥的实际长度是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值,计算即可.
【解答】解:93600000(厘米)
3600000厘米=36千米.
答:杭州湾跨海大桥的实际长度是36千米.
【点评】此题有计算公式可用,根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论.
例题5:在一幅地图上,量得广州到东莞的图上距离是4厘米,广州到东莞的实际距离大约是50千米.求这幅地图的比例尺是多少?
【答案】见试题解答内容
【分析】已知图上距离、实际距离,求比例尺,用比例尺=图上距离:实际距离,统一单位代入即可解决问题.
【解答】解:4厘米:50千米
=4厘米:5000000厘米
=1:1250000
答:这幅地图的比例尺是1:1250000.
【点评】本题考查了考查了比例尺的概念,图上距离、实际距离、比例尺三者之间的关系.
1.比例的意义和基本性质 【知识点归纳】 比例的意义:表示两个比相等的式子,叫做比例. 组成比例的四个数,叫做比例的项. 组成比例两端的两项叫做外项,中间的两项叫做内项. 比例的性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质. 如:4:5=16:20 4×20=5×16 2.正比例和反比例的意义 【知识点归纳】 1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为:k(一定). 2.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的乘积(一定),反比例的关系可以表示为:xy=k(一定). 3.辨识成正比例的量与成反比例的量 【知识点归纳】 1.成正比例的量: (1)“变化方向”相同,一种量扩大或缩小,另一种量也扩大或缩小. (2)相对应的两个数的比值(商)一定. (3)关系式:k(一定). 2.成反比例的量: (1)“变化方向”相反,一种量扩大或缩小,另一种量反而缩小或扩大. (2)相对应的两个数的乘积一定. (3)关系式:xy=k(一定). 3.判断方法:关键是看着两种相关量中相对应的两个数是商一定还是积一定,如果商一定,就成正比例;如果积一定,就成反比例. 4.解比例 【知识点归纳】 根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项.求比例中的未知项,叫做解比例. 一般来说,求比例的未知项有以下两种情况: (1)求未知外项 (2)求未知内项 5.比例的应用 【知识点归纳】 根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解. 6.比例尺 【知识点归纳】 1.比例尺: 表示图上距离比实地距离缩小的程度,因此也叫缩尺.图上距离和实际距离的比,叫做这幅图的比例尺. 即:图上距离:实际距离=图上距离÷比例尺 比例尺分类: 比例尺一般分为数值比例尺和线段比例尺: (1)数值比例尺:例如一幅图的比例尺是1:20000或.为了方便,通常把比例尺写成前项(或后项)是1的比. (2)线段比例尺是在图上附上一条标有数量的线段,用来表示实际相对应的距离. 2.比例尺表示方法: 用公式表示为:实际距离=图上距离÷比例尺.比例尺通常有三种表示方法. (1)数字式,用数字的比例式或分数式表示比例尺的大小.例如地图上1厘米代表实地距离500千米,可写成:1:50000000或写成:. (2)线段式,在地图上画一条线段,并注明地图上1厘米所代表的实际距离. (3)文字式,在地图上用文字直接写出地图上1厘米代表实地距离多少千米,如:图上1厘米相当于地面距离500千米,或五千万分之一. 3.比例尺公式: 图上距离=实际距离×比例尺 实际距离=图上距离÷比例尺 比例尺=图上距离÷实际距离.
1.车队向武汉灾区运送一批救援物资,去时每小时行50千米,6.4小时到达武汉;按原路返回,每小时行80千米,返回时间是多少?(用比例解)
2.身高1.8米的大卫在公园里观赏一尊雕像时,想知道雕像的高度。他灵机一动,站到雕像旁边拍了一张合影,然后量得照片上的他高3厘米,雕像高8厘米。因此很快算出了雕像的高度。你知道雕像的实际高度是多少米吗?
3.在比例尺1:2500000的的地图上量得A、B两地相距4.8厘米。甲骑自行车以每小时12km的速度从A地骑往B地,同时乙开车以每小时36km的速度从B开往A地。两人几小时后相遇?
4.如图,少年宫到市民广场的实际距离是1200米.这幅平面图的比例尺是多少?图书馆到市民广场的实际距离是多少米?
5.六一班有男生30人,女生18人,又转来一部分女生,这时,女生的人数与男生人数的比是2:3,又转来了多少名女生?
6.北京到广州的实际距离是2400千米,在某幅地图上量得北京到广州的图上距离是2.4厘米。求这幅地图的比例尺,并用线段比例尺表示出来。
7.一个手机零件长3mm,在一幅设计图上量得长9cm,这幅设计图的比例尺是多少?
8.一块梯形地的上底是40m,下底是60m,高是50m,如果将它画在比例尺为1:2000的图纸上,这块地在图纸上的面积是多少平方厘米?
9.在比例尺1:6000000的地图上,量得南京到北京的距离为15厘米.一列动车以每小时300千米的速度从南京开往北京,几小时能到达?
10.把线段比例尺改写成数值比例尺是多少?
11.修一条6400米的公路,修了20天后,还剩下4800米,照这样计算,剩下的路还要修多少天?(用比例解)
12.一辆汽车从甲地到乙地,平均每小时行80千米,12小时到达。回来时空车原路返回,10小时返回原地。返程时汽车的速度是多少?(用比例解)
13.一个零件在图纸上的宽度是9cm,已知这个零件的实际宽度是3mm,你能算出图纸的比例尺吗?
14.一块正方形地的边长是60米,如果把它的边长缩小到它的画在一张图纸上,图上的正方形边长应是多少厘米?
15.加工一批零件,第一天加工了总数的,第二天比第一天多加工5个,这时已加工的与未加工的零件个数比是7:5,这批零件共多少个?
16.一幅中国地图的比例尺是1:4000000.在这幅地图上,量得北京到上海的高铁路线长33厘米.一列高铁平均速度是每时300千米,它从北京到上海需要多长时间?
17.给客厅铺砖,如果用边长3分米的地砖需要400块。因为装饰需要改用面积是6平方分米的地砖,需要多少块?
18.希望小学教学楼的地基是长方形,长72米,宽24米,用1:1200的比例尺把它画在图纸上,图上长方形的面积是多少平方厘米?
19.“神舟”十二号是中国航天工程发射的第十二艘飞船,“神舟”十二号在太空球飞行10圈需用14小时,它飞行15圈要用多少小时?(用比例解答)
20.某校五年级只有两个班,全年级的男生人数与女生人数之比为8:7,已知一班男生有51人,女生有48人,二班的男生人数与女生人数之比为5:4,那么二班男生有多少人?女生有多少人?
21.在一幅比例尺是1:3000000的地图上,量得甲乙两地相距40cm,在另一幅地图上,量得甲乙两地相距20cm。另一幅地图的比例尺是多少?
22.大宝和小宝一起喝汤圆,本来大宝碗里的和小宝碗里的个数之比为2:3,后来大宝想要减肥,又夹了4个汤圆到小宝碗里,此时大小宝碗里汤圆之比为1:2,求两人一共有多少个汤圆?
23.王阿姨买了一辆电瓶车,七五折优惠付了1500元.这辆车比原来便宜了多少钱?先在线段图上补上缺少的信息和问题,再列式计算.
24.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
25.把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后,得到的卡片的面积是多少平方厘米?
26.甲、乙两人从A、B两地同时出发同向而行,甲、乙的速度之比为3:2,当甲追上乙时,甲比乙多走了500米,此时甲共走了多少米?
27.一种精密零件长5毫米,画在纸上长10厘米,这幅图纸的比例尺是多少?
28.在一幅比例尺是1:500000的地图上,量得甲、乙两地的距离是6.8厘米。如果把比例尺改为1:250000,画在新图上时甲、乙两地的距离是多少厘米?(列比例式解)
29.某地为便于残障人士的轮椅通行,发布了一项关于建筑物前斜坡高度的规定:每高1米的斜坡,至少需要12米的水平长度。某建筑物前的空地水平长度为18米,那么此处的斜坡高度最高为多少米?
30.计算机的CPU是计算机的心脏,将一个长30毫米的CPU零件画在图纸上,长为18厘米。这张图纸的比例尺是多少?
31.装订一批书籍,计划每天装订90本,20天装订完。实际提前5天完成任务,实际每天装订多少本?(用比例解)
32.一只瓢虫的实际长度是4毫米。画在图纸上的长度是2.4厘米,这幅图纸的比例尺是多少?
33.爸爸买一堆同样的铁钉。先数100根称了称是50克,又称了全部的质量是600克,这堆铁钉有多少根?(用比例解)
34.在一幅比例尺是1:2000000的地图上,量得A、B两地之间的距离是8.5cm,在另一幅比例尺是1:5000000的地图上,这两地之间的距离是多少厘米?
35.如图是乐乐绘制的校园平面图。
(1)图上1cm表示实际距离 。
(2)在平面图中,教学楼的长是2.5cm,宽是0.5cm,教学楼实际长 m,宽 m,教学楼实际占地面积是 m2。
(3)先量一量,再算一算校园的实际占地面积是 m2。
(4)王老师在黑板上画该校园的平面图,他用50cm表示校园的长。黑板上的平面图的比例尺是多少?
36.小明为准备学校读书竞赛,他要看完3本课外书,其中一本书共360页,他3天看了全书的25%。照这样的速度,看完这本书一共需要多少天?(用比例解)
37.学校组织同学们参观科技博物馆,如果每辆车坐35人,需要12辆车;如果每辆车坐28人,需要多少辆车?(用比例解)
38.某小区要修建一个长方体水池,在比例尺是1:200的设计图上,水池的长为14cm,宽为10cm,深为3cm.按图施工,这个水池的长、宽、深各应挖多少米?
39.李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
40.把下面左边的平行四边形按比例缩小后得到右边的平行四边形,那么缩小后的平行四边形的高是多少?
41.聪聪读一本《数学大王》,如果每天读20页,15天可以读完。聪聪想10天读完,那么平均每天要读多少页?(用比例的知识解)
42.一个精密零件,画在比例尺是25:1的图纸上,图上距离是12厘米,该零件的实际长度是多少?
43.一个飞机模型长15厘米,它的实际长度是60米,这个飞机模型的比例尺是多少?
44.在一幅比例尺是1:34000000的地图上,量得北京到上海的距离是3厘米.两地之间的实际距离是多少千米?
45.小明和小华吃鹤鹑蛋,原来小明和小华吃的鹤鹑蛋的个数比为2:3,后来小明又吃了4个,小华又吃了3个,此时小明和小华吃的鹤鹑蛋的个数比为3:4。原来两人各吃了多少个鹤鹑蛋?(用比例解)
46.2022年第24届冬季奥运会将在北京和张家口联合举办,北京至张家口的距离约为165km,在一幅冬奥会宣传图上,两地间的图上距离是55cm.
(1)这幅宣传图的比例尺是多少?
(2)北京至张家口将建设京张高铁,在宣传图上京张高铁全线长58cm,那么京张高铁全长多少千米?
47.一间房子要用方砖铺地,若用边长为4分米的方砖,需要72块,如果改用边长为6分米的方砖,需要多少块?(用比例解答)
48.强子的实际身高为1.6米,在照片上的身高为5厘米,照片的比例尺是多少?
49.把一个9毫米长的机器零件画在一张图纸上,量得零件的长是18厘米。这张图纸的比例尺是多少?
50.一种稀释消毒液,用药液和水按1:200配制而成。要配制这种稀释消毒液603千克,需要药液多少千克?(用比例知识解答)
参考答案与试题解析
1.车队向武汉灾区运送一批救援物资,去时每小时行50千米,6.4小时到达武汉;按原路返回,每小时行80千米,返回时间是多少?(用比例解)
【答案】4小时。
【分析】路程一定,速度和时间成反比例关系;去时速度×去时时间=回来时速度×回来时时间,据此列比例解答即可。
【解答】解:返回时间是x小时。
80x=50×6.4
80x=320
x=4
答:返回时间是4小时。
【点评】找出题中数量之间的比例关系,列出等量关系式,根据等量关系式列比例解答。
2.身高1.8米的大卫在公园里观赏一尊雕像时,想知道雕像的高度。他灵机一动,站到雕像旁边拍了一张合影,然后量得照片上的他高3厘米,雕像高8厘米。因此很快算出了雕像的高度。你知道雕像的实际高度是多少米吗?
【答案】4.8米。
【分析】设雕像的实际高度是x米,因为大卫和雕像在一张照片上,所以大卫的身高:照片上他的高度=雕像的实际高度:照片上雕像高度,列出比例解答即可。
【解答】解:设雕像的实际高度是x米。
1.8:3=x:8
3x=1.8×8
3x=14.4
x=4.8
答:雕像的实际高度是4.8米。
【点评】解答此题的关键是,判断实际高度与照片上高度成正比例,由此列出比例解决问题。
3.在比例尺1:2500000的的地图上量得A、B两地相距4.8厘米。甲骑自行车以每小时12km的速度从A地骑往B地,同时乙开车以每小时36km的速度从B开往A地。两人几小时后相遇?
【答案】2.5小时。
【分析】根据实际距离=图上距离÷比例尺,求出A,B两地的实际距离,再根据相遇时间=总路程÷速度和。
【解答】解:4.812000000(厘米)
12000000厘米=120千米
120÷(12+36)
=120÷48
=2.5(小时)
答:两人2.5小时后相遇。
【点评】此题考查了比例尺、图上距离和实际距离的关系以及时间、速度和路程的关系。
4.如图,少年宫到市民广场的实际距离是1200米.这幅平面图的比例尺是多少?图书馆到市民广场的实际距离是多少米?
【答案】见试题解答内容
【分析】(1)用直尺测量出少年宫到市民广场的图上距离是2厘米,根据图上距离:实际距离=比例尺,列式解答即可;
(2)用直尺测量出超图书馆到市民广场的图上距离;再根据实际距离=图上距离÷比例尺,据此解答.
【解答】解:(1)少年宫到市民广场的图上距离是2厘米;
1200米=120000厘米
2:120000=1:60000;
答:这幅平面图的比例尺是1:60000.
(2)图书馆到市民广场的图上距离1厘米
所以1×60000=60000(厘米)=600(米)
答:图书馆到市民广场的实际距离是600米.
【点评】本题主要考查了比例尺,图上距离与实际距离的关系.
5.六一班有男生30人,女生18人,又转来一部分女生,这时,女生的人数与男生人数的比是2:3,又转来了多少名女生?
【答案】2名。
【分析】设后来转来x个女生,这时女生的人数与男生人数的比是2:3,根据等量关系:(原有女生人数+后来转来女生人数):男生人数=2:3,列方程解答即可。
【解答】解:设又转来了x名女生。
(18+x):30=2:3
54+3x=60
3x=6
x=2
答:又转来了2名女生。
【点评】本题考查了比的应用,关键是根据等量关系:男生人数:(原有女生人数+后来转来女生人数):男生人数=2:3,列方程。
6.北京到广州的实际距离是2400千米,在某幅地图上量得北京到广州的图上距离是2.4厘米。求这幅地图的比例尺,并用线段比例尺表示出来。
【答案】1:100000000,。
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这幅图的比例尺。
【解答】解:2400千米=240000000厘米
2.4:240000000=1:100000000
100000000厘米=1000千米
答:这幅地图的比例尺是1:100000000,用线段比例尺表示出来是。
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算。
7.一个手机零件长3mm,在一幅设计图上量得长9cm,这幅设计图的比例尺是多少?
【答案】见试题解答内容
【分析】图上距离和实际距离已知,依据比例尺=图上距离:实际距离,即可求得这幅设计图的比例尺.
【解答】解:9cm=90mm
90:3=30:1
答:这幅设计图的比例尺为30:1.
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算.
8.一块梯形地的上底是40m,下底是60m,高是50m,如果将它画在比例尺为1:2000的图纸上,这块地在图纸上的面积是多少平方厘米?
【答案】见试题解答内容
【分析】根据图上距离=实际距离×比例尺,分别求出这个梯形画在图上的图上距离,再根据梯形的面积公式:S=(a+b)h÷2可求出图上的面积是多少.据此解答.
【解答】解:40m=4000厘米,60m=6000厘米,50m=5000厘米
40002(厘米)
60003(厘米)
50002.5(厘米)
(2+3)×2.5÷2
=5×1.25
=6.25(平方厘米)
答:这块地在图纸上的面积是6.25平方厘米.
【点评】本题的关键是根据图上距离=实际距离×比例尺,求出图上距离,再根据梯形的面积公式进行解答.
9.在比例尺1:6000000的地图上,量得南京到北京的距离为15厘米.一列动车以每小时300千米的速度从南京开往北京,几小时能到达?
【答案】见试题解答内容
【分析】这道题是已知比例尺、图上距离,求实际距离,根据图上距离÷比例尺=实际距离列式求得实际距离,再根据时间=路程÷速度即可解答.
【解答】解:1590000000(厘米)
90000000厘米=900(千米)
900÷300=3(小时)
答:3小时到达.
【点评】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,灵活变形列式解决问题.
10.把线段比例尺改写成数值比例尺是多少?
【答案】见试题解答内容
【分析】已知图上距离1cm、实际距离20km,求比例尺,用比例尺=图上距离:实际距离,统一单位代入数据即可解决问题.
【解答】解:1厘米:20千米
=1厘米:2000000厘米
=1:2000000
答:改写成数值比例尺为1:2000000.
【点评】本题考查了比例尺的意义,即比例尺=图上距离:实际距离,注意单位的统一.
11.修一条6400米的公路,修了20天后,还剩下4800米,照这样计算,剩下的路还要修多少天?(用比例解)
【答案】60天。
【分析】照这样计算,说明平均每天修路的米数是一定的,那么一共修的米数与修的天数的比值一定,即两种量成正比例,由此设出未知数,列比例解答问题。
【解答】解:设剩下的路还要修x天,由题意得:
(6400﹣4800):20=4800:x
1600x=20×4800
1600x=96000
x=60
答:剩下的路还要修60天。
【点评】此题主要考查对正比例意义的运用,解决此题关键是先用6400减去4800米求出余下的没修的米数,进而列比例解答。
12.一辆汽车从甲地到乙地,平均每小时行80千米,12小时到达。回来时空车原路返回,10小时返回原地。返程时汽车的速度是多少?(用比例解)
【答案】96米/时。
【分析】根据题意总路程不变,速度和时间成反比例,由此列式解答即可。
【解答】解:设返程时汽车的速度是x千米/时,
10x=80×12
10x=960
x=96
答:返程时汽车的速度是96千米/时。
【点评】解答此题的关键是弄清题意,找出相关联的量成什么比例,找准对应量,列式解答即可。
13.一个零件在图纸上的宽度是9cm,已知这个零件的实际宽度是3mm,你能算出图纸的比例尺吗?
【答案】见试题解答内容
【分析】根据比例尺=图上距离÷实际距离,代入数据解答即可.
【解答】解:9cm=90mm
90:3=30:1
答:图纸的比例尺是30:1.
【点评】解答此题的关键是掌握比例尺=图上距离÷实际距离这个公式及其变形.
14.一块正方形地的边长是60米,如果把它的边长缩小到它的画在一张图纸上,图上的正方形边长应是多少厘米?
【答案】见试题解答内容
【分析】实际距离和比例尺已知,依据“图上距离=实际距离×比例尺”即可求出图上的边长.
【解答】解:60米=6000厘米
60006(厘米)
答:图上的正方形边长应是6厘米.
【点评】此题主要考查图上距离、实际距离和比例尺的关系.
15.加工一批零件,第一天加工了总数的,第二天比第一天多加工5个,这时已加工的与未加工的零件个数比是7:5,这批零件共多少个?
【答案】420个。
【分析】这时已加工的与未加工的个数比是7:5,即此时已加工的占全部的,又第一天加工了总数的,所以第二天加工了全部的(),第二天比第一天多加工总数的(),根据分数除法的意义,用除法计算即可得这批零件一共的个数。
【解答】解:5÷()
=5÷[()]
=5÷[]
=5
=420(个)
答:这批零件共420个。
【点评】本题考查了比的应用,首先根据两天后已加工的与未加工的个数比求出此时已加工的占全部的分率是完成本题的关键。
16.一幅中国地图的比例尺是1:4000000.在这幅地图上,量得北京到上海的高铁路线长33厘米.一列高铁平均速度是每时300千米,它从北京到上海需要多长时间?
【答案】见试题解答内容
【分析】根据图上距离÷比例尺=实际距离列式求得北京到上海的实际距离,再根据路程、速度与时间的关系,列式即可解答.
【解答】解:33132000000(厘米)
132000000厘米=1320千米
1320÷300=4.4(小时)
答:它从北京到上海4.4小时.
【点评】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,以及时间=路程÷速度的实际应用.
17.给客厅铺砖,如果用边长3分米的地砖需要400块。因为装饰需要改用面积是6平方分米的地砖,需要多少块?
【答案】600块。
【分析】根据题意可知,每块地砖的面积×块数=铺地的面积(一定),所以每块地砖的面积和需要的块数成反比例,设需要x块,据此列方程解答。
【解答】解:设需要x块。
6×x=3×3×400
6x=9×400
x=600
答:需要600块。
【点评】此题主要考查正方形面积公式的灵活运用,反比例的意义及应用,注意:是每块地砖的面积和块成反比例,不是每块地砖的边长和块数成反比例。
18.希望小学教学楼的地基是长方形,长72米,宽24米,用1:1200的比例尺把它画在图纸上,图上长方形的面积是多少平方厘米?
【答案】见试题解答内容
【分析】根据比例尺的定义,图上距离=实际距离×比例尺,即可得到图形上的长和宽,再用长乘上宽即得面积.
【解答】解:因为72米=7200厘米,24米=2400厘米,
长:72006(厘米)
宽:24002(厘米)
面积:6×2=12(平方厘米)
答:图上长方形的面积是12平方厘米.
【点评】关键是理解比例尺的意义,注意单位的转换.
19.“神舟”十二号是中国航天工程发射的第十二艘飞船,“神舟”十二号在太空球飞行10圈需用14小时,它飞行15圈要用多少小时?(用比例解答)
【答案】21小时。
【分析】根据题意知道速度一定,路程和时间成正比例,据此列式解答即可。
【解答】解:设飞行15圈要用x小时,
10:14=15:x
10x=14×15
x=14×15÷10
x=21
答:它飞行15圈要用21小时。
【点评】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,再列出方程进行解答。
20.某校五年级只有两个班,全年级的男生人数与女生人数之比为8:7,已知一班男生有51人,女生有48人,二班的男生人数与女生人数之比为5:4,那么二班男生有多少人?女生有多少人?
【答案】二班男生有45人,女生有36人。
【分析】二班的男生人数与女生人数之比为5:4,设二班男生5x人,女生4x人,根据等量关系:(一班男生人数+二班男生人数):(一班女生人数+二班女生人数)=8:7,列方程解答即可。
【解答】解:设二班男生5x人,女生4x人,
(51+5x):(48+4x)=8:7
357+35x=384+32x
3x=27
x=9
9×5=45(人)
9×4=36(人)
答:二班男生有45人,女生有36人。
【点评】本题主要考查了比例的应用,关键是根据等量关系:(一班男生人数+二班男生人数):(一班女生人数+二班女生人数)=8:7,列方程。
21.在一幅比例尺是1:3000000的地图上,量得甲乙两地相距40cm,在另一幅地图上,量得甲乙两地相距20cm。另一幅地图的比例尺是多少?
【答案】1:6000000。
【分析】先根据“图上距离÷比例尺=实际距离”,求出甲乙两地间实际距离,求另一幅地图的比例尺,依据“比例尺=图上距离:实际距离”解答。
【解答】解:40120000000(厘米)
20:120000000=1:6000000
答:另一幅地图的比例尺是1:6000000。
【点评】此题考查的目的是理解掌握比例尺的意义及应用。根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可。
22.大宝和小宝一起喝汤圆,本来大宝碗里的和小宝碗里的个数之比为2:3,后来大宝想要减肥,又夹了4个汤圆到小宝碗里,此时大小宝碗里汤圆之比为1:2,求两人一共有多少个汤圆?
【答案】60个。
【分析】设两人一共有x个汤圆,则本来大宝碗里有x个,小宝碗里有x个,根据等量关系:(大宝碗里汤圆个数﹣4个):(小宝碗里汤圆个数+4个)=1:2,列方程解答即可。
【解答】解:设两人一共有x个汤圆,
(x﹣4):(x+4)=1:2
x+4x﹣8
x=12
x=60
答:两人一共有60个汤圆。
【点评】本题主要考查了比例的应用,关键是根据等量关系:(大宝碗里汤圆个数﹣4个):(小宝碗里汤圆个数+4个)=1:2,列方程。
23.王阿姨买了一辆电瓶车,七五折优惠付了1500元.这辆车比原来便宜了多少钱?先在线段图上补上缺少的信息和问题,再列式计算.
【答案】见试题解答内容
【分析】七五折是指现价是原价的75%,把原价看成单位“1”,它的75%对应的数量是现价1500元,根据已知一个数的百分之几是多少,用除法计算,求出原价,再用原价减去现价即可得出结论.
【解答】解
1500÷75%﹣1500
=2000﹣1500
=500(元)
答:这辆车比原来便宜了500元.
【点评】本题关键是理解打折的含义:打几几折,现价就是原价的百分之几十几.
24.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出甲车行驶的路程与行驶时间同时扩大或缩小的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)由图象可知:行驶150千米的路程甲车用的时间少,所以速度较快;据此解答即可.
【解答】解:(1)两辆车子所行的路程和时间成比例,因为是一条直线,所以成正比例;
(2)由图象可知:甲行驶150km,用4.2小时,乙行驶150km,用4.4小时,
4.2<4.4,
路程相同,用的时间越少,速度较快,即甲汽车的行驶速度快些;
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的比值一定,这两种量成正比例.
25.把一张长7厘米、宽5厘米的长方形卡片按3:1的比例放大后,得到的卡片的面积是多少平方厘米?
【答案】见试题解答内容
【分析】一个长7厘米、宽5厘米的长方形按3:1放大,即将这个长方形的长和宽同时扩大3倍,根据长方形的面积公式可知得到的图形的面积是:(7×3)×(5×3)=315(平方厘米).
【解答】解:(7×3)×(5×3)
=21×15
=315(平方厘米)
答:得到的卡片的面积是315平方厘米.
【点评】本题主要考查图形的放大或缩小,关键根据长方形的面积公式完成本题.
26.甲、乙两人从A、B两地同时出发同向而行,甲、乙的速度之比为3:2,当甲追上乙时,甲比乙多走了500米,此时甲共走了多少米?
【答案】1500米。
【分析】甲、乙的速度之比为3:2,因为走的时间相同,所以甲与乙走的路程比也为3:2,甲比乙多走的占甲走的,是500米,用除法计算即可得甲共走了多少米。
【解答】解:500
=500
=1500(米)
答:此时甲共走了1500米。
【点评】本题主要考查了比例的应用,已知一个数的几分之几是多少,求这个数,用除法计算。
27.一种精密零件长5毫米,画在纸上长10厘米,这幅图纸的比例尺是多少?
【答案】20:1。
【分析】依据比例尺的意义,即图上距离与实际距离的比即为比例尺,即可求解。
【解答】解:10厘米:5毫米
=100毫米:5毫米
=100:5
=20:1
答:这幅图纸的比例尺是20:1。
【点评】此题主要考查比例尺的意义,解答时要注意单位的换算。
28.在一幅比例尺是1:500000的地图上,量得甲、乙两地的距离是6.8厘米。如果把比例尺改为1:250000,画在新图上时甲、乙两地的距离是多少厘米?(列比例式解)
【答案】13.6厘米。
【分析】设画在新图上时甲、乙两地的距离是x厘米,根据图上距离÷比例尺=实际距离列比例式解答即可。
【解答】解:设画在新图上时甲、乙两地的距离是x厘米,
6.8:x:
x=6.8
x=13.6
答:设画在新图上时甲、乙两地的距离是13.6厘米。
【点评】解答此题应明确图上距离、比例尺和实际距离三者的关系。
29.某地为便于残障人士的轮椅通行,发布了一项关于建筑物前斜坡高度的规定:每高1米的斜坡,至少需要12米的水平长度。某建筑物前的空地水平长度为18米,那么此处的斜坡高度最高为多少米?
【答案】1.5米。
【分析】因为每1米高度的斜坡,至少需要12米的水平长度,也就是水平长度与斜坡的高度的比值是一定的,设此处斜坡最高x米,根据水平高度斜坡的高度的比值是一定的列出方程。
【解答】解:设此处斜坡最高x米。
12:1=18:x
12x=18
x=1.5
答:此处斜坡最高1.5米。
【点评】解答此题的关键是根据比例列方程。
30.计算机的CPU是计算机的心脏,将一个长30毫米的CPU零件画在图纸上,长为18厘米。这张图纸的比例尺是多少?
【答案】6:1。
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这张图纸的比例尺。
【解答】解:30毫米=3厘米
18厘米:3厘米=6:1
答:这张图纸的比例尺是6:1。
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算。
31.装订一批书籍,计划每天装订90本,20天装订完。实际提前5天完成任务,实际每天装订多少本?(用比例解)
【答案】120本。
【分析】每天装订的本数×天数=总本数(一定),每天装订的本数和天数成反比例关系。据此用比例求出实际每天装订多少本。
【解答】解:设实际每天装订x本。
90×20=(20﹣5)×x
15x=1800
x=120
答:实际每天装订120本。
【点评】如果相关的两个量的比值一定,这两个量成正比例关系,如果相关的两个量的乘积一定,这两个量成反比例关系。
32.一只瓢虫的实际长度是4毫米。画在图纸上的长度是2.4厘米,这幅图纸的比例尺是多少?
【答案】6:1。
【分析】比例尺=图上距离:实际距离,根据题意代入数据可直接得出这张地图的比例尺。
【解答】解:2.4厘米=24毫米
这幅地图的比例尺为24:4=6:1。
【点评】本题考查了比例尺的概念,掌握比例尺的计算方法,注意在求比的过程中,单位要统一。
33.爸爸买一堆同样的铁钉。先数100根称了称是50克,又称了全部的质量是600克,这堆铁钉有多少根?(用比例解)
【答案】1200根。
【分析】根据题意可知,每一根的质量是一定的,铁钉的根数与质量成正比例,依此列出比例解答。
【解答】解:设这堆铁钉有x根。
50x=100×600
50x÷50=60000÷50
x=1200
答:这堆铁钉有1200根。
【点评】根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解。
34.在一幅比例尺是1:2000000的地图上,量得A、B两地之间的距离是8.5cm,在另一幅比例尺是1:5000000的地图上,这两地之间的距离是多少厘米?
【答案】见试题解答内容
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出甲乙两地的实际距离,再据“图上距离=实际距离×比例尺”即可求出在另一幅图上的图上距离.
【解答】解:8.5
=17000000
=3.4(厘米)
答:在另一幅比例尺是1:5000000的地图上,这两地之间的距离是3.4厘米.
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算.
35.如图是乐乐绘制的校园平面图。
(1)图上1cm表示实际距离 25m 。
(2)在平面图中,教学楼的长是2.5cm,宽是0.5cm,教学楼实际长 62.5 m,宽 12.5 m,教学楼实际占地面积是 781.25 m2。
(3)先量一量,再算一算校园的实际占地面积是 11250 m2。
(4)王老师在黑板上画该校园的平面图,他用50cm表示校园的长。黑板上的平面图的比例尺是多少?
【答案】(1)25;(2)62.5,12.5,781.25;(3)11250;(4)1:300。
【分析】(1)因为比例尺1:2500表示图上距离1厘米代表实际距离2500厘米,又因2500厘米=25米,所以比例尺1:2500表示地图上1厘米的距离相当于地面上25米的实际距离。
(2)依据“实际距离=图上距离÷比例尺”即可求出长和宽的实际长度,进而依据长方形的面积公式即可求解。
(3)先量出校园的图上的长和宽,根据“实际距离=图上距离÷比例尺”即可求出长和宽的实际长度,进而依据长方形的面积公式即可求解。
(4)根据“比例尺=图上距离÷实际距离”计算即可。
【解答】解:(1)图上1cm表示实际距离25m。
(2)2.56250(cm)=62.5(m)
0.51250(cm)=12.5(m)
62.5×12.5=781.25(m2)
答:教学楼实际长62.5m,宽12.5m,教学楼实际占地面积是781.25m2。
(3)量得校园的长为6cm,宽为3cm,
615000(cm)=150(m)
37500(cm)=75(m)
150×75=11250(m2)
答:校园的实际占地面积是11250m2。
(4)150m=15000cm
50÷15000=1:300
答:黑板上的平面图的比例尺是1:300。
故答案为:25;62.5,12.5,781.25;11250。
【点评】此题是一道综合性的题目,涉及到了比例尺的应用,长方形得面积公式,要求学生要细心审题,仔细作答。
36.小明为准备学校读书竞赛,他要看完3本课外书,其中一本书共360页,他3天看了全书的25%。照这样的速度,看完这本书一共需要多少天?(用比例解)
【答案】12天。
【分析】根据每天看书的页数一定,书的页数和看此页数所需的天数成正比例,由此列比例解答即可。
【解答】解:设看完这本书一共需要x天,
3:25%=x:1
25%x=3×1
25%x÷25%=3÷25%
x=12
答:看完这本书一共需要12天。
【点评】根据题意,判断哪两种相关联的量成何种比例,由此列比例式解答即可。
37.学校组织同学们参观科技博物馆,如果每辆车坐35人,需要12辆车;如果每辆车坐28人,需要多少辆车?(用比例解)
【答案】15辆。
【分析】设需要x辆车,因为每辆车坐的人数×车的辆数=总人数(一定),所以每辆车坐的人数与车的辆数成反比例,列式解答即可。
【解答】解:设需要x辆车,
28x=35×12
28x=420
x=15
答:需要15辆车。
【点评】本题主要考查了比例的应用,关键是得出每辆车坐的人数与车的辆数成反比例。
38.某小区要修建一个长方体水池,在比例尺是1:200的设计图上,水池的长为14cm,宽为10cm,深为3cm.按图施工,这个水池的长、宽、深各应挖多少米?
【答案】见试题解答内容
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可分别求出水池的长、宽、深的实际长度.
【解答】解:142800(厘米)
2800厘米=28米
102000(厘米)
2000厘米=20米
3600(厘米)
600厘米=6米
答:按图施工,这个水池的长应挖28米,宽应挖20米,深应挖6米.
【点评】此题主要考查图上距离、实际距离和比例尺的关系的运用.
39.李明在电脑上把一张长6厘米,宽4厘米的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
【答案】9厘米。
【分析】由题意可知:放大前后的长及放大前后的宽的比是一定的,即放大前后的对应的边成正比例,由此列出比例解决问题。
【解答】解:设放大后照片的宽应是x厘米,
6:13.5=4:x
6x=54
x=9
答:宽是9厘米。
【点评】解答此题关键是明确按比例放大长与长的比等于宽与宽的比。
40.把下面左边的平行四边形按比例缩小后得到右边的平行四边形,那么缩小后的平行四边形的高是多少?
【答案】见试题解答内容
【分析】由题意可知:平行四边形各边缩小的倍数一定,则缩小后的边和高的长度与原来边与高的长度成正比,据此即可列比例求解.
【解答】解:设缩小后的平行四边形的高是xcm,根据题意可得:
24:36=x:24
36x=24×24
36x÷36=24×24÷36
x=16
答:缩小后的平行四边形的高是16厘米.
【点评】解答此题的关键是明白:平行四边形各边缩小的倍数一定,则缩小后的边和高的长度与原来边与高的长度成正比.
41.聪聪读一本《数学大王》,如果每天读20页,15天可以读完。聪聪想10天读完,那么平均每天要读多少页?(用比例的知识解)
【答案】30
【分析】根据题意可知:每天读的页×读的天数=这本书的页数(一定),所以每天读的页和读的天数成反比例,设平均每天要读x页,据此列比例解答。
【解答】解:设平均每天要读x页
10x=20×15
x=300÷10
x=30
答:平均每天要读30页。
故答案为:30
【点评】本题主要考查比例在日常生活中的应用,要正确判断哪两种量成反比例是解答关键。
42.一个精密零件,画在比例尺是25:1的图纸上,图上距离是12厘米,该零件的实际长度是多少?
【答案】见试题解答内容
【分析】根据实际距离=图上距离÷比例尺,代入数据解答即可.
【解答】解:12÷25=0.48(厘米)
答:该零件的实际长度是0.48厘米.
【点评】解答此题的关键是掌握比例尺=图上距离÷实际距离这个公式及其变形.
43.一个飞机模型长15厘米,它的实际长度是60米,这个飞机模型的比例尺是多少?
【答案】1:400。
【分析】根据比例尺的意义,图上距离:实际距离=比例尺,据此解答。
【解答】解:15厘米:60米
=15厘米:6000厘米
=1:400
答:这个飞机模型的比例尺是1:400。
【点评】此题考查的目的是理解掌握比例尺的意义,要熟练掌握。
44.在一幅比例尺是1:34000000的地图上,量得北京到上海的距离是3厘米.两地之间的实际距离是多少千米?
【答案】见试题解答内容
【分析】要求实际距离,根据“图上距离÷比例尺=实际距离”,代入数据,即可解决问题.
【解答】解:3102000000(厘米)
102000000厘米=1020千米;
答:这两地之间的实际距离是1020千米.
【点评】此题解题的关键是根据图上距离、实际距离和比例尺的三者之间的关系,进行列式解答即可得出结论.
45.小明和小华吃鹤鹑蛋,原来小明和小华吃的鹤鹑蛋的个数比为2:3,后来小明又吃了4个,小华又吃了3个,此时小明和小华吃的鹤鹑蛋的个数比为3:4。原来两人各吃了多少个鹤鹑蛋?(用比例解)
【答案】14个;21个。
【分析】设原来小明吃了2x个鹌鹑蛋,小华吃了3x个鹌鹑蛋,根据等量关系:(原来小明吃的个数+4个):(原来小华吃的个数+3个)=3:4,列方程解答即可。
【解答】解:设原来小明吃了2x个鹌鹑蛋,小华吃了3x个鹌鹑蛋。
(2x+4):(3x+3)=3:4
(3x+3)×3=(2x+4)×4
9x+9=8x+16
x=7
7×2=14(个)
7×3=21(个)
答:原来小明吃了14个鹌鹑蛋,小华吃了21个鹌鹑蛋。
【点评】本题主要考查了比例的应用,关键是根据等量关系:(原来小明吃的个数+4个):(原来小华吃的个数+3个)=3:4,列方程。
46.2022年第24届冬季奥运会将在北京和张家口联合举办,北京至张家口的距离约为165km,在一幅冬奥会宣传图上,两地间的图上距离是55cm.
(1)这幅宣传图的比例尺是多少?
(2)北京至张家口将建设京张高铁,在宣传图上京张高铁全线长58cm,那么京张高铁全长多少千米?
【答案】见试题解答内容
【分析】(1)根据比例尺=图上距离÷实际距离,代入数据解答即可.
(2)根据实际距离=图上距离÷比例尺,代入数据解答即可.
【解答】解:(1)165km=16500000cm
55:16500000=1:300000
答:这幅宣传图的比例尺是1:300000.
(2)5817400000(cm)
17400000cm=174km
答:京张高铁全长174千米.
【点评】解答此题的关键是掌握比例尺=图上距离÷实际距离这个公式及其变形.
47.一间房子要用方砖铺地,若用边长为4分米的方砖,需要72块,如果改用边长为6分米的方砖,需要多少块?(用比例解答)
【答案】32块。
【分析】根据题意知道,一间教室的地面的面积一定,一块方砖的面积×方砖的块数=一间教室的面积(一定),由此判断一块方砖的面积与方砖的块数成反比例,设出未知数,列比例解答即可
【解答】解:设需要x块,
6×6x=4×4×72
36x=1152
x=1152÷36
x=32
答:需要32块。
【点评】关键是判断出一块方砖的面积与方砖的块数成反比例,注意6分米与4分米是方砖的边长,不是方砖的面积。
48.强子的实际身高为1.6米,在照片上的身高为5厘米,照片的比例尺是多少?
【答案】1:32。
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】解:1.6米=160厘米
5:160
=(5÷5):(160÷5)
=1:32
答:照片的比例尺是1:32。
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
49.把一个9毫米长的机器零件画在一张图纸上,量得零件的长是18厘米。这张图纸的比例尺是多少?
【答案】20:1。
【分析】根据比例尺图上距离:实际距离,即可解答。
【解答】解:18厘米=180毫米
180:9=20:1
答:这张图纸的比例尺是20:1。
【点评】本题考查的是比例尺应用题,掌握比例尺图上距离:实际距离是解答关键。
50.一种稀释消毒液,用药液和水按1:200配制而成。要配制这种稀释消毒液603千克,需要药液多少千克?(用比例知识解答)
【答案】3千克。
【分析】由“用药液和水按照1:200配制而成”可以看出,农药的浓度一定,那么药液和农药的质量的比值一定,所以药液和农药的质量成正比例,设需要药液x千克,利用药液和农药的比,列出比例解答即可。
【解答】解:设需要药液x千克,
x:(603﹣x)=1:200
200x=603﹣x
201x=603
x=3
答:需要药液3千克。
【点评】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
21世纪教育网(www.21cnjy.com)
