第7单元 折线统计图高频易错培优讲练测(讲义)-2024-2025学年五年级下册数学人教版
文档属性
| 名称 | 第7单元 折线统计图高频易错培优讲练测(讲义)-2024-2025学年五年级下册数学人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览




文档简介
【思维导图+典型例题+知识精讲+高频真题+答案解析】
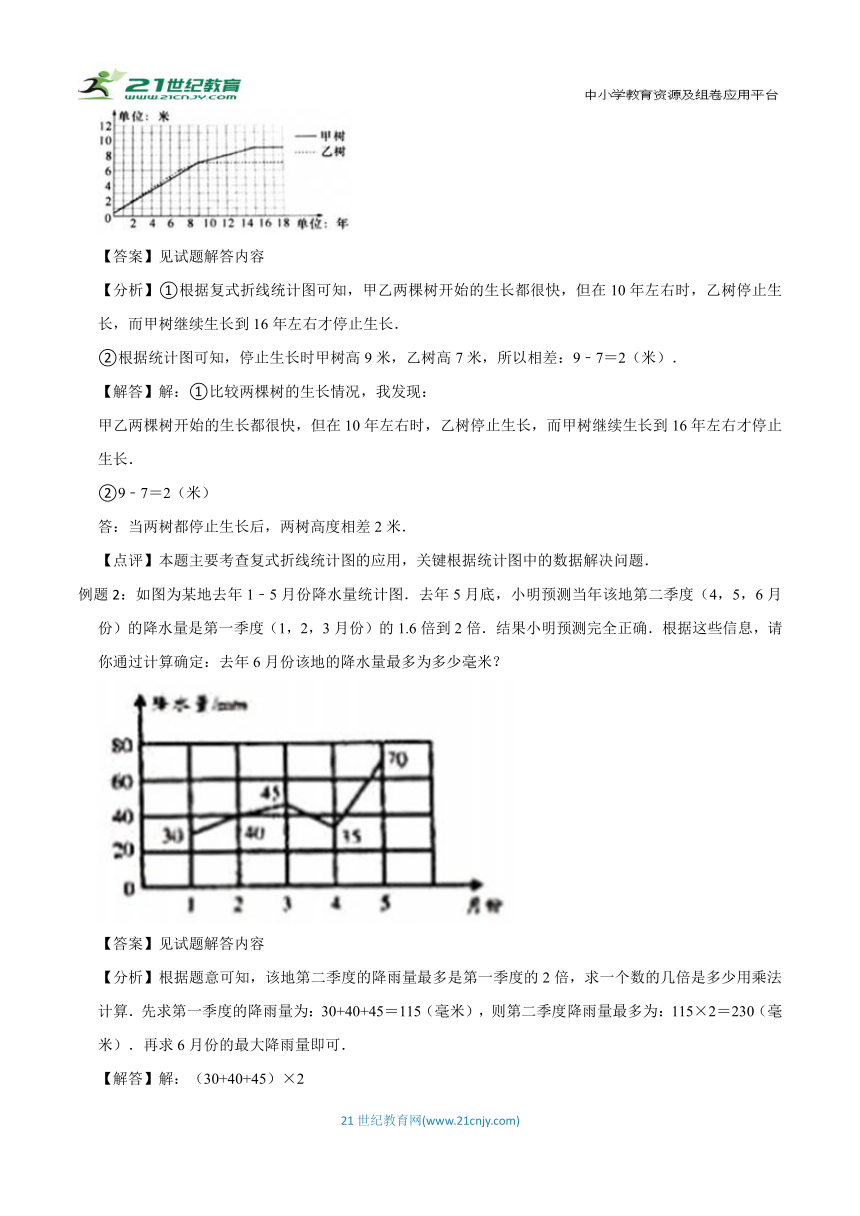
例题1:林场工作人员统计了两棵树木的生长情况,并制成了它们生长情况的统计图(如图)
①比较两棵树的生长情况,你发现了什么?
②当两树都停止生长后,两树高度相差多少米?
【答案】见试题解答内容
【分析】①根据复式折线统计图可知,甲乙两棵树开始的生长都很快,但在10年左右时,乙树停止生长,而甲树继续生长到16年左右才停止生长.
②根据统计图可知,停止生长时甲树高9米,乙树高7米,所以相差:9﹣7=2(米).
【解答】解:①比较两棵树的生长情况,我发现:
甲乙两棵树开始的生长都很快,但在10年左右时,乙树停止生长,而甲树继续生长到16年左右才停止生长.
②9﹣7=2(米)
答:当两树都停止生长后,两树高度相差2米.
【点评】本题主要考查复式折线统计图的应用,关键根据统计图中的数据解决问题.
例题2:如图为某地去年1﹣5月份降水量统计图.去年5月底,小明预测当年该地第二季度(4,5,6月份)的降水量是第一季度(1,2,3月份)的1.6倍到2倍.结果小明预测完全正确.根据这些信息,请你通过计算确定:去年6月份该地的降水量最多为多少毫米?
【答案】见试题解答内容
【分析】根据题意可知,该地第二季度的降雨量最多是第一季度的2倍,求一个数的几倍是多少用乘法计算.先求第一季度的降雨量为:30+40+45=115(毫米),则第二季度降雨量最多为:115×2=230(毫米).再求6月份的最大降雨量即可.
【解答】解:(30+40+45)×2
=115×2
=230(毫米)
则6月份的降雨量最多为:230﹣35﹣70=125(毫升)
答:去年6月份该地的降水量最多为125毫米.
【点评】本题主要考查折线统计图的应用,关键根据所给折线统计图,找到解决问题的条件,解决问题.
例题3:如图是陈明与李强绘制的自己10~14岁之间体重变化统计图,请根据统计图回答下列问题。
(1)陈明14岁时的体重比10岁时的体重增加了 0.667 倍。
(2)周宏说:“表示陈明体重变化的折线倾斜度较大,所以陈明的体重增长较快。”你认为她说的是否正确?简要说明理由。
【答案】(1)66.7;(2)不正确,陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
【分析】(1)用陈明14岁时的体重减10岁时的体重,再除以10岁时的体重即可。
(2)陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
【解答】解:(1)(50﹣30)÷30
=20÷30
≈0.667
答:陈明14岁时的体重比10岁时的体重增加了0.0667倍。
(2)她说的不正确,陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
故答案为:66.7。
【点评】本题是复式折线统计图,要通过坐标轴以及图例等读懂本图,根据图中所示的数量解决问题。
例题4:如图是阳阳和东东6~12岁的身高情况统计图,看图回答问题。
(1) 10 岁时,阳阳和东东一样高。
(2)12岁时,东东的身高比阳阳高多少?(请列式计算)
【答案】(1)10;(2)2%。
【分析】(1)观察复式折线统计图,两数据点重合,表示两人身高一样,找到横轴对应年龄即可;
12岁时东东和阳阳身高差既是答案。
【解答】解:(1)10岁时,阳阳和东东一样高。
(2)153﹣150=3(cm)
答:12岁时,东东的身高比阳阳高3cm。
故答案为:3cm。
【点评】本题考查了学生能读懂统计图并根据统计图解决问题的能力。
一、单式折线统计图 1.折线统计图: 用一个单位长度表示一定数量,用折线的上升或下降表示数量的多少和增减变化.容易看出数量的增减变化情况. 2.折现统计图制作步骤: (1)标题:根据统计表所反映的内容,在正上方写上统计图的名称; (2)画出横、纵轴:先画纵轴,后画横轴,横、纵轴都要有单位,按纸面的大小来确定用一定单位表示一定的数量; (3)描点、连线:根据数量的多少,在纵、横轴的恰当位置描出各点,然后把各点用线段顺序连接起来. 二、复式折线统计图 1.定义:用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段把各点顺次连接起来. 折线统计图不但可以表示项目的具体数量,又能清楚地反映事物变化的情况. 2.折线图特点:易于显示数据的变化的规律和趋势.可以用来作股市的跌涨和统计气温. 3.作用: 复式折线统计图一般用于两者之间比较,主要作用还是看两者之间的工作进度和增长. 折线统计图分单式或复式.复式的折线统计图有图例,用不同颜色或形状的线条区别开来. 4.区别: 与单式折线统计图相差最大的是多了一条线,和第二个单位,但仍然能看出他的上升趋势. 三、统计图的特点 1.折线统计图的特点:能够显示数据的变化趋势,反映事物的变化情况. 2.条形统计图的特点: (1)能够使人们一眼看出各个数据的大小. (2)易于比较数据之间的差别. 3.扇形统计图的特点: (1)用扇形的面积表示部分在总体中所占的百分比. (2)易于显示每组数据相对于总数的大小.
1.小丽驱车外出兜风,半途中突然有一只猫冲到车前,她用力刹车才没撞到它.小丽受惊后决定开车回家.以下的折线图是小丽行车的速度记录.
(1)小丽行车期间的最高车速是多少?
(2)小丽在什么时间为躲避那猫而踩刹车?
(3)由如图的数据,能否知道小丽回程的路线,是不是比她从家里出发到发生此意外事件的路线距离短?请解释你的答案.
2.杨庄小学2016年植树情况统计图如图,根据如图回答问题.
(1)植树最多的年级与最少的年级相差多少棵?
(2)三年级植树棵数比六年级少百分之几?
3.下面是航模兴趣小组制作的两架模型飞机在一次飞行中飞行时间和高度的记录.
(1)这两架模型飞机各飞行了多少秒?哪一架飞行时间长一些?
(2)起飞后第25秒甲模型飞机的飞行高度是多少米?乙模型飞机呢?
(3)起飞后第多少秒后两架飞机处于同一高度?起飞后第多少秒两架飞机的高度相差最大?
(4)说一说从起飞后,乙模型飞机第15秒至第20秒的飞行状态.
(5)从图上看,哪架模型飞机的性能好一些?为什么?
4.折线统计图是小玲爸爸的轿车去年下半年的用油量情况.
①这半年平均每月用油多少升?
②如果每升汽油售价是6.4元(以2017年4月上海市汽油价格为标准),参照去年下半年的平均每月用油量计算,小玲爸爸第二季度油卡里充值3500元,够用吗?
5.如图的折线统计图表示的是李叔叔从7时到9时,由李庄到张庄骑车行驶的路程。根据统计图回答下面的问题。
(1)李叔叔是几时从李庄出发的,几时到达张庄,两地间的路程是多少千米?
(2)李叔叔在中途停留了吗?停留了多长时间?
(3)李叔叔在骑车行驶的最后30分钟行驶了多少千米?比他行驶的第1小时的平均速度快了多少?
(4)李叔叔从李庄到张庄的平均速度是多少?
6.某班从一年级到六年级近视人数和未近视人数变化如图:
(1)近视人数和未近视人数相差最多的是 年级, 年级开始近视人数超过了未近视人数。
(2)六年级时近视人数占全班总人数的 。
(3) 年级至 年级近视人数增加最快。
7.如图是甲车行驶的路程与时间的关系图.甲车3.5时行驶多少千米?
8.下面是甲、乙两店2022年12月~2023年5月“午睡地垫”月销售量统计图。
(1)近半年以来,甲、乙两店“午睡地垫” 月销售相差最大,相差 万条。
(2)近半年销售量最高的是 店。
(3)如果你是校办老师,你会选择在哪家店购买,为什么?
9.如图是某城市10~15岁男女生平均身高折线统计图。
①当男女生 岁时,男生与女生平均身高一样,15岁时,男生平均身高比女生高 厘米。
②比较男生和女生的身高变化,你能得什么结论?
③把你的身高与平均值作比较,你有什么想法?
10.下表是某年云南省玉溪市和四川省成都市月平均气温统计表.(单位:C)(1分;
月份 1 2 3 4 5 6 7 8 9 10 11 12
玉溪市 16 18 21 25 27.5 28 27 26.5 26 25 22 17
成都市 4 5 10 16 21 26 29 29 23.5 17.5 11 5.5
(1)根据上表中的数据,绘制复式折线统计图.
(2)两个城市气温相差最大的是 月,相差 .
(3)简单描述两个城市全年气温变化情况.
(4)哪个城市全年气温相对稳定一些?
11.为了参加学校运动会的1分钟跳绳比赛,冬冬和平平提前10天进行训练,每天测试成绩如图:
(1)他们两人第1天的成绩相差多少个?第10天呢?
(2)你认为通过10天训练,谁的进步大一些?
12.第一小学的气象小组把某星期7天的最高气温和最低气温制成了下面的统计图。
(1)这个星期的最高气温从星期 到星期 保持不变。
(2)星期 的最高气温与前一天比相差最大。
(3)星期 的最高气温和最低气温相差最小。
13.下面是周阳(男)和赵娟(女)6到12岁的身高统计图。
请看图回答:
(1) 岁时,他们两人一样高。
(2)9岁时,周阳比赵娟高 厘米。
(3)从10岁到12岁, 的身高增长快。
14.兰兰和青青为了参加学校1分钟跳绳比赛,提前10天进行训练,如图是兰兰和青青每天测试成绩的折线统计图,请根据统计图,完成下面各题。
(1)青青第1天的成绩比她第10天的成绩少 下,第9天兰兰的成绩比青青的成绩多 下。
(2)兰兰和青青的训练成绩总体呈 趋势, 的进步幅度大一些。
(3)请你再提出一个数学问题,并解答。
15.如是汽车的耗油量与路程之间的关系的图象,根据图象回答问题.
(1)该汽车行驶20千米要耗油多少升?
(2)这次行程总共耗油多少升?大约行驶了多少千米?
16.小冬和爸爸爬山游玩,下图是他们两人爬山比赛情况的统计图,认真观察、分析统计图,回答下列问题。
(1) 在途中休息了 分钟。
(2)出发 分钟后,两人在距离起点 m处相遇。
(3) 先到达终点,早 分钟到达。
(4)在比赛的过程中,小冬走过的路程和时间成什么比例关系?请你根据图中的数据说明理由。
17.水池有A、B两个进水管,先开A管,过一段时间后两管同时打开.当A、B管同时打开后,每分钟水位上升多少分米?
18.下面是小明7~12岁的身高、体重与本市同龄儿童身高、体重平均水平比较的统计图。
(1)小明 岁时与本市同龄儿童的平均身高相差最大。
(2)小明 岁时与本市同龄儿童的平均体重相差最小。
19.根据下面的统计图回答问题.
(1)两个城市分别在哪个月降水量最多?哪个月降水量最少?
(2)两个城市最高降水量的差是多少?降水量对生活有什么影响?
20.仔细观察统计图并回答问题。
(1)从开始植树到第6年, 树生长较快。
(2)第 年,两棵树的高度一样。
(3)第15年,甲树的高度是乙树高度的几分之几?
21.(1)从统计图中可以看出,A城和B城的气温变化趋势 (填“相同”或“相反”).
(2)“A城属于温带季风气候,一年四季分明,6~8月为夏季,气候炎热”.根据这条信息可以看出,统计图中折线 表示的是A城的气温变化情况,折线 表示的是B城的气温变化情况.
(3)A城月平均气温最高的月份是 月,月平均气温最低的月份是 月.
(4)B城月平均气温最高的月份的平均气温是 ℃,这时A城的月平均气温是 ℃.
22.如图是根据某家电厂今年上半年销售微波炉情况绘制成的折线统计图.
(1)说一说上半年销售量的变化情况,想一想变化的原因.
(2)如果每月卖出900台微波炉便能收回成本,那么有哪几个月盈利?哪几个月亏本?哪几个月不亏不盈?
(3)从统计图中你还得到哪些信息?请你写下来.
23.爸爸从家出发,骑自行车去离家4800米远的银行,如图表示在这段时间里爸爸离家距离的变化情况.
(1)爸爸来回路上一共用了多少分钟?
(2)爸爸在银行办事用了多少分钟?
24.小强骑自行车到距家6km远的西湖去玩,根据如图的折线统计图回答问题.
(1)小强在西湖玩了多长时间?
(2)如果从出发起一直骑车不休息,几时几分可以到达西湖?
(3)求小强返回时骑车的速度.
25.如图是号称“天下第一泉“的趵突泉某段时间的喷水量和喷涌天数的统计表。
喷水量/m3 16万 32万 48万 64万 96万 ……
喷涌天数(天) 1 2 3 4 6 ……
(1)上表中趵突泉的喷水量和喷涌天数成什么比例关系?为什么?
(2)在如图中找出喷涌天数和对应喷水量的点,然后把它们连起来。
(3)利用图象回答:2.5天喷水 立方米,80万立方米的水量需要喷涌 天。
26.根据如图的统计图填空回答问题。
(1)两个车间 月份做衣服产量相差最大。
(2)第 车间这五个月的产量增长速度最快。
(3)4月份第一车间做衣服的产量是第二车间的几分之几?
(4)5月份第二车间衣服的产量占这个月两个车间总产量的几分之几?
27.如图所示是希望小学各年级学生近视人数统计图,看图回答问题。
(1)根据统计图,你能说说希望小学学生近视人数的变化趋势吗?
(2)六年级近视的人数比五年级多24%,六年级近视的人数是多少?
(3)根据以上信息,你想对同学们说些什么?
28.如图是小华骑自行车到6千米远的森林公园去游玩的情况.
(1)小华从出发到返回,一共经过了多长时间?
(2)返回前,小华在路上用的时间比在公园里玩的时间多多少分钟?
(3)返回时,小华骑自行车每分钟行走多少米?
29.下面是甲、乙两辆汽车与七星湖的距离统计图.
(1)如果甲,乙两辆汽车在同一条路上相向而行,那么点A说明了什么?
(2)你还能从图中知道什么?
30.如图是丽丽发热住院期间的体温记录情况统计图.
(1)这种统计图是 统计图.
(2)护士每 小时为丽丽量一次体温;丽丽体温最高是 摄氏度;丽丽4月8日12时的体温是 摄氏度.
(3)从体温看,丽丽的病情是恶化还是好转?为什么?
31.小乐到6千米远的西溪去玩。请你根据折线图回答:
(1)小乐在西溪玩了多少时间?
(2)如果一直走不休息,多少小时到达西溪?
(3)求出返回时小乐骑自行车的速度。
32.根据统计图,回答下面的问题.
(1)他们是同时开始竞走的吗?
(2)阳阳平均每分钟走多少米?甜甜平均每分钟走多少米?
33.A、B两地相距2400米,甲乙两人分别从A、B两地同时出发相向而行。两人行走情况如图。根据图意计算,两人出发后经过多少分钟相遇?
34.某市某出租车公司收费标准如图所示,如果小明只有13元钱,请计算出小明乘此出租车最远能到达的距离。
35.六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),如图反映的是大巴车行驶路程与时间之间的关系.请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距10km.
36.观察如图,完成问题.
(1)第1天 的成绩好,第2天 的成绩好.
(2)哪天两人成绩最接近?差多少下?
(3)如果从两人中选一人参加比赛,你会选准?并说明理由.
37.小甬和小真两人从甲地匀速步行到乙地,小甬出发5分钟后,小真以一定的速度沿同一路线行走,设小甬、小真两人相距s(米),小甬行走的时间为t(分),s(米)关于t(分)的图象如图所示,求a。
38.李欣和刘云为了参加学校运动会1分钟跳绳比赛,提前10天进行训练,每天测试成绩如图的统计图:
根据上面的统计图,回答问题。
(1)李欣和刘云第3天的成绩相差 次,第9天的成绩相差 次。
(2)李欣和刘云跳绳的成绩呈现 趋势, 的进步幅度大。
(3)李欣的最好跳绳成绩是1分钟跳 次,刘云的最好成绩是1分钟跳 次。
39.一辆汽车在公路上行驶,行驶的时间和路程如图.
(1)这辆车10小时行驶多少千米?
(2)行驶600千米要多少时?
40.某电动汽车经销部某一周销售情况如图:
(1)哪种型号的电动汽车销量大些?
(2)如果你是经销部经理,上图反映的信息对你有什么帮助?
41.如图,电车从A站经过B站到达C站,然后返回.去时在B站停车,而返回时不停车.已知去时的车速为48千米/小时,则返回时的车速是多少千米/小时?
参考答案与试题解析
1.小丽驱车外出兜风,半途中突然有一只猫冲到车前,她用力刹车才没撞到它.小丽受惊后决定开车回家.以下的折线图是小丽行车的速度记录.
(1)小丽行车期间的最高车速是多少?
(2)小丽在什么时间为躲避那猫而踩刹车?
(3)由如图的数据,能否知道小丽回程的路线,是不是比她从家里出发到发生此意外事件的路线距离短?请解释你的答案.
【答案】见试题解答内容
【分析】(1)通过观察统计图可知,小丽行车期间的最高车速是60千米/时.
(2)小丽在9:06为躲避那猫而踩刹车.
(3)由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.据此解答.
【解答】解:( 1 )小丽行车期间的最高车速是60千米/时.
( 2 )小丽在9:06为躲避那猫而踩刹车.
( 3 )答:由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.用的时间虽然相同,但回程时的速度却很慢,所以回程时的路线短.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
2.杨庄小学2016年植树情况统计图如图,根据如图回答问题.
(1)植树最多的年级与最少的年级相差多少棵?
(2)三年级植树棵数比六年级少百分之几?
【答案】见试题解答内容
【分析】(1)通过观察折线统计图可知,植树最多的年级是五年级,植树最少的年级是一年级,根据求一个数比另一个多或少几,用减法解答.
(2)把六年级植树的棵数看作单位“1”,先求出三年级比六年级少植树多少棵,再根据求一个数是另一个数的百分之几,用除法解答.
【解答】解:(1)645﹣200=445(棵)
答:植树最多的年级与最少的年级相差445棵.
(2)(500﹣400)÷500
=100÷500
=0.2
=20%
答:三年级植树棵数比六年级少20%.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
3.下面是航模兴趣小组制作的两架模型飞机在一次飞行中飞行时间和高度的记录.
(1)这两架模型飞机各飞行了多少秒?哪一架飞行时间长一些?
(2)起飞后第25秒甲模型飞机的飞行高度是多少米?乙模型飞机呢?
(3)起飞后第多少秒后两架飞机处于同一高度?起飞后第多少秒两架飞机的高度相差最大?
(4)说一说从起飞后,乙模型飞机第15秒至第20秒的飞行状态.
(5)从图上看,哪架模型飞机的性能好一些?为什么?
【答案】见试题解答内容
【分析】(1)观察统计图可知,甲飞机飞了40秒,乙飞机飞了35秒,甲飞机飞行的时间长一些,
(2)起飞后第25秒甲模型飞机的飞行高度是25米,乙模型飞机处在20米.
(3)起飞后大约15秒两架飞机的高度相差最大,第30秒两架飞机的高度相差最大.
(4)乙模型飞机第15秒至第20秒飞机的飞行水平行驶状态.
(5)从图上看,甲模型飞机的性能好一些.因为甲模型飞机不但飞得高,而且飞行时间长.
【解答】解:(1)这两架飞机中,甲飞机的飞行时间长一些.
(2)起飞后第25秒甲模型飞机的飞行高度是25米,乙模型飞机处在20米.
(3)起飞后大约15秒两架飞机的高度相差最大,第30秒两架飞机的高度相差最大.
(4)乙模型飞机第15秒至第20秒飞机的飞行水平行驶状态.
(5)从图上看,甲模型飞机的性能好一些.因为甲模型飞机不但飞得高,而且飞行时间长.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
4.折线统计图是小玲爸爸的轿车去年下半年的用油量情况.
①这半年平均每月用油多少升?
②如果每升汽油售价是6.4元(以2017年4月上海市汽油价格为标准),参照去年下半年的平均每月用油量计算,小玲爸爸第二季度油卡里充值3500元,够用吗?
【答案】见试题解答内容
【分析】①根据求平均数的方法,用7~12月份用油的总量除以6即可.
②根据下半年平均每月的用油量求出第二季度的用油量,然后根据单价×数量=总价,求出第二季度用汽油的总价,然后与3500元进行比较,如果小于3500元,说明够,如果大于3500元,说明不够.
【解答】解:①(180+160+0+100+280+240)÷6
=960÷6
=160(升);
答:这半年平均每月用油160升.
②6.4×(160×3)
=6.4×480
=3072(元),
3072元<3500元,
答:小玲爸爸第二季度油卡里充值3500元,够用.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
5.如图的折线统计图表示的是李叔叔从7时到9时,由李庄到张庄骑车行驶的路程。根据统计图回答下面的问题。
(1)李叔叔是几时从李庄出发的,几时到达张庄,两地间的路程是多少千米?
(2)李叔叔在中途停留了吗?停留了多长时间?
(3)李叔叔在骑车行驶的最后30分钟行驶了多少千米?比他行驶的第1小时的平均速度快了多少?
(4)李叔叔从李庄到张庄的平均速度是多少?
【答案】(1)7时,9时,30千米;(2)停留了,停留了30分钟;(3)15千米,15千米/时;(4)15千米/时。
【分析】(1)通过观察统计图可知:李叔叔是上午7时从李庄出发的,9时到达张庄,共行驶30千米;
(2)李叔叔8时至8时30分在途中停留,停留了30分钟;
(3)李叔叔在骑车行驶的最后30分钟行驶了30﹣15=15(千米),比他行驶的第1小时的平均速度快了多少,根据速度=路程÷时间分别求出第一小时行驶的速度和最后30分钟行驶的速度进行解答即可。
(4)求平均速度用总路程除以总时间即可。
【解答】解:(1)通过观察统计图可知:李叔叔是上午7时从李庄出发的,9时到达张庄,共行驶30千米;
(2)李叔叔8时至8时30分在途中停留,停留了30分钟;
(3)李叔叔在骑车行驶的最后30分钟行驶了30﹣15=15(千米),
第一小时行驶的速度:15÷1=15(千米/时)
最后30分钟行驶的速度:30分=0.5小时
15÷0.5=30(千米/时)
30﹣15=15(千米/时)
答:比他行驶的第1小时的平均速度快了15千米/时。
(4)李叔叔共行驶了2小时,走了30千米
30÷2=15(千米/时)
答:李叔叔从李庄到张庄的平均速度是15千米/时。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据折线统计图提供的信息,解决有关的实际问题。
6.某班从一年级到六年级近视人数和未近视人数变化如图:
(1)近视人数和未近视人数相差最多的是 一 年级, 五 年级开始近视人数超过了未近视人数。
(2)六年级时近视人数占全班总人数的 75% 。
(3) 五 年级至 六 年级近视人数增加最快。
【答案】(1)一,五;(2)75%;(3)五,六。
【分析】(1)根据图示可知,一年级未近视人数最多,近视人数最少,即一年级近视人数和未近视人数相差最多,五年级开始近视人数超过未近视人数;
(2)近视率=近视人数÷全班人数,据此解答;
(3)分别计算相邻两个年级近视人数的增加情况后比较大小即可作答。
【解答】解:(1)一年级未近视人数最多,近视人数最少,即一年级近视人数和未近视人数相差最多,五年级开始近视人数超过未近视人数;
(2)30÷(30+10)×100%
=30÷40×100%
=75%
答:六年级时近视人数占全班总人数的75%。
(3)5﹣3=2(人)
12﹣5=7(人)
16﹣12=4(人)
21﹣16=5(人)
30﹣21=9(人)
2<4<5<7<9,即五年级至六年级近视人数增加最快。
故答案为:(1)一,五;(2)75%;(3)五,六。
【点评】本题考查了学生能读懂统计图并根据统计图解决问题的能力。
7.如图是甲车行驶的路程与时间的关系图.甲车3.5时行驶多少千米?
【答案】见试题解答内容
【分析】通过观察折线统计图可知:甲车2小时行驶150千米,因为速度(一定),所以路程和时间成正比例,设3.5小时行驶x千米,据此列比例解答.
【解答】解:设3.5小时行驶x千米,
2x=3.5×150
x
x=262.5.
答:3.5小时行驶262.5千米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
8.下面是甲、乙两店2022年12月~2023年5月“午睡地垫”月销售量统计图。
(1)近半年以来,甲、乙两店“午睡地垫” 12 月销售相差最大,相差 0.8 万条。
(2)近半年销售量最高的是 甲 店。
(3)如果你是校办老师,你会选择在哪家店购买,为什么?
【答案】(1)12,0.8;
(2)甲;
(3)甲店,因为近半年销售量最高的是甲店。(答案不唯一)
【分析】(1)用减法列式分别计算6个月份两个店相差多少万条,由此解答本题;
(2)用加法列式计算两个店半年的销售量,由此解答本题;
(3)选择销量高的店,由此解答本题。
【解答】解:(1)2.4﹣1.6=0.8(万条)
2.6﹣1.9=0.7(万条)
2.7﹣2.0=0.7(万条)
2.4﹣1.9=0.5(万条)
2.1﹣2.0=0.1(万条)
2.4﹣1.8=0.6(万条)
0.8>0.7>0.6>0.5>0.1
答:近半年以来,甲、乙两店“午睡地垫”12月销售相差最大,相差0.8万条。
(2)2.4+2.6+2.7+2.4+2.0+1.8=13.9(万条)
1.6+1.9+2.0+1.9+2.1+2.4=11.9(万条)
答:近半年销售量最高的是甲店。
(3)我选择甲店来购买,因为近半年销售量最高的是甲店。(答案不唯一)
故答案为:12,0.8;甲。
【点评】本题考查的是复式折线统计图的应用。
9.如图是某城市10~15岁男女生平均身高折线统计图。
①当男女生 11 岁时,男生与女生平均身高一样,15岁时,男生平均身高比女生高 9 厘米。
②比较男生和女生的身高变化,你能得什么结论?
③把你的身高与平均值作比较,你有什么想法?
【答案】①11,9;
②在12之前女生的平均身高高于男生,从13岁到15岁,男生的平均身高高于女生。
③答案不唯一。我是一名男生,今年12岁,身高是154厘米,我的身高比平均身高稍高一些。我的想法是加强体育锻炼,增强体质。
【分析】①通过观察统计图可知,当男女生11岁时,男生与女生平均身高一样,再根据求一个数的比另一个数多几,用减法解答。
②在12之前女生的平均身高高于男生,从13岁到15岁,男生的平均身高高于女生。
③答案不唯一。我是一名男生,今年12岁,身高是154厘米,我的身高比平均身高稍高一些。我的想法是加强体育锻炼,增强体质。
【解答】解:①167﹣158=9(厘米)
答:当男女生11岁时,男生与女生平均身高一样,15岁时,男生平均身高比女生高9厘米。
②在12之前女生的平均身高高于男生,从13岁到15岁,男生的平均身高高于女生。
③答案不唯一。我是一名男生,今年12岁,身高是154厘米,我的身高比平均身高稍高一些。我的想法是加强体育锻炼,增强体质。
故答案为:11,9。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10.下表是某年云南省玉溪市和四川省成都市月平均气温统计表.(单位:C)(1分;
月份 1 2 3 4 5 6 7 8 9 10 11 12
玉溪市 16 18 21 25 27.5 28 27 26.5 26 25 22 17
成都市 4 5 10 16 21 26 29 29 23.5 17.5 11 5.5
(1)根据上表中的数据,绘制复式折线统计图.
(2)两个城市气温相差最大的是 2 月,相差 13℃ .
(3)简单描述两个城市全年气温变化情况.
(4)哪个城市全年气温相对稳定一些?
【答案】见试题解答内容
【分析】(1)根据折线统计图的绘制方法,按照统计表中的数据完成统计图.
(2)两个城市气温相差最大的是2月份,相差13℃.
(3)通过观察折线统计图可知:玉溪市月平均气温从1月到6月呈上升趋势,从7月到12月呈下降趋势;成都市月平均气温从1月到8月呈上升趋势,从9月到12月呈下降趋势.
(4)通过比较发现,玉溪市全年气温相对稳定一些.
【解答】解:(1)作图如下:
(2)18﹣5=13(℃);
答:两个城市气温相差最大的是2月份,相差13℃.
(3)通过观察折线统计图可知:玉溪市月平均气温从1月到6月呈上升趋势,从7月到12月呈下降趋势;成都市月平均气温从1月到8月呈上升趋势,从9月到12月呈下降趋势.
(4)通过比较发现,玉溪市全年气温相对稳定一些.
故答案为:2、13℃.
【点评】此题考查的目的是理解掌握折线统计图的绘制方法及应用,并且能够根据统计图提供的信息,解决有关的实际问题.
11.为了参加学校运动会的1分钟跳绳比赛,冬冬和平平提前10天进行训练,每天测试成绩如图:
(1)他们两人第1天的成绩相差多少个?第10天呢?
(2)你认为通过10天训练,谁的进步大一些?
【答案】(1)1个,2个;
(2)平平。
【分析】(1)根据求一个数比另一个数多或少几,用减法解答。
(2)通过观察统计图可知,通过10天的训练,我认为平平进步大一些。据此解答。
【解答】解:(1)153﹣152=1(个)
167﹣165=2(个)
答:他们两人第1天的成绩相差1个,第10天相差2个。
(2)通过10天的训练,我认为平平进步大一些。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
12.第一小学的气象小组把某星期7天的最高气温和最低气温制成了下面的统计图。
(1)这个星期的最高气温从星期 三 到星期 五 保持不变。
(2)星期 三 的最高气温与前一天比相差最大。
(3)星期 日 的最高气温和最低气温相差最小。
【答案】三,五;三;日。
【分析】(1)这个星期的最高气温从星期三到星期五保持不变;
(2)星期三的最高气温与前一天比相差最大;
(3)星期日的最高气温和最低气温相差最小。
【解答】解:(1)这个星期的最高气温从星期三到星期五保持不变;
(2)星期三的最高气温与前一天比相差最大;
(3)星期日的最高气温和最低气温相差最小。
故答案为:三,五;三;日。
【点评】仔细观察统计图,获取准确信息是解答关键。
13.下面是周阳(男)和赵娟(女)6到12岁的身高统计图。
请看图回答:
(1) 10 岁时,他们两人一样高。
(2)9岁时,周阳比赵娟高 2 厘米。
(3)从10岁到12岁, 赵娟 的身高增长快。
【答案】(1)10;
(2)2;
(3)赵娟。
【分析】(1)通过观察统计图直接回答问题。
(2)根据求一个数比另一个数多几,用减法解答。
(3)通过观察复式折线统计图可知,从10岁到12岁,赵娟的身高增长块。据此解答。
【解答】解:(1)10岁时,他们两人一样高。
(2)134﹣132=2(厘米)
答:9岁时,周阳比赵娟高2厘米。
(3)从10岁到12岁,赵娟的身高增长块。
故答案为:10;2;赵娟。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
14.兰兰和青青为了参加学校1分钟跳绳比赛,提前10天进行训练,如图是兰兰和青青每天测试成绩的折线统计图,请根据统计图,完成下面各题。
(1)青青第1天的成绩比她第10天的成绩少 13 下,第9天兰兰的成绩比青青的成绩多 5 下。
(2)兰兰和青青的训练成绩总体呈 上升 趋势, 兰兰 的进步幅度大一些。
(3)请你再提出一个数学问题,并解答。
【答案】(1)12,5;
(2)上升,兰兰;
(3)答案不唯一。兰兰第10天的成绩比第一天多多少下?
15下。
【分析】(1)根据求一个数比另一个数多或少几,用减法解答。
(2)兰兰和青青的训练成绩总体呈算式趋势,兰兰的进步幅度大一些。
(3)答案不唯一。兰兰第10天的成绩比第一天多多少下?根据求一个数比另一个数多几,用减法解答。
【解答】解:(1)165﹣153=12(下)
165﹣160=5(下)
答:青青第1天的成绩比她第10天的成绩少12下,第9天兰兰的成绩比青青的成绩多5下。
(2)兰兰和青青的训练成绩总体呈算式趋势,兰兰的进步幅度大一些。
(3)答案不唯一。兰兰第10天的成绩比第一天多多少下?
167﹣152=15(下)
答:兰兰第10天的成绩比第一天多15下。
故答案为:12,5;上升,兰兰。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
15.如是汽车的耗油量与路程之间的关系的图象,根据图象回答问题.
(1)该汽车行驶20千米要耗油多少升?
(2)这次行程总共耗油多少升?大约行驶了多少千米?
【答案】见试题解答内容
【分析】(1)通过观察折线统计图,计算该汽车行驶20千米要耗油多少升.
(2)这次行程总耗油量是20升,大约行驶了150千米.
【解答】解:(1)4÷30×20(升)
答:该汽车行驶20千米要耗油升.
30﹣10=20(升)
20÷(4÷30)=150(千米)
(2)答:这次行程总耗油量是20升,大约行驶了150千米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
16.小冬和爸爸爬山游玩,下图是他们两人爬山比赛情况的统计图,认真观察、分析统计图,回答下列问题。
(1) 爸爸 在途中休息了 5 分钟。
(2)出发 15 分钟后,两人在距离起点 300 m处相遇。
(3) 小冬 先到达终点,早 2.5 分钟到达。
(4)在比赛的过程中,小冬走过的路程和时间成什么比例关系?请你根据图中的数据说明理由。
【答案】见试题解答内容
【分析】(1)通过观察统计图可知:爸爸在途中休息了5分钟。
(2)出发后15分钟,两人在距离起点300米处相遇。
(3)小冬先达到终点,早2.5分钟。
(4)因为正比例的图象是一条直线,由此可知,在比赛的过程中,小冬走过的路程和时间成正比例关系。据此解答即可。
【解答】解:(1)爸爸在途中休息了5分钟。
(2)出发后15分钟,两人在距离起点300米处相遇。
(3)小冬先达到终点,早2.5分钟。
(4)因为正比例的图象是一条直线,由此可知,在比赛的过程中,小冬走过的路程和时间成正比例关系。
故答案为:爸爸、5;15、300;小冬、2.5。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用并且能够根据统计图提供的信息,解决有关的实际问题。
17.水池有A、B两个进水管,先开A管,过一段时间后两管同时打开.当A、B管同时打开后,每分钟水位上升多少分米?
【答案】见试题解答内容
【分析】通过观察折线统计图可知:单开A管15分钟水位上升到20分米,两管同时开5分钟水位上升了(40﹣20)分米,根据“等分”除法的意义,用除法解答即可.
【解答】解:(40﹣20)÷(20﹣15)
=20÷5
=4(分米),
答:每分钟水位上升4分米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
18.下面是小明7~12岁的身高、体重与本市同龄儿童身高、体重平均水平比较的统计图。
(1)小明 12 岁时与本市同龄儿童的平均身高相差最大。
(2)小明 7 岁时与本市同龄儿童的平均体重相差最小。
【答案】(1)12;
(2)7。
【分析】(1)通过观察统计图可知,小明12岁时与本市同龄儿童的平均身高相差最大。
(2)小明7岁时时与本市同龄儿童的平均体重相差最小。据此解答即可。
【解答】解:(1)小明12岁时与本市同龄儿童的平均身高相差最大。
(2)小明7岁时时与本市同龄儿童的平均体重相差最小。
故答案为:12;7。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
19.根据下面的统计图回答问题.
(1)两个城市分别在哪个月降水量最多?哪个月降水量最少?
(2)两个城市最高降水量的差是多少?降水量对生活有什么影响?
【答案】(1)7,南宁11月份,石家庄3月份.
(2)399,降水量的多少对人类的生产生活等各个领域有着极大影响.降水过多会导致洪涝灾害、滑坡、泥石流等自然灾害,对人类的生产生活造成极大的经济损失与不便;降水过少,则会给生活用水、农田浇灌等带来困难,只有适度的降水量才有益于我们的生产生活.(答案不唯一.)
【分析】(1)通过观察统计图可知,两个城市都是7月份降水量最多.南宁11月份的降水量最少,石家庄3月份的降水量最少.
(2)求两个城市最高降水量的差是多少,根据求一个数比另一个数多或少几,用减法解答;降水量的多少对人类的生产生活等各个领域有着极大影响.降水过多会导致洪涝灾害、滑坡、泥石流等自然灾害,对人类的生产生活造成极大的经济损失与不便;降水过少,则会给生活用水、农田浇灌等带来困难,只有适度的降水量才有益于我们的生产生活.据此解答.
【解答】解:(1)两个城市都是7月份降水量最多.南宁11月份的降水量最少,石家庄3月份的降水量最少.
(2)462.9﹣63.9=399 (毫米)
答:两个城市最高降水量的差399毫米.降水量的多少对人类的生产生活等各个领域有着极大影响.降水过多会导致洪涝灾害、滑坡、泥石流等自然灾害,对人类的生产生活造成极大的经济损失与不便;降水过少,则会给生活用水、农田浇灌等带来困难,只有适度的降水量才有益于我们的生产生活.
(答案不唯一.)
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,把能够根据统计图提供的信息,解决有关的实际问题.
20.仔细观察统计图并回答问题。
(1)从开始植树到第6年, 甲 树生长较快。
(2)第 9 年,两棵树的高度一样。
(3)第15年,甲树的高度是乙树高度的几分之几?
【答案】(1)甲;
(2)9;
(3)。
【分析】(1)通过观察统计图可知,从开始植树到第6年,甲树生长较快。
(2)第9年,两棵树的高度一样。
(3)把第15年乙树的高度看作单位“1”,根据求一个数是另一个数的几分之几,用除法解答。
【解答】解:(1)从开始植树到第6年,甲树生长较快。
(2)第9年,两棵树的高度一样。
(3)7÷9
答:第15年,甲树的高度是乙树高度的。
故答案为:甲;9;。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
21.(1)从统计图中可以看出,A城和B城的气温变化趋势 相反 (填“相同”或“相反”).
(2)“A城属于温带季风气候,一年四季分明,6~8月为夏季,气候炎热”.根据这条信息可以看出,统计图中折线 ② 表示的是A城的气温变化情况,折线 ① 表示的是B城的气温变化情况.
(3)A城月平均气温最高的月份是 7 月,月平均气温最低的月份是 1 月.
(4)B城月平均气温最高的月份的平均气温是 24.3 ℃,这时A城的月平均气温是 2 ℃.
【答案】见试题解答内容
【分析】(1)通过观察折线统计图可知,A城和B城的气温变化趋势相反.
(2)“A城属于温带季风气候,一年四季分明,6~8月为夏季,气候炎热”.根据这条信息可以看出,统计图中折线②表示的是A城的气温变化情况,折线①表示的是B城的气温变化情况.
(3)A城月平均气温最高的月份是7月份,月平均气温最低的月份是1月份.
(4)B城月平均气温最高的月份的平均气温是24.3℃,这时A城的月平均气温是2℃.据此解答即可.
【解答】解:(1)A城和B城的气温变化趋势相反.
(2)“A城属于温带季风气候,一年四季分明,6~8月为夏季,气候炎热”.根据这条信息可以看出,统计图中折线②表示的是A城的气温变化情况,折线①表示的是B城的气温变化情况.
(3)A城月平均气温最高的月份是7月份,月平均气温最低的月份是1月份.
(4)B城月平均气温最高的月份的平均气温是24.3℃,这时A城的月平均气温是2℃.
故答案为:相反;②、①;7、1;24.3、2.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
22.如图是根据某家电厂今年上半年销售微波炉情况绘制成的折线统计图.
(1)说一说上半年销售量的变化情况,想一想变化的原因.
(2)如果每月卖出900台微波炉便能收回成本,那么有哪几个月盈利?哪几个月亏本?哪几个月不亏不盈?
(3)从统计图中你还得到哪些信息?请你写下来.
【答案】见试题解答内容
【分析】(1)通过观察折线统计图发现,一月份到二月份销售量呈上升趋势,从二月份到六月份销售量呈下降趋势,这种变化的原因可能是宣传力度不够,另一个原因可能没有真正让利给顾客.
(2)如果每月卖出900台微波炉便能收回成本,一月份、二月份、四月份这三个月盈利,三月份和六月份亏本,四月份不亏不盈.
(3)从统计图中可以看出二月份销售量最多,三月份销售量最少.
【解答】解:(1)一月份到二月份销售量呈上升趋势,从二月份到六月份销售量呈下降趋势,这种变化的原因可能是宣传力度不够,另一个原因可能没有真正让利给顾客.
(2)如果每月卖出900台微波炉便能收回成本,四月份的销售量正好是900台,所以四月份不亏不盈.
1000﹣900=100(台)
1250﹣900=350(台)
940﹣900=40(台)
所以,一月份、二月份、四月份这三个月盈利,
900﹣760=140(台)
900﹣800=100(台)
所以,三月份和六月份亏本.
(3)从统计图中可以看出二月份销售量最多,是1250台;三月份销售量最少,是760台.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
23.爸爸从家出发,骑自行车去离家4800米远的银行,如图表示在这段时间里爸爸离家距离的变化情况.
(1)爸爸来回路上一共用了多少分钟?
(2)爸爸在银行办事用了多少分钟?
【答案】见试题解答内容
【分析】(1)通过观察统计图可知,去用了20分钟,返回用了30分钟,根据加法的意义,用加法解答.
(2)爸爸在银行办事用了40分钟.据此解答.
【解答】解:(1)20+30=50(分钟)
答:爸爸来回路上一共用了50分钟.
(2)60﹣20=40(分钟)
答:爸爸在银行办事用了40分钟.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
24.小强骑自行车到距家6km远的西湖去玩,根据如图的折线统计图回答问题.
(1)小强在西湖玩了多长时间?
(2)如果从出发起一直骑车不休息,几时几分可以到达西湖?
(3)求小强返回时骑车的速度.
【答案】30分钟;13时30分;200米/分.
【分析】(1)通过观察统计图可知,小强从14时~14时30分,在西湖玩了30分钟.
(2)如果从出发起一直骑车不休息,只需要30分钟就到,所以13时30分可以到达西湖.
(3)小强返回用了30分钟,根据速度=路程÷时间,据此列式解答.
【解答】解:(1)小强从14时~14时30分,在西湖玩了30分钟.
(2)如果从出发起一直骑车不休息,只需要30分钟就到,所以13时30分可以到达西湖.
(3)6千米=6000米
6000÷30=200(米/分)
答:小强返回时骑车的速度是每分钟行驶200米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
25.如图是号称“天下第一泉“的趵突泉某段时间的喷水量和喷涌天数的统计表。
喷水量/m3 16万 32万 48万 64万 96万 ……
喷涌天数(天) 1 2 3 4 6 ……
(1)上表中趵突泉的喷水量和喷涌天数成什么比例关系?为什么?
(2)在如图中找出喷涌天数和对应喷水量的点,然后把它们连起来。
(3)利用图象回答:2.5天喷水 40 立方米,80万立方米的水量需要喷涌 5 天。
【答案】(1)正比例关系,因为相对应的两个数的比值一定。
(2)
(3)40,5。
【分析】(1)根据正比例的意义,两种相关联的量,一种量变化,另一种量也随着变化,两种量中相对应的两个数的比值一定,这两种相关联的成正比例,它们的之间的关系是正比例关系。据此解答。
(2)先描出喷涌天数和对应喷水量的点,然后顺次连接各点画出图像。
(3)正比例图像是一条直线,利用图像直接回答问题。
【解答】解:(1)16:1=32:2=48:3=64:4......
所以上表中趵突泉的喷水量和喷涌天数成什么比例关系,因为相对应的两个数的比值一定。
(2)作图如下:
(3)答:2.5天喷水40立方米,80万立方米的水量需要喷涌5天。
故答案为:40,5。
【点评】此题考查的目的是理解掌握正比例的意义及应用,掌握正比例图像的画法及应用。
26.根据如图的统计图填空回答问题。
(1)两个车间 1 月份做衣服产量相差最大。
(2)第 二 车间这五个月的产量增长速度最快。
(3)4月份第一车间做衣服的产量是第二车间的几分之几?
(4)5月份第二车间衣服的产量占这个月两个车间总产量的几分之几?
【答案】(1)1;
(2)二;
(3)
(4)
【分析】(1)通过观察统计图直接回答问题。
(2)通过观察统计图可知,第二车间这五个月的产量增长速度最快。
(3)把4月份第二车间的产量看作单位“1”,根据求一个数是另一个数的几分之几,用除法解答。
(4)先求出5月份两个车间的总产量,把5月份两个车间的总产量看作单位“1”,根据求一个数是另一个数的几分之几,用除法解答。
【解答】解:(1)两个车间1月份做衣服产量相差最大。
(2)第二车间这五个月的产量增长速度最快。
(3)60÷70
答:4月份第一车间做衣服的产量是第二车间的。
(4)80÷(80+70)
=80÷150
答:5月份第二车间衣服的产量占这个月两个车间总产量的。
故答案为:1;二。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
27.如图所示是希望小学各年级学生近视人数统计图,看图回答问题。
(1)根据统计图,你能说说希望小学学生近视人数的变化趋势吗?
(2)六年级近视的人数比五年级多24%,六年级近视的人数是多少?
(3)根据以上信息,你想对同学们说些什么?
【答案】(1)上升趋势;
(2)62人;
(3)由于近似人数的上升,想对同学们说,在平时的学习中要注意用眼卫生,保护好我们的视力。(答案不唯一)
【分析】(1)根据统计图中折线的走势说出小学生近视眼变化的趋势;
(2)把五年级近视人数看作单位“1”,六年级比五年级多24%,六年级是五年级的(1+24%),用五年级近视人数乘(1+24%),即可求出六年级近视人数;
(3)根据折线的变化趋势,说出自己的建议,合理即可(答案不唯一)。
【解答】解:(1)从折线统计图中,折线的趋势可以看出,希望小学学生近视人数的变化趋势是上升趋势。
(2)50×(1+24%)
=50×1.24
=62(人)
答:六年级近视的人数是62人。
(3)由于近视人数的上升,想对同学们说,在平时的学习中要注意用眼卫生,保护好我们的视力。(答案不唯一)
【点评】本题考查折线统计图的实际应用,根据统计图提供的信息解答问题。
28.如图是小华骑自行车到6千米远的森林公园去游玩的情况.
(1)小华从出发到返回,一共经过了多长时间?
(2)返回前,小华在路上用的时间比在公园里玩的时间多多少分钟?
(3)返回时,小华骑自行车每分钟行走多少米?
【答案】见试题解答内容
【分析】(1)小华从1时出发到33时返回,求从出发到返回一共经过了多长时间就用返回的时间减去出发的时间解答.
(2)返回前,小华在路上用的时间是1小时,在公园里玩的时间是小时,求多多少分钟用减法解答,再化成分钟即可.
(3)先把时间化成分钟,把路程化成米,再用路程除以返回的时间解答.
【解答】解:(1)3
=3
(小时)
答:一共经过了2小时.
(2)1
=1
(小时)
答:返回前,小华在路上用的时间比在公园里玩的时间多20分钟.
(3)小时小时=40分钟,6千米=6000米
6000÷40=150(米)
答:返回时,小华骑自行车每分钟行走150米.
【点评】解答本题的关键是能从统计图中获取与问题有关的信息,再根据基本的数量关系解决问题.要注意单位的统一.
29.下面是甲、乙两辆汽车与七星湖的距离统计图.
(1)如果甲,乙两辆汽车在同一条路上相向而行,那么点A说明了什么?
(2)你还能从图中知道什么?
【答案】见试题解答内容
【分析】(1)通过观察折线统计图可知,如果甲,乙两辆汽车在同一条路上相向而行,那么点A说明了两车在此相遇.
(2)从图中可以知道甲车的速度比乙车的速度快.据此解答.
【解答】解:(1)如果甲,乙两辆汽车在同一条路上相向而行,那么点A说明了两车在此相遇.
(2)从图中可以知道甲车的速度比乙车的速度快.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
30.如图是丽丽发热住院期间的体温记录情况统计图.
(1)这种统计图是 折线 统计图.
(2)护士每 6 小时为丽丽量一次体温;丽丽体温最高是 39.5 摄氏度;丽丽4月8日12时的体温是 37.5 摄氏度.
(3)从体温看,丽丽的病情是恶化还是好转?为什么?
【答案】见试题解答内容
【分析】(1)这种统计图是折线统计图.
(2)护士每隔6小时为丽丽量一次体温,丽丽体温最高是39.5℃,丽丽4月8日12时的体温是37.5℃.
(3)从体温看,丽丽的病情是好转,因为她的体温逐渐接近正常体温.据此解答.
【解答】解:(1)这种统计图是折线统计图.
(2)护士每隔6小时为丽丽量一次体温,丽丽体温最高是39.5℃,丽丽4月8日12时的体温是37.5℃.
(3)从体温看,丽丽的病情是好转,因为她的体温逐渐接近正常体温.
故答案为:折线;6、39.5、37.5
【点评】此题考查的目的是理解掌握折线统计图的特点及主要,并且能够根据统计图提供的信息,解决有关的实际问题.
31.小乐到6千米远的西溪去玩。请你根据折线图回答:
(1)小乐在西溪玩了多少时间?
(2)如果一直走不休息,多少小时到达西溪?
(3)求出返回时小乐骑自行车的速度。
【答案】(1)30分钟,(2)小时,(3)12千米/小时。
【分析】(1)小乐2时到西溪,2时30分开始返回。
(2)小乐在去西溪的途中休息了20分钟,他是从1时出发,2时到达西溪,如果一直走不休息,到达西溪的用时就是1时减去20分钟。
(3)返回时小乐用时30分钟,路程除以时间等于速度。
【解答】解:(1)2:30﹣2:00=30(分钟)
答:小乐在西溪玩了30分钟。
(2)1时﹣20分钟=40分钟小时
答:如果一直走不休息,小时到达西溪。
(3)6÷0.5=12(千米/小时)
答:返回时小乐骑自行车每小时行12千米。
【点评】理解折线统计图的意义是解决本题的关键。
32.根据统计图,回答下面的问题.
(1)他们是同时开始竞走的吗?
(2)阳阳平均每分钟走多少米?甜甜平均每分钟走多少米?
【答案】见试题解答内容
【分析】(1)通过观察折线统计图可知,他们不是同时开始竞走的,阳阳比甜甜提前4分钟开始走.
(2)根据速度=路程÷时间,据此列式解答.
【解答】解:(1)阳阳比甜甜提前4分钟开始走,所以他们不是同时开始竞走的.
(2)800÷(50﹣30)
=800÷20
=40(米/分)
800÷(50﹣34)
=800÷16
=50(米/分)
答:阳阳平均每分钟走40米,甜甜平均每分钟走50米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
33.A、B两地相距2400米,甲乙两人分别从A、B两地同时出发相向而行。两人行走情况如图。根据图意计算,两人出发后经过多少分钟相遇?
【答案】分钟。
【分析】通过观察统计图可知,甲从A到B共用30分钟,乙从B到A共用24分钟,根据速度=路程÷时间,分别求出甲、乙平均每分钟走的速度,再根据相遇时间=路程÷速度和,列式解答即可。
【解答】解:2400÷(2400÷30+2400÷24)
=2400÷(80+100)
=2400÷180
(分钟)
答:两人出发后经过分钟相遇。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。关键是掌握相遇问题的基本数量关系及应用。
34.某市某出租车公司收费标准如图所示,如果小明只有13元钱,请计算出小明乘此出租车最远能到达的距离。
【答案】6千米。
【分析】通过观察折线统计图可知,某出租车的起步价是2千米内(包括2千米)5元,超过2千米每千米收费(11﹣5)÷(5﹣2)=2(元),如果小明只有13元,首先用13元减去起步价(5元),用剩下的钱除以超过2千米每千米的收费求出超过起步价以外行驶的距离,然后加上2千米就是最远能到达的距离。
【解答】解:(11﹣5)÷(5﹣2)
=6÷3
=2(元)
2+(13﹣5)÷2
=2+8÷2
=2+4
=6(千米)
答:如果小明只有13元钱,乘此出租车最远能到达的距离是6千米。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
35.六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),如图反映的是大巴车行驶路程与时间之间的关系.请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距10km.
【答案】见试题解答内容
【分析】通过观察统计图可知,大巴车从学校出发行驶1小时达到农场,学校距离农场40千米,根据时间=路程÷速度,据此列式解答即可.
【解答】解:去时:
10÷40=0.25(小时)
返回时:
3+0.25=3.25(小时)
答:去时大巴车离开学校0.25小时时,大巴车与农场相距10千米;返回时,大巴车离开学校3.25小时时,大巴车与农场相距10千米。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
36.观察如图,完成问题.
(1)第1天 穆欣 的成绩好,第2天 回媛媛 的成绩好.
(2)哪天两人成绩最接近?差多少下?
(3)如果从两人中选一人参加比赛,你会选准?并说明理由.
【答案】见试题解答内容
【分析】(1)比较两个人第一天和第二天的成绩即可解答.
(2)观察统计图发现第1天和第2天两人成绩最接近,再用减法求相差.
(3)观察统计图发现,回媛媛的成绩比穆欣的成绩好些,所以如果从两人中选一人参加比赛,会选回媛媛.
【解答】解:(1)因为153>152,155>154,所以第1天穆欣的成绩好,第2天回媛媛的成绩好.
(2)153﹣152=1(下)
155﹣154=1(下)
答:第1天和第2天两人成绩最接近,差1下.
(3)如果从两人中选一人参加比赛,会选回媛媛,因为回媛媛的成绩比穆欣的成绩好些,
故答案为:穆欣,回媛媛,回媛媛.
【点评】解答此题的关键是根据折线统计图提供的数据进行分析、计算、预测即可.
37.小甬和小真两人从甲地匀速步行到乙地,小甬出发5分钟后,小真以一定的速度沿同一路线行走,设小甬、小真两人相距s(米),小甬行走的时间为t(分),s(米)关于t(分)的图象如图所示,求a。
【答案】20
【分析】首先看懂图形表达的意思,前5分钟小真没有走,35分钟后,小真停下了,到40分钟小甬追上了小真,据此解答即可。
【解答】解:5+(40﹣35)
=5+5
=10(分)
5÷10
40﹣10=30(分)
3015(分)
a=15+5=20。
【点评】看懂图形表达的意思,是解答此题的关键。
38.李欣和刘云为了参加学校运动会1分钟跳绳比赛,提前10天进行训练,每天测试成绩如图的统计图:
根据上面的统计图,回答问题。
(1)李欣和刘云第3天的成绩相差 1 次,第9天的成绩相差 5 次。
(2)李欣和刘云跳绳的成绩呈现 上升 趋势, 刘云 的进步幅度大。
(3)李欣的最好跳绳成绩是1分钟跳 165 次,刘云的最好成绩是1分钟跳 167 次。
【答案】(1)1,5;
(2)上升,刘云;
(3)165,167。
【分析】统计图中纵轴表示天数,横轴表示跳绳次数;
(1)找出第3天李欣和刘云两人的跳绳成绩,相减求出第3天成绩相差几次,同样找出第9天李欣和刘云两人的跳绳成绩,相减求出第9天成绩相差几次;
(2)从图折线可以看出,虽然两人这10天的成绩有升有降,但总体呈上升趋势,其中李欣由最初的153次提升到最后的165次,刘云从最初的152次提升到最后的167次,分别求出两人提升的次数,提升次数较多的同学,进步幅度大;
(3)两人跳绳成绩的折线上最高点表示的成绩,是两人的最好成绩。
【解答】(1)159﹣158=1(次)
165﹣160=5(次)
答:李欣和刘云第3天的成绩相差1次,第9天的成绩相差5次。
(2)167﹣152=15(次)
165﹣153=12(次)
15>12
答:李欣和刘云跳绳的成绩呈现上升趋势,刘云的进步幅度大。
(3)李欣的最好跳绳成绩是1分钟跳165次,刘云的最好成绩是1分钟跳167次。
故答案为:1,5;上升,刘云;165,167。
【点评】此题主要考查从复式折线统计图中读取信息进行分析的能力。
39.一辆汽车在公路上行驶,行驶的时间和路程如图.
(1)这辆车10小时行驶多少千米?
(2)行驶600千米要多少时?
【答案】见试题解答内容
【分析】(1)根据图示可知,这辆车速度不变,路程乙时间成正比例,所以1小时行80千米,10小时行:80×10=800(千米).
(2)根据题意利用公式:时间=路程÷速度,行600千米所用时间为:600÷80=7.5(小时).
【解答】解:(1)80×10=800(千米)
答:这辆车10小时行驶800千米.
(2)600÷80=7.5(小时)
答:行驶600千米要7.5时.
【点评】本题主要考查单式折线统计图,关键根据统计图找对解决问题的条件,利用路程、速度和时间之间的关系做题.
40.某电动汽车经销部某一周销售情况如图:
(1)哪种型号的电动汽车销量大些?
(2)如果你是经销部经理,上图反映的信息对你有什么帮助?
【答案】见试题解答内容
【分析】(1)通过观察统计图,可知A型号的电动汽车销量大些;
(2)如果你是经销部经理,应多进A型号的电动汽车,因为A型号的电动汽车销售量大些.
【解答】解:(1)A型号的电动汽车销量大些;
(2)上图反映,应多进A型号的电动汽车,因为A型号的电动汽车销售量大些.
【点评】此题考查根据统计表提供的信息,解决实际问题的能力.
41.如图,电车从A站经过B站到达C站,然后返回.去时在B站停车,而返回时不停车.已知去时的车速为48千米/小时,则返回时的车速是多少千米/小时?
【答案】见试题解答内容
【分析】从统计图中可知电车从A站到达B站用了4分钟,并在B站休息了1分钟,从B站到达C站用了5分钟,所以电车从A站到达C站共行驶了4+5=9(分钟),根据“速度×时间=路程”求出从A站到C站的距离;电车在C站休息了3分钟,从第13分钟开始行驶到第19分钟返回A站,根据“速度=路程÷时间”即可得出答案.
【解答】解:10分钟﹣1分钟=9分钟小时
19分钟﹣13分钟=6分钟小时
48
=7.2
=72(千米/时)
答:返回时的车速是72千米/小时.
【点评】此题首先根据问题从图中找出所需要的信息,然后根据数量关系式:“速度×时间=路程”和“速度=路程÷时间”即可作出解答.
21世纪教育网(www.21cnjy.com)
例题1:林场工作人员统计了两棵树木的生长情况,并制成了它们生长情况的统计图(如图)
①比较两棵树的生长情况,你发现了什么?
②当两树都停止生长后,两树高度相差多少米?
【答案】见试题解答内容
【分析】①根据复式折线统计图可知,甲乙两棵树开始的生长都很快,但在10年左右时,乙树停止生长,而甲树继续生长到16年左右才停止生长.
②根据统计图可知,停止生长时甲树高9米,乙树高7米,所以相差:9﹣7=2(米).
【解答】解:①比较两棵树的生长情况,我发现:
甲乙两棵树开始的生长都很快,但在10年左右时,乙树停止生长,而甲树继续生长到16年左右才停止生长.
②9﹣7=2(米)
答:当两树都停止生长后,两树高度相差2米.
【点评】本题主要考查复式折线统计图的应用,关键根据统计图中的数据解决问题.
例题2:如图为某地去年1﹣5月份降水量统计图.去年5月底,小明预测当年该地第二季度(4,5,6月份)的降水量是第一季度(1,2,3月份)的1.6倍到2倍.结果小明预测完全正确.根据这些信息,请你通过计算确定:去年6月份该地的降水量最多为多少毫米?
【答案】见试题解答内容
【分析】根据题意可知,该地第二季度的降雨量最多是第一季度的2倍,求一个数的几倍是多少用乘法计算.先求第一季度的降雨量为:30+40+45=115(毫米),则第二季度降雨量最多为:115×2=230(毫米).再求6月份的最大降雨量即可.
【解答】解:(30+40+45)×2
=115×2
=230(毫米)
则6月份的降雨量最多为:230﹣35﹣70=125(毫升)
答:去年6月份该地的降水量最多为125毫米.
【点评】本题主要考查折线统计图的应用,关键根据所给折线统计图,找到解决问题的条件,解决问题.
例题3:如图是陈明与李强绘制的自己10~14岁之间体重变化统计图,请根据统计图回答下列问题。
(1)陈明14岁时的体重比10岁时的体重增加了 0.667 倍。
(2)周宏说:“表示陈明体重变化的折线倾斜度较大,所以陈明的体重增长较快。”你认为她说的是否正确?简要说明理由。
【答案】(1)66.7;(2)不正确,陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
【分析】(1)用陈明14岁时的体重减10岁时的体重,再除以10岁时的体重即可。
(2)陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
【解答】解:(1)(50﹣30)÷30
=20÷30
≈0.667
答:陈明14岁时的体重比10岁时的体重增加了0.0667倍。
(2)她说的不正确,陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
故答案为:66.7。
【点评】本题是复式折线统计图,要通过坐标轴以及图例等读懂本图,根据图中所示的数量解决问题。
例题4:如图是阳阳和东东6~12岁的身高情况统计图,看图回答问题。
(1) 10 岁时,阳阳和东东一样高。
(2)12岁时,东东的身高比阳阳高多少?(请列式计算)
【答案】(1)10;(2)2%。
【分析】(1)观察复式折线统计图,两数据点重合,表示两人身高一样,找到横轴对应年龄即可;
12岁时东东和阳阳身高差既是答案。
【解答】解:(1)10岁时,阳阳和东东一样高。
(2)153﹣150=3(cm)
答:12岁时,东东的身高比阳阳高3cm。
故答案为:3cm。
【点评】本题考查了学生能读懂统计图并根据统计图解决问题的能力。
一、单式折线统计图 1.折线统计图: 用一个单位长度表示一定数量,用折线的上升或下降表示数量的多少和增减变化.容易看出数量的增减变化情况. 2.折现统计图制作步骤: (1)标题:根据统计表所反映的内容,在正上方写上统计图的名称; (2)画出横、纵轴:先画纵轴,后画横轴,横、纵轴都要有单位,按纸面的大小来确定用一定单位表示一定的数量; (3)描点、连线:根据数量的多少,在纵、横轴的恰当位置描出各点,然后把各点用线段顺序连接起来. 二、复式折线统计图 1.定义:用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段把各点顺次连接起来. 折线统计图不但可以表示项目的具体数量,又能清楚地反映事物变化的情况. 2.折线图特点:易于显示数据的变化的规律和趋势.可以用来作股市的跌涨和统计气温. 3.作用: 复式折线统计图一般用于两者之间比较,主要作用还是看两者之间的工作进度和增长. 折线统计图分单式或复式.复式的折线统计图有图例,用不同颜色或形状的线条区别开来. 4.区别: 与单式折线统计图相差最大的是多了一条线,和第二个单位,但仍然能看出他的上升趋势. 三、统计图的特点 1.折线统计图的特点:能够显示数据的变化趋势,反映事物的变化情况. 2.条形统计图的特点: (1)能够使人们一眼看出各个数据的大小. (2)易于比较数据之间的差别. 3.扇形统计图的特点: (1)用扇形的面积表示部分在总体中所占的百分比. (2)易于显示每组数据相对于总数的大小.
1.小丽驱车外出兜风,半途中突然有一只猫冲到车前,她用力刹车才没撞到它.小丽受惊后决定开车回家.以下的折线图是小丽行车的速度记录.
(1)小丽行车期间的最高车速是多少?
(2)小丽在什么时间为躲避那猫而踩刹车?
(3)由如图的数据,能否知道小丽回程的路线,是不是比她从家里出发到发生此意外事件的路线距离短?请解释你的答案.
2.杨庄小学2016年植树情况统计图如图,根据如图回答问题.
(1)植树最多的年级与最少的年级相差多少棵?
(2)三年级植树棵数比六年级少百分之几?
3.下面是航模兴趣小组制作的两架模型飞机在一次飞行中飞行时间和高度的记录.
(1)这两架模型飞机各飞行了多少秒?哪一架飞行时间长一些?
(2)起飞后第25秒甲模型飞机的飞行高度是多少米?乙模型飞机呢?
(3)起飞后第多少秒后两架飞机处于同一高度?起飞后第多少秒两架飞机的高度相差最大?
(4)说一说从起飞后,乙模型飞机第15秒至第20秒的飞行状态.
(5)从图上看,哪架模型飞机的性能好一些?为什么?
4.折线统计图是小玲爸爸的轿车去年下半年的用油量情况.
①这半年平均每月用油多少升?
②如果每升汽油售价是6.4元(以2017年4月上海市汽油价格为标准),参照去年下半年的平均每月用油量计算,小玲爸爸第二季度油卡里充值3500元,够用吗?
5.如图的折线统计图表示的是李叔叔从7时到9时,由李庄到张庄骑车行驶的路程。根据统计图回答下面的问题。
(1)李叔叔是几时从李庄出发的,几时到达张庄,两地间的路程是多少千米?
(2)李叔叔在中途停留了吗?停留了多长时间?
(3)李叔叔在骑车行驶的最后30分钟行驶了多少千米?比他行驶的第1小时的平均速度快了多少?
(4)李叔叔从李庄到张庄的平均速度是多少?
6.某班从一年级到六年级近视人数和未近视人数变化如图:
(1)近视人数和未近视人数相差最多的是 年级, 年级开始近视人数超过了未近视人数。
(2)六年级时近视人数占全班总人数的 。
(3) 年级至 年级近视人数增加最快。
7.如图是甲车行驶的路程与时间的关系图.甲车3.5时行驶多少千米?
8.下面是甲、乙两店2022年12月~2023年5月“午睡地垫”月销售量统计图。
(1)近半年以来,甲、乙两店“午睡地垫” 月销售相差最大,相差 万条。
(2)近半年销售量最高的是 店。
(3)如果你是校办老师,你会选择在哪家店购买,为什么?
9.如图是某城市10~15岁男女生平均身高折线统计图。
①当男女生 岁时,男生与女生平均身高一样,15岁时,男生平均身高比女生高 厘米。
②比较男生和女生的身高变化,你能得什么结论?
③把你的身高与平均值作比较,你有什么想法?
10.下表是某年云南省玉溪市和四川省成都市月平均气温统计表.(单位:C)(1分;
月份 1 2 3 4 5 6 7 8 9 10 11 12
玉溪市 16 18 21 25 27.5 28 27 26.5 26 25 22 17
成都市 4 5 10 16 21 26 29 29 23.5 17.5 11 5.5
(1)根据上表中的数据,绘制复式折线统计图.
(2)两个城市气温相差最大的是 月,相差 .
(3)简单描述两个城市全年气温变化情况.
(4)哪个城市全年气温相对稳定一些?
11.为了参加学校运动会的1分钟跳绳比赛,冬冬和平平提前10天进行训练,每天测试成绩如图:
(1)他们两人第1天的成绩相差多少个?第10天呢?
(2)你认为通过10天训练,谁的进步大一些?
12.第一小学的气象小组把某星期7天的最高气温和最低气温制成了下面的统计图。
(1)这个星期的最高气温从星期 到星期 保持不变。
(2)星期 的最高气温与前一天比相差最大。
(3)星期 的最高气温和最低气温相差最小。
13.下面是周阳(男)和赵娟(女)6到12岁的身高统计图。
请看图回答:
(1) 岁时,他们两人一样高。
(2)9岁时,周阳比赵娟高 厘米。
(3)从10岁到12岁, 的身高增长快。
14.兰兰和青青为了参加学校1分钟跳绳比赛,提前10天进行训练,如图是兰兰和青青每天测试成绩的折线统计图,请根据统计图,完成下面各题。
(1)青青第1天的成绩比她第10天的成绩少 下,第9天兰兰的成绩比青青的成绩多 下。
(2)兰兰和青青的训练成绩总体呈 趋势, 的进步幅度大一些。
(3)请你再提出一个数学问题,并解答。
15.如是汽车的耗油量与路程之间的关系的图象,根据图象回答问题.
(1)该汽车行驶20千米要耗油多少升?
(2)这次行程总共耗油多少升?大约行驶了多少千米?
16.小冬和爸爸爬山游玩,下图是他们两人爬山比赛情况的统计图,认真观察、分析统计图,回答下列问题。
(1) 在途中休息了 分钟。
(2)出发 分钟后,两人在距离起点 m处相遇。
(3) 先到达终点,早 分钟到达。
(4)在比赛的过程中,小冬走过的路程和时间成什么比例关系?请你根据图中的数据说明理由。
17.水池有A、B两个进水管,先开A管,过一段时间后两管同时打开.当A、B管同时打开后,每分钟水位上升多少分米?
18.下面是小明7~12岁的身高、体重与本市同龄儿童身高、体重平均水平比较的统计图。
(1)小明 岁时与本市同龄儿童的平均身高相差最大。
(2)小明 岁时与本市同龄儿童的平均体重相差最小。
19.根据下面的统计图回答问题.
(1)两个城市分别在哪个月降水量最多?哪个月降水量最少?
(2)两个城市最高降水量的差是多少?降水量对生活有什么影响?
20.仔细观察统计图并回答问题。
(1)从开始植树到第6年, 树生长较快。
(2)第 年,两棵树的高度一样。
(3)第15年,甲树的高度是乙树高度的几分之几?
21.(1)从统计图中可以看出,A城和B城的气温变化趋势 (填“相同”或“相反”).
(2)“A城属于温带季风气候,一年四季分明,6~8月为夏季,气候炎热”.根据这条信息可以看出,统计图中折线 表示的是A城的气温变化情况,折线 表示的是B城的气温变化情况.
(3)A城月平均气温最高的月份是 月,月平均气温最低的月份是 月.
(4)B城月平均气温最高的月份的平均气温是 ℃,这时A城的月平均气温是 ℃.
22.如图是根据某家电厂今年上半年销售微波炉情况绘制成的折线统计图.
(1)说一说上半年销售量的变化情况,想一想变化的原因.
(2)如果每月卖出900台微波炉便能收回成本,那么有哪几个月盈利?哪几个月亏本?哪几个月不亏不盈?
(3)从统计图中你还得到哪些信息?请你写下来.
23.爸爸从家出发,骑自行车去离家4800米远的银行,如图表示在这段时间里爸爸离家距离的变化情况.
(1)爸爸来回路上一共用了多少分钟?
(2)爸爸在银行办事用了多少分钟?
24.小强骑自行车到距家6km远的西湖去玩,根据如图的折线统计图回答问题.
(1)小强在西湖玩了多长时间?
(2)如果从出发起一直骑车不休息,几时几分可以到达西湖?
(3)求小强返回时骑车的速度.
25.如图是号称“天下第一泉“的趵突泉某段时间的喷水量和喷涌天数的统计表。
喷水量/m3 16万 32万 48万 64万 96万 ……
喷涌天数(天) 1 2 3 4 6 ……
(1)上表中趵突泉的喷水量和喷涌天数成什么比例关系?为什么?
(2)在如图中找出喷涌天数和对应喷水量的点,然后把它们连起来。
(3)利用图象回答:2.5天喷水 立方米,80万立方米的水量需要喷涌 天。
26.根据如图的统计图填空回答问题。
(1)两个车间 月份做衣服产量相差最大。
(2)第 车间这五个月的产量增长速度最快。
(3)4月份第一车间做衣服的产量是第二车间的几分之几?
(4)5月份第二车间衣服的产量占这个月两个车间总产量的几分之几?
27.如图所示是希望小学各年级学生近视人数统计图,看图回答问题。
(1)根据统计图,你能说说希望小学学生近视人数的变化趋势吗?
(2)六年级近视的人数比五年级多24%,六年级近视的人数是多少?
(3)根据以上信息,你想对同学们说些什么?
28.如图是小华骑自行车到6千米远的森林公园去游玩的情况.
(1)小华从出发到返回,一共经过了多长时间?
(2)返回前,小华在路上用的时间比在公园里玩的时间多多少分钟?
(3)返回时,小华骑自行车每分钟行走多少米?
29.下面是甲、乙两辆汽车与七星湖的距离统计图.
(1)如果甲,乙两辆汽车在同一条路上相向而行,那么点A说明了什么?
(2)你还能从图中知道什么?
30.如图是丽丽发热住院期间的体温记录情况统计图.
(1)这种统计图是 统计图.
(2)护士每 小时为丽丽量一次体温;丽丽体温最高是 摄氏度;丽丽4月8日12时的体温是 摄氏度.
(3)从体温看,丽丽的病情是恶化还是好转?为什么?
31.小乐到6千米远的西溪去玩。请你根据折线图回答:
(1)小乐在西溪玩了多少时间?
(2)如果一直走不休息,多少小时到达西溪?
(3)求出返回时小乐骑自行车的速度。
32.根据统计图,回答下面的问题.
(1)他们是同时开始竞走的吗?
(2)阳阳平均每分钟走多少米?甜甜平均每分钟走多少米?
33.A、B两地相距2400米,甲乙两人分别从A、B两地同时出发相向而行。两人行走情况如图。根据图意计算,两人出发后经过多少分钟相遇?
34.某市某出租车公司收费标准如图所示,如果小明只有13元钱,请计算出小明乘此出租车最远能到达的距离。
35.六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),如图反映的是大巴车行驶路程与时间之间的关系.请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距10km.
36.观察如图,完成问题.
(1)第1天 的成绩好,第2天 的成绩好.
(2)哪天两人成绩最接近?差多少下?
(3)如果从两人中选一人参加比赛,你会选准?并说明理由.
37.小甬和小真两人从甲地匀速步行到乙地,小甬出发5分钟后,小真以一定的速度沿同一路线行走,设小甬、小真两人相距s(米),小甬行走的时间为t(分),s(米)关于t(分)的图象如图所示,求a。
38.李欣和刘云为了参加学校运动会1分钟跳绳比赛,提前10天进行训练,每天测试成绩如图的统计图:
根据上面的统计图,回答问题。
(1)李欣和刘云第3天的成绩相差 次,第9天的成绩相差 次。
(2)李欣和刘云跳绳的成绩呈现 趋势, 的进步幅度大。
(3)李欣的最好跳绳成绩是1分钟跳 次,刘云的最好成绩是1分钟跳 次。
39.一辆汽车在公路上行驶,行驶的时间和路程如图.
(1)这辆车10小时行驶多少千米?
(2)行驶600千米要多少时?
40.某电动汽车经销部某一周销售情况如图:
(1)哪种型号的电动汽车销量大些?
(2)如果你是经销部经理,上图反映的信息对你有什么帮助?
41.如图,电车从A站经过B站到达C站,然后返回.去时在B站停车,而返回时不停车.已知去时的车速为48千米/小时,则返回时的车速是多少千米/小时?
参考答案与试题解析
1.小丽驱车外出兜风,半途中突然有一只猫冲到车前,她用力刹车才没撞到它.小丽受惊后决定开车回家.以下的折线图是小丽行车的速度记录.
(1)小丽行车期间的最高车速是多少?
(2)小丽在什么时间为躲避那猫而踩刹车?
(3)由如图的数据,能否知道小丽回程的路线,是不是比她从家里出发到发生此意外事件的路线距离短?请解释你的答案.
【答案】见试题解答内容
【分析】(1)通过观察统计图可知,小丽行车期间的最高车速是60千米/时.
(2)小丽在9:06为躲避那猫而踩刹车.
(3)由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.据此解答.
【解答】解:( 1 )小丽行车期间的最高车速是60千米/时.
( 2 )小丽在9:06为躲避那猫而踩刹车.
( 3 )答:由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.用的时间虽然相同,但回程时的速度却很慢,所以回程时的路线短.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
2.杨庄小学2016年植树情况统计图如图,根据如图回答问题.
(1)植树最多的年级与最少的年级相差多少棵?
(2)三年级植树棵数比六年级少百分之几?
【答案】见试题解答内容
【分析】(1)通过观察折线统计图可知,植树最多的年级是五年级,植树最少的年级是一年级,根据求一个数比另一个多或少几,用减法解答.
(2)把六年级植树的棵数看作单位“1”,先求出三年级比六年级少植树多少棵,再根据求一个数是另一个数的百分之几,用除法解答.
【解答】解:(1)645﹣200=445(棵)
答:植树最多的年级与最少的年级相差445棵.
(2)(500﹣400)÷500
=100÷500
=0.2
=20%
答:三年级植树棵数比六年级少20%.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
3.下面是航模兴趣小组制作的两架模型飞机在一次飞行中飞行时间和高度的记录.
(1)这两架模型飞机各飞行了多少秒?哪一架飞行时间长一些?
(2)起飞后第25秒甲模型飞机的飞行高度是多少米?乙模型飞机呢?
(3)起飞后第多少秒后两架飞机处于同一高度?起飞后第多少秒两架飞机的高度相差最大?
(4)说一说从起飞后,乙模型飞机第15秒至第20秒的飞行状态.
(5)从图上看,哪架模型飞机的性能好一些?为什么?
【答案】见试题解答内容
【分析】(1)观察统计图可知,甲飞机飞了40秒,乙飞机飞了35秒,甲飞机飞行的时间长一些,
(2)起飞后第25秒甲模型飞机的飞行高度是25米,乙模型飞机处在20米.
(3)起飞后大约15秒两架飞机的高度相差最大,第30秒两架飞机的高度相差最大.
(4)乙模型飞机第15秒至第20秒飞机的飞行水平行驶状态.
(5)从图上看,甲模型飞机的性能好一些.因为甲模型飞机不但飞得高,而且飞行时间长.
【解答】解:(1)这两架飞机中,甲飞机的飞行时间长一些.
(2)起飞后第25秒甲模型飞机的飞行高度是25米,乙模型飞机处在20米.
(3)起飞后大约15秒两架飞机的高度相差最大,第30秒两架飞机的高度相差最大.
(4)乙模型飞机第15秒至第20秒飞机的飞行水平行驶状态.
(5)从图上看,甲模型飞机的性能好一些.因为甲模型飞机不但飞得高,而且飞行时间长.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
4.折线统计图是小玲爸爸的轿车去年下半年的用油量情况.
①这半年平均每月用油多少升?
②如果每升汽油售价是6.4元(以2017年4月上海市汽油价格为标准),参照去年下半年的平均每月用油量计算,小玲爸爸第二季度油卡里充值3500元,够用吗?
【答案】见试题解答内容
【分析】①根据求平均数的方法,用7~12月份用油的总量除以6即可.
②根据下半年平均每月的用油量求出第二季度的用油量,然后根据单价×数量=总价,求出第二季度用汽油的总价,然后与3500元进行比较,如果小于3500元,说明够,如果大于3500元,说明不够.
【解答】解:①(180+160+0+100+280+240)÷6
=960÷6
=160(升);
答:这半年平均每月用油160升.
②6.4×(160×3)
=6.4×480
=3072(元),
3072元<3500元,
答:小玲爸爸第二季度油卡里充值3500元,够用.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
5.如图的折线统计图表示的是李叔叔从7时到9时,由李庄到张庄骑车行驶的路程。根据统计图回答下面的问题。
(1)李叔叔是几时从李庄出发的,几时到达张庄,两地间的路程是多少千米?
(2)李叔叔在中途停留了吗?停留了多长时间?
(3)李叔叔在骑车行驶的最后30分钟行驶了多少千米?比他行驶的第1小时的平均速度快了多少?
(4)李叔叔从李庄到张庄的平均速度是多少?
【答案】(1)7时,9时,30千米;(2)停留了,停留了30分钟;(3)15千米,15千米/时;(4)15千米/时。
【分析】(1)通过观察统计图可知:李叔叔是上午7时从李庄出发的,9时到达张庄,共行驶30千米;
(2)李叔叔8时至8时30分在途中停留,停留了30分钟;
(3)李叔叔在骑车行驶的最后30分钟行驶了30﹣15=15(千米),比他行驶的第1小时的平均速度快了多少,根据速度=路程÷时间分别求出第一小时行驶的速度和最后30分钟行驶的速度进行解答即可。
(4)求平均速度用总路程除以总时间即可。
【解答】解:(1)通过观察统计图可知:李叔叔是上午7时从李庄出发的,9时到达张庄,共行驶30千米;
(2)李叔叔8时至8时30分在途中停留,停留了30分钟;
(3)李叔叔在骑车行驶的最后30分钟行驶了30﹣15=15(千米),
第一小时行驶的速度:15÷1=15(千米/时)
最后30分钟行驶的速度:30分=0.5小时
15÷0.5=30(千米/时)
30﹣15=15(千米/时)
答:比他行驶的第1小时的平均速度快了15千米/时。
(4)李叔叔共行驶了2小时,走了30千米
30÷2=15(千米/时)
答:李叔叔从李庄到张庄的平均速度是15千米/时。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据折线统计图提供的信息,解决有关的实际问题。
6.某班从一年级到六年级近视人数和未近视人数变化如图:
(1)近视人数和未近视人数相差最多的是 一 年级, 五 年级开始近视人数超过了未近视人数。
(2)六年级时近视人数占全班总人数的 75% 。
(3) 五 年级至 六 年级近视人数增加最快。
【答案】(1)一,五;(2)75%;(3)五,六。
【分析】(1)根据图示可知,一年级未近视人数最多,近视人数最少,即一年级近视人数和未近视人数相差最多,五年级开始近视人数超过未近视人数;
(2)近视率=近视人数÷全班人数,据此解答;
(3)分别计算相邻两个年级近视人数的增加情况后比较大小即可作答。
【解答】解:(1)一年级未近视人数最多,近视人数最少,即一年级近视人数和未近视人数相差最多,五年级开始近视人数超过未近视人数;
(2)30÷(30+10)×100%
=30÷40×100%
=75%
答:六年级时近视人数占全班总人数的75%。
(3)5﹣3=2(人)
12﹣5=7(人)
16﹣12=4(人)
21﹣16=5(人)
30﹣21=9(人)
2<4<5<7<9,即五年级至六年级近视人数增加最快。
故答案为:(1)一,五;(2)75%;(3)五,六。
【点评】本题考查了学生能读懂统计图并根据统计图解决问题的能力。
7.如图是甲车行驶的路程与时间的关系图.甲车3.5时行驶多少千米?
【答案】见试题解答内容
【分析】通过观察折线统计图可知:甲车2小时行驶150千米,因为速度(一定),所以路程和时间成正比例,设3.5小时行驶x千米,据此列比例解答.
【解答】解:设3.5小时行驶x千米,
2x=3.5×150
x
x=262.5.
答:3.5小时行驶262.5千米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
8.下面是甲、乙两店2022年12月~2023年5月“午睡地垫”月销售量统计图。
(1)近半年以来,甲、乙两店“午睡地垫” 12 月销售相差最大,相差 0.8 万条。
(2)近半年销售量最高的是 甲 店。
(3)如果你是校办老师,你会选择在哪家店购买,为什么?
【答案】(1)12,0.8;
(2)甲;
(3)甲店,因为近半年销售量最高的是甲店。(答案不唯一)
【分析】(1)用减法列式分别计算6个月份两个店相差多少万条,由此解答本题;
(2)用加法列式计算两个店半年的销售量,由此解答本题;
(3)选择销量高的店,由此解答本题。
【解答】解:(1)2.4﹣1.6=0.8(万条)
2.6﹣1.9=0.7(万条)
2.7﹣2.0=0.7(万条)
2.4﹣1.9=0.5(万条)
2.1﹣2.0=0.1(万条)
2.4﹣1.8=0.6(万条)
0.8>0.7>0.6>0.5>0.1
答:近半年以来,甲、乙两店“午睡地垫”12月销售相差最大,相差0.8万条。
(2)2.4+2.6+2.7+2.4+2.0+1.8=13.9(万条)
1.6+1.9+2.0+1.9+2.1+2.4=11.9(万条)
答:近半年销售量最高的是甲店。
(3)我选择甲店来购买,因为近半年销售量最高的是甲店。(答案不唯一)
故答案为:12,0.8;甲。
【点评】本题考查的是复式折线统计图的应用。
9.如图是某城市10~15岁男女生平均身高折线统计图。
①当男女生 11 岁时,男生与女生平均身高一样,15岁时,男生平均身高比女生高 9 厘米。
②比较男生和女生的身高变化,你能得什么结论?
③把你的身高与平均值作比较,你有什么想法?
【答案】①11,9;
②在12之前女生的平均身高高于男生,从13岁到15岁,男生的平均身高高于女生。
③答案不唯一。我是一名男生,今年12岁,身高是154厘米,我的身高比平均身高稍高一些。我的想法是加强体育锻炼,增强体质。
【分析】①通过观察统计图可知,当男女生11岁时,男生与女生平均身高一样,再根据求一个数的比另一个数多几,用减法解答。
②在12之前女生的平均身高高于男生,从13岁到15岁,男生的平均身高高于女生。
③答案不唯一。我是一名男生,今年12岁,身高是154厘米,我的身高比平均身高稍高一些。我的想法是加强体育锻炼,增强体质。
【解答】解:①167﹣158=9(厘米)
答:当男女生11岁时,男生与女生平均身高一样,15岁时,男生平均身高比女生高9厘米。
②在12之前女生的平均身高高于男生,从13岁到15岁,男生的平均身高高于女生。
③答案不唯一。我是一名男生,今年12岁,身高是154厘米,我的身高比平均身高稍高一些。我的想法是加强体育锻炼,增强体质。
故答案为:11,9。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10.下表是某年云南省玉溪市和四川省成都市月平均气温统计表.(单位:C)(1分;
月份 1 2 3 4 5 6 7 8 9 10 11 12
玉溪市 16 18 21 25 27.5 28 27 26.5 26 25 22 17
成都市 4 5 10 16 21 26 29 29 23.5 17.5 11 5.5
(1)根据上表中的数据,绘制复式折线统计图.
(2)两个城市气温相差最大的是 2 月,相差 13℃ .
(3)简单描述两个城市全年气温变化情况.
(4)哪个城市全年气温相对稳定一些?
【答案】见试题解答内容
【分析】(1)根据折线统计图的绘制方法,按照统计表中的数据完成统计图.
(2)两个城市气温相差最大的是2月份,相差13℃.
(3)通过观察折线统计图可知:玉溪市月平均气温从1月到6月呈上升趋势,从7月到12月呈下降趋势;成都市月平均气温从1月到8月呈上升趋势,从9月到12月呈下降趋势.
(4)通过比较发现,玉溪市全年气温相对稳定一些.
【解答】解:(1)作图如下:
(2)18﹣5=13(℃);
答:两个城市气温相差最大的是2月份,相差13℃.
(3)通过观察折线统计图可知:玉溪市月平均气温从1月到6月呈上升趋势,从7月到12月呈下降趋势;成都市月平均气温从1月到8月呈上升趋势,从9月到12月呈下降趋势.
(4)通过比较发现,玉溪市全年气温相对稳定一些.
故答案为:2、13℃.
【点评】此题考查的目的是理解掌握折线统计图的绘制方法及应用,并且能够根据统计图提供的信息,解决有关的实际问题.
11.为了参加学校运动会的1分钟跳绳比赛,冬冬和平平提前10天进行训练,每天测试成绩如图:
(1)他们两人第1天的成绩相差多少个?第10天呢?
(2)你认为通过10天训练,谁的进步大一些?
【答案】(1)1个,2个;
(2)平平。
【分析】(1)根据求一个数比另一个数多或少几,用减法解答。
(2)通过观察统计图可知,通过10天的训练,我认为平平进步大一些。据此解答。
【解答】解:(1)153﹣152=1(个)
167﹣165=2(个)
答:他们两人第1天的成绩相差1个,第10天相差2个。
(2)通过10天的训练,我认为平平进步大一些。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
12.第一小学的气象小组把某星期7天的最高气温和最低气温制成了下面的统计图。
(1)这个星期的最高气温从星期 三 到星期 五 保持不变。
(2)星期 三 的最高气温与前一天比相差最大。
(3)星期 日 的最高气温和最低气温相差最小。
【答案】三,五;三;日。
【分析】(1)这个星期的最高气温从星期三到星期五保持不变;
(2)星期三的最高气温与前一天比相差最大;
(3)星期日的最高气温和最低气温相差最小。
【解答】解:(1)这个星期的最高气温从星期三到星期五保持不变;
(2)星期三的最高气温与前一天比相差最大;
(3)星期日的最高气温和最低气温相差最小。
故答案为:三,五;三;日。
【点评】仔细观察统计图,获取准确信息是解答关键。
13.下面是周阳(男)和赵娟(女)6到12岁的身高统计图。
请看图回答:
(1) 10 岁时,他们两人一样高。
(2)9岁时,周阳比赵娟高 2 厘米。
(3)从10岁到12岁, 赵娟 的身高增长快。
【答案】(1)10;
(2)2;
(3)赵娟。
【分析】(1)通过观察统计图直接回答问题。
(2)根据求一个数比另一个数多几,用减法解答。
(3)通过观察复式折线统计图可知,从10岁到12岁,赵娟的身高增长块。据此解答。
【解答】解:(1)10岁时,他们两人一样高。
(2)134﹣132=2(厘米)
答:9岁时,周阳比赵娟高2厘米。
(3)从10岁到12岁,赵娟的身高增长块。
故答案为:10;2;赵娟。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
14.兰兰和青青为了参加学校1分钟跳绳比赛,提前10天进行训练,如图是兰兰和青青每天测试成绩的折线统计图,请根据统计图,完成下面各题。
(1)青青第1天的成绩比她第10天的成绩少 13 下,第9天兰兰的成绩比青青的成绩多 5 下。
(2)兰兰和青青的训练成绩总体呈 上升 趋势, 兰兰 的进步幅度大一些。
(3)请你再提出一个数学问题,并解答。
【答案】(1)12,5;
(2)上升,兰兰;
(3)答案不唯一。兰兰第10天的成绩比第一天多多少下?
15下。
【分析】(1)根据求一个数比另一个数多或少几,用减法解答。
(2)兰兰和青青的训练成绩总体呈算式趋势,兰兰的进步幅度大一些。
(3)答案不唯一。兰兰第10天的成绩比第一天多多少下?根据求一个数比另一个数多几,用减法解答。
【解答】解:(1)165﹣153=12(下)
165﹣160=5(下)
答:青青第1天的成绩比她第10天的成绩少12下,第9天兰兰的成绩比青青的成绩多5下。
(2)兰兰和青青的训练成绩总体呈算式趋势,兰兰的进步幅度大一些。
(3)答案不唯一。兰兰第10天的成绩比第一天多多少下?
167﹣152=15(下)
答:兰兰第10天的成绩比第一天多15下。
故答案为:12,5;上升,兰兰。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
15.如是汽车的耗油量与路程之间的关系的图象,根据图象回答问题.
(1)该汽车行驶20千米要耗油多少升?
(2)这次行程总共耗油多少升?大约行驶了多少千米?
【答案】见试题解答内容
【分析】(1)通过观察折线统计图,计算该汽车行驶20千米要耗油多少升.
(2)这次行程总耗油量是20升,大约行驶了150千米.
【解答】解:(1)4÷30×20(升)
答:该汽车行驶20千米要耗油升.
30﹣10=20(升)
20÷(4÷30)=150(千米)
(2)答:这次行程总耗油量是20升,大约行驶了150千米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
16.小冬和爸爸爬山游玩,下图是他们两人爬山比赛情况的统计图,认真观察、分析统计图,回答下列问题。
(1) 爸爸 在途中休息了 5 分钟。
(2)出发 15 分钟后,两人在距离起点 300 m处相遇。
(3) 小冬 先到达终点,早 2.5 分钟到达。
(4)在比赛的过程中,小冬走过的路程和时间成什么比例关系?请你根据图中的数据说明理由。
【答案】见试题解答内容
【分析】(1)通过观察统计图可知:爸爸在途中休息了5分钟。
(2)出发后15分钟,两人在距离起点300米处相遇。
(3)小冬先达到终点,早2.5分钟。
(4)因为正比例的图象是一条直线,由此可知,在比赛的过程中,小冬走过的路程和时间成正比例关系。据此解答即可。
【解答】解:(1)爸爸在途中休息了5分钟。
(2)出发后15分钟,两人在距离起点300米处相遇。
(3)小冬先达到终点,早2.5分钟。
(4)因为正比例的图象是一条直线,由此可知,在比赛的过程中,小冬走过的路程和时间成正比例关系。
故答案为:爸爸、5;15、300;小冬、2.5。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用并且能够根据统计图提供的信息,解决有关的实际问题。
17.水池有A、B两个进水管,先开A管,过一段时间后两管同时打开.当A、B管同时打开后,每分钟水位上升多少分米?
【答案】见试题解答内容
【分析】通过观察折线统计图可知:单开A管15分钟水位上升到20分米,两管同时开5分钟水位上升了(40﹣20)分米,根据“等分”除法的意义,用除法解答即可.
【解答】解:(40﹣20)÷(20﹣15)
=20÷5
=4(分米),
答:每分钟水位上升4分米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
18.下面是小明7~12岁的身高、体重与本市同龄儿童身高、体重平均水平比较的统计图。
(1)小明 12 岁时与本市同龄儿童的平均身高相差最大。
(2)小明 7 岁时与本市同龄儿童的平均体重相差最小。
【答案】(1)12;
(2)7。
【分析】(1)通过观察统计图可知,小明12岁时与本市同龄儿童的平均身高相差最大。
(2)小明7岁时时与本市同龄儿童的平均体重相差最小。据此解答即可。
【解答】解:(1)小明12岁时与本市同龄儿童的平均身高相差最大。
(2)小明7岁时时与本市同龄儿童的平均体重相差最小。
故答案为:12;7。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
19.根据下面的统计图回答问题.
(1)两个城市分别在哪个月降水量最多?哪个月降水量最少?
(2)两个城市最高降水量的差是多少?降水量对生活有什么影响?
【答案】(1)7,南宁11月份,石家庄3月份.
(2)399,降水量的多少对人类的生产生活等各个领域有着极大影响.降水过多会导致洪涝灾害、滑坡、泥石流等自然灾害,对人类的生产生活造成极大的经济损失与不便;降水过少,则会给生活用水、农田浇灌等带来困难,只有适度的降水量才有益于我们的生产生活.(答案不唯一.)
【分析】(1)通过观察统计图可知,两个城市都是7月份降水量最多.南宁11月份的降水量最少,石家庄3月份的降水量最少.
(2)求两个城市最高降水量的差是多少,根据求一个数比另一个数多或少几,用减法解答;降水量的多少对人类的生产生活等各个领域有着极大影响.降水过多会导致洪涝灾害、滑坡、泥石流等自然灾害,对人类的生产生活造成极大的经济损失与不便;降水过少,则会给生活用水、农田浇灌等带来困难,只有适度的降水量才有益于我们的生产生活.据此解答.
【解答】解:(1)两个城市都是7月份降水量最多.南宁11月份的降水量最少,石家庄3月份的降水量最少.
(2)462.9﹣63.9=399 (毫米)
答:两个城市最高降水量的差399毫米.降水量的多少对人类的生产生活等各个领域有着极大影响.降水过多会导致洪涝灾害、滑坡、泥石流等自然灾害,对人类的生产生活造成极大的经济损失与不便;降水过少,则会给生活用水、农田浇灌等带来困难,只有适度的降水量才有益于我们的生产生活.
(答案不唯一.)
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,把能够根据统计图提供的信息,解决有关的实际问题.
20.仔细观察统计图并回答问题。
(1)从开始植树到第6年, 甲 树生长较快。
(2)第 9 年,两棵树的高度一样。
(3)第15年,甲树的高度是乙树高度的几分之几?
【答案】(1)甲;
(2)9;
(3)。
【分析】(1)通过观察统计图可知,从开始植树到第6年,甲树生长较快。
(2)第9年,两棵树的高度一样。
(3)把第15年乙树的高度看作单位“1”,根据求一个数是另一个数的几分之几,用除法解答。
【解答】解:(1)从开始植树到第6年,甲树生长较快。
(2)第9年,两棵树的高度一样。
(3)7÷9
答:第15年,甲树的高度是乙树高度的。
故答案为:甲;9;。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
21.(1)从统计图中可以看出,A城和B城的气温变化趋势 相反 (填“相同”或“相反”).
(2)“A城属于温带季风气候,一年四季分明,6~8月为夏季,气候炎热”.根据这条信息可以看出,统计图中折线 ② 表示的是A城的气温变化情况,折线 ① 表示的是B城的气温变化情况.
(3)A城月平均气温最高的月份是 7 月,月平均气温最低的月份是 1 月.
(4)B城月平均气温最高的月份的平均气温是 24.3 ℃,这时A城的月平均气温是 2 ℃.
【答案】见试题解答内容
【分析】(1)通过观察折线统计图可知,A城和B城的气温变化趋势相反.
(2)“A城属于温带季风气候,一年四季分明,6~8月为夏季,气候炎热”.根据这条信息可以看出,统计图中折线②表示的是A城的气温变化情况,折线①表示的是B城的气温变化情况.
(3)A城月平均气温最高的月份是7月份,月平均气温最低的月份是1月份.
(4)B城月平均气温最高的月份的平均气温是24.3℃,这时A城的月平均气温是2℃.据此解答即可.
【解答】解:(1)A城和B城的气温变化趋势相反.
(2)“A城属于温带季风气候,一年四季分明,6~8月为夏季,气候炎热”.根据这条信息可以看出,统计图中折线②表示的是A城的气温变化情况,折线①表示的是B城的气温变化情况.
(3)A城月平均气温最高的月份是7月份,月平均气温最低的月份是1月份.
(4)B城月平均气温最高的月份的平均气温是24.3℃,这时A城的月平均气温是2℃.
故答案为:相反;②、①;7、1;24.3、2.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
22.如图是根据某家电厂今年上半年销售微波炉情况绘制成的折线统计图.
(1)说一说上半年销售量的变化情况,想一想变化的原因.
(2)如果每月卖出900台微波炉便能收回成本,那么有哪几个月盈利?哪几个月亏本?哪几个月不亏不盈?
(3)从统计图中你还得到哪些信息?请你写下来.
【答案】见试题解答内容
【分析】(1)通过观察折线统计图发现,一月份到二月份销售量呈上升趋势,从二月份到六月份销售量呈下降趋势,这种变化的原因可能是宣传力度不够,另一个原因可能没有真正让利给顾客.
(2)如果每月卖出900台微波炉便能收回成本,一月份、二月份、四月份这三个月盈利,三月份和六月份亏本,四月份不亏不盈.
(3)从统计图中可以看出二月份销售量最多,三月份销售量最少.
【解答】解:(1)一月份到二月份销售量呈上升趋势,从二月份到六月份销售量呈下降趋势,这种变化的原因可能是宣传力度不够,另一个原因可能没有真正让利给顾客.
(2)如果每月卖出900台微波炉便能收回成本,四月份的销售量正好是900台,所以四月份不亏不盈.
1000﹣900=100(台)
1250﹣900=350(台)
940﹣900=40(台)
所以,一月份、二月份、四月份这三个月盈利,
900﹣760=140(台)
900﹣800=100(台)
所以,三月份和六月份亏本.
(3)从统计图中可以看出二月份销售量最多,是1250台;三月份销售量最少,是760台.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
23.爸爸从家出发,骑自行车去离家4800米远的银行,如图表示在这段时间里爸爸离家距离的变化情况.
(1)爸爸来回路上一共用了多少分钟?
(2)爸爸在银行办事用了多少分钟?
【答案】见试题解答内容
【分析】(1)通过观察统计图可知,去用了20分钟,返回用了30分钟,根据加法的意义,用加法解答.
(2)爸爸在银行办事用了40分钟.据此解答.
【解答】解:(1)20+30=50(分钟)
答:爸爸来回路上一共用了50分钟.
(2)60﹣20=40(分钟)
答:爸爸在银行办事用了40分钟.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
24.小强骑自行车到距家6km远的西湖去玩,根据如图的折线统计图回答问题.
(1)小强在西湖玩了多长时间?
(2)如果从出发起一直骑车不休息,几时几分可以到达西湖?
(3)求小强返回时骑车的速度.
【答案】30分钟;13时30分;200米/分.
【分析】(1)通过观察统计图可知,小强从14时~14时30分,在西湖玩了30分钟.
(2)如果从出发起一直骑车不休息,只需要30分钟就到,所以13时30分可以到达西湖.
(3)小强返回用了30分钟,根据速度=路程÷时间,据此列式解答.
【解答】解:(1)小强从14时~14时30分,在西湖玩了30分钟.
(2)如果从出发起一直骑车不休息,只需要30分钟就到,所以13时30分可以到达西湖.
(3)6千米=6000米
6000÷30=200(米/分)
答:小强返回时骑车的速度是每分钟行驶200米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
25.如图是号称“天下第一泉“的趵突泉某段时间的喷水量和喷涌天数的统计表。
喷水量/m3 16万 32万 48万 64万 96万 ……
喷涌天数(天) 1 2 3 4 6 ……
(1)上表中趵突泉的喷水量和喷涌天数成什么比例关系?为什么?
(2)在如图中找出喷涌天数和对应喷水量的点,然后把它们连起来。
(3)利用图象回答:2.5天喷水 40 立方米,80万立方米的水量需要喷涌 5 天。
【答案】(1)正比例关系,因为相对应的两个数的比值一定。
(2)
(3)40,5。
【分析】(1)根据正比例的意义,两种相关联的量,一种量变化,另一种量也随着变化,两种量中相对应的两个数的比值一定,这两种相关联的成正比例,它们的之间的关系是正比例关系。据此解答。
(2)先描出喷涌天数和对应喷水量的点,然后顺次连接各点画出图像。
(3)正比例图像是一条直线,利用图像直接回答问题。
【解答】解:(1)16:1=32:2=48:3=64:4......
所以上表中趵突泉的喷水量和喷涌天数成什么比例关系,因为相对应的两个数的比值一定。
(2)作图如下:
(3)答:2.5天喷水40立方米,80万立方米的水量需要喷涌5天。
故答案为:40,5。
【点评】此题考查的目的是理解掌握正比例的意义及应用,掌握正比例图像的画法及应用。
26.根据如图的统计图填空回答问题。
(1)两个车间 1 月份做衣服产量相差最大。
(2)第 二 车间这五个月的产量增长速度最快。
(3)4月份第一车间做衣服的产量是第二车间的几分之几?
(4)5月份第二车间衣服的产量占这个月两个车间总产量的几分之几?
【答案】(1)1;
(2)二;
(3)
(4)
【分析】(1)通过观察统计图直接回答问题。
(2)通过观察统计图可知,第二车间这五个月的产量增长速度最快。
(3)把4月份第二车间的产量看作单位“1”,根据求一个数是另一个数的几分之几,用除法解答。
(4)先求出5月份两个车间的总产量,把5月份两个车间的总产量看作单位“1”,根据求一个数是另一个数的几分之几,用除法解答。
【解答】解:(1)两个车间1月份做衣服产量相差最大。
(2)第二车间这五个月的产量增长速度最快。
(3)60÷70
答:4月份第一车间做衣服的产量是第二车间的。
(4)80÷(80+70)
=80÷150
答:5月份第二车间衣服的产量占这个月两个车间总产量的。
故答案为:1;二。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
27.如图所示是希望小学各年级学生近视人数统计图,看图回答问题。
(1)根据统计图,你能说说希望小学学生近视人数的变化趋势吗?
(2)六年级近视的人数比五年级多24%,六年级近视的人数是多少?
(3)根据以上信息,你想对同学们说些什么?
【答案】(1)上升趋势;
(2)62人;
(3)由于近似人数的上升,想对同学们说,在平时的学习中要注意用眼卫生,保护好我们的视力。(答案不唯一)
【分析】(1)根据统计图中折线的走势说出小学生近视眼变化的趋势;
(2)把五年级近视人数看作单位“1”,六年级比五年级多24%,六年级是五年级的(1+24%),用五年级近视人数乘(1+24%),即可求出六年级近视人数;
(3)根据折线的变化趋势,说出自己的建议,合理即可(答案不唯一)。
【解答】解:(1)从折线统计图中,折线的趋势可以看出,希望小学学生近视人数的变化趋势是上升趋势。
(2)50×(1+24%)
=50×1.24
=62(人)
答:六年级近视的人数是62人。
(3)由于近视人数的上升,想对同学们说,在平时的学习中要注意用眼卫生,保护好我们的视力。(答案不唯一)
【点评】本题考查折线统计图的实际应用,根据统计图提供的信息解答问题。
28.如图是小华骑自行车到6千米远的森林公园去游玩的情况.
(1)小华从出发到返回,一共经过了多长时间?
(2)返回前,小华在路上用的时间比在公园里玩的时间多多少分钟?
(3)返回时,小华骑自行车每分钟行走多少米?
【答案】见试题解答内容
【分析】(1)小华从1时出发到33时返回,求从出发到返回一共经过了多长时间就用返回的时间减去出发的时间解答.
(2)返回前,小华在路上用的时间是1小时,在公园里玩的时间是小时,求多多少分钟用减法解答,再化成分钟即可.
(3)先把时间化成分钟,把路程化成米,再用路程除以返回的时间解答.
【解答】解:(1)3
=3
(小时)
答:一共经过了2小时.
(2)1
=1
(小时)
答:返回前,小华在路上用的时间比在公园里玩的时间多20分钟.
(3)小时小时=40分钟,6千米=6000米
6000÷40=150(米)
答:返回时,小华骑自行车每分钟行走150米.
【点评】解答本题的关键是能从统计图中获取与问题有关的信息,再根据基本的数量关系解决问题.要注意单位的统一.
29.下面是甲、乙两辆汽车与七星湖的距离统计图.
(1)如果甲,乙两辆汽车在同一条路上相向而行,那么点A说明了什么?
(2)你还能从图中知道什么?
【答案】见试题解答内容
【分析】(1)通过观察折线统计图可知,如果甲,乙两辆汽车在同一条路上相向而行,那么点A说明了两车在此相遇.
(2)从图中可以知道甲车的速度比乙车的速度快.据此解答.
【解答】解:(1)如果甲,乙两辆汽车在同一条路上相向而行,那么点A说明了两车在此相遇.
(2)从图中可以知道甲车的速度比乙车的速度快.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
30.如图是丽丽发热住院期间的体温记录情况统计图.
(1)这种统计图是 折线 统计图.
(2)护士每 6 小时为丽丽量一次体温;丽丽体温最高是 39.5 摄氏度;丽丽4月8日12时的体温是 37.5 摄氏度.
(3)从体温看,丽丽的病情是恶化还是好转?为什么?
【答案】见试题解答内容
【分析】(1)这种统计图是折线统计图.
(2)护士每隔6小时为丽丽量一次体温,丽丽体温最高是39.5℃,丽丽4月8日12时的体温是37.5℃.
(3)从体温看,丽丽的病情是好转,因为她的体温逐渐接近正常体温.据此解答.
【解答】解:(1)这种统计图是折线统计图.
(2)护士每隔6小时为丽丽量一次体温,丽丽体温最高是39.5℃,丽丽4月8日12时的体温是37.5℃.
(3)从体温看,丽丽的病情是好转,因为她的体温逐渐接近正常体温.
故答案为:折线;6、39.5、37.5
【点评】此题考查的目的是理解掌握折线统计图的特点及主要,并且能够根据统计图提供的信息,解决有关的实际问题.
31.小乐到6千米远的西溪去玩。请你根据折线图回答:
(1)小乐在西溪玩了多少时间?
(2)如果一直走不休息,多少小时到达西溪?
(3)求出返回时小乐骑自行车的速度。
【答案】(1)30分钟,(2)小时,(3)12千米/小时。
【分析】(1)小乐2时到西溪,2时30分开始返回。
(2)小乐在去西溪的途中休息了20分钟,他是从1时出发,2时到达西溪,如果一直走不休息,到达西溪的用时就是1时减去20分钟。
(3)返回时小乐用时30分钟,路程除以时间等于速度。
【解答】解:(1)2:30﹣2:00=30(分钟)
答:小乐在西溪玩了30分钟。
(2)1时﹣20分钟=40分钟小时
答:如果一直走不休息,小时到达西溪。
(3)6÷0.5=12(千米/小时)
答:返回时小乐骑自行车每小时行12千米。
【点评】理解折线统计图的意义是解决本题的关键。
32.根据统计图,回答下面的问题.
(1)他们是同时开始竞走的吗?
(2)阳阳平均每分钟走多少米?甜甜平均每分钟走多少米?
【答案】见试题解答内容
【分析】(1)通过观察折线统计图可知,他们不是同时开始竞走的,阳阳比甜甜提前4分钟开始走.
(2)根据速度=路程÷时间,据此列式解答.
【解答】解:(1)阳阳比甜甜提前4分钟开始走,所以他们不是同时开始竞走的.
(2)800÷(50﹣30)
=800÷20
=40(米/分)
800÷(50﹣34)
=800÷16
=50(米/分)
答:阳阳平均每分钟走40米,甜甜平均每分钟走50米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
33.A、B两地相距2400米,甲乙两人分别从A、B两地同时出发相向而行。两人行走情况如图。根据图意计算,两人出发后经过多少分钟相遇?
【答案】分钟。
【分析】通过观察统计图可知,甲从A到B共用30分钟,乙从B到A共用24分钟,根据速度=路程÷时间,分别求出甲、乙平均每分钟走的速度,再根据相遇时间=路程÷速度和,列式解答即可。
【解答】解:2400÷(2400÷30+2400÷24)
=2400÷(80+100)
=2400÷180
(分钟)
答:两人出发后经过分钟相遇。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。关键是掌握相遇问题的基本数量关系及应用。
34.某市某出租车公司收费标准如图所示,如果小明只有13元钱,请计算出小明乘此出租车最远能到达的距离。
【答案】6千米。
【分析】通过观察折线统计图可知,某出租车的起步价是2千米内(包括2千米)5元,超过2千米每千米收费(11﹣5)÷(5﹣2)=2(元),如果小明只有13元,首先用13元减去起步价(5元),用剩下的钱除以超过2千米每千米的收费求出超过起步价以外行驶的距离,然后加上2千米就是最远能到达的距离。
【解答】解:(11﹣5)÷(5﹣2)
=6÷3
=2(元)
2+(13﹣5)÷2
=2+8÷2
=2+4
=6(千米)
答:如果小明只有13元钱,乘此出租车最远能到达的距离是6千米。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
35.六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),如图反映的是大巴车行驶路程与时间之间的关系.请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距10km.
【答案】见试题解答内容
【分析】通过观察统计图可知,大巴车从学校出发行驶1小时达到农场,学校距离农场40千米,根据时间=路程÷速度,据此列式解答即可.
【解答】解:去时:
10÷40=0.25(小时)
返回时:
3+0.25=3.25(小时)
答:去时大巴车离开学校0.25小时时,大巴车与农场相距10千米;返回时,大巴车离开学校3.25小时时,大巴车与农场相距10千米。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
36.观察如图,完成问题.
(1)第1天 穆欣 的成绩好,第2天 回媛媛 的成绩好.
(2)哪天两人成绩最接近?差多少下?
(3)如果从两人中选一人参加比赛,你会选准?并说明理由.
【答案】见试题解答内容
【分析】(1)比较两个人第一天和第二天的成绩即可解答.
(2)观察统计图发现第1天和第2天两人成绩最接近,再用减法求相差.
(3)观察统计图发现,回媛媛的成绩比穆欣的成绩好些,所以如果从两人中选一人参加比赛,会选回媛媛.
【解答】解:(1)因为153>152,155>154,所以第1天穆欣的成绩好,第2天回媛媛的成绩好.
(2)153﹣152=1(下)
155﹣154=1(下)
答:第1天和第2天两人成绩最接近,差1下.
(3)如果从两人中选一人参加比赛,会选回媛媛,因为回媛媛的成绩比穆欣的成绩好些,
故答案为:穆欣,回媛媛,回媛媛.
【点评】解答此题的关键是根据折线统计图提供的数据进行分析、计算、预测即可.
37.小甬和小真两人从甲地匀速步行到乙地,小甬出发5分钟后,小真以一定的速度沿同一路线行走,设小甬、小真两人相距s(米),小甬行走的时间为t(分),s(米)关于t(分)的图象如图所示,求a。
【答案】20
【分析】首先看懂图形表达的意思,前5分钟小真没有走,35分钟后,小真停下了,到40分钟小甬追上了小真,据此解答即可。
【解答】解:5+(40﹣35)
=5+5
=10(分)
5÷10
40﹣10=30(分)
3015(分)
a=15+5=20。
【点评】看懂图形表达的意思,是解答此题的关键。
38.李欣和刘云为了参加学校运动会1分钟跳绳比赛,提前10天进行训练,每天测试成绩如图的统计图:
根据上面的统计图,回答问题。
(1)李欣和刘云第3天的成绩相差 1 次,第9天的成绩相差 5 次。
(2)李欣和刘云跳绳的成绩呈现 上升 趋势, 刘云 的进步幅度大。
(3)李欣的最好跳绳成绩是1分钟跳 165 次,刘云的最好成绩是1分钟跳 167 次。
【答案】(1)1,5;
(2)上升,刘云;
(3)165,167。
【分析】统计图中纵轴表示天数,横轴表示跳绳次数;
(1)找出第3天李欣和刘云两人的跳绳成绩,相减求出第3天成绩相差几次,同样找出第9天李欣和刘云两人的跳绳成绩,相减求出第9天成绩相差几次;
(2)从图折线可以看出,虽然两人这10天的成绩有升有降,但总体呈上升趋势,其中李欣由最初的153次提升到最后的165次,刘云从最初的152次提升到最后的167次,分别求出两人提升的次数,提升次数较多的同学,进步幅度大;
(3)两人跳绳成绩的折线上最高点表示的成绩,是两人的最好成绩。
【解答】(1)159﹣158=1(次)
165﹣160=5(次)
答:李欣和刘云第3天的成绩相差1次,第9天的成绩相差5次。
(2)167﹣152=15(次)
165﹣153=12(次)
15>12
答:李欣和刘云跳绳的成绩呈现上升趋势,刘云的进步幅度大。
(3)李欣的最好跳绳成绩是1分钟跳165次,刘云的最好成绩是1分钟跳167次。
故答案为:1,5;上升,刘云;165,167。
【点评】此题主要考查从复式折线统计图中读取信息进行分析的能力。
39.一辆汽车在公路上行驶,行驶的时间和路程如图.
(1)这辆车10小时行驶多少千米?
(2)行驶600千米要多少时?
【答案】见试题解答内容
【分析】(1)根据图示可知,这辆车速度不变,路程乙时间成正比例,所以1小时行80千米,10小时行:80×10=800(千米).
(2)根据题意利用公式:时间=路程÷速度,行600千米所用时间为:600÷80=7.5(小时).
【解答】解:(1)80×10=800(千米)
答:这辆车10小时行驶800千米.
(2)600÷80=7.5(小时)
答:行驶600千米要7.5时.
【点评】本题主要考查单式折线统计图,关键根据统计图找对解决问题的条件,利用路程、速度和时间之间的关系做题.
40.某电动汽车经销部某一周销售情况如图:
(1)哪种型号的电动汽车销量大些?
(2)如果你是经销部经理,上图反映的信息对你有什么帮助?
【答案】见试题解答内容
【分析】(1)通过观察统计图,可知A型号的电动汽车销量大些;
(2)如果你是经销部经理,应多进A型号的电动汽车,因为A型号的电动汽车销售量大些.
【解答】解:(1)A型号的电动汽车销量大些;
(2)上图反映,应多进A型号的电动汽车,因为A型号的电动汽车销售量大些.
【点评】此题考查根据统计表提供的信息,解决实际问题的能力.
41.如图,电车从A站经过B站到达C站,然后返回.去时在B站停车,而返回时不停车.已知去时的车速为48千米/小时,则返回时的车速是多少千米/小时?
【答案】见试题解答内容
【分析】从统计图中可知电车从A站到达B站用了4分钟,并在B站休息了1分钟,从B站到达C站用了5分钟,所以电车从A站到达C站共行驶了4+5=9(分钟),根据“速度×时间=路程”求出从A站到C站的距离;电车在C站休息了3分钟,从第13分钟开始行驶到第19分钟返回A站,根据“速度=路程÷时间”即可得出答案.
【解答】解:10分钟﹣1分钟=9分钟小时
19分钟﹣13分钟=6分钟小时
48
=7.2
=72(千米/时)
答:返回时的车速是72千米/小时.
【点评】此题首先根据问题从图中找出所需要的信息,然后根据数量关系式:“速度×时间=路程”和“速度=路程÷时间”即可作出解答.
21世纪教育网(www.21cnjy.com)
