2024-2025学年小升初数学备考真题分类汇编(湖北地区专版)专题3 填空题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(湖北地区专版)专题3 填空题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 243.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 07:43:49 | ||
图片预览




文档简介
专题3填空题-2023-2024学年
小升初数学备考真题分类汇编(湖北地区专版)
试卷说明:
本试卷试题精选自湖北省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合湖北省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、填空题
1.(2024·石首)2024年巴黎奥运会开幕式的日期很特别,表示月份的数是一位数中最大的质数;表示日子的数是一个两位数,十位上是最小的质数,个位上是3的倍数而且是偶数。巴黎奥运会开幕式的日期是 。
2.(2024·沙市区)2024年五一期间,荆州古城、荆州博物馆、方特等地人山人海。据荆州文旅局统计,全市A级旅游景区共接待游客867600人次,横线上的数改写成用“万人”作单位的数是 万人次;综合收入达五亿六千零八万元,横线上的数写作 。
3.(2024·石首)有若干名教师和医生,他们的平均年龄为40岁,其中教师的平均年龄为35岁,医生的平均年龄为50岁,教师人数与医生人数的比是 。
4.(2024·襄城)有一组图形,它的排列规律如图。第5个图形中有 个三角形,第n个图形中有 个三角形。
5.(2024·建始)学校组织研学旅行活动,五年级共有350名同学参加,至少有 人在同一个月过生日。在开展“找次品”比赛活动中,老师拿来13个乒乓球,有12个质量相同,另有一个较轻一点,如果用天平称,至少称 次保证能找出这个乒乓球。
6.(2024·阳新)如果规定:1!=1;2!=1×2;3!=1×2×3;4!=1×2×3×4。那么= ,= 。(写出得数)
7.(2024·黄陂)妈妈把10000元钱存入银行,定期一年,年利率是2.25%,到期时妈妈共可以取回 元,我用数量关系式是 求利息的.
8.(2024·阳新)已知自然数x、y满足“x÷y=50……4”,当y最小时,x= 。
9.(2024·阳新)750ml= L
平方千米= 公顷
6时24分= 时
10.(2024·黄陂)如图,一个立体图形从正面看到的图形是A,从上面看到的图形是B,这个立体图形的体积是 立方厘米;如果用一个长方体盒子包装它,这个盒子的容积至少是 立方厘米。
11.(2024·黄陂)转化思想作为重要的数学思想方法之一,在我们的学习生活中,无处不在。一个瓶子里装有一些水(如图),根据图中标出的数据,可得瓶中水的体积占瓶子容积的 。
12.(2024·黄陂)一个笔记本a元,一支钢笔b元,一个笔记本比一支钢笔贵 元,买5个笔记本和15支钢笔共 元。
13.(2024·黄陂) :24= =14÷ =0.875= %
14.(2023·浠水)如图,一张桌子可坐4人,2张桌子拼起来可坐6人,3张桌子拼起来可坐8人。像这样 张桌子拼起来可坐38人,10张桌子可坐 人。
15.(2023·浠水)小圆的半径是3厘米,大圆的半径是4厘米,大圆和小圆周长的比是 ,面积的比是 。
16.(2023·浠水)一副扑克牌有4种花色(大小王除外),每种花色有13张,从中任意抽牌,最少要抽 张牌,才能保证有4张牌是同一花色的。
17.(2024·沙市区)如下图所示三个图形的周长相等,那么a:b:c= : : 。
请写出你的推理过程。
18.(2023·浠水)一个平行四边形和一个三角形等底等高。已知平行四边形的面积是60平方厘米,那么三角形的面积是 平方厘米。将这个三角形按2:1放大,得到的三角形的面积是 平方厘米。
19.(2023·浠水)今年可欣a岁,梦琪比她大3岁,那么今年梦琪年龄是 岁。5年后,梦琪比可欣大 岁。
20.(2023·浠水)9÷ == :20= %。
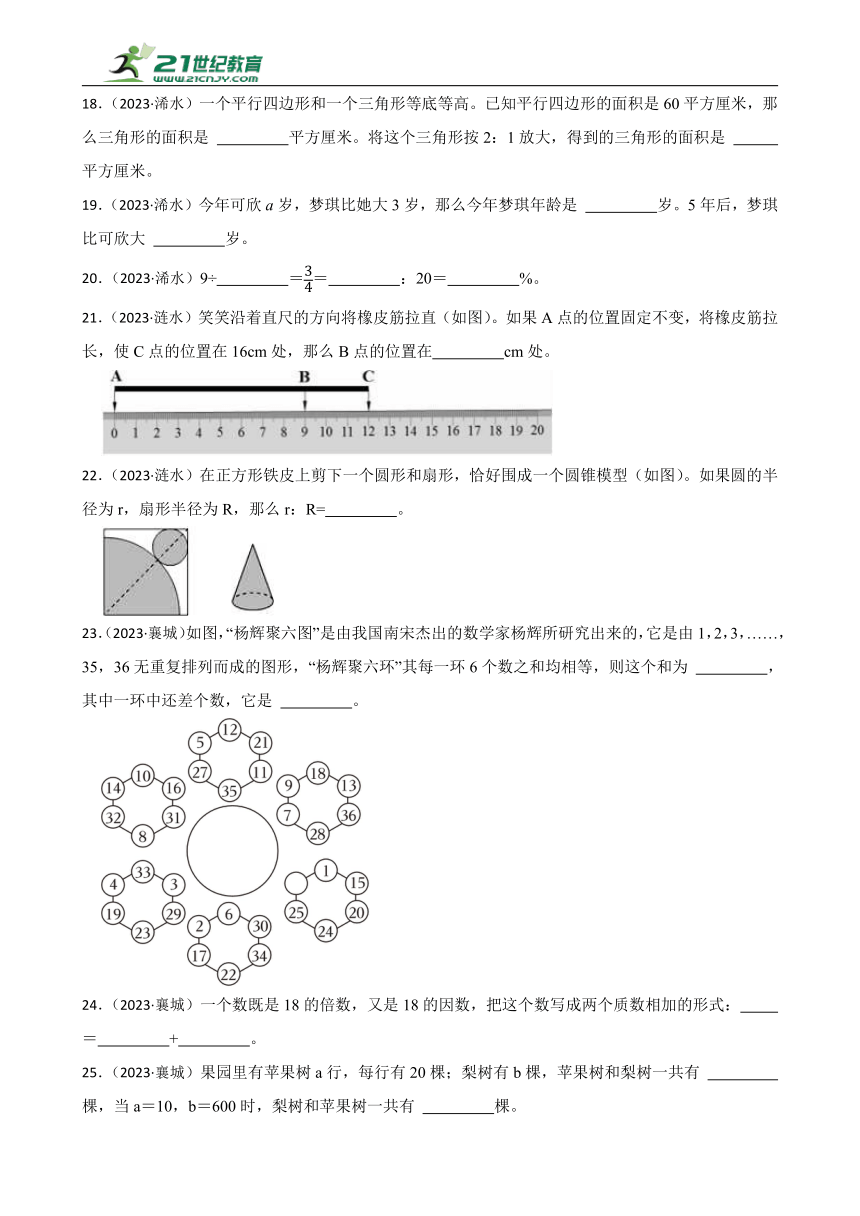
21.(2023·涟水)笑笑沿着直尺的方向将橡皮筋拉直(如图)。如果A点的位置固定不变,将橡皮筋拉长,使C点的位置在16cm处,那么B点的位置在 cm处。
22.(2023·涟水)在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型(如图)。如果圆的半径为r,扇形半径为R,那么r:R= 。
23.(2023·襄城)如图,“杨辉聚六图”是由我国南宋杰出的数学家杨辉所研究出来的,它是由1,2,3,……,35,36无重复排列而成的图形,“杨辉聚六环”其每一环6个数之和均相等,则这个和为 ,其中一环中还差个数,它是 。
24.(2023·襄城)一个数既是18的倍数,又是18的因数,把这个数写成两个质数相加的形式: = + 。
25.(2023·襄城)果园里有苹果树a行,每行有20棵;梨树有b棵,苹果树和梨树一共有 棵,当a=10,b=600时,梨树和苹果树一共有 棵。
26.(2023·襄城)A、B、C三个数的比是5:7:9,如果A=150,则A、B和C三个数的平均数是 。
27.(2023·襄城)一条项链长60cm,每隔5cm有一颗水晶.这条项链上共有 颗水晶.
28.(2023·襄城) = %= ÷160= = (填小数)
29.(2023·襄城)数据显示,2023年“五一”假日期间,某市旅游总收入七十八亿五千万元,写作 元,改写成以“亿”为单位的数是 亿元。
30.(2023·梁子湖)观察图,想一想,填一填。用棋子摆方阵,那么图6要摆 枚棋子,图n要摆 枚棋子。
31.(2023·梁子湖)一个圆锥的底面积是9dm2,高是6dm,它的体积是 dm3,与它等底等高的圆柱的体积是 dm3。
32.(2023·梁子湖)如图,圆的面积与长方形的面积相等。已知长方形的长是15.7cm,圆的半径是 cm。
33.(2023·梁子湖)轩轩的存钱罐里有5元和1元的纸币共9张,总共25元。他有 张5元纸币。
34.(2023·梁子湖)李师傅和徒弟一起生产一种零件。李师傅每小时比徒弟多生产40个,已知两人每小时生产的零件个数的比是10:9,徒弟每小时生产 个零件。
35.(2023·梁子湖)一个数的亿位和千万位上的数字都是一位数中最大的质数,百万位上的数字是最小的质数,其余各位上的数字都是0,这个数写作 ,读作 ,省略亿位后面的尾数约是 亿。
36.(2023·梁子湖)红星面粉厂生产的一种袋装面粉,注明“净含量10kg±0.5kg”,李叔叔买了一袋这样的面粉,质量最少是 kg。
37.(2023·崇阳)按如图的方式摆下去,摆n个连着的正六边形需要 根小棒。
38.(2023·崇阳)在一个边长为20cm的正方形木板上,锯掉一个最大的圆,这个圆的面积是 cm2,剩下的面积占木板面积的 %。
39.(2023·崇阳) :40=4÷5= = %= 折。
40.(2023·广水)我们学过“+、﹣、×、÷”四种运算。若规定“*”是一种新运算,A*B表示(A+2)B。如:3*5=(3+2)×5=25。那么8*8= 。
41.(2023·广水)把一个底面周长是9.42dm,高6dm的圆柱,沿底面直径切成两个半圆柱后,表面积共增加了 dm2。
42.(2023·广水)妈妈买回一袋苹果,每6个装一盘或每8个装一盘都余2个,这袋苹果最少有 个。
43.(2023·广水)一种果汁,零售每瓶5元,商场促销:“买四赠一”。商场优惠了 %。
44.(2023·崇阳)若三角形的面积一定,它的底和高成 比例,如果Y=8X,那么X和Y成 比例。
45.(2023·崇阳)今年妈妈把10万元钱存入银行,存定期二年,年利率是2.25%,到期时妈妈获得利息 元。
46.(2024·沙市区)甲店销售量的恰好等于乙店销售量的,则甲、乙两店销售量的最简整数比是 。
47.(2024·沙市区)如下图,三角形ABC以直角边AC所在的直线为轴旋转一周,所形成的立体图形的体积是 cm3。
48.(2024·沙市区)如下图,李老师用下面装置做排水实验:他把等底等高的圆锥和圆柱体铁块全部浸入水中,圆锥的体积是 cm3。
49.(2024·沙市区)商店原有400个足球,卖出a箱,每箱20个,商店还剩下 个足球;当a=14时,商店还剩下 个足球。
50.(2024·沙市区)中国嫦娥六号探测器上有一个精密零件长5毫米,画在图纸上是10厘米,这幅图的比例尺是 。
答案解析部分
1.7月26日
解:月份是7月,日期是26日,则巴黎奥运会开幕式的日期是7月26日。
故答案为:7月26日。
月份是一位数中最大的质数是7;十位上是最小的质数2,个位上的数=3×2=6。巴黎奥运会开幕式的日期是7月26日。
2.86.76;560080000
解:867600=86.76万;五亿六千零八万写作:560080000。
故答案为:86.76;560080000。
在万位后面点上小数点,去掉末尾的0,在后面加上万字即可改写成用万作单位的数。写数时从高位到低位按照数位顺序写,有几个计数单位就在相应的数位上写几,没有就写0。
3.2:1
解:设教师人数为x,医生人数为y。
40(x + y) = 35x + 50y
40x + 40y = 35x + 50y
5x = 10y
x =2y,所以,教师人数与医生人数的比是2:1。
故答案为:2:1。
首先,我们设立未知数,设教师人数为x,医生人数为y。然后,根据题目给出的平均年龄信息,我们可以建立一个方程。接着,我们对方程进行化简和求解,得到教师人数与医生人数的比例关系。
4.16;4(n﹣1)
解:第5个图形中:(5-1)×4=16(个)。
第n个图形中有4(n-1)个三角形。
故答案为:16;4(n-1)。
第二个图形中有4个三角形,第三个图中有(2×4)个三角形,三角形个数=(图形个数-1)×4,由此计算第5个图形中三角形的个数,并用含有字母的式子表示第n个图形中三角形的个数。
5.30;3
解:第一问:350÷12=29……2,29+1=30(人),至少有30人在同一个月过生日。
第二问:把13个乒乓球分成4、4、5共三份,第一次:在天平两端各放4个乒乓球,如果平衡,较轻的就在剩下的5个中;如果不平衡,上升那端的4个中有一个是轻的。第二次:如果在5个中,天平两端各放2个,如果平衡,剩下的那个就是轻的;如果不平衡,上升那端的2个中有1个是轻的,再称第三次就能找出轻的;如果在4个中,天平两端各放2个,上升那端有1个是轻的,这样再称第三次就能找出轻的。
故答案为:30;3。
第一问:用350除以12求出商是29,余数是2,从最不利的情况考虑,每个月都有29人生日,那么剩下的2人无论在哪个月出生都至少有30人在同一个月过生日;
第二问:把物品平均分成3份,如果不能平均分也要使其中一份比另外两份多或少1个,这样称一次就能把次品缩小到最小范围;按照这样的方法确定称的次数即可。
6.;2024
解: ==;
==2024。
故答案为:;2024。
依据的新定义分别写出分子、分母相乘的形式,然后再约分。
7.10225;利息=本金×利率×时间
解:10000×1×2.25%+10000
=225+10000
=10225(元)
利息=本金×利率×时间。
故答案为:10225;利息=本金×利率×时间。
到期时妈妈共可以取回的钱数=利息+本金,其中,利息=本金×利率×时间。
8.254
解:50×(4+1)+4
=250+4
=254。
故答案为:254。
在有余数的除法中,除数最小=余数+1;此时,被除数=商×除数+余数。
9.0.75;40;6.4
解:750÷1000=0.75(升)
×100=40(公顷)
6+24÷60
=6+0.4
=6.4(时)。
故答案为:0.75;40;6.4。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
10.12.56;48
解:3.14×22×3÷3
=12.56×3÷3
=12.56(立方厘米)
2×2=4(厘米)
4×4×3
=16×3
=48(立方厘米)。
故答案为:12.56;48。
这个立体图形的体积=圆锥的体积=π×半径2×高÷3;这个盒子的容积至少=长×宽×高;其中,长=宽=底面圆的直径,高=圆锥的高。
11.
解:7÷(7+18)
=7÷25
=。
故答案为:。
瓶中水的体积占瓶子容积的分率=正放时水的高度÷(正放时水的高度+倒放时水的高度) 。
12.(a-b);(5a+15b)
解:a-b=(a-b)(元);
5a+15b=(5a+15b)(元)。
故答案为:(a-b);(5a+15b)。
一个笔记本比一支钢笔贵的钱数=笔记本的单价-钢笔的单价;买5个笔记本和15支钢笔的总钱数=笔记本的单价×笔记本的数量+钢笔的单价×钢笔的数量。
13.21;7;16;87.5
解:0.875×24=21;
0.875×8=7;
14÷0.875=16;
0.875=87.5%;
所以21:24==14÷16=87.5%。
故答案为:21;7;16;87.5。
比的前项=比值×比的后项,分子=分母×分数值,除数=被除数÷商;小数化成百分数,把小数的小数点向右移动两位,再加上百分号。
14.18;22
解:一张桌子可坐2+2×1=4人,
2张桌子拼起来可坐2+2×2=6人,
3张桌子拼起来可坐2+2×3=8人,
·····
n张桌子拼起来可坐2+2×n=2n+2人,
2n+2=38,
n=18,
2×10+2=22(人);
故答案为:18;22。
一张桌子可坐2+2×1=4人,2张桌子拼起来可坐2+2×2=6人,3张桌子拼起来可坐2+2×3=8人,由此可以发现规律,n张桌子拼起来可坐2+2×n=2n+2人,将38和10代入求解即可。
15.4:3;16:9
解:小圆周长:大圆周长
=(3×2×π)∶(4×2×π)
=6π∶8π
=3∶4;
小圆面积:大圆面积
=(32×π)∶(42×π)
=9π∶16π
=9∶16;
故答案为:4:3;16:9。
根据圆的周长公式:C=2πr,面积公式:S=πr2,把数据分别代入公式求出大小圆的周长、面积,进而求出它们的比即可。
16.13
解:每种花色各选3张,一共12张,再任取一张即可,
所以从中任意抽牌,最少要抽13张牌,才能保证有4张牌是同一花色的;
故答案为:13。
根据抽屉原理,如果每个抽屉代表一个集合,每一个物体就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定至少有一个集合里有两个元素,每种花色各选3张,一共12张,可见抽12张牌不能保证有4张牌是同一花色的.如果抽13张牌,由于花色只有4种,其中必有一种多于3张,即必有4张牌同一花色。
17.8;4;5
解:根据第一个和第三个图形可知,2a+b=5b,则2a=4b,a=2b;
根据第二个和第三个图形可知,4c=5b,c=b;
a:b:c=2b:b:b=8b:4b:5b=8:4:5。
故答案为:8;4;5。
因为三个图形周长相等,根据第一个和第三个图形的周长确定a=2b;根据第二个和第三个图形可知c=b,由此写a、b、c的比,化简后写出最简整数比即可。
18.30;120
解:60÷2=30(平方厘米)
30×4=120(平方厘米)
故答案为:30;120。
根据等底等高的三角形的面积是平行四边形的面积的一半,由此用平行四边形的面积除以2求出三角形的面积,再根据图形放大与缩小的意义,沿将这个三角形按2∶1放大,其底和高就都扩大到原来的2倍,面积比原来扩大到原来的2×2=4倍,即用原来的面积乘4就是扩大后的面积。
19.a+3;3
解:可欣的年龄+3=梦琪的年龄,
今年梦琪的年龄是a+3岁,5年后,梦琪比可欣大3岁;
故答案为:a+3;3。
根据题意,可欣的年龄+3=梦琪的年龄,两人的年龄差是不变的,梦琪比可欣大3岁,5年后,梦琪还是比可欣大3岁,据此解答。
20.12;15;75
解:=3÷4=(3×3)÷(4×3)=9÷12;
=3:4=(3×5)÷(4×5)=15:20;
=3÷4=0.75=75%;
故答案为:12;15;75。
根据分数与除法的关系,=3÷4,再根据商不变的性质,被除数、除数都乘3就是9÷12;根据比与分数的关系,=3:4,再根据比的基本性质,比的前、后项都乘5就是15:20;=3÷4=0.75,把0.75的小数点向右移动两位,添上百分号就是75%。
21.12
解:设B点的位置在x厘米处。
12:9=16:x
12x=16×9
x=144÷12
x=12
故答案为:12。
AC与AB的长度比的比值是不变的,因此设B点的位置在x厘米处,根据两次拉伸皮筋AC与AB的长度比不变列出比例解答即可。
22.1:4
解:2πr=2πR×
r=R
r:R=1:4
故答案为:1:4。
圆的周长=扇形的弧长,就此解答即可。
23.111;26
解:5+12+21+11+35+27
=17+21+11+35+27
=38+11+35+27
=49+35+27
=84+27
=111;
111-1-15-20-24-25
=110-15-20-24-25
=95-20-24-25
=75-24-25
=51-25
=26。
故答案为:111;26。
每一环6个数之和=任意一环中的6个数相加;其中一环中还差的数=每一环6个数之和-其余的5个数。
24.18;11;7
解:18=11+7。
故答案为:18;11;7。
一个数既是18的倍数,又是18的因数,则这个数是18,18=11+7。
25.(20a+b);800
解:20×a+b=(20a+b)(棵);
当a=10,b=600时
20a+b
=20×10+600
=200+600
=800(棵)。
故答案为:(20a+b);800。
苹果树和梨树一共的棵数=苹果树的行数×平均每行苹果树的棵数+梨树的棵数;然后把a=10,b=600代入计算。
26.210
解:150÷5=30
(150+30×7+30×9)÷3
=(150+210+270)÷3
=630÷3
=210。
故答案为:210。
A、B和C三个数的平均数=A、B、C三个数的和÷3;其中,B、C代表的数=A÷A占的份数×B、C分别占的份数。
27.12
解:60÷5=12(颗)。
故答案为:12。
封闭图形的植树问题,棵数=间隔数,所以这条项链上共有水晶的颗数=项链的总长÷间距。
28.62.5;100;72;0.625
解:=5÷8=0.625=62.5%;
=(5×20)÷(8×20)=100÷160;
==;
所以=62.5%=100÷160=0.625。
故答案为:62.5;100;72;0.625。
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
29.7850000000;78.5
解:七十八亿五千万写作:7850000000;
7850000000÷100000000=78.5亿。
故答案为:7850000000;78.5。
亿以上的数的写法,先看这个数有几级,再从最高级写起,哪个数位上一个单位也没有,就在那个数位上写0;用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
30.25;(4n+1)
解:4×6+1
=24+1
=25(枚)
图n要摆(4n+1)枚棋子。
故答案为:25;(4n+1)。
图n需要棋子的枚数=(4n+1)枚,然后代入计算即可。
31.18;54
解:9×6×
=54×
=18(立方分米)
18×3=54(立方分米)。
故答案为:18;54。
圆锥的体积=底面积×高×;与它等底等高的圆柱的体积=圆锥的体积×3。
32.5
解:设圆的半径是r厘米。
3.14×r2=15.7×r
3.14×r=15.7
r=15.7÷3.14
r=5。
故答案为:5。
依据等量关系式:π×半径2=长方形的长×宽,列方程,求出半径的值。
33.4
解:假设全部是1元纸币,则5元纸币的张数是:
(25-9×1)÷(5-1)
=(25-9)÷4
=16÷4
=4(张)。
故答案为:4。
假设全部是1元纸币,则5元纸币的张数=(总钱数-1元×总张数)÷(5-1)。
34.360
解:40÷(10-9)×9
=40÷1×9
=40×9
=360(个)。
故答案为:360。
徒弟每小时生产零件的个数=李师傅每小时比徒弟多生产零件的个数÷师徒二人份数的差×徒弟生产的份数。
35.772000000;七亿七千二百万;8
解:这个数写作:772000000;读作:七亿七千二百万
772000000≈8亿。
故答案为:772000000;七亿七千二百万;8。
最大的一位质数是7,最小的质数是2,其余各位上的数字都是0,这个数是772000000;亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零;用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
36.9.5
解:10-0.5=9.5(千克)。
故答案为:9.5。
红星面粉厂生产的一种袋装面粉,注明“净含量10kg±0.5kg”,表示质量最多=10+0.5,质量最少=10-0.5。
37.(5n+1)
解:5×n+1=(5n+1)(根)。
故答案为:(5n+1)。
摆n个连着的正六边形需要小棒的根数=5×连着的正六边形的个数+1根。
38.314;21.5
解:20÷2=10(厘米)
3.14×102
=3.14×100
=314(平方厘米)
(20×20-314)÷(20×20)
=(400-314)÷400
=86÷400
=21.5%。
故答案为:314;21.5。
这个圆的面积=π×半径2;剩下的面积占木板面积的分率=(正方形的边长×边长-圆的面积)÷(正方形的边长×边长)。
39.32;12;80;八
解:4÷5=(4×8):(5×8)=32:40;
4÷5==;
4÷5=0.8=80%=八折;
所以32:40=4÷5==80%=八折。
故答案为:32;12;80;八。
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;百分之几十就是几折。
40.80
解:8*8=(8+2)×8=10×8=80。
故答案为:80。
“*”表示的运算是“*”前面的数加2,再用和乘“*”后面的数。
41.36
解:9.42÷3.14=3(分米)
3×6×2=18×2=36(平方分米)
故答案为:36。
底面周长÷3.14=底面直径,底面直径×高=一个切面的面积,一个切面的面积×2=2个切面的面积。
42.26
解:6和8的最小公倍数是24
24+2=26(个)
这袋苹果最少有26个
故答案为:26。
6和8的最小公倍数+2个苹果=这袋苹果最少的个数。
43.20
解:4÷(4+1)=4÷5=80%;1-80%=20%;
商场优惠了20%。
故答案为:20。
买的瓶数÷实际得到的瓶数=打的折扣,1-打的折扣=优惠的折扣。
44.反;正
解:底×高÷2=三角形的面积(一定),三角形的面积一定,它的底和高成反比例;
Y=8X
=8(一定),如果Y=8X,那么X和Y成正比例。
故答案为:反;正。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
45.5000
解:100000×2×2.25%
=200000×2.25%
=5000(元)。
故答案为:5000。
到期时妈妈获得利息=本金×年利率×妈妈存定期的时间。
46.6:5
解::=12:10=6:5。
故答案为:6:5。
根据分数乘法的意义可知,甲店的销量×=乙店的销量×,可以把甲看作,乙看作,由此写出甲、乙两个店销量的比并写出最简整数比即可。
47.37.68
解:3.14×32×4×
=3.14×36×
=3.14×12
=37.68(cm3)
故答案为:37.68。
圆锥的体积=底面积×高×。以直角三角形的哪条直角边为轴,旋转一周后得到的圆锥的高就是这条直角边,另一条直角边就是圆锥的底面半径。
48.37.5
解:150÷(3+1)
=150÷4
=37.5(cm3)
故答案为:37.5。
放入圆柱和圆锥后排出水的体积就是圆柱和圆锥的体积和,体积和是150立方厘米。等底等高的圆柱体积是圆锥体积的3倍,圆锥的体积是1份,则这个圆柱的体积就是3份,由此用体积和除以份数和即可求出每份的体积,也就是圆锥的体积。
49.(400﹣20a);120
解:商店原有400个足球,卖出a箱,每箱20个,商店还剩下(400-20a)个足球;当a=14时,商店还剩下:400-20×14=400-280=120(个)。
故答案为:(400-20a);120。
用每箱的个数乘卖出的箱数表示出卖出的个数,用总数减去卖出的个数表示出还剩下的足球个数即可。把式子中的a代换成14求出还剩下的足球个数即可。
50.20:1
解:10厘米=100毫米,100:5=20:1。
故答案为:20:1。
图上距离:实际距离=比例尺,把图上距离换算成毫米,写出图上距离与实际距离的比并化成后项是1的比即可。
小升初数学备考真题分类汇编(湖北地区专版)
试卷说明:
本试卷试题精选自湖北省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合湖北省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、填空题
1.(2024·石首)2024年巴黎奥运会开幕式的日期很特别,表示月份的数是一位数中最大的质数;表示日子的数是一个两位数,十位上是最小的质数,个位上是3的倍数而且是偶数。巴黎奥运会开幕式的日期是 。
2.(2024·沙市区)2024年五一期间,荆州古城、荆州博物馆、方特等地人山人海。据荆州文旅局统计,全市A级旅游景区共接待游客867600人次,横线上的数改写成用“万人”作单位的数是 万人次;综合收入达五亿六千零八万元,横线上的数写作 。
3.(2024·石首)有若干名教师和医生,他们的平均年龄为40岁,其中教师的平均年龄为35岁,医生的平均年龄为50岁,教师人数与医生人数的比是 。
4.(2024·襄城)有一组图形,它的排列规律如图。第5个图形中有 个三角形,第n个图形中有 个三角形。
5.(2024·建始)学校组织研学旅行活动,五年级共有350名同学参加,至少有 人在同一个月过生日。在开展“找次品”比赛活动中,老师拿来13个乒乓球,有12个质量相同,另有一个较轻一点,如果用天平称,至少称 次保证能找出这个乒乓球。
6.(2024·阳新)如果规定:1!=1;2!=1×2;3!=1×2×3;4!=1×2×3×4。那么= ,= 。(写出得数)
7.(2024·黄陂)妈妈把10000元钱存入银行,定期一年,年利率是2.25%,到期时妈妈共可以取回 元,我用数量关系式是 求利息的.
8.(2024·阳新)已知自然数x、y满足“x÷y=50……4”,当y最小时,x= 。
9.(2024·阳新)750ml= L
平方千米= 公顷
6时24分= 时
10.(2024·黄陂)如图,一个立体图形从正面看到的图形是A,从上面看到的图形是B,这个立体图形的体积是 立方厘米;如果用一个长方体盒子包装它,这个盒子的容积至少是 立方厘米。
11.(2024·黄陂)转化思想作为重要的数学思想方法之一,在我们的学习生活中,无处不在。一个瓶子里装有一些水(如图),根据图中标出的数据,可得瓶中水的体积占瓶子容积的 。
12.(2024·黄陂)一个笔记本a元,一支钢笔b元,一个笔记本比一支钢笔贵 元,买5个笔记本和15支钢笔共 元。
13.(2024·黄陂) :24= =14÷ =0.875= %
14.(2023·浠水)如图,一张桌子可坐4人,2张桌子拼起来可坐6人,3张桌子拼起来可坐8人。像这样 张桌子拼起来可坐38人,10张桌子可坐 人。
15.(2023·浠水)小圆的半径是3厘米,大圆的半径是4厘米,大圆和小圆周长的比是 ,面积的比是 。
16.(2023·浠水)一副扑克牌有4种花色(大小王除外),每种花色有13张,从中任意抽牌,最少要抽 张牌,才能保证有4张牌是同一花色的。
17.(2024·沙市区)如下图所示三个图形的周长相等,那么a:b:c= : : 。
请写出你的推理过程。
18.(2023·浠水)一个平行四边形和一个三角形等底等高。已知平行四边形的面积是60平方厘米,那么三角形的面积是 平方厘米。将这个三角形按2:1放大,得到的三角形的面积是 平方厘米。
19.(2023·浠水)今年可欣a岁,梦琪比她大3岁,那么今年梦琪年龄是 岁。5年后,梦琪比可欣大 岁。
20.(2023·浠水)9÷ == :20= %。
21.(2023·涟水)笑笑沿着直尺的方向将橡皮筋拉直(如图)。如果A点的位置固定不变,将橡皮筋拉长,使C点的位置在16cm处,那么B点的位置在 cm处。
22.(2023·涟水)在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型(如图)。如果圆的半径为r,扇形半径为R,那么r:R= 。
23.(2023·襄城)如图,“杨辉聚六图”是由我国南宋杰出的数学家杨辉所研究出来的,它是由1,2,3,……,35,36无重复排列而成的图形,“杨辉聚六环”其每一环6个数之和均相等,则这个和为 ,其中一环中还差个数,它是 。
24.(2023·襄城)一个数既是18的倍数,又是18的因数,把这个数写成两个质数相加的形式: = + 。
25.(2023·襄城)果园里有苹果树a行,每行有20棵;梨树有b棵,苹果树和梨树一共有 棵,当a=10,b=600时,梨树和苹果树一共有 棵。
26.(2023·襄城)A、B、C三个数的比是5:7:9,如果A=150,则A、B和C三个数的平均数是 。
27.(2023·襄城)一条项链长60cm,每隔5cm有一颗水晶.这条项链上共有 颗水晶.
28.(2023·襄城) = %= ÷160= = (填小数)
29.(2023·襄城)数据显示,2023年“五一”假日期间,某市旅游总收入七十八亿五千万元,写作 元,改写成以“亿”为单位的数是 亿元。
30.(2023·梁子湖)观察图,想一想,填一填。用棋子摆方阵,那么图6要摆 枚棋子,图n要摆 枚棋子。
31.(2023·梁子湖)一个圆锥的底面积是9dm2,高是6dm,它的体积是 dm3,与它等底等高的圆柱的体积是 dm3。
32.(2023·梁子湖)如图,圆的面积与长方形的面积相等。已知长方形的长是15.7cm,圆的半径是 cm。
33.(2023·梁子湖)轩轩的存钱罐里有5元和1元的纸币共9张,总共25元。他有 张5元纸币。
34.(2023·梁子湖)李师傅和徒弟一起生产一种零件。李师傅每小时比徒弟多生产40个,已知两人每小时生产的零件个数的比是10:9,徒弟每小时生产 个零件。
35.(2023·梁子湖)一个数的亿位和千万位上的数字都是一位数中最大的质数,百万位上的数字是最小的质数,其余各位上的数字都是0,这个数写作 ,读作 ,省略亿位后面的尾数约是 亿。
36.(2023·梁子湖)红星面粉厂生产的一种袋装面粉,注明“净含量10kg±0.5kg”,李叔叔买了一袋这样的面粉,质量最少是 kg。
37.(2023·崇阳)按如图的方式摆下去,摆n个连着的正六边形需要 根小棒。
38.(2023·崇阳)在一个边长为20cm的正方形木板上,锯掉一个最大的圆,这个圆的面积是 cm2,剩下的面积占木板面积的 %。
39.(2023·崇阳) :40=4÷5= = %= 折。
40.(2023·广水)我们学过“+、﹣、×、÷”四种运算。若规定“*”是一种新运算,A*B表示(A+2)B。如:3*5=(3+2)×5=25。那么8*8= 。
41.(2023·广水)把一个底面周长是9.42dm,高6dm的圆柱,沿底面直径切成两个半圆柱后,表面积共增加了 dm2。
42.(2023·广水)妈妈买回一袋苹果,每6个装一盘或每8个装一盘都余2个,这袋苹果最少有 个。
43.(2023·广水)一种果汁,零售每瓶5元,商场促销:“买四赠一”。商场优惠了 %。
44.(2023·崇阳)若三角形的面积一定,它的底和高成 比例,如果Y=8X,那么X和Y成 比例。
45.(2023·崇阳)今年妈妈把10万元钱存入银行,存定期二年,年利率是2.25%,到期时妈妈获得利息 元。
46.(2024·沙市区)甲店销售量的恰好等于乙店销售量的,则甲、乙两店销售量的最简整数比是 。
47.(2024·沙市区)如下图,三角形ABC以直角边AC所在的直线为轴旋转一周,所形成的立体图形的体积是 cm3。
48.(2024·沙市区)如下图,李老师用下面装置做排水实验:他把等底等高的圆锥和圆柱体铁块全部浸入水中,圆锥的体积是 cm3。
49.(2024·沙市区)商店原有400个足球,卖出a箱,每箱20个,商店还剩下 个足球;当a=14时,商店还剩下 个足球。
50.(2024·沙市区)中国嫦娥六号探测器上有一个精密零件长5毫米,画在图纸上是10厘米,这幅图的比例尺是 。
答案解析部分
1.7月26日
解:月份是7月,日期是26日,则巴黎奥运会开幕式的日期是7月26日。
故答案为:7月26日。
月份是一位数中最大的质数是7;十位上是最小的质数2,个位上的数=3×2=6。巴黎奥运会开幕式的日期是7月26日。
2.86.76;560080000
解:867600=86.76万;五亿六千零八万写作:560080000。
故答案为:86.76;560080000。
在万位后面点上小数点,去掉末尾的0,在后面加上万字即可改写成用万作单位的数。写数时从高位到低位按照数位顺序写,有几个计数单位就在相应的数位上写几,没有就写0。
3.2:1
解:设教师人数为x,医生人数为y。
40(x + y) = 35x + 50y
40x + 40y = 35x + 50y
5x = 10y
x =2y,所以,教师人数与医生人数的比是2:1。
故答案为:2:1。
首先,我们设立未知数,设教师人数为x,医生人数为y。然后,根据题目给出的平均年龄信息,我们可以建立一个方程。接着,我们对方程进行化简和求解,得到教师人数与医生人数的比例关系。
4.16;4(n﹣1)
解:第5个图形中:(5-1)×4=16(个)。
第n个图形中有4(n-1)个三角形。
故答案为:16;4(n-1)。
第二个图形中有4个三角形,第三个图中有(2×4)个三角形,三角形个数=(图形个数-1)×4,由此计算第5个图形中三角形的个数,并用含有字母的式子表示第n个图形中三角形的个数。
5.30;3
解:第一问:350÷12=29……2,29+1=30(人),至少有30人在同一个月过生日。
第二问:把13个乒乓球分成4、4、5共三份,第一次:在天平两端各放4个乒乓球,如果平衡,较轻的就在剩下的5个中;如果不平衡,上升那端的4个中有一个是轻的。第二次:如果在5个中,天平两端各放2个,如果平衡,剩下的那个就是轻的;如果不平衡,上升那端的2个中有1个是轻的,再称第三次就能找出轻的;如果在4个中,天平两端各放2个,上升那端有1个是轻的,这样再称第三次就能找出轻的。
故答案为:30;3。
第一问:用350除以12求出商是29,余数是2,从最不利的情况考虑,每个月都有29人生日,那么剩下的2人无论在哪个月出生都至少有30人在同一个月过生日;
第二问:把物品平均分成3份,如果不能平均分也要使其中一份比另外两份多或少1个,这样称一次就能把次品缩小到最小范围;按照这样的方法确定称的次数即可。
6.;2024
解: ==;
==2024。
故答案为:;2024。
依据的新定义分别写出分子、分母相乘的形式,然后再约分。
7.10225;利息=本金×利率×时间
解:10000×1×2.25%+10000
=225+10000
=10225(元)
利息=本金×利率×时间。
故答案为:10225;利息=本金×利率×时间。
到期时妈妈共可以取回的钱数=利息+本金,其中,利息=本金×利率×时间。
8.254
解:50×(4+1)+4
=250+4
=254。
故答案为:254。
在有余数的除法中,除数最小=余数+1;此时,被除数=商×除数+余数。
9.0.75;40;6.4
解:750÷1000=0.75(升)
×100=40(公顷)
6+24÷60
=6+0.4
=6.4(时)。
故答案为:0.75;40;6.4。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
10.12.56;48
解:3.14×22×3÷3
=12.56×3÷3
=12.56(立方厘米)
2×2=4(厘米)
4×4×3
=16×3
=48(立方厘米)。
故答案为:12.56;48。
这个立体图形的体积=圆锥的体积=π×半径2×高÷3;这个盒子的容积至少=长×宽×高;其中,长=宽=底面圆的直径,高=圆锥的高。
11.
解:7÷(7+18)
=7÷25
=。
故答案为:。
瓶中水的体积占瓶子容积的分率=正放时水的高度÷(正放时水的高度+倒放时水的高度) 。
12.(a-b);(5a+15b)
解:a-b=(a-b)(元);
5a+15b=(5a+15b)(元)。
故答案为:(a-b);(5a+15b)。
一个笔记本比一支钢笔贵的钱数=笔记本的单价-钢笔的单价;买5个笔记本和15支钢笔的总钱数=笔记本的单价×笔记本的数量+钢笔的单价×钢笔的数量。
13.21;7;16;87.5
解:0.875×24=21;
0.875×8=7;
14÷0.875=16;
0.875=87.5%;
所以21:24==14÷16=87.5%。
故答案为:21;7;16;87.5。
比的前项=比值×比的后项,分子=分母×分数值,除数=被除数÷商;小数化成百分数,把小数的小数点向右移动两位,再加上百分号。
14.18;22
解:一张桌子可坐2+2×1=4人,
2张桌子拼起来可坐2+2×2=6人,
3张桌子拼起来可坐2+2×3=8人,
·····
n张桌子拼起来可坐2+2×n=2n+2人,
2n+2=38,
n=18,
2×10+2=22(人);
故答案为:18;22。
一张桌子可坐2+2×1=4人,2张桌子拼起来可坐2+2×2=6人,3张桌子拼起来可坐2+2×3=8人,由此可以发现规律,n张桌子拼起来可坐2+2×n=2n+2人,将38和10代入求解即可。
15.4:3;16:9
解:小圆周长:大圆周长
=(3×2×π)∶(4×2×π)
=6π∶8π
=3∶4;
小圆面积:大圆面积
=(32×π)∶(42×π)
=9π∶16π
=9∶16;
故答案为:4:3;16:9。
根据圆的周长公式:C=2πr,面积公式:S=πr2,把数据分别代入公式求出大小圆的周长、面积,进而求出它们的比即可。
16.13
解:每种花色各选3张,一共12张,再任取一张即可,
所以从中任意抽牌,最少要抽13张牌,才能保证有4张牌是同一花色的;
故答案为:13。
根据抽屉原理,如果每个抽屉代表一个集合,每一个物体就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定至少有一个集合里有两个元素,每种花色各选3张,一共12张,可见抽12张牌不能保证有4张牌是同一花色的.如果抽13张牌,由于花色只有4种,其中必有一种多于3张,即必有4张牌同一花色。
17.8;4;5
解:根据第一个和第三个图形可知,2a+b=5b,则2a=4b,a=2b;
根据第二个和第三个图形可知,4c=5b,c=b;
a:b:c=2b:b:b=8b:4b:5b=8:4:5。
故答案为:8;4;5。
因为三个图形周长相等,根据第一个和第三个图形的周长确定a=2b;根据第二个和第三个图形可知c=b,由此写a、b、c的比,化简后写出最简整数比即可。
18.30;120
解:60÷2=30(平方厘米)
30×4=120(平方厘米)
故答案为:30;120。
根据等底等高的三角形的面积是平行四边形的面积的一半,由此用平行四边形的面积除以2求出三角形的面积,再根据图形放大与缩小的意义,沿将这个三角形按2∶1放大,其底和高就都扩大到原来的2倍,面积比原来扩大到原来的2×2=4倍,即用原来的面积乘4就是扩大后的面积。
19.a+3;3
解:可欣的年龄+3=梦琪的年龄,
今年梦琪的年龄是a+3岁,5年后,梦琪比可欣大3岁;
故答案为:a+3;3。
根据题意,可欣的年龄+3=梦琪的年龄,两人的年龄差是不变的,梦琪比可欣大3岁,5年后,梦琪还是比可欣大3岁,据此解答。
20.12;15;75
解:=3÷4=(3×3)÷(4×3)=9÷12;
=3:4=(3×5)÷(4×5)=15:20;
=3÷4=0.75=75%;
故答案为:12;15;75。
根据分数与除法的关系,=3÷4,再根据商不变的性质,被除数、除数都乘3就是9÷12;根据比与分数的关系,=3:4,再根据比的基本性质,比的前、后项都乘5就是15:20;=3÷4=0.75,把0.75的小数点向右移动两位,添上百分号就是75%。
21.12
解:设B点的位置在x厘米处。
12:9=16:x
12x=16×9
x=144÷12
x=12
故答案为:12。
AC与AB的长度比的比值是不变的,因此设B点的位置在x厘米处,根据两次拉伸皮筋AC与AB的长度比不变列出比例解答即可。
22.1:4
解:2πr=2πR×
r=R
r:R=1:4
故答案为:1:4。
圆的周长=扇形的弧长,就此解答即可。
23.111;26
解:5+12+21+11+35+27
=17+21+11+35+27
=38+11+35+27
=49+35+27
=84+27
=111;
111-1-15-20-24-25
=110-15-20-24-25
=95-20-24-25
=75-24-25
=51-25
=26。
故答案为:111;26。
每一环6个数之和=任意一环中的6个数相加;其中一环中还差的数=每一环6个数之和-其余的5个数。
24.18;11;7
解:18=11+7。
故答案为:18;11;7。
一个数既是18的倍数,又是18的因数,则这个数是18,18=11+7。
25.(20a+b);800
解:20×a+b=(20a+b)(棵);
当a=10,b=600时
20a+b
=20×10+600
=200+600
=800(棵)。
故答案为:(20a+b);800。
苹果树和梨树一共的棵数=苹果树的行数×平均每行苹果树的棵数+梨树的棵数;然后把a=10,b=600代入计算。
26.210
解:150÷5=30
(150+30×7+30×9)÷3
=(150+210+270)÷3
=630÷3
=210。
故答案为:210。
A、B和C三个数的平均数=A、B、C三个数的和÷3;其中,B、C代表的数=A÷A占的份数×B、C分别占的份数。
27.12
解:60÷5=12(颗)。
故答案为:12。
封闭图形的植树问题,棵数=间隔数,所以这条项链上共有水晶的颗数=项链的总长÷间距。
28.62.5;100;72;0.625
解:=5÷8=0.625=62.5%;
=(5×20)÷(8×20)=100÷160;
==;
所以=62.5%=100÷160=0.625。
故答案为:62.5;100;72;0.625。
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
29.7850000000;78.5
解:七十八亿五千万写作:7850000000;
7850000000÷100000000=78.5亿。
故答案为:7850000000;78.5。
亿以上的数的写法,先看这个数有几级,再从最高级写起,哪个数位上一个单位也没有,就在那个数位上写0;用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
30.25;(4n+1)
解:4×6+1
=24+1
=25(枚)
图n要摆(4n+1)枚棋子。
故答案为:25;(4n+1)。
图n需要棋子的枚数=(4n+1)枚,然后代入计算即可。
31.18;54
解:9×6×
=54×
=18(立方分米)
18×3=54(立方分米)。
故答案为:18;54。
圆锥的体积=底面积×高×;与它等底等高的圆柱的体积=圆锥的体积×3。
32.5
解:设圆的半径是r厘米。
3.14×r2=15.7×r
3.14×r=15.7
r=15.7÷3.14
r=5。
故答案为:5。
依据等量关系式:π×半径2=长方形的长×宽,列方程,求出半径的值。
33.4
解:假设全部是1元纸币,则5元纸币的张数是:
(25-9×1)÷(5-1)
=(25-9)÷4
=16÷4
=4(张)。
故答案为:4。
假设全部是1元纸币,则5元纸币的张数=(总钱数-1元×总张数)÷(5-1)。
34.360
解:40÷(10-9)×9
=40÷1×9
=40×9
=360(个)。
故答案为:360。
徒弟每小时生产零件的个数=李师傅每小时比徒弟多生产零件的个数÷师徒二人份数的差×徒弟生产的份数。
35.772000000;七亿七千二百万;8
解:这个数写作:772000000;读作:七亿七千二百万
772000000≈8亿。
故答案为:772000000;七亿七千二百万;8。
最大的一位质数是7,最小的质数是2,其余各位上的数字都是0,这个数是772000000;亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个零;用“四舍五入”法求近似数,看需要保留的下一位数,是0~4舍去,是5~9向前一位进一。
36.9.5
解:10-0.5=9.5(千克)。
故答案为:9.5。
红星面粉厂生产的一种袋装面粉,注明“净含量10kg±0.5kg”,表示质量最多=10+0.5,质量最少=10-0.5。
37.(5n+1)
解:5×n+1=(5n+1)(根)。
故答案为:(5n+1)。
摆n个连着的正六边形需要小棒的根数=5×连着的正六边形的个数+1根。
38.314;21.5
解:20÷2=10(厘米)
3.14×102
=3.14×100
=314(平方厘米)
(20×20-314)÷(20×20)
=(400-314)÷400
=86÷400
=21.5%。
故答案为:314;21.5。
这个圆的面积=π×半径2;剩下的面积占木板面积的分率=(正方形的边长×边长-圆的面积)÷(正方形的边长×边长)。
39.32;12;80;八
解:4÷5=(4×8):(5×8)=32:40;
4÷5==;
4÷5=0.8=80%=八折;
所以32:40=4÷5==80%=八折。
故答案为:32;12;80;八。
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;百分之几十就是几折。
40.80
解:8*8=(8+2)×8=10×8=80。
故答案为:80。
“*”表示的运算是“*”前面的数加2,再用和乘“*”后面的数。
41.36
解:9.42÷3.14=3(分米)
3×6×2=18×2=36(平方分米)
故答案为:36。
底面周长÷3.14=底面直径,底面直径×高=一个切面的面积,一个切面的面积×2=2个切面的面积。
42.26
解:6和8的最小公倍数是24
24+2=26(个)
这袋苹果最少有26个
故答案为:26。
6和8的最小公倍数+2个苹果=这袋苹果最少的个数。
43.20
解:4÷(4+1)=4÷5=80%;1-80%=20%;
商场优惠了20%。
故答案为:20。
买的瓶数÷实际得到的瓶数=打的折扣,1-打的折扣=优惠的折扣。
44.反;正
解:底×高÷2=三角形的面积(一定),三角形的面积一定,它的底和高成反比例;
Y=8X
=8(一定),如果Y=8X,那么X和Y成正比例。
故答案为:反;正。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
45.5000
解:100000×2×2.25%
=200000×2.25%
=5000(元)。
故答案为:5000。
到期时妈妈获得利息=本金×年利率×妈妈存定期的时间。
46.6:5
解::=12:10=6:5。
故答案为:6:5。
根据分数乘法的意义可知,甲店的销量×=乙店的销量×,可以把甲看作,乙看作,由此写出甲、乙两个店销量的比并写出最简整数比即可。
47.37.68
解:3.14×32×4×
=3.14×36×
=3.14×12
=37.68(cm3)
故答案为:37.68。
圆锥的体积=底面积×高×。以直角三角形的哪条直角边为轴,旋转一周后得到的圆锥的高就是这条直角边,另一条直角边就是圆锥的底面半径。
48.37.5
解:150÷(3+1)
=150÷4
=37.5(cm3)
故答案为:37.5。
放入圆柱和圆锥后排出水的体积就是圆柱和圆锥的体积和,体积和是150立方厘米。等底等高的圆柱体积是圆锥体积的3倍,圆锥的体积是1份,则这个圆柱的体积就是3份,由此用体积和除以份数和即可求出每份的体积,也就是圆锥的体积。
49.(400﹣20a);120
解:商店原有400个足球,卖出a箱,每箱20个,商店还剩下(400-20a)个足球;当a=14时,商店还剩下:400-20×14=400-280=120(个)。
故答案为:(400-20a);120。
用每箱的个数乘卖出的箱数表示出卖出的个数,用总数减去卖出的个数表示出还剩下的足球个数即可。把式子中的a代换成14求出还剩下的足球个数即可。
50.20:1
解:10厘米=100毫米,100:5=20:1。
故答案为:20:1。
图上距离:实际距离=比例尺,把图上距离换算成毫米,写出图上距离与实际距离的比并化成后项是1的比即可。
同课章节目录
