2024-2025学年小升初数学备考真题分类汇编(湖北地区专版)专题2 单项选择题(含解析)
文档属性
| 名称 | 2024-2025学年小升初数学备考真题分类汇编(湖北地区专版)专题2 单项选择题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 326.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 07:45:06 | ||
图片预览




文档简介
专题2单项选择题-2023-2024学年
小升初数学备考真题分类汇编(湖北地区专版)
试卷说明:
本试卷试题精选自湖北省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合湖北省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
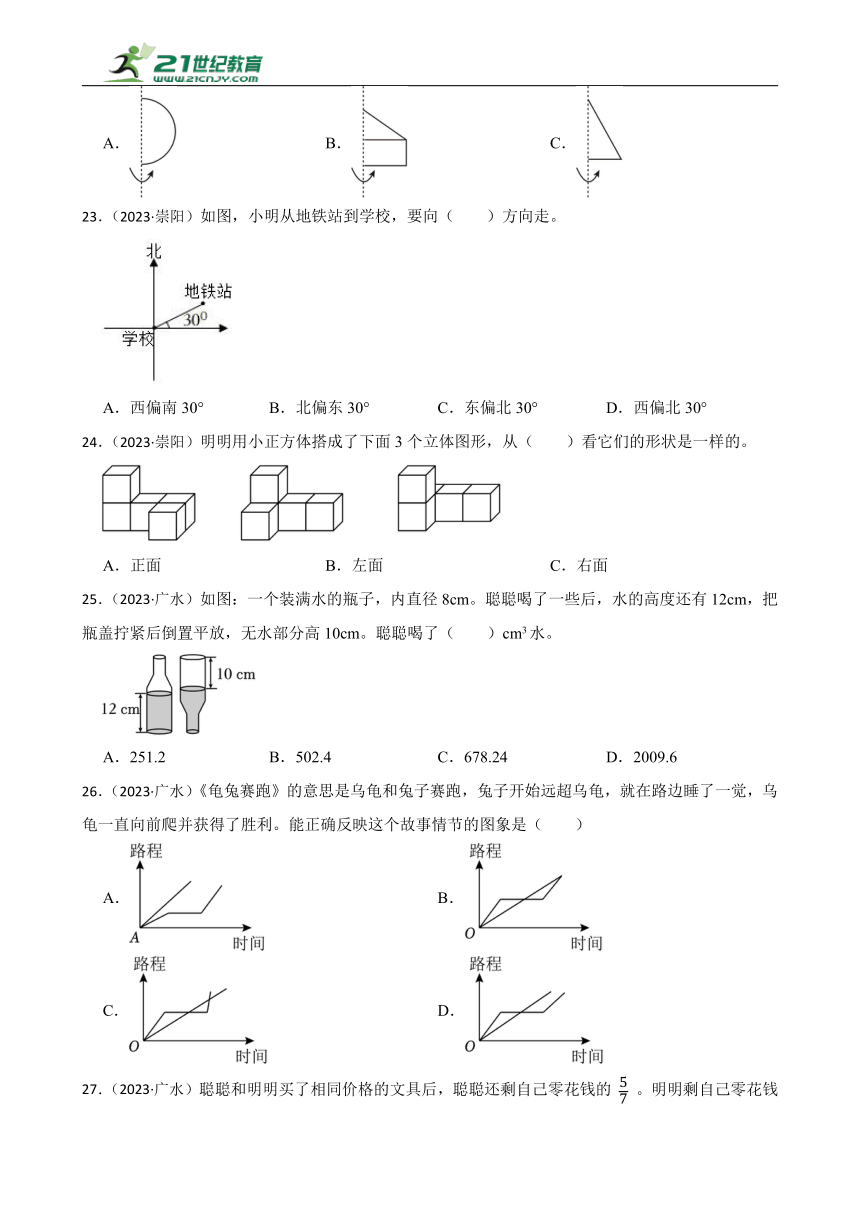
1.(2024·沙市区)如下图为甲、乙两辆汽车从A地到B地行驶的路程与相应时间关系的图像,下列关于图像描述错误的是( )
A.两辆汽车行驶的路程和时间都成正比例关系。
B.从A地到B地大约360千米,甲车从A地到B地大约需要4小时。
C.乙车4小时大约行驶了180千米。
D.从图像上看乙车的速度比甲车快。
2.(2024·襄城)旋转得到4个立方体,其中体积最大的是( )
A. B.
C. D.
3.(2024·沙市区)如下图,沙北实验学校组建了两个社团,下面说法正确的是( )
A.科学组女生人数和艺术组男生一样多。
B.两个小组的人数同样多。
C.艺术组里女生多,科学组里男生多。
D.艺术组女生人数比科学组男生多。
4.(2024·沙市区)下列各数量关系中,成正比例关系的是( )
A.修一条路,已修的米数和未修的米数。
B.圆锥的体积一定,它的底面积和高。
C.看一本书,每天看的页数和看的天数。
D.圆的周长和它的半径。
5.(2024·襄城)苗苗家在笑笑家北偏东40°方向上,那么笑笑家在苗苗家( )
A.东偏南40° B.北偏西50° C.南偏西40° D.西偏北50°
6.(2024·沙市区)如下图所示,阴影部分的面积是大圆面积的,是小圆面积的,那么大圆和小圆的面积比是( )
A.4:3 B.3:4 C.5:4 D.4:5
7.(2024·沙市区)体育老师对六年级同学进行跳绳测试,如果以每分钟跳80个为合格,王明每分钟跳90个,记作+10。张兰的成绩记作﹣5,则她实际跳了( )个。
A.75 B.85 C.90 D.95
8.(2024·石首)虚线框中与左侧圆锥体积相等的图形有( )个。
A.0 B.1 C.2 D.3
9.(2024·石首)如下图,如果△ABC的顶点B的位置用数对(1,1)表示,顶点C的位置用数对(4,1)表示,那么将这个△ABC绕点C顺时针转90°,顶点A旋转到点A',点A'的位置用数对( )表示。
A.(6,4) B.(4,6) C.(7,3) D.(4,5)
10.(2024·石首)晓晓在探究图形面积和周长之间的关系时,画了如下图四幅图,其中空白部分与阴影部分的周长相等但面积不相等的是图( )
A. B.
C. D.
11.(2023·硚口模拟)对于“米”理解,下面选项中( )是错误的.
A.等于9厘米 B.相当于1米的
C.相当于1米的9% D.可以改写成9%
12.(2024·石首)一种头饰在甲、乙、丙三个商店销售时原价都是每个6元,现在这三个商店分别以不同的方式促销。甲商店打八五折;乙商店购买商品满50元打八折;丙商店买3送1。东东要买8个这种头饰,想花钱最少,应该到( )去买。
A.甲商店 B.乙商店
C.丙商店 D.哪个商店都一样
13.(2024·石首)能表示a>b的式子是( )
A.a:b=1 B.<(c≠0)
C.>1 D.b﹣a=1
14.(2024·石首)晓晓想用计算器计算900÷15,他错误地输入了900÷5,接下来,下面( )的做法可以弥补他的错误。
A.乘3 B.除以10 C.除以3 D.加上3
15.(2024·石首)往350g含糖率为25%的糖水中加入10g糖和10g水,这时糖水中的含糖率( )
A.大于25% B.等于25% C.小于25% D.无法确定
16.(2024·黄陂)六(1)班有36名同学,按学号依次轮流当值日班长,这学期有22周,每人至少轮到 ( )次。
A.2 B.3 C.4 D.5
17.(2023·浠水)小丽想研究成年人每天不同时段的体温变化情况,她记录了本周爸爸和妈妈在相应五个不同时段的体温,她选择用( )统计图来呈现爸爸和妈妈的体温数据比较适合。
A.复式条形 B.复式折线 C.扇形 D.单式条形
18.(2023·浠水)有甲乙两根绳子,甲剪去全长的 ,乙剪去 米,两根绳子都还剩 米。那么原来甲乙两根绳子的长度相比,( )。
A.甲绳长 B.乙绳长
C.两绳长度相等 D.无法比较
19.(2023·浠水)把一个数的小数点先向右移动两位,再把得到的数缩小到它的 后是3.6,原数是( )。
A.36 B.3.6 C.0.36 D.360
20.(2023·梁子湖)五月一日李阿姨开车从家到省博物馆玩,如图是汽车行驶的时间和路程的变化情况。她上午9时从家出发,汽车在途中停车加油一次。下面表述中不正确的是( )
A.汽车行驶到一半路程时,停车加油10分钟
B.路上一共用了75分,上午10时15分到达省博物馆
C.汽车加油前后的速度一样快
D.加油后汽车行驶的速度是45千米/时
21.(2023·梁子湖)用5个大小相等的小正方体搭成下面两个立体图形,从( )看这两个立体图形所看到的图形是完全一样的。
A.正面 B.左面 C.上面
22.(2023·梁子湖)下面选项中以虚线为轴旋转一周,( )能得到。
A. B. C.
23.(2023·崇阳)如图,小明从地铁站到学校,要向( )方向走。
A.西偏南30° B.北偏东30° C.东偏北30° D.西偏北30°
24.(2023·崇阳)明明用小正方体搭成了下面3个立体图形,从( )看它们的形状是一样的。
A.正面 B.左面 C.右面
25.(2023·广水)如图:一个装满水的瓶子,内直径8cm。聪聪喝了一些后,水的高度还有12cm,把瓶盖拧紧后倒置平放,无水部分高10cm。聪聪喝了( )cm3水。
A.251.2 B.502.4 C.678.24 D.2009.6
26.(2023·广水)《龟兔赛跑》的意思是乌龟和兔子赛跑,兔子开始远超乌龟,就在路边睡了一觉,乌龟一直向前爬并获得了胜利。能正确反映这个故事情节的图象是( )
A. B.
C. D.
27.(2023·广水)聪聪和明明买了相同价格的文具后,聪聪还剩自己零花钱的 。明明剩自己零花钱75%,聪聪和明明原来的零花钱相比,( )
A.聪聪比明明多 B.明明比聪聪多
C.一样多 D.无法比较
28.(2023·广水)把一些规格相同的杯子叠起来(如图),4个杯子叠起来高20厘米,6个杯子叠起来高26厘米。n个杯子叠起来的高度可以用下面( )的关系式来表示。
A.6n﹣10 B.3n+11 C.6n﹣4 D.3n+8
29.(2023·广水)和0.2表示的意思相同的数是( )
A. B.2 C. D.
30.(2023·崇阳)下面说法错误的有( ) 个。
①圆的周长和直径成正比例
②20%去掉百分号大小不变
③小数点的后面添上或去掉0,小数大小不变
④半圆有无数条对称轴
A.1 B.2 C.3 D.4
31.(2023·黄梅模拟)某机械加工车间,完成了一批同规格零件的加工工作。这种零件的标准外直径是585mm.质检部门在抽检这批零件时,为了记录每个抽检零件外直径与标准的误差,把1号零件外直径记作+2mm,那么2号零件外直径记作( )
A.+582mm B.+3mm C.-582mm D.-3mm
32.(2023·硚口模拟)比的前项扩大原来的3倍,后项缩小为原来的,比值将( )
A.扩大为原来的9倍 B.缩小为原来的
C.扩大为原来的3倍 D.缩小为原来的
33.(2023·硚口模拟)下面哪一种情况选用扇形统计图更合适?( )
A.运动员一周训练的成绩变化记录
B.商场各种商品的销售情况
C.李老师家每月各项生活费用与家庭总收入的关系
D.六年级男、女生身高统计情况
34.(2023·硚口模拟)直角三角形中,一个锐角与直角的度数比是4:15,则两个锐角的度数比( )
A.4:5 B.4:11 C.11:15 D.15:11
35.(2023·硚口模拟)陈老师晚上8点从北京乘高铁到南京,3小时行驶了全程的,他到南京时看到的景象是( )
A.夜深入静 B.夕阳西下 C.艳阳高照 D.旭日东升
36.(2023·郧阳模拟)一长方形沿长和宽可以围成不同的圆柱。如图,圆柱A的侧面积( )圆柱B的侧面积。
A.等于 B.大于 C.小于 D.无法确定
37.(2023·郧阳模拟) :的前项乘,若使原来的比值不变,则后项应( )
A.乘 B.除以 C.乘 D.除以
答案解析部分
1.D
解:A:两辆汽车行驶的路程和时间都成正比例关系。正确;
B:从A地到B地大约360千米,甲车从A地到B地大约需要4小时。正确;
C:乙车4小时大约行驶了180千米。正确;
D:从图像上看乙车的速度比甲车慢。原来说法错误。
故答案为:D。
A:表示时间和路程的关系的图像都是经过原点的直线,是成正比例关系;
B:A地到B地的最远距离是360千米,所以两地的距离就是360千米;
C:乙车4小时对应的路程是180千米;
D:甲车到B地用了4小时,乙车到B地用了8小时,所以甲车速度比乙车快。
2.C
解:A:3.14×42×6=3.14×96;
B:3.14×42×9×=3.14×48;
C:3.14×42×8-3.14×42×4×=3.14×128-3.14×=106×3.14;
D:3.14×42×4+3.14×42×4×=3.14×64+3.14×=85×3.14;
所以体积最大的是106×3.14。
故答案为:C。
圆柱的体积=底面积×高,圆锥的体积=底面积×高×;
A:得到的是一个底面半径是4cm,高是6cm的圆柱;
B:得到的是两个底面半径都是4cm,高度和是9cm的圆锥;
C:得到的图形是一个底面半径4cm,高8cm的圆柱,减去一个底面半径4cm,高4cm的圆锥;
D:得到的图形是一个底面半径4cm,高4cm的圆柱,加上一个底面半径4cm,高4cm的圆锥。
3.C
解:艺术组:60%>40%,女生多;
科学组:60%>40%,男生多。
故答案为:C。
由于不知道艺术组和科学组各有多少人,所以无法比较两个组中男生和女生的人数;只有每个小组内的男生和女生可以比较多少。
4.D
解:A:已修的米数+未修的米数=这条路总长度,已修的米数和未修的米数不成比例;
B:底面积×高=圆锥体体积×3,所以它的底面积和高成反比例关系;
C:每天看的页数×看的天数=总页数,每天看的页数和看的天数成反比例关系;
D:圆的周长÷半径=圆周率×2,圆的周长和半径成正比例关系。
故答案为:D。
根据数量关系判断相关联的两个量的乘积一定还是商一定,如果乘积一定就成反比例关系;如果商一定就成正比例关系;否则不成比例。
5.C
解:苗苗家在笑笑家北偏东40°方向上,那么笑笑家在苗苗家南偏西40°方向。
故答案为:C。
观测点相反,夹角度数不变,那么方向刚好相反,所以苗苗家在笑笑家北偏东40°方向上,那么笑笑家在苗苗家南偏西40°方向上或西偏南50°方向。
6.C
解:阴影部分为1,则大圆和小圆的面积比是:(1÷):(1÷)=5:4。
故答案为:C。
假设阴影部分是1,根据分数除法的意义分别求出大圆和小圆的面积,然后写出面积的最简整数比即可。
7.A
解:80-5=75(个)
故答案为:A。
张兰的成绩记作-5,说明张兰比合格数少5个,因此用80减去5就是张兰实际跳的个数。
8.D
解:50×36÷3
=1800÷3
=600(立方厘米)
①50×12=600(立方厘米)
②150×4=600(立方厘米)
③150×12÷3
=1800÷3
=600(立方厘米)。
故答案为:D。
圆锥的体积=底面积×高÷3,圆柱的体积=底面积×高,长方体的体积=底面积×高,据此计算。
9.A
解: 点A'的位置在第6列,第4行,用数对(6,4)表示。
故答案为:A。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数。
10.B
解:A项:空白部分周长=阴影部分的周长,空白部分的面积=阴影部分的面积;
B项:空白部分周长=阴影部分的周长,空白部分的面积<阴影部分的面积;
C项:空白部分周长>阴影部分的周长,空白部分的面积=阴影部分的面积;
D项:空白部分周长>阴影部分的周长,空白部分的面积>阴影部分的面积。
故答案为:B。
A项:空白部分周长与阴影部分的周长相等,是圆的面积,空白部分的面积与阴影部分的面积相等,是半圆的面积;
B项:空白部分周长与阴影部分的周长相等,是正方形的边长×2+圆的周长÷4,空白部分的面积=正方形的面积-阴影部分的面积,阴影部分的面积=π×半径2÷4;
C项:三角形的面积=底×高÷2,空白部分周长>阴影部分的周长,空白部分的面积=阴影部分的面积=三角形面积的一半;
D项:三角形的面积=底×高÷2,空白部分周长>阴影部分的周长,空白部分的面积>阴影部分的面积。
11.D
解:A:×100=9厘米,此选项正确;
B:相当于1米的,此选项正确;
C:相当于1米的9%,此选项正确;
D:不能改写成9%,此选项错误。
故答案为:D。
百分数表示一个数是另一个数的百分之几,不表示实际的量,所以米不能用百分数表示。
12.C
解:甲商店:6×8×85%=40.8(元)
乙商店:6×8=48(元)
丙商店:8÷3=2(组)······2(个)
(8-2)×6
=6×6
=36(元)
48>40.8>36。
故答案为:C。
甲商店现价=原价×数量×折扣;乙商店现价=原价×数量;丙商店现价=原价×(要买的数量-送的数量)。
13.B
解:A项:a=b×1=b;
B项:<,分子相等,分母小的分数大,则a>b;
C项:>1 ,则b>a;
D项:b-a=1,则b=a+1,b>a。
故答案为:B。
A项:比的前项=比值×比的后项;
B项:同分子分数,分母小的就大;
C项:分子比分母大的分数大于1;
D项:被减数=差+件数,然后再比较a与b的大小。
14.C
解:15÷5=3,接下来他可以除以3。
故答案为:C。
被除数不变,除数缩小3倍,则被除数扩大3倍,要使结果不变,他可以除以3。
15.A
解:(350×25%+10)÷(350+10+10)
=97.5÷370
≈26%
26%>25%。
故答案为:A。
这时糖水的含糖率=(原来糖水的质量×原来的含糖率+加入糖的质量) ÷(原来糖水的质量+加入糖的质量+加入水的质量),然后与原来的含糖率比较大小。
16.A
解:36÷22=1(次)······14(周)
1+1=2(次)。
故答案为:A。
抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
17.B
解:要研究成年人每天不同时刻的体温变化情况,复式折线统计图可以同时反映爸爸和妈妈体温数据的增减变化情况;
故答案为:B。
条形统计图:从图中直观地看出数量的多少,便于比较;折线统计图:不仅能看清数量的多少,还能反映数量的增减变化情况;扇形统计图:清楚地看出各部分数量与总数量之间的关系;据此解答。
18.B
解: 原来甲乙两根绳子的长度相比 乙绳长。
故答案为:B。
甲剪去全长的 ,则甲绳长(米);乙绳长(米);。
19.A
解:原数是36。
故答案为:A。
“再把得到的数缩小到它的 ”,是小数点向左移动三位,本题的意思是这个数小数点向左动了一位,得到的是3.6,原数就是36。
20.C
解:30÷25=1.2(千米/分)
30÷(75-35)
=30÷40
=0.75(千米/分)
1.2>0.75,汽车加油前后的速度不同。
故答案为:C。
汽车加油前的速度=行驶的路程30千米÷所用的时间25分钟;汽车加油后的速度=行驶的路程30千米÷(到达的时间-加油后出发的时间),然后比较大小。
21.A
解:从正面看这两个立体图形所看到的图形是完全一样的。
故答案为:A。
这两个立体图形,从正面看,都是看到两层,下面一层三个正方形,上面一层一个正方形,并且左侧对齐。
22.C
解:以虚线为轴旋转一周,能得到。
故答案为:C。
以直角三角形的一条直角边为轴,旋转一周可以得到一个圆锥。
23.A
解:小明从地铁站到学校,要向西偏南30°方向走。
故答案为:A。
在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对;西南和东北相对,西北和东南相对。
24.A
解:从正面看它们的形状是一样的。
故答案为:A。
从正面看它们的形状是一样的,都是看到两层,下面一层三个正方形,上面一层一个正方形,并且左侧对齐。
25.B
解:8÷2=4(厘米)
3.14×4×4×12=50.24×10=502.4(立方厘米)
故答案为:B。
直径÷2=半径,π×底面半径的平方×无水部分高=聪聪喝的水的体积。
26.D
解:第四个折线统计图能正确反映这个故事情节的图象。
故答案为:D。
乌龟一直向前爬并获得了胜利。说明乌龟的图像是一条射线且比兔子用的时间少,B、C错误;兔子开始远超乌龟,说明开始兔子跑的路程比乌龟多,这一段路程,表示兔子的路程应该在乌龟的上面,据此可知A错误。
27.B
解:=5÷7≈0.71;75%=0.75;
0.75>0.71,明明比聪聪原来的零花钱多。
故答案为:B。
他们原来的钱数-花的钱数=剩下的钱数,花的钱数相同,剩下的钱数越多,说明他们原来的钱数越多,据此解答。
28.D
解:(26-20)÷(5-3)
=6÷2
=3(厘米)
20-3×3=20-9=11(厘米)
n个杯子叠起来的高度是11+3×(n-1)
=11+3n-3
=3n+8
故答案为:D。
6个杯子叠起来高-4个杯子叠起来高=上面2个间隔的高度,上面2个间隔的高度÷2=上面1个间隔的高度;20厘米-上面1个间隔的高度×3=杯子的高度;n个杯子叠起来的高度=杯子的高度+3×(杯子数-1),据此解答。
29.C
解:0.2=,和0.2表示的意思相同的数是。
故答案为:C。
小数化分数,小数点后有几位小数,就在1后面添几个0做分母,小数点去掉做分子。
30.C
解:①圆的周长÷直径=π(一定),圆的周长和直径成正比例,原题干说法正确;
②20%<20,原题干说法错误;
③小数的末尾添上或去掉0,小数大小不变,原题干说法错误;
④半圆有1数条对称轴,原题干说法错误。
故答案为:C。
①两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;
②20%去掉百分号后扩大了100倍;
③小数的基本性质:在小数的末尾添上0或者去掉0,小数的大小不变;
④依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;其中的这条直线就是对称轴。
31.D
解:587-2=585(mm),585-582=3(mm),那么2号零件外直径记作-3mm。
故答案为:D。
因为587mm比准确值多2mm,则准确值就是585mm,582mm低于585mm,那么低于标准尺寸的部分就记作负。
32.A
解:比的前项扩大原来的3倍,后项缩小为原来的,比值将扩大为原来的9倍。
故答案为:A。
比的前项扩大到原来的3倍,比值就扩大到原来的3倍;比的后项缩小为原来的,比值扩大3倍。所以比值会扩大到原来的9倍。
33.C
解:A:应选用折线统计图;
B:应选用条形统计图;
C:应选用扇形统计图;
D:应选用条形统计图。
故答案为:C。
条形统计图能清楚地表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图表示部分与整体之间的关系。
34.B
解:4:(15-4)=4:11。
故答案为:B。
因为直角三角形两个锐角的度数和是90°,所以可以用15减去4求出另一个锐角的份数,然后写出两个锐角的度数比即可。
35.A
解:3÷=4(小时),晚上8点过4小时是12点,此时看到的景象是夜深入静。
故答案为:A。
根据分数除法的意义,用3除以求出行完全程需要的时间,然后判断到达南京的时间。根据这个时间确定看到的景象即可。
36.A
解:圆柱A的侧面积=圆柱B的侧面积。
故答案为:A。
不管怎么围,侧面积都是这张长方形的纸,所以侧面积相等。
37.A
解:若使原来的比值不变,则后项应乘。
故答案为:A。
比的基本性质:比的前项和后项同时乘或除以(0除外)相同的数,比值不变。
小升初数学备考真题分类汇编(湖北地区专版)
试卷说明:
本试卷试题精选自湖北省各市,县2024、2023近两年六年级下学期小升初期末真题试卷,难易度均衡,适合湖北省各市,县的六年级学生小升初择校考、分班考等复习备考使用!
一、单选题
1.(2024·沙市区)如下图为甲、乙两辆汽车从A地到B地行驶的路程与相应时间关系的图像,下列关于图像描述错误的是( )
A.两辆汽车行驶的路程和时间都成正比例关系。
B.从A地到B地大约360千米,甲车从A地到B地大约需要4小时。
C.乙车4小时大约行驶了180千米。
D.从图像上看乙车的速度比甲车快。
2.(2024·襄城)旋转得到4个立方体,其中体积最大的是( )
A. B.
C. D.
3.(2024·沙市区)如下图,沙北实验学校组建了两个社团,下面说法正确的是( )
A.科学组女生人数和艺术组男生一样多。
B.两个小组的人数同样多。
C.艺术组里女生多,科学组里男生多。
D.艺术组女生人数比科学组男生多。
4.(2024·沙市区)下列各数量关系中,成正比例关系的是( )
A.修一条路,已修的米数和未修的米数。
B.圆锥的体积一定,它的底面积和高。
C.看一本书,每天看的页数和看的天数。
D.圆的周长和它的半径。
5.(2024·襄城)苗苗家在笑笑家北偏东40°方向上,那么笑笑家在苗苗家( )
A.东偏南40° B.北偏西50° C.南偏西40° D.西偏北50°
6.(2024·沙市区)如下图所示,阴影部分的面积是大圆面积的,是小圆面积的,那么大圆和小圆的面积比是( )
A.4:3 B.3:4 C.5:4 D.4:5
7.(2024·沙市区)体育老师对六年级同学进行跳绳测试,如果以每分钟跳80个为合格,王明每分钟跳90个,记作+10。张兰的成绩记作﹣5,则她实际跳了( )个。
A.75 B.85 C.90 D.95
8.(2024·石首)虚线框中与左侧圆锥体积相等的图形有( )个。
A.0 B.1 C.2 D.3
9.(2024·石首)如下图,如果△ABC的顶点B的位置用数对(1,1)表示,顶点C的位置用数对(4,1)表示,那么将这个△ABC绕点C顺时针转90°,顶点A旋转到点A',点A'的位置用数对( )表示。
A.(6,4) B.(4,6) C.(7,3) D.(4,5)
10.(2024·石首)晓晓在探究图形面积和周长之间的关系时,画了如下图四幅图,其中空白部分与阴影部分的周长相等但面积不相等的是图( )
A. B.
C. D.
11.(2023·硚口模拟)对于“米”理解,下面选项中( )是错误的.
A.等于9厘米 B.相当于1米的
C.相当于1米的9% D.可以改写成9%
12.(2024·石首)一种头饰在甲、乙、丙三个商店销售时原价都是每个6元,现在这三个商店分别以不同的方式促销。甲商店打八五折;乙商店购买商品满50元打八折;丙商店买3送1。东东要买8个这种头饰,想花钱最少,应该到( )去买。
A.甲商店 B.乙商店
C.丙商店 D.哪个商店都一样
13.(2024·石首)能表示a>b的式子是( )
A.a:b=1 B.<(c≠0)
C.>1 D.b﹣a=1
14.(2024·石首)晓晓想用计算器计算900÷15,他错误地输入了900÷5,接下来,下面( )的做法可以弥补他的错误。
A.乘3 B.除以10 C.除以3 D.加上3
15.(2024·石首)往350g含糖率为25%的糖水中加入10g糖和10g水,这时糖水中的含糖率( )
A.大于25% B.等于25% C.小于25% D.无法确定
16.(2024·黄陂)六(1)班有36名同学,按学号依次轮流当值日班长,这学期有22周,每人至少轮到 ( )次。
A.2 B.3 C.4 D.5
17.(2023·浠水)小丽想研究成年人每天不同时段的体温变化情况,她记录了本周爸爸和妈妈在相应五个不同时段的体温,她选择用( )统计图来呈现爸爸和妈妈的体温数据比较适合。
A.复式条形 B.复式折线 C.扇形 D.单式条形
18.(2023·浠水)有甲乙两根绳子,甲剪去全长的 ,乙剪去 米,两根绳子都还剩 米。那么原来甲乙两根绳子的长度相比,( )。
A.甲绳长 B.乙绳长
C.两绳长度相等 D.无法比较
19.(2023·浠水)把一个数的小数点先向右移动两位,再把得到的数缩小到它的 后是3.6,原数是( )。
A.36 B.3.6 C.0.36 D.360
20.(2023·梁子湖)五月一日李阿姨开车从家到省博物馆玩,如图是汽车行驶的时间和路程的变化情况。她上午9时从家出发,汽车在途中停车加油一次。下面表述中不正确的是( )
A.汽车行驶到一半路程时,停车加油10分钟
B.路上一共用了75分,上午10时15分到达省博物馆
C.汽车加油前后的速度一样快
D.加油后汽车行驶的速度是45千米/时
21.(2023·梁子湖)用5个大小相等的小正方体搭成下面两个立体图形,从( )看这两个立体图形所看到的图形是完全一样的。
A.正面 B.左面 C.上面
22.(2023·梁子湖)下面选项中以虚线为轴旋转一周,( )能得到。
A. B. C.
23.(2023·崇阳)如图,小明从地铁站到学校,要向( )方向走。
A.西偏南30° B.北偏东30° C.东偏北30° D.西偏北30°
24.(2023·崇阳)明明用小正方体搭成了下面3个立体图形,从( )看它们的形状是一样的。
A.正面 B.左面 C.右面
25.(2023·广水)如图:一个装满水的瓶子,内直径8cm。聪聪喝了一些后,水的高度还有12cm,把瓶盖拧紧后倒置平放,无水部分高10cm。聪聪喝了( )cm3水。
A.251.2 B.502.4 C.678.24 D.2009.6
26.(2023·广水)《龟兔赛跑》的意思是乌龟和兔子赛跑,兔子开始远超乌龟,就在路边睡了一觉,乌龟一直向前爬并获得了胜利。能正确反映这个故事情节的图象是( )
A. B.
C. D.
27.(2023·广水)聪聪和明明买了相同价格的文具后,聪聪还剩自己零花钱的 。明明剩自己零花钱75%,聪聪和明明原来的零花钱相比,( )
A.聪聪比明明多 B.明明比聪聪多
C.一样多 D.无法比较
28.(2023·广水)把一些规格相同的杯子叠起来(如图),4个杯子叠起来高20厘米,6个杯子叠起来高26厘米。n个杯子叠起来的高度可以用下面( )的关系式来表示。
A.6n﹣10 B.3n+11 C.6n﹣4 D.3n+8
29.(2023·广水)和0.2表示的意思相同的数是( )
A. B.2 C. D.
30.(2023·崇阳)下面说法错误的有( ) 个。
①圆的周长和直径成正比例
②20%去掉百分号大小不变
③小数点的后面添上或去掉0,小数大小不变
④半圆有无数条对称轴
A.1 B.2 C.3 D.4
31.(2023·黄梅模拟)某机械加工车间,完成了一批同规格零件的加工工作。这种零件的标准外直径是585mm.质检部门在抽检这批零件时,为了记录每个抽检零件外直径与标准的误差,把1号零件外直径记作+2mm,那么2号零件外直径记作( )
A.+582mm B.+3mm C.-582mm D.-3mm
32.(2023·硚口模拟)比的前项扩大原来的3倍,后项缩小为原来的,比值将( )
A.扩大为原来的9倍 B.缩小为原来的
C.扩大为原来的3倍 D.缩小为原来的
33.(2023·硚口模拟)下面哪一种情况选用扇形统计图更合适?( )
A.运动员一周训练的成绩变化记录
B.商场各种商品的销售情况
C.李老师家每月各项生活费用与家庭总收入的关系
D.六年级男、女生身高统计情况
34.(2023·硚口模拟)直角三角形中,一个锐角与直角的度数比是4:15,则两个锐角的度数比( )
A.4:5 B.4:11 C.11:15 D.15:11
35.(2023·硚口模拟)陈老师晚上8点从北京乘高铁到南京,3小时行驶了全程的,他到南京时看到的景象是( )
A.夜深入静 B.夕阳西下 C.艳阳高照 D.旭日东升
36.(2023·郧阳模拟)一长方形沿长和宽可以围成不同的圆柱。如图,圆柱A的侧面积( )圆柱B的侧面积。
A.等于 B.大于 C.小于 D.无法确定
37.(2023·郧阳模拟) :的前项乘,若使原来的比值不变,则后项应( )
A.乘 B.除以 C.乘 D.除以
答案解析部分
1.D
解:A:两辆汽车行驶的路程和时间都成正比例关系。正确;
B:从A地到B地大约360千米,甲车从A地到B地大约需要4小时。正确;
C:乙车4小时大约行驶了180千米。正确;
D:从图像上看乙车的速度比甲车慢。原来说法错误。
故答案为:D。
A:表示时间和路程的关系的图像都是经过原点的直线,是成正比例关系;
B:A地到B地的最远距离是360千米,所以两地的距离就是360千米;
C:乙车4小时对应的路程是180千米;
D:甲车到B地用了4小时,乙车到B地用了8小时,所以甲车速度比乙车快。
2.C
解:A:3.14×42×6=3.14×96;
B:3.14×42×9×=3.14×48;
C:3.14×42×8-3.14×42×4×=3.14×128-3.14×=106×3.14;
D:3.14×42×4+3.14×42×4×=3.14×64+3.14×=85×3.14;
所以体积最大的是106×3.14。
故答案为:C。
圆柱的体积=底面积×高,圆锥的体积=底面积×高×;
A:得到的是一个底面半径是4cm,高是6cm的圆柱;
B:得到的是两个底面半径都是4cm,高度和是9cm的圆锥;
C:得到的图形是一个底面半径4cm,高8cm的圆柱,减去一个底面半径4cm,高4cm的圆锥;
D:得到的图形是一个底面半径4cm,高4cm的圆柱,加上一个底面半径4cm,高4cm的圆锥。
3.C
解:艺术组:60%>40%,女生多;
科学组:60%>40%,男生多。
故答案为:C。
由于不知道艺术组和科学组各有多少人,所以无法比较两个组中男生和女生的人数;只有每个小组内的男生和女生可以比较多少。
4.D
解:A:已修的米数+未修的米数=这条路总长度,已修的米数和未修的米数不成比例;
B:底面积×高=圆锥体体积×3,所以它的底面积和高成反比例关系;
C:每天看的页数×看的天数=总页数,每天看的页数和看的天数成反比例关系;
D:圆的周长÷半径=圆周率×2,圆的周长和半径成正比例关系。
故答案为:D。
根据数量关系判断相关联的两个量的乘积一定还是商一定,如果乘积一定就成反比例关系;如果商一定就成正比例关系;否则不成比例。
5.C
解:苗苗家在笑笑家北偏东40°方向上,那么笑笑家在苗苗家南偏西40°方向。
故答案为:C。
观测点相反,夹角度数不变,那么方向刚好相反,所以苗苗家在笑笑家北偏东40°方向上,那么笑笑家在苗苗家南偏西40°方向上或西偏南50°方向。
6.C
解:阴影部分为1,则大圆和小圆的面积比是:(1÷):(1÷)=5:4。
故答案为:C。
假设阴影部分是1,根据分数除法的意义分别求出大圆和小圆的面积,然后写出面积的最简整数比即可。
7.A
解:80-5=75(个)
故答案为:A。
张兰的成绩记作-5,说明张兰比合格数少5个,因此用80减去5就是张兰实际跳的个数。
8.D
解:50×36÷3
=1800÷3
=600(立方厘米)
①50×12=600(立方厘米)
②150×4=600(立方厘米)
③150×12÷3
=1800÷3
=600(立方厘米)。
故答案为:D。
圆锥的体积=底面积×高÷3,圆柱的体积=底面积×高,长方体的体积=底面积×高,据此计算。
9.A
解: 点A'的位置在第6列,第4行,用数对(6,4)表示。
故答案为:A。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数。
10.B
解:A项:空白部分周长=阴影部分的周长,空白部分的面积=阴影部分的面积;
B项:空白部分周长=阴影部分的周长,空白部分的面积<阴影部分的面积;
C项:空白部分周长>阴影部分的周长,空白部分的面积=阴影部分的面积;
D项:空白部分周长>阴影部分的周长,空白部分的面积>阴影部分的面积。
故答案为:B。
A项:空白部分周长与阴影部分的周长相等,是圆的面积,空白部分的面积与阴影部分的面积相等,是半圆的面积;
B项:空白部分周长与阴影部分的周长相等,是正方形的边长×2+圆的周长÷4,空白部分的面积=正方形的面积-阴影部分的面积,阴影部分的面积=π×半径2÷4;
C项:三角形的面积=底×高÷2,空白部分周长>阴影部分的周长,空白部分的面积=阴影部分的面积=三角形面积的一半;
D项:三角形的面积=底×高÷2,空白部分周长>阴影部分的周长,空白部分的面积>阴影部分的面积。
11.D
解:A:×100=9厘米,此选项正确;
B:相当于1米的,此选项正确;
C:相当于1米的9%,此选项正确;
D:不能改写成9%,此选项错误。
故答案为:D。
百分数表示一个数是另一个数的百分之几,不表示实际的量,所以米不能用百分数表示。
12.C
解:甲商店:6×8×85%=40.8(元)
乙商店:6×8=48(元)
丙商店:8÷3=2(组)······2(个)
(8-2)×6
=6×6
=36(元)
48>40.8>36。
故答案为:C。
甲商店现价=原价×数量×折扣;乙商店现价=原价×数量;丙商店现价=原价×(要买的数量-送的数量)。
13.B
解:A项:a=b×1=b;
B项:<,分子相等,分母小的分数大,则a>b;
C项:>1 ,则b>a;
D项:b-a=1,则b=a+1,b>a。
故答案为:B。
A项:比的前项=比值×比的后项;
B项:同分子分数,分母小的就大;
C项:分子比分母大的分数大于1;
D项:被减数=差+件数,然后再比较a与b的大小。
14.C
解:15÷5=3,接下来他可以除以3。
故答案为:C。
被除数不变,除数缩小3倍,则被除数扩大3倍,要使结果不变,他可以除以3。
15.A
解:(350×25%+10)÷(350+10+10)
=97.5÷370
≈26%
26%>25%。
故答案为:A。
这时糖水的含糖率=(原来糖水的质量×原来的含糖率+加入糖的质量) ÷(原来糖水的质量+加入糖的质量+加入水的质量),然后与原来的含糖率比较大小。
16.A
解:36÷22=1(次)······14(周)
1+1=2(次)。
故答案为:A。
抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1。
17.B
解:要研究成年人每天不同时刻的体温变化情况,复式折线统计图可以同时反映爸爸和妈妈体温数据的增减变化情况;
故答案为:B。
条形统计图:从图中直观地看出数量的多少,便于比较;折线统计图:不仅能看清数量的多少,还能反映数量的增减变化情况;扇形统计图:清楚地看出各部分数量与总数量之间的关系;据此解答。
18.B
解: 原来甲乙两根绳子的长度相比 乙绳长。
故答案为:B。
甲剪去全长的 ,则甲绳长(米);乙绳长(米);。
19.A
解:原数是36。
故答案为:A。
“再把得到的数缩小到它的 ”,是小数点向左移动三位,本题的意思是这个数小数点向左动了一位,得到的是3.6,原数就是36。
20.C
解:30÷25=1.2(千米/分)
30÷(75-35)
=30÷40
=0.75(千米/分)
1.2>0.75,汽车加油前后的速度不同。
故答案为:C。
汽车加油前的速度=行驶的路程30千米÷所用的时间25分钟;汽车加油后的速度=行驶的路程30千米÷(到达的时间-加油后出发的时间),然后比较大小。
21.A
解:从正面看这两个立体图形所看到的图形是完全一样的。
故答案为:A。
这两个立体图形,从正面看,都是看到两层,下面一层三个正方形,上面一层一个正方形,并且左侧对齐。
22.C
解:以虚线为轴旋转一周,能得到。
故答案为:C。
以直角三角形的一条直角边为轴,旋转一周可以得到一个圆锥。
23.A
解:小明从地铁站到学校,要向西偏南30°方向走。
故答案为:A。
在地图上的方位是上北,下南,左西,右东;东和西相对,南和北相对;西南和东北相对,西北和东南相对。
24.A
解:从正面看它们的形状是一样的。
故答案为:A。
从正面看它们的形状是一样的,都是看到两层,下面一层三个正方形,上面一层一个正方形,并且左侧对齐。
25.B
解:8÷2=4(厘米)
3.14×4×4×12=50.24×10=502.4(立方厘米)
故答案为:B。
直径÷2=半径,π×底面半径的平方×无水部分高=聪聪喝的水的体积。
26.D
解:第四个折线统计图能正确反映这个故事情节的图象。
故答案为:D。
乌龟一直向前爬并获得了胜利。说明乌龟的图像是一条射线且比兔子用的时间少,B、C错误;兔子开始远超乌龟,说明开始兔子跑的路程比乌龟多,这一段路程,表示兔子的路程应该在乌龟的上面,据此可知A错误。
27.B
解:=5÷7≈0.71;75%=0.75;
0.75>0.71,明明比聪聪原来的零花钱多。
故答案为:B。
他们原来的钱数-花的钱数=剩下的钱数,花的钱数相同,剩下的钱数越多,说明他们原来的钱数越多,据此解答。
28.D
解:(26-20)÷(5-3)
=6÷2
=3(厘米)
20-3×3=20-9=11(厘米)
n个杯子叠起来的高度是11+3×(n-1)
=11+3n-3
=3n+8
故答案为:D。
6个杯子叠起来高-4个杯子叠起来高=上面2个间隔的高度,上面2个间隔的高度÷2=上面1个间隔的高度;20厘米-上面1个间隔的高度×3=杯子的高度;n个杯子叠起来的高度=杯子的高度+3×(杯子数-1),据此解答。
29.C
解:0.2=,和0.2表示的意思相同的数是。
故答案为:C。
小数化分数,小数点后有几位小数,就在1后面添几个0做分母,小数点去掉做分子。
30.C
解:①圆的周长÷直径=π(一定),圆的周长和直径成正比例,原题干说法正确;
②20%<20,原题干说法错误;
③小数的末尾添上或去掉0,小数大小不变,原题干说法错误;
④半圆有1数条对称轴,原题干说法错误。
故答案为:C。
①两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;
②20%去掉百分号后扩大了100倍;
③小数的基本性质:在小数的末尾添上0或者去掉0,小数的大小不变;
④依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;其中的这条直线就是对称轴。
31.D
解:587-2=585(mm),585-582=3(mm),那么2号零件外直径记作-3mm。
故答案为:D。
因为587mm比准确值多2mm,则准确值就是585mm,582mm低于585mm,那么低于标准尺寸的部分就记作负。
32.A
解:比的前项扩大原来的3倍,后项缩小为原来的,比值将扩大为原来的9倍。
故答案为:A。
比的前项扩大到原来的3倍,比值就扩大到原来的3倍;比的后项缩小为原来的,比值扩大3倍。所以比值会扩大到原来的9倍。
33.C
解:A:应选用折线统计图;
B:应选用条形统计图;
C:应选用扇形统计图;
D:应选用条形统计图。
故答案为:C。
条形统计图能清楚地表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图表示部分与整体之间的关系。
34.B
解:4:(15-4)=4:11。
故答案为:B。
因为直角三角形两个锐角的度数和是90°,所以可以用15减去4求出另一个锐角的份数,然后写出两个锐角的度数比即可。
35.A
解:3÷=4(小时),晚上8点过4小时是12点,此时看到的景象是夜深入静。
故答案为:A。
根据分数除法的意义,用3除以求出行完全程需要的时间,然后判断到达南京的时间。根据这个时间确定看到的景象即可。
36.A
解:圆柱A的侧面积=圆柱B的侧面积。
故答案为:A。
不管怎么围,侧面积都是这张长方形的纸,所以侧面积相等。
37.A
解:若使原来的比值不变,则后项应乘。
故答案为:A。
比的基本性质:比的前项和后项同时乘或除以(0除外)相同的数,比值不变。
同课章节目录
