人教版(2024)七年级下册 第10章 二元一次方程组 单元测试卷(含答案)
文档属性
| 名称 | 人教版(2024)七年级下册 第10章 二元一次方程组 单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 78.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 15:42:20 | ||
图片预览




文档简介
人教版2025年七年级(下)第10章《二元一次方程组》单元测试卷
满分120分 时间120分钟
班级__________ 姓名__________ 学号__________
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程是二元一次方程的是( )
A.x+2=1 B.x2+2y=2 C.y2+y=4 D.x+5y=0
2.下列哪组x,y的值是二元一次方程x+2y=5的解( )
A. B.
C. D.
3.下列各组值中,是方程组的解是( )
A. B. C. D.
4.用代入法解方程组时,代入正确的是( )
A.2x﹣3+x=5 B.2x﹣3﹣x=5 C.2x+3+x=5 D.2x+3﹣x=5
5.小丽在用“加减消元法”解二元一次方程组时,利用①×a+②×b消去y,则a、b的值可能是( )
A.a=3,b=2 B.a=2,b=3 C.a=﹣2,b=3 D.a=3,b=﹣2
6.已知|2x+y+3|+(x﹣y+3)2=0,则(x+y)2025=( )
A.2025 B.1 C.﹣2025 D.﹣1
7.下列四组数值中,为方程组的解是( )
A. B.
C. D.
8.若关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值为( )
A. B. C. D.
9.如表,在3×3的方格中做填字游戏,要求每行、每列及对角线上三个方格中的数字和都相等,则表格中x,y的值是( )
A. B. C. D.
10.已知关于x,y的二元一次方程组,下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣4;
②当a=1时,方程组的解也是方程x+y=3+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y,则.
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题(共5小题,满分15分,每小题3分)
11.已知方程4x﹣2y=5,用含x的式子表示y为y= .
12.已知(5﹣a)x+y|a|﹣4=2是关于x,y的二元一次方程,则a的值是 .
13.若是方程ax+y=6的解,则a的值为 .
14.小明在校园自动售货机上购买了橡皮、圆规两种文具,共用去13元.若橡皮的单价为3元/块,圆规的单价为4元/个,则他购买了 块橡皮.
15.若方程组的解为,则方程组的解为 .
三.解答题(共8小题,满分75分)
16.(7分)解下列方程(组):
(1); (2).
17.(7分)下面是张亮同学的一道作业题,请认真阅读并完成相应任务.
解:.
第一步:由①得,x=2y+1③;
第二步:将③代入②,得2×2y+1+2y=5;
第三步:解得;
第四步:将y=1代入③,解得;
第五步:所以原方程组的解为.
任务一:张亮解方程组用的方法是 消元法(填“代入”或“加减”);
任务二:仔细检查后,发现张亮的答案是错误的,他从第 步开始出现错误;
任务三:请写出正确的解答过程.
18.(7分)已知关于x,y的方程组.若原方程组的解也是二元一次方程2x+y=7的一个解,求m的值.
19.(9分)乐乐,果果两人同解方程组时,乐乐看错了方程①中的a,解得,果果看错了方程②中的b,解得,求的值.
20.(9分)若方程组和方程组有相同的解.
(1)求方程组正确的解.
(2)求a,b的值.
21.(9分)某校准备组织七年级400名学生参加综合实践活动,已知用1辆小客车和2辆大客车均满载,每次可运送学生110名;用3辆小客车和1辆大客车均满载,每次可运送学生105名.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若学校计划租用小客车x辆,大客车y辆,一次送完,且恰好每辆车都坐满.
①请你设计出所有的租车方案;
②若小客车每辆需租金1600元,大客车每辆需租金2700元,请选出最省钱的租车方案,并求出最少租金.
22.(13分)在解方程组时,某同学发现:如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错,如果把方程组中的2x+3y、4x﹣3y分别看作一个整体,通过换元:设m=2x+3y、n=4x﹣3y,可以将原方程组化为,解得,把代入m=2x+3y、n=4x﹣3y,得,解得,所以原方程组解为.
(1)若方程组的解为,则方程组的解为 ;
(2)若方程组的解为,其中k为常数.求方程组的解.
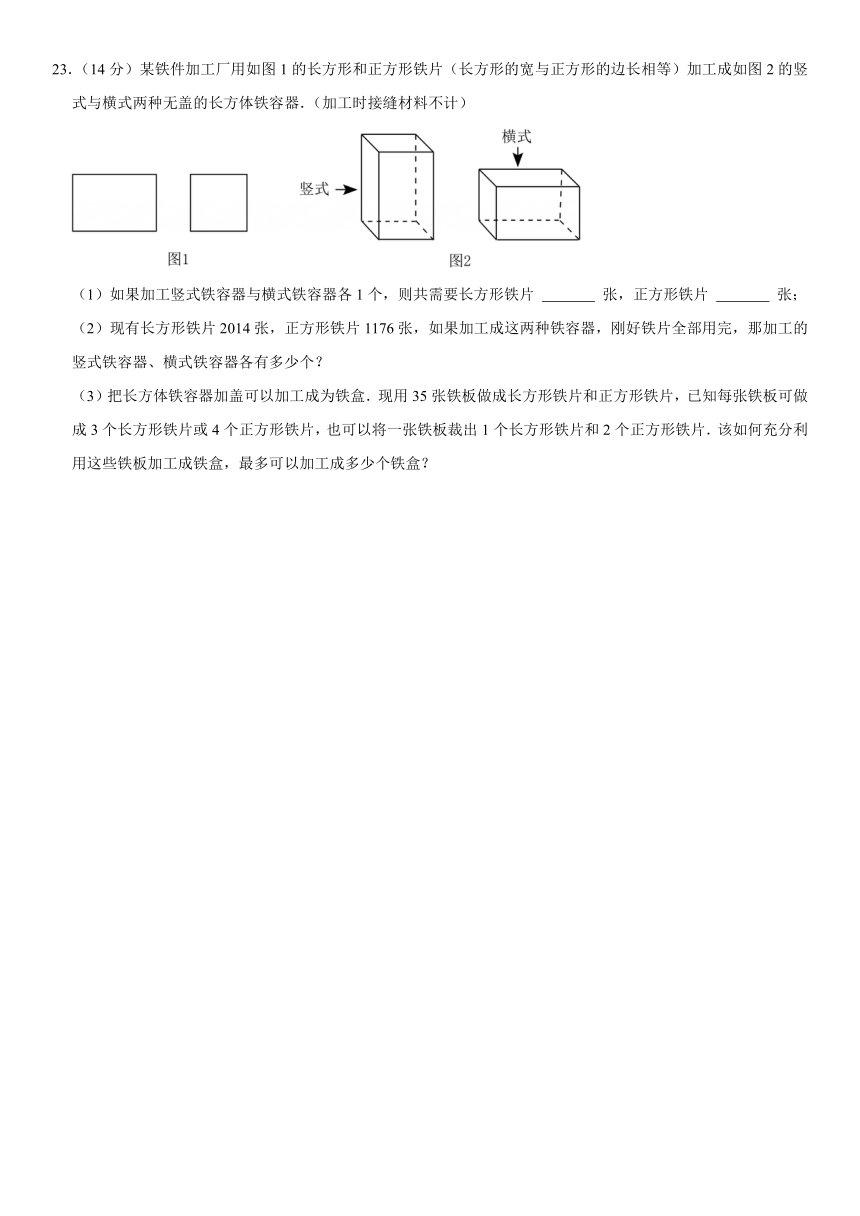
23.(14分)某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片 张,正方形铁片 张;
(2)现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成3个长方形铁片或4个正方形铁片,也可以将一张铁板裁出1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒?
参考答案
一.选择题(共10小题,满分30分,每小题3分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B A A D. D A B A
二.填空题(共5小题,满分15分,每小题3分)
11.解:4x﹣2y=5,移项,可得2y=4x﹣5,
系数化为1,可得y.
故答案为:.
12.解:由题意可得,5﹣a≠0,|a|﹣4=1,
解得:a=﹣5.
故答案为:﹣5.
13.解:把代入方程ax+y=6中,得a+2=6,
解得a=4,
故答案为:4.
14.解:设他购买了x块橡皮,y个圆规,
根据题意得:3x+4y=13,
∴x,
又∵x,y均为正整数,
∴,
∴他购买了2块橡皮.
故答案为:2.
15.解:设m=x+1,n=y+1,则方程组可化为,
已知的解为,
∴对于方程组的解为,
∵m=x+1,n=y+1,
∴
解得x=0,y=﹣2,
∴方程组的解为,
故答案为:,
三.解答题(共8小题,满分75分)
16.解:(1),
①+②,得5x=10,
解得:x=2,
把x=2代入①,得2×2﹣y=3,
解得:y=1,
∴方程组的解为;
(2),
由②,得y=2x+8③,
把③代入①,得3x+4(2x+8)=21,
去括号,得3x+8x+32=21,
解得:x=﹣1,
把x=﹣1代入②,得2×(﹣1)﹣y=﹣8,
解得:y=6,
∴方程组的解为.
17.解:任务一:根据题意可得,用的方法是代入消元法.
故答案为:代入;
任务二:他从第二步开始错误,错误的原因:整体代入未添加括号.
故答案为:二;
任务三:正确的解答过程:由①得x=2y+1 ③,
将③代入②,得2(2y+1)+2y=5,
解得:,
把代入③,得=22,
∴原方程组的解为:.
18.解:关于x,y的方程组标号得,
①+②得2x+y=2+m,
∴2+m=7,
∴m=5.
19.解:根据题意可知,把代入②,
得﹣12=﹣b﹣2,
解得:b=10,
把代入①,
得5a+20=15,
解得:a=﹣1,
∴原式
=1﹣1
=0.
20.解:(1)∵方程组和方程组有相同的解,
∴,
①+②得3x﹣y+2x+y=7+8,解得x=3,
将x=3代入①得y=2,
∴方程组的解为.
(2)∵方程组和方程组有相同的解,
∴可得新方程组,
解得:,
把,代入,得,
解得.
故a的值是,b的值是.
21.解:(1)设每辆小客车能坐a名学生,每辆大客车能坐b名学生,
根据题意得:,
解得:,
答:每辆小客车能坐20名学生,每辆大客车能坐45名学生;
(2)①∵学校计划租用小客车x辆,大客车y辆,某校准备组织七年级400名学生参加综合实践活动,
∴20x+45y=400,
整理得:x=20y,
∵x,y为非负整数,
∴或或,
∴学校租车方案有3种:
方案1:小客车20辆,大客车0辆;
方案2:小客车11辆,大客车4辆;
方案3:小客车2辆,大客车8辆;
②由①可知,方案1的租金为:1600×20=32000(元);
方案2的租金为:1600×11+2700×4=28400(元);
方案3的租金为:1600×2+2700×8=24800(元),
∵32000>28400>24800,
∴学校最省钱的租车方案为2辆小客车,8辆大客车,最少租金为24800元.
22.解:(1)∵的解为,
∴的解为,
设x﹣2=m,y+2=n,
则方程组可变为:,
∴,
解得:.
故答案为:.
(2)设,,
则原方程组可变为:,
∵的解为,
∴的解为,
即,
解得:.
23.解:(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片7张,正方形铁片3张;
(2)设加工的竖式铁容器有x个,横式铁容器有y个,根据题意得,
解得
答:竖式铁容器加工100个,横式铁容器加工538个;
(3)设做长方形铁片的铁板为m块,做正方形铁片的铁板为n块,
依题意,得:,
解得:.
∵在这35块铁板中,25块做长方形铁片可做25×3=75(张),9块做正方形铁片可做9×4=36(张),剩下1块可裁出1张长方形铁片和2张正方形铁片,
∴共做长方形铁片75+1=76(张),正方形铁片36+2=38(张),
∴可做铁盒76÷4=19(个).
答:最多可以加工成19个铁盒.
解法二:设做长方形铁片的铁板为m块,做正方形铁片的铁板为n块,则(35﹣m﹣n)按1个长方形铁片和2个正方形铁片截.
由题意2[3m+(35﹣m﹣n)]=4[4n+2(35﹣m﹣n)],
整理得6m﹣5n=105,其中1m+n≤35且m,n是正整数,
解得或,
可以加工成铁盒的数量为,
当m=20,n=3时,18(个),
当m=25,n=9时,19(个).
答:25张铁板按3个长方形截,9张铁板按4个正方形截,1张铁板按1个长方形2个正方形截,最多可以加工成19个铁盒.
满分120分 时间120分钟
班级__________ 姓名__________ 学号__________
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程是二元一次方程的是( )
A.x+2=1 B.x2+2y=2 C.y2+y=4 D.x+5y=0
2.下列哪组x,y的值是二元一次方程x+2y=5的解( )
A. B.
C. D.
3.下列各组值中,是方程组的解是( )
A. B. C. D.
4.用代入法解方程组时,代入正确的是( )
A.2x﹣3+x=5 B.2x﹣3﹣x=5 C.2x+3+x=5 D.2x+3﹣x=5
5.小丽在用“加减消元法”解二元一次方程组时,利用①×a+②×b消去y,则a、b的值可能是( )
A.a=3,b=2 B.a=2,b=3 C.a=﹣2,b=3 D.a=3,b=﹣2
6.已知|2x+y+3|+(x﹣y+3)2=0,则(x+y)2025=( )
A.2025 B.1 C.﹣2025 D.﹣1
7.下列四组数值中,为方程组的解是( )
A. B.
C. D.
8.若关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值为( )
A. B. C. D.
9.如表,在3×3的方格中做填字游戏,要求每行、每列及对角线上三个方格中的数字和都相等,则表格中x,y的值是( )
A. B. C. D.
10.已知关于x,y的二元一次方程组,下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣4;
②当a=1时,方程组的解也是方程x+y=3+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y,则.
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题(共5小题,满分15分,每小题3分)
11.已知方程4x﹣2y=5,用含x的式子表示y为y= .
12.已知(5﹣a)x+y|a|﹣4=2是关于x,y的二元一次方程,则a的值是 .
13.若是方程ax+y=6的解,则a的值为 .
14.小明在校园自动售货机上购买了橡皮、圆规两种文具,共用去13元.若橡皮的单价为3元/块,圆规的单价为4元/个,则他购买了 块橡皮.
15.若方程组的解为,则方程组的解为 .
三.解答题(共8小题,满分75分)
16.(7分)解下列方程(组):
(1); (2).
17.(7分)下面是张亮同学的一道作业题,请认真阅读并完成相应任务.
解:.
第一步:由①得,x=2y+1③;
第二步:将③代入②,得2×2y+1+2y=5;
第三步:解得;
第四步:将y=1代入③,解得;
第五步:所以原方程组的解为.
任务一:张亮解方程组用的方法是 消元法(填“代入”或“加减”);
任务二:仔细检查后,发现张亮的答案是错误的,他从第 步开始出现错误;
任务三:请写出正确的解答过程.
18.(7分)已知关于x,y的方程组.若原方程组的解也是二元一次方程2x+y=7的一个解,求m的值.
19.(9分)乐乐,果果两人同解方程组时,乐乐看错了方程①中的a,解得,果果看错了方程②中的b,解得,求的值.
20.(9分)若方程组和方程组有相同的解.
(1)求方程组正确的解.
(2)求a,b的值.
21.(9分)某校准备组织七年级400名学生参加综合实践活动,已知用1辆小客车和2辆大客车均满载,每次可运送学生110名;用3辆小客车和1辆大客车均满载,每次可运送学生105名.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若学校计划租用小客车x辆,大客车y辆,一次送完,且恰好每辆车都坐满.
①请你设计出所有的租车方案;
②若小客车每辆需租金1600元,大客车每辆需租金2700元,请选出最省钱的租车方案,并求出最少租金.
22.(13分)在解方程组时,某同学发现:如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错,如果把方程组中的2x+3y、4x﹣3y分别看作一个整体,通过换元:设m=2x+3y、n=4x﹣3y,可以将原方程组化为,解得,把代入m=2x+3y、n=4x﹣3y,得,解得,所以原方程组解为.
(1)若方程组的解为,则方程组的解为 ;
(2)若方程组的解为,其中k为常数.求方程组的解.
23.(14分)某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片 张,正方形铁片 张;
(2)现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成3个长方形铁片或4个正方形铁片,也可以将一张铁板裁出1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒?
参考答案
一.选择题(共10小题,满分30分,每小题3分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B A A D. D A B A
二.填空题(共5小题,满分15分,每小题3分)
11.解:4x﹣2y=5,移项,可得2y=4x﹣5,
系数化为1,可得y.
故答案为:.
12.解:由题意可得,5﹣a≠0,|a|﹣4=1,
解得:a=﹣5.
故答案为:﹣5.
13.解:把代入方程ax+y=6中,得a+2=6,
解得a=4,
故答案为:4.
14.解:设他购买了x块橡皮,y个圆规,
根据题意得:3x+4y=13,
∴x,
又∵x,y均为正整数,
∴,
∴他购买了2块橡皮.
故答案为:2.
15.解:设m=x+1,n=y+1,则方程组可化为,
已知的解为,
∴对于方程组的解为,
∵m=x+1,n=y+1,
∴
解得x=0,y=﹣2,
∴方程组的解为,
故答案为:,
三.解答题(共8小题,满分75分)
16.解:(1),
①+②,得5x=10,
解得:x=2,
把x=2代入①,得2×2﹣y=3,
解得:y=1,
∴方程组的解为;
(2),
由②,得y=2x+8③,
把③代入①,得3x+4(2x+8)=21,
去括号,得3x+8x+32=21,
解得:x=﹣1,
把x=﹣1代入②,得2×(﹣1)﹣y=﹣8,
解得:y=6,
∴方程组的解为.
17.解:任务一:根据题意可得,用的方法是代入消元法.
故答案为:代入;
任务二:他从第二步开始错误,错误的原因:整体代入未添加括号.
故答案为:二;
任务三:正确的解答过程:由①得x=2y+1 ③,
将③代入②,得2(2y+1)+2y=5,
解得:,
把代入③,得=22,
∴原方程组的解为:.
18.解:关于x,y的方程组标号得,
①+②得2x+y=2+m,
∴2+m=7,
∴m=5.
19.解:根据题意可知,把代入②,
得﹣12=﹣b﹣2,
解得:b=10,
把代入①,
得5a+20=15,
解得:a=﹣1,
∴原式
=1﹣1
=0.
20.解:(1)∵方程组和方程组有相同的解,
∴,
①+②得3x﹣y+2x+y=7+8,解得x=3,
将x=3代入①得y=2,
∴方程组的解为.
(2)∵方程组和方程组有相同的解,
∴可得新方程组,
解得:,
把,代入,得,
解得.
故a的值是,b的值是.
21.解:(1)设每辆小客车能坐a名学生,每辆大客车能坐b名学生,
根据题意得:,
解得:,
答:每辆小客车能坐20名学生,每辆大客车能坐45名学生;
(2)①∵学校计划租用小客车x辆,大客车y辆,某校准备组织七年级400名学生参加综合实践活动,
∴20x+45y=400,
整理得:x=20y,
∵x,y为非负整数,
∴或或,
∴学校租车方案有3种:
方案1:小客车20辆,大客车0辆;
方案2:小客车11辆,大客车4辆;
方案3:小客车2辆,大客车8辆;
②由①可知,方案1的租金为:1600×20=32000(元);
方案2的租金为:1600×11+2700×4=28400(元);
方案3的租金为:1600×2+2700×8=24800(元),
∵32000>28400>24800,
∴学校最省钱的租车方案为2辆小客车,8辆大客车,最少租金为24800元.
22.解:(1)∵的解为,
∴的解为,
设x﹣2=m,y+2=n,
则方程组可变为:,
∴,
解得:.
故答案为:.
(2)设,,
则原方程组可变为:,
∵的解为,
∴的解为,
即,
解得:.
23.解:(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片7张,正方形铁片3张;
(2)设加工的竖式铁容器有x个,横式铁容器有y个,根据题意得,
解得
答:竖式铁容器加工100个,横式铁容器加工538个;
(3)设做长方形铁片的铁板为m块,做正方形铁片的铁板为n块,
依题意,得:,
解得:.
∵在这35块铁板中,25块做长方形铁片可做25×3=75(张),9块做正方形铁片可做9×4=36(张),剩下1块可裁出1张长方形铁片和2张正方形铁片,
∴共做长方形铁片75+1=76(张),正方形铁片36+2=38(张),
∴可做铁盒76÷4=19(个).
答:最多可以加工成19个铁盒.
解法二:设做长方形铁片的铁板为m块,做正方形铁片的铁板为n块,则(35﹣m﹣n)按1个长方形铁片和2个正方形铁片截.
由题意2[3m+(35﹣m﹣n)]=4[4n+2(35﹣m﹣n)],
整理得6m﹣5n=105,其中1m+n≤35且m,n是正整数,
解得或,
可以加工成铁盒的数量为,
当m=20,n=3时,18(个),
当m=25,n=9时,19(个).
答:25张铁板按3个长方形截,9张铁板按4个正方形截,1张铁板按1个长方形2个正方形截,最多可以加工成19个铁盒.
同课章节目录
