白鹭洲中学2009—2010学年高一年级上学期第二次月考
文档属性
| 名称 | 白鹭洲中学2009—2010学年高一年级上学期第二次月考 |  | |
| 格式 | zip | ||
| 文件大小 | 193.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-05 10:59:00 | ||
图片预览



文档简介
白鹭洲中学2009—2010学年高一年级上学期第二次月考
数学试卷
命题:傅金梅 董永芳 审题:张子路
考生注意:
1.本试卷设试卷Ⅰ、Ⅱ卷和答题卡纸三部分,试卷所有答案都必须写在答题纸上.
2.答题纸与试卷在试题编号上是一一对应的,答题时应特别注意,不能错位.
3.考试时间为120分钟,试卷满分为150.
4. 345678班做B题 ,其它班做A题(其中12,15,21题分AB题)
第Ⅰ卷 (选择题 共60分)
选择题:(本大题共有12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.)
1.的值为( )
A. B. C. D.
2. 函数都是增加的一个区间是( )
A. B. C.[0,] D.[,]
3. 半径为2cm,中心角为120o的扇形面积为 ( )
A. B. C. D.
4.的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程的一个近似根(精确到)为( )
A. B. C. D. 5.( )
A B
C D
6. 已知函数的最小正周期为,为了得到函数
的图象,只要将的图象( )
A 向左平移个单位长度 B 向右平移个单位长度
C 向左平移个单位长度 D 向右平移个单位长度
7.已知函数 的图象与函数的图象关于直线对称,则( )
A. B.
C. D.
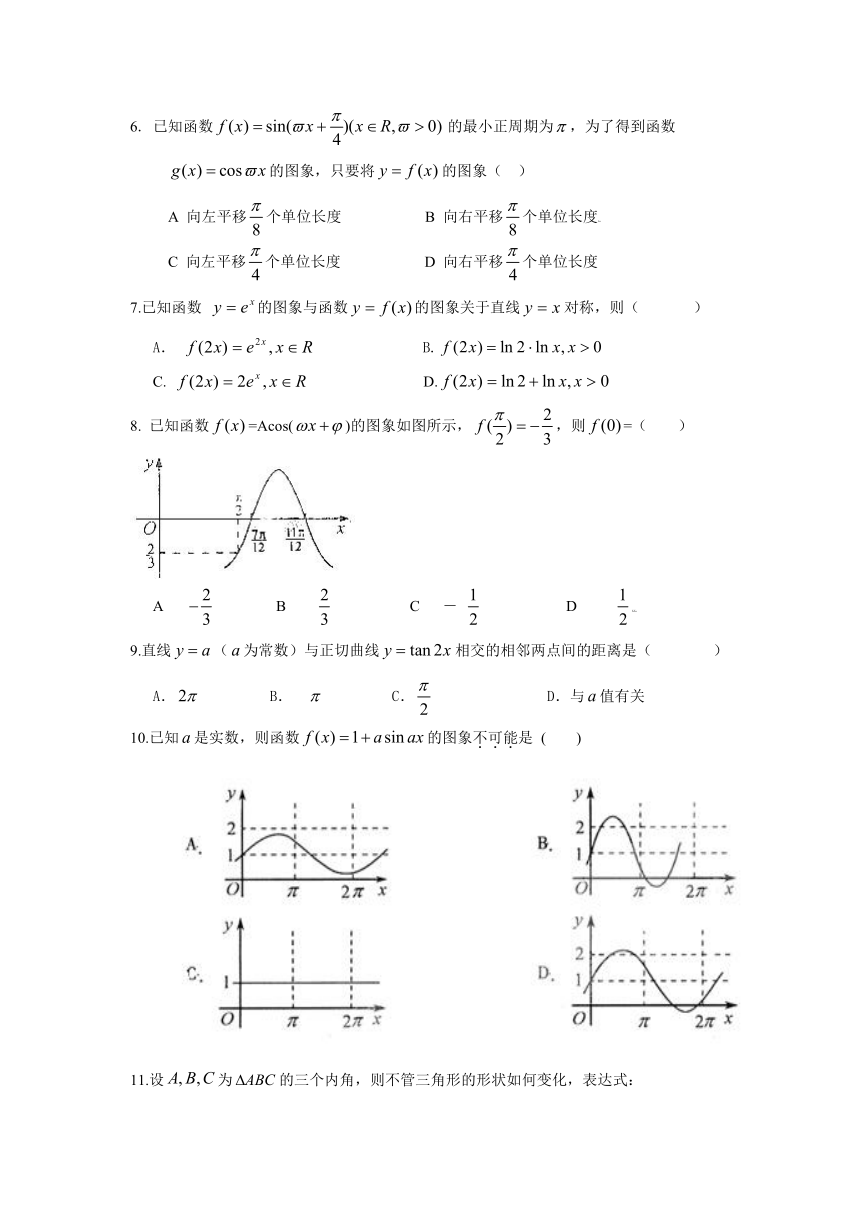
8. 已知函数=Acos()的图象如图所示,,则=( )
A B C - D
9.直线(为常数)与正切曲线相交的相邻两点间的距离是( )
A. B. C. D.与值有关
10.已知是实数,则函数的图象不可能是 ( )
( http: / / www. )11.设为的三个内角,则不管三角形的形状如何变化,表达式:
(2)(3)
(4) 始终是常数的有( )个
A 1 B 2 C 3 D 4
12.(A) 函数的零点个数是( )
A 0 B 1 C 2 D 3
(B)函数的零点个数是( )
A 7 B 6 C 5 D 4
二.填空题:(本大题共4小题,每小题4分,共16分.将答案填在答题卡上的相应位置.)
13.若A为三角形的内角,,则的范围
14.已知是定义在上的减函数,图象经过点,,则不等式 的解集是
15.(A)设是定义在R上奇函数,且当时,,则当时,
表达式为 .
(B)设f(x)是定义在R上奇函数,且f(x+1)=-f(x),当时,
则时,表达式为 .
16.关于有如下说法:
若,则是的整数倍,
函数解析式可改为,
函数图象关于对称,
函数图象关于点对称。
其中正确的是(填正确的序号)
三、解答题:本大题共6小题,共74分. 解答应写出必要的文字说明、证明过程或演算步骤.
17.已知角的顶点与直角坐标系的原点重合,始边在x轴的正半轴上,
终边经过点P(-1,2),
求(1)
18.已知关于x的方程的两根为和,,求:(1)的值;
(2) 的值;
(3) 方程的两根及此时的值.
已知函数有最大值,试求实数的值 ( http: / / wxc. / )
20.某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件元,预计年销售量将减少p万件.
(1)将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函
数的定义域;
(2)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征
收管理费的比率p%的范围是多少?
(3)第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金
额,则p应为多少?
21.(A)已知,函数,当时,.(1)求常数的值
(2)设,求的单调区间
(B)已知,函数,当时,.
(1)求常数的值
(2)当a>0时,设,且,求的单调区间
22.已知,函数.
当时,求所有使成立的的值;
(2)当时,求函数在闭区间上的最小值;
(3)(345678班做,其它班不做)试讨论函数的图像与直线的交点个数.
第二次月考(数学)答题卷
一.选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二.填空题(每小题4分,共16分)
13 . 14 .
15 . 16 .
解答题(本大题共6个小题,共74分)
17.(本小题满分12分)
18(本小题满分12分)
19(本小题满分12分)
20(本小题满分12分)
21(本小题满分12分)
22(本小题满分14分)
高一数学参考答案及评分标准
一、选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 A B C C B A D B C D C B
二、填空题(每小题5分,共20分)
13. () 14.
15. (A)(B) 16. (2)(3)
三、解答题
解:(1)
(2)原式=
18.解:⑴由题意得
⑶
19、 解:,令,
则,,对称轴为
当时,即,,(舍)
当时,即,,(舍)
当时,即,,(舍)
所以。
20. 解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为(11.8-p)万元,?
则商场该年对该商品征收的总管理费为(11.8-p)p%(万元).
故所求函数为:y=(118-10p)p.
11.8-p>0及p>0得定义域为0<p<.
(2)由y≥14,得(118-10p)p≥14.?
化简得p2-12p+20≤0,即(p-2)(p-10)≤0,解得2≤p≤10.?
故当比率在[2%,10%]内时,商场收取的管理费将不少于14万元.
(3)第二年,当商场收取的管理费不少于14万元时,
厂家的销售收入为g(p)=(11.8-p)(2≤p≤10).
∵g(p)=(11.8-p)=700(10+)为减函数,?
∴g(p)max=g(2)=700(万元).?
故当比率为2%时,厂家销售金额最大,且商场所收管理费又不少于14万元
21、解:(A)(1)
则,,则,
(2) ,
的单调递增区间为
的单调递减区间为
(B)(1)
则,当a=0不合题意
,则,
则,
(2),即a=2,b=-5时,且即
的单调递增区间为
的单调递减区间为
22解:(1)所以或;
(2),
1O.当时,,这时,对称轴,
所以函数在区间上递增,;
2O.当时,时函数;
3O.当时,,这时,对称轴, 所以函数;
(3)因为所以,所以在上递增;
在递增,在上递减.
因为,所以当时,函数的图像与直线有2个交点;
又当且仅当时,等号成立.
所以,当时,函数的图像与直线有1个交点;
当时,函数的图像与直线有2个交点;
当时,函数的图像与直线有3个交点;
当时,函数的图像与直线有2个交点;
当时,函数的图像与直线有3个交点.
班级 姓名 学号
数学试卷
命题:傅金梅 董永芳 审题:张子路
考生注意:
1.本试卷设试卷Ⅰ、Ⅱ卷和答题卡纸三部分,试卷所有答案都必须写在答题纸上.
2.答题纸与试卷在试题编号上是一一对应的,答题时应特别注意,不能错位.
3.考试时间为120分钟,试卷满分为150.
4. 345678班做B题 ,其它班做A题(其中12,15,21题分AB题)
第Ⅰ卷 (选择题 共60分)
选择题:(本大题共有12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.)
1.的值为( )
A. B. C. D.
2. 函数都是增加的一个区间是( )
A. B. C.[0,] D.[,]
3. 半径为2cm,中心角为120o的扇形面积为 ( )
A. B. C. D.
4.的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程的一个近似根(精确到)为( )
A. B. C. D. 5.( )
A B
C D
6. 已知函数的最小正周期为,为了得到函数
的图象,只要将的图象( )
A 向左平移个单位长度 B 向右平移个单位长度
C 向左平移个单位长度 D 向右平移个单位长度
7.已知函数 的图象与函数的图象关于直线对称,则( )
A. B.
C. D.
8. 已知函数=Acos()的图象如图所示,,则=( )
A B C - D
9.直线(为常数)与正切曲线相交的相邻两点间的距离是( )
A. B. C. D.与值有关
10.已知是实数,则函数的图象不可能是 ( )
( http: / / www. )11.设为的三个内角,则不管三角形的形状如何变化,表达式:
(2)(3)
(4) 始终是常数的有( )个
A 1 B 2 C 3 D 4
12.(A) 函数的零点个数是( )
A 0 B 1 C 2 D 3
(B)函数的零点个数是( )
A 7 B 6 C 5 D 4
二.填空题:(本大题共4小题,每小题4分,共16分.将答案填在答题卡上的相应位置.)
13.若A为三角形的内角,,则的范围
14.已知是定义在上的减函数,图象经过点,,则不等式 的解集是
15.(A)设是定义在R上奇函数,且当时,,则当时,
表达式为 .
(B)设f(x)是定义在R上奇函数,且f(x+1)=-f(x),当时,
则时,表达式为 .
16.关于有如下说法:
若,则是的整数倍,
函数解析式可改为,
函数图象关于对称,
函数图象关于点对称。
其中正确的是(填正确的序号)
三、解答题:本大题共6小题,共74分. 解答应写出必要的文字说明、证明过程或演算步骤.
17.已知角的顶点与直角坐标系的原点重合,始边在x轴的正半轴上,
终边经过点P(-1,2),
求(1)
18.已知关于x的方程的两根为和,,求:(1)的值;
(2) 的值;
(3) 方程的两根及此时的值.
已知函数有最大值,试求实数的值 ( http: / / wxc. / )
20.某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件元,预计年销售量将减少p万件.
(1)将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函
数的定义域;
(2)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征
收管理费的比率p%的范围是多少?
(3)第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金
额,则p应为多少?
21.(A)已知,函数,当时,.(1)求常数的值
(2)设,求的单调区间
(B)已知,函数,当时,.
(1)求常数的值
(2)当a>0时,设,且,求的单调区间
22.已知,函数.
当时,求所有使成立的的值;
(2)当时,求函数在闭区间上的最小值;
(3)(345678班做,其它班不做)试讨论函数的图像与直线的交点个数.
第二次月考(数学)答题卷
一.选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二.填空题(每小题4分,共16分)
13 . 14 .
15 . 16 .
解答题(本大题共6个小题,共74分)
17.(本小题满分12分)
18(本小题满分12分)
19(本小题满分12分)
20(本小题满分12分)
21(本小题满分12分)
22(本小题满分14分)
高一数学参考答案及评分标准
一、选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 A B C C B A D B C D C B
二、填空题(每小题5分,共20分)
13. () 14.
15. (A)(B) 16. (2)(3)
三、解答题
解:(1)
(2)原式=
18.解:⑴由题意得
⑶
19、 解:,令,
则,,对称轴为
当时,即,,(舍)
当时,即,,(舍)
当时,即,,(舍)
所以。
20. 解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为(11.8-p)万元,?
则商场该年对该商品征收的总管理费为(11.8-p)p%(万元).
故所求函数为:y=(118-10p)p.
11.8-p>0及p>0得定义域为0<p<.
(2)由y≥14,得(118-10p)p≥14.?
化简得p2-12p+20≤0,即(p-2)(p-10)≤0,解得2≤p≤10.?
故当比率在[2%,10%]内时,商场收取的管理费将不少于14万元.
(3)第二年,当商场收取的管理费不少于14万元时,
厂家的销售收入为g(p)=(11.8-p)(2≤p≤10).
∵g(p)=(11.8-p)=700(10+)为减函数,?
∴g(p)max=g(2)=700(万元).?
故当比率为2%时,厂家销售金额最大,且商场所收管理费又不少于14万元
21、解:(A)(1)
则,,则,
(2) ,
的单调递增区间为
的单调递减区间为
(B)(1)
则,当a=0不合题意
,则,
则,
(2),即a=2,b=-5时,且即
的单调递增区间为
的单调递减区间为
22解:(1)所以或;
(2),
1O.当时,,这时,对称轴,
所以函数在区间上递增,;
2O.当时,时函数;
3O.当时,,这时,对称轴, 所以函数;
(3)因为所以,所以在上递增;
在递增,在上递减.
因为,所以当时,函数的图像与直线有2个交点;
又当且仅当时,等号成立.
所以,当时,函数的图像与直线有1个交点;
当时,函数的图像与直线有2个交点;
当时,函数的图像与直线有3个交点;
当时,函数的图像与直线有2个交点;
当时,函数的图像与直线有3个交点.
班级 姓名 学号
