4.5.3一次函数的应用 教案

中小学教育资源及组卷应用平台
分课时教学设计
第9课时《4.5.3一次函数的应用 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 使学生经历探索 、合作、交流的学习过程，激发学生对数学的兴趣，获得成功的体验．
学习者分析 让学生经历观察、操作、合作、探究、交流、推理等活动，体会数学的建模、数形结合思想，进一步发展推理能力及有条理表达能力．
教学目标 1.会综合运用一次函数的解析式和图象解决简单实际问题； 2.了解直角坐标系中两条直线（不平行于坐标轴）的交点坐标与两条直线的函数解析式所组成的二元一次方程组的解之间的关系； 3.会用一次函数的图象求二元一次方程组的解（包括近似解）．
教学重点 运用一次函数的解析式和图象等解决简单实际问题．
教学难点 构造数学模型（包括函数解析式和图象）与实际问题情景之间的对应关系.
学习活动设计
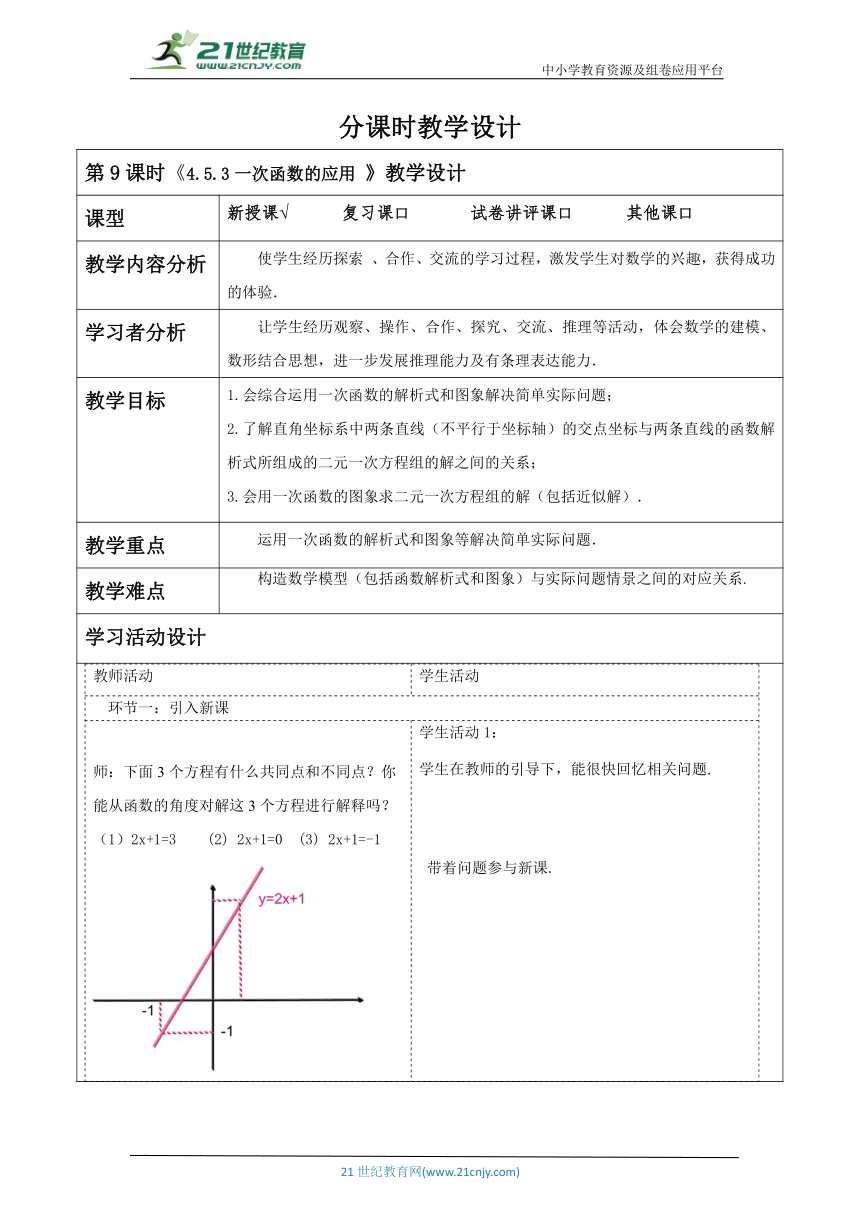
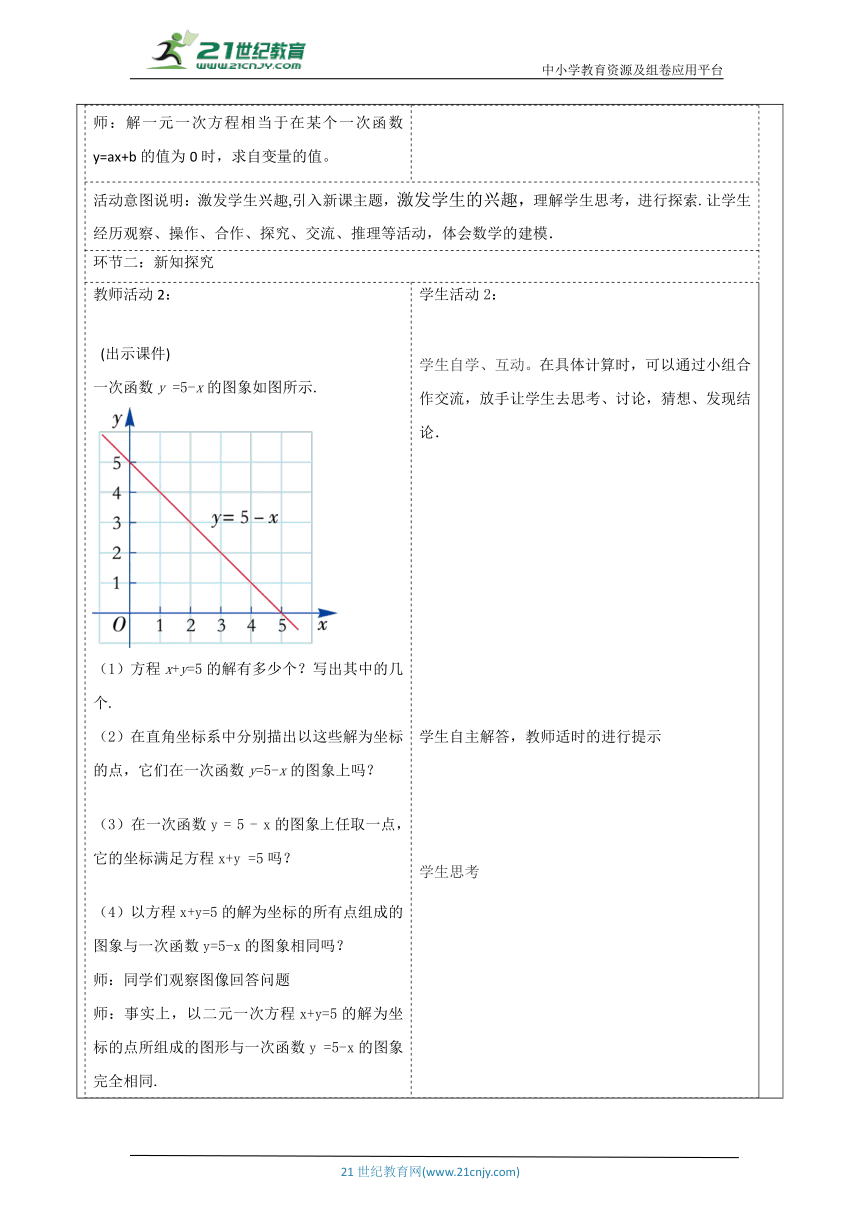
教师活动学生活动环节一：引入新课 师：下面3个方程有什么共同点和不同点？你能从函数的角度对解这3个方程进行解释吗？ （1）2x+1=3 (2) 2x+1=0 (3) 2x+1=-1 师：解一元一次方程相当于在某个一次函数y=ax+b的值为0时，求自变量的值。学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，进行探索.让学生经历观察、操作、合作、探究、交流、推理等活动，体会数学的建模． 环节二：新知探究教师活动2： (出示课件) 一次函数y =5-x的图象如图所示. （1）方程x+y=5的解有多少个？写出其中的几个. （2）在直角坐标系中分别描出以这些解为坐标的点，它们在一次函数y=5-x的图象上吗？ （3）在一次函数y = 5 - x的图象上任取一点，它的坐标满足方程x+y =5吗？ （4）以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5-x的图象相同吗？ 师：同学们观察图像回答问题 师：事实上，以二元一次方程x+y=5的解为坐标的点所组成的图形与一次函数y =5-x的图象完全相同. 师：通过上面的学习，我们来总结一下 生：一般地，一次函数y=kx+b图象上任意一点的坐标都是二元一次方程kx-y+b=0的一个解，以二元一次方程kx-y+b =0的解为坐标的点都在一次函数y=kx+b的图象上. 师：我们再来看这个问题 你能找到下面两个问题之间的联系吗？ （1） 解方程： 3x - 6 = 0. （2） 已知一次函数y = 3x - 6，问x取何值时，y = 0？ 师：同学们画出函数y = 3x - 6的图象 生： 从图中可以看出，一次函数y =3x-6的图象与x 轴交于点（2，0），这就是当y =0时，得x=2，而x=2正是方程3x-6=0的解. 师：同学们一次函数与方程的关系是怎样的？ 师：我们来小练一下 课件展示： 如图，过点Q(0，3.5)的一次函数的图象与正比例函数y=2x的图象相交于点P，能表示这个一次函数图象的方程是( ) A.3x-2y+3.5=0 B.3x-2y-3.5=0 C.3x-2y+7=0 D.3x+2y-7=0 学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．了解直角坐标系中两条直线（不平行于坐标轴）的交点坐标与两条直线的函数解析式所组成的二元一次方程组的解之间的关系．环节三：典例精析 例1、已知一次函数y = 2x + 6， 求这个函数的图象与x轴交点的横坐标. 解法一：（1） 令y = 0， 解方程2x + 6 = 0， 得x = -3. 所以一次函数y = 2x + 6的图象与x轴交点的横坐标为-3. 解法二：画出函数y = 2x + 6的图象， 直线y = 2x + 6与x 轴交于点（-3，0），所以该图象与x轴交点的横坐标为-3. 学生活动3： 参与教师分析和讲例题． 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，运用一次函数的解析式和图象等解决简单实际问题．
板书设计
课堂练习 【知识技能类作业】 必做题： 1、方程2x+12=0的解是直线y=2x+12( ) A.与y轴交点的横坐标 B.与y轴交点的纵坐标 C.与x轴交点的横坐标 D.与x轴交点的纵坐标 选做题： 2.已知关于x的方程mx+n=0的解是x=-2，则直线y=mx+n与x轴的交点坐标是__________. 【综合拓展类作业】 3.一次函数y=kx+b(k,b为常数，且k≠0)的图象如图所示，根据图象信息可求得关于x的方程kx+b=4的解为多少？
课堂总结
作业设计 【知识技能类作业】 必做题： 1、一次函数y=kx+b的图象如图所示，则方程kx+b=0的解为( ) A.x=2 B.y=2 C.x=-1 D.y=-1 选做题： 2．将直角坐标系中一次函数的图象与坐标轴围成的三角形，叫做此一次函数的坐标三角形.例如，图中的一次函数图象与x，y轴分别交于点A，B，则△ABO为此一次函数的坐标三角形，一次函数y=- / x+4的坐标三角形的周长是______. 【综合拓展类作业】 3、已知二元一次方程y-kx-2k+4=0化为一次函数后，经过画图发现，它与x轴的交点为-1. (1)请将二元一次方程化为一次函数的形式； (2)这个函数的图象不经过第几象限？ (3)求这个一次函数的图象与y轴的交点坐标.
教学反思
21世纪教育网(www.21cnjy.com)