湖南省永州市祁阳市浯溪一中2025年中考模拟数学试卷(三)(含答案)
文档属性
| 名称 | 湖南省永州市祁阳市浯溪一中2025年中考模拟数学试卷(三)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 904.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 09:49:12 | ||
图片预览


文档简介
湖南省祁阳市浯溪一中2025年中考模拟数学试卷(三)
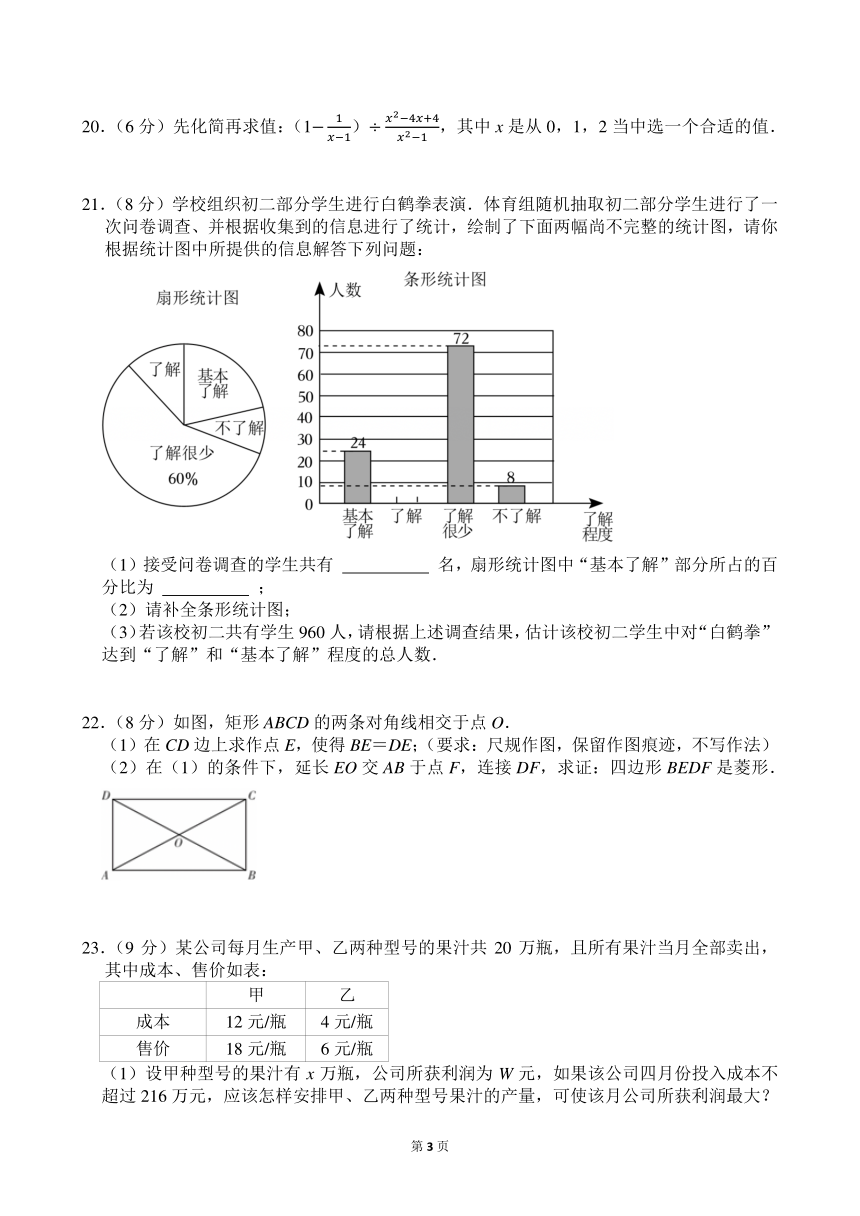
一.选择题(共10小题,满分30分,每小题3分)
1.实数2,0,,﹣3中,最大的数是( )
A.2 B.0 C.﹣3 D.
2.下列图形中,是中心对称图形的是( )
A.B. C. D.
3.如图是一个由6个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
4.用反证法证明命题:“在△ABC中,∠B≠∠C,则AB≠AC”.应先假设( )
A.AB>AC B.AB<AC C.AB=AC D.∠B=∠C
5.高老师准备从超市购买一些奖品.如图,高老师从学校出发,随机选择一条道路,需先经过广场,最终到达超市,则这条路线恰好是最短路线的概率是( )
A. B. C. D.
6.如图,△ABC的顶点A(﹣8,0),B(﹣2,8),点C在y轴的正半轴上,AB=AC,将△ABC向右平移得到△A'B'C',若A'B'经过点C,则点C'的坐标为( )
A. B.(3,6) C. D.(4,6)
第5题图 第6题图 第7题图 第8题图
7.如图,以矩形ABCD的顶点A为圆心,AD长为半径画弧交CB的延长线于E;过点D作DF∥AE交BC于点F,连接AF.AB=4,AD=5,则AF的长是( )
A. B. C.3 D.
8.如图,在△ABC中,DE∥BC,若S△ADE:S△BDE=1:2,S△ADE=2,则S△ABC为( )
A.4 B.6 C.16 D.18
9.如图1是一盏亮度可调节的台灯,通过调节总电阻R来控制电流I实现灯光亮度的变化.电流I(A)与电阻R(Ω)之间的函数关系如图2所示.下列结论正确的是( )
A. B.当I>10时,R>22
C.当I=5时,R=40 D.当I>2时,0<R<110
10.已知关于x的一元二次方程x2﹣2x+c=0无实数根,则抛物线y=x2﹣2x+c的顶点所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
第9题图 第13题图 第16题图 第17题图
二.填空题(共8小题,满分24分,每小题3分)
11.若m﹣n=﹣6,则代数式2037+2m﹣2n的值等于 .
12.2021年11月3日揭晓的2020年度国家自然科学奖,共评出了两项一等奖,其中一项是“有序介孔高分子和碳材料的创制应用”.有序介孔材料是上世纪90年代迅速兴起的新型纳米材料,孔径在0.000000002米~0.000000005米范围内.数据0.000000002用科学记数法可表示为 .
13.如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.那么小明一共走了 米.
14.若数据1,2,4,3,5的平均数是3,则中位数是 .
15.对于实数对(a,b),定义偏左数为,偏右数为.对于实数对(2x﹣2,3﹣x),若Pl﹣Pr≤1,则x的最大整数值是 .
16.为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽AC的长是 米.(π取3.14,计算结果精确到0.1)
17.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点A的坐标为(﹣1,0),固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,此时∠ABC'=120°,则点C的对应点C′的坐标为 .
18.某商品原价100元,经过连续两次降价后,售价为81元,设平均每次降价的百分率为x,则x的值为 .
三.解答题(共8小题,满分66分)
19.(6分)计算:|﹣4|﹣(﹣2)﹣2+(π﹣3.14)0.
20.(6分)先化简再求值:(1),其中x是从0,1,2当中选一个合适的值.
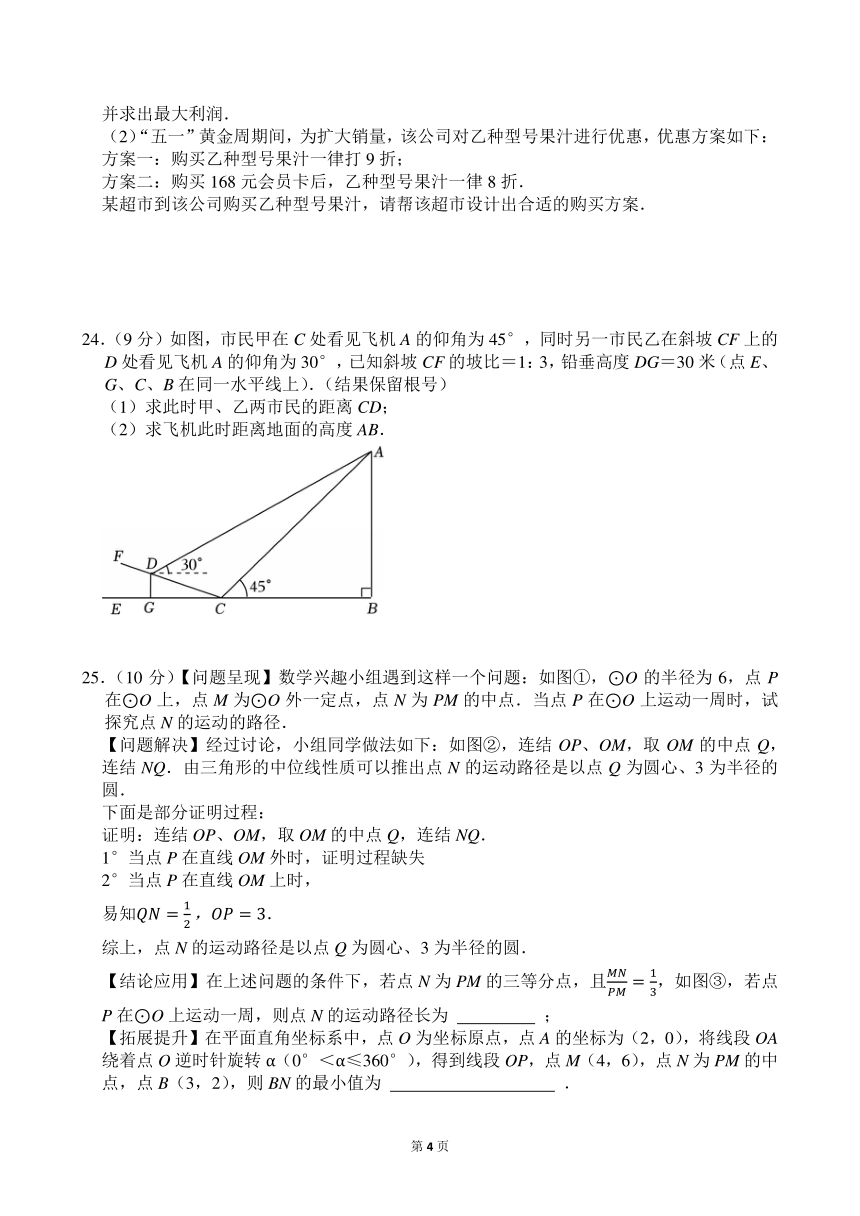
21.(8分)学校组织初二部分学生进行白鹤拳表演.体育组随机抽取初二部分学生进行了一次问卷调查、并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 名,扇形统计图中“基本了解”部分所占的百分比为 ;
(2)请补全条形统计图;
(3)若该校初二共有学生960人,请根据上述调查结果,估计该校初二学生中对“白鹤拳”达到“了解”和“基本了解”程度的总人数.
22.(8分)如图,矩形ABCD的两条对角线相交于点O.
(1)在CD边上求作点E,使得BE=DE;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,延长EO交AB于点F,连接DF,求证:四边形BEDF是菱形.
23.(9分)某公司每月生产甲、乙两种型号的果汁共20万瓶,且所有果汁当月全部卖出,其中成本、售价如表:
甲 乙
成本 12元/瓶 4元/瓶
售价 18元/瓶 6元/瓶
(1)设甲种型号的果汁有x万瓶,公司所获利润为W元,如果该公司四月份投入成本不超过216万元,应该怎样安排甲、乙两种型号果汁的产量,可使该月公司所获利润最大?并求出最大利润.
(2)“五一”黄金周期间,为扩大销量,该公司对乙种型号果汁进行优惠,优惠方案如下:
方案一:购买乙种型号果汁一律打9折;
方案二:购买168元会员卡后,乙种型号果汁一律8折.
某超市到该公司购买乙种型号果汁,请帮该超市设计出合适的购买方案.
24.(9分)如图,市民甲在C处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°,已知斜坡CF的坡比=1:3,铅垂高度DG=30米(点E、G、C、B在同一水平线上).(结果保留根号)
(1)求此时甲、乙两市民的距离CD;
(2)求飞机此时距离地面的高度AB.
25.(10分)【问题呈现】数学兴趣小组遇到这样一个问题:如图①,⊙O的半径为6,点P在⊙O上,点M为⊙O外一定点,点N为PM的中点.当点P在⊙O上运动一周时,试探究点N的运动的路径.
【问题解决】经过讨论,小组同学做法如下:如图②,连结OP、OM,取OM的中点Q,连结NQ.由三角形的中位线性质可以推出点N的运动路径是以点Q为圆心、3为半径的圆.
下面是部分证明过程:
证明:连结OP、OM,取OM的中点Q,连结NQ.
1°当点P在直线OM外时,证明过程缺失
2°当点P在直线OM上时,
易知.
综上,点N的运动路径是以点Q为圆心、3为半径的圆.
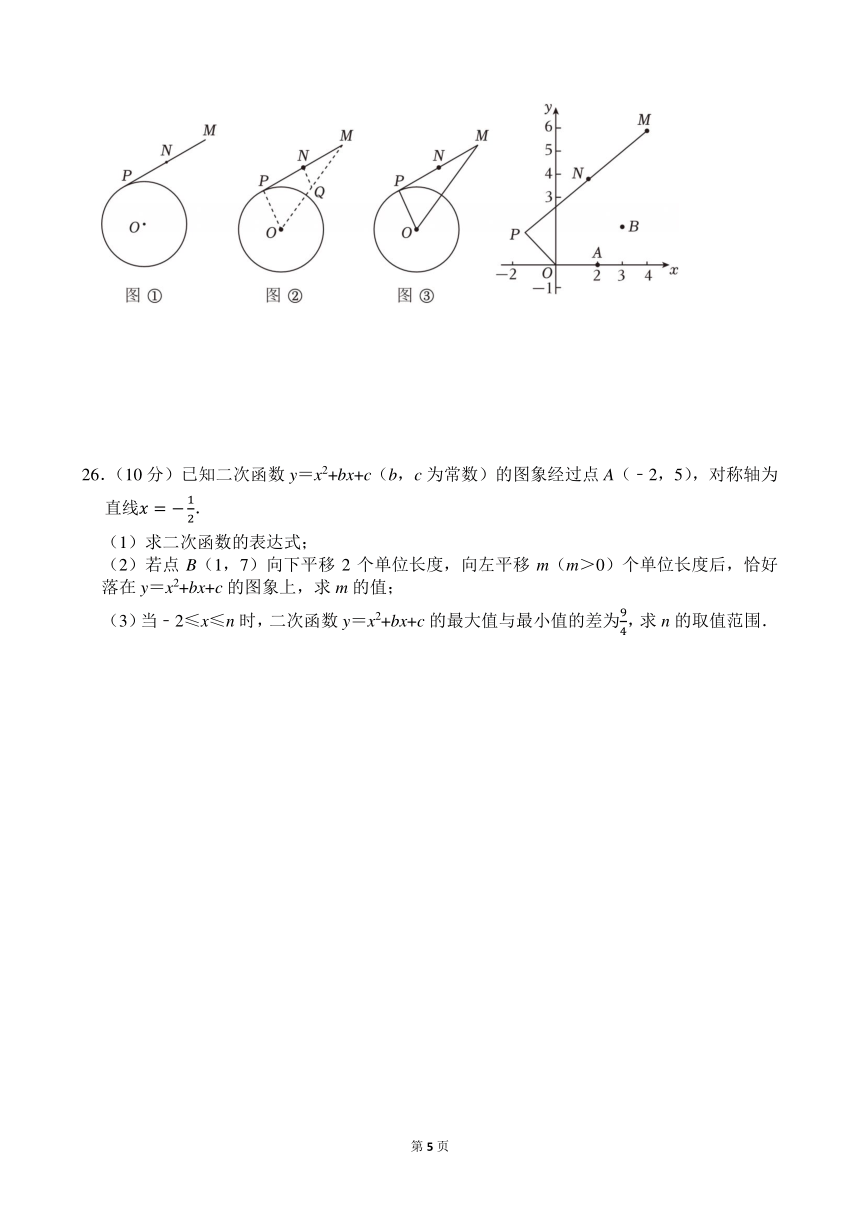
【结论应用】在上述问题的条件下,若点N为PM的三等分点,且,如图③,若点P在⊙O上运动一周,则点N的运动路径长为 ;
【拓展提升】在平面直角坐标系中,点O为坐标原点,点A的坐标为(2,0),将线段OA绕着点O逆时针旋转α(0°<α≤360°),得到线段OP,点M(4,6),点N为PM的中点,点B(3,2),则BN的最小值为 .
26.(10分)已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(﹣2,5),对称轴为直线.
(1)求二次函数的表达式;
(2)若点B(1,7)向下平移2个单位长度,向左平移m(m>0)个单位长度后,恰好落在y=x2+bx+c的图象上,求m的值;
(3)当﹣2≤x≤n时,二次函数y=x2+bx+c的最大值与最小值的差为,求n的取值范围.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A. A D C D C A D D A
6.解析:过点B作BG⊥x轴于点G,
∵A(﹣8,0),B(﹣2,8),AB=AC,
∴OA=8,BG=8,OG=2,
∴AG=6,
∵BG2+AG2=AB2,
∴82+62=AB2,
∴AB=10,
∴AC=10,
在Rt△AOC,AC2=OA2+OC2,
∴OC=6,
点C(0,6);
设直线AB的解析式为:y=kx+b(k≠0),
∴,
解得,
∴;
设△ABC向右平移n个单位长度得到△A'B'C',
∴直线A'B'的解析式为:,∵点C(0,6)在直线A'B'上,∴,∴,∴△ABC向右平移个单位长度得到△A'B'C',
∴点,
7.解析:由矩形的性质得AD∥BC,∠ABC=90°,则∠ABE=90°,再证明四边形ADFE是平行四边形,由作图得AE=AD=5,则四边形ADFE是菱形,所以FE=AE=5,则BE3,可求得BF=2,则AF2,于是得到问题的答案.
8.解析:设点E到AB的距离为h,则,所以,则,由DE∥BC,证明△ADE∽△ABC,则,所以S△ABC=9S△ADE=18,于是得到问题的答案.
11.2025.
12.2×10﹣9m.
13.180.
14.3.
15.2.解析:∵对于实数对(a,b),定义偏左数为,偏右数为,∴对于实数对(2x﹣2,3﹣x),Pl,Pr,∵Pl﹣Pr≤1,∴1,∴3x﹣5≤3,∴x,∴x的最大整数值是2.
16.28.7.
19.解;|﹣4|﹣(﹣2)﹣2+(π﹣3.14)0 .
20.解:(1) ,∵x≠1,x≠2,
∴x=0时,原式.
21.解:(1)接受问卷调查的学生共有:72÷60%=120(名),
扇形统计图中“基本了解”部分所对应扇形的圆心角为:100%=20%,
故答案为:120,20%;
(2)“了解”的人数为:120﹣24﹣72﹣8=16(人),
补全条形统计图如下:
(3)(人),
答:估计该校初二学生中对将“白鹤拳”达到“了解”和“基本了解”程度的总人数为320人.
22.(1)解:如图,点E为所作;
(2)证明:∵四边形ABCD是矩形,
∴DO=OB,CD∥AB,
∴∠CDB=∠ABD,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA),
∴DE=BF,
而DE∥BF,
∴四边形BEDF是平行四边形,
∵BE=DE,
∴平行四边形BEDF是菱形.
23.解:(1)∵该公司每月生产甲、乙两种型号的果汁共20万瓶,且甲种型号的果汁生产了x万瓶,
∴乙种型号的果汁生产了(20﹣x)万瓶.
根据题意得:12x+4(20﹣x)≤216,
解得:x≤17.
∵公司所获利润为W元,
∴W=(18﹣12)x+(6﹣4)(20﹣x),
∴W=4x+40,
∵4>0,
∴W随x的增大而增大,
∴当x=17时,W取得最大值,最大值为4×17+40=108,此时20﹣x=20﹣17=3.
答:当甲种型号的果汁生产了17万瓶,乙种型号的果汁生产了3万瓶时,该月公司所获利润最大,最大利润为108万元;
(2)设该超市到该公司购买乙种型号果汁y瓶,则选择方案一所需费用为6×0.9y=5.4y元;选择方案二所需费用为168+6×0.8y=(168+4.8y)元.
若5.4y<168+4.8y,则y<280,
∴当0<y<280时,选择方案一购买更合算;
若5.4y=168+4.8y,则y=280,
∴当y=280时,选择两优惠方案所需费用相同;
若5.4y>168+4.8y,则y>280,
∴当y>280时,选择方案二购买更合算.
答:当0<y<280时,选择方案一购买更合算;当y=280时,选择两优惠方案所需费用相同;当y>280时,选择方案二购买更合算.
24.解:(1)过点D作DH⊥AB于点H,如图,
∵斜坡CF的坡比=1:3,
∴,
∵铅垂高度DG=30米,
∴CG=90米,
∴CD30(米),
答:甲、乙两市民的距离CD为30米;
(2)∵DG⊥BG,AB⊥BG,
∴四边形BHDG是矩形,
∴BH=DG=30米,DH=BG,
∵∠ABC=90°,∠ACB=45°,
∴△ABC是等腰直角三角形,
∴AB=BC,
设AB=BC=x米,则AH=AB﹣BH=(x﹣30)米,
DH=BG=CG+BC=(x+90)米,
∵,
∴,
解得,
∴米,
答:飞机距离地面的高度为米.
25.解:【结论应用】如图所示,在OM上取点Q,使,连接NQ,
1°当点P在直线OM外时,
∵,∠M=∠M,
∴△MPO∽△MNQ,
∴,即,
∴NQ=2;
2°当点P在线段OM上时,
∵,
∴,
∵,
∴,
∴,
3°当点P在MO延长线上时,
同理可得,,
综上,点N的运动路径是以点Q为圆心、2为半径的圆.
∴点N的运动路径长为2π×2=4π,
故答案为:4π;
【拓展提升】如图所示,
∵点A的坐标为(2,0),
∴OA=2,
∵将线段OA绕着点O逆时针旋转α(0°<α≤60°),
∴OP=OA=2,
∴点P在以点O为圆心,半径为2的圆上运动,
连接OM,取中点Q,
∵点N是OM的中点,
∴QN是三角形MOP的中位线,
∴,
∴点Q在以点N为圆心,半径为1的圆上运动,
∴BN≥BQ﹣QN,
∴当点Q,B,N三点共线,且点N运动到线段QB上时,BN有最小值,即BQ﹣QN的值,
∵O(0,0),M(4,6),点Q是OM的中点,
∴Q(2,3),
∵B(3,2),
∴,
∴,
∴BN的最小值为,
故答案为:.
26.解:(1)设,
把A(﹣2,5)代入得,
解得,
∴;
(2)点B平移后的点的坐标为(1﹣m,5),
则5=(1﹣m)2+(1﹣m)+3,
解得m=3或m=0(舍),
∴m的值为3;
(3)当时,
∴最大值与最小值的差为,
解得:不符合题意,舍去;
当时,
∴最大值与最小值的差为,符合题意;
当n>1时,
最大值与最小值的差为,
解得n1=1或n2=﹣2(舍去);
综上所述,n的取值范围为.
第1页
一.选择题(共10小题,满分30分,每小题3分)
1.实数2,0,,﹣3中,最大的数是( )
A.2 B.0 C.﹣3 D.
2.下列图形中,是中心对称图形的是( )
A.B. C. D.
3.如图是一个由6个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
4.用反证法证明命题:“在△ABC中,∠B≠∠C,则AB≠AC”.应先假设( )
A.AB>AC B.AB<AC C.AB=AC D.∠B=∠C
5.高老师准备从超市购买一些奖品.如图,高老师从学校出发,随机选择一条道路,需先经过广场,最终到达超市,则这条路线恰好是最短路线的概率是( )
A. B. C. D.
6.如图,△ABC的顶点A(﹣8,0),B(﹣2,8),点C在y轴的正半轴上,AB=AC,将△ABC向右平移得到△A'B'C',若A'B'经过点C,则点C'的坐标为( )
A. B.(3,6) C. D.(4,6)
第5题图 第6题图 第7题图 第8题图
7.如图,以矩形ABCD的顶点A为圆心,AD长为半径画弧交CB的延长线于E;过点D作DF∥AE交BC于点F,连接AF.AB=4,AD=5,则AF的长是( )
A. B. C.3 D.
8.如图,在△ABC中,DE∥BC,若S△ADE:S△BDE=1:2,S△ADE=2,则S△ABC为( )
A.4 B.6 C.16 D.18
9.如图1是一盏亮度可调节的台灯,通过调节总电阻R来控制电流I实现灯光亮度的变化.电流I(A)与电阻R(Ω)之间的函数关系如图2所示.下列结论正确的是( )
A. B.当I>10时,R>22
C.当I=5时,R=40 D.当I>2时,0<R<110
10.已知关于x的一元二次方程x2﹣2x+c=0无实数根,则抛物线y=x2﹣2x+c的顶点所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
第9题图 第13题图 第16题图 第17题图
二.填空题(共8小题,满分24分,每小题3分)
11.若m﹣n=﹣6,则代数式2037+2m﹣2n的值等于 .
12.2021年11月3日揭晓的2020年度国家自然科学奖,共评出了两项一等奖,其中一项是“有序介孔高分子和碳材料的创制应用”.有序介孔材料是上世纪90年代迅速兴起的新型纳米材料,孔径在0.000000002米~0.000000005米范围内.数据0.000000002用科学记数法可表示为 .
13.如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.那么小明一共走了 米.
14.若数据1,2,4,3,5的平均数是3,则中位数是 .
15.对于实数对(a,b),定义偏左数为,偏右数为.对于实数对(2x﹣2,3﹣x),若Pl﹣Pr≤1,则x的最大整数值是 .
16.为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽AC的长是 米.(π取3.14,计算结果精确到0.1)
17.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,点A的坐标为(﹣1,0),固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,此时∠ABC'=120°,则点C的对应点C′的坐标为 .
18.某商品原价100元,经过连续两次降价后,售价为81元,设平均每次降价的百分率为x,则x的值为 .
三.解答题(共8小题,满分66分)
19.(6分)计算:|﹣4|﹣(﹣2)﹣2+(π﹣3.14)0.
20.(6分)先化简再求值:(1),其中x是从0,1,2当中选一个合适的值.
21.(8分)学校组织初二部分学生进行白鹤拳表演.体育组随机抽取初二部分学生进行了一次问卷调查、并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 名,扇形统计图中“基本了解”部分所占的百分比为 ;
(2)请补全条形统计图;
(3)若该校初二共有学生960人,请根据上述调查结果,估计该校初二学生中对“白鹤拳”达到“了解”和“基本了解”程度的总人数.
22.(8分)如图,矩形ABCD的两条对角线相交于点O.
(1)在CD边上求作点E,使得BE=DE;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,延长EO交AB于点F,连接DF,求证:四边形BEDF是菱形.
23.(9分)某公司每月生产甲、乙两种型号的果汁共20万瓶,且所有果汁当月全部卖出,其中成本、售价如表:
甲 乙
成本 12元/瓶 4元/瓶
售价 18元/瓶 6元/瓶
(1)设甲种型号的果汁有x万瓶,公司所获利润为W元,如果该公司四月份投入成本不超过216万元,应该怎样安排甲、乙两种型号果汁的产量,可使该月公司所获利润最大?并求出最大利润.
(2)“五一”黄金周期间,为扩大销量,该公司对乙种型号果汁进行优惠,优惠方案如下:
方案一:购买乙种型号果汁一律打9折;
方案二:购买168元会员卡后,乙种型号果汁一律8折.
某超市到该公司购买乙种型号果汁,请帮该超市设计出合适的购买方案.
24.(9分)如图,市民甲在C处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°,已知斜坡CF的坡比=1:3,铅垂高度DG=30米(点E、G、C、B在同一水平线上).(结果保留根号)
(1)求此时甲、乙两市民的距离CD;
(2)求飞机此时距离地面的高度AB.
25.(10分)【问题呈现】数学兴趣小组遇到这样一个问题:如图①,⊙O的半径为6,点P在⊙O上,点M为⊙O外一定点,点N为PM的中点.当点P在⊙O上运动一周时,试探究点N的运动的路径.
【问题解决】经过讨论,小组同学做法如下:如图②,连结OP、OM,取OM的中点Q,连结NQ.由三角形的中位线性质可以推出点N的运动路径是以点Q为圆心、3为半径的圆.
下面是部分证明过程:
证明:连结OP、OM,取OM的中点Q,连结NQ.
1°当点P在直线OM外时,证明过程缺失
2°当点P在直线OM上时,
易知.
综上,点N的运动路径是以点Q为圆心、3为半径的圆.
【结论应用】在上述问题的条件下,若点N为PM的三等分点,且,如图③,若点P在⊙O上运动一周,则点N的运动路径长为 ;
【拓展提升】在平面直角坐标系中,点O为坐标原点,点A的坐标为(2,0),将线段OA绕着点O逆时针旋转α(0°<α≤360°),得到线段OP,点M(4,6),点N为PM的中点,点B(3,2),则BN的最小值为 .
26.(10分)已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(﹣2,5),对称轴为直线.
(1)求二次函数的表达式;
(2)若点B(1,7)向下平移2个单位长度,向左平移m(m>0)个单位长度后,恰好落在y=x2+bx+c的图象上,求m的值;
(3)当﹣2≤x≤n时,二次函数y=x2+bx+c的最大值与最小值的差为,求n的取值范围.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A. A D C D C A D D A
6.解析:过点B作BG⊥x轴于点G,
∵A(﹣8,0),B(﹣2,8),AB=AC,
∴OA=8,BG=8,OG=2,
∴AG=6,
∵BG2+AG2=AB2,
∴82+62=AB2,
∴AB=10,
∴AC=10,
在Rt△AOC,AC2=OA2+OC2,
∴OC=6,
点C(0,6);
设直线AB的解析式为:y=kx+b(k≠0),
∴,
解得,
∴;
设△ABC向右平移n个单位长度得到△A'B'C',
∴直线A'B'的解析式为:,∵点C(0,6)在直线A'B'上,∴,∴,∴△ABC向右平移个单位长度得到△A'B'C',
∴点,
7.解析:由矩形的性质得AD∥BC,∠ABC=90°,则∠ABE=90°,再证明四边形ADFE是平行四边形,由作图得AE=AD=5,则四边形ADFE是菱形,所以FE=AE=5,则BE3,可求得BF=2,则AF2,于是得到问题的答案.
8.解析:设点E到AB的距离为h,则,所以,则,由DE∥BC,证明△ADE∽△ABC,则,所以S△ABC=9S△ADE=18,于是得到问题的答案.
11.2025.
12.2×10﹣9m.
13.180.
14.3.
15.2.解析:∵对于实数对(a,b),定义偏左数为,偏右数为,∴对于实数对(2x﹣2,3﹣x),Pl,Pr,∵Pl﹣Pr≤1,∴1,∴3x﹣5≤3,∴x,∴x的最大整数值是2.
16.28.7.
19.解;|﹣4|﹣(﹣2)﹣2+(π﹣3.14)0 .
20.解:(1) ,∵x≠1,x≠2,
∴x=0时,原式.
21.解:(1)接受问卷调查的学生共有:72÷60%=120(名),
扇形统计图中“基本了解”部分所对应扇形的圆心角为:100%=20%,
故答案为:120,20%;
(2)“了解”的人数为:120﹣24﹣72﹣8=16(人),
补全条形统计图如下:
(3)(人),
答:估计该校初二学生中对将“白鹤拳”达到“了解”和“基本了解”程度的总人数为320人.
22.(1)解:如图,点E为所作;
(2)证明:∵四边形ABCD是矩形,
∴DO=OB,CD∥AB,
∴∠CDB=∠ABD,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA),
∴DE=BF,
而DE∥BF,
∴四边形BEDF是平行四边形,
∵BE=DE,
∴平行四边形BEDF是菱形.
23.解:(1)∵该公司每月生产甲、乙两种型号的果汁共20万瓶,且甲种型号的果汁生产了x万瓶,
∴乙种型号的果汁生产了(20﹣x)万瓶.
根据题意得:12x+4(20﹣x)≤216,
解得:x≤17.
∵公司所获利润为W元,
∴W=(18﹣12)x+(6﹣4)(20﹣x),
∴W=4x+40,
∵4>0,
∴W随x的增大而增大,
∴当x=17时,W取得最大值,最大值为4×17+40=108,此时20﹣x=20﹣17=3.
答:当甲种型号的果汁生产了17万瓶,乙种型号的果汁生产了3万瓶时,该月公司所获利润最大,最大利润为108万元;
(2)设该超市到该公司购买乙种型号果汁y瓶,则选择方案一所需费用为6×0.9y=5.4y元;选择方案二所需费用为168+6×0.8y=(168+4.8y)元.
若5.4y<168+4.8y,则y<280,
∴当0<y<280时,选择方案一购买更合算;
若5.4y=168+4.8y,则y=280,
∴当y=280时,选择两优惠方案所需费用相同;
若5.4y>168+4.8y,则y>280,
∴当y>280时,选择方案二购买更合算.
答:当0<y<280时,选择方案一购买更合算;当y=280时,选择两优惠方案所需费用相同;当y>280时,选择方案二购买更合算.
24.解:(1)过点D作DH⊥AB于点H,如图,
∵斜坡CF的坡比=1:3,
∴,
∵铅垂高度DG=30米,
∴CG=90米,
∴CD30(米),
答:甲、乙两市民的距离CD为30米;
(2)∵DG⊥BG,AB⊥BG,
∴四边形BHDG是矩形,
∴BH=DG=30米,DH=BG,
∵∠ABC=90°,∠ACB=45°,
∴△ABC是等腰直角三角形,
∴AB=BC,
设AB=BC=x米,则AH=AB﹣BH=(x﹣30)米,
DH=BG=CG+BC=(x+90)米,
∵,
∴,
解得,
∴米,
答:飞机距离地面的高度为米.
25.解:【结论应用】如图所示,在OM上取点Q,使,连接NQ,
1°当点P在直线OM外时,
∵,∠M=∠M,
∴△MPO∽△MNQ,
∴,即,
∴NQ=2;
2°当点P在线段OM上时,
∵,
∴,
∵,
∴,
∴,
3°当点P在MO延长线上时,
同理可得,,
综上,点N的运动路径是以点Q为圆心、2为半径的圆.
∴点N的运动路径长为2π×2=4π,
故答案为:4π;
【拓展提升】如图所示,
∵点A的坐标为(2,0),
∴OA=2,
∵将线段OA绕着点O逆时针旋转α(0°<α≤60°),
∴OP=OA=2,
∴点P在以点O为圆心,半径为2的圆上运动,
连接OM,取中点Q,
∵点N是OM的中点,
∴QN是三角形MOP的中位线,
∴,
∴点Q在以点N为圆心,半径为1的圆上运动,
∴BN≥BQ﹣QN,
∴当点Q,B,N三点共线,且点N运动到线段QB上时,BN有最小值,即BQ﹣QN的值,
∵O(0,0),M(4,6),点Q是OM的中点,
∴Q(2,3),
∵B(3,2),
∴,
∴,
∴BN的最小值为,
故答案为:.
26.解:(1)设,
把A(﹣2,5)代入得,
解得,
∴;
(2)点B平移后的点的坐标为(1﹣m,5),
则5=(1﹣m)2+(1﹣m)+3,
解得m=3或m=0(舍),
∴m的值为3;
(3)当时,
∴最大值与最小值的差为,
解得:不符合题意,舍去;
当时,
∴最大值与最小值的差为,符合题意;
当n>1时,
最大值与最小值的差为,
解得n1=1或n2=﹣2(舍去);
综上所述,n的取值范围为.
第1页
同课章节目录
