专题八 一线三等角模型(含答案) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题八 一线三等角模型(含答案) 2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 488.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 16:15:09 | ||
图片预览



文档简介
一线三等角模型
1.一线三等角
【核心考点】:
只要在一条直线上出现三个角相等,一般都可以构造全等三角形解决问题.
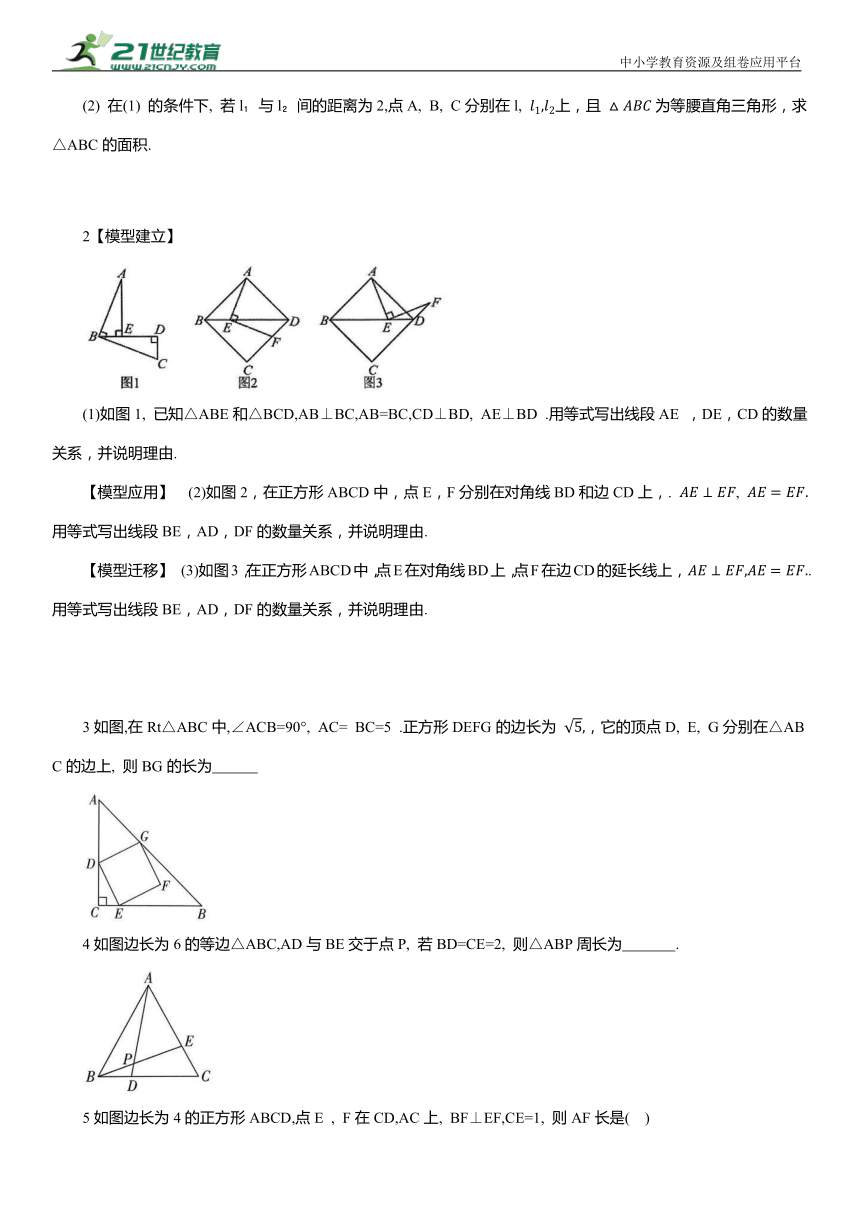
【经典图形】:
2.高分宝典
(1)模型识别:
①一条直线上出现三个直角 ,考虑一线三垂直
②一条直线上出现三个相等的角,考虑一线三等角
(2)辅助线构造:
①一线三垂直:见于一条直线过直角顶点,且已过45°角顶点向直线作垂,构成完整的三垂模型.
②一线三等角:一半不需要自己构造辅助线,观察出全等关系即可.
真题精炼
1.如图, 已知直线l //l .
(1)在l ,l 所在的平面内求作直线l,使得 ,且l与l 间的距离恰好等于l与l 间的距离;(要求:尺规作图,不写作法,保留作图痕迹)
(2) 在(1) 的条件下, 若l 与l 间的距离为2,点A, B, C分别在l, 上,且 为等腰直角三角形,求△ABC的面积.
2【模型建立】
(1)如图1, 已知△ABE和△BCD,AB⊥BC,AB=BC,CD⊥BD, AE⊥BD .用等式写出线段AE ,DE,CD的数量关系,并说明理由.
【模型应用】 (2)如图2,在正方形ABCD中,点E,F分别在对角线BD和边CD上,. , 用等式写出线段BE,AD,DF的数量关系,并说明理由.
【模型迁移】 (3)如图3,在正方形ABCD中,点E在对角线BD上,点F在边CD的延长线上, .用等式写出线段BE,AD,DF的数量关系,并说明理由.
3如图,在Rt△ABC中,∠ACB=90°, AC= BC=5 .正方形DEFG的边长为 ,它的顶点D, E, G分别在△ABC的边上, 则BG的长为
4如图边长为6的等边△ABC,AD与BE交于点P, 若BD=CE=2, 则△ABP周长为 .
5如图边长为4的正方形ABCD,点E , F在CD,AC上, BF⊥EF,CE=1, 则AF长是( )
6如图,正比例函数y=x的图象与反比例函数 的图象交于点A(1,a), 在△ABC中,∠ACB=90°,CA=CB,点C坐标为(-2,0).
(1) 求k的值.
(2)求AB所在直线的解析式.
7如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, OA=2, 将△AOB绕点O逆时针旋转90°, 点B的对应点B'的坐标是( )
8在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 则点A的坐标为( )
9如图A(2,0), B(0,1), AC由AB绕点A顺时针旋转90°而得, 则AC所在直线解析式是
10正方形和等腰Rt△AEF, AB=5,AE=4.△AEF绕A转,∠ ABF最大,
11如图.已知点A(4,3),点B为直线y =-2上的一动点,点C(0,n),-212如图,在Rt△ABC中,CA=CB, M是AB的中点,点D在BM上, 垂足分别为E, F,连接EM .则下列结论中:①BF=CE;②∠AEM =∠DEM ;③ ⑤若AE平分 则EF ⑥CF·DM=BM·DE,正确的有 . (只填序号)
13如图正方形ABCD对角线AC上有一点E,且( ,过点E作 ,交CB延长线于点G,连接GF并延长,交AC延长线于点P ,若 ,则线段EP的长是
14回答下列问题.
(1) 如图,在四边形ABCD中,. ,点E在边CD上,. ,求证:
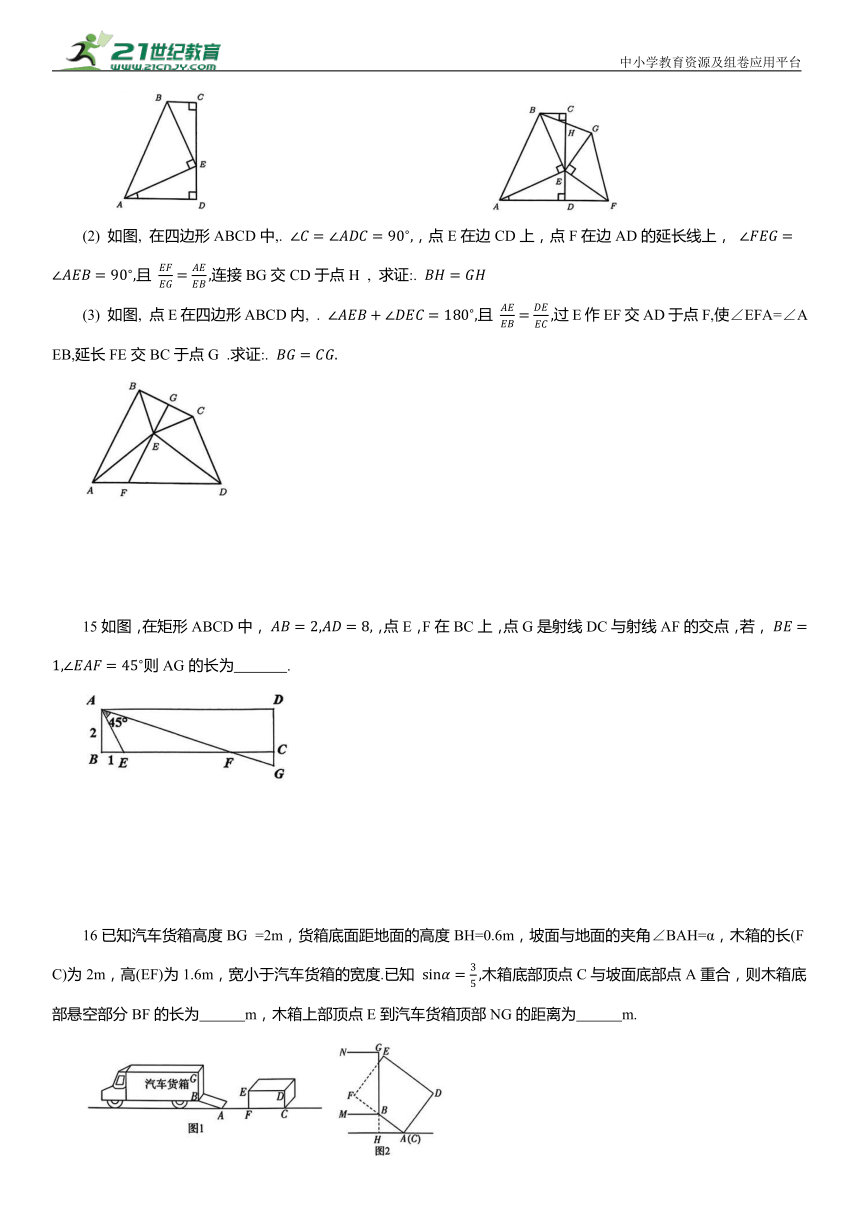
(2) 如图, 在四边形ABCD中,. ,点E在边CD上,点F在边AD的延长线上, 且 连接BG交CD于点H , 求证:.
(3) 如图, 点E在四边形ABCD内, . 且 过E作EF交AD于点F,使∠EFA=∠AEB,延长FE交BC于点G .求证:.
15如图,在矩形ABCD中, ,点E,F在BC上,点G是射线DC与射线AF的交点,若, 则AG的长为 .
16已知汽车货箱高度BG =2m,货箱底面距地面的高度BH=0.6m,坡面与地面的夹角∠BAH=α,木箱的长(FC)为2m,高(EF)为1.6m,宽小于汽车货箱的宽度.已知 木箱底部顶点C与坡面底部点A重合,则木箱底部悬空部分BF的长为 m,木箱上部顶点E到汽车货箱顶部NG的距离为 m.
17如图,在直角坐标系中,点A、点B分别是x轴正半轴,y轴正半轴上的动点,以AB为直角边作等腰直角三角形ABC,其中点A为直角顶点,点P为斜边BC的中点,则下列说法中正确的有( )
①若点A、点B选择适当位置,则可能有OP⊥BC;
②若点A(a,0) , 点B(0,b), 则C点的坐标必是(
③无论AB怎样运动, 都有OP≤AB .
A. ①② B. ②③ C. ①③ D. ①②③
18如图将正方形OABC放在坐标系中,A的坐标为( ,则点C的坐标为 .
19如图正方形ABCD中,E是边AB上的一动点(不与点A,B重合),点A关于直线DE的对称点为F ,连接EF并延长交BC于点G,连接DG,过点E作 交DG的延长线于点H ,连接BH .
(1) 求证:
(2)用等式表示线段BH与AE的数量关系,并证明.
1如图,已知直线l //l .
(1)在l ,l 所在的平面内求作直线l,使得l//l //l ,且l与l 间的距离恰好等于l与l 间的距离;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若l 与l 间的距离为2,点A,B,C分别在l,l ,l 上,且△ABC为等腰直角三角形,求△ABC的面积.
【答案】(1)见解析
(2)1或
【解析】(1)如图,直线l即为所求作的直线.
(2) ①当∠BAC=90°,AB=AC时,如图1,
∵l//l //l ,直线l 与l 间的距离为2,且l与l 间的距离等于l与l 间的距离,根据图形的对称性可知:BC=2,
②当∠ABC=90°,BA=BC时,
如图2,分别过点A,C作直线l 的垂线,垂足为M,N,
∴∠AMB=∠BNC=90°,
∵l//l //l ,直线l 与l 间的距离为2,且l与l 间的距离等于l与l 间的距离,
∴CN=2,AM=1,
·∠MAB+∠ABM=90°,∠NBC+∠ABM=90°,
∴∠MAB=∠NBC,
∴△AMB≌△BNC(AAS),
∴BM=CN=2,
在Rt△ABM中,由勾股定理得
③当∠ACB=90°,CA=CB时,同理②可得,
综上所述,△ABC的面积为1或
【标注】 【知识点】AAS
2.【模型建立】
(1)如图1,已知△ABE和△BCD,AB⊥BC,AB=BC,CD⊥BD,AE⊥BD.用等式写出线段AE,DE,CD的数量关系,并说明理由.
【模型应用】
(2)如图2,在正方形ABCD中,点E,F分别在对角线BD和边CD上, AE⊥EF,AE=EF用等式写出线段BE,AD,DF的数量关系,并说明理由
【模型迁移】
(3)如图3,在正方形ABCD中,点E在对角线BD上,点F在边CD的延长线上, AE⊥EF,AE=EF.用等式写出线段BE,AD,DF的数量关系,并说明理由.
【答案】(1)DE+CD=AE,理由见详解, 理由见详解,
理由见详解
【解析】
【分析】
(1) 直接证明△ABE≌△BCD,即可证明;
(2)过E点作EM⊥AD于点M,过E点作EN⊥CD于点N,先证明Rt△AEM≌Rt△FEN,可得AM=NF,结合等腰直角三角形的性质可得: NF=ND-DF=MD-DF,即有 进而可得 即可证;
(3)过A点作AH⊥BD于点H,过F点作FG⊥BD,交BD的延长线于点G,先证明△HAEg△GEF,再结合等腰直角三角形的性质,即可证明.
【详解】
(1) DE+CD=AE,理由如下:
∵CD⊥BD,AE⊥BD,AB⊥BC,
∴∠ABC=∠D=∠AEB=90°,
∴∠ABE+∠CBD=∠C+∠CBD=90°,
∴∠ABE=∠C,
∵AB=BC,
∴△ABE≌△BCD,
∴BE=CD,AE=BD,
∴DE=BD-BE=AE-CD,
∴DE+CD=AE;
理由如下:
过E点作EM⊥AD于点M,过E点作EN⊥CD于点N,如图,
∵四边形ABCD是正方形,BD是正方形的对角线,
∴∠ADB=∠CDB=45°,BD平分∠ADC,∠ADC=90°,
即
:EN⊥CD,EM⊥AD,
. EM=EN,
:AE=EF.
. Rt△AEM≌Rt△FEN,
AM=NF,
EM=EN,EN⊥CD,EM⊥AD,∠ADC=90°,
∴四边形EMDN是正方形,
∵ED是正方形EMDN对角线, MD=ND,
即
即有
理由见详解,
过A点作AH⊥BD于点H,过F点作FG⊥BD,交BD的延长线于点G,如图,
∵AH⊥BD, FG⊥BD,AE⊥EF,
∴∠AHE=∠G=∠AEF=90°,
∴∠AEH+∠HAE=∠AEH+∠FEG=90°,
∴∠HAE=∠FEG,
又∵AE=AF,
∴△HAE≌△GEF,
∴HE=FG,
∵在正方形ABCD中,∠BDC =45°,
∴∠DFG=45°,
∴△DFG是等腰直角三角形,
∵∠ADB=45°,AH⊥HD,
∴△ADH是等腰直角三角形,
【点睛】
本题主要考查了正方形的性质,等腰直角三角形的性质,全等三角形的判定与性质,角平分线的性质等知识,题目难度中等,作出合理的辅助线,灵活证明三角形的全等,并准确表示出各个边之间的数量关系,是解答本题的关键.
【标注】 【知识点】正方形的性质
【知识点】勾股定理
【知识点】角分线性质定理
【业务题型】证明题
3.如图,在Rt△ABC中,∠ACB=90°,AC= BC =5.正方形DEFG的边长为 ,它的顶点D,E,G分别在△ABC的边上,则BG的长为 .
【答案】3
【解析】解:过点G作GH⊥AC,则:∠AHG=∠GHD=90°,
∴∠DGH+∠HDG=90°,
∵∠ACB=90°,AC=BC=5,
∴AH=HG,
设AH=HG=x,则:CH=AC-AH=5-x,
∵正方形DEFG,
∴DG=DE,∠GDE=90°,
∴∠HDG+∠CDE=90°.
∴∠HGD=∠CDE.
∵∠C=∠GHD=90°,
∴△GHD≌△DCE,
∴CD=GH=x,
∴DH=CH--CD=5-2x,
Rt△GHD中,由勾股定理,得:(
解得:x=2,
∴AH=2,CH=3,
∵∠C=∠AHD=90°,
∴HG∥BC,
故答案为:3
【标注】【知识点】正方形与全等综合
4如图,在边长为6的等边△ABC中,D、E分别为边BC、AC上的点,AD与BE相交于点P,若BD=CE=2,则△ABP的周长为 .
【答案】
【解析】如下图所示,过点E作EF⊥AB于F,
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BAC=∠BCE=60°,
∵CE=BD=2,AB=AC=6.
∴AE=4,
∴AF=AE·cos∠EAF=2,EF=AE·sin∠EAF=2
∴BF=4.
又∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,AD=BE,
又∵∠BDP=∠ADB,
∴△BDP∽△ADB,
∴△ABP的周长:
因此正确答案为:
【标注】 【知识点】等腰三角形
5如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上,BF⊥EF,CE=1,则AF的长是( ).
A.2
【答案】B
【解析】如图所示,过F作AB的垂线分别交AB,CD于N,M,
∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠BNM=90°,AB=BC=OD=4,
∴四边形CMNB是矩形,
∴MN=BC=4,CM=BN,
∵BF⊥EF,
∴∠EFB=∠FNB=90°,
∴∠FBN+∠NFB=∠NFB+∠EFM,
∴∠FBN=∠EFM,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴∠MFC=∠MCF=45°,
∴MF=MC=NB,
在△MEF和△NFB中,
∴△MEF≌△NFB(AAS),
∴ME=FN,
设ME=FN=x,则MC=MF=BN=1+x,
:MN=MF+FN,即1+x+x=4,解得
∵四边形ABCD是正方形, MN⊥AB,
∴∠NAF=∠AFN=45°,
∴FN=AN,
故选B.
【标注】 【知识点】特殊平行四边形
6如图,正比例函数y=x的图象与反比例函数 的图象交于点A(1,a),在△ABO中,∠ACB=90°,CA=CB,点C坐标为(-2,0).
(1)求k的值.
(2)求AB所在直线的解析式.
【答案】(1) k=1.
【解析】(1)∵正比例函数y=x的图象与反比例函数 的图象交于点A(1,a),
∴a=1,
∴A(1,1),
∴k=1×1=1.
(2)过点A作AD⊥x轴于点D ,过点B作BE⊥x轴于点E,
∵C(-2,0),A(1,1),
∴OD=1,OC=2,
∴CD=OC+OD=2+1=3,DA=1,
∵CA=CB,∠BEC=∠CDA=90°,∠ACB=90°,
∴∠1=∠3,
∴△CBE≌△ACD(AAS),
∴EB=CD=3,EC=DA=1,
∴OE=OC+EC=2+1=3,
∴B(-3,3),
设yAB= kx+b,
解得
∴AB所在直线的解析式为
【标注】 【知识点】反比例函数与一次函数综合
7如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( ) .
A.(- B. (-3, C.(- ,2+ D.(-1,2+
【答案】A
【解析】如图,过点B'作B'H⊥y轴于H,
∵∠AOB=∠B=30°.
. AB=OA=2,
.. A'B'=AB=2,
在Rt△A'B'H中,
∵A'B'=2,∠B'A'H=60°,
∴OH=2+1=3,
故选A.
【标注】【知识点】旋转的性质
8在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 则点A的坐标为( ).
c (2,
【答案】A
【解析】设A的坐标为 设C的坐标为
∵矩形OABC,画出如图,
AB与1/轴交于E,OC与 交于F,
∵BF∥1轴,BC∥AO,如图,
∴∠CBF=∠AOE.
在△BCF与△OAE中
∴△BCF≌△OAE(ASA),
∴△BCF中BF边上的高=△OAE中OE边上的高,
即
∴C点坐标为
∵O(0,0),
∴OA直线方程为y
设y= kx+b,将O(0,0),A(xA, )f代入,解得
设y= kx+b,将O(0,0). 代入解得A
b=0,
∴OC直线方程为
∵OC⊥OA,
解得 舍去,
故选A.
【标注】【知识点】反比例函数与四边形综合
9如图,在平面直角坐标系中,A(2,0),B(0,1), AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是 .
【答案】y=2x-4
【解析】∵A(2,0), B(0,1)
∴OA=2,OB=1,
过点C作CD⊥x轴于点D,
则易知△ACD≌△BAO(AAS) ,
∴AD=OB=1,CD=OA=2,
∴C(3,2),
设直线AC的解析式为y=kx+b,将点A,点C坐标代入得
∴直线AC的解析式为y=2x-4.
故答案为:y=2x-4.
【标注】 【知识点】根据条件写一次函数解析式
10如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,
【答案】6
【解析】作DH⊥AE于H,如图,
:AF=4,当△AEF绕点A旋转时,点F在以A为圆心,4为半径的圆上,
∴当BF为此圆的切线时,∠ABF最大,即BF⊥AF,
在Rt△ABF中,
∵∠EAF=90°,
∴∠DAH=∠BAF,
在△ADH和△ABF中,
∴△ADH≌△ABF(AAS),
∴DH=BF=3,
故答案为:6.
【标注】【知识点】正方形与全等综合
11如图.已知点A(4,3),点B为直线y=-2上的一动点,点C(0,n),-2【答案】
【解析】过点A作AM⊥y轴于点M, AN⊥BN于点N,
∵直线y=-2//z轴,
故∠ABN=α,
当sinα的值最大时, 值最大,
故当BN最小,即BG最大时, tanα最大,
即当BG最大时,sinα的值最大,
设BG=y,
则AM=4,GC=n+2,CM=3-π,
∵∠ACM+∠MAC=90°,
∠ACM+∠BCG=90°,
∴∠CAM=∠BCG,
.. tan∠CAM=tan∠BCG,
即
故当 时,y取得最大值,
故
故答案为。
12如图,在Rt△ABC中,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥CD,垂足分别为E,F,连接EM .则下列结论中:①BF=CE;②∠AEM=∠DEM;③ ;⑤若AE平分∠BAC,则EF:BF= :1;⑥CF-DM=BM·DE,正确的有 .(只填序号)
【答案】①②③④⑤⑥
【解析】∵∠ACB=90°,
∴∠ACE=∠CBF,
又∵∠BFD=90°=∠AEC,AC=BC,
∴△BCF≌△CAE(AAS),
∴BF=CE,故①正确;
由全等可得:AE=CF,BF=CE,
'. AE-CE=CF--CE=EF,连接FM,OM,
∵点M是AB中点,
在△BDF和△CDM中,
∠BFD=∠CMD,∠BDF=∠CDM,
∴∠DBF=∠DCM,又BM=CM,BF=CE,
∴△BFM≌△CEM,
∴FM=EM,∠BMF=∠CME,
∵∠BMC=90°,
.∠EMF=90°, 即△EMF为等腰直角三角形,
,故③正确;
∴∠MEF=∠AEM=45°,故②正确;
设AE与CM交于点N,连接DN,
∵∠DMF=∠NME,FM=EM,
∠DFM=∠DEM=∠AEM =45°,
∴△DFM≌△NEM,
∴DF=EN,DM=MN,
∴△DMN为等腰直角三角形,
而
故④正确;
∵AC=BC,∠ACB=90°,
∴∠CAB=45°,
∵AE平分∠BAC,
∴∠DAE=∠CAE=22.5°,∠ADE=67.5°,
∵∠DEM=45°,
∴∠EMD=67.5°,即DE=EM,
∵AE=AE,∠AED=∠AEC,∠DAE=∠CAE,
∴△ADE≌△ACE,
∴DE=CE,
∵△MEF为等腰直角三角形,
故⑤正确;
∵∠CDM=∠ADE,∠CMD=∠AED=90°,
∴△CDM∽△ADE,
BM=CM,AE=CF,
.. CF·DM=BM·DE,故⑥正确;
故答案为:①②③④⑤⑥.
【标注】 【知识点】相似三角形的性质与判定综合
13如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接GF并延长,交AC的延长线于点P,若AB=5,CF=2,则线段EP的长是 .
【答案】
【解析】如图,作FH⊥PE于H.
∵四边形ABCD是正方形, AB=5,
AC=5 ,∠ACD=∠FCH=45°,
:∠FHC=90°,CF=2,
∴CH=HF=
∵CE=4AE,
∴EH=5
在Rt△EFH中,
∴E,G,F,C四点共圆,
∴∠EFG=∠ECG=45°,
∴∠ECF=∠EFP=135°,
∵∠CEF=∠FEP,
∴△CEF∽△FEP.
故答案为
【标注】 【知识点】相似三角形的性质与判定综合
14回答下列问题.
(1) 如图,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°,求证:
(2)如图,在四边形ABCD中,. 点E在边CD上,点F在边AD的延长线上,∠FEG=∠AEB=90°,且. 连接BG交CD于点H,求证: BH=GH
(3)如图,点E在四边形ABCD内,∠AEB+∠DEC=180°,且 过E作EF交AD于点F ,使∠EFA=∠AEB,延长FE交BC于点G.求证:BG=CG.
【答案】(1)证明见解析.
(2)证明见解析.
(3)证明见解析.
【解析】(1)∵∠C =∠D =∠AEB=90°,
.∠BEC+∠AED=∠AED+∠EAD=90°,
∴∠BEC=∠EAD,
.△AED∽△EBC,
(2)如图,过点G作GM⊥CD于点M,
同(1)的方法可知
. BC=GM,
又∵∠C=∠GMH=90°,∠CHB=∠MHG,
∴△BCH≌△GMH(AAS).
∴BH=GH.
(3)方法一:如图,在EG上取点M,使∠BME=∠AFE,过点C作CN//BM,交EG的延长线于点N,则∠N=∠BMG,
∵∠EAF+∠AFE+∠AEF
=∠AEF+∠AEB+∠BEM
=180°,
∠EFA=∠AEB,
∴∠EAF=∠BEM,
∴△AEF∽△EBM,
∵∠AEB+∠DEC=180°,∠EFA+∠DFE=180°,
而∠EFA=∠AEB,
∴∠CED=∠EFD,
∵∠BMG+∠BME=180°,
∠N=∠BMG,
∠BME=∠AFE,
∴∠N=∠EFD,
∵∠EFD+∠EDF+∠FED
=∠FED+∠DEC+∠CEN
∴∠EDF=∠CEN,
∴△DEF∽△EON,
∴BM=CN,
又∵∠N=∠BMG,∠BGM=∠CGN,
∴△BGM≌△CGN(AAS),
∴BG=CG.
方法二:作BH//CE交EG延长线于点G,
∴∠EBH+∠BEC=180°,
∵∠AED+∠BEC=180°,
∴∠EBH=∠AED,
又∵∠BEH=∠EAD(外角) ,
∴△BEH∽△EAD,
又 (已知) ,
∴BH=EC,
∴△BGH≌△EGC,
∴BG=CG.
【标注】【知识点】相似三角形的性质与判定综合
15如图,在矩形ABCD中,AB=2,AD=8,点E,F在BC上,点G是射线DC与射线AF的交点.若,BE=1,∠EAF=45°则AG的长为 .
【答案】
【解析】
故答案为
【标注】 【知识点】动点与特殊平行四边形问题;相似三角形的性质;三垂直模型
16如图1,这是一个装有货物的长方体形状的木箱沿着坡面装进汽车货箱的立体示意图,图2是它的平面示意图.已知汽车货箱高度BG=2m,货箱底面距地面的高度BH=0.6m,坡面与地面的夹角∠BAH=α,木箱的长(FC)为2m,高(EF)为1.6m,宽小于汽车货箱的宽度.已知 木箱底部顶点C与坡面底部点A重合,则木箱底部悬空部分BF的长为 m,木箱上部顶点E到汽车货箱顶部NG的距离为 m.
【答案】1;0.12
【解析】∵BH=0.6米,
(米) ,
(米) ,
∵AF=FC=2(米) ,
∴BF=AF-AB=2-1=1(米),
作FJ⊥BG于点J, EK⊥FJ于点K,
则∠EKF=∠FJB=∠AHB=∠EFA=90°,易得∠EFK=∠FBJ=∠ABH,
∴△EFK∽△FBJ∽△ABH,
∵FB=AB,
∴△FBJ≌△ABH
(米) ,
∴EK =1.28(米) ,
. BJ+EK=0.6+1.28=1.88(米),
∴点E到NG的距离为2-1.88 =0.12(米) ,
故答案为:1,0.12.
17如图,在直角坐标系中,点A、点B分别是x轴正半轴,y轴正半轴上的动点,以AB为直角边作等腰直角三角形ABC,其中点A为直角顶点,点P为斜边BC的中点,则下列说法中正确的有( )
①若点A、点B选择适当位置,则可能有OP⊥BC;
②若点A(a,0),点B(0,b),则C点的坐标必是(a+b,a);
③无论AB怎样运动,都有OP≤AB.
A. ①② B. ②③ C. ①③ D.①②③
【答案】B
【解析】解:①由等腰直角三角形ABC,P是斜边BC的中点,得AP⊥BC,过一点有且只有一条直线与已知直线垂直,OP不能垂直斜边BC,故①错误;
②如图:作CD⊥x轴于点D,由余角的性质,得∠OBA=∠DAC,
在Rt△OBA和Rt△DAC中,
Rt△OBA≌Rt△DAC(AAS),
∴AD=OB=b,DC=OA=a.
由线段的和差,得OD=OA+AD=a+b,即C点坐标是(a+b,a),故②正确;
③由勾股定理,得
平方,
即AB≥OP,故③正确.
【标注】【知识点】勾股定理与全等
18如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为 .
【答案】
【解析】如图,作CE⊥x轴,AD⊥x轴,BF⊥AD,
易证△OCE≌△AOD,△BAF≌△AOD,
∴OE= ,CE=1,BF= ,AF=1,
如图作AF⊥x轴于F,CE⊥x轴于E.
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
:∠COE+∠AOF=90°,∠AOF+∠OAF=90°,
∴∠COE=∠OAF,
在△COE和△OAF中,
∴△COE≌△OAF,
∴CE=OF,OE=AF,
∵A(1, ),
∴CE=OF=1,OE=AF=
∴点C坐标(- ,1).
故答案为(- ,1).
【标注】【知识点】三垂直模型
19如图,在正方形ABCD中,E是边AB上的一动点(不与点A,B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1) 求证:GF=GC.
(2)用等式表示线段BH与AE的数量关系,并证明.
【答案】(1)证明见解析.
证明见解析.
【解析】(1)连接DF,
点A关于直线DE的对称点为F,
∴AE=EF,∠AED=∠FED,
在△ADE和△FDE中,
∴△ADE≌△FDE(SAS),
∴AD=DF,∠DFE=∠A,
在正方形ABCD中,AD=DC,
∴DF=DC,
在Rt△DFG和Rt△DCG中,
∴Rt△DFG≌Rt△DCG(HL),
∴GF=GC.
(2)方法一:过B点作HP⊥AB于P点,
∴∠CDG=∠FDG,
∵△ADE≌△FDE,
∴∠ADE=∠FDE,
在正方形ABOD中,∠ADC=90°,
∵DE⊥EH,
∴△DEH为等腰直角三角形,
∴DE=EH,
在Rt△ADE中,∠1+∠2=90°,
∴∠1=∠3,
在△ADE和△PEH中
∴△ADE≌△PEH(AAS),
∴AE=HP,DA=EP,
∵AD=AB,
∴AB=EP,
∴AE=BP,
∴BP=HP,
∴△BHP为等腰直角三角形,
中小学教育资源及组卷应用平台
方法二:如图,在线段AD上截取AM,使AM= AE,
∵AD=AB,
∴DM=BE;
由(1)知:∠1=∠2,∠3=∠4,
∵∠ADC=90°,
∴∠1+∠2+∠3+∠4=90°,
∴2∠2+2∠3=90°,
即
∵EH⊥DE,
∴∠DEH=90°,△DEH是等腰直角三角形,
∴∠AED+∠BEH=∠AED+∠1=90°,DE=EH,
∴∠1=∠BEH,
在△DME和△EBH中,
∴△DME≌△EBH(SAS),
∴EM=BH,
在Rt△AEM中,∠A=90°,AM=AE,
∴EM= AE,
∴B.
故答案为:
【标注】【知识点】正方形与全等综合
1.一线三等角
【核心考点】:
只要在一条直线上出现三个角相等,一般都可以构造全等三角形解决问题.
【经典图形】:
2.高分宝典
(1)模型识别:
①一条直线上出现三个直角 ,考虑一线三垂直
②一条直线上出现三个相等的角,考虑一线三等角
(2)辅助线构造:
①一线三垂直:见于一条直线过直角顶点,且已过45°角顶点向直线作垂,构成完整的三垂模型.
②一线三等角:一半不需要自己构造辅助线,观察出全等关系即可.
真题精炼
1.如图, 已知直线l //l .
(1)在l ,l 所在的平面内求作直线l,使得 ,且l与l 间的距离恰好等于l与l 间的距离;(要求:尺规作图,不写作法,保留作图痕迹)
(2) 在(1) 的条件下, 若l 与l 间的距离为2,点A, B, C分别在l, 上,且 为等腰直角三角形,求△ABC的面积.
2【模型建立】
(1)如图1, 已知△ABE和△BCD,AB⊥BC,AB=BC,CD⊥BD, AE⊥BD .用等式写出线段AE ,DE,CD的数量关系,并说明理由.
【模型应用】 (2)如图2,在正方形ABCD中,点E,F分别在对角线BD和边CD上,. , 用等式写出线段BE,AD,DF的数量关系,并说明理由.
【模型迁移】 (3)如图3,在正方形ABCD中,点E在对角线BD上,点F在边CD的延长线上, .用等式写出线段BE,AD,DF的数量关系,并说明理由.
3如图,在Rt△ABC中,∠ACB=90°, AC= BC=5 .正方形DEFG的边长为 ,它的顶点D, E, G分别在△ABC的边上, 则BG的长为
4如图边长为6的等边△ABC,AD与BE交于点P, 若BD=CE=2, 则△ABP周长为 .
5如图边长为4的正方形ABCD,点E , F在CD,AC上, BF⊥EF,CE=1, 则AF长是( )
6如图,正比例函数y=x的图象与反比例函数 的图象交于点A(1,a), 在△ABC中,∠ACB=90°,CA=CB,点C坐标为(-2,0).
(1) 求k的值.
(2)求AB所在直线的解析式.
7如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, OA=2, 将△AOB绕点O逆时针旋转90°, 点B的对应点B'的坐标是( )
8在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 则点A的坐标为( )
9如图A(2,0), B(0,1), AC由AB绕点A顺时针旋转90°而得, 则AC所在直线解析式是
10正方形和等腰Rt△AEF, AB=5,AE=4.△AEF绕A转,∠ ABF最大,
11如图.已知点A(4,3),点B为直线y =-2上的一动点,点C(0,n),-2
13如图正方形ABCD对角线AC上有一点E,且( ,过点E作 ,交CB延长线于点G,连接GF并延长,交AC延长线于点P ,若 ,则线段EP的长是
14回答下列问题.
(1) 如图,在四边形ABCD中,. ,点E在边CD上,. ,求证:
(2) 如图, 在四边形ABCD中,. ,点E在边CD上,点F在边AD的延长线上, 且 连接BG交CD于点H , 求证:.
(3) 如图, 点E在四边形ABCD内, . 且 过E作EF交AD于点F,使∠EFA=∠AEB,延长FE交BC于点G .求证:.
15如图,在矩形ABCD中, ,点E,F在BC上,点G是射线DC与射线AF的交点,若, 则AG的长为 .
16已知汽车货箱高度BG =2m,货箱底面距地面的高度BH=0.6m,坡面与地面的夹角∠BAH=α,木箱的长(FC)为2m,高(EF)为1.6m,宽小于汽车货箱的宽度.已知 木箱底部顶点C与坡面底部点A重合,则木箱底部悬空部分BF的长为 m,木箱上部顶点E到汽车货箱顶部NG的距离为 m.
17如图,在直角坐标系中,点A、点B分别是x轴正半轴,y轴正半轴上的动点,以AB为直角边作等腰直角三角形ABC,其中点A为直角顶点,点P为斜边BC的中点,则下列说法中正确的有( )
①若点A、点B选择适当位置,则可能有OP⊥BC;
②若点A(a,0) , 点B(0,b), 则C点的坐标必是(
③无论AB怎样运动, 都有OP≤AB .
A. ①② B. ②③ C. ①③ D. ①②③
18如图将正方形OABC放在坐标系中,A的坐标为( ,则点C的坐标为 .
19如图正方形ABCD中,E是边AB上的一动点(不与点A,B重合),点A关于直线DE的对称点为F ,连接EF并延长交BC于点G,连接DG,过点E作 交DG的延长线于点H ,连接BH .
(1) 求证:
(2)用等式表示线段BH与AE的数量关系,并证明.
1如图,已知直线l //l .
(1)在l ,l 所在的平面内求作直线l,使得l//l //l ,且l与l 间的距离恰好等于l与l 间的距离;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若l 与l 间的距离为2,点A,B,C分别在l,l ,l 上,且△ABC为等腰直角三角形,求△ABC的面积.
【答案】(1)见解析
(2)1或
【解析】(1)如图,直线l即为所求作的直线.
(2) ①当∠BAC=90°,AB=AC时,如图1,
∵l//l //l ,直线l 与l 间的距离为2,且l与l 间的距离等于l与l 间的距离,根据图形的对称性可知:BC=2,
②当∠ABC=90°,BA=BC时,
如图2,分别过点A,C作直线l 的垂线,垂足为M,N,
∴∠AMB=∠BNC=90°,
∵l//l //l ,直线l 与l 间的距离为2,且l与l 间的距离等于l与l 间的距离,
∴CN=2,AM=1,
·∠MAB+∠ABM=90°,∠NBC+∠ABM=90°,
∴∠MAB=∠NBC,
∴△AMB≌△BNC(AAS),
∴BM=CN=2,
在Rt△ABM中,由勾股定理得
③当∠ACB=90°,CA=CB时,同理②可得,
综上所述,△ABC的面积为1或
【标注】 【知识点】AAS
2.【模型建立】
(1)如图1,已知△ABE和△BCD,AB⊥BC,AB=BC,CD⊥BD,AE⊥BD.用等式写出线段AE,DE,CD的数量关系,并说明理由.
【模型应用】
(2)如图2,在正方形ABCD中,点E,F分别在对角线BD和边CD上, AE⊥EF,AE=EF用等式写出线段BE,AD,DF的数量关系,并说明理由
【模型迁移】
(3)如图3,在正方形ABCD中,点E在对角线BD上,点F在边CD的延长线上, AE⊥EF,AE=EF.用等式写出线段BE,AD,DF的数量关系,并说明理由.
【答案】(1)DE+CD=AE,理由见详解, 理由见详解,
理由见详解
【解析】
【分析】
(1) 直接证明△ABE≌△BCD,即可证明;
(2)过E点作EM⊥AD于点M,过E点作EN⊥CD于点N,先证明Rt△AEM≌Rt△FEN,可得AM=NF,结合等腰直角三角形的性质可得: NF=ND-DF=MD-DF,即有 进而可得 即可证;
(3)过A点作AH⊥BD于点H,过F点作FG⊥BD,交BD的延长线于点G,先证明△HAEg△GEF,再结合等腰直角三角形的性质,即可证明.
【详解】
(1) DE+CD=AE,理由如下:
∵CD⊥BD,AE⊥BD,AB⊥BC,
∴∠ABC=∠D=∠AEB=90°,
∴∠ABE+∠CBD=∠C+∠CBD=90°,
∴∠ABE=∠C,
∵AB=BC,
∴△ABE≌△BCD,
∴BE=CD,AE=BD,
∴DE=BD-BE=AE-CD,
∴DE+CD=AE;
理由如下:
过E点作EM⊥AD于点M,过E点作EN⊥CD于点N,如图,
∵四边形ABCD是正方形,BD是正方形的对角线,
∴∠ADB=∠CDB=45°,BD平分∠ADC,∠ADC=90°,
即
:EN⊥CD,EM⊥AD,
. EM=EN,
:AE=EF.
. Rt△AEM≌Rt△FEN,
AM=NF,
EM=EN,EN⊥CD,EM⊥AD,∠ADC=90°,
∴四边形EMDN是正方形,
∵ED是正方形EMDN对角线, MD=ND,
即
即有
理由见详解,
过A点作AH⊥BD于点H,过F点作FG⊥BD,交BD的延长线于点G,如图,
∵AH⊥BD, FG⊥BD,AE⊥EF,
∴∠AHE=∠G=∠AEF=90°,
∴∠AEH+∠HAE=∠AEH+∠FEG=90°,
∴∠HAE=∠FEG,
又∵AE=AF,
∴△HAE≌△GEF,
∴HE=FG,
∵在正方形ABCD中,∠BDC =45°,
∴∠DFG=45°,
∴△DFG是等腰直角三角形,
∵∠ADB=45°,AH⊥HD,
∴△ADH是等腰直角三角形,
【点睛】
本题主要考查了正方形的性质,等腰直角三角形的性质,全等三角形的判定与性质,角平分线的性质等知识,题目难度中等,作出合理的辅助线,灵活证明三角形的全等,并准确表示出各个边之间的数量关系,是解答本题的关键.
【标注】 【知识点】正方形的性质
【知识点】勾股定理
【知识点】角分线性质定理
【业务题型】证明题
3.如图,在Rt△ABC中,∠ACB=90°,AC= BC =5.正方形DEFG的边长为 ,它的顶点D,E,G分别在△ABC的边上,则BG的长为 .
【答案】3
【解析】解:过点G作GH⊥AC,则:∠AHG=∠GHD=90°,
∴∠DGH+∠HDG=90°,
∵∠ACB=90°,AC=BC=5,
∴AH=HG,
设AH=HG=x,则:CH=AC-AH=5-x,
∵正方形DEFG,
∴DG=DE,∠GDE=90°,
∴∠HDG+∠CDE=90°.
∴∠HGD=∠CDE.
∵∠C=∠GHD=90°,
∴△GHD≌△DCE,
∴CD=GH=x,
∴DH=CH--CD=5-2x,
Rt△GHD中,由勾股定理,得:(
解得:x=2,
∴AH=2,CH=3,
∵∠C=∠AHD=90°,
∴HG∥BC,
故答案为:3
【标注】【知识点】正方形与全等综合
4如图,在边长为6的等边△ABC中,D、E分别为边BC、AC上的点,AD与BE相交于点P,若BD=CE=2,则△ABP的周长为 .
【答案】
【解析】如下图所示,过点E作EF⊥AB于F,
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BAC=∠BCE=60°,
∵CE=BD=2,AB=AC=6.
∴AE=4,
∴AF=AE·cos∠EAF=2,EF=AE·sin∠EAF=2
∴BF=4.
又∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,AD=BE,
又∵∠BDP=∠ADB,
∴△BDP∽△ADB,
∴△ABP的周长:
因此正确答案为:
【标注】 【知识点】等腰三角形
5如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上,BF⊥EF,CE=1,则AF的长是( ).
A.2
【答案】B
【解析】如图所示,过F作AB的垂线分别交AB,CD于N,M,
∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠BNM=90°,AB=BC=OD=4,
∴四边形CMNB是矩形,
∴MN=BC=4,CM=BN,
∵BF⊥EF,
∴∠EFB=∠FNB=90°,
∴∠FBN+∠NFB=∠NFB+∠EFM,
∴∠FBN=∠EFM,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴∠MFC=∠MCF=45°,
∴MF=MC=NB,
在△MEF和△NFB中,
∴△MEF≌△NFB(AAS),
∴ME=FN,
设ME=FN=x,则MC=MF=BN=1+x,
:MN=MF+FN,即1+x+x=4,解得
∵四边形ABCD是正方形, MN⊥AB,
∴∠NAF=∠AFN=45°,
∴FN=AN,
故选B.
【标注】 【知识点】特殊平行四边形
6如图,正比例函数y=x的图象与反比例函数 的图象交于点A(1,a),在△ABO中,∠ACB=90°,CA=CB,点C坐标为(-2,0).
(1)求k的值.
(2)求AB所在直线的解析式.
【答案】(1) k=1.
【解析】(1)∵正比例函数y=x的图象与反比例函数 的图象交于点A(1,a),
∴a=1,
∴A(1,1),
∴k=1×1=1.
(2)过点A作AD⊥x轴于点D ,过点B作BE⊥x轴于点E,
∵C(-2,0),A(1,1),
∴OD=1,OC=2,
∴CD=OC+OD=2+1=3,DA=1,
∵CA=CB,∠BEC=∠CDA=90°,∠ACB=90°,
∴∠1=∠3,
∴△CBE≌△ACD(AAS),
∴EB=CD=3,EC=DA=1,
∴OE=OC+EC=2+1=3,
∴B(-3,3),
设yAB= kx+b,
解得
∴AB所在直线的解析式为
【标注】 【知识点】反比例函数与一次函数综合
7如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( ) .
A.(- B. (-3, C.(- ,2+ D.(-1,2+
【答案】A
【解析】如图,过点B'作B'H⊥y轴于H,
∵∠AOB=∠B=30°.
. AB=OA=2,
.. A'B'=AB=2,
在Rt△A'B'H中,
∵A'B'=2,∠B'A'H=60°,
∴OH=2+1=3,
故选A.
【标注】【知识点】旋转的性质
8在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 则点A的坐标为( ).
c (2,
【答案】A
【解析】设A的坐标为 设C的坐标为
∵矩形OABC,画出如图,
AB与1/轴交于E,OC与 交于F,
∵BF∥1轴,BC∥AO,如图,
∴∠CBF=∠AOE.
在△BCF与△OAE中
∴△BCF≌△OAE(ASA),
∴△BCF中BF边上的高=△OAE中OE边上的高,
即
∴C点坐标为
∵O(0,0),
∴OA直线方程为y
设y= kx+b,将O(0,0),A(xA, )f代入,解得
设y= kx+b,将O(0,0). 代入解得A
b=0,
∴OC直线方程为
∵OC⊥OA,
解得 舍去,
故选A.
【标注】【知识点】反比例函数与四边形综合
9如图,在平面直角坐标系中,A(2,0),B(0,1), AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是 .
【答案】y=2x-4
【解析】∵A(2,0), B(0,1)
∴OA=2,OB=1,
过点C作CD⊥x轴于点D,
则易知△ACD≌△BAO(AAS) ,
∴AD=OB=1,CD=OA=2,
∴C(3,2),
设直线AC的解析式为y=kx+b,将点A,点C坐标代入得
∴直线AC的解析式为y=2x-4.
故答案为:y=2x-4.
【标注】 【知识点】根据条件写一次函数解析式
10如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,
【答案】6
【解析】作DH⊥AE于H,如图,
:AF=4,当△AEF绕点A旋转时,点F在以A为圆心,4为半径的圆上,
∴当BF为此圆的切线时,∠ABF最大,即BF⊥AF,
在Rt△ABF中,
∵∠EAF=90°,
∴∠DAH=∠BAF,
在△ADH和△ABF中,
∴△ADH≌△ABF(AAS),
∴DH=BF=3,
故答案为:6.
【标注】【知识点】正方形与全等综合
11如图.已知点A(4,3),点B为直线y=-2上的一动点,点C(0,n),-2
【解析】过点A作AM⊥y轴于点M, AN⊥BN于点N,
∵直线y=-2//z轴,
故∠ABN=α,
当sinα的值最大时, 值最大,
故当BN最小,即BG最大时, tanα最大,
即当BG最大时,sinα的值最大,
设BG=y,
则AM=4,GC=n+2,CM=3-π,
∵∠ACM+∠MAC=90°,
∠ACM+∠BCG=90°,
∴∠CAM=∠BCG,
.. tan∠CAM=tan∠BCG,
即
故当 时,y取得最大值,
故
故答案为。
12如图,在Rt△ABC中,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥CD,垂足分别为E,F,连接EM .则下列结论中:①BF=CE;②∠AEM=∠DEM;③ ;⑤若AE平分∠BAC,则EF:BF= :1;⑥CF-DM=BM·DE,正确的有 .(只填序号)
【答案】①②③④⑤⑥
【解析】∵∠ACB=90°,
∴∠ACE=∠CBF,
又∵∠BFD=90°=∠AEC,AC=BC,
∴△BCF≌△CAE(AAS),
∴BF=CE,故①正确;
由全等可得:AE=CF,BF=CE,
'. AE-CE=CF--CE=EF,连接FM,OM,
∵点M是AB中点,
在△BDF和△CDM中,
∠BFD=∠CMD,∠BDF=∠CDM,
∴∠DBF=∠DCM,又BM=CM,BF=CE,
∴△BFM≌△CEM,
∴FM=EM,∠BMF=∠CME,
∵∠BMC=90°,
.∠EMF=90°, 即△EMF为等腰直角三角形,
,故③正确;
∴∠MEF=∠AEM=45°,故②正确;
设AE与CM交于点N,连接DN,
∵∠DMF=∠NME,FM=EM,
∠DFM=∠DEM=∠AEM =45°,
∴△DFM≌△NEM,
∴DF=EN,DM=MN,
∴△DMN为等腰直角三角形,
而
故④正确;
∵AC=BC,∠ACB=90°,
∴∠CAB=45°,
∵AE平分∠BAC,
∴∠DAE=∠CAE=22.5°,∠ADE=67.5°,
∵∠DEM=45°,
∴∠EMD=67.5°,即DE=EM,
∵AE=AE,∠AED=∠AEC,∠DAE=∠CAE,
∴△ADE≌△ACE,
∴DE=CE,
∵△MEF为等腰直角三角形,
故⑤正确;
∵∠CDM=∠ADE,∠CMD=∠AED=90°,
∴△CDM∽△ADE,
BM=CM,AE=CF,
.. CF·DM=BM·DE,故⑥正确;
故答案为:①②③④⑤⑥.
【标注】 【知识点】相似三角形的性质与判定综合
13如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接GF并延长,交AC的延长线于点P,若AB=5,CF=2,则线段EP的长是 .
【答案】
【解析】如图,作FH⊥PE于H.
∵四边形ABCD是正方形, AB=5,
AC=5 ,∠ACD=∠FCH=45°,
:∠FHC=90°,CF=2,
∴CH=HF=
∵CE=4AE,
∴EH=5
在Rt△EFH中,
∴E,G,F,C四点共圆,
∴∠EFG=∠ECG=45°,
∴∠ECF=∠EFP=135°,
∵∠CEF=∠FEP,
∴△CEF∽△FEP.
故答案为
【标注】 【知识点】相似三角形的性质与判定综合
14回答下列问题.
(1) 如图,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°,求证:
(2)如图,在四边形ABCD中,. 点E在边CD上,点F在边AD的延长线上,∠FEG=∠AEB=90°,且. 连接BG交CD于点H,求证: BH=GH
(3)如图,点E在四边形ABCD内,∠AEB+∠DEC=180°,且 过E作EF交AD于点F ,使∠EFA=∠AEB,延长FE交BC于点G.求证:BG=CG.
【答案】(1)证明见解析.
(2)证明见解析.
(3)证明见解析.
【解析】(1)∵∠C =∠D =∠AEB=90°,
.∠BEC+∠AED=∠AED+∠EAD=90°,
∴∠BEC=∠EAD,
.△AED∽△EBC,
(2)如图,过点G作GM⊥CD于点M,
同(1)的方法可知
. BC=GM,
又∵∠C=∠GMH=90°,∠CHB=∠MHG,
∴△BCH≌△GMH(AAS).
∴BH=GH.
(3)方法一:如图,在EG上取点M,使∠BME=∠AFE,过点C作CN//BM,交EG的延长线于点N,则∠N=∠BMG,
∵∠EAF+∠AFE+∠AEF
=∠AEF+∠AEB+∠BEM
=180°,
∠EFA=∠AEB,
∴∠EAF=∠BEM,
∴△AEF∽△EBM,
∵∠AEB+∠DEC=180°,∠EFA+∠DFE=180°,
而∠EFA=∠AEB,
∴∠CED=∠EFD,
∵∠BMG+∠BME=180°,
∠N=∠BMG,
∠BME=∠AFE,
∴∠N=∠EFD,
∵∠EFD+∠EDF+∠FED
=∠FED+∠DEC+∠CEN
∴∠EDF=∠CEN,
∴△DEF∽△EON,
∴BM=CN,
又∵∠N=∠BMG,∠BGM=∠CGN,
∴△BGM≌△CGN(AAS),
∴BG=CG.
方法二:作BH//CE交EG延长线于点G,
∴∠EBH+∠BEC=180°,
∵∠AED+∠BEC=180°,
∴∠EBH=∠AED,
又∵∠BEH=∠EAD(外角) ,
∴△BEH∽△EAD,
又 (已知) ,
∴BH=EC,
∴△BGH≌△EGC,
∴BG=CG.
【标注】【知识点】相似三角形的性质与判定综合
15如图,在矩形ABCD中,AB=2,AD=8,点E,F在BC上,点G是射线DC与射线AF的交点.若,BE=1,∠EAF=45°则AG的长为 .
【答案】
【解析】
故答案为
【标注】 【知识点】动点与特殊平行四边形问题;相似三角形的性质;三垂直模型
16如图1,这是一个装有货物的长方体形状的木箱沿着坡面装进汽车货箱的立体示意图,图2是它的平面示意图.已知汽车货箱高度BG=2m,货箱底面距地面的高度BH=0.6m,坡面与地面的夹角∠BAH=α,木箱的长(FC)为2m,高(EF)为1.6m,宽小于汽车货箱的宽度.已知 木箱底部顶点C与坡面底部点A重合,则木箱底部悬空部分BF的长为 m,木箱上部顶点E到汽车货箱顶部NG的距离为 m.
【答案】1;0.12
【解析】∵BH=0.6米,
(米) ,
(米) ,
∵AF=FC=2(米) ,
∴BF=AF-AB=2-1=1(米),
作FJ⊥BG于点J, EK⊥FJ于点K,
则∠EKF=∠FJB=∠AHB=∠EFA=90°,易得∠EFK=∠FBJ=∠ABH,
∴△EFK∽△FBJ∽△ABH,
∵FB=AB,
∴△FBJ≌△ABH
(米) ,
∴EK =1.28(米) ,
. BJ+EK=0.6+1.28=1.88(米),
∴点E到NG的距离为2-1.88 =0.12(米) ,
故答案为:1,0.12.
17如图,在直角坐标系中,点A、点B分别是x轴正半轴,y轴正半轴上的动点,以AB为直角边作等腰直角三角形ABC,其中点A为直角顶点,点P为斜边BC的中点,则下列说法中正确的有( )
①若点A、点B选择适当位置,则可能有OP⊥BC;
②若点A(a,0),点B(0,b),则C点的坐标必是(a+b,a);
③无论AB怎样运动,都有OP≤AB.
A. ①② B. ②③ C. ①③ D.①②③
【答案】B
【解析】解:①由等腰直角三角形ABC,P是斜边BC的中点,得AP⊥BC,过一点有且只有一条直线与已知直线垂直,OP不能垂直斜边BC,故①错误;
②如图:作CD⊥x轴于点D,由余角的性质,得∠OBA=∠DAC,
在Rt△OBA和Rt△DAC中,
Rt△OBA≌Rt△DAC(AAS),
∴AD=OB=b,DC=OA=a.
由线段的和差,得OD=OA+AD=a+b,即C点坐标是(a+b,a),故②正确;
③由勾股定理,得
平方,
即AB≥OP,故③正确.
【标注】【知识点】勾股定理与全等
18如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为 .
【答案】
【解析】如图,作CE⊥x轴,AD⊥x轴,BF⊥AD,
易证△OCE≌△AOD,△BAF≌△AOD,
∴OE= ,CE=1,BF= ,AF=1,
如图作AF⊥x轴于F,CE⊥x轴于E.
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
:∠COE+∠AOF=90°,∠AOF+∠OAF=90°,
∴∠COE=∠OAF,
在△COE和△OAF中,
∴△COE≌△OAF,
∴CE=OF,OE=AF,
∵A(1, ),
∴CE=OF=1,OE=AF=
∴点C坐标(- ,1).
故答案为(- ,1).
【标注】【知识点】三垂直模型
19如图,在正方形ABCD中,E是边AB上的一动点(不与点A,B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1) 求证:GF=GC.
(2)用等式表示线段BH与AE的数量关系,并证明.
【答案】(1)证明见解析.
证明见解析.
【解析】(1)连接DF,
点A关于直线DE的对称点为F,
∴AE=EF,∠AED=∠FED,
在△ADE和△FDE中,
∴△ADE≌△FDE(SAS),
∴AD=DF,∠DFE=∠A,
在正方形ABCD中,AD=DC,
∴DF=DC,
在Rt△DFG和Rt△DCG中,
∴Rt△DFG≌Rt△DCG(HL),
∴GF=GC.
(2)方法一:过B点作HP⊥AB于P点,
∴∠CDG=∠FDG,
∵△ADE≌△FDE,
∴∠ADE=∠FDE,
在正方形ABOD中,∠ADC=90°,
∵DE⊥EH,
∴△DEH为等腰直角三角形,
∴DE=EH,
在Rt△ADE中,∠1+∠2=90°,
∴∠1=∠3,
在△ADE和△PEH中
∴△ADE≌△PEH(AAS),
∴AE=HP,DA=EP,
∵AD=AB,
∴AB=EP,
∴AE=BP,
∴BP=HP,
∴△BHP为等腰直角三角形,
中小学教育资源及组卷应用平台
方法二:如图,在线段AD上截取AM,使AM= AE,
∵AD=AB,
∴DM=BE;
由(1)知:∠1=∠2,∠3=∠4,
∵∠ADC=90°,
∴∠1+∠2+∠3+∠4=90°,
∴2∠2+2∠3=90°,
即
∵EH⊥DE,
∴∠DEH=90°,△DEH是等腰直角三角形,
∴∠AED+∠BEH=∠AED+∠1=90°,DE=EH,
∴∠1=∠BEH,
在△DME和△EBH中,
∴△DME≌△EBH(SAS),
∴EM=BH,
在Rt△AEM中,∠A=90°,AM=AE,
∴EM= AE,
∴B.
故答案为:
【标注】【知识点】正方形与全等综合
同课章节目录
