专题九 半角模型(含答案) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题九 半角模型(含答案) 2025年中考数学几何模型专题讲练 | 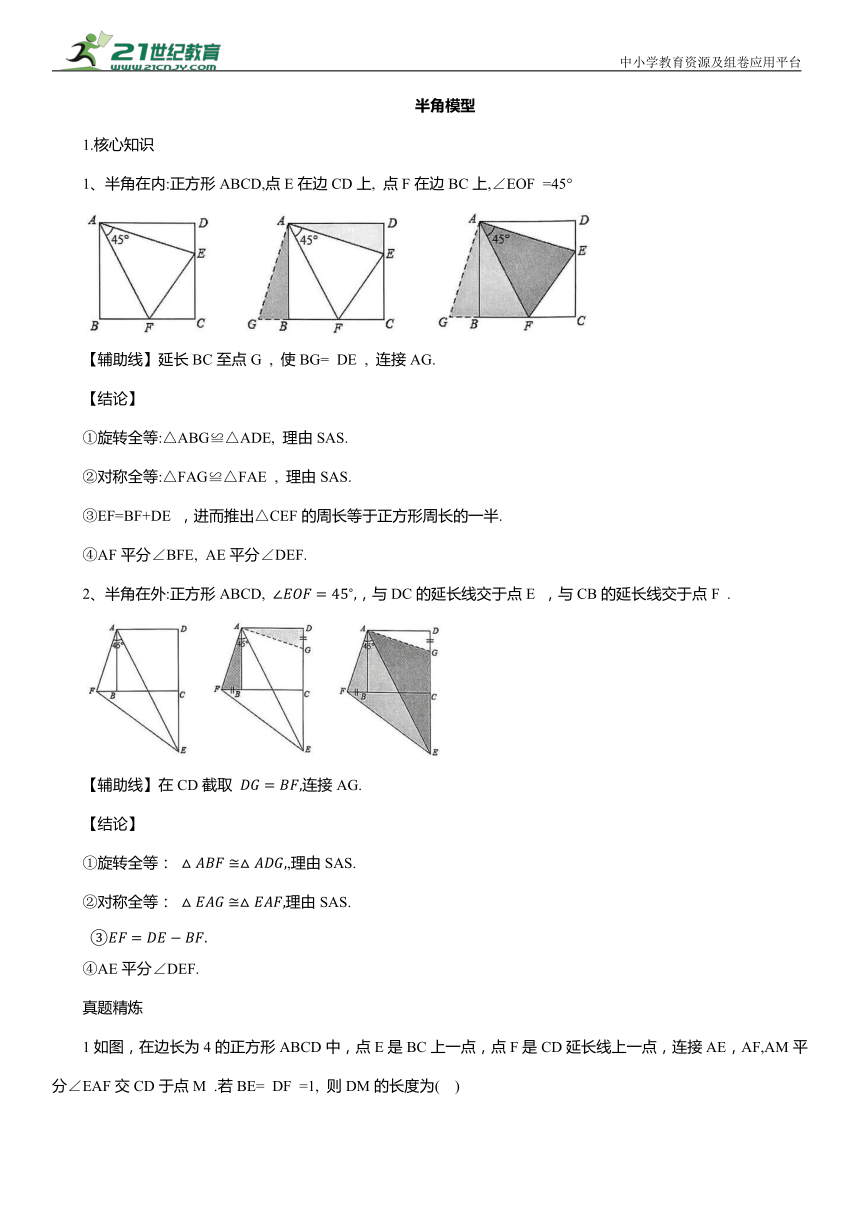 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 16:15:56 | ||
图片预览


文档简介
半角模型
1.核心知识
1、半角在内:正方形ABCD,点E在边CD上, 点F在边BC上,∠EOF =45°
【辅助线】延长BC至点G , 使BG= DE , 连接AG.
【结论】
①旋转全等:△ABG≌△ADE, 理由SAS.
②对称全等:△FAG≌△FAE , 理由SAS.
③EF=BF+DE ,进而推出△CEF的周长等于正方形周长的一半.
④AF平分∠BFE, AE平分∠DEF.
2、半角在外:正方形ABCD, ,与DC的延长线交于点E ,与CB的延长线交于点F .
【辅助线】在CD截取 连接AG.
【结论】
①旋转全等: ,理由SAS.
②对称全等: 理由SAS.
④AE平分∠DEF.
真题精炼
1如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M .若BE= DF =1, 则DM的长度为( )
A.2
2正方形ABCD中,点E在边BC ,CD上运动(不与正方形顶点重合).作射线AE,将射线AE绕点A逆时针旋转45°,交射线CD于点F .
(1)如图,点E在边BC上,BE =DF ,则图中与线段AE相等的线段是
(2) 过点E作EG⊥AF, 垂足为G, 连接DG, 求∠GDC的度数.
3在复习课上,刘老师先引导学生解决以下问题: 【问题情境】如图1,在△ABC中,∠BAC=90°,AB= AC,点D、E在边BC上,且∠DAE=45°,BD=3,CE=4,求DE的长.解:如图2, 将△ABD绕点A逆时针旋转90°得到△ACD', 连结ED' .
由旋转的特征得∠BAD=∠CAD',∠B=∠ACD', AD= AD',BD=CD'.∵∠BAC=90°,∠DAE=45°,∴∠BAD+∠EAC=45°.∵∠BAD=∠CAD',∴∠CAD'+∠EAC=45°,即∠EAD'=45°.∴∠DAE=∠D'AE.在△DAE和 中, ∠DAE=∠D'AE, AE=AE,∴ ① .∴DE=D'E .又∵
∠ECD'=∠ECA+∠ACD'=∠ECA+∠B=90°,∴在Rt△ECD'中, ② .
∵CD'=BD=3,CE=4,
【问题解决】上述问题情境中, “①”处应填: ; “②”处应填: ; “③”处应填: .刘老师进一步谈到:图形的变化强调从运动变化的观点来研究,只要我们抓住了变化中的不变量,就能以不变应万变.
【知识迁移】如图3,在正方形ABCD中,点E、F分别在边BC、 CD上,满足△CEF的周长等于正方形ABCD的周长的一半,连结AE、 AF,分别与对角线BD交于M、N两点.探究BM、MN、 DN的数量关系并证明.
【拓展应用】如图4,在矩形ABCD中,点E、F分别在边BC、 CD上,且∠EAF=∠CEF=45°.探究BE、EF、 DF的数量关系:
【问题再探】如图5,在△ABC中,∠ABC=90°,AB=4,BC=3,点D、E在边AC上,且∠DBE=45°.设AD=x,CE=y,求y与x的函数关系式.
4(1)操作一:如图①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则 度.
(2)操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N .我们发现,当点E的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上,则 度.
(3)在图②中,运用以上操作所得结论,解答下列问题:
① 设AM与NF的交点为点P .求证:
② 若 则线段AP的长为 .
5数学实践活动 ,是一种非常有效的学习方式.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF,连接EF ,如图1.
,写出图中两个等腰三角形 : (不需要添加字母);
转一转:将图1中的 绕点A旋转,使它的两边分别交边BC、CD于点P、Q,连接PQ,如图2.
(2) 线段BP、PQ、DQ之间的数量关系为 .
(3)连接正方形对角线BD ,若图2中的. 的边AP、AQ分别交对角线BD于点M、点N,如图3,则
剪一剪:将图3中的正方形纸片沿对角线BD剪开,如图4.
(4) 求证 :
6如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作 交BC于点F ,连接AF、EF , AF交BD于G, 现有以下结论:①AP =PF;②DE+BF=EF;③PB--PD= BF ;④S△AEF为定值;⑤S四边形PEFG = S△APG .以上结论正确的有 (填入正确的序号即可).
7如图正方形ABCD中,. 且 将 绕点A沿顺时针方向旋转90°后与 重合,连接EF,过点B作 交AF于点M,则以下结论:① 中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
8如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),. 点F在射线AM上,且 CF与AD相交于点G ,连接EC、EF、EG,则下列结论:
①∠ECF=45°;
②△AEG的周长为
④△EAF的面积的最大值是
⑤当 时,G是线段AD的中点 .其中正确的结论是( )
A. ①②③ B. ②④⑤ C. ①③④ D. ①④⑤
9如图,在平面直角坐标系中, 以坐标原点O(0,0), A(0,4), B(3,0)为顶点的Rt△AOB, 其两个锐角对应的外角的平分线相交于点P,且点P恰好在反比例函数 的图象上,则k的值为( )
A.36 B. 48 C. 49 D.64
10如图,在正方形ABCD中, AB=6,G是BC的中点,将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( ) .
A. 1 B. 1.5 C. 2 D. 2.5
11矩形ABCD中,AB=2,BC=4,若 则AF的长为
12如图1,已知四边形ABCD是正方形,将 分别沿DE,DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点) , 若 ,则DG的长为 .
13如图,已知正方形ABCD的边长为a,E为CD边上一点(不与端点重合),将 沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF .给出下列判断:
②若 则AG//CF;
③若E为CD的中点,则△GFC的面积为 ④若CF=FG ,则.
⑤BG·DE+AF·GE=a .其中正确的是 .
14如图正方形中,△ABC绕点A逆时针旋转到 交对角线于点E, F,若AE=4 ,则EF·ED为 .
15如图①, E、F是等腰Rt△ABC的斜边BC上的两动点, ∠ C且CD=BE.
(1) 求证:△ABE≌△ACD .
(2) 求证:
(3) 如图②, 作AH⊥BC, 垂足为H ,设 不妨设 请利用(2) 的结论证明:当α+β=45°时, 成立.
16在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
(2) 如图2,当AB=5,且AF·FD=10时,求BC的长.
(3) 如图3,延长EF,与∠ABF的角平分线交于点M , BM交AD于点N ,当 时,求 的值.
17如图1,在正方形ABCD内作 ,AE交BC于点E , AF交CD于点F , 连接EF , 过点A作AH⊥EF,垂足为H .
(1) 如图2, 将△ADF绕点A顺时针旋转90°得到△AB
① 求证:△AGE≌△AFE.
② 若BE=2, DF =3,求AH的长.
(2) 如图3,连接BD交AE于点M,交AF于点N .请探究并猜想:线段BM , MN , ND之间有什么数量关系 并说明理由.
18如图,正方形ABCD的边长为6,若 且∠ECF=45°,则CF的长为( )
19如图,在正方形ABCD内作∠EAF =45°, 连接EF, 过点A作AH⊥EF ,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE =2, DF=3,则AH的长为 .
20在等边 的两边AB、AC所在直线上分别有两点M、N ,D为△ABC外一点,且 .探究:当点M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.
(1) 如图1,当点M、N在边AB、AC上,且DM =DN时, BM、CN、MN之间的数量关系是 ;此时
(2) 如图2,当点M、N在边AB、AC上,且当DM≠DN时, 猜想(1) 问的两个结论还成立吗 写出你的猜想并加以证明.
(3) 如图3,当点M、N分别在边AB、CA的延长线上时,若AN=x,则Q=
21如图△ABC中, ,E、F为线段AB上两动点,且. ,过点E、F分别作BC、AC的垂线相交于点M .以下结论: ②当点E与点B重合时, ③AF+BE=EF; ④MG·MH= $,其中正确结论为( )
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
22如图,在△ABC中, AB = AC,∠BAC=120°,点D、E在边BC上,且 将△ADE沿AE翻折, 点D的对应点是D', 连接CD' , 若 ,则DE的长为( ) .
23如图,点E, F分别为正方形ABCD的边上一点, AC, BD交于点O,且∠EAF =45°,AE,AF分别交对角线BD于点M , N , 则有以下结论:①∠AEB =∠AEF =∠ANM ;②EF =BE+DF;③△AOM ∽△ADF;④S△AEF =2S△AMN.正确的是 .
24正方形ABCD中,且∠EAF=45°.下列结论:①AB =BN·DM;②AF平分∠DFE;③AM·AE=AN·AF;④BE+DF= MN.其中正确的结论是( ).
A. ①② B. ①③ C. ①②③ D. ①②③④
25正方形ABCD中, E是BC边上的一点, BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AC,如下结论:①∠EAG=45°;②FG=FC;③FC//AG;④S△GFC =14 .正确结论个数是( )
A.1 B.2 C. 3 D.4
26如图1,在四边形ABCD中, AB=AD ,∠B+∠ADC=180°,点E、F分别在四边形ABCD的边BC、CD上, 连接EF ,试猜想EF、BE、DF之间的数量关系.
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG, 使AB与AD重合, 由 得∠FDG=180°, 即点F、D、G三点共线, 易证△AFG≌ , 故EF、BE、DF之间的数量关系为 .
(2)类比引申
如图2,在图1的条件下,若点E、F由原来的位置分别变到四边形ABCD的边CB、DC延长线上, 连接EF ,试猜想EF、BE、DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D , E均在边BC上,且∠DAE=45°,若BD=1, EC=2,则DE的长为 .
27旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知, 中, 点D、E在边BC上, 且
(1) 如图a,当 时,将 绕点A顺时针旋转60°到△AFB的位置,连接DF .
①求 的度数.
② 求证:
(2) 如图b,当 时,猜想BD、DE、CE的数量关系,并说明理由.
(3) 如图c,当 时,请直接写出DE的长为 .
1如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AP,AM平分∠EAF交CD于点M ,若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
2.【答案】(1) AF
(2)过G点作GM⊥AD交于M,延长MG交BC于N点,
∴∠AMG=∠DMG=∠GNE=90°,
.四边形CDMN是矩形,
.∠AGM+∠MAG=90°,
:EG⊥AF,∠EAF=45°,
∴∠AGM+∠EGN=90°
∵∠AGE=90°,∠EAF=45°
∴△AEG是等腰直角三角形,
∴AG=EG,
∴∠EGN=∠MAG,
∴△AMG≌△GNE(AAS),
∴AM=GN,
∵AM+MD=GN+MG,
∴MD=MG,
∴△MDG为等腰直角三角形,
∴∠MDG=45°,
∴∠GDC=45°;
当点E在CD边上时,如图,
过点G作GN⊥DF交于N,延长NG交BA延长线于点M,∴四边形ADNM是矩形,
同理,△AMG≌△GNE(AAS).
∴GN=AM=DN,
∴△NDG为等腰直角三角形,
∴∠GDN=45°,
∴∠GDC=180°-45°=135°,
综上所述:∠GDC的度数为45°或135°.
【标注】【知识点】正方形与全等综合
3【问题情境】
如图1,在△ABC中,∠BAC=90°,AB=AC,点D、E在边BC上,且∠DAE=45°,BD=3,CE=4,求DE的长.
解:如图2,将△ABD绕点A逆时针旋转90°得到△ACD',连结ED'.
由旋转的特征得∠BAD=∠CAD',∠B=∠ACD',AD=AD',BD=CD'.
∵∠BAC=90°,∠DAE=45°,
∠BAD+∠EAC=45°.
∴∠BAD=∠CAD',
..∠CAD'+∠EAC=45°,即∠EAD'=45°.
∴∠DAE=∠D'AE.
在△DAE和△D'AE中,
AD=AD',∠DAE=∠D'AE,AE=AE,
.① .
DE=D'E.
又∵∠ECD'=∠ECA+∠ACD'=∠ECA+∠B=90°,
∴在Rt△ECD'中, ② .
∵CD'=BD=3,CE=4,
∴DE=D'E= ③ .
【问题解决】
上述问题情境中, “①”处应填: ;“②”处应填: ;“③”处应填: .
刘老师进一步谈到:图形的变化强调从运动变化的观点来研究,只要我们抓住了变化中的不变量,就能以不变应万变.
【知识迁移】
如图3,在正方形ABCD中,点E、F分别在边BC、CD上,满足△CEF的周长等于正方形ABCD的周长的一半,连结AE、AF,分别与对角线BD交于M、N两点.探究BM、MN、DN的数量关系并证明.
如图4,在矩形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CEF =45°.探究BE、EF、DF的数量关系: (直接写出结论,不必证明).
中小学教育资源及组卷应用平台
如图5,在△ABC中,∠ABC=90°,AB=4,BC=3,点D、E在边AC上,且∠DBE=45°.设AD=x,CE=y,求y与x的函数关系式.
【答案】 【问题解决】①△ADE≌△AD'E;②EC +CD =ED ;③5;【知识迁移】 见解析;【拓展应用】 【问题再探】
【解析】
【分析】
(1)【问题解决】根据题中思路解答即可;
(2)【知识迁移】如图,将△ABE绕点A逆时针旋转90°,得到△ADF'过点D作DH⊥BD交边AF'于点H,连结NH,由旋转的特征得AE=AF',BE=DF',∠BAE=∠DAF'.结合题意得 .证明△AEF≌AF'F,得出∠EAF=∠F'AF.根据正方形性质得出∠ABD=∠ADB=45°.结合DH⊥BD,得出∠ADH=∠HDB-∠ADB=45°.证明△ABM≌△ADH,得出AM=AH;BM=DH.证明△AMN △AHN.得出MN=HN.在Rt△HND中,根据勾股定理即可求解;
(3)【拓展应用】如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连接HM,HE.则△ADF≌△AGH.则DF=GH,AG=AD,AF=AH,∠DAF=∠HAG,根据∠EAF=45°,证明△AEH≌△AEF,得出EF=HE,过点H作HO⊥CB交CB于点O,过点H作HG⊥BM交BM于点M,则四边形OHGB为矩形.得出OH=BG,OB=HG,证明△BME,△DNF,△CEF,△AMN是等腰直角三角形,得出GM=DN=DF=HG,∠HME=90°,在Rt△OHE中,根据勾股定理即可证明;
(4)【问题再探】如图,将△BEC绕点B逆时针旋转90°,得到BE'C',连结E'D.过点E作EG⊥BC,垂足为点G,过点E'作EG'⊥BC',垂足为G',过点E'作E'F∥BA,过点D作DF∥BC交AB于点H,E'F、DF交于点F.由旋转的特征得
BE=BE',∠CBE=∠C'BE',EG=E'G',BG=BG'.根据∠ABC=90°,∠DBE=45°,得出∠DBE'=45°,证明△EBD≌△E'BD,得出DE=DE',根据勾股定理算出AC,根据AD=z,CE=y,表示出DE'=5-x-y,证明△AHD∽△ABC,根据相似三角形的性质表示出 同理可得
证明四边形FE'G'H为矩形.得出
在Rt△E'FD中,根据勾股定理即可求解;
【详解】
解: (1)【问题解决】解:如图2,将△ABD绕点A逆时针旋转90°得到△ACD',连结ED'
由旋转的特征得∠BAD=∠CAD',∠B=∠ACD',AD=AD',BD=CD'.
∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠EAC=45°
∵∠BAD=∠CAD',
∴∠CAD'+∠EAC=45°,即∠EAD'=45°.
∴∠DAE=∠D'AE.
在△DAE和△D'AE中,AD=AD',∠DAE=∠D'AE,AE=AE,
∴①△ADE≌△AD'E.
∴DE=D'E.
又∵∠ECD'=∠ECA+∠ACD'=∠ECA+∠B=90°,
∴在Rt△ECD'中,(
∵OD'=BD=3,CE=4,
(2)【知识迁移】
证明:如图,将△ABE绕点A逆时针旋转90°,得到△ADF'.
过点D作DH⊥BD交边AF'于点H,连结NH.
由旋转的特征得AE=AF',BE=DF',∠BAE=∠DAF'.
由题意得EF+EC+FC=DC+BC=DF+FC+EC+BE,
∴EF=DF+BE=DF+DF'=F'F.
在△AEF和△AF'F中,AE=AF',EF=F'F,AF=AF,
∴△AEF≌AF'F(SSS). quadquad
∴∠EAF=∠F'AF.
又∵BD为正方形ABCD的对角线,
∴∠ABD=∠ADB=45°.
∵DH⊥BD,
∴∠ADH=∠HDB=∠ADB=45°
在△ABM和△ADH中,∠BAM=∠DAH,AB=AD,∠ABM=∠ADH,
∴△ABM≌△ADH(ASA),
∴AM=AH,BM=DH.
在△AMN和△AHN中, AM=AH ∠MAN=∠HAN,AN=AN,
∴△AMN≌△AHN(SAS).
∴MN=HN.
在Rt△HND中,
(3)【拓展应用】
证明:如图所示,延长EF交AB延长线于M点,交AD延长线于N点.
将△ADF绕着点A顺时针旋转90°,得到△AGH,连接HM,HE.
则△ADF≌△AGH.
则DF=GH,AG=AD,AF=AH,∠DAF=∠HAG,
∵∠EAF=45°,
∴∠HAE=∠HAG+∠GAE=∠DAF+∠GAE=45°,
在△AEH和△AFE中
∴△AEH≌△AEF(SAS),
∴EF=HE,
过点H作HO⊥CB交CB于点O,过点H作HG⊥BM交BM于点M,则四边形OHGB为矩形.
∴OH=BG,OB=HG,
∵∠CEF=45°,
∴∠CEF=∠CFE=∠DFN=∠DNF=∠BME=∠BEM=45°,
∴△BME,△DNF,△CEF,△AMN是等腰直角三角形,
∴CE=CF,BE=BM,DN=DF,AN=AM,
∴AM-AG=AN-AD,
∴GM=DN=DF=HG,
∴∠HMG=45°,
在Rt△OHE中,
即
又∴ ,
即2
(4)【问题再探】如图,将△BEC绕点B逆时针旋转90°,得到△BE'C',连结E'D.过点E作EG⊥BC,垂足为点G,过点E'作EG'⊥BC',垂足为G'.过点E'作E'F∥BA,过点D作DF∥BC交AB于点H,E'F、DF交于点F
由旋转的特征得BE=BE',∠CBE=∠C'BE',EG=E'G',BG= BG'.
∵∠ABC=90°,∠DBE=45°
∴∠CBE+∠DBA=45°,
∴∠C'BE'+∠DBA=45°,即.
在△EBD和△E'BD中,BE=BE',∠DBE=∠DBE',BD=BD.
∴△EBD≌△E'BD(SAS),
∴DE=DE',
:∠ABC=90°,AB=4,BC=3,
又∵AD=x,CE=y,
∴DE'=DE=5-x-y,
∵DF∥BC,
∴∠ADH=∠C,∠AHD=∠ABC=90°,
∴△AHD∽△ABC,
即
同理可得
∵E'G'⊥AB,∠ABC=90°,
∴E'G'∥BC∥FD,
又∵E'F∥AB,∠FHG'=∠AHD=90°,
∴四边形FE'G'H为矩形
在Rt△ E'FD中,
解得
【点睛】
本题是四边形的综合题,考查的是旋转变换的性质、矩形的性质和判定、正方形的性质和判定、勾股定理、等腰直角三角形的性质和判定、全等三角形的判定和性质,相似三角形的判定和性质,灵活运用旋转变换作图,掌握以上知识点是解题的关键.
4实践与探究.
(1)操作一:如图①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M ,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则∠EAF= 度.
(2)操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N .我们发现,当点B的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上.则∠AEF= 度.
(3)在图②中,运用以上操作所得结论,解答下列问题:
①设AM与NF的交点为点P .求证:△ANP≌△FNE;
② 若 则线段AP的长为 .
【答案】(1)45
(2)60
(3)①证明见解析.
【解析】(1)∵四边形ABCD是正方形,
..∠BAD=90°,
由折叠的性质可知,△ABE≌△AME,△ADF≌△AMF.
∴∠BAE=∠MAE,∠DAF=∠MAF,
:∠BAE+∠MAE+∠DAF+∠MAF=∠BAD=90°,
:2∠MAE+2∠MAF=90°,
∴∠MAE+∠MAF=45°,
即∠EAF=45°.
(2)由折叠的性质可知,
△ABE≌△AME,△FCE≌△FNE,
∴∠AEB=∠AEM ,∠AEM=∠CEF,
∴∠AEB=∠AEM=∠CEF.
∵∠AEB+∠AEM+∠CEF=180°.
∴∠AEB=∠AEM=∠CEF=60°.
即∠AEF=60°.
(3)① ∵四边形ABCD是正方形,
由折叠的性质可知,△ABE≌△AME,△FNE≌△FCE,
∴∠AME=∠B=90°,∠FNE=∠C=90°,
:∠EAF=45°,
∴∠AFN=∠FNE-∠EAF=45°,
∴∠AFN=∠EAF,
∴AN=FN,
∴∠NAP=∠NFE,
在△ANP和△FNE中,
∴△ANP≌△FNE(ASA).
② ∵在Rt△ABE中,∠AEB=60°,AB=
∵四边形ABCD是正方形,
∵∠C=90°,∠FEC=60°,
∴∠EFC=30°,
∵△ANP≌△FNE,
【标注】 【知识点】四边形与折叠问题
5综合与实践.
数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思维空间,丰富数学体验.让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF,连接EF,如图1.
(1)∠EAF= ,写出图中两个等腰三角形: (不需要添加字母);
转一转:将图1中的∠EAF绕点A旋转,使它的两边分别交边BC、CD于点P、Q,连接PQ,如图2.
(2)线段BP、PQ、DQ之间的数量关系为 .
(3)连接正方形对角线BD ,若图2中的∠PAQ的边AP、AQ分别交对角线BD于点M、点N,如图3,则
剪一剪:将图3中的正方形纸片沿对角线BD剪开,如图4.
(4) 求证:.
【答案】(1)45°;△AEF,△CEF
(2) BP+DQ=PQ
(3)
(4)证明见解析.
【解析】(1)如图1中,
∵四边形ABCD是正方形,
.. AB=AD=BC=CD,∠BAD=90°.
∴△ABC,△ADC都是等腰三角形,
:∠BAE=∠CAE,∠DAF=∠CAF,
∵∠BAE=∠DAF=22.5°,∠B=∠D=90°,AB=AD,
∴△BAE≌△DAF(ASA),
.. BE=DF,AE=AF,
∵CB=CD,
CE=CF.
.△AEF,△CEF都是等腰三角形.
(2) 结论:PQ=BP+DQ.
理由:如图2中,延长CB到T,使得BT=DQ,
∵AD=AB,∠ADQ=∠ABT=90°,DQ=BT,
∴△ADQ≌△ABT(SAS),
∴AT=AQ,∠DAQ=∠BAT,
∵∠PAQ=45°,
∵AP=AP,
∴△PAT≌△PAQ(SAS),
∴PQ=PT,
∵PT=PB+BT=PB+DQ,
∴PQ=BP+DQ.
故答案为:PQ=BP+DQ.
如图3中,
∵四边形ABCD是正方形,
∴∠ABM=∠ACQ=∠BAC=45°,AC= AB,
∠BAC=∠PAQ=45°,
∴∠BAM=∠CAQ,
∴△CAQ∽△BAM,
故答案为:
(4) 如图4中,将△ADN绕点A顺时针旋转90°得到△ABR,连接RM,
∵∠BAD=90°,∠MAN=45°,
∴∠DAN=∠BAR,
∵AR=AN,AM=AM,
∴△AMR≌△AMN(SAS),
∴RM=NM,
∵∠D=∠ABR=∠ABD=45°.
∵DN=BR,MN=RM,
【标注】 【知识点】旋转的性质
6如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作PF⊥AP交BC于点F,连接AF、EF, AF交BD于G,现有以下结论:①AP=PF;②DE+BF=EF;③PB-PD= BF ;④S△AEP为定值;⑤ 以上结论正确的有 (填入正确的序号即可)
【答案】①②③⑤
【解析】∵四边形ABCD是正方形, PF⊥AP,
∴∠APF=∠ABC=∠ADE=∠C=90°,AD=AB,∠ABD=45°,
①∵∠ABC+∠APF=180°,
∴由四边形内角和可得∠BAP+∠BFP=180°,
∴点A、B、F、P四点共圆,
∴∠AFP=∠ABD=45°,
∴△APF是等腰直角三角形,
∴AP=PF,故①正确;
②把△AED绕点A顺时针旋转90°得到△ABH,如图所示:
∴DE=BH,∠DAE=∠BAH,∠HAE=90°,AH=AE,
∴∠HAF=∠EAF=45°,
∵AF=AF,
∴△AEP≌△AHF(SAS),
∴HF=EF,
∵HF=BH+BF,
∴DE+BF=EF;故②正确;
③连接AC,在BP上截取BM=DP,连接AM ,如图所示:
∵点O是对角线BD的中点,
∴OB=OD,BD⊥AC,
∴OP=OM,△AOB是等腰直角三角形,
由①可得点A、B、F、P四点共圆,
∴∠APO=∠AFB,
∵∠ABF=∠AOP=90°,
∴△AOP∽△ABF,
∵BP-DP=BP-BM=PM=2OP,
故③正确;
④过点A作AN⊥EF于点N,如图所示:
由②可得∠AFB=∠AFN
∵∠ABF=∠ANF=90°,AF=AF,
∴△ABF≌△ANF(AAS).
. AN=AB,
若△AEF的面积为定值,则EF为定值,
∵点P在线段OD上,
∴EF的长不可能为定值,故④错误;
⑤由③可得
∵∠AFB=∠AFN=∠APG,∠FAE=∠PAG,
∴△APG∽△AFE,
故⑤正确;
综上所述:以上结论正确的有①②③⑤;
故答案为①②③⑤.
【标注】【知识点】四点共圆的应用
7已知,如图,在正方形ABCD中,AD=4,E,F分别是CD,BC上的点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论: 中正确的是( ).
A. ①②③ B. ②③④ C. ①③④ D.①②④
【答案】D
【解析】∵AG=AE,∠FAE=∠FAG=45°,AF=AF.
.△AFE≌△AFG(SAS),
∴EF=FG,
DE=BG,
.. EF=FG=BG+FB=DE+BF,故①正确,
BC=CD=AD=4,EC=1,
∴DE=3,设BF=x,则EF=x+3,CF=4-x,
在Rt△ECF中,
解得
故②正确,③错误,
:BM//AG,
.△FBM∽△FGA,
故④正确.
故选:D.
【标注】【知识点】正方形中的半角模型
8如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合), 点F在射线AM上,且 CF与AD相交于点G,连接EC、EF、EG,则下列结论:
①∠ECF=45°;
②△AEG的周长为
④△EAF的面积的最大值是
⑤当 a时,G是线段AD的中点.
其中正确的结论是( )
A. ①②③ B. ②④⑤ C. ①③④ D.①④⑤
【答案】D
【解析】如图1中,在BC上截取BH=BE,连接EH,
∵BE=BH ,∠EBH=90°,
∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°.
∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,∴AE=HC,
∴△FAE≌△EHC(SAS),
∴EF=EC,∠AEF=∠ECH,
∴∠FEC=90°,
∴∠ECF=∠EFC=45°,故①正确;
如图2中,延长AD到H,使得DH= BE,
则△CBE≌△CDH(SAS),
∴∠ECB=∠DCH,
CG=CG,CE=CH,
∴△GCE≌△GCH(SAS),
∴EG=GH,
∵GH=DG+DH,DH=BE,
∴EG=BE+DG,故③错误;
∴△AEG的周长=AE+EG+AG=AE+AD+DH
=AE+AD+EB=AB+AD=2a,故②错误;
设BE=x,则AE=a-x,AF= x,
当a a时,△AEF的面积的最大值为 a ,故④正确;
如图3,延长AD到H,使得DH= BE,
同理,EG=GH,
则
设AG=y,则DG=a-y,
在Rt△AEG中,
艮
解得
∴当 a时,G是线段AD的中点,故⑤正确.
综上,①④⑤正确.
故选:D.
【标注】 【知识点】正方形与全等综合
9如图,在平面直角坐标系中,以坐标原点O(0,0),A(0,4), B(3,0)为顶点的Rt△AOB,其两个锐角对应的外角的平分线相交于点P,且点P恰好在反比例函数 的图象上,则k的值为( ).
A.36 B.48 C.49 D.64
【答案】A
【解析】过点P分别作AB、x轴、y轴的垂线,垂足分别为C、D、E,如图,
∵A(0,4), B(3,0),
∴OA=4,OB=3,
∵△OAB的两个锐角对应的外角的平分线相交于点P,
∵PE=PC,PD=PC,
∴PE=PC=PD,
设P(t,t),则PC=t,
= txt,
解得t=6,
∴P(6,6),
把P(6,6)代入y= kz得k=6×6=36.
故选:A.
【标注】 【知识点】反比例函数的系数k的几何意义
10如图,在正方形ABCD中,AB=6,G是BC的中点,将△ABG沿AG对折至△AFG,延长GF交DC于点E ,则DE的长是( ) .
A.1 B. 1.5 C. 2 D.2.5
【答案】C
【解析】如图,连接AE,
∴AB=AD=AF,∠D=∠AFE=90°,
在Rt△AFE和Rt△ADE中,
. Rt△AFE≌Rt△ADE,
∴EF=DE,
设DE=FE=x,则EC=6-x.
∵G为BC中点,BC=6,
∴CG=3,
在Rt△ECG中,根据勾股定理,得:
解得x=2.
则DE=2.
【标注】 【知识点】翻折问题与勾股定理
11如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ∠EAF=45°,则AF的长为 .
【答案】
【解析】取AB的中点M ,连接ME,在AD上截取ND=DF,
^
设DF=DN=x,
∵四边形ABCD是矩形,
∴∠D=∠BAD=∠B=90°,AD=BC=4,
∴NF= x,AN=4-x,
∵AB=2,
∴AM=BM=1,
∵AE= ,AB=2,
∴BE=1,
∴∠MEA=∠NAF,
∴△AME∽△FNA,
解得
【标注】 【知识点】相似三角形的性质与判定综合
12如图1,已知四边形ABCD是正方形,将△DAE,△DCF分别沿DE,DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点),若GF=4,EG=6,则DG的长为
【答案】12
【解析】设正方形ABCD的边长为x,由翻折可得:
DG=DA=DC=∞,
∵GF=4,EG=6,
∴AE=EG=6,CF=GF=4,
∴BE=x-6,BF=x-4,EF=6+4=10,如图1所示:
在Rt△BEF中,由勾股定理得:
∴(x+2)(x-12)=0,
∴x =-2 (舍),x =12,
∴DG=12.
故答案为:12.
【标注】 【知识点】翻折问题与勾股定理
13如图,已知正方形ABCD的边长为a,E为CD边上一点(不与端点重合),将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.
给出下列判断:
①∠EAG =45°;
②若 则AG//CF;
③若E为CD的中点,则△GFC的面积为 ;
④若CF=FG,则
⑤BG·DE+AF·GE=a
其中正确的是 .(写出所有正确判断的序号)
【答案】①②④⑤
【解析】①∵四边形ABCD是正方形,
∴AB=BC=AD=a,
∵将△ADE沿AE对折至△AFE,
∴∠AFE=∠ADE=∠ABG=90°,AF=AD=AB,EF=DE,∠DAE=∠FAE,
在Rt△ABG和Rt△AFG中
∴Rt△ABG≌Rt△AFG(HL) ,
∴∠BAG=∠FAG,
故①正确;
②∴BG=GF,∠BGA=∠FGA,
设BG=GF=x,∵DE= a,
∴CG=a-x,
在Rt△EGC中, 由勾股定理可得
解得 此时
∴∠GFC=∠GCF,
且∠BGF=∠GFC+∠GCF=2∠GCF,
∴2∠AGB=2∠GCF,
∴∠AGB=∠GCF,
∴AG//CF,
∴②正确;
③若E为CD的中点,则
设BG=GF=y,则CG=a-y,
艮
解得
故③错误;
④当CF=FG,则∠FGC=∠FCG,
∵∠FGC+∠FEC=∠FCG+∠FCE=90°,
∴∠FEC=∠FCE.
. EF=CF=GF,
∴BG=GF=EF=DE,
∴EG=2DE,CG=CE=a-DE,
∴CE=EG,即
故④正确;
⑤设BG=GF=b,DE=EF=c,则CG=a-b,CE=a-c,
由勾股定理得, 整理得
即S△CEG=BG·DE,
∵S△ABG=S△APG,S△AEF=S△ADE,
故⑤正确.
故答案为:①②④⑤.
【标注】【知识点】正方形与全等综合
14如图,正方形ABCD中,△ABC绕点A逆时针旋转到△AB'C', AB',AC'分别交对角线BD于点E, F ,若AE=4,则EF. ED的值为
【答案】16
【解析】∵∠EAF=∠EDA=45°,∠AEF=∠DEA,
∴△AEF∽△DEA,
15如图①,E、F是等腰Rt△ABC的斜边BC上的两动点,∠EAF=45°,CD⊥BC且CD=BE.
(1) 求证:△ABE≌△ACD.
(2)求证:
(3)如图②,作AH⊥BC,垂足为H,设∠EAH=α,∠FAH=β,不妨设 请利用(2)的结论证明:当α+β=45°时 成立.
【答案】(1)证明见解析.
(2)证明见解析.
(3)证明见解析.
【解析】(1)∵△ABC是等腰直角三角形,
∴AB=AC,
∵CD⊥BC,
∴∠AOD=∠BCD-∠ACB=45°=∠B,在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
(2)由(1)知,△ABE≌△ACD,
∴AE=AD,∠BAE=∠CAD,
∵∠BAO=90°,
∴∠EAD=∠CAE+∠CAD=∠CAE+∠BAE=∠BAC=90°,
∵∠EAF=45°,
∴∠DAF=∠DAE-∠EAF=45°=∠EAF,
∵AF=AF,
∴△AEF≌△ADF(SAS),
∴DF=EF,
在Rt△DCF中,根据勾股定理得,
∵CD=BE,
(3)在Rt△ABC中,AC=AB=
∵AH⊥BC,
∴BE=1-EH,CF=1-FH,
由(2)知,
∵EF=EH+FH,
∴1-EH·FH=EH+FH,
在Rt△AHE中,
在Rt△AHF中,
∴右边
=1.
∴左边
∴左边=右边,
即当α+β=45°时,
成立.
【标注】 【知识点】解直角三角形的综合应用
16在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
(1)如图1,若BC=2BA,求∠CBE的度数.
(2)如图2,当AB=5,且AF·FD=10时,求BC的长.
(3) 如图3,延长EF,与∠ABF的角平分线交于点M , BM交AD于点N ,当NF=AN+FD时, 求ABC的值.
【答案】(1)15°.
(2)3
(3)
【解析】(1)由△BCE翻折得到△BFE,可知BC=BF,∠CBE=∠FBE.
又∵BC=2BA=BF,
∴在Rt△ABF中,
又:
(2) 由翻折可知:∠BFE=∠BCE=90°,
∴可得∠AFB+∠DFE=90°.
又∵在△AFB中,.
在Rt△DEF中,∠DFE+∠DEF=90°,
故可得∠DFE=∠ABF,∠AFB=∠DEF,
∴△AFB∽△DEF,
故AB·DE=AF·DF,
即5·DE=10,
∴DE=2,
.. EF=CE=5-2=3.
设DF为a,在Rt△DEF中,
可得 即
又∵AF·DF=10,
故
(3)如图,过N点作NH⊥BF于H点.
∴∠NFH=∠BFA,∠NHF=∠BAF=90°,
∴△NFH∽△BFA,
#
又∵NF=AN+FD,
设NH=a,又因为BN为角平分线,NA⊥AB,NH⊥BF,
∴AN=HN=a.
在Rt△ABN和Rt△HBN中,
∴Rt△ABN≌Rt△HBN(HL),
故BH=AB=2NH=2a.
设FN=b,|由
可得
在Rt△NHF中,
由( 得
解得
【标注】 【知识点】翻折问题与勾股定理
17如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E, AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE.
②若BE=2,DF=3,求AH的长.
(2) 如图3,连接BD交AE于点M ,交AF于点N .请探究并猜想:线段BM ,MN,ND之间有什么数量关系 并说明理由.
【答案】(1)①证明见解析.
② AH=6.
【解析】(1)①由旋转的性质可知:AF=AG ,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中
∴△GAE≌△FAE.
② ∵△GAE≌△FAE,AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x-2,FC=x-3.
在Rt△EFC中,
由勾股定理得:
即
解得:x=6.
∴AB=6.
.. AH=6.
(2) 如图所示:将△ABM逆时针旋转90°得△ADM'.
∵四边形ABCD为正方形,
.∠ABD=∠ADB=45°
由旋转的性质可知:∠ABM=∠ADM'=45°,BE=DM'.
.∠NDM'=90°.
:∠EAM'=90°,∠EAF=45°,
.∠EAF=∠FAM'=45°
在△AMN和△ANM'中,
∴△AMN≌△ANM'.
∴MN=NM'
又∵BM=DM',
【标注】 【知识点】正方形与全等综合
18如图,正方形ABCD的边长为6,点E、F分别在AB、AD上,若CE=3 ,且∠ECF=45°,则CF的长为( ) .
A.2 B.3 D.
【答案】A
【解析】如图,延长FD到G,使DG=BE,
连接CG、EF.
∵四边形ABCD为正方形,
在△BCE与△DCG中,
∴△BCE≌△DCG(SAS),
∴CG=CE=3 ,∠DCG=∠BCE.
∵∠BCE+∠FCD=∠FCD+∠DCG=90°-∠ECF=45°,
∴△GCF≌△ECF(SAS).
∴AE=3.
设AF=x,则DF=6-x,GF=9-x,
解得x=4,
∴DF=2.
在Rt△CDF中,
∴CF=2
【标注】 【知识点】正方形中的半角模型
19如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 .
【答案】6
【解析】由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°
∴∠BAG+∠BAE=45°
∴∠GAE=∠FAE.
在△GAE和△FAE中
△GAE≌△FAE.
AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x-2,FC=x-3.
在Rt△EFC中,由勾股定理得: 即
解得:x=6.
∴AB=6.
∴AH=6.
【标注】【知识点】方程思想在勾股定理的应用;正方形中的半角模型
20在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=CD.探究:当点M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.
(1) 如图1,当点M、N在边AB、AC上,且DM=DN时,BM、CN、MN之间的数量关系是 ;此时
(2)如图2,当点M、N在边AB、AC上,且当DM≠DN时,猜想(1)问的两个结论还成立吗 写出你的猜想并加以证明.
(3)如图3,当点M、N分别在边AB、CA的延长线上时,若AN=x,则Q= .(用z、L表示)
【答案】
(2)猜想:结论依然成立,证明见解析.
【解析】(1)如图1,猜想:MN=BM+NC,理由是:
∵DM=DN,∠MDN=60°,
△MDN是等边三角形.
. MN=DM=DN.
:∠BDC=120°,BD=DC,
∴∠DBC=∠DCB=30°.
∵△ABC是等边三角形,
∵BD=CD,DM=DN,
∴Rt△DBM≌Rt△DCN.
∴∠BDM=∠CDN=30°,BM=CN.
∴DM=2BM.
∴DM=MN=2BM=BM+NC.
:AB=AC,BM=CN,
∴AM=AN
:∠A=60°,
∴△AMN是等边三角形.
∴△AMN的周长Q=3MN=6BM
等边△ABC的周长L=3AB=3(AM+BM)=9BM,
故答案为:.
(2)猜想:结论依然成立.
如图,延长AC至E,使得CE=BM ,连接DE,
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°.
又∵△ABC为等边三角形,
∴∠MBD=∠NCD=90°.
在△MBD与△ECD中,
∴△MBD≌△ECD(SAS).
∴DM=DE,∠BDM=∠CDE,
∴∠EDN=∠BDC-∠MDN=60°.
在△MDN与△EDN中,
∴△MDN≌△EDN(SAS),
∴MN=NE=BM+ON,
△AMN的周长Q=AM+AN+MN=AB+AC,
(3)如图3,∵等边△ABC的周长为L,
△AMN的周长Q=MN+AN+AM
=FN+AN+AB+BM
=AN+AF+AN+AB+CF
=2x+2AB
故答案为:
【标注】 【知识点】多边形中的半角模型
21如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M ,垂足分别为H、G.现有以下结论:①AB= ②当点E与点B重合时,MH= ;③AF+BE=EF;④MG·MH= ,其中正确结论为( ).
A. ①②③ B. ①③④ C. ①②④ D.①②③④
【答案】C
【解析】①由题意可知,△ABC是等腰直角三角形,
故①正确;
②如图1,当点E与点B重合时,点H与点B重合,
∴MB⊥BC,∠MBC=90°,
∵MG⊥AC,
∠MGC=90°=∠ACB=∠MBC,
∴MG∥BC,四边形MGCB是矩形,
∴MH=MB=CG,
∵∠FCE=45°=∠ABC,∠A=∠ACF=45°,
∴CE=AF=BF,
:FG是△ACB的中位线,
故②正确;
③如图②,
∵AC=BC,∠ACB=90°,
∴∠A=∠5=45°,
将△ACF顺时针旋转90°至△BCD,
则CF=CD,∠1=∠4,∠A=∠6=45°,BD=AF,
∵∠2=45°,
∴∠1+∠3=∠3+∠4=45°,
∴∠DCE=∠2,
在△ECF和△ECD中,
∴△ECF≌△ECD(SAS) ,
∴EF=DE,
∵∠5=45°,
∴∠DBE=90°,
即 故③错误;
④方法一:由题意可知四边形CHMG是矩形,
∴∠A=∠MEF,∠AGF=∠EMF,
∴△AGF∽△EMF,
同理可得△EHB∽△EMF,
则
由③得,EF =AF +BE ,
即,
即△ABC的面积等于矩形GCHM的面积,
故④正确;
:∠7=∠1+∠A=∠1+45°=∠1+∠2=∠ACE,
∵∠A=∠5=45°,
∴△ACE∽△BFC,
∴AE·BF=AC·BC=1,
由题意知四边形CHMG是矩形,
∴MG∥BC,MH=CG,
MG=CH,MH//AC,
故④正确.
④方法二:
同理可得:
由③可知:
故④正确.
所以正确的结论有①②④三个,故选C
【标注】 【知识点】相似8字型
22如图,在△ABC中,AB=AC,∠BAC=120°,点D、E在边BC上,且∠DAE=60°,将△ADE沿AE翻折,点D的对应点是D',连接CD',若BD=4,CE=5,则DE的长为( )
A B. C. D.2
【答案】B
【解析】如图,作D'H⊥EC于H.
∵∠DAE=∠EAD'=60°,∠BAC=120°,
∴∠BAD+∠EAC=60°,∠EAC+∠CAD'=60°,
∴∠BAD=∠CAD',
∵AB=AC,AD=AD',
∴△BAD≌△CAD',
∴CD'=BD=4,∠B=∠ACD'=∠ACB=30°,
∴∠D'CH=60°,∠CD'H=30°,
在Rt△D'EH中,
故选:B.
23如图,点E,F分别为正方形ABCD的边BC,CD上一点,AC,BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M, N,则有以下结论:①∠AEB=∠AEF=∠ANM;②EF=BE+DF;③△AOM∽△ADF;④S△ABF=2S△AMN.
以上结论中,正确的是 (请把正确结论的序号都填上)
【答案】①②③④
【解析】如图,把△ADF绕点A顺时针旋转90°得到△ABH.
由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,
∵∠EAF=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°-∠EAF=45°.
∴∠EAH=∠EAF=45°,
在△AEF和△AEH中,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∴∠AEB=∠AEF,
∴BE+BH=BE+DF=EF,故②正确;
∵∠ANM=∠ADB+∠DAN=45°+∠DAN,
∠AEB=90°-∠BAE=90°-(∠HAE-∠BAH)=90°-(45°-∠BAH)=45°+∠BAH'
∴∠ANM=∠AEB,
∴∠AEB=∠AEF=∠ANM;故①正确;
∵AC⊥BD,
∴∠AOM=∠ADF=90°,
∵∠MAO=45°-∠NAO,∠DAF=45°-∠NAO,
∴△OAM∽△DAF,故③正确;
连接NE,
∵∠MAN=∠MBE=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∴△AMB∽△NME,
∴∠AEN=∠ABD=45°,
∴△AEN是等腰直角三角形,
∵△AMN∽△BME,△AFE∽△BME,
∴△AMN∽△AFE,
.故④正确.
故答案为:①②③④.
【标注】 【知识点】正方形中的半角模型
24如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M、N .下列结论:①AB =BN·DM;②AF平分∠DFE;③AM·AE=AN·AF 其中正确的结论是( )
A. ①② B. ①③ C. ①②③ D.①②③④
【答案】D
【解析】①∵∠BAN=∠BAM+∠MAN
∴∠BAN=∠AMD.
又∠ABN=∠ADM=45°,
∴△ABN-△ADM,
∴AB:BN=DM:AD.
∵AD=AB,
故①正确;
②把△ABE绕点A逆时针旋转90°,得到△ADH.
∵∠BAD=90°,∠EAF=45°,
∴∠EAF=∠HAF.
∵AE=AH,AF=AF,
∴△AEF≌△AHF,
∴∠AFH=∠AFE,即AF平分∠DFE.
故②正确;
③∵AB∥CD,
∴∠DFA=∠BAN
∵∠AFE=∠AFD,∠BAN=∠AMD,
∴∠AFE=∠AMN.
又∠MAN=∠FAE,
∴△AMN-△AFE.
. AM:AF=AN:AE,即AM·AE=AN·AF.
故③正确;
④由②得BE+DF=DH+DF=FH=FE.
过A作AO⊥BD,AG⊥EF.
则△AFE与△AMN的相似比就是AG:AO.
易证△ADF≌△AGF(AAS),
则可知
从而得证故④正确.
故选:D.
【标注】 【知识点】正方形中的半角模型
25如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AC,现在有如下4个结论:
①∠EAG=45°;②FG=FC;③FC//AG;④S△GFC=14.
A.1 B.2 C.3 D.4
【答案】B
【解析】如图,连接DF.
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠ABE=∠BAD=∠ADG=∠ECG=90°,由翻折可知:AB=AF,∠ABE=∠AFE=∠AFG=90°,BE=EF=4,∠BAE=∠EAF,
∵∠AFG=∠ADG=90°,AG=AG,AD=AF,
∴Rt△AGD≌Rt△AGF(HL),
∴DG=FG,∠GAF=∠GAD,设GD=GF=x,
故①正确;在Rt△ECG中,
∴x=6,
∵OD=BC=BE+EC=12,
∴DG=CG=6,
∴FG=GC,
易知△GFC不是等边三角形,显然FG≠FC,故②错误;
∵GF=GD=GC,
∴CF⊥DF,
∵AD=AF,GD=GF,
∴AG⊥DF,
∴CF//AG,故③正确;
∵S△BCG= ×6×8=24,FG:FE=6:4=3:2,
∴FG:EG=3:5,
故④错误;
故选B.
【标注】 【知识点】其它翻折问题
26如图1,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在四边形ABCD的边BC、CD上, 连接EF,试猜想EF、BE、DF之间的数量关系.
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F、D、G三点共线,易证△AFG≌ ,故EF、BE、DF之间的数量关系为 .
(2)类比引申
如图2,在图1的条件下,若点E、F由原来的位置分别变到四边形ABCD的边CB、DC延长线上, 连接EF ,试猜想EF、BE、DF之间的数量关系,并给出证明、
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,则DE的长为 .
【答案】(1)△AFE;EF=BE+DF
(2) EF、BE、DF之间的数量关系是EF=DF-BE,证明见解析.
(3)
【解析】(1)将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,:∠B+∠ADC=180°,
∴∠FDG=180°,即点F , D , G三点共线,
∴∠EAF=∠GAF.
在△AFG和△AFE中,
∴△AFG≌△AFE,
∴EF=FG=FD+FG=FD+BE.
(2)将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',
则△ABE≌△ADE',
..∠DAE'=∠BAE,AE'=AE,DE'=BE,∠ADE'=∠ABE,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
.∠ADE'=∠ADC,即E'、D、F三点共线,
∴∠E'AF=∠BAD-(∠BAF+∠DAE')
=∠BAD-(∠BAF+∠BAE)
∴∠EAF=∠E'AF,
在△AEF和△AE'F中,
∴△AFE≌△AFE'(SAS),
∴EF=DF-BE;
(3) 将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',
由(1)得,△AED≌AED',
∴DE=D'E.
在Rt△ECD'中, 即
27旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且
(1) 如图a,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连接DF.
①求∠DAF的度数.
② 求证:△ADE≌△ADF.
(2)如图b,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由.
(3)如图c,当α=120°,BD=4,CE=5时,请直接写出DE的长为 .
【答案】(1)① 30°.
② 证明见解析.
证明见解析.
【解析】(1)①由旋转得,∠FAB=∠CAE,
∴∠DAF=∠BAD+∠BAF=∠BAD+∠CAE=30°.
②由旋转得,AF=AE
在△ADE和△ADF中
∴△ADE≌△ADF.
(2)如图,
将△AEC绕点A顺时针旋转90°到△AFB的位置,连接DF,
∴BF=CE,∠ABF=∠ACB,
由(1)得△ADE≌△ADF
∴DF=DE
∵AB=AC,∠BAC=90°,
∴∠ABC=∠AOB=45°,
∴∠DBF=∠ABC+∠ABF=∠ABC+∠ACB=90°,
∴在Rt△BDF中,
(3)如图3,
将△AEC绕点A顺时针旋转90°到△AFB的位置,连接DF,
∴BF=CE,∠ABF=∠ACB,
由(1)知,△ADE≌△ADF,
∴DE=DF,BF=CE=5,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=30°,
∴∠DBF=∠ABC+∠ABF=∠ABC+∠ACB=60°,过点F作FM⊥BC于M,
在Rt△BMF中,∠BFM=90°-∠DBF=30°,BF=5,
∵BD=4,
根据勾股定理得
故答案为:
1.核心知识
1、半角在内:正方形ABCD,点E在边CD上, 点F在边BC上,∠EOF =45°
【辅助线】延长BC至点G , 使BG= DE , 连接AG.
【结论】
①旋转全等:△ABG≌△ADE, 理由SAS.
②对称全等:△FAG≌△FAE , 理由SAS.
③EF=BF+DE ,进而推出△CEF的周长等于正方形周长的一半.
④AF平分∠BFE, AE平分∠DEF.
2、半角在外:正方形ABCD, ,与DC的延长线交于点E ,与CB的延长线交于点F .
【辅助线】在CD截取 连接AG.
【结论】
①旋转全等: ,理由SAS.
②对称全等: 理由SAS.
④AE平分∠DEF.
真题精炼
1如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M .若BE= DF =1, 则DM的长度为( )
A.2
2正方形ABCD中,点E在边BC ,CD上运动(不与正方形顶点重合).作射线AE,将射线AE绕点A逆时针旋转45°,交射线CD于点F .
(1)如图,点E在边BC上,BE =DF ,则图中与线段AE相等的线段是
(2) 过点E作EG⊥AF, 垂足为G, 连接DG, 求∠GDC的度数.
3在复习课上,刘老师先引导学生解决以下问题: 【问题情境】如图1,在△ABC中,∠BAC=90°,AB= AC,点D、E在边BC上,且∠DAE=45°,BD=3,CE=4,求DE的长.解:如图2, 将△ABD绕点A逆时针旋转90°得到△ACD', 连结ED' .
由旋转的特征得∠BAD=∠CAD',∠B=∠ACD', AD= AD',BD=CD'.∵∠BAC=90°,∠DAE=45°,∴∠BAD+∠EAC=45°.∵∠BAD=∠CAD',∴∠CAD'+∠EAC=45°,即∠EAD'=45°.∴∠DAE=∠D'AE.在△DAE和 中, ∠DAE=∠D'AE, AE=AE,∴ ① .∴DE=D'E .又∵
∠ECD'=∠ECA+∠ACD'=∠ECA+∠B=90°,∴在Rt△ECD'中, ② .
∵CD'=BD=3,CE=4,
【问题解决】上述问题情境中, “①”处应填: ; “②”处应填: ; “③”处应填: .刘老师进一步谈到:图形的变化强调从运动变化的观点来研究,只要我们抓住了变化中的不变量,就能以不变应万变.
【知识迁移】如图3,在正方形ABCD中,点E、F分别在边BC、 CD上,满足△CEF的周长等于正方形ABCD的周长的一半,连结AE、 AF,分别与对角线BD交于M、N两点.探究BM、MN、 DN的数量关系并证明.
【拓展应用】如图4,在矩形ABCD中,点E、F分别在边BC、 CD上,且∠EAF=∠CEF=45°.探究BE、EF、 DF的数量关系:
【问题再探】如图5,在△ABC中,∠ABC=90°,AB=4,BC=3,点D、E在边AC上,且∠DBE=45°.设AD=x,CE=y,求y与x的函数关系式.
4(1)操作一:如图①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则 度.
(2)操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N .我们发现,当点E的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上,则 度.
(3)在图②中,运用以上操作所得结论,解答下列问题:
① 设AM与NF的交点为点P .求证:
② 若 则线段AP的长为 .
5数学实践活动 ,是一种非常有效的学习方式.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF,连接EF ,如图1.
,写出图中两个等腰三角形 : (不需要添加字母);
转一转:将图1中的 绕点A旋转,使它的两边分别交边BC、CD于点P、Q,连接PQ,如图2.
(2) 线段BP、PQ、DQ之间的数量关系为 .
(3)连接正方形对角线BD ,若图2中的. 的边AP、AQ分别交对角线BD于点M、点N,如图3,则
剪一剪:将图3中的正方形纸片沿对角线BD剪开,如图4.
(4) 求证 :
6如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作 交BC于点F ,连接AF、EF , AF交BD于G, 现有以下结论:①AP =PF;②DE+BF=EF;③PB--PD= BF ;④S△AEF为定值;⑤S四边形PEFG = S△APG .以上结论正确的有 (填入正确的序号即可).
7如图正方形ABCD中,. 且 将 绕点A沿顺时针方向旋转90°后与 重合,连接EF,过点B作 交AF于点M,则以下结论:① 中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
8如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),. 点F在射线AM上,且 CF与AD相交于点G ,连接EC、EF、EG,则下列结论:
①∠ECF=45°;
②△AEG的周长为
④△EAF的面积的最大值是
⑤当 时,G是线段AD的中点 .其中正确的结论是( )
A. ①②③ B. ②④⑤ C. ①③④ D. ①④⑤
9如图,在平面直角坐标系中, 以坐标原点O(0,0), A(0,4), B(3,0)为顶点的Rt△AOB, 其两个锐角对应的外角的平分线相交于点P,且点P恰好在反比例函数 的图象上,则k的值为( )
A.36 B. 48 C. 49 D.64
10如图,在正方形ABCD中, AB=6,G是BC的中点,将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( ) .
A. 1 B. 1.5 C. 2 D. 2.5
11矩形ABCD中,AB=2,BC=4,若 则AF的长为
12如图1,已知四边形ABCD是正方形,将 分别沿DE,DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点) , 若 ,则DG的长为 .
13如图,已知正方形ABCD的边长为a,E为CD边上一点(不与端点重合),将 沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF .给出下列判断:
②若 则AG//CF;
③若E为CD的中点,则△GFC的面积为 ④若CF=FG ,则.
⑤BG·DE+AF·GE=a .其中正确的是 .
14如图正方形中,△ABC绕点A逆时针旋转到 交对角线于点E, F,若AE=4 ,则EF·ED为 .
15如图①, E、F是等腰Rt△ABC的斜边BC上的两动点, ∠ C且CD=BE.
(1) 求证:△ABE≌△ACD .
(2) 求证:
(3) 如图②, 作AH⊥BC, 垂足为H ,设 不妨设 请利用(2) 的结论证明:当α+β=45°时, 成立.
16在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
(2) 如图2,当AB=5,且AF·FD=10时,求BC的长.
(3) 如图3,延长EF,与∠ABF的角平分线交于点M , BM交AD于点N ,当 时,求 的值.
17如图1,在正方形ABCD内作 ,AE交BC于点E , AF交CD于点F , 连接EF , 过点A作AH⊥EF,垂足为H .
(1) 如图2, 将△ADF绕点A顺时针旋转90°得到△AB
① 求证:△AGE≌△AFE.
② 若BE=2, DF =3,求AH的长.
(2) 如图3,连接BD交AE于点M,交AF于点N .请探究并猜想:线段BM , MN , ND之间有什么数量关系 并说明理由.
18如图,正方形ABCD的边长为6,若 且∠ECF=45°,则CF的长为( )
19如图,在正方形ABCD内作∠EAF =45°, 连接EF, 过点A作AH⊥EF ,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE =2, DF=3,则AH的长为 .
20在等边 的两边AB、AC所在直线上分别有两点M、N ,D为△ABC外一点,且 .探究:当点M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.
(1) 如图1,当点M、N在边AB、AC上,且DM =DN时, BM、CN、MN之间的数量关系是 ;此时
(2) 如图2,当点M、N在边AB、AC上,且当DM≠DN时, 猜想(1) 问的两个结论还成立吗 写出你的猜想并加以证明.
(3) 如图3,当点M、N分别在边AB、CA的延长线上时,若AN=x,则Q=
21如图△ABC中, ,E、F为线段AB上两动点,且. ,过点E、F分别作BC、AC的垂线相交于点M .以下结论: ②当点E与点B重合时, ③AF+BE=EF; ④MG·MH= $,其中正确结论为( )
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
22如图,在△ABC中, AB = AC,∠BAC=120°,点D、E在边BC上,且 将△ADE沿AE翻折, 点D的对应点是D', 连接CD' , 若 ,则DE的长为( ) .
23如图,点E, F分别为正方形ABCD的边上一点, AC, BD交于点O,且∠EAF =45°,AE,AF分别交对角线BD于点M , N , 则有以下结论:①∠AEB =∠AEF =∠ANM ;②EF =BE+DF;③△AOM ∽△ADF;④S△AEF =2S△AMN.正确的是 .
24正方形ABCD中,且∠EAF=45°.下列结论:①AB =BN·DM;②AF平分∠DFE;③AM·AE=AN·AF;④BE+DF= MN.其中正确的结论是( ).
A. ①② B. ①③ C. ①②③ D. ①②③④
25正方形ABCD中, E是BC边上的一点, BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AC,如下结论:①∠EAG=45°;②FG=FC;③FC//AG;④S△GFC =14 .正确结论个数是( )
A.1 B.2 C. 3 D.4
26如图1,在四边形ABCD中, AB=AD ,∠B+∠ADC=180°,点E、F分别在四边形ABCD的边BC、CD上, 连接EF ,试猜想EF、BE、DF之间的数量关系.
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG, 使AB与AD重合, 由 得∠FDG=180°, 即点F、D、G三点共线, 易证△AFG≌ , 故EF、BE、DF之间的数量关系为 .
(2)类比引申
如图2,在图1的条件下,若点E、F由原来的位置分别变到四边形ABCD的边CB、DC延长线上, 连接EF ,试猜想EF、BE、DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D , E均在边BC上,且∠DAE=45°,若BD=1, EC=2,则DE的长为 .
27旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知, 中, 点D、E在边BC上, 且
(1) 如图a,当 时,将 绕点A顺时针旋转60°到△AFB的位置,连接DF .
①求 的度数.
② 求证:
(2) 如图b,当 时,猜想BD、DE、CE的数量关系,并说明理由.
(3) 如图c,当 时,请直接写出DE的长为 .
1如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AP,AM平分∠EAF交CD于点M ,若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
2.【答案】(1) AF
(2)过G点作GM⊥AD交于M,延长MG交BC于N点,
∴∠AMG=∠DMG=∠GNE=90°,
.四边形CDMN是矩形,
.∠AGM+∠MAG=90°,
:EG⊥AF,∠EAF=45°,
∴∠AGM+∠EGN=90°
∵∠AGE=90°,∠EAF=45°
∴△AEG是等腰直角三角形,
∴AG=EG,
∴∠EGN=∠MAG,
∴△AMG≌△GNE(AAS),
∴AM=GN,
∵AM+MD=GN+MG,
∴MD=MG,
∴△MDG为等腰直角三角形,
∴∠MDG=45°,
∴∠GDC=45°;
当点E在CD边上时,如图,
过点G作GN⊥DF交于N,延长NG交BA延长线于点M,∴四边形ADNM是矩形,
同理,△AMG≌△GNE(AAS).
∴GN=AM=DN,
∴△NDG为等腰直角三角形,
∴∠GDN=45°,
∴∠GDC=180°-45°=135°,
综上所述:∠GDC的度数为45°或135°.
【标注】【知识点】正方形与全等综合
3【问题情境】
如图1,在△ABC中,∠BAC=90°,AB=AC,点D、E在边BC上,且∠DAE=45°,BD=3,CE=4,求DE的长.
解:如图2,将△ABD绕点A逆时针旋转90°得到△ACD',连结ED'.
由旋转的特征得∠BAD=∠CAD',∠B=∠ACD',AD=AD',BD=CD'.
∵∠BAC=90°,∠DAE=45°,
∠BAD+∠EAC=45°.
∴∠BAD=∠CAD',
..∠CAD'+∠EAC=45°,即∠EAD'=45°.
∴∠DAE=∠D'AE.
在△DAE和△D'AE中,
AD=AD',∠DAE=∠D'AE,AE=AE,
.① .
DE=D'E.
又∵∠ECD'=∠ECA+∠ACD'=∠ECA+∠B=90°,
∴在Rt△ECD'中, ② .
∵CD'=BD=3,CE=4,
∴DE=D'E= ③ .
【问题解决】
上述问题情境中, “①”处应填: ;“②”处应填: ;“③”处应填: .
刘老师进一步谈到:图形的变化强调从运动变化的观点来研究,只要我们抓住了变化中的不变量,就能以不变应万变.
【知识迁移】
如图3,在正方形ABCD中,点E、F分别在边BC、CD上,满足△CEF的周长等于正方形ABCD的周长的一半,连结AE、AF,分别与对角线BD交于M、N两点.探究BM、MN、DN的数量关系并证明.
如图4,在矩形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CEF =45°.探究BE、EF、DF的数量关系: (直接写出结论,不必证明).
中小学教育资源及组卷应用平台
如图5,在△ABC中,∠ABC=90°,AB=4,BC=3,点D、E在边AC上,且∠DBE=45°.设AD=x,CE=y,求y与x的函数关系式.
【答案】 【问题解决】①△ADE≌△AD'E;②EC +CD =ED ;③5;【知识迁移】 见解析;【拓展应用】 【问题再探】
【解析】
【分析】
(1)【问题解决】根据题中思路解答即可;
(2)【知识迁移】如图,将△ABE绕点A逆时针旋转90°,得到△ADF'过点D作DH⊥BD交边AF'于点H,连结NH,由旋转的特征得AE=AF',BE=DF',∠BAE=∠DAF'.结合题意得 .证明△AEF≌AF'F,得出∠EAF=∠F'AF.根据正方形性质得出∠ABD=∠ADB=45°.结合DH⊥BD,得出∠ADH=∠HDB-∠ADB=45°.证明△ABM≌△ADH,得出AM=AH;BM=DH.证明△AMN △AHN.得出MN=HN.在Rt△HND中,根据勾股定理即可求解;
(3)【拓展应用】如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连接HM,HE.则△ADF≌△AGH.则DF=GH,AG=AD,AF=AH,∠DAF=∠HAG,根据∠EAF=45°,证明△AEH≌△AEF,得出EF=HE,过点H作HO⊥CB交CB于点O,过点H作HG⊥BM交BM于点M,则四边形OHGB为矩形.得出OH=BG,OB=HG,证明△BME,△DNF,△CEF,△AMN是等腰直角三角形,得出GM=DN=DF=HG,∠HME=90°,在Rt△OHE中,根据勾股定理即可证明;
(4)【问题再探】如图,将△BEC绕点B逆时针旋转90°,得到BE'C',连结E'D.过点E作EG⊥BC,垂足为点G,过点E'作EG'⊥BC',垂足为G',过点E'作E'F∥BA,过点D作DF∥BC交AB于点H,E'F、DF交于点F.由旋转的特征得
BE=BE',∠CBE=∠C'BE',EG=E'G',BG=BG'.根据∠ABC=90°,∠DBE=45°,得出∠DBE'=45°,证明△EBD≌△E'BD,得出DE=DE',根据勾股定理算出AC,根据AD=z,CE=y,表示出DE'=5-x-y,证明△AHD∽△ABC,根据相似三角形的性质表示出 同理可得
证明四边形FE'G'H为矩形.得出
在Rt△E'FD中,根据勾股定理即可求解;
【详解】
解: (1)【问题解决】解:如图2,将△ABD绕点A逆时针旋转90°得到△ACD',连结ED'
由旋转的特征得∠BAD=∠CAD',∠B=∠ACD',AD=AD',BD=CD'.
∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠EAC=45°
∵∠BAD=∠CAD',
∴∠CAD'+∠EAC=45°,即∠EAD'=45°.
∴∠DAE=∠D'AE.
在△DAE和△D'AE中,AD=AD',∠DAE=∠D'AE,AE=AE,
∴①△ADE≌△AD'E.
∴DE=D'E.
又∵∠ECD'=∠ECA+∠ACD'=∠ECA+∠B=90°,
∴在Rt△ECD'中,(
∵OD'=BD=3,CE=4,
(2)【知识迁移】
证明:如图,将△ABE绕点A逆时针旋转90°,得到△ADF'.
过点D作DH⊥BD交边AF'于点H,连结NH.
由旋转的特征得AE=AF',BE=DF',∠BAE=∠DAF'.
由题意得EF+EC+FC=DC+BC=DF+FC+EC+BE,
∴EF=DF+BE=DF+DF'=F'F.
在△AEF和△AF'F中,AE=AF',EF=F'F,AF=AF,
∴△AEF≌AF'F(SSS). quadquad
∴∠EAF=∠F'AF.
又∵BD为正方形ABCD的对角线,
∴∠ABD=∠ADB=45°.
∵DH⊥BD,
∴∠ADH=∠HDB=∠ADB=45°
在△ABM和△ADH中,∠BAM=∠DAH,AB=AD,∠ABM=∠ADH,
∴△ABM≌△ADH(ASA),
∴AM=AH,BM=DH.
在△AMN和△AHN中, AM=AH ∠MAN=∠HAN,AN=AN,
∴△AMN≌△AHN(SAS).
∴MN=HN.
在Rt△HND中,
(3)【拓展应用】
证明:如图所示,延长EF交AB延长线于M点,交AD延长线于N点.
将△ADF绕着点A顺时针旋转90°,得到△AGH,连接HM,HE.
则△ADF≌△AGH.
则DF=GH,AG=AD,AF=AH,∠DAF=∠HAG,
∵∠EAF=45°,
∴∠HAE=∠HAG+∠GAE=∠DAF+∠GAE=45°,
在△AEH和△AFE中
∴△AEH≌△AEF(SAS),
∴EF=HE,
过点H作HO⊥CB交CB于点O,过点H作HG⊥BM交BM于点M,则四边形OHGB为矩形.
∴OH=BG,OB=HG,
∵∠CEF=45°,
∴∠CEF=∠CFE=∠DFN=∠DNF=∠BME=∠BEM=45°,
∴△BME,△DNF,△CEF,△AMN是等腰直角三角形,
∴CE=CF,BE=BM,DN=DF,AN=AM,
∴AM-AG=AN-AD,
∴GM=DN=DF=HG,
∴∠HMG=45°,
在Rt△OHE中,
即
又∴ ,
即2
(4)【问题再探】如图,将△BEC绕点B逆时针旋转90°,得到△BE'C',连结E'D.过点E作EG⊥BC,垂足为点G,过点E'作EG'⊥BC',垂足为G'.过点E'作E'F∥BA,过点D作DF∥BC交AB于点H,E'F、DF交于点F
由旋转的特征得BE=BE',∠CBE=∠C'BE',EG=E'G',BG= BG'.
∵∠ABC=90°,∠DBE=45°
∴∠CBE+∠DBA=45°,
∴∠C'BE'+∠DBA=45°,即.
在△EBD和△E'BD中,BE=BE',∠DBE=∠DBE',BD=BD.
∴△EBD≌△E'BD(SAS),
∴DE=DE',
:∠ABC=90°,AB=4,BC=3,
又∵AD=x,CE=y,
∴DE'=DE=5-x-y,
∵DF∥BC,
∴∠ADH=∠C,∠AHD=∠ABC=90°,
∴△AHD∽△ABC,
即
同理可得
∵E'G'⊥AB,∠ABC=90°,
∴E'G'∥BC∥FD,
又∵E'F∥AB,∠FHG'=∠AHD=90°,
∴四边形FE'G'H为矩形
在Rt△ E'FD中,
解得
【点睛】
本题是四边形的综合题,考查的是旋转变换的性质、矩形的性质和判定、正方形的性质和判定、勾股定理、等腰直角三角形的性质和判定、全等三角形的判定和性质,相似三角形的判定和性质,灵活运用旋转变换作图,掌握以上知识点是解题的关键.
4实践与探究.
(1)操作一:如图①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M ,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则∠EAF= 度.
(2)操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N .我们发现,当点B的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上.则∠AEF= 度.
(3)在图②中,运用以上操作所得结论,解答下列问题:
①设AM与NF的交点为点P .求证:△ANP≌△FNE;
② 若 则线段AP的长为 .
【答案】(1)45
(2)60
(3)①证明见解析.
【解析】(1)∵四边形ABCD是正方形,
..∠BAD=90°,
由折叠的性质可知,△ABE≌△AME,△ADF≌△AMF.
∴∠BAE=∠MAE,∠DAF=∠MAF,
:∠BAE+∠MAE+∠DAF+∠MAF=∠BAD=90°,
:2∠MAE+2∠MAF=90°,
∴∠MAE+∠MAF=45°,
即∠EAF=45°.
(2)由折叠的性质可知,
△ABE≌△AME,△FCE≌△FNE,
∴∠AEB=∠AEM ,∠AEM=∠CEF,
∴∠AEB=∠AEM=∠CEF.
∵∠AEB+∠AEM+∠CEF=180°.
∴∠AEB=∠AEM=∠CEF=60°.
即∠AEF=60°.
(3)① ∵四边形ABCD是正方形,
由折叠的性质可知,△ABE≌△AME,△FNE≌△FCE,
∴∠AME=∠B=90°,∠FNE=∠C=90°,
:∠EAF=45°,
∴∠AFN=∠FNE-∠EAF=45°,
∴∠AFN=∠EAF,
∴AN=FN,
∴∠NAP=∠NFE,
在△ANP和△FNE中,
∴△ANP≌△FNE(ASA).
② ∵在Rt△ABE中,∠AEB=60°,AB=
∵四边形ABCD是正方形,
∵∠C=90°,∠FEC=60°,
∴∠EFC=30°,
∵△ANP≌△FNE,
【标注】 【知识点】四边形与折叠问题
5综合与实践.
数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思维空间,丰富数学体验.让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF,连接EF,如图1.
(1)∠EAF= ,写出图中两个等腰三角形: (不需要添加字母);
转一转:将图1中的∠EAF绕点A旋转,使它的两边分别交边BC、CD于点P、Q,连接PQ,如图2.
(2)线段BP、PQ、DQ之间的数量关系为 .
(3)连接正方形对角线BD ,若图2中的∠PAQ的边AP、AQ分别交对角线BD于点M、点N,如图3,则
剪一剪:将图3中的正方形纸片沿对角线BD剪开,如图4.
(4) 求证:.
【答案】(1)45°;△AEF,△CEF
(2) BP+DQ=PQ
(3)
(4)证明见解析.
【解析】(1)如图1中,
∵四边形ABCD是正方形,
.. AB=AD=BC=CD,∠BAD=90°.
∴△ABC,△ADC都是等腰三角形,
:∠BAE=∠CAE,∠DAF=∠CAF,
∵∠BAE=∠DAF=22.5°,∠B=∠D=90°,AB=AD,
∴△BAE≌△DAF(ASA),
.. BE=DF,AE=AF,
∵CB=CD,
CE=CF.
.△AEF,△CEF都是等腰三角形.
(2) 结论:PQ=BP+DQ.
理由:如图2中,延长CB到T,使得BT=DQ,
∵AD=AB,∠ADQ=∠ABT=90°,DQ=BT,
∴△ADQ≌△ABT(SAS),
∴AT=AQ,∠DAQ=∠BAT,
∵∠PAQ=45°,
∵AP=AP,
∴△PAT≌△PAQ(SAS),
∴PQ=PT,
∵PT=PB+BT=PB+DQ,
∴PQ=BP+DQ.
故答案为:PQ=BP+DQ.
如图3中,
∵四边形ABCD是正方形,
∴∠ABM=∠ACQ=∠BAC=45°,AC= AB,
∠BAC=∠PAQ=45°,
∴∠BAM=∠CAQ,
∴△CAQ∽△BAM,
故答案为:
(4) 如图4中,将△ADN绕点A顺时针旋转90°得到△ABR,连接RM,
∵∠BAD=90°,∠MAN=45°,
∴∠DAN=∠BAR,
∵AR=AN,AM=AM,
∴△AMR≌△AMN(SAS),
∴RM=NM,
∵∠D=∠ABR=∠ABD=45°.
∵DN=BR,MN=RM,
【标注】 【知识点】旋转的性质
6如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作PF⊥AP交BC于点F,连接AF、EF, AF交BD于G,现有以下结论:①AP=PF;②DE+BF=EF;③PB-PD= BF ;④S△AEP为定值;⑤ 以上结论正确的有 (填入正确的序号即可)
【答案】①②③⑤
【解析】∵四边形ABCD是正方形, PF⊥AP,
∴∠APF=∠ABC=∠ADE=∠C=90°,AD=AB,∠ABD=45°,
①∵∠ABC+∠APF=180°,
∴由四边形内角和可得∠BAP+∠BFP=180°,
∴点A、B、F、P四点共圆,
∴∠AFP=∠ABD=45°,
∴△APF是等腰直角三角形,
∴AP=PF,故①正确;
②把△AED绕点A顺时针旋转90°得到△ABH,如图所示:
∴DE=BH,∠DAE=∠BAH,∠HAE=90°,AH=AE,
∴∠HAF=∠EAF=45°,
∵AF=AF,
∴△AEP≌△AHF(SAS),
∴HF=EF,
∵HF=BH+BF,
∴DE+BF=EF;故②正确;
③连接AC,在BP上截取BM=DP,连接AM ,如图所示:
∵点O是对角线BD的中点,
∴OB=OD,BD⊥AC,
∴OP=OM,△AOB是等腰直角三角形,
由①可得点A、B、F、P四点共圆,
∴∠APO=∠AFB,
∵∠ABF=∠AOP=90°,
∴△AOP∽△ABF,
∵BP-DP=BP-BM=PM=2OP,
故③正确;
④过点A作AN⊥EF于点N,如图所示:
由②可得∠AFB=∠AFN
∵∠ABF=∠ANF=90°,AF=AF,
∴△ABF≌△ANF(AAS).
. AN=AB,
若△AEF的面积为定值,则EF为定值,
∵点P在线段OD上,
∴EF的长不可能为定值,故④错误;
⑤由③可得
∵∠AFB=∠AFN=∠APG,∠FAE=∠PAG,
∴△APG∽△AFE,
故⑤正确;
综上所述:以上结论正确的有①②③⑤;
故答案为①②③⑤.
【标注】【知识点】四点共圆的应用
7已知,如图,在正方形ABCD中,AD=4,E,F分别是CD,BC上的点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论: 中正确的是( ).
A. ①②③ B. ②③④ C. ①③④ D.①②④
【答案】D
【解析】∵AG=AE,∠FAE=∠FAG=45°,AF=AF.
.△AFE≌△AFG(SAS),
∴EF=FG,
DE=BG,
.. EF=FG=BG+FB=DE+BF,故①正确,
BC=CD=AD=4,EC=1,
∴DE=3,设BF=x,则EF=x+3,CF=4-x,
在Rt△ECF中,
解得
故②正确,③错误,
:BM//AG,
.△FBM∽△FGA,
故④正确.
故选:D.
【标注】【知识点】正方形中的半角模型
8如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合), 点F在射线AM上,且 CF与AD相交于点G,连接EC、EF、EG,则下列结论:
①∠ECF=45°;
②△AEG的周长为
④△EAF的面积的最大值是
⑤当 a时,G是线段AD的中点.
其中正确的结论是( )
A. ①②③ B. ②④⑤ C. ①③④ D.①④⑤
【答案】D
【解析】如图1中,在BC上截取BH=BE,连接EH,
∵BE=BH ,∠EBH=90°,
∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°.
∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,∴AE=HC,
∴△FAE≌△EHC(SAS),
∴EF=EC,∠AEF=∠ECH,
∴∠FEC=90°,
∴∠ECF=∠EFC=45°,故①正确;
如图2中,延长AD到H,使得DH= BE,
则△CBE≌△CDH(SAS),
∴∠ECB=∠DCH,
CG=CG,CE=CH,
∴△GCE≌△GCH(SAS),
∴EG=GH,
∵GH=DG+DH,DH=BE,
∴EG=BE+DG,故③错误;
∴△AEG的周长=AE+EG+AG=AE+AD+DH
=AE+AD+EB=AB+AD=2a,故②错误;
设BE=x,则AE=a-x,AF= x,
当a a时,△AEF的面积的最大值为 a ,故④正确;
如图3,延长AD到H,使得DH= BE,
同理,EG=GH,
则
设AG=y,则DG=a-y,
在Rt△AEG中,
艮
解得
∴当 a时,G是线段AD的中点,故⑤正确.
综上,①④⑤正确.
故选:D.
【标注】 【知识点】正方形与全等综合
9如图,在平面直角坐标系中,以坐标原点O(0,0),A(0,4), B(3,0)为顶点的Rt△AOB,其两个锐角对应的外角的平分线相交于点P,且点P恰好在反比例函数 的图象上,则k的值为( ).
A.36 B.48 C.49 D.64
【答案】A
【解析】过点P分别作AB、x轴、y轴的垂线,垂足分别为C、D、E,如图,
∵A(0,4), B(3,0),
∴OA=4,OB=3,
∵△OAB的两个锐角对应的外角的平分线相交于点P,
∵PE=PC,PD=PC,
∴PE=PC=PD,
设P(t,t),则PC=t,
= txt,
解得t=6,
∴P(6,6),
把P(6,6)代入y= kz得k=6×6=36.
故选:A.
【标注】 【知识点】反比例函数的系数k的几何意义
10如图,在正方形ABCD中,AB=6,G是BC的中点,将△ABG沿AG对折至△AFG,延长GF交DC于点E ,则DE的长是( ) .
A.1 B. 1.5 C. 2 D.2.5
【答案】C
【解析】如图,连接AE,
∴AB=AD=AF,∠D=∠AFE=90°,
在Rt△AFE和Rt△ADE中,
. Rt△AFE≌Rt△ADE,
∴EF=DE,
设DE=FE=x,则EC=6-x.
∵G为BC中点,BC=6,
∴CG=3,
在Rt△ECG中,根据勾股定理,得:
解得x=2.
则DE=2.
【标注】 【知识点】翻折问题与勾股定理
11如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ∠EAF=45°,则AF的长为 .
【答案】
【解析】取AB的中点M ,连接ME,在AD上截取ND=DF,
^
设DF=DN=x,
∵四边形ABCD是矩形,
∴∠D=∠BAD=∠B=90°,AD=BC=4,
∴NF= x,AN=4-x,
∵AB=2,
∴AM=BM=1,
∵AE= ,AB=2,
∴BE=1,
∴∠MEA=∠NAF,
∴△AME∽△FNA,
解得
【标注】 【知识点】相似三角形的性质与判定综合
12如图1,已知四边形ABCD是正方形,将△DAE,△DCF分别沿DE,DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点),若GF=4,EG=6,则DG的长为
【答案】12
【解析】设正方形ABCD的边长为x,由翻折可得:
DG=DA=DC=∞,
∵GF=4,EG=6,
∴AE=EG=6,CF=GF=4,
∴BE=x-6,BF=x-4,EF=6+4=10,如图1所示:
在Rt△BEF中,由勾股定理得:
∴(x+2)(x-12)=0,
∴x =-2 (舍),x =12,
∴DG=12.
故答案为:12.
【标注】 【知识点】翻折问题与勾股定理
13如图,已知正方形ABCD的边长为a,E为CD边上一点(不与端点重合),将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.
给出下列判断:
①∠EAG =45°;
②若 则AG//CF;
③若E为CD的中点,则△GFC的面积为 ;
④若CF=FG,则
⑤BG·DE+AF·GE=a
其中正确的是 .(写出所有正确判断的序号)
【答案】①②④⑤
【解析】①∵四边形ABCD是正方形,
∴AB=BC=AD=a,
∵将△ADE沿AE对折至△AFE,
∴∠AFE=∠ADE=∠ABG=90°,AF=AD=AB,EF=DE,∠DAE=∠FAE,
在Rt△ABG和Rt△AFG中
∴Rt△ABG≌Rt△AFG(HL) ,
∴∠BAG=∠FAG,
故①正确;
②∴BG=GF,∠BGA=∠FGA,
设BG=GF=x,∵DE= a,
∴CG=a-x,
在Rt△EGC中, 由勾股定理可得
解得 此时
∴∠GFC=∠GCF,
且∠BGF=∠GFC+∠GCF=2∠GCF,
∴2∠AGB=2∠GCF,
∴∠AGB=∠GCF,
∴AG//CF,
∴②正确;
③若E为CD的中点,则
设BG=GF=y,则CG=a-y,
艮
解得
故③错误;
④当CF=FG,则∠FGC=∠FCG,
∵∠FGC+∠FEC=∠FCG+∠FCE=90°,
∴∠FEC=∠FCE.
. EF=CF=GF,
∴BG=GF=EF=DE,
∴EG=2DE,CG=CE=a-DE,
∴CE=EG,即
故④正确;
⑤设BG=GF=b,DE=EF=c,则CG=a-b,CE=a-c,
由勾股定理得, 整理得
即S△CEG=BG·DE,
∵S△ABG=S△APG,S△AEF=S△ADE,
故⑤正确.
故答案为:①②④⑤.
【标注】【知识点】正方形与全等综合
14如图,正方形ABCD中,△ABC绕点A逆时针旋转到△AB'C', AB',AC'分别交对角线BD于点E, F ,若AE=4,则EF. ED的值为
【答案】16
【解析】∵∠EAF=∠EDA=45°,∠AEF=∠DEA,
∴△AEF∽△DEA,
15如图①,E、F是等腰Rt△ABC的斜边BC上的两动点,∠EAF=45°,CD⊥BC且CD=BE.
(1) 求证:△ABE≌△ACD.
(2)求证:
(3)如图②,作AH⊥BC,垂足为H,设∠EAH=α,∠FAH=β,不妨设 请利用(2)的结论证明:当α+β=45°时 成立.
【答案】(1)证明见解析.
(2)证明见解析.
(3)证明见解析.
【解析】(1)∵△ABC是等腰直角三角形,
∴AB=AC,
∵CD⊥BC,
∴∠AOD=∠BCD-∠ACB=45°=∠B,在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
(2)由(1)知,△ABE≌△ACD,
∴AE=AD,∠BAE=∠CAD,
∵∠BAO=90°,
∴∠EAD=∠CAE+∠CAD=∠CAE+∠BAE=∠BAC=90°,
∵∠EAF=45°,
∴∠DAF=∠DAE-∠EAF=45°=∠EAF,
∵AF=AF,
∴△AEF≌△ADF(SAS),
∴DF=EF,
在Rt△DCF中,根据勾股定理得,
∵CD=BE,
(3)在Rt△ABC中,AC=AB=
∵AH⊥BC,
∴BE=1-EH,CF=1-FH,
由(2)知,
∵EF=EH+FH,
∴1-EH·FH=EH+FH,
在Rt△AHE中,
在Rt△AHF中,
∴右边
=1.
∴左边
∴左边=右边,
即当α+β=45°时,
成立.
【标注】 【知识点】解直角三角形的综合应用
16在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
(1)如图1,若BC=2BA,求∠CBE的度数.
(2)如图2,当AB=5,且AF·FD=10时,求BC的长.
(3) 如图3,延长EF,与∠ABF的角平分线交于点M , BM交AD于点N ,当NF=AN+FD时, 求ABC的值.
【答案】(1)15°.
(2)3
(3)
【解析】(1)由△BCE翻折得到△BFE,可知BC=BF,∠CBE=∠FBE.
又∵BC=2BA=BF,
∴在Rt△ABF中,
又:
(2) 由翻折可知:∠BFE=∠BCE=90°,
∴可得∠AFB+∠DFE=90°.
又∵在△AFB中,.
在Rt△DEF中,∠DFE+∠DEF=90°,
故可得∠DFE=∠ABF,∠AFB=∠DEF,
∴△AFB∽△DEF,
故AB·DE=AF·DF,
即5·DE=10,
∴DE=2,
.. EF=CE=5-2=3.
设DF为a,在Rt△DEF中,
可得 即
又∵AF·DF=10,
故
(3)如图,过N点作NH⊥BF于H点.
∴∠NFH=∠BFA,∠NHF=∠BAF=90°,
∴△NFH∽△BFA,
#
又∵NF=AN+FD,
设NH=a,又因为BN为角平分线,NA⊥AB,NH⊥BF,
∴AN=HN=a.
在Rt△ABN和Rt△HBN中,
∴Rt△ABN≌Rt△HBN(HL),
故BH=AB=2NH=2a.
设FN=b,|由
可得
在Rt△NHF中,
由( 得
解得
【标注】 【知识点】翻折问题与勾股定理
17如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E, AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE.
②若BE=2,DF=3,求AH的长.
(2) 如图3,连接BD交AE于点M ,交AF于点N .请探究并猜想:线段BM ,MN,ND之间有什么数量关系 并说明理由.
【答案】(1)①证明见解析.
② AH=6.
【解析】(1)①由旋转的性质可知:AF=AG ,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中
∴△GAE≌△FAE.
② ∵△GAE≌△FAE,AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x-2,FC=x-3.
在Rt△EFC中,
由勾股定理得:
即
解得:x=6.
∴AB=6.
.. AH=6.
(2) 如图所示:将△ABM逆时针旋转90°得△ADM'.
∵四边形ABCD为正方形,
.∠ABD=∠ADB=45°
由旋转的性质可知:∠ABM=∠ADM'=45°,BE=DM'.
.∠NDM'=90°.
:∠EAM'=90°,∠EAF=45°,
.∠EAF=∠FAM'=45°
在△AMN和△ANM'中,
∴△AMN≌△ANM'.
∴MN=NM'
又∵BM=DM',
【标注】 【知识点】正方形与全等综合
18如图,正方形ABCD的边长为6,点E、F分别在AB、AD上,若CE=3 ,且∠ECF=45°,则CF的长为( ) .
A.2 B.3 D.
【答案】A
【解析】如图,延长FD到G,使DG=BE,
连接CG、EF.
∵四边形ABCD为正方形,
在△BCE与△DCG中,
∴△BCE≌△DCG(SAS),
∴CG=CE=3 ,∠DCG=∠BCE.
∵∠BCE+∠FCD=∠FCD+∠DCG=90°-∠ECF=45°,
∴△GCF≌△ECF(SAS).
∴AE=3.
设AF=x,则DF=6-x,GF=9-x,
解得x=4,
∴DF=2.
在Rt△CDF中,
∴CF=2
【标注】 【知识点】正方形中的半角模型
19如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 .
【答案】6
【解析】由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°
∴∠BAG+∠BAE=45°
∴∠GAE=∠FAE.
在△GAE和△FAE中
△GAE≌△FAE.
AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x-2,FC=x-3.
在Rt△EFC中,由勾股定理得: 即
解得:x=6.
∴AB=6.
∴AH=6.
【标注】【知识点】方程思想在勾股定理的应用;正方形中的半角模型
20在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=CD.探究:当点M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.
(1) 如图1,当点M、N在边AB、AC上,且DM=DN时,BM、CN、MN之间的数量关系是 ;此时
(2)如图2,当点M、N在边AB、AC上,且当DM≠DN时,猜想(1)问的两个结论还成立吗 写出你的猜想并加以证明.
(3)如图3,当点M、N分别在边AB、CA的延长线上时,若AN=x,则Q= .(用z、L表示)
【答案】
(2)猜想:结论依然成立,证明见解析.
【解析】(1)如图1,猜想:MN=BM+NC,理由是:
∵DM=DN,∠MDN=60°,
△MDN是等边三角形.
. MN=DM=DN.
:∠BDC=120°,BD=DC,
∴∠DBC=∠DCB=30°.
∵△ABC是等边三角形,
∵BD=CD,DM=DN,
∴Rt△DBM≌Rt△DCN.
∴∠BDM=∠CDN=30°,BM=CN.
∴DM=2BM.
∴DM=MN=2BM=BM+NC.
:AB=AC,BM=CN,
∴AM=AN
:∠A=60°,
∴△AMN是等边三角形.
∴△AMN的周长Q=3MN=6BM
等边△ABC的周长L=3AB=3(AM+BM)=9BM,
故答案为:.
(2)猜想:结论依然成立.
如图,延长AC至E,使得CE=BM ,连接DE,
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°.
又∵△ABC为等边三角形,
∴∠MBD=∠NCD=90°.
在△MBD与△ECD中,
∴△MBD≌△ECD(SAS).
∴DM=DE,∠BDM=∠CDE,
∴∠EDN=∠BDC-∠MDN=60°.
在△MDN与△EDN中,
∴△MDN≌△EDN(SAS),
∴MN=NE=BM+ON,
△AMN的周长Q=AM+AN+MN=AB+AC,
(3)如图3,∵等边△ABC的周长为L,
△AMN的周长Q=MN+AN+AM
=FN+AN+AB+BM
=AN+AF+AN+AB+CF
=2x+2AB
故答案为:
【标注】 【知识点】多边形中的半角模型
21如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M ,垂足分别为H、G.现有以下结论:①AB= ②当点E与点B重合时,MH= ;③AF+BE=EF;④MG·MH= ,其中正确结论为( ).
A. ①②③ B. ①③④ C. ①②④ D.①②③④
【答案】C
【解析】①由题意可知,△ABC是等腰直角三角形,
故①正确;
②如图1,当点E与点B重合时,点H与点B重合,
∴MB⊥BC,∠MBC=90°,
∵MG⊥AC,
∠MGC=90°=∠ACB=∠MBC,
∴MG∥BC,四边形MGCB是矩形,
∴MH=MB=CG,
∵∠FCE=45°=∠ABC,∠A=∠ACF=45°,
∴CE=AF=BF,
:FG是△ACB的中位线,
故②正确;
③如图②,
∵AC=BC,∠ACB=90°,
∴∠A=∠5=45°,
将△ACF顺时针旋转90°至△BCD,
则CF=CD,∠1=∠4,∠A=∠6=45°,BD=AF,
∵∠2=45°,
∴∠1+∠3=∠3+∠4=45°,
∴∠DCE=∠2,
在△ECF和△ECD中,
∴△ECF≌△ECD(SAS) ,
∴EF=DE,
∵∠5=45°,
∴∠DBE=90°,
即 故③错误;
④方法一:由题意可知四边形CHMG是矩形,
∴∠A=∠MEF,∠AGF=∠EMF,
∴△AGF∽△EMF,
同理可得△EHB∽△EMF,
则
由③得,EF =AF +BE ,
即,
即△ABC的面积等于矩形GCHM的面积,
故④正确;
:∠7=∠1+∠A=∠1+45°=∠1+∠2=∠ACE,
∵∠A=∠5=45°,
∴△ACE∽△BFC,
∴AE·BF=AC·BC=1,
由题意知四边形CHMG是矩形,
∴MG∥BC,MH=CG,
MG=CH,MH//AC,
故④正确.
④方法二:
同理可得:
由③可知:
故④正确.
所以正确的结论有①②④三个,故选C
【标注】 【知识点】相似8字型
22如图,在△ABC中,AB=AC,∠BAC=120°,点D、E在边BC上,且∠DAE=60°,将△ADE沿AE翻折,点D的对应点是D',连接CD',若BD=4,CE=5,则DE的长为( )
A B. C. D.2
【答案】B
【解析】如图,作D'H⊥EC于H.
∵∠DAE=∠EAD'=60°,∠BAC=120°,
∴∠BAD+∠EAC=60°,∠EAC+∠CAD'=60°,
∴∠BAD=∠CAD',
∵AB=AC,AD=AD',
∴△BAD≌△CAD',
∴CD'=BD=4,∠B=∠ACD'=∠ACB=30°,
∴∠D'CH=60°,∠CD'H=30°,
在Rt△D'EH中,
故选:B.
23如图,点E,F分别为正方形ABCD的边BC,CD上一点,AC,BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M, N,则有以下结论:①∠AEB=∠AEF=∠ANM;②EF=BE+DF;③△AOM∽△ADF;④S△ABF=2S△AMN.
以上结论中,正确的是 (请把正确结论的序号都填上)
【答案】①②③④
【解析】如图,把△ADF绕点A顺时针旋转90°得到△ABH.
由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,
∵∠EAF=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°-∠EAF=45°.
∴∠EAH=∠EAF=45°,
在△AEF和△AEH中,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∴∠AEB=∠AEF,
∴BE+BH=BE+DF=EF,故②正确;
∵∠ANM=∠ADB+∠DAN=45°+∠DAN,
∠AEB=90°-∠BAE=90°-(∠HAE-∠BAH)=90°-(45°-∠BAH)=45°+∠BAH'
∴∠ANM=∠AEB,
∴∠AEB=∠AEF=∠ANM;故①正确;
∵AC⊥BD,
∴∠AOM=∠ADF=90°,
∵∠MAO=45°-∠NAO,∠DAF=45°-∠NAO,
∴△OAM∽△DAF,故③正确;
连接NE,
∵∠MAN=∠MBE=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∴△AMB∽△NME,
∴∠AEN=∠ABD=45°,
∴△AEN是等腰直角三角形,
∵△AMN∽△BME,△AFE∽△BME,
∴△AMN∽△AFE,
.故④正确.
故答案为:①②③④.
【标注】 【知识点】正方形中的半角模型
24如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M、N .下列结论:①AB =BN·DM;②AF平分∠DFE;③AM·AE=AN·AF 其中正确的结论是( )
A. ①② B. ①③ C. ①②③ D.①②③④
【答案】D
【解析】①∵∠BAN=∠BAM+∠MAN
∴∠BAN=∠AMD.
又∠ABN=∠ADM=45°,
∴△ABN-△ADM,
∴AB:BN=DM:AD.
∵AD=AB,
故①正确;
②把△ABE绕点A逆时针旋转90°,得到△ADH.
∵∠BAD=90°,∠EAF=45°,
∴∠EAF=∠HAF.
∵AE=AH,AF=AF,
∴△AEF≌△AHF,
∴∠AFH=∠AFE,即AF平分∠DFE.
故②正确;
③∵AB∥CD,
∴∠DFA=∠BAN
∵∠AFE=∠AFD,∠BAN=∠AMD,
∴∠AFE=∠AMN.
又∠MAN=∠FAE,
∴△AMN-△AFE.
. AM:AF=AN:AE,即AM·AE=AN·AF.
故③正确;
④由②得BE+DF=DH+DF=FH=FE.
过A作AO⊥BD,AG⊥EF.
则△AFE与△AMN的相似比就是AG:AO.
易证△ADF≌△AGF(AAS),
则可知
从而得证故④正确.
故选:D.
【标注】 【知识点】正方形中的半角模型
25如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AC,现在有如下4个结论:
①∠EAG=45°;②FG=FC;③FC//AG;④S△GFC=14.
A.1 B.2 C.3 D.4
【答案】B
【解析】如图,连接DF.
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠ABE=∠BAD=∠ADG=∠ECG=90°,由翻折可知:AB=AF,∠ABE=∠AFE=∠AFG=90°,BE=EF=4,∠BAE=∠EAF,
∵∠AFG=∠ADG=90°,AG=AG,AD=AF,
∴Rt△AGD≌Rt△AGF(HL),
∴DG=FG,∠GAF=∠GAD,设GD=GF=x,
故①正确;在Rt△ECG中,
∴x=6,
∵OD=BC=BE+EC=12,
∴DG=CG=6,
∴FG=GC,
易知△GFC不是等边三角形,显然FG≠FC,故②错误;
∵GF=GD=GC,
∴CF⊥DF,
∵AD=AF,GD=GF,
∴AG⊥DF,
∴CF//AG,故③正确;
∵S△BCG= ×6×8=24,FG:FE=6:4=3:2,
∴FG:EG=3:5,
故④错误;
故选B.
【标注】 【知识点】其它翻折问题
26如图1,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在四边形ABCD的边BC、CD上, 连接EF,试猜想EF、BE、DF之间的数量关系.
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F、D、G三点共线,易证△AFG≌ ,故EF、BE、DF之间的数量关系为 .
(2)类比引申
如图2,在图1的条件下,若点E、F由原来的位置分别变到四边形ABCD的边CB、DC延长线上, 连接EF ,试猜想EF、BE、DF之间的数量关系,并给出证明、
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,则DE的长为 .
【答案】(1)△AFE;EF=BE+DF
(2) EF、BE、DF之间的数量关系是EF=DF-BE,证明见解析.
(3)
【解析】(1)将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,:∠B+∠ADC=180°,
∴∠FDG=180°,即点F , D , G三点共线,
∴∠EAF=∠GAF.
在△AFG和△AFE中,
∴△AFG≌△AFE,
∴EF=FG=FD+FG=FD+BE.
(2)将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',
则△ABE≌△ADE',
..∠DAE'=∠BAE,AE'=AE,DE'=BE,∠ADE'=∠ABE,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
.∠ADE'=∠ADC,即E'、D、F三点共线,
∴∠E'AF=∠BAD-(∠BAF+∠DAE')
=∠BAD-(∠BAF+∠BAE)
∴∠EAF=∠E'AF,
在△AEF和△AE'F中,
∴△AFE≌△AFE'(SAS),
∴EF=DF-BE;
(3) 将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',
由(1)得,△AED≌AED',
∴DE=D'E.
在Rt△ECD'中, 即
27旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且
(1) 如图a,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连接DF.
①求∠DAF的度数.
② 求证:△ADE≌△ADF.
(2)如图b,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由.
(3)如图c,当α=120°,BD=4,CE=5时,请直接写出DE的长为 .
【答案】(1)① 30°.
② 证明见解析.
证明见解析.
【解析】(1)①由旋转得,∠FAB=∠CAE,
∴∠DAF=∠BAD+∠BAF=∠BAD+∠CAE=30°.
②由旋转得,AF=AE
在△ADE和△ADF中
∴△ADE≌△ADF.
(2)如图,
将△AEC绕点A顺时针旋转90°到△AFB的位置,连接DF,
∴BF=CE,∠ABF=∠ACB,
由(1)得△ADE≌△ADF
∴DF=DE
∵AB=AC,∠BAC=90°,
∴∠ABC=∠AOB=45°,
∴∠DBF=∠ABC+∠ABF=∠ABC+∠ACB=90°,
∴在Rt△BDF中,
(3)如图3,
将△AEC绕点A顺时针旋转90°到△AFB的位置,连接DF,
∴BF=CE,∠ABF=∠ACB,
由(1)知,△ADE≌△ADF,
∴DE=DF,BF=CE=5,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=30°,
∴∠DBF=∠ABC+∠ABF=∠ABC+∠ACB=60°,过点F作FM⊥BC于M,
在Rt△BMF中,∠BFM=90°-∠DBF=30°,BF=5,
∵BD=4,
根据勾股定理得
故答案为:
同课章节目录
