专题一 将军饮马最值模型(含答案) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题一 将军饮马最值模型(含答案) 2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 969.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 16:16:22 | ||
图片预览


文档简介
将军饮马最值模型
1.类型一 “将军饮马”问题
【结论】:
如图,在定直线l上找一动点P ,使点P到两定点A与B的距离之和最小,即 最小.
作对称点的作用:
1.将直线同侧两点问题转化为直线异侧两点问题;
2.利用轴对称的性质可以将相等的线段转化.
2.类型二 矩形纸片折叠问题
1.翻折后对应角相等.2.翻折问题中的计算常用勾股定理.
3.类型三 图形中的对称问题
1 .点线对称;对称点连线被折痕垂直平分. 2.三角形直线对称;对称前后全等;
4.类型四 轴对称图形的构造及应用
策略总结:可考虑对称
板块1:将军饮马最值模型
真题精炼
1.坐标系+将军饮马+两定一动——24成都+填空压轴+初二/初三
如图,在平面直角坐标系xOy中,已知A(3,0),B(0,2),过点B作y轴的垂线l,P为直线l上一动点, 连接PO , PA ,则PO +PA的最小值为
2.三角形内心 °角+将军饮马+两定一动——24内江+填空压轴+初二/初三
如图,在 中, ,E是BC边上一点,且 点I是△ABC的内心, BI的延长线交AC于点D , P是BD上一动点, 连接PE、PC,则 的最小值为 .
3.正方形+8字相似+将军饮马+两定一动——23泸州+填空压轴+初三
如图,E ,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当 取得最小值时, 的值是
板块1:将军饮马最值模型
4.矩形+周长最小值+将军饮马+两定两动+瓜豆原理——24大庆+选择压轴+初二
如图,在矩形ABCD中, ,点M是AB边的中点 ,点N是AD边上任意一点,将线段MN绕点M顺时针旋转 点N旋转到点 则 周长的最小值为( )
A. 15 D.18
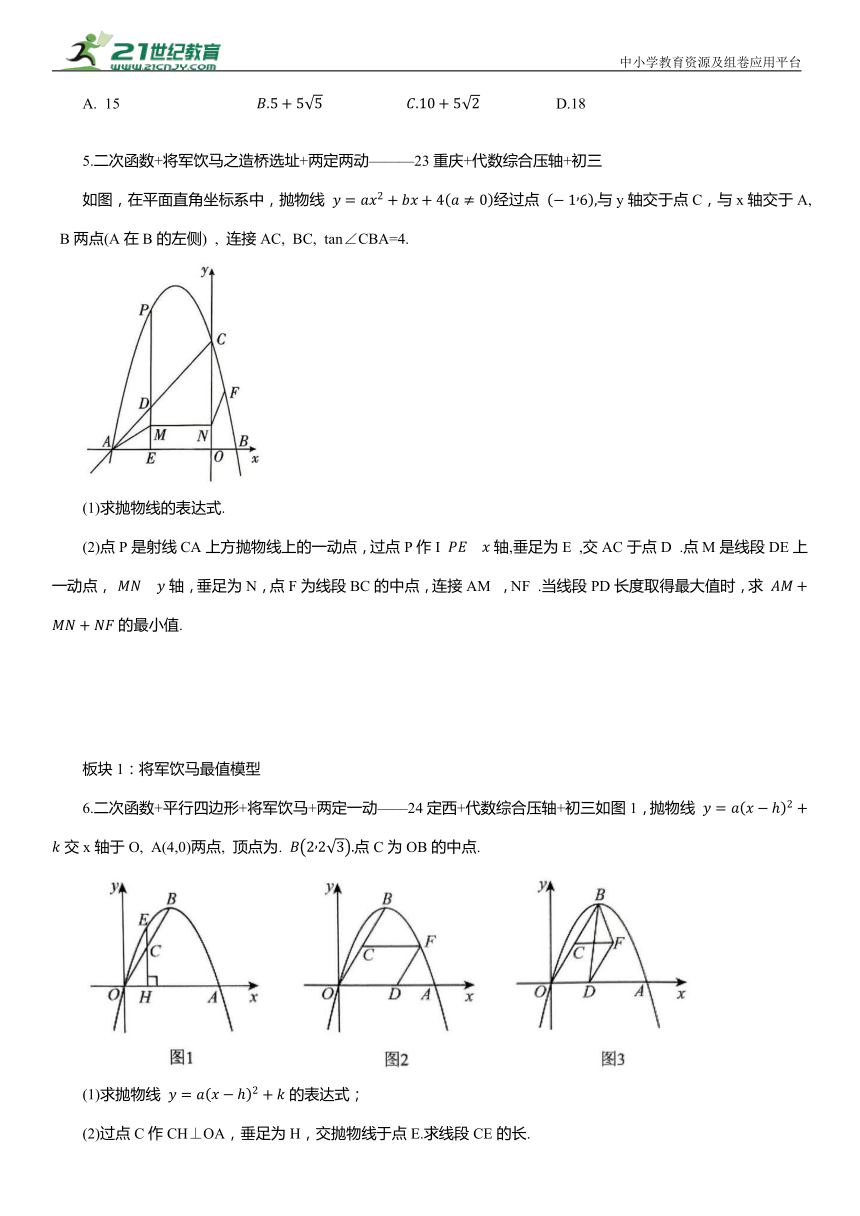
5.二次函数+将军饮马之造桥选址+两定两动———23重庆+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 经过点 与y轴交于点C,与x轴交于A, B两点(A在B的左侧) , 连接AC, BC, tan∠CBA=4.
(1)求抛物线的表达式.
(2)点P是射线CA上方抛物线上的一动点,过点P作I 轴,垂足为E ,交AC于点D .点M是线段DE上一动点, 轴,垂足为N,点F为线段BC的中点,连接AM ,NF .当线段PD长度取得最大值时,求 的最小值.
板块1:将军饮马最值模型
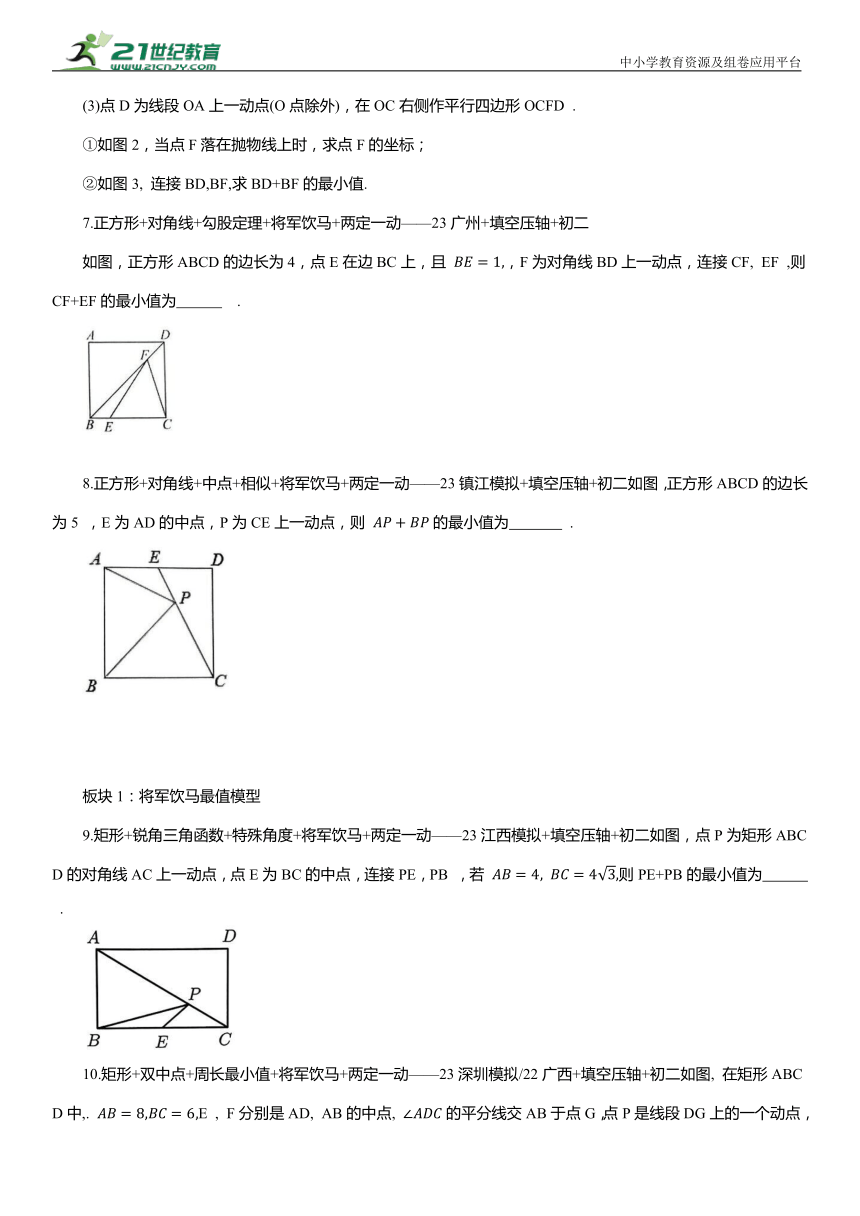
6.二次函数+平行四边形+将军饮马+两定一动——24定西+代数综合压轴+初三如图1,抛物线 交x轴于O, A(4,0)两点, 顶点为. 点C为OB的中点.
(1)求抛物线 的表达式;
(2)过点C作CH⊥OA,垂足为H,交抛物线于点E.求线段CE的长.
(3)点D为线段OA上一动点(O点除外),在OC右侧作平行四边形OCFD .
①如图2,当点F落在抛物线上时,求点F的坐标;
②如图3, 连接BD,BF,求BD+BF的最小值.
7.正方形+对角线+勾股定理+将军饮马+两定一动——23广州+填空压轴+初二
如图,正方形ABCD的边长为4,点E在边BC上,且 ,F为对角线BD上一动点,连接CF, EF ,则CF+EF的最小值为 .
8.正方形+对角线+中点+相似+将军饮马+两定一动——23镇江模拟+填空压轴+初二如图,正方形ABCD的边长为5 ,E为AD的中点,P为CE上一动点,则 的最小值为 .
板块1:将军饮马最值模型
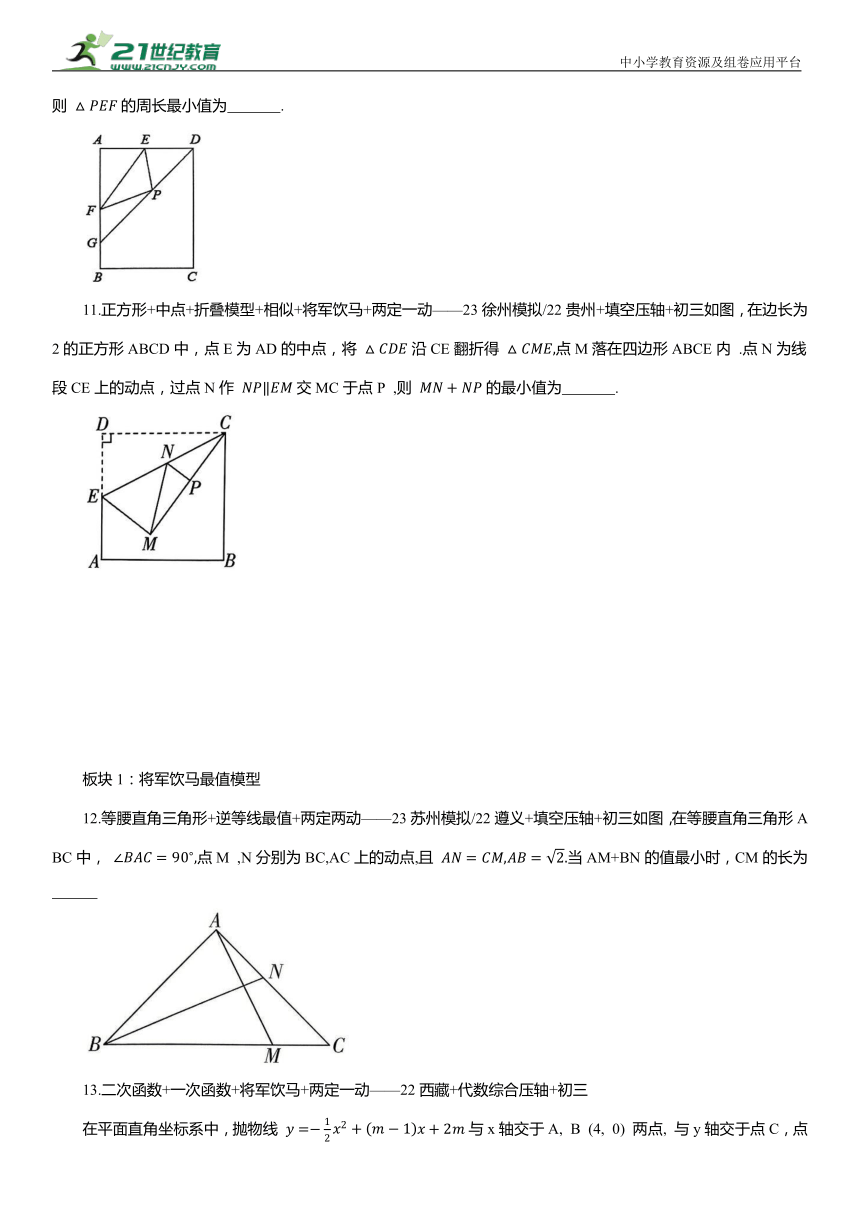
9.矩形+锐角三角函数+特殊角度+将军饮马+两定一动——23江西模拟+填空压轴+初二如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB ,若 则PE+PB的最小值为 .
10.矩形+双中点+周长最小值+将军饮马+两定一动——23深圳模拟/22广西+填空压轴+初二如图, 在矩形ABCD中,. E , F分别是AD, AB的中点, 的平分线交AB于点G,点P是线段DG上的一个动点,则 的周长最小值为 .
11.正方形+中点+折叠模型+相似+将军饮马+两定一动——23徐州模拟/22贵州+填空压轴+初三如图,在边长为2的正方形ABCD中,点E为AD的中点,将 沿CE翻折得 点M落在四边形ABCE内 .点N为线段CE上的动点,过点N作 交MC于点P ,则 的最小值为 .
板块1:将军饮马最值模型
12.等腰直角三角形+逆等线最值+两定两动——23苏州模拟/22遵义+填空压轴+初三如图,在等腰直角三角形ABC中, 点M ,N分别为BC,AC上的动点,且 当AM+BN的值最小时,CM的长为
13.二次函数+一次函数+将军饮马+两定一动——22西藏+代数综合压轴+初三
在平面直角坐标系中,抛物线 与x轴交于A, B (4, 0) 两点, 与y轴交于点C,点P是抛物线在第一象限内的一个动点.
(1)求抛物线的解析式,并直接写出点A,C的坐标;(2)如图甲,点M是直线BC上的一个动点,连接AM,OM ,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;
14.二次函数+线段和最小值+将军饮马+两定两动——22天津+代数综合压轴+初三已知抛物线 (a,b,c是常数,a>0)的顶点为P ,与x轴相交于点 和点B .
( 1 ) 若b=-2,c=-3.
① 求点P的坐标.
② 直线x=m(m是常数,1(2)若3b=2c,直线x=2与抛物线相交于点N ,E是x轴的正半轴上的动点,F是y轴的负半轴上的动点,当PF+FE+EN的最小值为5时,求点E,F的坐标.
15.特殊角+线段和最小值+双对称+两定两动————22泰安+选择压轴+初二
如图, ,点M、N分别在边OA、 OB上, 且( ,点P、Q分别在边OB、 OA上,则MP+PQ+QN的最小值是( )
矩形+将军饮马造桥选址+两定两动————23济南模拟/22内江+填空压轴+初二
如图,矩形ABCD中,AB=6, AD=4,点E、F分别是AB、DC上的动点, EF∥BC,则AF+CE的最小 值是 .
17.等边三角形+中垂线+将军饮马+两定一动——24大庆模拟+选择压轴+初二
如图 ,在等边 中,点E是AC边的中点,点P是△ABC的中线AD上的动点,且 则EP+CF 的最小值是( )
A. 12 B. 9 C. 6 D.3
18.矩形+中点+将军遛马+两定两动——23青岛模拟/22自贡+填空压轴+初二
如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为
19.菱形+特殊角60°+对角线+将军饮马+两定一动——23丹东模拟/22黑龙江+填空压轴+初二如图, 菱形ABCD中, 对角线AC, BD相交于点O,. AH是∠BAC的 平分线,CE⊥AH于点E,点P是直线AB上的一个动点,则OP+PE的最小值是
20.特殊角+将军饮马+两定一动——21黑龙江+选择压轴+初二
已知在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,点E为边AC上的动点,点F为边AB上的动点,则线段FE+EB的最小值是( )
21.圆+正方形+周长最小值+将军遛马+两动一定——23宁波模拟/21连云港+选择压轴+初二如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π, MN=1, 则△AMN周长的最小值是( )
A.3 B.4 C. 5 D.6
22.圆+将军饮马+两定一动——23宿迁模拟+填空压轴+初二
如图,在] 中, 以点O为圆心,3为半径的⊙O,与OB交于点C,过点C作 交AB于点D,点P是边OA上的动点,则 D的最小值为 .
23.矩形+折叠模型+将军饮马+两定一动———23深圳模拟/21盘锦+填空压轴+初二如图,四边形ABCD为矩形, 点P为边AB上一点.以DP为折痕将△DAP翻 折, 点A的对应点为点A'.连结AA', AA'交PD于点M,点Q为线段BC上一点, 连结AQ, MQ,则 的最小值是
24.直角三角形+特殊角度+将军饮马+两定一动———23鄂州模拟/21西藏+选择压轴+初二如图,在 中, ,点P是线段AC上一 动点,点M在线段AB上,当 时, 1的最小值为( )
正方形+隐形圆+将军饮马+点圆最值+两动一定——22无锡模拟/21鄂尔多斯+填空压轴+初三
如图,已知正方形ABCD的边长为6,点F是正方形内一点,连接CF,DF,且 点E是AD边上一动点,连接EB,EF,则 长度的最小值为
26.二次函数+将军遛马+两定两动——22泰安模拟/21广元+代数综合压轴+初三
如图1,在平面直角坐标系xOy中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:
x -1 0 1 2 3
y 0 3 4 3 0
(1)求出这条抛物线的解析式及顶点M的坐标.
(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求 的最小值.
27.矩形+平四存在性+线段差最大值+线段和最小值+将军饮马——23无锡模拟+选择压轴+初三如图,在矩形ABCD中, ,把边AB沿对角线BD平移,点 分别对应点A,B.给出下列结论:
①顺次连接点A',B',C,D的图形是平行四边形;
②点C到它关于直线. 的对称点的距离为48;
的最大值为15 ;
的最小值为
其中正确结论的个数是 ().
A. 1 B. 2 C. 3 D.4
28.二次函数+将军遛马+两定两动+四边形周长最小———22广州模拟/21遂宁+代数综合压轴+初三
如图,已知二次函数的图象与x轴交于A和. 两点,与y轴交于( 对称轴为直线 直线 经过点A ,且与y轴交于点D,与抛物线交于点E ,与对称轴交于点F .
(1)求抛物线的解析式和m的值.
(2) 直线 上有M、N两点(M在N的左侧 ),且 ,若将线段MN在直线 上平移,当它移动到某一位置时,四边形MEFN的周长会达到最小,请求出周长的最小值(结果保留根号)
29.正方形+隐形圆+将军饮马+两定两动———23湖州模拟/20广西+选择压轴+初三
如图,动点M在边长为2的正方形ABCD内 ,且 ,P是CD边上的一个动点,E是AD边的中点,则线段 的最小值为( )
等边三角形+中垂线+将军饮马+两定一动——22凉山模拟/21西宁+填空压轴+初二
如图, 是等边三角形,. ,N是AB的中点,AD是BC边上的中线,M是AD上的一个动点, 连接BM,MN,则 的最小值是 .
31.坐标系+将军遛马+两定两动———22广州模拟/20荆门+选择压轴+初二
在平面直角坐标系中,长为2的线段CD (点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接AC、BD,则. 的最小值为( ).
32.坐标系+将军遛马+两定两动——23长沙模拟/21聊城+填空压轴+初二
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(-4,6), D(0,4),线段EF在边OA上移动, 保持1 ,当四边形BDEF的周长最小时,点E的坐标为
33.正方形+对角线+将军饮马+两定一动——21青海+填空压轴+初二
如图,正方形ABCD的边长为8,M在DC上,且 N是AC上一动点,则 + MN的最小值为 .
34.正方形+多选+将军饮马+两定一动———21黄冈+填空压轴+初三
如图,正方形ABCD中, AB=1,连接AC,∠ACD的角平分线交AD于点E,在AB上截取 ,连接DF ,分别交CE, CA于点G , H ,点P是线段GC上的动点, PQ⊥AC于点Q,连接PH .下列结论:①CE⊥DF;②DE+DC=AC;③EA= AH;④PH+PQ的的最小值是 其中正确结论的序号是
35.特殊角+三角形周长最小值+将军饮马+两动一定——22泰州模拟+选择压轴+初二如图,∠AOB=60°, 点P是∠AOB内的定点且( 若点M、N分别是射线OA、 OB上异于点O的动点,则△PMN周长的最小值是( )
C. 6 D.3
36.菱形+特殊角度+将军饮马+两定一动——20广西+填空压轴+初二
如图,四边形ABCD是菱形,对角线AC,BD相交于点O, 点P是AC上一动点,点E是AB的中点,则 的最小值为
板块1:将军饮马最值模型
扇形+阴影面积+周长最小值+将军饮马+两定一动——22南通模拟/20河南+填空压轴+初三
如图,在扇形BOC中, OD平分 交 于点D ,点E为半径OB上一动点.若 则阴影部分周长的最小值为
坐标系+三角形周长最小+特殊角+将军饮马两动一定——21武威模拟/20永州+填空压轴+初二
在平面直角坐标系中的位置如图所示,且 在 内有一点P(4,3), M、N分别是OA,OB边上的动点, 连接PM , PN , MN,则 周长的最小值是 .
等边三角形+点线最值+特殊角度——20营口+填空压轴+初二
如图, 为等边三角形,边长为6,. ,垂足为点D ,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为
板块1:将军饮马最值模型
40.矩形+特殊角度+将军饮马+两定一动——22成都模拟/20内江+填空压轴+初三
如图,在矩形ABCD中, ,若点M、N分别是线段DB、AB上的两个动点,则. 的最小值为 .
41.正方形+平移+将军饮马+两定两动——20黑龙江+填空压轴+初二
如图,在边长为4的正方形ABCD中将 沿射线BD平移,得到 ,连接EC、GC,则 的最小值为 .
42.坐标系+四边形周长最小值+将军饮马+两定一动————20聊城+填空压轴+初二
如图,在直角坐标系中,点A(1,1),B(3,3)是第一象限角平分线上的两点,点C的纵坐标为1,且 在y轴上取一点D,连接AC,BC,AD,BD,使得四边形ACBD的周长最小,这个最小周长的值为 .
43.坐标系+将军遛马+两定两动——20辽宁+填空压轴+初三
如图,在平面直角坐标系中,已知A(3,6),. ,在x轴上取两点C,D(点C在点D的左侧),且始终保持线段CD在x轴上平移,当 的值最小时,点C的坐标为 .
1.坐标系+将军饮马+两定一动
——24成都+填空压轴+初二/初三
如图,在平面直角坐标系xOy中,已知A(3,0),B(0,2),过点B作y轴的垂线l,P为直线l上一动点,连接PO, PA,则PO+PA的最小值为 .
【答案】5
【解析】取点O'(0,4),连接O'P,O'A,如图,
∵B(0,2), 过点B作y轴的垂线l,
∴点O'(0,4)与点O(0,0)关于直线l对称,
∴PO'=PO.
∴PO+PA=PO'+PA≥O'A,
即PO+PA的最小值为O'A的长,
在Rt△O'AO中,
∵OA=3,OO'=4,
∴由勾股定理,得(
∴PO+PA的最小值为5.
故答案为:5.
【标注】 【知识点】线段和的最小值
2.三角形内心+30°角+将军饮马+两定一动1——24内江+填空压轴+初二/初三
如图,在△ABC中,∠ABC=60°,BC=8,E是BC边上一点,且BE=2,点I是△ABC的内心,BI的延长线交AC于点D,P是BD上一动点,连接PE、PC,则PE+PC的最小值为 .
【答案】2
【解析】
【分析】
在AB取点F,使BF=BE=2,连接PF,CF ,过点F作FH⊥BC于H,利用三角形内心的定义可得出∠ABD=∠CBD,利用SAS证明△BFPa△BEP,得出PF=PB,则
PE+PC=PF+PC≥OF,当C、P、F三点共线时,PE+PC最小,最小值为CF,利用含30°的直角三角形的性质求出BH,利用勾股定理求出FH ,CF即可.
【详解】
解:在AB取点F,使BF=BE=2,连接PF,CF,过点F作FH⊥BC于H,
∵是△ABC的内心,
.. BI平分∠ABC,
∴∠ABD=∠CBD,
又BP=BP,
∴△BFP≌△BEP(SAS),
∴PF=PE,
∴PE+PC=PF+PC≥CF,
当C、P、F三点共线时, PE+PC最小,最小值为CF,
∵FH⊥BC,∠ABC=60°,
∴∠BFH=30°,
∴PE+PC的最小值为2
故答案为:2
【点睛】
本题考查了三角形的内心,全等三角形的判定与性质,含30°的直角三角形的性质,勾股定理等知识,明确题意,添加合适辅助线,构造全等三角形和含30°的直角三角形是解题的关键.
【标注】 【知识点】三角形内切圆
【知识点】全等三角形的判定
【知识点】勾股定理
【知识点】30°特殊角的性质应用
3.正方形+8字相似+将军饮马+两定一动23泸州+填空压轴+初三
如图,E,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当PE+PF取得最小值时,APC的值是 .
【答案】2
【解析】
【分析】
作点/关于AC的对称点F',连接EF'交AC于点P',此时PE+PF取得最小值,过点F'作AD的垂线段,交AC于点K,根据题意可知点F'落在AD上,设正方形的边长为a,求得AK的边长,证明△AEP'∽△KF'P',可得 即可解答.
【详解】
解:作点F关于AC的对称点F',连接EF'交AC于点P',过点F'作AD的垂线段,交AC于点K.
由题意得:此时F'落在AD上,且根据对称的性质,当P点与P'重合时PE+PF取得最小值,
设正方形ABCD的边长为a,则
∵四边形ABCD是正方形,
∴∠F'AK=45°,∠P'AE=45°,AC=
∵F'K⊥AF',
∴当PE+PF取得最小值时, 的值是为
故答案为:
【点睛】
本题考查了四边形的最值问题,轴对称的性质,相似三角形的证明与性质,正方形的性质,正确画出辅助线是解题的关键.
【标注】 【知识点】坐标系中的对称
【知识点】相似三角形的性质与判定综合
【知识点】四边形综合
【知识点】正方形的性质
4.矩形+周长最小值+将军饮马+两定两动+瓜豆原理--24大庆+选择压轴+初二
如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N',则△MBN'周长的最小值为( )
A. 15 D.18
【答案】B
【解析】
【分析】
本题考查了旋转的性质,矩形的性质,勾股定理,确定点N'的轨迹是解题的关键.由旋转的性质结合AAS证明△AMN≌△GMN',推出MG=AM=5,得到点N'在平行于AB,且与AB的距离为5的直线上运动,作点M关于直线EF的对称点M',连接M'B交直线EF于点N',此时△MBN'周长取得最小值,由勾股定理可求解.
【详解】
解:过点N'作EF∥AB,交AD、BC于E、F,过点M作MG⊥EF垂足为G,
矩形ABCD,
∴AB∥CD,
∴AB∥EF∥CD,
∴四边形AMGE和BMGF都是矩形,
由旋转的性质得
∴∠AMN=90°-∠NMG=∠GMN',
∴△AMN≌△GMN'(AAS),
∴MG=AM=5,
∴点N'在平行于AB,且与AB的距离为5的直线上运动,作点M关于直线EF的对称点M',连接M'B交直线EF于点N',此时△MBN'周长取得最小值,最小值为BM+BM',
故选:B.
【标注】 【知识点】勾股定理
【知识点】全等三角形的判定
【知识点】矩形的性质
【知识点】旋转的性质
5.二次函数+将军饮马之造桥选址+两定两动———23重庆+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 )经过点(-1,6),与y轴交于点C,与x轴交于A,B两点(A在B的左侧) ,连接AC,BC,tan∠CBA=4.
(1)求抛物线的表达式.
(2)点P是射线CA上方抛物线上的一动点,过点P作PE⊥x轴,垂足为E,交AC于点D.点M是线段DE上一动点,MN⊥y轴,垂足为N ,点F为线段BC的中点,连接AM,NF .当线段PD长度取得最大值时,求AM+MN+NF的最小值.
【答案】
【解析】(1)由抛物线的表达式知,OC=4,
∵tan∠CBA=4,则OB=1,
即点B(1,0),
由题意得:
解得:
则抛物线的表达式为
(2) 由抛物线的表达式知,点A、B、C的坐标分别为:(-4,0)、(1,0)、(0,4),则点
由点A、C的坐标得,直线AC的表达式为:y=x+4,
设点 则点D(x,x+4),
则
当x=-2时,PD取得最大值,则点E(-2,0)、D(-2,2),则MN=2,
将点A向右平移2个单位得到点A'(-2,0), 连接A'F交y轴于点N, 过点N作NM⊥PE,连接AM,
则四边形MNA'A为平行四边形,则AM=A'N,
则此时
为最小.
【标注】 【知识点】二次函数与角度问题
6.二次函数+平行四边形+将军饮马+两定一动—24定西+代数综合压轴+初三
如图1,抛物线 k交x轴于O, A(4,0)两点,顶点为B(2,2 ).点C为OB的中点.
(1)求抛物线 k的表达式;
(2)过点C作CH⊥OA,垂足为H,交抛物线于点E .求线段CE的长.
(3)点D为线段OA上一动点(O点除外),在OC右侧作平行四边形OCFD.
①如图2,当点F落在抛物线上时,求点/的坐标;
②如图3,连接BD,BF,求BD+BF的最小值.
【答案】
【解析】
【分析】
(1)根据顶点为B(2,2 ).设抛物线 把A(4,0)代入解析式,计算求解即可;
(2)根据顶点为B(2,2 ).点C为OB的中点,得到C(1, ),当x=1时, 得到E 结合CH⊥OA,垂足为H,得到 的长.
(3)①根据题意,得C(1, ),结合四边形OCFD是平行四边形,设F(m, ),结合点F落在抛物线上,得到 解得即可;
②过点B作BN⊥y轴于点N,作点D关于直线BN的对称点G,过点G作GH⊥y轴于点H,连接DG,CH,FG,利用平行四边形的判定和性质,三角形不等式,勾股定理,矩形判定和性质,计算解答即可.
【详解】
(1)∵抛物线的顶点坐标为B(2,2 ).
设抛物线
把A(4,0)代入解析式,得
解得
(2)∵顶点为B(2,2 ).点C为OB的中点,
∴c(1, ),
∵CH⊥OA,
∵CH∥y轴,
∴E的横坐标为1,
设E(1,m),
当x=1时
(3)①根据题意,得C(1, ),
∵四边形OCFD是平行四边形,
∴点C,点/的纵坐标相同,
设F(m, ),
∵点/落在抛物线上,
解得 (舍去):
故F
②过点B作BN⊥g轴于点N,作点D关于直线BN的对称点G,过点G作GH⊥g轴于点H,连接DG,CH,FG,
则四边形ODGH是矩形,
∴OD=HG,OD∥HG,
∵四边形OCFD是平行四边形,
∴OD=CF,OD∥CF,
∴GH=CF,GH∥CF,
∴四边形CFGH是平行四边形,
∴FG=CH,
∵BG+BF≥FG,
故当B、G、F三点共线时,BG+BF取得最小值,
∵BG=BD,
∴BG+BF的最小值,就是BD+BF的最小值,且最小值就是CH,
延长FC交y轴于点M,
∵OD∥CF,
∵C(1,
∵B(2,2 ).
故BD+BF的最小值是2
本题考查了二次函数待定系数法,中点坐标公式,平行四边形的判定和性质,矩形的判定和性质,勾股定理,轴对称,三角形不等式求线段和的最小值,熟练掌握平行四边形的性质,轴对称,三角形不等式求线段和的最小值是解题的关键.
【标注】【知识点】勾股定理
【知识点】二次函数与特殊平行四边形
【知识点】二次函数与平行四边形
【知识点】二次函数解析式
【业务题型】运算题
7.正方形+对角线+勾股定理+将军饮马+两定一动——23广州+填空压轴+初二
如图,正方形ABCD的边长为4,点E在边BC上,且BE=1,F为对角线BD上一动点,连接CF,EF,则CF+EF的最小值为
【答案】
【解析】解:如图,连接AE交BD于一点F ,连接CF,∵四边形ABCD是正方形,∴点A与点C关于BD对称,∴AF=CF,∴CF+EF=AF+EF=AE,此时CF+EF最小,∵正方形ABCD的边长为4,∴AD=4,∠ABC=90°,∵点E在AB上,且BE=1,∴
F的最小值为 故答案为:
【标注】 【知识点】勾股定理
【知识点】正方形的性质
8.正方形+对角线+中点+相似+将军饮马+两定一动—23镇江模拟+填空压轴+初二
如图,正方形ABCD的边长为5,E为AD的中点,P为CE上一动点,则AP+BP的最小值为 .
【答案】
【解析】建立平面直角坐标系如下图所示,
作点B关于CE的对称点F,BF交CE于点H,连接AF交CE于点P,过点F作FG⊥x轴于点G,
∴BP=FP
根据“两点之间,线段最短”可知,AP+BP的最小值为A/的长,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=5,∠BCD=∠D=90°
∴∠DCE+∠BCH=90°,A(0,5)
点E为AB的贵点,
由勾股定理得,
又BH⊥CE,
∴∠HBC+∠BCH=90
∠HBC=∠DCE
∴△HBC~△DCE
∵∠CBH=∠FBG,∠BHC=∠FGB=90°,
∴△BHC~△BGF,
∴BG=8,FG=4
∴F(8,4)
又A(0,5)
∴AP+BP的最小值为
因此正确答案为
【标注】 【知识点】最短路径问题
9.矩形+锐角三角函数+特殊角度+将军饮马+两定一动——23江西模拟+填空压轴+初二
如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB,若AB=4,BC=4 ,则PE+PB的最小值为
【答案】6
【解析】如图,作点B关于AC的对称点B',交AC于点F ,连接B'E交AC于点P,则PE+PB的最小值为B'E的长度.
∵AC是矩形的对角线,
∴AB=CD=4,∠ABC=90°
在直角△ABC中,AB=4,BC=4
∴∠ACB=30°.
由对称的性质,得B'B=2BF,B'B⊥AC,
∴△BEF是等边三角形.
∴BE=BF=B'F.
∴△BEB'是直角三角形.
∴PE+PB的最小值为6.
故答案为:6.
【标注】【知识点】最短路径问题
10.矩形+双中点+周长最小值+将军饮马+两定一动——23深圳模拟/22广西+填空压轴+初二
如图,在矩形ABCD中,AB=8,BC=6,E,F分别是AD,AB的中点,∠ADC的平分线交AB于点G,点P是线段DG上的一个动点,则△PEF的周长最小值为 .
【答案】
【解析】
解:如下图所示,在CD上取点H,使DH=DE,连接EH,PH,过点F作FK⊥CD于点K,
在矩形ABCD中,∠A=∠ADC=90°,AD=BC=6,CD=AB=8,
∴△DEH为等腰直角三角形,
∵DG平分∠ADC,
∴DG垂直平分EH,
∴PE=PH,
∴△PEF的周长等于PE+PF+EF=PH+PF+EF≥FH+EF,
∴当点F、P、H三点共线时,△PEF的周长最小,最小值为FH+EF,
∵E,F分别是AD,AB的中点,
∴AE=DE=DH=3,AF=4,
∴EF=5,
∵FK⊥CD,
∴四边形ADKF为矩形,
∴DK=AF=4, FK=AD=6,
∴HK=1,
即△PEF的周长最小为
因此正确答案为:
【标注】 【知识点】特殊平行四边形
11.正方形+中点+折叠模型+相似+将军饮马+两定一动—23徐州模拟/22贵州+填空压轴+初三
如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为 .
【答案】
【解析】作点P关于CE的对称点P'.
由折叠的性质知CE是∠DCM的平分线,
∴点P'在CD上.
过点M作MF⊥CD于F,交CE于点G,
∵MN+NP=MN+NP'≥MF,
∴MN+NP的最小值为MF的长.
连接DG, DM,
由折叠的性质知CE为线段DM的垂直平分线,
∵AD=CD=2,DE=1,
∵MF⊥CD,∠EDC=90°,
∴DE∥MF.
∴∠EDO=∠GMO.
∵CE为线段DM的垂直平分线,
∴DO=OM,∠DOE=∠MOG=90°.
∴△DOE≌△MOG、
∴DE=GM.
.四边形DEMG为平行四边形.
∠MOG=90°,
∴四边形DEMG为菱形.
∵DE//MF,即DE//GF,
∴△CFG∽△CDE.
艮
∴MN+NP的最小值为
故答案为:
【标注】 【知识点】动点与特殊平行四边形问题
12.等腰直角三角形+逆等线最值+两定两动——23苏州模拟/22遵义+填空压轴+初三
如图,在等腰直角三角形ABC中,∠BAC=90°,点M ,N分别为BC,AC上的动点,且AN=CM,AB= .当AM+BN的值最小时,CM的长为
【答案】
【解析】如下图所示,过点A作AD∥BC,且AD=AC,连接DN,
∴∠DAN=∠ACM,又AN=CM,
∴△AND≌△CMA,
∴AM=DN,
∴BN+AM=BN+DN≥BD,
当B,N,D三点共线时,BN+AM取得最小值,此时如下图所示,
∵在等腰直角三角形ABO中,∠BAC=90°,AB=
△AND≌△CMA,
∴∠ADN=∠CAM,
∵AD=AC=AB,
∴∠ADN=∠ABN,
:AD//BC,
∴∠ADN=∠MBN,
∴∠ABN=∠MBN,
设∠MAC=α,
∴AB=BM=
即BN+AM的值最小值时,CM的长为2-
因此正确答案为:2-
【标注】【知识点】最短路径问题
13二次函数+一次函数+将军饮马+两定一动———22西藏+代数综合压轴+初三
在平面直角坐标系中,抛物线 与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.
(1)求抛物线的解析式,并直接写出点A,C的坐标;(2)如图甲,点M是直线BC上的一个动点,连接AM,OM ,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;
【答案】 ,A(-2,0);C(0,4)(2)存在点M使AM+OM最小, M
【解析】 【分析】(1)将B(4,0)代入 求出函数解析式即可求解; (2)作O点关于BC的对称点O',连接AO'交BC'于点M ,连接BO',当A、M、O'三点共线时,AM+OM有最小值,分别求出直线AO'的解析式和直线BC的解析式,两直线的交点即为M点; (1)将B(4,0)代入y=- w +(m-1)x+2m,..-8+4(m-1)+2m=0,1解得 令x=0,则y=4,∴C(0,4),令y=0,
AM+OM最小,理由如下:作O点关于BC的对称点O',连接AO'交BC于点M ,连接BO',由对称性可知,OM=O'M ,∴AM+OM=AM+O'M≥AO',当A、M、O'三点共线时,
AM+OM有最小值,∵B(4,0) ,C(0,4),. OB=OC,∴∠CBO=45°,由对称性可知 由一次函数关系即可得到M点坐标为
【点睛】本题考查二次函数的图像及性质,熟练掌握二次函数的图像及性质,轴对称求最短距离的方法,平行线的性质是解题的关键.
【标注】 【知识点】二次函数y=ax^2+bx+c的图象和性质
【知识点】二次函数解析式
【知识点】平行线分线段成比例定理
【知识点】轴对称应用
【业务题型】其他
14.二次函数+线段和最小值+将军饮马+两定两动——22天津+代数综合压轴+初三
已知抛物线 a,b,c是常数,a>0)的顶点为P,与x轴相交于点A(-1,0)和点B.
(1) 若b=-2,c=-3.
① 求点P的坐标
②直线x=m(m是常数,1(2)若3b=2c,直线x=2与抛物线相交于点N ,E是a轴的正半轴上的动点,F是y轴的负半轴上的动点,当PF+FE+EN的最小值为5时,求点E,F的坐标.
【答案】(1)① P(1,-4)
② M(2,-3),G(2,-2)
【解析】(1)①若b=-2,c=-3,
则抛物线
∵抛物线 与x轴相交于点A(-1,0),
解得a=1,
∴抛物线为
∴顶点P的坐标为(1,-4).
②当y=0时,
解得x =-1,x =3,
∴B(3,0),
设直线BP的解析式为y= kx+n,
解得
∴直线BP的解析式为y=2x-6,
∵直线x=m(m是常数,1设点M 则G(m,2m-6),
∴当m=2时, MG取得最大值1,
此时,点M(2,-3),则G(2,-2).
(2) ∵抛物线y 与x轴相交于点A(-1,0),
∴a-b+c=0,
又3b=2c,
b=-2a,c=-3a(a>0),
∴抛物线的解析式为
∴顶点P的坐标为(1,-4a),
∵直线x=2与抛物线相交于点N,
∴点N的坐标为(2,-3a),
作点P关于y轴的对称点P',作点N关于x轴的对称点N',连接P'N',
得点P'的坐标为(-1,-4a) ,点N'的坐标为(2,3a),
当满足条件的点E,F落在直线P'N'上时,PF+FE+EN取得最小值,此时,
延长P'P与直线x=2相交于点H ,则P'H⊥N'H.
在Rt△P'HN'中,P'H=3,HN'=3a-(-4a)=7a.
解得 (舍)
∴点P'的坐标为 点N'的坐标为
∴直线P'N'的解析式为
∴点E 点
【标注】 【知识点】二次函数与轴对称问题
15.特殊角+线段和最小值+双对称+两定两动——22泰安+选择压轴+初二
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=3,ON=5,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )
A. B.
【答案】A
【解析】解:作M关于OB的对称点M,作N关于OA的对称点N,如下图所示:
连接MN,即为MP+PQ+QM的最小值
根据轴对称的定义可知:ON△=ON=5, OM^'=OM=3,∠NOQ=∠M'OB=30°,
∴△ONN为等边三角形,△OMM'为等边三角形,
∴∠NOM=90°,
∴在Rt△MON中,
因此正确答案为:A.
【标注】 【知识点】最短路径问题
16.矩形+将军饮马造桥选址+两定两动——23济南模拟/22内江+填空压轴+初二
如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点, EFIBC,则AF+CE的最小值是 .
【答案】10
【解析】解:延长BC到G,使CG=EF,连接FG,
EF∥CG,EF=CG,
∴四边形EFGC是平行四边形,
∴CE=FG,
∴AF+CE=AF+FG,
∴当点A、F、G三点共线时, AF+CE的值最小为AG.
由勾股定理得
∴AF+CE的最小值为10,
因此正确答案为:10.
【标注】 【知识点】最短路径问题
17.等边三角形+中垂线+将军饮马+两定一动 -24大庆模拟+选择压轴+初二
如图,在等边△ABC中,点E是AC边的中点, 点P是△ABC的中线AD上的动点,且AD=6,则EP+CP的最小值是( )
A.12 B. 9 C. 6 D.3
【答案】C
【解析】
【分析】
要求EP+CP的最小值,需考虑通过作辅助线转化EP,CP的值,从而找出其最小值求解即可.
【详解】
解:作点E关于AD的对称点F,连接CF,
·△ABC是等边三角形,AD是BC边上的中线,
∴AD⊥BC,
∴AD是BC的垂直平分线,
∴点E关于AD的对应点为点F,
∴CF就是EP+CP的最小值.
∵△ABC是等边三角形,E是AC边的中点,
∴F是AB的中点,
∴CF是△ABC的中线,
∴CF=AD=6,
即EP+CP的最小值为6,
故选:C.
【点睛】
本题主要考查了轴对称-最短路线问题以及等边三角形的性质,熟练掌握等边三角形和轴对称的性质是解题的关键.
【标注】 【知识点】等边三角形的性质
18.矩形+中点+将军遛马+两定两动——23青岛模拟/22自贡+填空压轴+初二
如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 .
【答案】3
【解析】如图,作G关于AB的对称点G',在CD上截取CH=1,然后连接HG'交AB于E,在EB上截取EF=1,此时GE+CF的值最小,
∵OH=EF=1,CH∥EF,
∴四边形EFCH是平行四边形,
∴EH=CF,
∴G'H=EG'+EH=EG+CF,
∵AB=4,BC=AD=2,G为边AD的中点,
∴DG'=AD+AG'=2+1=3,DH=4-1=3,
由勾股定理得:
即GE+CF的最小值为3
故答案为:3
【标注】 【知识点】线段和的最小值
19.菱形+特殊角60°+对角线+将军饮马+两定一动——23丹东模拟/22黑龙江+填空压轴+初二
如图,菱形ABCD中,对角线AC,BD相交于点O,∠BAD=60°, AD=3,AH是∠BAC的平分线,CE⊥AH于点E,点P是直线AB上的一个动点,则OP+PE的最小值是 .
【答案】
【解析】如图,连接OE,作点O关于AB的对称点F,连接OF交AB于G,连接PE交直线AB于P ,连接PO,
则PO=PF,此时,PO+PE最小,最小值=EF,
∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC,OB=OD,AD=AB=3.
∵∠BAD=60°,
∴△ABD是等边三角形.
∴BD=AB=3,∠BAO=30°
∵点O和点F关于直线AB对称,
∴OF⊥AB,OF=2OG=OA=
中小学教育资源及组卷应用平台
∴∠AOG=60°.
∵CE⊥AH于E,OA=OC,
∴∠CAE=∠OEA,
:AH平分∠BAC,
∴∠CAE=15°
在Rt∠EOF中,由勾股定理,得
∴PO+PE的最小值为
故答案为:
【标注】【知识点】特殊平行四边形
20.特殊角+将军饮马+两定一动1———21黑龙江+选择压轴+初二
已知在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,点E为边AC上的动点,点F为边AB上的动点,则线段FE+EB的最小值是( )
B. C. D.
【答案】B
【解析】作F关于AC的对称点F',延长AF'、BC交于点B',连接BF'、BD.
FE+EB=BE+EF',
∴当B、E、F'共线且与AB'垂直时,长度最小,
即作BD⊥AB'于D,
在Rt△ABD中,
∴FE+EB的最小值为
故选B.
【标注】【知识点】线段和的最小值
21.圆+正方形+周长最小值+将军遛马+两动一定————23宁波模拟/21连云港+选择压轴+初二
如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是().
A.3 B.4 C.5 D.6
【答案】B
【解析】⊙O的面积为2π,则圆的半径为 则
由正方形的性质,可知点C是点A关于BD的对称点,
过点C作CA'//BD,且使CA'=1,
连接AA'交BD于点N,取NM =1,连接AM、CM,则点M、N为所求点,
A'C//MN,且A'C= MN,则四边形MCA'N为平行四边形,
则A'N=CM=AM,
故△AMN的周长=AM+AN+MN=AA'+1时取得最小值,
则
则△AMN的周长的最小值为3+1=4,
故选:B.
22.圆+将军饮马+两定一动——23宿迁模拟+填空压轴+初二
如图,在Rt△AOB中,∠AOB=90°,OA=4,OB=6,以点O为圆心,3为半径的⊙O,与OB交于点C,过点C作CD⊥OB交AB于点D ,点P是边OA上的动点,则PC+PD的最小值为 .
【答案】2
【解析】∵OB=6,OC=3,
∴点C为OB的中点,
∵OA⊥OB,CD⊥OB,
∴OA//CD,
延长CO与⊙O相交于C',连接C'D与OA相交于P,如图,
∴在Rt△C'CD中,
23.矩形+折叠模型+将军饮马+两定一动1 ———23深圳模拟/21盘锦+填空压轴+初二
如图,四边形ABCD为矩形, 点P为边AB上一点.以DP为折痕将△DAP翻折,点A的对应点为点A'.连结AA',AA'交PD于点M ,点Q为线段BC上一点,连结AQ,MQ,则AQ+MQ的最小值是
【答案】4
【解析】解:如下图所示,作点A关于BC的对称点T,取AD的中点R,连接BT, QT, RT, RM.
∵四边形ABCD是矩形,
∴∠RAT=90°,
∵A,A关于DP对称,
∴AA'⊥DP,
∴∠AMD=90°,
:AR=RD,
∵MT≥RT-RM,
∴M7的最小值为4
∵QA+QM=QT+QM≥MT,
∴QA+QM≥4
∴QA+QM的最小值为4
因此正确答案为:4
【标注】【知识点】特殊平行四边形
24.直角三角形+特殊角度+将军饮马+两定一动——23鄂州模拟/21西藏+选择压轴+初二
如图,在Rt△ABC中,∠A=30°,∠C=90°, AB=6,点P是线段AC上一动点,点M在线段AB上,当 AB时, PB+PM的最小值为()
A.3 B.2 C. 2 +2 D.3 +3
【答案】B
【解析】解:作B点关于AC的对称点B',连接B'M交AC于点P,
BP=B'P,
∴PB+PM=B'P+PM≥B'M,
∴PB+PM的最小值为B'M的长,
过点B'作B'H⊥AB于H点,
∵∠A=30°,∠C=90°,
∴∠CBA=60°,
:AB=6,
. BC=3,
∴BB'=6,
在Rt△BB'H中,
:AH=3,
∴AM=2,
∴MH=1,
在Rt△MHB'中,
∴PB+PM的最小值为2
故选:B.
25.正方形+隐形圆+将军饮马+点圆最值+两动一定——22无锡模拟/21鄂尔多斯+填空压轴+初三
如图,已知正方形ABCD的边长为6,点/是正方形内一点,连接CF,DF,且∠ADF=∠DCF,点E是AD边上一动点,连接EB,EF,则EB+EF长度的最小值为 .
【答案】
【解析】解:∵四边形ABCD是正方形,
∴∠ADC=90°,
∵∠ADF=∠DCF,
∴点R在以DC为直径的半圆上移动,
如下图所示,设CD的中点为O,作正方形ABCD关于直线AD对称的正方形APGD,则点B的对应点是P,
连接PO交AD于E,交半圆O于F,则线段FP的长即为BE+FE的长度最小值,OF=3,
∵∠G=90°,PG=DG=AB=6,
∴OG=9,
∴BE+FE的长度最小值为3
因此正确答案为:3
【标注】【知识点】轴对称应用
【知识点】圆心角和圆周角
【知识点】勾股定理
【知识点】正方形的性质
26.二次函数+将军遛马+两定两动22泰安模拟/21广元+代数综合压轴+初三
如图1,在平面直角坐标系xOy中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:
x ..+ -1 0 1 2 3 ...
y ++ 0 3 4 3 0 ..
(1)求出这条抛物线的解析式及顶点M的坐标.
(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求AQ+QP+PC的最小值.
【答案】
【解析】(1)由表格数据可知,顶点坐标为(1,4),
设抛物线解析式为:
将点(0,3)代入解析式得:3=a+4,
∴a=-1,
∴抛物线解析式为: 顶点坐标M(1,4).
(2) 由表格可知,抛物线经过点A(-1,0),C(0,3),
如图3,将A点向上平移一个单位,得到A'(-1,1),
则AA'//PQ,AA'=PQ,
∴四边形AA'PQ是平行四边形,
∴PA'=QA,
作A'关于MQ的对称点E ,则E(3,1),
∴PA'=PE,
∴AQ+QP+PC=PE+1+PC,
当P、B、C三点共线时,PE+PC最短,
设直线CE的解析式为:y= mx+n,
将C、E两点坐标代入解析式可得
∴直线CE的解析式为
令x=1,则
∴当P的坐标为 时, P、E、C三点共线,
此时 最短,
∴AQ+QP+PC的最小值为
【标注】 【知识点】二次函数与圆的综合问题
27.矩形+平行四边形存在性+线段差最大值+线段和最小值+将军饮马
——23无锡模拟+选择压轴+初三
如图,在矩形ABCD中,AB=15,BC=20,把边AB沿对角线BD平移,点A',B'分别对应点A,B.给出下列结论:
①顺次连接点A',B',C,D的图形是平行四边形;
②点C到它关于直线AA'的对称点的距离为48;
③A'C-B'C的最大值为15;
④A'C+B'C的最小值为9
其中正确结论的个数是( ).
A.1 B. 2 C.3 D.4
【答案】D
【解析】如图1,
∵AB=A'B',AB//A'B',AB=CD,AB//CD,
∴A'B'=CD,A'B'//CD,
∴四边形A'B'CD是平行四边形,故①正确,
作点C关于直线AA'的对称点E,连接CE交AA'于T,交BD于点O,则CE=4OC.
∵四边形ABCD是矩形,
∴EC=48,故②正确,
∵A'C-B'C≤A'B',
∴A'C-B'C≤15,
∴A'C-B'C的最大值为15,故③正确,
如图2,
∵B'C=A'D.
.. A'C+B'C=A'C+A'D,
作点D关于AA'的对称点D',
连接DD'交AA'于J,过点D'作D'E⊥CD交CD的延长线于E ,连接CD'交AA'于A',此时CB'+CA'的值最小,最小值=CD',
由△AJD∽△DAB,
可得
∴DJ=12,
注可得:
∴A'C+B'C的最小值为9 故④正确.,;
故选:D.
28.二次函数+将军遛马+两定两动+四边形周长最小值——22广州模拟/21遂宁+代数综合压轴+初三
如图,已知二次函数的图象与x轴交于A和B(-3,0)两点,与y轴交于C(0,-3),对称轴为直线x=-1,直线y=-2x+m经过点A,且与y轴交于点D,与抛物线交于点E,与对称轴交于点P.
(1)求抛物线的解析式和m的值.
(2) 直线y=1上有M、N两点(M在N的左侧) ,且MN=2,若将线段MN在直线y=1上平移,当它移动到某一位置时,四边形MEFN的周长会达到最小,请求出周长的最小值(结果保留根号).
【答案】
【解析】(1)∵抛物线的对称轴为直线x=-1, 与x轴的交点为A, B(-3,0),
. A(1,0),
∴可以设抛物线的解析式为y=a(x+3)(x-1),
把C(0,-3)代入得到,a=1,
∴抛物线的解析式为
直线y= - 2x+m经过点A(1,0),
∴0=-2+m,
∴m=2.
(2) ∵点E、F均为定点,
∴线段EF长为定值,
∴当EM+FN为最小值时,四边形MEFN的周长最小,
如图2,画出直线y=1,将点F向左平移2个单位得到F',作点E关于y=1的对称点E',连接E'F'与直线y=1交于点M ,过点F作FN//E'F', 交直线y=1于点N ,
由作图可知:EM=E'M,F'M=FN,
又∵E',M , F'三点共线,
此时,EM+FN的值最小,
∵点F为直线y=-2x+2与直线x=-1的交点,
∴F(-1,4),
∴F'(-3,4),
∵E(-5,12),
∴E'(-5,-10),
如图,延长FF'交线段EE'于点W,
∵FF'//直线y=1,
∴FW⊥EE', W(-5,4),
∵在Rt△EWF中,
由勾股定理得:
在Rt△E'WF'中,
∴四边形MEFN的周长最小值
=ME+FN+EF+MN
【标注】 【知识点】二次函数与动点问题
29.正方形+隐形圆+将军饮马+两定两动——23湖州模拟/20广西+选择压轴+初三
如图,动点M在边长为2的正方形ABCD内,且AM⊥BM,P是CD边上的一个动点,E是AD边的中点,则线段PE+PM的最小值为 ( )
A. -1 B. +1 C.
【答案】A
【解析】解答:解:作点E关于DC的对称点E',设AB的中点为点O,连接OE',交DC于点P,连接PE,如图:
∵动点M在边长为2的正方形ABCD内,且AM⊥BM,
∴点M在以AB为直径的圆上,
∵正方形ABCD的边长为2,∴AD=AB=2,∠DAB=90°,
∴E是AD的中点,
∵点E与点E'关于DC对称,
∴DE'=DE=1, PE=PE',
∴AE'=AD+DE'=2+1=3,
在Rt△AOE'中,
∴线段PE+PM的最小值为:
因此正确答案为:A.
【标注】 【知识点】勾股定理
【知识点】圆心角和圆周角
【知识点】有关公理-两点之间线段最短
【知识点】正方形的性质
30.等边三角形+中垂线+将军饮马+两定一动——22凉山模拟/21西宁+填空压轴+初二
如图,△ABC是等边三角形,AB=6,N是AB的中点,AD是BC边上的中线,M是AD上的一个动点,连接BM,MN,则BM+MN的最小值是 .
【答案】3
【解析】解:连接CN,与AD交于点M,连接BM.(根据两点之间线段最短;点到直线垂直距离最短) ,AD是BC边上的中线即C和B关于AD对称,则BM+MN=CN,则CN就是BM+MN的最小值.
∵△ABC是等边三角形, AB=6, N是AB的中点,
即BM+MN的最小值为3
因此正确答案为:3
【标注】【知识点】等腰三角形
31.坐标系+将军遛马+两定两动——22广州模拟/20荆门+选择压轴+初二
在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接AC、BD,则AC+BD的最小值为( )
A.2 C.6 D.3
【答案】B
【解析】如图,将线段AC沿x轴方向平移2个单位得到A'D,
则A'D=AC
作A'关于x轴的对称点A",连接A"B ,
则
∴AC+BD的最小值为A” B的长度.
过A"作A"E⊥y轴于E点,
在Rt△A"BE中,
BE=4+2=6,A"E=2,
即AC+BD的最小值为2
故选B.
【标注】 【知识点】直接用勾股求边长
32.坐标系+将军遛马+两定两动
1——23长沙模拟/21聊城+填空压轴+初二
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,O分别在x轴,y轴上,B,D两点坐标分别为B(-4,6),D(0,4),线段EF在边OA上移动,保持EF =3,当四边形BDEF的周长最小时,点E的坐标为 .
【答案】
【解析】在线段BC上取点M,使得BM=EF,作M点关于a轴的对称点N,连接EM, EN,MN,
∵四边形OABC是矩形,
∴BC∥OA,BC⊥OC,
∵EF=3,
. BM=EF=3.
∵BM∥EF,
∴四边形BFEM是平行四边形,
∴BF=ME,
·B点坐标为(-4,6), D点坐标为(0,4),
∵BM=3,
∴M点坐标为(-1,6),
∵M、N关于x轴对称,
∴N点坐标为(-1,-6), EM=EN,
∴当且仅当N,E ,D三点共线时,
四边形BDEF的周长取得最小值,
设直线DN的解析式为y= kx+b,
∴y=10x+4,
令y=0,10x+4=0,
解得
∴当四边形BDEF的周长最小时,
点E的坐标为
故答案为:
【标注】 【知识点】四边形周长最小
33.正方形+对角线+将军饮马+两定一动——21青海+填空压轴+初二
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为 .
【答案】10
【解析】根据题意,连接BN、BM,如图,
根据正方形的性质,点N在对角线AC上,
∴BN=DN,
∴DN+MN=BN+MN,
当B,N,M三点共线时,取最小值,
则BM就是所求DN+MN的最小值.
在Rt△BCM中,BC=8,CM=6.
根据勾股定理得: 即DN+MN的最小值为10.
【标注】 【知识点】线段和的最小值
34.正方形+多选+将军饮马+两定一动——21黄冈+填空压轴+初三
如图,正方形ABCD中,AB=1,连接AC,∠ACD的角平分线交AD于点E,在AB上截取AF=DE,连接DF,分别交CE,CA于点G ,H,点P是线段GC上的动点,PQ⊥AC于点Q ,连接PH 下列结论:①CE⊥DF;②DE+DC=AC;③EA= AH;④PH+PQ的最小值是 其中正确结论的序号是
【答案】①②④
【解析】在正方形ABCD中,
CD=AD,∠CDE=∠DAF=90°,
在△CDE与△DAF中,
∴△CDE≌△DAF(SAS),
∴∠DCE=∠ADF,
∴∠ADF+∠CDF=90°,
∴∠DGC=90°,
∴CE⊥DF,
∴①正确.
∵CE平分∠ACD,CE⊥DF,
∴CD=CH,
∵AB∥CD,
∴△AHF∽△CHD,
∴AH=AF,
∴DE+DC=AF+CH
=AH+CH
=AC.
∴②正确.
:CE平分∠ACD,
∴③错误.
过P作PQ'⊥CD.
∵CE平分∠ACD,
∴PH+PQ=PH+PQ',
当HQ'⊥CD时,
PH+PQ'最小,
艮
∴④正确.
∴综上①②④正确.
【标注】 【知识点】动点与特殊平行四边形问题
35.特殊角+三角形周长最小值+将军饮马+两动一定———22泰州模拟+选择压轴+初二
如图,∠AOB=60°,点P是∠AOB内的定点且 若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( ).
C. 6 D.3
【答案】D
【解析】作P点分别关于OA、OB的对称点C、D,
连接OD分别交OA、OB于M、N,如图,则OA、OB分别是线段PC、PD垂直平分线,
∴MP=MC,NP=ND,OP=OD=OC= ,∠BOP=∠BOD,
∠AOP=∠AOC,
∴PN+PM+MN=ND+MN+NC=DC
∠COD=∠BOP+∠BOD+∠AOP+∠AOC
=2∠AOB=120°.
利用两点之间线段最短,即△PMN的周长围为线段DC的长度,
∵两点之间线段的距离最小,
∴此时△PMN周长最小,
作OH⊥CD于H,则CH = DH,
∴OD=2CH=3.
故选D.
【标注】【知识点】三角形周长最小
36.菱形+特殊角度+将军饮马+两定一动
———20广西+填空压轴+初二
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=6 ,BD=6,,点P是AC上一动点,点E是AB的中点,则PD+PE的最小值为 .
【答案】3
【解析】如下图所示,连接DE,
∵四边形ABCD是菱形,对角线AC,BD相交于点O, AC=6 ,BD=6,
AB=AD=BD,即△ABD是等边三角形,
又∵E是AB的中点,
. DE⊥AB,
∵DP+PE≥DE,
∴PD+PE的最小值为DE的长.
即PD+PE的最小值为3
因此正确答案为:3
【标注】 【知识点】特殊平行四边形
37.扇形+阴影面积+周长最小值+将军饮马+两定一动———22南通模拟/20河南+填空压轴+初三
如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交BC于点D ,点E为半径OB上一动点若OB=2,则阴影部分周长的最小值为 .
【答案】
【解析】作点D关于OB的对称点D',再连接CD'与OB的交点即为点E,
此时阴影部分周长最小,最后再连接OD',
∵∠BOC=60°且OD平分∠BOC,
∵OB=2,
∵点D与D'关于OB轴对称,
∴∠BOD'=∠BOD=30°,OD'=OD, DE=D'E,
∴CE+DE的最小值=CD'=2
∴阴影部分周长的最小值为(
【标注】 【知识点】与圆有关的不规则图形的周长与面积计算
38.坐标系+三角形周长最小值+特殊角度+将军饮马+两动一定21武威模拟/20永州+填空压轴+初二
∠AOB在平面直角坐标系中的位置如图所示,且∠AOB=60°,在∠AOB内有一点P(4,3), M、N分别是OA,OB边上的动点,连接PM,PN,MN,则△PMN周长的最小值是 .
【答案】5
【解析】分别作点P关于OA,OB的对称点P ,P ,连接P P 交OA于点M ,交OB于点N,连接OP ,OP ,OP,
则OP =OP=OP ,∠P OA=∠POA,∠POB=∠P OB,
∴PM=P M,PN=P N,
则△PMN的周长最小值为P P 的长度,
过点O作OQ⊥P P 于点Q,
∵P点坐标为(4,3),
∴OP=5,
∵∠POA=∠P OA,∠P OB=∠POB,∠POA+∠POB=∠AOB=60°,
又:
在Rt△OP Q中,
在等腰三角形OP P 中,OQ为P P 边上的高线,
即△PMN周长最小值为5
故答案为:5
【标注】【知识点】轴对称的性质
39.等边三角形+点线最值+特殊角度———20营口+填空压轴+初二
如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为 .
【答案】3
【解析】如图所示,过点O作ON⊥AB于点N,交AD于点M,
∵点E为AD上的动点,点F为AB上的动点,
.当点E与点M重合,点F与点N重合时,CE+EF取最小值ON.
∵△ABC为等边三角形,边长为6,
∴BO=6,∠B=60°,
Rt△CBN中,
故CE+EF的最小值为(
故答案为:3
【标注】 【知识点】等边三角形的性质
【能力】推理论证能力
40.矩形+特殊角度+将军饮马+两定一动
11 ——22成都模拟/20内江+填空压轴+初三
如图,在矩形ABCD中, BC=10,∠ABD=30°,若点M、N分别是线段DB、AB上的两个动点,则AM+MN的最小值为 .
【答案】15
【解析】如图,过A作AG⊥BD于G.延长AG,使AG=EG.过E作EN⊥AB于N,交BD于M,
则AM+MN=EN最短,
∵四边形ABCD为矩形,BC=10,∠ABD=30°,
.. AD=10,BD=20,AB=BD·cos30°=10
∵AG·BD=AD·AB,
∴20AG=10×10
∴AG=5 ,AE=2AG=10
∵AE⊥BD,EN⊥AB,∠EMG=∠BMN,
∴∠E=∠ABD=30°,
∴AM+MN=15,
即AM+MN的最小值为15.
故答案为:15.
【标注】【知识点】矩形的性质
【能力】推理论证能力
41.正方形+平移+将军饮马+两定两动
———20黑龙江+填空压轴+初二
如图,在边长为4的正方形ABCD中将△ABD沿射线BD平移,得到△EGF,连接EC、GC,则EC+GC的最小值为
【答案】4
【解析】如图,将△ABC沿射线CA平移到△AB'C'的位置,连接C'E、AE、DE.
:AB//GE//DC且AB=GE=DC,
∴四边形ABGE和四边形EGCD均为平行四边形,
∴AE∥BG,CG=DE,
∴AE⊥OO'
由作图易得,点C与点C'关于AE对称,C'E=CE.
又∵CG=DE,
∴EC+GC=C'E+ED,
当点C'、E、D在同一直线上时,C'E+ED的值最小,
此时,在Rt△C'DB'中,
即EC+GC的最小值为4
故答案为:4
【标注】[知识点】线段和的最小值
42.坐标系+四边形周长最小值+将军饮马+两定一动 ---20聊城+填空压轴+初二
如图,在直角坐标系中,点A(1,1),B(3,3)是第一象限角平分线上的两点,点C的纵坐标为1,且CA=CB,在y轴上取一点D ,连接AC,BO,AD,BD,使得四边形ACBD的周长最小,这个最小周长的值为 .
【答案】
【解析】由点A与点C的纵坐标均为1,可知AC//x轴,
又因为点A,B是第一象限角平分线上的两点,
则AC-BC=2.
如图,作点A关于y轴的对称点E,连接BE交y轴于点D,
此时AD+BD的值愿小,为线段BE的长.由轴对称性可知AB=2,则EC=4,
在Rt△BCE中,根据勾股定理,得 ∴四边形ACBD的最小周长为
【标注】【知识点】轴对称的性质
43.坐标系+将军遛马+两定两动———20辽宁+填空压轴+初三
如图,在平面直角坐标系中,已知A(3,6), B(-2,2),在x轴上取两点C,D(点C在点D的左侧),且始终保持CD=1,线段CD在x轴上平移,当AD+BC的值最小时,点C的坐标为 .
【答案】(-1,0)
【解析】把A(3,6)向左平移1得A'(2,6),
作点B关于x轴的对称点B',连接B'A'交x轴于C,在x轴上取点D(点C在点D的左侧),使CD=1,连接AD,
则AD+BC的值最小,
∵B(-2,2),
∵. B'(-2,-2),
设直线B'A'的解析式为y= kx+b,
解得:
∴直线H'A'的解析式为y =2x+2,
当y=0时,x=-1,
∴C(-1,0),
故答案为:(-1,0).
【标注】 【知识点】坐标轴上点的坐标特征
1.类型一 “将军饮马”问题
【结论】:
如图,在定直线l上找一动点P ,使点P到两定点A与B的距离之和最小,即 最小.
作对称点的作用:
1.将直线同侧两点问题转化为直线异侧两点问题;
2.利用轴对称的性质可以将相等的线段转化.
2.类型二 矩形纸片折叠问题
1.翻折后对应角相等.2.翻折问题中的计算常用勾股定理.
3.类型三 图形中的对称问题
1 .点线对称;对称点连线被折痕垂直平分. 2.三角形直线对称;对称前后全等;
4.类型四 轴对称图形的构造及应用
策略总结:可考虑对称
板块1:将军饮马最值模型
真题精炼
1.坐标系+将军饮马+两定一动——24成都+填空压轴+初二/初三
如图,在平面直角坐标系xOy中,已知A(3,0),B(0,2),过点B作y轴的垂线l,P为直线l上一动点, 连接PO , PA ,则PO +PA的最小值为
2.三角形内心 °角+将军饮马+两定一动——24内江+填空压轴+初二/初三
如图,在 中, ,E是BC边上一点,且 点I是△ABC的内心, BI的延长线交AC于点D , P是BD上一动点, 连接PE、PC,则 的最小值为 .
3.正方形+8字相似+将军饮马+两定一动——23泸州+填空压轴+初三
如图,E ,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当 取得最小值时, 的值是
板块1:将军饮马最值模型
4.矩形+周长最小值+将军饮马+两定两动+瓜豆原理——24大庆+选择压轴+初二
如图,在矩形ABCD中, ,点M是AB边的中点 ,点N是AD边上任意一点,将线段MN绕点M顺时针旋转 点N旋转到点 则 周长的最小值为( )
A. 15 D.18
5.二次函数+将军饮马之造桥选址+两定两动———23重庆+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 经过点 与y轴交于点C,与x轴交于A, B两点(A在B的左侧) , 连接AC, BC, tan∠CBA=4.
(1)求抛物线的表达式.
(2)点P是射线CA上方抛物线上的一动点,过点P作I 轴,垂足为E ,交AC于点D .点M是线段DE上一动点, 轴,垂足为N,点F为线段BC的中点,连接AM ,NF .当线段PD长度取得最大值时,求 的最小值.
板块1:将军饮马最值模型
6.二次函数+平行四边形+将军饮马+两定一动——24定西+代数综合压轴+初三如图1,抛物线 交x轴于O, A(4,0)两点, 顶点为. 点C为OB的中点.
(1)求抛物线 的表达式;
(2)过点C作CH⊥OA,垂足为H,交抛物线于点E.求线段CE的长.
(3)点D为线段OA上一动点(O点除外),在OC右侧作平行四边形OCFD .
①如图2,当点F落在抛物线上时,求点F的坐标;
②如图3, 连接BD,BF,求BD+BF的最小值.
7.正方形+对角线+勾股定理+将军饮马+两定一动——23广州+填空压轴+初二
如图,正方形ABCD的边长为4,点E在边BC上,且 ,F为对角线BD上一动点,连接CF, EF ,则CF+EF的最小值为 .
8.正方形+对角线+中点+相似+将军饮马+两定一动——23镇江模拟+填空压轴+初二如图,正方形ABCD的边长为5 ,E为AD的中点,P为CE上一动点,则 的最小值为 .
板块1:将军饮马最值模型
9.矩形+锐角三角函数+特殊角度+将军饮马+两定一动——23江西模拟+填空压轴+初二如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB ,若 则PE+PB的最小值为 .
10.矩形+双中点+周长最小值+将军饮马+两定一动——23深圳模拟/22广西+填空压轴+初二如图, 在矩形ABCD中,. E , F分别是AD, AB的中点, 的平分线交AB于点G,点P是线段DG上的一个动点,则 的周长最小值为 .
11.正方形+中点+折叠模型+相似+将军饮马+两定一动——23徐州模拟/22贵州+填空压轴+初三如图,在边长为2的正方形ABCD中,点E为AD的中点,将 沿CE翻折得 点M落在四边形ABCE内 .点N为线段CE上的动点,过点N作 交MC于点P ,则 的最小值为 .
板块1:将军饮马最值模型
12.等腰直角三角形+逆等线最值+两定两动——23苏州模拟/22遵义+填空压轴+初三如图,在等腰直角三角形ABC中, 点M ,N分别为BC,AC上的动点,且 当AM+BN的值最小时,CM的长为
13.二次函数+一次函数+将军饮马+两定一动——22西藏+代数综合压轴+初三
在平面直角坐标系中,抛物线 与x轴交于A, B (4, 0) 两点, 与y轴交于点C,点P是抛物线在第一象限内的一个动点.
(1)求抛物线的解析式,并直接写出点A,C的坐标;(2)如图甲,点M是直线BC上的一个动点,连接AM,OM ,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;
14.二次函数+线段和最小值+将军饮马+两定两动——22天津+代数综合压轴+初三已知抛物线 (a,b,c是常数,a>0)的顶点为P ,与x轴相交于点 和点B .
( 1 ) 若b=-2,c=-3.
① 求点P的坐标.
② 直线x=m(m是常数,1
15.特殊角+线段和最小值+双对称+两定两动————22泰安+选择压轴+初二
如图, ,点M、N分别在边OA、 OB上, 且( ,点P、Q分别在边OB、 OA上,则MP+PQ+QN的最小值是( )
矩形+将军饮马造桥选址+两定两动————23济南模拟/22内江+填空压轴+初二
如图,矩形ABCD中,AB=6, AD=4,点E、F分别是AB、DC上的动点, EF∥BC,则AF+CE的最小 值是 .
17.等边三角形+中垂线+将军饮马+两定一动——24大庆模拟+选择压轴+初二
如图 ,在等边 中,点E是AC边的中点,点P是△ABC的中线AD上的动点,且 则EP+CF 的最小值是( )
A. 12 B. 9 C. 6 D.3
18.矩形+中点+将军遛马+两定两动——23青岛模拟/22自贡+填空压轴+初二
如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为
19.菱形+特殊角60°+对角线+将军饮马+两定一动——23丹东模拟/22黑龙江+填空压轴+初二如图, 菱形ABCD中, 对角线AC, BD相交于点O,. AH是∠BAC的 平分线,CE⊥AH于点E,点P是直线AB上的一个动点,则OP+PE的最小值是
20.特殊角+将军饮马+两定一动——21黑龙江+选择压轴+初二
已知在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,点E为边AC上的动点,点F为边AB上的动点,则线段FE+EB的最小值是( )
21.圆+正方形+周长最小值+将军遛马+两动一定——23宁波模拟/21连云港+选择压轴+初二如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π, MN=1, 则△AMN周长的最小值是( )
A.3 B.4 C. 5 D.6
22.圆+将军饮马+两定一动——23宿迁模拟+填空压轴+初二
如图,在] 中, 以点O为圆心,3为半径的⊙O,与OB交于点C,过点C作 交AB于点D,点P是边OA上的动点,则 D的最小值为 .
23.矩形+折叠模型+将军饮马+两定一动———23深圳模拟/21盘锦+填空压轴+初二如图,四边形ABCD为矩形, 点P为边AB上一点.以DP为折痕将△DAP翻 折, 点A的对应点为点A'.连结AA', AA'交PD于点M,点Q为线段BC上一点, 连结AQ, MQ,则 的最小值是
24.直角三角形+特殊角度+将军饮马+两定一动———23鄂州模拟/21西藏+选择压轴+初二如图,在 中, ,点P是线段AC上一 动点,点M在线段AB上,当 时, 1的最小值为( )
正方形+隐形圆+将军饮马+点圆最值+两动一定——22无锡模拟/21鄂尔多斯+填空压轴+初三
如图,已知正方形ABCD的边长为6,点F是正方形内一点,连接CF,DF,且 点E是AD边上一动点,连接EB,EF,则 长度的最小值为
26.二次函数+将军遛马+两定两动——22泰安模拟/21广元+代数综合压轴+初三
如图1,在平面直角坐标系xOy中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:
x -1 0 1 2 3
y 0 3 4 3 0
(1)求出这条抛物线的解析式及顶点M的坐标.
(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求 的最小值.
27.矩形+平四存在性+线段差最大值+线段和最小值+将军饮马——23无锡模拟+选择压轴+初三如图,在矩形ABCD中, ,把边AB沿对角线BD平移,点 分别对应点A,B.给出下列结论:
①顺次连接点A',B',C,D的图形是平行四边形;
②点C到它关于直线. 的对称点的距离为48;
的最大值为15 ;
的最小值为
其中正确结论的个数是 ().
A. 1 B. 2 C. 3 D.4
28.二次函数+将军遛马+两定两动+四边形周长最小———22广州模拟/21遂宁+代数综合压轴+初三
如图,已知二次函数的图象与x轴交于A和. 两点,与y轴交于( 对称轴为直线 直线 经过点A ,且与y轴交于点D,与抛物线交于点E ,与对称轴交于点F .
(1)求抛物线的解析式和m的值.
(2) 直线 上有M、N两点(M在N的左侧 ),且 ,若将线段MN在直线 上平移,当它移动到某一位置时,四边形MEFN的周长会达到最小,请求出周长的最小值(结果保留根号)
29.正方形+隐形圆+将军饮马+两定两动———23湖州模拟/20广西+选择压轴+初三
如图,动点M在边长为2的正方形ABCD内 ,且 ,P是CD边上的一个动点,E是AD边的中点,则线段 的最小值为( )
等边三角形+中垂线+将军饮马+两定一动——22凉山模拟/21西宁+填空压轴+初二
如图, 是等边三角形,. ,N是AB的中点,AD是BC边上的中线,M是AD上的一个动点, 连接BM,MN,则 的最小值是 .
31.坐标系+将军遛马+两定两动———22广州模拟/20荆门+选择压轴+初二
在平面直角坐标系中,长为2的线段CD (点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接AC、BD,则. 的最小值为( ).
32.坐标系+将军遛马+两定两动——23长沙模拟/21聊城+填空压轴+初二
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(-4,6), D(0,4),线段EF在边OA上移动, 保持1 ,当四边形BDEF的周长最小时,点E的坐标为
33.正方形+对角线+将军饮马+两定一动——21青海+填空压轴+初二
如图,正方形ABCD的边长为8,M在DC上,且 N是AC上一动点,则 + MN的最小值为 .
34.正方形+多选+将军饮马+两定一动———21黄冈+填空压轴+初三
如图,正方形ABCD中, AB=1,连接AC,∠ACD的角平分线交AD于点E,在AB上截取 ,连接DF ,分别交CE, CA于点G , H ,点P是线段GC上的动点, PQ⊥AC于点Q,连接PH .下列结论:①CE⊥DF;②DE+DC=AC;③EA= AH;④PH+PQ的的最小值是 其中正确结论的序号是
35.特殊角+三角形周长最小值+将军饮马+两动一定——22泰州模拟+选择压轴+初二如图,∠AOB=60°, 点P是∠AOB内的定点且( 若点M、N分别是射线OA、 OB上异于点O的动点,则△PMN周长的最小值是( )
C. 6 D.3
36.菱形+特殊角度+将军饮马+两定一动——20广西+填空压轴+初二
如图,四边形ABCD是菱形,对角线AC,BD相交于点O, 点P是AC上一动点,点E是AB的中点,则 的最小值为
板块1:将军饮马最值模型
扇形+阴影面积+周长最小值+将军饮马+两定一动——22南通模拟/20河南+填空压轴+初三
如图,在扇形BOC中, OD平分 交 于点D ,点E为半径OB上一动点.若 则阴影部分周长的最小值为
坐标系+三角形周长最小+特殊角+将军饮马两动一定——21武威模拟/20永州+填空压轴+初二
在平面直角坐标系中的位置如图所示,且 在 内有一点P(4,3), M、N分别是OA,OB边上的动点, 连接PM , PN , MN,则 周长的最小值是 .
等边三角形+点线最值+特殊角度——20营口+填空压轴+初二
如图, 为等边三角形,边长为6,. ,垂足为点D ,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为
板块1:将军饮马最值模型
40.矩形+特殊角度+将军饮马+两定一动——22成都模拟/20内江+填空压轴+初三
如图,在矩形ABCD中, ,若点M、N分别是线段DB、AB上的两个动点,则. 的最小值为 .
41.正方形+平移+将军饮马+两定两动——20黑龙江+填空压轴+初二
如图,在边长为4的正方形ABCD中将 沿射线BD平移,得到 ,连接EC、GC,则 的最小值为 .
42.坐标系+四边形周长最小值+将军饮马+两定一动————20聊城+填空压轴+初二
如图,在直角坐标系中,点A(1,1),B(3,3)是第一象限角平分线上的两点,点C的纵坐标为1,且 在y轴上取一点D,连接AC,BC,AD,BD,使得四边形ACBD的周长最小,这个最小周长的值为 .
43.坐标系+将军遛马+两定两动——20辽宁+填空压轴+初三
如图,在平面直角坐标系中,已知A(3,6),. ,在x轴上取两点C,D(点C在点D的左侧),且始终保持线段CD在x轴上平移,当 的值最小时,点C的坐标为 .
1.坐标系+将军饮马+两定一动
——24成都+填空压轴+初二/初三
如图,在平面直角坐标系xOy中,已知A(3,0),B(0,2),过点B作y轴的垂线l,P为直线l上一动点,连接PO, PA,则PO+PA的最小值为 .
【答案】5
【解析】取点O'(0,4),连接O'P,O'A,如图,
∵B(0,2), 过点B作y轴的垂线l,
∴点O'(0,4)与点O(0,0)关于直线l对称,
∴PO'=PO.
∴PO+PA=PO'+PA≥O'A,
即PO+PA的最小值为O'A的长,
在Rt△O'AO中,
∵OA=3,OO'=4,
∴由勾股定理,得(
∴PO+PA的最小值为5.
故答案为:5.
【标注】 【知识点】线段和的最小值
2.三角形内心+30°角+将军饮马+两定一动1——24内江+填空压轴+初二/初三
如图,在△ABC中,∠ABC=60°,BC=8,E是BC边上一点,且BE=2,点I是△ABC的内心,BI的延长线交AC于点D,P是BD上一动点,连接PE、PC,则PE+PC的最小值为 .
【答案】2
【解析】
【分析】
在AB取点F,使BF=BE=2,连接PF,CF ,过点F作FH⊥BC于H,利用三角形内心的定义可得出∠ABD=∠CBD,利用SAS证明△BFPa△BEP,得出PF=PB,则
PE+PC=PF+PC≥OF,当C、P、F三点共线时,PE+PC最小,最小值为CF,利用含30°的直角三角形的性质求出BH,利用勾股定理求出FH ,CF即可.
【详解】
解:在AB取点F,使BF=BE=2,连接PF,CF,过点F作FH⊥BC于H,
∵是△ABC的内心,
.. BI平分∠ABC,
∴∠ABD=∠CBD,
又BP=BP,
∴△BFP≌△BEP(SAS),
∴PF=PE,
∴PE+PC=PF+PC≥CF,
当C、P、F三点共线时, PE+PC最小,最小值为CF,
∵FH⊥BC,∠ABC=60°,
∴∠BFH=30°,
∴PE+PC的最小值为2
故答案为:2
【点睛】
本题考查了三角形的内心,全等三角形的判定与性质,含30°的直角三角形的性质,勾股定理等知识,明确题意,添加合适辅助线,构造全等三角形和含30°的直角三角形是解题的关键.
【标注】 【知识点】三角形内切圆
【知识点】全等三角形的判定
【知识点】勾股定理
【知识点】30°特殊角的性质应用
3.正方形+8字相似+将军饮马+两定一动23泸州+填空压轴+初三
如图,E,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当PE+PF取得最小值时,APC的值是 .
【答案】2
【解析】
【分析】
作点/关于AC的对称点F',连接EF'交AC于点P',此时PE+PF取得最小值,过点F'作AD的垂线段,交AC于点K,根据题意可知点F'落在AD上,设正方形的边长为a,求得AK的边长,证明△AEP'∽△KF'P',可得 即可解答.
【详解】
解:作点F关于AC的对称点F',连接EF'交AC于点P',过点F'作AD的垂线段,交AC于点K.
由题意得:此时F'落在AD上,且根据对称的性质,当P点与P'重合时PE+PF取得最小值,
设正方形ABCD的边长为a,则
∵四边形ABCD是正方形,
∴∠F'AK=45°,∠P'AE=45°,AC=
∵F'K⊥AF',
∴当PE+PF取得最小值时, 的值是为
故答案为:
【点睛】
本题考查了四边形的最值问题,轴对称的性质,相似三角形的证明与性质,正方形的性质,正确画出辅助线是解题的关键.
【标注】 【知识点】坐标系中的对称
【知识点】相似三角形的性质与判定综合
【知识点】四边形综合
【知识点】正方形的性质
4.矩形+周长最小值+将军饮马+两定两动+瓜豆原理--24大庆+选择压轴+初二
如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N',则△MBN'周长的最小值为( )
A. 15 D.18
【答案】B
【解析】
【分析】
本题考查了旋转的性质,矩形的性质,勾股定理,确定点N'的轨迹是解题的关键.由旋转的性质结合AAS证明△AMN≌△GMN',推出MG=AM=5,得到点N'在平行于AB,且与AB的距离为5的直线上运动,作点M关于直线EF的对称点M',连接M'B交直线EF于点N',此时△MBN'周长取得最小值,由勾股定理可求解.
【详解】
解:过点N'作EF∥AB,交AD、BC于E、F,过点M作MG⊥EF垂足为G,
矩形ABCD,
∴AB∥CD,
∴AB∥EF∥CD,
∴四边形AMGE和BMGF都是矩形,
由旋转的性质得
∴∠AMN=90°-∠NMG=∠GMN',
∴△AMN≌△GMN'(AAS),
∴MG=AM=5,
∴点N'在平行于AB,且与AB的距离为5的直线上运动,作点M关于直线EF的对称点M',连接M'B交直线EF于点N',此时△MBN'周长取得最小值,最小值为BM+BM',
故选:B.
【标注】 【知识点】勾股定理
【知识点】全等三角形的判定
【知识点】矩形的性质
【知识点】旋转的性质
5.二次函数+将军饮马之造桥选址+两定两动———23重庆+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 )经过点(-1,6),与y轴交于点C,与x轴交于A,B两点(A在B的左侧) ,连接AC,BC,tan∠CBA=4.
(1)求抛物线的表达式.
(2)点P是射线CA上方抛物线上的一动点,过点P作PE⊥x轴,垂足为E,交AC于点D.点M是线段DE上一动点,MN⊥y轴,垂足为N ,点F为线段BC的中点,连接AM,NF .当线段PD长度取得最大值时,求AM+MN+NF的最小值.
【答案】
【解析】(1)由抛物线的表达式知,OC=4,
∵tan∠CBA=4,则OB=1,
即点B(1,0),
由题意得:
解得:
则抛物线的表达式为
(2) 由抛物线的表达式知,点A、B、C的坐标分别为:(-4,0)、(1,0)、(0,4),则点
由点A、C的坐标得,直线AC的表达式为:y=x+4,
设点 则点D(x,x+4),
则
当x=-2时,PD取得最大值,则点E(-2,0)、D(-2,2),则MN=2,
将点A向右平移2个单位得到点A'(-2,0), 连接A'F交y轴于点N, 过点N作NM⊥PE,连接AM,
则四边形MNA'A为平行四边形,则AM=A'N,
则此时
为最小.
【标注】 【知识点】二次函数与角度问题
6.二次函数+平行四边形+将军饮马+两定一动—24定西+代数综合压轴+初三
如图1,抛物线 k交x轴于O, A(4,0)两点,顶点为B(2,2 ).点C为OB的中点.
(1)求抛物线 k的表达式;
(2)过点C作CH⊥OA,垂足为H,交抛物线于点E .求线段CE的长.
(3)点D为线段OA上一动点(O点除外),在OC右侧作平行四边形OCFD.
①如图2,当点F落在抛物线上时,求点/的坐标;
②如图3,连接BD,BF,求BD+BF的最小值.
【答案】
【解析】
【分析】
(1)根据顶点为B(2,2 ).设抛物线 把A(4,0)代入解析式,计算求解即可;
(2)根据顶点为B(2,2 ).点C为OB的中点,得到C(1, ),当x=1时, 得到E 结合CH⊥OA,垂足为H,得到 的长.
(3)①根据题意,得C(1, ),结合四边形OCFD是平行四边形,设F(m, ),结合点F落在抛物线上,得到 解得即可;
②过点B作BN⊥y轴于点N,作点D关于直线BN的对称点G,过点G作GH⊥y轴于点H,连接DG,CH,FG,利用平行四边形的判定和性质,三角形不等式,勾股定理,矩形判定和性质,计算解答即可.
【详解】
(1)∵抛物线的顶点坐标为B(2,2 ).
设抛物线
把A(4,0)代入解析式,得
解得
(2)∵顶点为B(2,2 ).点C为OB的中点,
∴c(1, ),
∵CH⊥OA,
∵CH∥y轴,
∴E的横坐标为1,
设E(1,m),
当x=1时
(3)①根据题意,得C(1, ),
∵四边形OCFD是平行四边形,
∴点C,点/的纵坐标相同,
设F(m, ),
∵点/落在抛物线上,
解得 (舍去):
故F
②过点B作BN⊥g轴于点N,作点D关于直线BN的对称点G,过点G作GH⊥g轴于点H,连接DG,CH,FG,
则四边形ODGH是矩形,
∴OD=HG,OD∥HG,
∵四边形OCFD是平行四边形,
∴OD=CF,OD∥CF,
∴GH=CF,GH∥CF,
∴四边形CFGH是平行四边形,
∴FG=CH,
∵BG+BF≥FG,
故当B、G、F三点共线时,BG+BF取得最小值,
∵BG=BD,
∴BG+BF的最小值,就是BD+BF的最小值,且最小值就是CH,
延长FC交y轴于点M,
∵OD∥CF,
∵C(1,
∵B(2,2 ).
故BD+BF的最小值是2
本题考查了二次函数待定系数法,中点坐标公式,平行四边形的判定和性质,矩形的判定和性质,勾股定理,轴对称,三角形不等式求线段和的最小值,熟练掌握平行四边形的性质,轴对称,三角形不等式求线段和的最小值是解题的关键.
【标注】【知识点】勾股定理
【知识点】二次函数与特殊平行四边形
【知识点】二次函数与平行四边形
【知识点】二次函数解析式
【业务题型】运算题
7.正方形+对角线+勾股定理+将军饮马+两定一动——23广州+填空压轴+初二
如图,正方形ABCD的边长为4,点E在边BC上,且BE=1,F为对角线BD上一动点,连接CF,EF,则CF+EF的最小值为
【答案】
【解析】解:如图,连接AE交BD于一点F ,连接CF,∵四边形ABCD是正方形,∴点A与点C关于BD对称,∴AF=CF,∴CF+EF=AF+EF=AE,此时CF+EF最小,∵正方形ABCD的边长为4,∴AD=4,∠ABC=90°,∵点E在AB上,且BE=1,∴
F的最小值为 故答案为:
【标注】 【知识点】勾股定理
【知识点】正方形的性质
8.正方形+对角线+中点+相似+将军饮马+两定一动—23镇江模拟+填空压轴+初二
如图,正方形ABCD的边长为5,E为AD的中点,P为CE上一动点,则AP+BP的最小值为 .
【答案】
【解析】建立平面直角坐标系如下图所示,
作点B关于CE的对称点F,BF交CE于点H,连接AF交CE于点P,过点F作FG⊥x轴于点G,
∴BP=FP
根据“两点之间,线段最短”可知,AP+BP的最小值为A/的长,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=5,∠BCD=∠D=90°
∴∠DCE+∠BCH=90°,A(0,5)
点E为AB的贵点,
由勾股定理得,
又BH⊥CE,
∴∠HBC+∠BCH=90
∠HBC=∠DCE
∴△HBC~△DCE
∵∠CBH=∠FBG,∠BHC=∠FGB=90°,
∴△BHC~△BGF,
∴BG=8,FG=4
∴F(8,4)
又A(0,5)
∴AP+BP的最小值为
因此正确答案为
【标注】 【知识点】最短路径问题
9.矩形+锐角三角函数+特殊角度+将军饮马+两定一动——23江西模拟+填空压轴+初二
如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB,若AB=4,BC=4 ,则PE+PB的最小值为
【答案】6
【解析】如图,作点B关于AC的对称点B',交AC于点F ,连接B'E交AC于点P,则PE+PB的最小值为B'E的长度.
∵AC是矩形的对角线,
∴AB=CD=4,∠ABC=90°
在直角△ABC中,AB=4,BC=4
∴∠ACB=30°.
由对称的性质,得B'B=2BF,B'B⊥AC,
∴△BEF是等边三角形.
∴BE=BF=B'F.
∴△BEB'是直角三角形.
∴PE+PB的最小值为6.
故答案为:6.
【标注】【知识点】最短路径问题
10.矩形+双中点+周长最小值+将军饮马+两定一动——23深圳模拟/22广西+填空压轴+初二
如图,在矩形ABCD中,AB=8,BC=6,E,F分别是AD,AB的中点,∠ADC的平分线交AB于点G,点P是线段DG上的一个动点,则△PEF的周长最小值为 .
【答案】
【解析】
解:如下图所示,在CD上取点H,使DH=DE,连接EH,PH,过点F作FK⊥CD于点K,
在矩形ABCD中,∠A=∠ADC=90°,AD=BC=6,CD=AB=8,
∴△DEH为等腰直角三角形,
∵DG平分∠ADC,
∴DG垂直平分EH,
∴PE=PH,
∴△PEF的周长等于PE+PF+EF=PH+PF+EF≥FH+EF,
∴当点F、P、H三点共线时,△PEF的周长最小,最小值为FH+EF,
∵E,F分别是AD,AB的中点,
∴AE=DE=DH=3,AF=4,
∴EF=5,
∵FK⊥CD,
∴四边形ADKF为矩形,
∴DK=AF=4, FK=AD=6,
∴HK=1,
即△PEF的周长最小为
因此正确答案为:
【标注】 【知识点】特殊平行四边形
11.正方形+中点+折叠模型+相似+将军饮马+两定一动—23徐州模拟/22贵州+填空压轴+初三
如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为 .
【答案】
【解析】作点P关于CE的对称点P'.
由折叠的性质知CE是∠DCM的平分线,
∴点P'在CD上.
过点M作MF⊥CD于F,交CE于点G,
∵MN+NP=MN+NP'≥MF,
∴MN+NP的最小值为MF的长.
连接DG, DM,
由折叠的性质知CE为线段DM的垂直平分线,
∵AD=CD=2,DE=1,
∵MF⊥CD,∠EDC=90°,
∴DE∥MF.
∴∠EDO=∠GMO.
∵CE为线段DM的垂直平分线,
∴DO=OM,∠DOE=∠MOG=90°.
∴△DOE≌△MOG、
∴DE=GM.
.四边形DEMG为平行四边形.
∠MOG=90°,
∴四边形DEMG为菱形.
∵DE//MF,即DE//GF,
∴△CFG∽△CDE.
艮
∴MN+NP的最小值为
故答案为:
【标注】 【知识点】动点与特殊平行四边形问题
12.等腰直角三角形+逆等线最值+两定两动——23苏州模拟/22遵义+填空压轴+初三
如图,在等腰直角三角形ABC中,∠BAC=90°,点M ,N分别为BC,AC上的动点,且AN=CM,AB= .当AM+BN的值最小时,CM的长为
【答案】
【解析】如下图所示,过点A作AD∥BC,且AD=AC,连接DN,
∴∠DAN=∠ACM,又AN=CM,
∴△AND≌△CMA,
∴AM=DN,
∴BN+AM=BN+DN≥BD,
当B,N,D三点共线时,BN+AM取得最小值,此时如下图所示,
∵在等腰直角三角形ABO中,∠BAC=90°,AB=
△AND≌△CMA,
∴∠ADN=∠CAM,
∵AD=AC=AB,
∴∠ADN=∠ABN,
:AD//BC,
∴∠ADN=∠MBN,
∴∠ABN=∠MBN,
设∠MAC=α,
∴AB=BM=
即BN+AM的值最小值时,CM的长为2-
因此正确答案为:2-
【标注】【知识点】最短路径问题
13二次函数+一次函数+将军饮马+两定一动———22西藏+代数综合压轴+初三
在平面直角坐标系中,抛物线 与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.
(1)求抛物线的解析式,并直接写出点A,C的坐标;(2)如图甲,点M是直线BC上的一个动点,连接AM,OM ,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;
【答案】 ,A(-2,0);C(0,4)(2)存在点M使AM+OM最小, M
【解析】 【分析】(1)将B(4,0)代入 求出函数解析式即可求解; (2)作O点关于BC的对称点O',连接AO'交BC'于点M ,连接BO',当A、M、O'三点共线时,AM+OM有最小值,分别求出直线AO'的解析式和直线BC的解析式,两直线的交点即为M点; (1)将B(4,0)代入y=- w +(m-1)x+2m,..-8+4(m-1)+2m=0,1解得 令x=0,则y=4,∴C(0,4),令y=0,
AM+OM最小,理由如下:作O点关于BC的对称点O',连接AO'交BC于点M ,连接BO',由对称性可知,OM=O'M ,∴AM+OM=AM+O'M≥AO',当A、M、O'三点共线时,
AM+OM有最小值,∵B(4,0) ,C(0,4),. OB=OC,∴∠CBO=45°,由对称性可知 由一次函数关系即可得到M点坐标为
【点睛】本题考查二次函数的图像及性质,熟练掌握二次函数的图像及性质,轴对称求最短距离的方法,平行线的性质是解题的关键.
【标注】 【知识点】二次函数y=ax^2+bx+c的图象和性质
【知识点】二次函数解析式
【知识点】平行线分线段成比例定理
【知识点】轴对称应用
【业务题型】其他
14.二次函数+线段和最小值+将军饮马+两定两动——22天津+代数综合压轴+初三
已知抛物线 a,b,c是常数,a>0)的顶点为P,与x轴相交于点A(-1,0)和点B.
(1) 若b=-2,c=-3.
① 求点P的坐标
②直线x=m(m是常数,1
【答案】(1)① P(1,-4)
② M(2,-3),G(2,-2)
【解析】(1)①若b=-2,c=-3,
则抛物线
∵抛物线 与x轴相交于点A(-1,0),
解得a=1,
∴抛物线为
∴顶点P的坐标为(1,-4).
②当y=0时,
解得x =-1,x =3,
∴B(3,0),
设直线BP的解析式为y= kx+n,
解得
∴直线BP的解析式为y=2x-6,
∵直线x=m(m是常数,1
∴当m=2时, MG取得最大值1,
此时,点M(2,-3),则G(2,-2).
(2) ∵抛物线y 与x轴相交于点A(-1,0),
∴a-b+c=0,
又3b=2c,
b=-2a,c=-3a(a>0),
∴抛物线的解析式为
∴顶点P的坐标为(1,-4a),
∵直线x=2与抛物线相交于点N,
∴点N的坐标为(2,-3a),
作点P关于y轴的对称点P',作点N关于x轴的对称点N',连接P'N',
得点P'的坐标为(-1,-4a) ,点N'的坐标为(2,3a),
当满足条件的点E,F落在直线P'N'上时,PF+FE+EN取得最小值,此时,
延长P'P与直线x=2相交于点H ,则P'H⊥N'H.
在Rt△P'HN'中,P'H=3,HN'=3a-(-4a)=7a.
解得 (舍)
∴点P'的坐标为 点N'的坐标为
∴直线P'N'的解析式为
∴点E 点
【标注】 【知识点】二次函数与轴对称问题
15.特殊角+线段和最小值+双对称+两定两动——22泰安+选择压轴+初二
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=3,ON=5,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )
A. B.
【答案】A
【解析】解:作M关于OB的对称点M,作N关于OA的对称点N,如下图所示:
连接MN,即为MP+PQ+QM的最小值
根据轴对称的定义可知:ON△=ON=5, OM^'=OM=3,∠NOQ=∠M'OB=30°,
∴△ONN为等边三角形,△OMM'为等边三角形,
∴∠NOM=90°,
∴在Rt△MON中,
因此正确答案为:A.
【标注】 【知识点】最短路径问题
16.矩形+将军饮马造桥选址+两定两动——23济南模拟/22内江+填空压轴+初二
如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点, EFIBC,则AF+CE的最小值是 .
【答案】10
【解析】解:延长BC到G,使CG=EF,连接FG,
EF∥CG,EF=CG,
∴四边形EFGC是平行四边形,
∴CE=FG,
∴AF+CE=AF+FG,
∴当点A、F、G三点共线时, AF+CE的值最小为AG.
由勾股定理得
∴AF+CE的最小值为10,
因此正确答案为:10.
【标注】 【知识点】最短路径问题
17.等边三角形+中垂线+将军饮马+两定一动 -24大庆模拟+选择压轴+初二
如图,在等边△ABC中,点E是AC边的中点, 点P是△ABC的中线AD上的动点,且AD=6,则EP+CP的最小值是( )
A.12 B. 9 C. 6 D.3
【答案】C
【解析】
【分析】
要求EP+CP的最小值,需考虑通过作辅助线转化EP,CP的值,从而找出其最小值求解即可.
【详解】
解:作点E关于AD的对称点F,连接CF,
·△ABC是等边三角形,AD是BC边上的中线,
∴AD⊥BC,
∴AD是BC的垂直平分线,
∴点E关于AD的对应点为点F,
∴CF就是EP+CP的最小值.
∵△ABC是等边三角形,E是AC边的中点,
∴F是AB的中点,
∴CF是△ABC的中线,
∴CF=AD=6,
即EP+CP的最小值为6,
故选:C.
【点睛】
本题主要考查了轴对称-最短路线问题以及等边三角形的性质,熟练掌握等边三角形和轴对称的性质是解题的关键.
【标注】 【知识点】等边三角形的性质
18.矩形+中点+将军遛马+两定两动——23青岛模拟/22自贡+填空压轴+初二
如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 .
【答案】3
【解析】如图,作G关于AB的对称点G',在CD上截取CH=1,然后连接HG'交AB于E,在EB上截取EF=1,此时GE+CF的值最小,
∵OH=EF=1,CH∥EF,
∴四边形EFCH是平行四边形,
∴EH=CF,
∴G'H=EG'+EH=EG+CF,
∵AB=4,BC=AD=2,G为边AD的中点,
∴DG'=AD+AG'=2+1=3,DH=4-1=3,
由勾股定理得:
即GE+CF的最小值为3
故答案为:3
【标注】 【知识点】线段和的最小值
19.菱形+特殊角60°+对角线+将军饮马+两定一动——23丹东模拟/22黑龙江+填空压轴+初二
如图,菱形ABCD中,对角线AC,BD相交于点O,∠BAD=60°, AD=3,AH是∠BAC的平分线,CE⊥AH于点E,点P是直线AB上的一个动点,则OP+PE的最小值是 .
【答案】
【解析】如图,连接OE,作点O关于AB的对称点F,连接OF交AB于G,连接PE交直线AB于P ,连接PO,
则PO=PF,此时,PO+PE最小,最小值=EF,
∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC,OB=OD,AD=AB=3.
∵∠BAD=60°,
∴△ABD是等边三角形.
∴BD=AB=3,∠BAO=30°
∵点O和点F关于直线AB对称,
∴OF⊥AB,OF=2OG=OA=
中小学教育资源及组卷应用平台
∴∠AOG=60°.
∵CE⊥AH于E,OA=OC,
∴∠CAE=∠OEA,
:AH平分∠BAC,
∴∠CAE=15°
在Rt∠EOF中,由勾股定理,得
∴PO+PE的最小值为
故答案为:
【标注】【知识点】特殊平行四边形
20.特殊角+将军饮马+两定一动1———21黑龙江+选择压轴+初二
已知在Rt△ACB中,∠C=90°,∠ABC=75°,AB=5,点E为边AC上的动点,点F为边AB上的动点,则线段FE+EB的最小值是( )
B. C. D.
【答案】B
【解析】作F关于AC的对称点F',延长AF'、BC交于点B',连接BF'、BD.
FE+EB=BE+EF',
∴当B、E、F'共线且与AB'垂直时,长度最小,
即作BD⊥AB'于D,
在Rt△ABD中,
∴FE+EB的最小值为
故选B.
【标注】【知识点】线段和的最小值
21.圆+正方形+周长最小值+将军遛马+两动一定————23宁波模拟/21连云港+选择压轴+初二
如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是().
A.3 B.4 C.5 D.6
【答案】B
【解析】⊙O的面积为2π,则圆的半径为 则
由正方形的性质,可知点C是点A关于BD的对称点,
过点C作CA'//BD,且使CA'=1,
连接AA'交BD于点N,取NM =1,连接AM、CM,则点M、N为所求点,
A'C//MN,且A'C= MN,则四边形MCA'N为平行四边形,
则A'N=CM=AM,
故△AMN的周长=AM+AN+MN=AA'+1时取得最小值,
则
则△AMN的周长的最小值为3+1=4,
故选:B.
22.圆+将军饮马+两定一动——23宿迁模拟+填空压轴+初二
如图,在Rt△AOB中,∠AOB=90°,OA=4,OB=6,以点O为圆心,3为半径的⊙O,与OB交于点C,过点C作CD⊥OB交AB于点D ,点P是边OA上的动点,则PC+PD的最小值为 .
【答案】2
【解析】∵OB=6,OC=3,
∴点C为OB的中点,
∵OA⊥OB,CD⊥OB,
∴OA//CD,
延长CO与⊙O相交于C',连接C'D与OA相交于P,如图,
∴在Rt△C'CD中,
23.矩形+折叠模型+将军饮马+两定一动1 ———23深圳模拟/21盘锦+填空压轴+初二
如图,四边形ABCD为矩形, 点P为边AB上一点.以DP为折痕将△DAP翻折,点A的对应点为点A'.连结AA',AA'交PD于点M ,点Q为线段BC上一点,连结AQ,MQ,则AQ+MQ的最小值是
【答案】4
【解析】解:如下图所示,作点A关于BC的对称点T,取AD的中点R,连接BT, QT, RT, RM.
∵四边形ABCD是矩形,
∴∠RAT=90°,
∵A,A关于DP对称,
∴AA'⊥DP,
∴∠AMD=90°,
:AR=RD,
∵MT≥RT-RM,
∴M7的最小值为4
∵QA+QM=QT+QM≥MT,
∴QA+QM≥4
∴QA+QM的最小值为4
因此正确答案为:4
【标注】【知识点】特殊平行四边形
24.直角三角形+特殊角度+将军饮马+两定一动——23鄂州模拟/21西藏+选择压轴+初二
如图,在Rt△ABC中,∠A=30°,∠C=90°, AB=6,点P是线段AC上一动点,点M在线段AB上,当 AB时, PB+PM的最小值为()
A.3 B.2 C. 2 +2 D.3 +3
【答案】B
【解析】解:作B点关于AC的对称点B',连接B'M交AC于点P,
BP=B'P,
∴PB+PM=B'P+PM≥B'M,
∴PB+PM的最小值为B'M的长,
过点B'作B'H⊥AB于H点,
∵∠A=30°,∠C=90°,
∴∠CBA=60°,
:AB=6,
. BC=3,
∴BB'=6,
在Rt△BB'H中,
:AH=3,
∴AM=2,
∴MH=1,
在Rt△MHB'中,
∴PB+PM的最小值为2
故选:B.
25.正方形+隐形圆+将军饮马+点圆最值+两动一定——22无锡模拟/21鄂尔多斯+填空压轴+初三
如图,已知正方形ABCD的边长为6,点/是正方形内一点,连接CF,DF,且∠ADF=∠DCF,点E是AD边上一动点,连接EB,EF,则EB+EF长度的最小值为 .
【答案】
【解析】解:∵四边形ABCD是正方形,
∴∠ADC=90°,
∵∠ADF=∠DCF,
∴点R在以DC为直径的半圆上移动,
如下图所示,设CD的中点为O,作正方形ABCD关于直线AD对称的正方形APGD,则点B的对应点是P,
连接PO交AD于E,交半圆O于F,则线段FP的长即为BE+FE的长度最小值,OF=3,
∵∠G=90°,PG=DG=AB=6,
∴OG=9,
∴BE+FE的长度最小值为3
因此正确答案为:3
【标注】【知识点】轴对称应用
【知识点】圆心角和圆周角
【知识点】勾股定理
【知识点】正方形的性质
26.二次函数+将军遛马+两定两动22泰安模拟/21广元+代数综合压轴+初三
如图1,在平面直角坐标系xOy中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:
x ..+ -1 0 1 2 3 ...
y ++ 0 3 4 3 0 ..
(1)求出这条抛物线的解析式及顶点M的坐标.
(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求AQ+QP+PC的最小值.
【答案】
【解析】(1)由表格数据可知,顶点坐标为(1,4),
设抛物线解析式为:
将点(0,3)代入解析式得:3=a+4,
∴a=-1,
∴抛物线解析式为: 顶点坐标M(1,4).
(2) 由表格可知,抛物线经过点A(-1,0),C(0,3),
如图3,将A点向上平移一个单位,得到A'(-1,1),
则AA'//PQ,AA'=PQ,
∴四边形AA'PQ是平行四边形,
∴PA'=QA,
作A'关于MQ的对称点E ,则E(3,1),
∴PA'=PE,
∴AQ+QP+PC=PE+1+PC,
当P、B、C三点共线时,PE+PC最短,
设直线CE的解析式为:y= mx+n,
将C、E两点坐标代入解析式可得
∴直线CE的解析式为
令x=1,则
∴当P的坐标为 时, P、E、C三点共线,
此时 最短,
∴AQ+QP+PC的最小值为
【标注】 【知识点】二次函数与圆的综合问题
27.矩形+平行四边形存在性+线段差最大值+线段和最小值+将军饮马
——23无锡模拟+选择压轴+初三
如图,在矩形ABCD中,AB=15,BC=20,把边AB沿对角线BD平移,点A',B'分别对应点A,B.给出下列结论:
①顺次连接点A',B',C,D的图形是平行四边形;
②点C到它关于直线AA'的对称点的距离为48;
③A'C-B'C的最大值为15;
④A'C+B'C的最小值为9
其中正确结论的个数是( ).
A.1 B. 2 C.3 D.4
【答案】D
【解析】如图1,
∵AB=A'B',AB//A'B',AB=CD,AB//CD,
∴A'B'=CD,A'B'//CD,
∴四边形A'B'CD是平行四边形,故①正确,
作点C关于直线AA'的对称点E,连接CE交AA'于T,交BD于点O,则CE=4OC.
∵四边形ABCD是矩形,
∴EC=48,故②正确,
∵A'C-B'C≤A'B',
∴A'C-B'C≤15,
∴A'C-B'C的最大值为15,故③正确,
如图2,
∵B'C=A'D.
.. A'C+B'C=A'C+A'D,
作点D关于AA'的对称点D',
连接DD'交AA'于J,过点D'作D'E⊥CD交CD的延长线于E ,连接CD'交AA'于A',此时CB'+CA'的值最小,最小值=CD',
由△AJD∽△DAB,
可得
∴DJ=12,
注可得:
∴A'C+B'C的最小值为9 故④正确.,;
故选:D.
28.二次函数+将军遛马+两定两动+四边形周长最小值——22广州模拟/21遂宁+代数综合压轴+初三
如图,已知二次函数的图象与x轴交于A和B(-3,0)两点,与y轴交于C(0,-3),对称轴为直线x=-1,直线y=-2x+m经过点A,且与y轴交于点D,与抛物线交于点E,与对称轴交于点P.
(1)求抛物线的解析式和m的值.
(2) 直线y=1上有M、N两点(M在N的左侧) ,且MN=2,若将线段MN在直线y=1上平移,当它移动到某一位置时,四边形MEFN的周长会达到最小,请求出周长的最小值(结果保留根号).
【答案】
【解析】(1)∵抛物线的对称轴为直线x=-1, 与x轴的交点为A, B(-3,0),
. A(1,0),
∴可以设抛物线的解析式为y=a(x+3)(x-1),
把C(0,-3)代入得到,a=1,
∴抛物线的解析式为
直线y= - 2x+m经过点A(1,0),
∴0=-2+m,
∴m=2.
(2) ∵点E、F均为定点,
∴线段EF长为定值,
∴当EM+FN为最小值时,四边形MEFN的周长最小,
如图2,画出直线y=1,将点F向左平移2个单位得到F',作点E关于y=1的对称点E',连接E'F'与直线y=1交于点M ,过点F作FN//E'F', 交直线y=1于点N ,
由作图可知:EM=E'M,F'M=FN,
又∵E',M , F'三点共线,
此时,EM+FN的值最小,
∵点F为直线y=-2x+2与直线x=-1的交点,
∴F(-1,4),
∴F'(-3,4),
∵E(-5,12),
∴E'(-5,-10),
如图,延长FF'交线段EE'于点W,
∵FF'//直线y=1,
∴FW⊥EE', W(-5,4),
∵在Rt△EWF中,
由勾股定理得:
在Rt△E'WF'中,
∴四边形MEFN的周长最小值
=ME+FN+EF+MN
【标注】 【知识点】二次函数与动点问题
29.正方形+隐形圆+将军饮马+两定两动——23湖州模拟/20广西+选择压轴+初三
如图,动点M在边长为2的正方形ABCD内,且AM⊥BM,P是CD边上的一个动点,E是AD边的中点,则线段PE+PM的最小值为 ( )
A. -1 B. +1 C.
【答案】A
【解析】解答:解:作点E关于DC的对称点E',设AB的中点为点O,连接OE',交DC于点P,连接PE,如图:
∵动点M在边长为2的正方形ABCD内,且AM⊥BM,
∴点M在以AB为直径的圆上,
∵正方形ABCD的边长为2,∴AD=AB=2,∠DAB=90°,
∴E是AD的中点,
∵点E与点E'关于DC对称,
∴DE'=DE=1, PE=PE',
∴AE'=AD+DE'=2+1=3,
在Rt△AOE'中,
∴线段PE+PM的最小值为:
因此正确答案为:A.
【标注】 【知识点】勾股定理
【知识点】圆心角和圆周角
【知识点】有关公理-两点之间线段最短
【知识点】正方形的性质
30.等边三角形+中垂线+将军饮马+两定一动——22凉山模拟/21西宁+填空压轴+初二
如图,△ABC是等边三角形,AB=6,N是AB的中点,AD是BC边上的中线,M是AD上的一个动点,连接BM,MN,则BM+MN的最小值是 .
【答案】3
【解析】解:连接CN,与AD交于点M,连接BM.(根据两点之间线段最短;点到直线垂直距离最短) ,AD是BC边上的中线即C和B关于AD对称,则BM+MN=CN,则CN就是BM+MN的最小值.
∵△ABC是等边三角形, AB=6, N是AB的中点,
即BM+MN的最小值为3
因此正确答案为:3
【标注】【知识点】等腰三角形
31.坐标系+将军遛马+两定两动——22广州模拟/20荆门+选择压轴+初二
在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接AC、BD,则AC+BD的最小值为( )
A.2 C.6 D.3
【答案】B
【解析】如图,将线段AC沿x轴方向平移2个单位得到A'D,
则A'D=AC
作A'关于x轴的对称点A",连接A"B ,
则
∴AC+BD的最小值为A” B的长度.
过A"作A"E⊥y轴于E点,
在Rt△A"BE中,
BE=4+2=6,A"E=2,
即AC+BD的最小值为2
故选B.
【标注】 【知识点】直接用勾股求边长
32.坐标系+将军遛马+两定两动
1——23长沙模拟/21聊城+填空压轴+初二
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,O分别在x轴,y轴上,B,D两点坐标分别为B(-4,6),D(0,4),线段EF在边OA上移动,保持EF =3,当四边形BDEF的周长最小时,点E的坐标为 .
【答案】
【解析】在线段BC上取点M,使得BM=EF,作M点关于a轴的对称点N,连接EM, EN,MN,
∵四边形OABC是矩形,
∴BC∥OA,BC⊥OC,
∵EF=3,
. BM=EF=3.
∵BM∥EF,
∴四边形BFEM是平行四边形,
∴BF=ME,
·B点坐标为(-4,6), D点坐标为(0,4),
∵BM=3,
∴M点坐标为(-1,6),
∵M、N关于x轴对称,
∴N点坐标为(-1,-6), EM=EN,
∴当且仅当N,E ,D三点共线时,
四边形BDEF的周长取得最小值,
设直线DN的解析式为y= kx+b,
∴y=10x+4,
令y=0,10x+4=0,
解得
∴当四边形BDEF的周长最小时,
点E的坐标为
故答案为:
【标注】 【知识点】四边形周长最小
33.正方形+对角线+将军饮马+两定一动——21青海+填空压轴+初二
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为 .
【答案】10
【解析】根据题意,连接BN、BM,如图,
根据正方形的性质,点N在对角线AC上,
∴BN=DN,
∴DN+MN=BN+MN,
当B,N,M三点共线时,取最小值,
则BM就是所求DN+MN的最小值.
在Rt△BCM中,BC=8,CM=6.
根据勾股定理得: 即DN+MN的最小值为10.
【标注】 【知识点】线段和的最小值
34.正方形+多选+将军饮马+两定一动——21黄冈+填空压轴+初三
如图,正方形ABCD中,AB=1,连接AC,∠ACD的角平分线交AD于点E,在AB上截取AF=DE,连接DF,分别交CE,CA于点G ,H,点P是线段GC上的动点,PQ⊥AC于点Q ,连接PH 下列结论:①CE⊥DF;②DE+DC=AC;③EA= AH;④PH+PQ的最小值是 其中正确结论的序号是
【答案】①②④
【解析】在正方形ABCD中,
CD=AD,∠CDE=∠DAF=90°,
在△CDE与△DAF中,
∴△CDE≌△DAF(SAS),
∴∠DCE=∠ADF,
∴∠ADF+∠CDF=90°,
∴∠DGC=90°,
∴CE⊥DF,
∴①正确.
∵CE平分∠ACD,CE⊥DF,
∴CD=CH,
∵AB∥CD,
∴△AHF∽△CHD,
∴AH=AF,
∴DE+DC=AF+CH
=AH+CH
=AC.
∴②正确.
:CE平分∠ACD,
∴③错误.
过P作PQ'⊥CD.
∵CE平分∠ACD,
∴PH+PQ=PH+PQ',
当HQ'⊥CD时,
PH+PQ'最小,
艮
∴④正确.
∴综上①②④正确.
【标注】 【知识点】动点与特殊平行四边形问题
35.特殊角+三角形周长最小值+将军饮马+两动一定———22泰州模拟+选择压轴+初二
如图,∠AOB=60°,点P是∠AOB内的定点且 若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( ).
C. 6 D.3
【答案】D
【解析】作P点分别关于OA、OB的对称点C、D,
连接OD分别交OA、OB于M、N,如图,则OA、OB分别是线段PC、PD垂直平分线,
∴MP=MC,NP=ND,OP=OD=OC= ,∠BOP=∠BOD,
∠AOP=∠AOC,
∴PN+PM+MN=ND+MN+NC=DC
∠COD=∠BOP+∠BOD+∠AOP+∠AOC
=2∠AOB=120°.
利用两点之间线段最短,即△PMN的周长围为线段DC的长度,
∵两点之间线段的距离最小,
∴此时△PMN周长最小,
作OH⊥CD于H,则CH = DH,
∴OD=2CH=3.
故选D.
【标注】【知识点】三角形周长最小
36.菱形+特殊角度+将军饮马+两定一动
———20广西+填空压轴+初二
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=6 ,BD=6,,点P是AC上一动点,点E是AB的中点,则PD+PE的最小值为 .
【答案】3
【解析】如下图所示,连接DE,
∵四边形ABCD是菱形,对角线AC,BD相交于点O, AC=6 ,BD=6,
AB=AD=BD,即△ABD是等边三角形,
又∵E是AB的中点,
. DE⊥AB,
∵DP+PE≥DE,
∴PD+PE的最小值为DE的长.
即PD+PE的最小值为3
因此正确答案为:3
【标注】 【知识点】特殊平行四边形
37.扇形+阴影面积+周长最小值+将军饮马+两定一动———22南通模拟/20河南+填空压轴+初三
如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交BC于点D ,点E为半径OB上一动点若OB=2,则阴影部分周长的最小值为 .
【答案】
【解析】作点D关于OB的对称点D',再连接CD'与OB的交点即为点E,
此时阴影部分周长最小,最后再连接OD',
∵∠BOC=60°且OD平分∠BOC,
∵OB=2,
∵点D与D'关于OB轴对称,
∴∠BOD'=∠BOD=30°,OD'=OD, DE=D'E,
∴CE+DE的最小值=CD'=2
∴阴影部分周长的最小值为(
【标注】 【知识点】与圆有关的不规则图形的周长与面积计算
38.坐标系+三角形周长最小值+特殊角度+将军饮马+两动一定21武威模拟/20永州+填空压轴+初二
∠AOB在平面直角坐标系中的位置如图所示,且∠AOB=60°,在∠AOB内有一点P(4,3), M、N分别是OA,OB边上的动点,连接PM,PN,MN,则△PMN周长的最小值是 .
【答案】5
【解析】分别作点P关于OA,OB的对称点P ,P ,连接P P 交OA于点M ,交OB于点N,连接OP ,OP ,OP,
则OP =OP=OP ,∠P OA=∠POA,∠POB=∠P OB,
∴PM=P M,PN=P N,
则△PMN的周长最小值为P P 的长度,
过点O作OQ⊥P P 于点Q,
∵P点坐标为(4,3),
∴OP=5,
∵∠POA=∠P OA,∠P OB=∠POB,∠POA+∠POB=∠AOB=60°,
又:
在Rt△OP Q中,
在等腰三角形OP P 中,OQ为P P 边上的高线,
即△PMN周长最小值为5
故答案为:5
【标注】【知识点】轴对称的性质
39.等边三角形+点线最值+特殊角度———20营口+填空压轴+初二
如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为 .
【答案】3
【解析】如图所示,过点O作ON⊥AB于点N,交AD于点M,
∵点E为AD上的动点,点F为AB上的动点,
.当点E与点M重合,点F与点N重合时,CE+EF取最小值ON.
∵△ABC为等边三角形,边长为6,
∴BO=6,∠B=60°,
Rt△CBN中,
故CE+EF的最小值为(
故答案为:3
【标注】 【知识点】等边三角形的性质
【能力】推理论证能力
40.矩形+特殊角度+将军饮马+两定一动
11 ——22成都模拟/20内江+填空压轴+初三
如图,在矩形ABCD中, BC=10,∠ABD=30°,若点M、N分别是线段DB、AB上的两个动点,则AM+MN的最小值为 .
【答案】15
【解析】如图,过A作AG⊥BD于G.延长AG,使AG=EG.过E作EN⊥AB于N,交BD于M,
则AM+MN=EN最短,
∵四边形ABCD为矩形,BC=10,∠ABD=30°,
.. AD=10,BD=20,AB=BD·cos30°=10
∵AG·BD=AD·AB,
∴20AG=10×10
∴AG=5 ,AE=2AG=10
∵AE⊥BD,EN⊥AB,∠EMG=∠BMN,
∴∠E=∠ABD=30°,
∴AM+MN=15,
即AM+MN的最小值为15.
故答案为:15.
【标注】【知识点】矩形的性质
【能力】推理论证能力
41.正方形+平移+将军饮马+两定两动
———20黑龙江+填空压轴+初二
如图,在边长为4的正方形ABCD中将△ABD沿射线BD平移,得到△EGF,连接EC、GC,则EC+GC的最小值为
【答案】4
【解析】如图,将△ABC沿射线CA平移到△AB'C'的位置,连接C'E、AE、DE.
:AB//GE//DC且AB=GE=DC,
∴四边形ABGE和四边形EGCD均为平行四边形,
∴AE∥BG,CG=DE,
∴AE⊥OO'
由作图易得,点C与点C'关于AE对称,C'E=CE.
又∵CG=DE,
∴EC+GC=C'E+ED,
当点C'、E、D在同一直线上时,C'E+ED的值最小,
此时,在Rt△C'DB'中,
即EC+GC的最小值为4
故答案为:4
【标注】[知识点】线段和的最小值
42.坐标系+四边形周长最小值+将军饮马+两定一动 ---20聊城+填空压轴+初二
如图,在直角坐标系中,点A(1,1),B(3,3)是第一象限角平分线上的两点,点C的纵坐标为1,且CA=CB,在y轴上取一点D ,连接AC,BO,AD,BD,使得四边形ACBD的周长最小,这个最小周长的值为 .
【答案】
【解析】由点A与点C的纵坐标均为1,可知AC//x轴,
又因为点A,B是第一象限角平分线上的两点,
则AC-BC=2.
如图,作点A关于y轴的对称点E,连接BE交y轴于点D,
此时AD+BD的值愿小,为线段BE的长.由轴对称性可知AB=2,则EC=4,
在Rt△BCE中,根据勾股定理,得 ∴四边形ACBD的最小周长为
【标注】【知识点】轴对称的性质
43.坐标系+将军遛马+两定两动———20辽宁+填空压轴+初三
如图,在平面直角坐标系中,已知A(3,6), B(-2,2),在x轴上取两点C,D(点C在点D的左侧),且始终保持CD=1,线段CD在x轴上平移,当AD+BC的值最小时,点C的坐标为 .
【答案】(-1,0)
【解析】把A(3,6)向左平移1得A'(2,6),
作点B关于x轴的对称点B',连接B'A'交x轴于C,在x轴上取点D(点C在点D的左侧),使CD=1,连接AD,
则AD+BC的值最小,
∵B(-2,2),
∵. B'(-2,-2),
设直线B'A'的解析式为y= kx+b,
解得:
∴直线H'A'的解析式为y =2x+2,
当y=0时,x=-1,
∴C(-1,0),
故答案为:(-1,0).
【标注】 【知识点】坐标轴上点的坐标特征
同课章节目录
