专题二 胡不归最值模型(含答案) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题二 胡不归最值模型(含答案) 2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 494.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 16:16:40 | ||
图片预览


文档简介
胡不归最值模型
知识回顾
1. “胡不归”问题
我们学过将军饮马模型,知道怎么求解PA+PB的最小值,但是有时候还会见到下面这种,即“PB+nPA”最小值问题(n≠1),这是近几年考试热点也是难点,本讲内容主要来研究这个问题.
从前,有一个小伙子在外地当学徒,当他获悉老父亲病危后,便立即启程赶路.由于他只考虑了两点之间线段最短的原理,所以选择了全是砂砾地带的直线路径A →B (如图所示),而忽视了走折线虽然路程多但速度快的情况,当他到家时,老人刚咽气.老人弥留之际不断念叨着“胡不归 胡不归 何以归” .这个传说,引起思考,能否提前到家 应该选择一条怎样的路线呢 这就是的“胡不归”问题.
将问题简化:在直线AC上有一个动点P ,点B是直线外一点 ,求 的最小值.
特点:①两定一动 . A、B是两个定点,点P是一个动点.②动点P在直线上运动.
“胡不归”问题总结
由构造 可知,我们构造的直角三角形中, 所以在解决 这类问题时,我们只需要构造一个含∠A的Rt△APH , 使得 即可.
3、特殊情况:如果n值大于1,则要先提取n,再进行求解.
如:PA+3PB转为求 转为求
品真题精炼
1.二次函数+胡不归最大值+两动一定——24重庆+代数综合压轴+初三
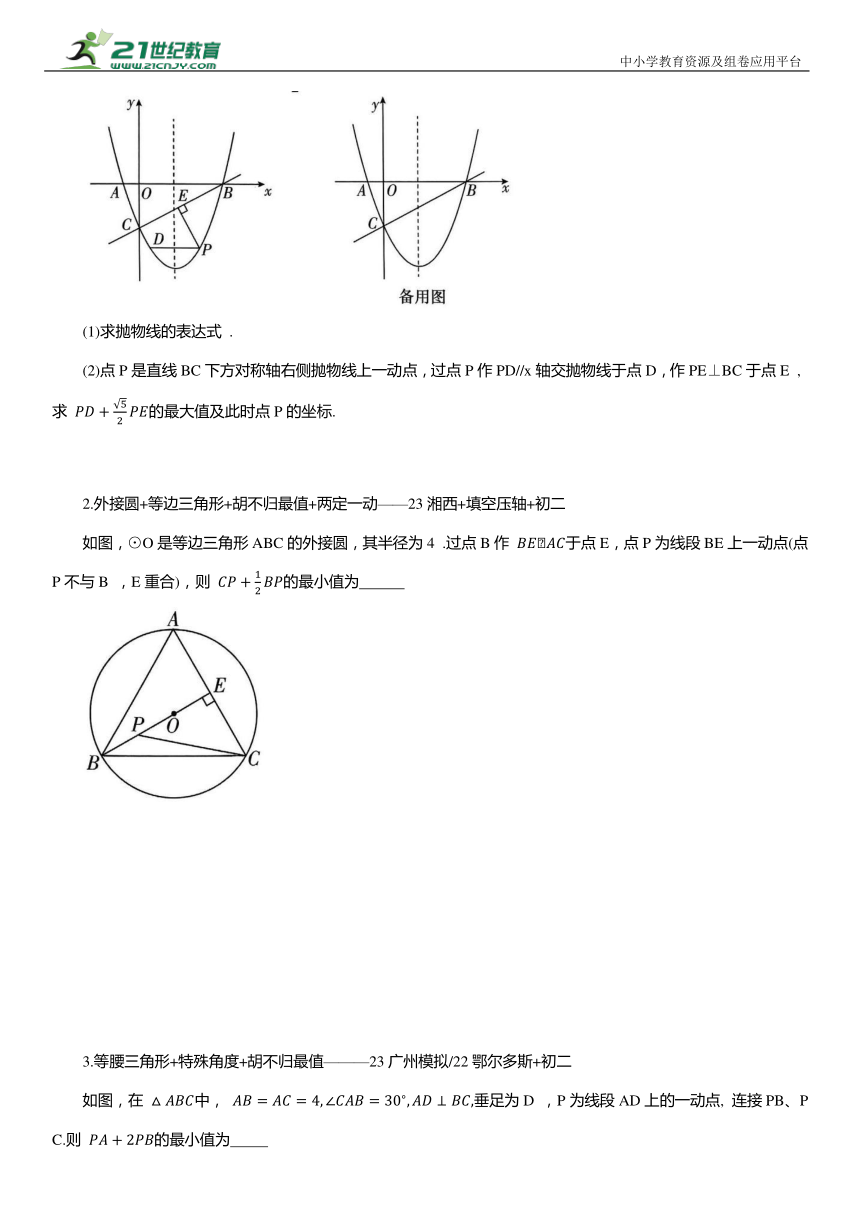
如图,在平面直角坐标系中,抛物线 与x轴交于 B两点,交y轴于点C,抛物线的对称轴是直线
(1)求抛物线的表达式 .
(2)点P是直线BC下方对称轴右侧抛物线上一动点,过点P作PD//x轴交抛物线于点D,作PE⊥BC于点E , 求 的最大值及此时点P的坐标.
2.外接圆+等边三角形+胡不归最值+两定一动——23湘西+填空压轴+初二
如图,⊙O是等边三角形ABC的外接圆,其半径为4 .过点B作 于点E,点P为线段BE上一动点(点P不与B ,E重合),则 的最小值为
3.等腰三角形+特殊角度+胡不归最值———23广州模拟/22鄂尔多斯+初二
如图,在 中, 垂足为D ,P为线段AD上的一动点, 连接PB、PC.则 的最小值为
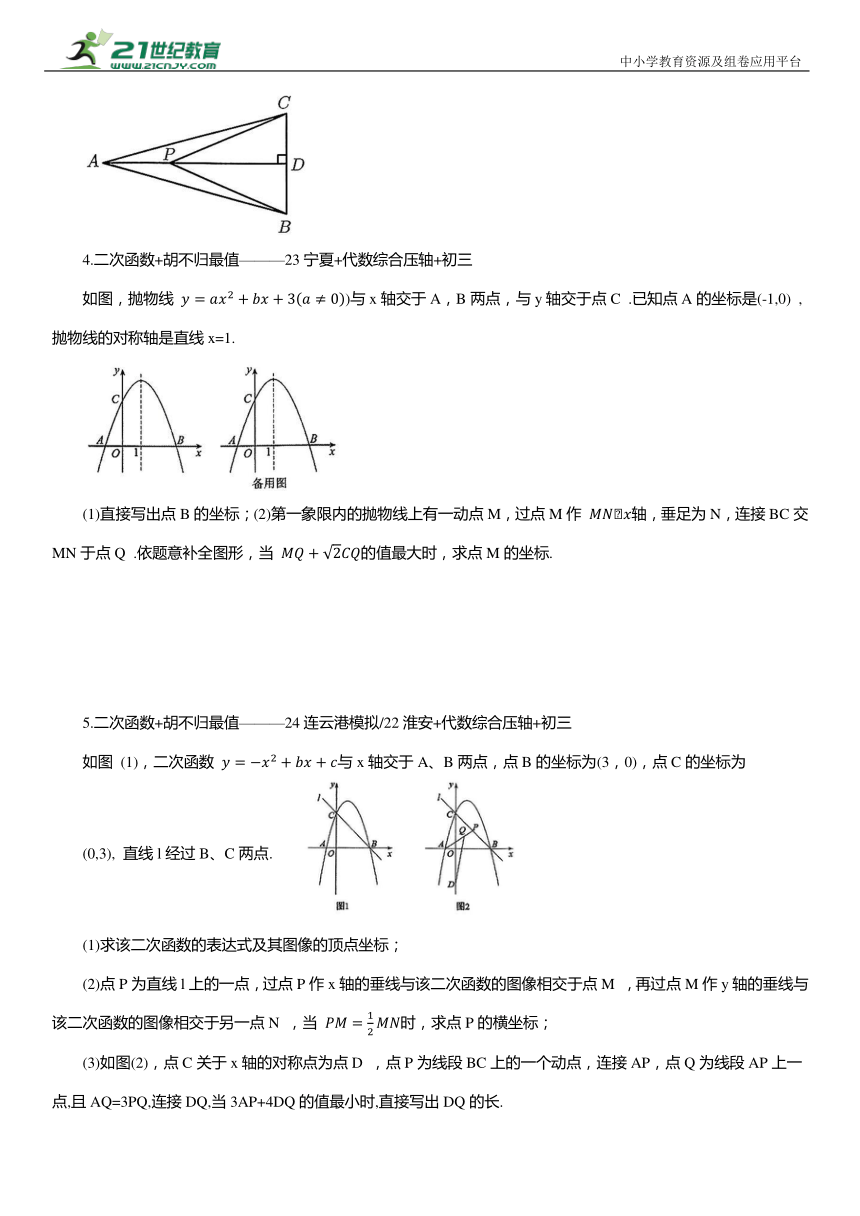
4.二次函数+胡不归最值———23宁夏+代数综合压轴+初三
如图,抛物线 )与x轴交于A,B两点,与y轴交于点C .已知点A的坐标是(-1,0) ,抛物线的对称轴是直线x=1.
(1)直接写出点B的坐标;(2)第一象限内的抛物线上有一动点M,过点M作 轴,垂足为N,连接BC交MN于点Q .依题意补全图形,当 的值最大时,求点M的坐标.
5.二次函数+胡不归最值———24连云港模拟/22淮安+代数综合压轴+初三
如图 (1),二次函数 与x轴交于A、B两点,点B的坐标为(3,0),点C的坐标为
(0,3), 直线l经过B、C两点.
(1)求该二次函数的表达式及其图像的顶点坐标;
(2)点P为直线l上的一点,过点P作x轴的垂线与该二次函数的图像相交于点M ,再过点M作y轴的垂线与该二次函数的图像相交于另一点N ,当 时,求点P的横坐标;
(3)如图(2),点C关于x轴的对称点为点D ,点P为线段BC上的一个动点,连接AP,点Q为线段AP上一点,且AQ=3PQ,连接DQ,当3AP+4DQ的值最小时,直接写出DQ的长.
6.胡不归最值+锐角三角函数+点线最值———22长春模拟/21郴州+填空压轴+初三如图,在△ABC中, 交AC于点D .点P为线段BD上的动点,则 的最小值为
7.胡不归最值+锐角三角函数+点线最值——22四川模拟+填空压轴+初三如图,△ABC中,AB=AC=10,tanA=3,CD⊥AB于点D ,点E是线段CD的一个动点,则 的最小值是 .
8.二次函数+四边形+胡不归最值+平移————22宜宾+代数综合压轴+初三
如图 c与x轴交于A(3,0)、B(-1,0)两点,与y轴交于点C(0,3), 其顶点为点D, 连结AC.
求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E ,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标;(3)在(2)的条件下,将点D向下平移5个单位得到点M,点P为抛物线的对称轴上一动点,求 的最小值.
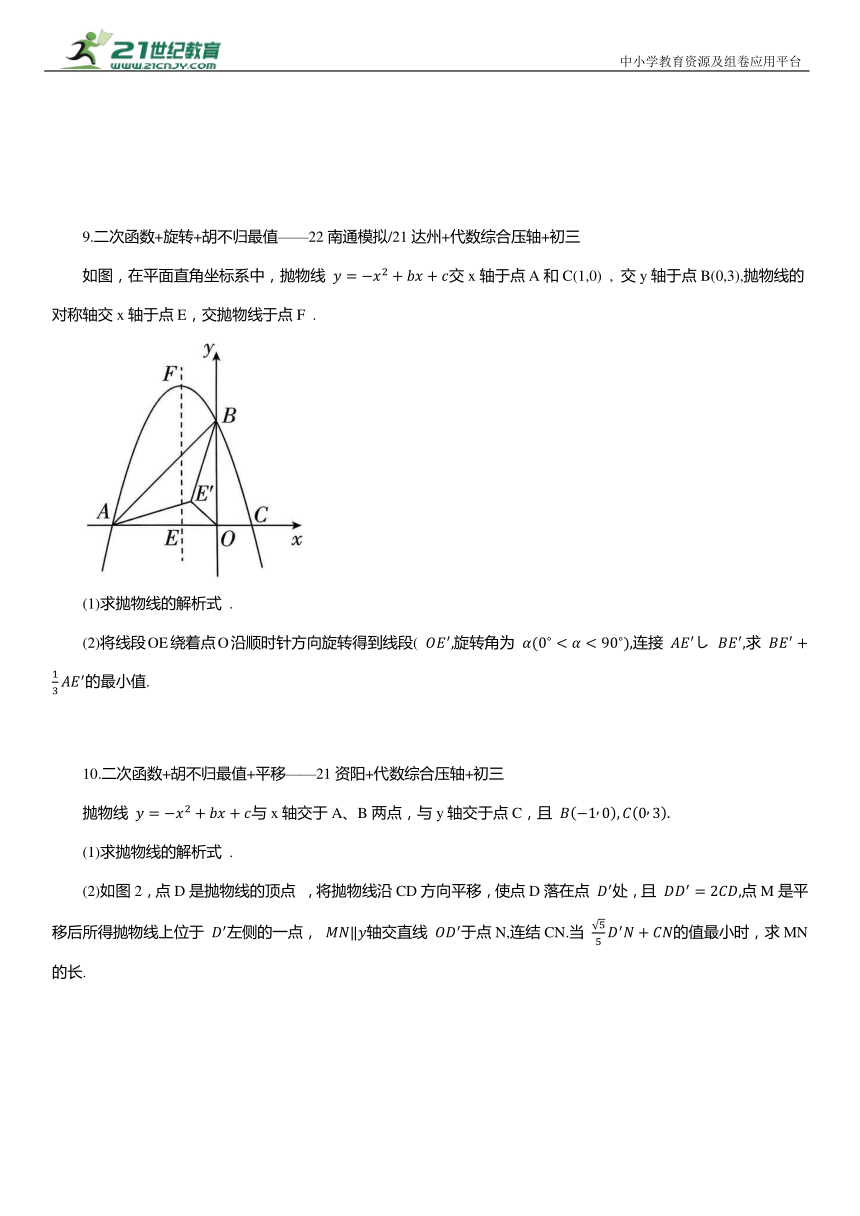
9.二次函数+旋转+胡不归最值——22南通模拟/21达州+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 交x轴于点A和C(1,0) , 交y轴于点B(0,3),抛物线的对称轴交x轴于点E,交抛物线于点F .
(1)求抛物线的解析式 .
(2)将线段OE绕着点O沿顺时针方向旋转得到线段( 旋转角为 连接 し 求 的最小值.
10.二次函数+胡不归最值+平移——21资阳+代数综合压轴+初三
抛物线 与x轴交于A、B两点,与y轴交于点C,且
(1)求抛物线的解析式 .
(2)如图2,点D是抛物线的顶点 ,将抛物线沿CD方向平移,使点D落在点 处,且 点M是平移后所得抛物线上位于 左侧的一点, 轴交直线 于点N,连结CN.当 的值最小时,求MN的长.
11.菱形+对角线+胡不归+点线最值——22天津模拟+填空压轴+初三
如图, 在菱形ABCD中,. ,对角线AC、BD相交于点O,点M在线段AC上,且 点P为线段BD上的一个动点,则 的最小值是 .
12.直角三角形+特殊角度+胡不归最值——22四川模拟/20新疆+填空压轴+初二如图, 在△ABC中, ,若D是BC边上的动点 , 则2AD+DC的 最小值为 .
13.等腰三角形+锐角三角函数+胡不归最值——22芜湖模拟+填空压轴+初三如图,在△ABC中, AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点 ,则 的最小值是( )
D.10
14.平行四边形+特殊角度+胡不归最值——22徐州模拟+填空压轴+初三如图,在平行四边形ABCD中, ,P为边CD上的一动点,则 的最小值等于 .
15.圆+特殊角度+胡不归最值——21台州模拟+选择压轴+初三
如图,AB是⊙O的直径,AB =2 ,点C是圆上一点,且 点P是AB上的动点,则 的最小值为( )
A. 1 B. D.2
16.二次函数+平移+胡不归最小值———23广元模拟+代数综合压轴+初三
在平面直角坐标系中,将二次函数 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧), 经过点A的一次函数y = kx+b(k≠0)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D, 的面积为5 .
(1)求抛物线和一次函数的解析式.
(2)抛物线上的动点E在一次函数的图象下方,求 面积的最大值,并求出此时点E的坐标.
(3)若点P为x轴上任意一点,在(2)的结论下,求 的最小值.
17.等腰三角形+锐角三角函数+线段和差+胡不归最值——22成都模拟+填空压轴+初三如图,在等腰三角形ABC中, BD为高, M , N分别是BD , CD上的动点,若 E是AB的中点, 连接EM , MN, 则 的最小值为 .
18.菱形+对角线+特殊角度+胡不归最值——22山西模拟+填空压轴+初三
如图,已知菱形ABCD的面积为 ,对角线AC、BD交于点O,若点P为对角线AC上一点,则 的最小值是 .
1.二次函数+胡不归最大值+两动一定::1———24重庆+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线y 与x轴交于A(-1,0), B两点, 交y轴于点C,抛物线的对称轴是直线
(1)求抛物线的表达式.
(2)点P是直线BC下方对称轴右侧抛物线上一动点,过点P作PD//x轴交抛物线于点D,作PE⊥BC于点E,求 的最大值及此时点P的坐标.
【答案】
(2)最大值为 ,P(5,-3)
【解析】(1)∵抛物线 与x轴交于A(-1,0), B两点, 交y轴于点C,抛物线的对称轴是直线x
解得
∴抛物线的表达式为
(2)如图,延长PE交x轴于G,过P作PH//y轴于H,
在 3中,令y=0得
解得:z =-1,x =6,
∴B(6,0),
当x=0时,y=-3,
∴C(0,-3),
∴sin
∵PD//x轴,
∴∠PHE=∠BCO,
∴si
由B(6,0),C(0,-3)得直线BC为
设 则H
∵抛物线 的对称轴为直线
∴当 PE取得最大值,最大值为 ,此时 P(5,-3).
【标注】 【知识点】二次函数与几何最值问题
2外接圆+等边三角形+胡不归最值÷两定一动l ——23湘西+填空压轴+初二
如图,⊙O是等边三角形ABC的外接圆,其半径为4 .过点B作BE⊥AC于点E ,点P为线段BE上一动点(点P不与B,E重合),则 的最小值为 .
【答案】6
【解析】如图所示,过点P作PD⊥AB,连接CO并延长交AB于点F,连接AO,
∵△ABC是等边三角形, BE⊥AC,
∵⊙O是等边三角形ABC的外接圆,其半径为4,
∴OA=OB=4,OF⊥AB,
∵BE⊥AC,
∴BE=BO+EO=6,
∵PD⊥AB,∠ABE=30°,
BP的最小值为CF的长度,
∵△ABC是等边三角形,BE⊥AC,CF⊥AB,
∴CF=BE=6,
BP的最小值为6.
故答案为:6.
【标注】 【知识点】30°特殊角的性质应用
【知识点】勾股定理
【知识点】正多边形与圆
【知识点】三角形的外接圆
3.等最三角形+特殊角度+胡不归最值——23广州模拟/22鄂尔多斯+初二
如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
【答案】4
【解析】如图,
在∠BAC的外部作∠CAE=15°,作BF⊥AE于F,交AD于P,
此时PA+2PB最小,
∵BF⊥AE,
∴∠AFB=90°
∵AB=AC,AD⊥BC,
∴∠EAD=∠CAE+∠CAD=30°.
∵C(0,3),
∴3=-3a,
∴a=-1,
设]
则:N(m,0),
由(2)知:直线BC:y=-x+3,
∴Q(m -m+3),
∵C(0,3),B(3,0),
∴OC=OB=3,BN=3-m,
∴当 时, 有最大值,
此时.
【标注】 【知识点】二次函数
4.二次函数+胡不归最值——24连云港模拟/22淮安+代数综合压轴+初三
如图(1),二次函数 c的图像与x轴交于A、B两点,与y轴交于C点,点B的坐标
为(3,0),点C的坐标为(0,3),直线l经过B、C两点.
在Rt△ABF中,AB=4,∠BAF=∠BAC+∠CAE=45°,
故答案为:4
【标注】【知识点】最短路径问题
5.二次函数。胡不归最值——23宁夏+代数综合压轴+初三
如图,抛物线 与x轴交于A,B两点,与y轴交于点C .已知点A的坐标是(-1,0) ,抛物线的对称轴是直线x=1.
(1)直接写出点B的坐标;(2)第一象限内的抛物线上有一动点M ,过点M作MN⊥α轴,垂足为N连接BC交MN于点Q .依题意补全图形,当 的值最大时,求点M的坐标.
【答案】
【解析】(1)解:∵点A(-1,0)关于对称轴的对称点为点B,对称轴为直线x=1,∴点B为(3,0);
(2)过点M作MN⊥x轴,垂足为N,连接BC交MN于点Q ,如图所示,
∵A(-1,0),B(3,0),
设抛物线的解析式为:y=a(x+1)(x-3),
(1)求该二次函数的表达式及其图像的顶点坐标;
(2)点P为直线l上的一点,过点P作x轴的垂线与该二次函数的图像相交于点M ,再过点M作y轴的垂线与该二次函数的图像相交于另一点N,当 时,求点P的横坐标;
(3)如图(2),点C关于x轴的对称点为点D ,点P为线段BC上的一个动点,连接AP,点Q为线段AP上一点,且AQ=3PQ,连接DQ,当3AP +4DQ的值最小时,直接写出DQ的长.
【答案】 顶点坐标(1,4)
(2) P点横坐标为1+
【解析】(1) (1)解:将点B(3,0),C(0,3)代.顶点坐标(1,4); .
(2)解:设直线BC的解析式为 解得设P(t,-t+3),则A ∴t -3t= (2-2t)或 当 时,整理得 解得 当 时,整理得( 解得e ∴P点横坐标为
(3) 解:∵C(0,3), D点与C点关于x轴对称,∴D(0,-3),令y=0,则 解得x=-1或x=3,∴A(-1,0),∴AB=4,∵AQ=3PQ ,∴Q点在平行于BC的线段上,设此线段与x轴的交点为G,. AG=3,∴G(2,0),∵OB=OC,∴∠OBC=45°,作A点关于CQ的对称点A',连接AD与AP交于点Q,
. AQ=A'Q,∴AQ+DQ=A'Q+DQ≥A'D,∴
∠QGA=∠CBO=45°,AA'⊥QG,∴∠A'AG=45°,∵AG=A'G,∴
∠AA'G=45°,∴∠AGA'=90°,∴A'(2,3), 设直线DA'的解析式为y= kx+b,∴
解得 同理可求直线QG的解析式为y=-x+2
,联立方程组 解得
【标注】 【知识点】二次函数解析式
【知识点】二次函数的其他实际问题
【知识点】二次函数 的对称轴
【知识点】平行线分线段成比例定理
【业务题型】运算题
6.胡不归最值+锐角三角函数+点线最值——22长春模拟/21郴州+填空压轴+初三
如图,在△ABC中,AB=5,AC=4,sinA= BD⊥AC交AC于点D .点P为线段BD上的动点,则 PB的最小值为
【答案】
【解析】过点P作PE⊥AB于点E,过点C作CH⊥AB于点H,
∵BD⊥AC,
∴∠ADB=90°,
∴BD=4,
由勾股定理得
即点C,P,E三点共线时, PB最小,
PB的最小值为CH的长,
∴4×4=5×CH,
PB的最小值为
故答案为:
【标注】 【知识点】最短路径问题
7.胡不归最值+锐角三角函数+点线最值——22四川模拟+填空压轴+初三
如图,△ABC中,AB=AC=10,tanA=3,CD⊥AB于点D ,点E是线段CD的一个动点,则 E的最小值是 .
中小学教育资源及组卷应用平台
【答案】3
【解析】
【分析】
作EG⊥AC于G, BH⊥AC于H,由 设AD=a, CD=3a,利用勾股定理构建方程求出a,再证明 推出 由垂线段最短即可解决问题.
【详解】
解:如图,作EG⊥AC于G, BH⊥AC于H,
∵CD⊥AB,
设AD=a,CD=3a,
则有:
(舍),
∵AB=AC,CD⊥AB, BH⊥AC,
∵∠ECG=∠ACD,∠CGE=∠CDA,
∴BE+EG≥BH,
EC的最小值为3
故答案为:
【点睛】
本题考查解直角三角形,等腰三角形的性质,垂线段最短等知识,解题的关键是学会添加常用辅助线,用转化的思想思考问题,属于中考常考题型、
【标注】【知识点】解直角三角形的定义及常见类型
【知识点】等腰三角形的性质-等边对等角
【知识点】垂线段最短
8.二次函数+四边形+胡不归最值+平移——22宜宾+代数综合压轴+初三
如图,抛物线 c与x轴交于A(3,0)、B(-1,0)两点,与y轴交于点C(0,3),其顶点为点D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标;
(3)在(2)的条件下,将点D向下平移5个单位得到点M,点P为抛物线的对称轴上一动点,求 的最小值.
【答案】 顶点D的坐标为(1,4)
(2)F(-2,-5)或F(4,-5)
(3)
【解析】
(1)解:∵抛物线 c经过点A(3,0), B(-1,0),C(0,3),
解得:
∴抛物线的解析式为:
∴顶点D的坐标为(1,4);
(2)解:设直线AC的解析式为:y= kx+b,
把点A(3,0),C(0,3)代入得:k=-1,b=3,
∴直线AC解析式为:y=-x+3,
过点/作FG⊥DE于点G,
∵以A、C、E、A四点为顶点的四边形是以AC为边的平行四边形,
∴AC∥EF,AC=EF,
又∵OA∥FG,
..∠OAC=∠GFE
∴△OAC≌△GFE,
∴OA=GF=3,
设F点的坐标为
则G点的坐标为
∴FG=|m-1|=3,
∴m=-2或m=4,当m=-2时,
∴F (-2,-5),
当m=4时,
∴F (4,-5),
∴F(-2,-5)或F(4,-5);
(3)解:通过题意,得点M的坐标为(1,-1),
通过题意知: 点F (4,-5)与点F (-2,-5)关于对称轴x=1对称,
连结F F ,对称轴于点H,连结F M、F M ,过点F 作F N⊥F M于点N,交对称轴于点P,则MH=4,HF =3,MF =5.
在Rt△MHF 中, 则在Rt△MPN中,
又∵PF =PF
为最小值,
又1
∴求得 的最小值为
【标注】 【知识点】二次函数与特殊平行四边形
【知识点】二次函数与平行四边形
【知识点】二次函数解析式
【知识点】二次函数的其他实际问题
【知识点】解直角三角形的定义及常见类型
【业务题型】运算题
9二次函数+旋转+胡不归最值————22南通模拟/21达州+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 c交x轴于点A和C(1,0), 交y轴于点B(0,3)抛物线的对称轴交a轴于点E ,交抛物线于点F.
(1)求抛物线的解析式.
(2)将线段OE绕着点O沿顺时针方向旋转得到线段OE',旋转角为( 连接AE',BE',求 的最小值.
【答案】
【解析】(1)∵y=-x + bx+c过C(1,0), B(0,3),
∴b=-2,c=3,
∴抛物线的解析式为
(2)在OE上取一点D ,使得 连接DE',BD,
对称轴2
∴ 3,
∴△DOE'∽△E'OA,
当B,E', D三点在同一点直线上时, BE'+DE'最小为BD.
在Rt△BOD中,
最小值为
【标注】 【知识点】二次函数与相似三角形结合
10.抛物线3 与x轴交于A、B两点,与y轴交于点C,且B(-1,0), C(0,3).
(1)求抛物线的解析式.
(2)如图2,点D是抛物线的顶点,将抛物线沿CD方向平移,使点D落在点D'处,且DD'=2CD,点M是平移后所得抛物线上位于D'左侧的一点,MN//y轴交直线OD'于点N,连结ON.当 的值最小时,求MN的长.
【答案】
【解析】
(2) ∵D为顶点,
∴D(1,4),
由题
∴D'(3,6).
∵VOD'=2x,
过D'作y轴平行线l,过N作NP⊥D'P,
在Rt△NPD'中,
当CP'⊥l时 取最小值,
最小值为3,
yN= yc=3,
【标注】 【知识点】二次函数与轴对称问题
11.菱形+对角线+胡不归+点线最值——22天津模拟+填空压轴+初三
如图,在菱形ABCD中, AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则 PB的最小值是
【答案】
【解析】易知△ABC与△ACD为正三角形, 边长为10.
过P作PQ⊥BC交BC于Q ,过点M作MN⊥BC于点N.
显然M,P,Q三点共线时最小,即为MN的长,
∠MCQ=60°,MC=AC-AM=10-3=7,
即 B最小为
12..直角三角形+特殊角度+胡不归最值
——22四川模拟/20新疆+填空压轴+初二
如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为 .
【答案】6
【解析】如图所示,作点A关于BC的对称点A',连接AA',A'D,过点D作DE⊥AC于点E,AA'交BC于点H,
∵△ABC中,∠BAC=90°,∠B=60°,AB=2,
∴BH=1,AH= ,AA'=2 ,∠C=30°,
∴Rt△CDE中, 即2DE=CD,
∵A与A'关于BC对称,
∴AD=A'D,
∴AD+DE=A'D+DE,
∴当A',D , E在同一直线上时, AD+DE的最小值等于A'E的长,
此时,Rt△AA'E中,
∵AD+DE的最小值为3,
即2AD+CD的最小值为6.
故答案为:6.
【标注】 【知识点】轴对称的性质
【能力】推理论证能力
13..等腰三角形+锐角三角函数+胡不归最值——22芜湖模拟+填空压轴+初三
如图,在△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则 的最小值是( )
A.2 B.4 C.5 D.10
【答案】B
【解析】方法一:在Rt△ABE中
∴AE:BE:AB=1:2:
如图,过D作DF⊥AB,垂足为F,
在Rt△BDF中,
如图,过C作CG⊥AB,垂足为G,
故选B.
方法二:如图,作DH⊥AB于H,CM⊥AB于M.
∵BE⊥AO,
∴设AE=a,BE=2a,
则有
∴a=2 或-2 (舍去) ,
∵AB=AC,BE⊥AC,CM⊥AB,
等腰三角形两腰上的高相等),
∵∠DBH=∠ABE,∠BHD=∠BEA,
BD的最小值为4
故选B.
【标注】【知识点】胡不归问题
14..平行四边形+特殊角度+胡不归最值——22徐州模拟+填空压轴+初三
如图,在平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于 .
【答案】3
【解析】
过点P作PF⊥AD,交AD延长线于点F,
过点B作BE⊥AD ,交AD延长线于点E,
在Rt△AEB中,
∵∠DAB=60°,AB=6,
又∵AD=BC=2,
∴AE>AD,
∴E在AD的延长线上.
在Rt△PFD中,
∵∠PDF=∠DAB=60°,
易知当B、P、F三点共线时PB+PF取最小值,
即 的最小值为
故答案为:3
【标注】【知识点】胡不归问题
15.圆+特殊角度+胡不归最值
——21台州模拟+选择压轴+初三
如图,AB是⊙O的直径,AB=2,点C是圆上一点,且∠BAC=30°,点P是AB上的动点,则 AP的最小值为( ).
A.1 B. C. D.2
【答案】B
【解析】作∠BAD=30°,过P作PH⊥AD于H,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,AB=2,
∵PH⊥AD,
∴∠PHA=90°,
∵∠DAB=30°,
∴当且仅当C、P、H三点共线且CH⊥AD时, 取得最小值.
∵∠CAD=∠BAC+∠BAD=60°,
的最小值为
故选B.
【标注】 【知识点】胡不归问题
16..二次函数+平移+胡不归最小值——23广元模拟+代数综合压轴+初三
在平面直角坐标系中,将二次函数 )的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与a轴交于点A、B(点A在点B的左侧),OA =1,经过点A的一次函数y=kx+b(k≠0)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)求抛物线和一次函数的解析式.
(2)抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E的坐标.
(3)若点P为x轴上任意一点,在(2)的结论下,求 A的最小值.
【答案】(1)见解析
(2)见解析
(3)见解析
【解析】(1)解:将二次函数 )的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
∵OA=1,
∴点A的坐标为(-1,0),代入抛物线的解析式得,4a-2=0,
∴抛物线的解析式为 即
令y=0,解得<
∴B(3,0),
∴AB=OA+OB=4,
∵△ABD的面积为5,
代入抛物线解析式得
解得x =-2,z =4,
设直线AD的解析式为y= kx+b,
解得:
∴直线AD的解析式为
(2)过点E作EM//v轴交AD于M,如图,设E 则
∴当 时,△ACE的面积有最大值,最大值是 ,此时E点坐标为
(3)作点E关于x轴的对称点F,连接EF交x轴于点G,过点F作FH⊥AE于点H ,交x轴于点P,
∵∠AGE=∠AHP=90°
∵E、F关于x轴对称,
∴PE=PF,
此时FH最小,
4的最小值是3.
【标注】 【知识点】胡不归问题
17.等腰三角形+锐角三角函数+线段和差+胡不归最值————22成都模拟+填空压轴+初三
如图,在等腰三角形ABC中,AC=BC=50,tanA=3,BD为高,M,N分别是BD,CD上的动点,若DN-AD=2DM,E是AB的中点,连接EM,MN,则 的最小值为 .
【答案】5
【解析】E为AB中点,且三角形ABC为等腰三角形,连接CE,则CE为AB垂直平分线,
即CE=3AE,且
AD=AB×cosA=10,BD=AB×sinA=30,
作DF⊥AB,垂足为F,作MG⊥AB,垂足为G,
DF=AD·sinA=3 ,AF=AD·cosA= ,BF=AB-AF=9
设DM=x,则DN=2x+10,MB=30-x,
则 ME+MN
可看作x轴上动点H(x,0)到点P(15,5)和Q(-4,-2)的距离之和,
且
即 ME+MN的最小值为5
【标注】 【知识点】胡不归问题
18.菱形+对角线+特殊角度+胡不归最值—22山西模拟+填空压轴+初三
如图,已知菱形ABCD的面积为8 ,∠BAD=60°,对角线AC、BD交于点O,若点P为对角线AC上一点,则 的最小值是
【答案】2
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
又∵∠BAD=60°,
∴△ABD为等边三角形.
又∵菱形的对角线互相垂直平分且平分每一对角,
设OD=OB=x,在Rt△AOB中,
∵线段长度应该大于0,
∴x=2,即OB=OD=2,AO=OC=2
∴AB=BD=2OB=4.
过P点作PQ⊥AD于Q点,
∵∠DAC=30°,
当B、P、Q三点共线且BQ⊥AD时,BQ取得最小值,
此时 最小值为BQ的长度.
在Rt△ABQ中,
良 P的最小值为2
【标注】【知识点】胡不归问题
知识回顾
1. “胡不归”问题
我们学过将军饮马模型,知道怎么求解PA+PB的最小值,但是有时候还会见到下面这种,即“PB+nPA”最小值问题(n≠1),这是近几年考试热点也是难点,本讲内容主要来研究这个问题.
从前,有一个小伙子在外地当学徒,当他获悉老父亲病危后,便立即启程赶路.由于他只考虑了两点之间线段最短的原理,所以选择了全是砂砾地带的直线路径A →B (如图所示),而忽视了走折线虽然路程多但速度快的情况,当他到家时,老人刚咽气.老人弥留之际不断念叨着“胡不归 胡不归 何以归” .这个传说,引起思考,能否提前到家 应该选择一条怎样的路线呢 这就是的“胡不归”问题.
将问题简化:在直线AC上有一个动点P ,点B是直线外一点 ,求 的最小值.
特点:①两定一动 . A、B是两个定点,点P是一个动点.②动点P在直线上运动.
“胡不归”问题总结
由构造 可知,我们构造的直角三角形中, 所以在解决 这类问题时,我们只需要构造一个含∠A的Rt△APH , 使得 即可.
3、特殊情况:如果n值大于1,则要先提取n,再进行求解.
如:PA+3PB转为求 转为求
品真题精炼
1.二次函数+胡不归最大值+两动一定——24重庆+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 与x轴交于 B两点,交y轴于点C,抛物线的对称轴是直线
(1)求抛物线的表达式 .
(2)点P是直线BC下方对称轴右侧抛物线上一动点,过点P作PD//x轴交抛物线于点D,作PE⊥BC于点E , 求 的最大值及此时点P的坐标.
2.外接圆+等边三角形+胡不归最值+两定一动——23湘西+填空压轴+初二
如图,⊙O是等边三角形ABC的外接圆,其半径为4 .过点B作 于点E,点P为线段BE上一动点(点P不与B ,E重合),则 的最小值为
3.等腰三角形+特殊角度+胡不归最值———23广州模拟/22鄂尔多斯+初二
如图,在 中, 垂足为D ,P为线段AD上的一动点, 连接PB、PC.则 的最小值为
4.二次函数+胡不归最值———23宁夏+代数综合压轴+初三
如图,抛物线 )与x轴交于A,B两点,与y轴交于点C .已知点A的坐标是(-1,0) ,抛物线的对称轴是直线x=1.
(1)直接写出点B的坐标;(2)第一象限内的抛物线上有一动点M,过点M作 轴,垂足为N,连接BC交MN于点Q .依题意补全图形,当 的值最大时,求点M的坐标.
5.二次函数+胡不归最值———24连云港模拟/22淮安+代数综合压轴+初三
如图 (1),二次函数 与x轴交于A、B两点,点B的坐标为(3,0),点C的坐标为
(0,3), 直线l经过B、C两点.
(1)求该二次函数的表达式及其图像的顶点坐标;
(2)点P为直线l上的一点,过点P作x轴的垂线与该二次函数的图像相交于点M ,再过点M作y轴的垂线与该二次函数的图像相交于另一点N ,当 时,求点P的横坐标;
(3)如图(2),点C关于x轴的对称点为点D ,点P为线段BC上的一个动点,连接AP,点Q为线段AP上一点,且AQ=3PQ,连接DQ,当3AP+4DQ的值最小时,直接写出DQ的长.
6.胡不归最值+锐角三角函数+点线最值———22长春模拟/21郴州+填空压轴+初三如图,在△ABC中, 交AC于点D .点P为线段BD上的动点,则 的最小值为
7.胡不归最值+锐角三角函数+点线最值——22四川模拟+填空压轴+初三如图,△ABC中,AB=AC=10,tanA=3,CD⊥AB于点D ,点E是线段CD的一个动点,则 的最小值是 .
8.二次函数+四边形+胡不归最值+平移————22宜宾+代数综合压轴+初三
如图 c与x轴交于A(3,0)、B(-1,0)两点,与y轴交于点C(0,3), 其顶点为点D, 连结AC.
求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E ,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标;(3)在(2)的条件下,将点D向下平移5个单位得到点M,点P为抛物线的对称轴上一动点,求 的最小值.
9.二次函数+旋转+胡不归最值——22南通模拟/21达州+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 交x轴于点A和C(1,0) , 交y轴于点B(0,3),抛物线的对称轴交x轴于点E,交抛物线于点F .
(1)求抛物线的解析式 .
(2)将线段OE绕着点O沿顺时针方向旋转得到线段( 旋转角为 连接 し 求 的最小值.
10.二次函数+胡不归最值+平移——21资阳+代数综合压轴+初三
抛物线 与x轴交于A、B两点,与y轴交于点C,且
(1)求抛物线的解析式 .
(2)如图2,点D是抛物线的顶点 ,将抛物线沿CD方向平移,使点D落在点 处,且 点M是平移后所得抛物线上位于 左侧的一点, 轴交直线 于点N,连结CN.当 的值最小时,求MN的长.
11.菱形+对角线+胡不归+点线最值——22天津模拟+填空压轴+初三
如图, 在菱形ABCD中,. ,对角线AC、BD相交于点O,点M在线段AC上,且 点P为线段BD上的一个动点,则 的最小值是 .
12.直角三角形+特殊角度+胡不归最值——22四川模拟/20新疆+填空压轴+初二如图, 在△ABC中, ,若D是BC边上的动点 , 则2AD+DC的 最小值为 .
13.等腰三角形+锐角三角函数+胡不归最值——22芜湖模拟+填空压轴+初三如图,在△ABC中, AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点 ,则 的最小值是( )
D.10
14.平行四边形+特殊角度+胡不归最值——22徐州模拟+填空压轴+初三如图,在平行四边形ABCD中, ,P为边CD上的一动点,则 的最小值等于 .
15.圆+特殊角度+胡不归最值——21台州模拟+选择压轴+初三
如图,AB是⊙O的直径,AB =2 ,点C是圆上一点,且 点P是AB上的动点,则 的最小值为( )
A. 1 B. D.2
16.二次函数+平移+胡不归最小值———23广元模拟+代数综合压轴+初三
在平面直角坐标系中,将二次函数 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧), 经过点A的一次函数y = kx+b(k≠0)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D, 的面积为5 .
(1)求抛物线和一次函数的解析式.
(2)抛物线上的动点E在一次函数的图象下方,求 面积的最大值,并求出此时点E的坐标.
(3)若点P为x轴上任意一点,在(2)的结论下,求 的最小值.
17.等腰三角形+锐角三角函数+线段和差+胡不归最值——22成都模拟+填空压轴+初三如图,在等腰三角形ABC中, BD为高, M , N分别是BD , CD上的动点,若 E是AB的中点, 连接EM , MN, 则 的最小值为 .
18.菱形+对角线+特殊角度+胡不归最值——22山西模拟+填空压轴+初三
如图,已知菱形ABCD的面积为 ,对角线AC、BD交于点O,若点P为对角线AC上一点,则 的最小值是 .
1.二次函数+胡不归最大值+两动一定::1———24重庆+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线y 与x轴交于A(-1,0), B两点, 交y轴于点C,抛物线的对称轴是直线
(1)求抛物线的表达式.
(2)点P是直线BC下方对称轴右侧抛物线上一动点,过点P作PD//x轴交抛物线于点D,作PE⊥BC于点E,求 的最大值及此时点P的坐标.
【答案】
(2)最大值为 ,P(5,-3)
【解析】(1)∵抛物线 与x轴交于A(-1,0), B两点, 交y轴于点C,抛物线的对称轴是直线x
解得
∴抛物线的表达式为
(2)如图,延长PE交x轴于G,过P作PH//y轴于H,
在 3中,令y=0得
解得:z =-1,x =6,
∴B(6,0),
当x=0时,y=-3,
∴C(0,-3),
∴sin
∵PD//x轴,
∴∠PHE=∠BCO,
∴si
由B(6,0),C(0,-3)得直线BC为
设 则H
∵抛物线 的对称轴为直线
∴当 PE取得最大值,最大值为 ,此时 P(5,-3).
【标注】 【知识点】二次函数与几何最值问题
2外接圆+等边三角形+胡不归最值÷两定一动l ——23湘西+填空压轴+初二
如图,⊙O是等边三角形ABC的外接圆,其半径为4 .过点B作BE⊥AC于点E ,点P为线段BE上一动点(点P不与B,E重合),则 的最小值为 .
【答案】6
【解析】如图所示,过点P作PD⊥AB,连接CO并延长交AB于点F,连接AO,
∵△ABC是等边三角形, BE⊥AC,
∵⊙O是等边三角形ABC的外接圆,其半径为4,
∴OA=OB=4,OF⊥AB,
∵BE⊥AC,
∴BE=BO+EO=6,
∵PD⊥AB,∠ABE=30°,
BP的最小值为CF的长度,
∵△ABC是等边三角形,BE⊥AC,CF⊥AB,
∴CF=BE=6,
BP的最小值为6.
故答案为:6.
【标注】 【知识点】30°特殊角的性质应用
【知识点】勾股定理
【知识点】正多边形与圆
【知识点】三角形的外接圆
3.等最三角形+特殊角度+胡不归最值——23广州模拟/22鄂尔多斯+初二
如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
【答案】4
【解析】如图,
在∠BAC的外部作∠CAE=15°,作BF⊥AE于F,交AD于P,
此时PA+2PB最小,
∵BF⊥AE,
∴∠AFB=90°
∵AB=AC,AD⊥BC,
∴∠EAD=∠CAE+∠CAD=30°.
∵C(0,3),
∴3=-3a,
∴a=-1,
设]
则:N(m,0),
由(2)知:直线BC:y=-x+3,
∴Q(m -m+3),
∵C(0,3),B(3,0),
∴OC=OB=3,BN=3-m,
∴当 时, 有最大值,
此时.
【标注】 【知识点】二次函数
4.二次函数+胡不归最值——24连云港模拟/22淮安+代数综合压轴+初三
如图(1),二次函数 c的图像与x轴交于A、B两点,与y轴交于C点,点B的坐标
为(3,0),点C的坐标为(0,3),直线l经过B、C两点.
在Rt△ABF中,AB=4,∠BAF=∠BAC+∠CAE=45°,
故答案为:4
【标注】【知识点】最短路径问题
5.二次函数。胡不归最值——23宁夏+代数综合压轴+初三
如图,抛物线 与x轴交于A,B两点,与y轴交于点C .已知点A的坐标是(-1,0) ,抛物线的对称轴是直线x=1.
(1)直接写出点B的坐标;(2)第一象限内的抛物线上有一动点M ,过点M作MN⊥α轴,垂足为N连接BC交MN于点Q .依题意补全图形,当 的值最大时,求点M的坐标.
【答案】
【解析】(1)解:∵点A(-1,0)关于对称轴的对称点为点B,对称轴为直线x=1,∴点B为(3,0);
(2)过点M作MN⊥x轴,垂足为N,连接BC交MN于点Q ,如图所示,
∵A(-1,0),B(3,0),
设抛物线的解析式为:y=a(x+1)(x-3),
(1)求该二次函数的表达式及其图像的顶点坐标;
(2)点P为直线l上的一点,过点P作x轴的垂线与该二次函数的图像相交于点M ,再过点M作y轴的垂线与该二次函数的图像相交于另一点N,当 时,求点P的横坐标;
(3)如图(2),点C关于x轴的对称点为点D ,点P为线段BC上的一个动点,连接AP,点Q为线段AP上一点,且AQ=3PQ,连接DQ,当3AP +4DQ的值最小时,直接写出DQ的长.
【答案】 顶点坐标(1,4)
(2) P点横坐标为1+
【解析】(1) (1)解:将点B(3,0),C(0,3)代.顶点坐标(1,4); .
(2)解:设直线BC的解析式为 解得设P(t,-t+3),则A ∴t -3t= (2-2t)或 当 时,整理得 解得 当 时,整理得( 解得e ∴P点横坐标为
(3) 解:∵C(0,3), D点与C点关于x轴对称,∴D(0,-3),令y=0,则 解得x=-1或x=3,∴A(-1,0),∴AB=4,∵AQ=3PQ ,∴Q点在平行于BC的线段上,设此线段与x轴的交点为G,. AG=3,∴G(2,0),∵OB=OC,∴∠OBC=45°,作A点关于CQ的对称点A',连接AD与AP交于点Q,
. AQ=A'Q,∴AQ+DQ=A'Q+DQ≥A'D,∴
∠QGA=∠CBO=45°,AA'⊥QG,∴∠A'AG=45°,∵AG=A'G,∴
∠AA'G=45°,∴∠AGA'=90°,∴A'(2,3), 设直线DA'的解析式为y= kx+b,∴
解得 同理可求直线QG的解析式为y=-x+2
,联立方程组 解得
【标注】 【知识点】二次函数解析式
【知识点】二次函数的其他实际问题
【知识点】二次函数 的对称轴
【知识点】平行线分线段成比例定理
【业务题型】运算题
6.胡不归最值+锐角三角函数+点线最值——22长春模拟/21郴州+填空压轴+初三
如图,在△ABC中,AB=5,AC=4,sinA= BD⊥AC交AC于点D .点P为线段BD上的动点,则 PB的最小值为
【答案】
【解析】过点P作PE⊥AB于点E,过点C作CH⊥AB于点H,
∵BD⊥AC,
∴∠ADB=90°,
∴BD=4,
由勾股定理得
即点C,P,E三点共线时, PB最小,
PB的最小值为CH的长,
∴4×4=5×CH,
PB的最小值为
故答案为:
【标注】 【知识点】最短路径问题
7.胡不归最值+锐角三角函数+点线最值——22四川模拟+填空压轴+初三
如图,△ABC中,AB=AC=10,tanA=3,CD⊥AB于点D ,点E是线段CD的一个动点,则 E的最小值是 .
中小学教育资源及组卷应用平台
【答案】3
【解析】
【分析】
作EG⊥AC于G, BH⊥AC于H,由 设AD=a, CD=3a,利用勾股定理构建方程求出a,再证明 推出 由垂线段最短即可解决问题.
【详解】
解:如图,作EG⊥AC于G, BH⊥AC于H,
∵CD⊥AB,
设AD=a,CD=3a,
则有:
(舍),
∵AB=AC,CD⊥AB, BH⊥AC,
∵∠ECG=∠ACD,∠CGE=∠CDA,
∴BE+EG≥BH,
EC的最小值为3
故答案为:
【点睛】
本题考查解直角三角形,等腰三角形的性质,垂线段最短等知识,解题的关键是学会添加常用辅助线,用转化的思想思考问题,属于中考常考题型、
【标注】【知识点】解直角三角形的定义及常见类型
【知识点】等腰三角形的性质-等边对等角
【知识点】垂线段最短
8.二次函数+四边形+胡不归最值+平移——22宜宾+代数综合压轴+初三
如图,抛物线 c与x轴交于A(3,0)、B(-1,0)两点,与y轴交于点C(0,3),其顶点为点D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标;
(3)在(2)的条件下,将点D向下平移5个单位得到点M,点P为抛物线的对称轴上一动点,求 的最小值.
【答案】 顶点D的坐标为(1,4)
(2)F(-2,-5)或F(4,-5)
(3)
【解析】
(1)解:∵抛物线 c经过点A(3,0), B(-1,0),C(0,3),
解得:
∴抛物线的解析式为:
∴顶点D的坐标为(1,4);
(2)解:设直线AC的解析式为:y= kx+b,
把点A(3,0),C(0,3)代入得:k=-1,b=3,
∴直线AC解析式为:y=-x+3,
过点/作FG⊥DE于点G,
∵以A、C、E、A四点为顶点的四边形是以AC为边的平行四边形,
∴AC∥EF,AC=EF,
又∵OA∥FG,
..∠OAC=∠GFE
∴△OAC≌△GFE,
∴OA=GF=3,
设F点的坐标为
则G点的坐标为
∴FG=|m-1|=3,
∴m=-2或m=4,当m=-2时,
∴F (-2,-5),
当m=4时,
∴F (4,-5),
∴F(-2,-5)或F(4,-5);
(3)解:通过题意,得点M的坐标为(1,-1),
通过题意知: 点F (4,-5)与点F (-2,-5)关于对称轴x=1对称,
连结F F ,对称轴于点H,连结F M、F M ,过点F 作F N⊥F M于点N,交对称轴于点P,则MH=4,HF =3,MF =5.
在Rt△MHF 中, 则在Rt△MPN中,
又∵PF =PF
为最小值,
又1
∴求得 的最小值为
【标注】 【知识点】二次函数与特殊平行四边形
【知识点】二次函数与平行四边形
【知识点】二次函数解析式
【知识点】二次函数的其他实际问题
【知识点】解直角三角形的定义及常见类型
【业务题型】运算题
9二次函数+旋转+胡不归最值————22南通模拟/21达州+代数综合压轴+初三
如图,在平面直角坐标系中,抛物线 c交x轴于点A和C(1,0), 交y轴于点B(0,3)抛物线的对称轴交a轴于点E ,交抛物线于点F.
(1)求抛物线的解析式.
(2)将线段OE绕着点O沿顺时针方向旋转得到线段OE',旋转角为( 连接AE',BE',求 的最小值.
【答案】
【解析】(1)∵y=-x + bx+c过C(1,0), B(0,3),
∴b=-2,c=3,
∴抛物线的解析式为
(2)在OE上取一点D ,使得 连接DE',BD,
对称轴2
∴ 3,
∴△DOE'∽△E'OA,
当B,E', D三点在同一点直线上时, BE'+DE'最小为BD.
在Rt△BOD中,
最小值为
【标注】 【知识点】二次函数与相似三角形结合
10.抛物线3 与x轴交于A、B两点,与y轴交于点C,且B(-1,0), C(0,3).
(1)求抛物线的解析式.
(2)如图2,点D是抛物线的顶点,将抛物线沿CD方向平移,使点D落在点D'处,且DD'=2CD,点M是平移后所得抛物线上位于D'左侧的一点,MN//y轴交直线OD'于点N,连结ON.当 的值最小时,求MN的长.
【答案】
【解析】
(2) ∵D为顶点,
∴D(1,4),
由题
∴D'(3,6).
∵VOD'=2x,
过D'作y轴平行线l,过N作NP⊥D'P,
在Rt△NPD'中,
当CP'⊥l时 取最小值,
最小值为3,
yN= yc=3,
【标注】 【知识点】二次函数与轴对称问题
11.菱形+对角线+胡不归+点线最值——22天津模拟+填空压轴+初三
如图,在菱形ABCD中, AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则 PB的最小值是
【答案】
【解析】易知△ABC与△ACD为正三角形, 边长为10.
过P作PQ⊥BC交BC于Q ,过点M作MN⊥BC于点N.
显然M,P,Q三点共线时最小,即为MN的长,
∠MCQ=60°,MC=AC-AM=10-3=7,
即 B最小为
12..直角三角形+特殊角度+胡不归最值
——22四川模拟/20新疆+填空压轴+初二
如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为 .
【答案】6
【解析】如图所示,作点A关于BC的对称点A',连接AA',A'D,过点D作DE⊥AC于点E,AA'交BC于点H,
∵△ABC中,∠BAC=90°,∠B=60°,AB=2,
∴BH=1,AH= ,AA'=2 ,∠C=30°,
∴Rt△CDE中, 即2DE=CD,
∵A与A'关于BC对称,
∴AD=A'D,
∴AD+DE=A'D+DE,
∴当A',D , E在同一直线上时, AD+DE的最小值等于A'E的长,
此时,Rt△AA'E中,
∵AD+DE的最小值为3,
即2AD+CD的最小值为6.
故答案为:6.
【标注】 【知识点】轴对称的性质
【能力】推理论证能力
13..等腰三角形+锐角三角函数+胡不归最值——22芜湖模拟+填空压轴+初三
如图,在△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则 的最小值是( )
A.2 B.4 C.5 D.10
【答案】B
【解析】方法一:在Rt△ABE中
∴AE:BE:AB=1:2:
如图,过D作DF⊥AB,垂足为F,
在Rt△BDF中,
如图,过C作CG⊥AB,垂足为G,
故选B.
方法二:如图,作DH⊥AB于H,CM⊥AB于M.
∵BE⊥AO,
∴设AE=a,BE=2a,
则有
∴a=2 或-2 (舍去) ,
∵AB=AC,BE⊥AC,CM⊥AB,
等腰三角形两腰上的高相等),
∵∠DBH=∠ABE,∠BHD=∠BEA,
BD的最小值为4
故选B.
【标注】【知识点】胡不归问题
14..平行四边形+特殊角度+胡不归最值——22徐州模拟+填空压轴+初三
如图,在平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于 .
【答案】3
【解析】
过点P作PF⊥AD,交AD延长线于点F,
过点B作BE⊥AD ,交AD延长线于点E,
在Rt△AEB中,
∵∠DAB=60°,AB=6,
又∵AD=BC=2,
∴AE>AD,
∴E在AD的延长线上.
在Rt△PFD中,
∵∠PDF=∠DAB=60°,
易知当B、P、F三点共线时PB+PF取最小值,
即 的最小值为
故答案为:3
【标注】【知识点】胡不归问题
15.圆+特殊角度+胡不归最值
——21台州模拟+选择压轴+初三
如图,AB是⊙O的直径,AB=2,点C是圆上一点,且∠BAC=30°,点P是AB上的动点,则 AP的最小值为( ).
A.1 B. C. D.2
【答案】B
【解析】作∠BAD=30°,过P作PH⊥AD于H,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,AB=2,
∵PH⊥AD,
∴∠PHA=90°,
∵∠DAB=30°,
∴当且仅当C、P、H三点共线且CH⊥AD时, 取得最小值.
∵∠CAD=∠BAC+∠BAD=60°,
的最小值为
故选B.
【标注】 【知识点】胡不归问题
16..二次函数+平移+胡不归最小值——23广元模拟+代数综合压轴+初三
在平面直角坐标系中,将二次函数 )的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与a轴交于点A、B(点A在点B的左侧),OA =1,经过点A的一次函数y=kx+b(k≠0)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)求抛物线和一次函数的解析式.
(2)抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E的坐标.
(3)若点P为x轴上任意一点,在(2)的结论下,求 A的最小值.
【答案】(1)见解析
(2)见解析
(3)见解析
【解析】(1)解:将二次函数 )的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
∵OA=1,
∴点A的坐标为(-1,0),代入抛物线的解析式得,4a-2=0,
∴抛物线的解析式为 即
令y=0,解得<
∴B(3,0),
∴AB=OA+OB=4,
∵△ABD的面积为5,
代入抛物线解析式得
解得x =-2,z =4,
设直线AD的解析式为y= kx+b,
解得:
∴直线AD的解析式为
(2)过点E作EM//v轴交AD于M,如图,设E 则
∴当 时,△ACE的面积有最大值,最大值是 ,此时E点坐标为
(3)作点E关于x轴的对称点F,连接EF交x轴于点G,过点F作FH⊥AE于点H ,交x轴于点P,
∵∠AGE=∠AHP=90°
∵E、F关于x轴对称,
∴PE=PF,
此时FH最小,
4的最小值是3.
【标注】 【知识点】胡不归问题
17.等腰三角形+锐角三角函数+线段和差+胡不归最值————22成都模拟+填空压轴+初三
如图,在等腰三角形ABC中,AC=BC=50,tanA=3,BD为高,M,N分别是BD,CD上的动点,若DN-AD=2DM,E是AB的中点,连接EM,MN,则 的最小值为 .
【答案】5
【解析】E为AB中点,且三角形ABC为等腰三角形,连接CE,则CE为AB垂直平分线,
即CE=3AE,且
AD=AB×cosA=10,BD=AB×sinA=30,
作DF⊥AB,垂足为F,作MG⊥AB,垂足为G,
DF=AD·sinA=3 ,AF=AD·cosA= ,BF=AB-AF=9
设DM=x,则DN=2x+10,MB=30-x,
则 ME+MN
可看作x轴上动点H(x,0)到点P(15,5)和Q(-4,-2)的距离之和,
且
即 ME+MN的最小值为5
【标注】 【知识点】胡不归问题
18.菱形+对角线+特殊角度+胡不归最值—22山西模拟+填空压轴+初三
如图,已知菱形ABCD的面积为8 ,∠BAD=60°,对角线AC、BD交于点O,若点P为对角线AC上一点,则 的最小值是
【答案】2
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
又∵∠BAD=60°,
∴△ABD为等边三角形.
又∵菱形的对角线互相垂直平分且平分每一对角,
设OD=OB=x,在Rt△AOB中,
∵线段长度应该大于0,
∴x=2,即OB=OD=2,AO=OC=2
∴AB=BD=2OB=4.
过P点作PQ⊥AD于Q点,
∵∠DAC=30°,
当B、P、Q三点共线且BQ⊥AD时,BQ取得最小值,
此时 最小值为BQ的长度.
在Rt△ABQ中,
良 P的最小值为2
【标注】【知识点】胡不归问题
同课章节目录
