专题三 阿氏圆最值模型(含答案) 2025年中考数学几何模型专题讲练
文档属性
| 名称 | 专题三 阿氏圆最值模型(含答案) 2025年中考数学几何模型专题讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 458.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 16:16:55 | ||
图片预览



文档简介
阿氏圆最值模型
知识回顾
1. “阿氏圆”问题
我们学过将军饮马模型,知道怎么求解PA+PB的最小值,但是有时候我们还会见到下面这种,即“PB+nPA"的最小值问题(n≠1),这是近几年考试热点也是难点,本讲内容主要来研究这个问题.
“阿氏圆”问题总结
1、特点:①两定一动.点A 、B是定点,点P是动点.②动点P在圆周上运动.
2、解题步骤:
①连接动点P和圆心O .将系数不为1的线段的两个端点分别与圆心连接,如图线段OP、OA
②计算出所连接的这两条线段的长度 .③计算这两条线段的长度比.即
④在线段上取点Q ,使得 得到△OPQ ∽△OAP ,则PQ=n·PA
⑤连接BQ ,与圆交点即为当“PB+nPA”的值最小时,点P的位置.
3、 “阿氏圆”问题本质是构造字母型相似,如图1 .
构造 得 所以.PQ=n·PA
4、特殊情况:如果n值大于1,则要先提取n,再跟据思路2进行求解.
如: 的最小值转化为求
求2PA+3PB的最小值转化为求
品真题精炼
1.二次函数+一次函数+阿氏圆最值——24济南模拟/23烟台+代数综合压轴+初三
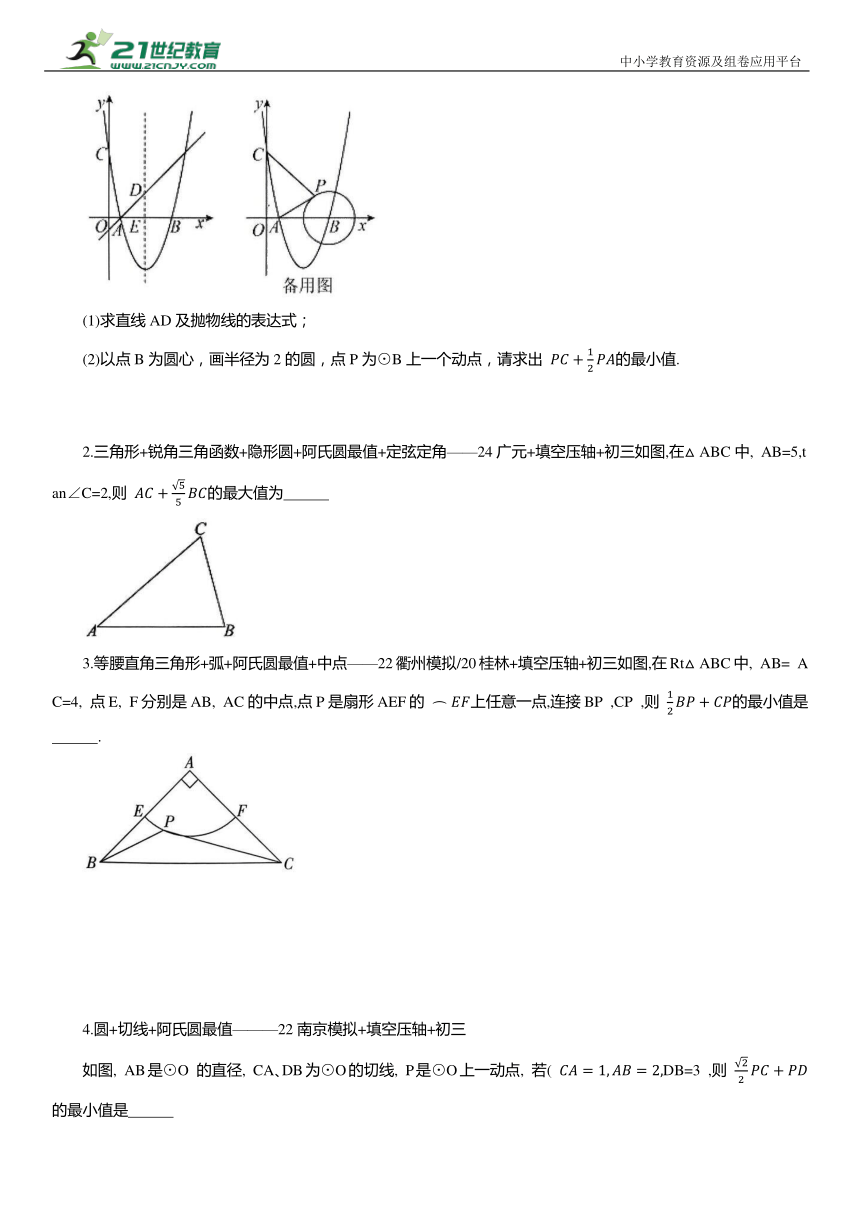
如图,抛物线 与x轴交于A,B两点,与y轴交于点C,. 抛物线的对称轴 与经过点A的直线 交于点D,与x轴交于点E .
(1)求直线AD及抛物线的表达式;
(2)以点B为圆心,画半径为2的圆,点P为⊙B上一个动点,请求出 的最小值.
2.三角形+锐角三角函数+隐形圆+阿氏圆最值+定弦定角——24广元+填空压轴+初三如图,在△ABC中, AB=5,tan∠C=2,则 的最大值为
3.等腰直角三角形+弧+阿氏圆最值+中点——22衢州模拟/20桂林+填空压轴+初三如图,在Rt△ABC中, AB= AC=4, 点E, F分别是AB, AC的中点,点P是扇形AEF的 上任意一点,连接BP ,CP ,则 的最小值是 .
4.圆+切线+阿氏圆最值———22南京模拟+填空压轴+初三
如图, AB是⊙O 的直径, CA、DB为⊙O的切线, P是⊙O上一动点, 若( DB=3 ,则 的最小值是
5.直角三角形+圆+阿氏圆最值——23宁波模拟+填空压轴+初三
在△ABC中,. ,以点C为圆心,4为半径的圆上有一动点D ,连接AD,BD,CD,则 的最小值是
6.矩形+圆+阿氏圆最值——23扬州模拟+填空压轴+初三
如图,已知矩形ABCD, AB=8,BC=6,以点A为圆心、5为半径作圆, M为⊙A上一动点,连接CM、DM,则 的最小值为 .
7直角三角形+圆+阿氏圆最值——22温州模拟+填空压轴+初三
如图所示,在△ABC中,. 以点C为圆心、2为半径的圆上有一动点D, 连接AD, BD , CD, 则 的最小值是
8.圆+切线+阿氏圆最值——23盐城模拟+几何解答题+初三
已知⊙O半径为1, AC、BD为切线,. ,P为弧AB上一动点,试求 的最小值.
9.特殊角度+圆+阿氏圆最值——23宿迁模拟+填空压轴+初三
在△ABC中, ,圆A的半径为6 ,P是圆A上的动点,连接PB、PC, 则3PC+2PB的最小值为 .
10.扇形+特殊角度+阿氏圆最值+中点——22眉山模拟+选择压轴+初三
如图,在扇形CAB中, ,D为CA的中点, P为. 上一动点(不与C,B重合),则 的最小值为( )
C. 10
11.二次函数+圆+阿氏圆最值——23广州模拟+填空压轴+初三
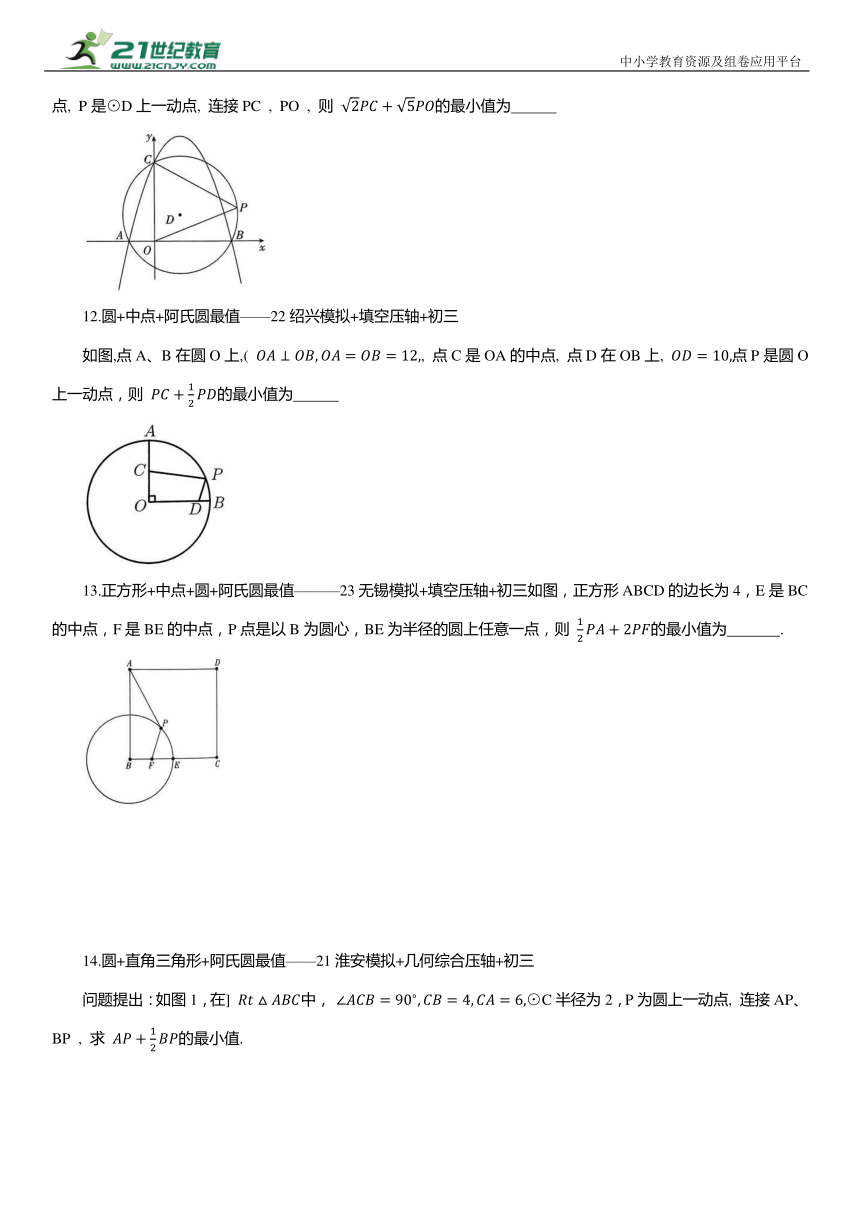
如图,抛物线 与x轴交于A、B两点(A在B的左侧) , 与y轴交于点C , ⊙D过A, B,C三点, P是⊙D上一动点, 连接PC , PO , 则 的最小值为
12.圆+中点+阿氏圆最值——22绍兴模拟+填空压轴+初三
如图,点A、B在圆O上,( , 点C是OA的中点, 点D在OB上, 点P是圆O上一动点,则 的最小值为
13.正方形+中点+圆+阿氏圆最值———23无锡模拟+填空压轴+初三如图,正方形ABCD的边长为4,E是BC的中点,F是BE的中点,P点是以B为圆心,BE为半径的圆上任意一点,则 的最小值为 .
14.圆+直角三角形+阿氏圆最值——21淮安模拟+几何综合压轴+初三
问题提出:如图1,在] 中, ⊙C半径为2,P为圆上一动点, 连接AP、BP , 求 的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使 则有 又∵
请你完成余下的思考,并直接写出答案: 的最小值为 .
(2)自主探索:在“问题提出”的条件不变的情况下, 的最小值为 .
15.几何综合+胡不归最值+阿氏圆最值——22陕西+几何综合压轴+初三
(1) 【问题发现】
如图1, 已知线段AC和BC ,. ,则线段AB的最小值为 .
(2) 【问题探究】
如图2,在矩形ABCD中,. P为矩形内部一点 ,分别连接AP、BP、CP,且PB=3,延长CP交AB于点F ,若 求 的值.
(3) 【问题解决】
如图3是某街心花园的一角 ,在扇形AOB中,. 米,在矮围墙OA和OB上分别有两个入口C和D,. 米,D为OB的中点.现要在 上找一个出口E,沿CE、DE从入口到出口铺设两条景观小路.已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元,则在 上是否存在点E ,使铺设小路CE和DE的总造价最低 若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.(小路的宽度忽略不计)
16.二次函数+矩形+圆+阿氏圆最值———21连云港模拟+代数综合压轴+初三
如图,抛物线 与直线AB交于A(-4,-4), B(0,4)两点, 直线AC: 交y轴于点C.点E是直线AB上的动点,过点E作 轴交AC于点F ,交抛物线于点G.
(1)求抛物线 c的表达式.
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标.
(3)解答下列各题:
① 在y轴上存在一点H,连接EH ,HF ,当点E运动到什么位置时,以A,E ,F ,H为顶点的四边形是矩形 求出此时点E ,H的坐标.
② 在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求 的最小值.
1.如图,抛物线y 与x轴交于A,B两点,与y轴交于点C,AB=4.抛物线的对称轴x=3与经过点A的直线y=kx-1交于点D,与x轴交于点E.
(1)求直线AD及抛物线的表达式;
(2)以点B为圆心,画半径为2的圆,点P为⊙B上一个动点,请求出 PA的最小值.
【答案】(1)直线AD的解析式为y=x-1;抛物线解析式为
【解析】(1)解:∵抛物线的对称轴x=3,AB=4,∴A(1,0),B(5,0),将A(1,0)代入直线y= kx-1,得k-1=0,解得k=1,∴直线AD的解析式为y=x-1;将A(1,0),B(5,0)代 得 解得 .抛物线的解析式为
(2)如下图所示,在AB上取点F,使BF=1,连接CF, 又∵∠PBF=∠ABP,∴△PBF∽△ABP,. 即 ∴当点C、P、F三点共线时, A的值最小,即为线段CF的长,∵OC=5,OF=OB-1=5-1=4 A的最小值为
【标注】 【知识点】二次函数解析式
2.如图,在△ABC中,AB=5,tan∠C=2,则 BC的最大值为 .
【答案】5
【解析】
【分析】
过点B作BD⊥AC,垂足为D,如图所示,利用三角函数定义得到 ,延长DC到E,使EC=CD=x,连接BE,如图所示,从而确定
,再由辅助圆-定弦定角模型得到点E在⊙O上运动,AE是⊙O的弦,求 的最大值就是求弦AE的最大值,即AE是直径时,取到最大值,由圆周角定理及勾股定理求解即可得到答案.
【详解】
解:过点B作BD⊥AC,垂足为D,如图所示:
∵tan∠C=2,
∴在Rt△BCD中,设DC=x,则BD=2x,由勾股定理可得
即
延长DC到E,使EC=CD=x,连接BE,如图所示:
∵BD⊥DE,DE=2x=BD,
∴△BDE是等腰直角三角形,则∠E=45°,
在△ABE中,AB=5,∠E=45°,由辅助圆-定弦定角模型,作△ABE的外接圆,如图所示:
∴由圆周角定理可知,点E在⊙O上运动,AE是⊙O的弦,求 的最大值就是求弦AE的最大值,根据圆的性质可知,当弦AE过圆心O,即AE是直径时,弦最大,如图所示:
∵AE是⊙O的直径,
∴∠ABE=90°,
∴△ABE是等腰直角三角形,
∵AB=5,
∴BE=AB=5,则由勾股定理可得 即 C的最大值为5
故答案为:5
【点睛】
本题考查动点最值问题,涉及解三角形、勾股定理、等腰直角三角形的判定与性质、圆的性质、圆周角定理、动点最值问题-定弦定角模型等知识,熟练掌握动点最值问题-定弦定角横型的解法是解决问题的关键.
【标注】 【知识点】圆心角和圆周角
【知识点】等腰三角形的性质与判定综合问题
【知识点】勾股定理
【知识点】正切的定义
3.如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的EF上任意一点,连接BP,CP,则 的最小值是 .
【答案】
【解析】在AB上取一点T,使得AT=1,连接PT,PA,CT.
∵PA=2,AT=1,AB=4,
∵∠PAT=∠PAB,
∴△COP∽△POE,
过点E作AB的平行线分别交CA,DB于点F,G,
则
的最小值是
【标注】【知识点】阿氏圆问题
4在△ABC中,∠ACB=90°,BC=8,AC=6,以点O为圆心,4为半径的圆上有一动点D,连接AD,BD,CD,则 的最小值是
【答案】
【解析】如图,在CB上取一点,使得CF=2,连接FD、AF,
在Rt△ACT中,∵∠CAT=90°, AT=1,AC=4,
的最小值为
故答案为:
【标注】 【知识点】阿氏圆问题
5.如图,AB是⊙O的直径,CA、DB为⊙O的切线,P是⊙O上一动点,若CA=1 ,AB=2,DB=3 ,则 的最小值是
【答案】
【解析】如图,连接OC,OP,取OC的中点E,连接DE,PE,
则CA=OA=OP=1,
又∠OOP=∠POE,
∴CD=4,CF=2,CB=8,
·∠FCD=∠DCB,
.△FCD∽△DCB.
的最小值是2
【标注】【知识点】阿氏圆问题
6.如图,已知矩形ABCD,AB=8,BC=6,以点A为圆心、5为半径作圆, M为⊙A上一动点,连接CM、DM,则 的最小值为 .
【答案】
【解析】连接AO交⊙A于点E,取AE的中点N,连接MN,ND,
则 的最小值为DN的长,
∵矩形ABCD中,AB=8,BC=6,
∵AM=5,AN=2.5,
∵∠MAN=∠CAM(公共角) ,
∴△MAN∽△CAM,
即
∴ CM+MD=MN+DM≥DN.
当N、M、D三点共线时等号成立,即 的最小值就是DN的长.
作NH⊥AD,易求得
故答案为:
【标注】【知识点】阿氏圆问题
7如图所示,在△ABC中,∠ACB=90°,BC=4 ,AC=3,以点C为圆心、2为半径的圆上有一动点D,连接AD,BD,CD,则 的最小值是 .
【答案】
【解析】如图,在CB上取一点F,使得CF=1,连接FD, AF.
∴CD=2,CF=1,CB=4,
∵∠FCD=∠DCB,
∴△FCD∽△DCB,
的最小值是
故答案为:
【标注】 【知识点】阿氏圆问题
8已知⊙O半径为1,AC、BD为切线,AC=1,BD=2,P为弧AB上一动点,试求 的最小值.
【答案】
【解析】连接OC ,在线段OC取一点E,使
且∠EOP=∠POC,
的最小值等于EP+PD最小值.
作EM⊥AB于M,EN⊥BD于N,
即 最小值为
【标注】 【知识点】阿氏圆问题
9.在△ABC中,AB=9,BC=8,∠ABC=60°,圆A的半径为6,P是圆A上的动点,连接 PbPC,则3PC+2PB的最小值为
【答案】21
【解析】在AB上取Q点,连接AP、PQ,使得AQ=4.则△AQP∽△APB,且相似比为2:3,则
在△BQC中用余弦定理求得
QC=7,则所求为21.
【标注】 【知识点】阿氏圆问题
10.如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为BC上一动点(不与C,B重合) ,则2PD+PB的最小值为( )
B. 4 C.10 D.4 +4
【答案】B
【解析】方法一:如图,作∠PAP'=120°,则AP'=2AB=8,连接PP',BP',
则∠1=∠2,
∴△APD∽△AP'B,
∴BP'=2PD,
过点P作PE⊥P'A交P'A的延长线于点E,
在Rt△PEP'中,I
∴2PD+PB的最小值为4
方法二:如图,延长AC到E,使得CE=AC,连接BE交⊙A于P',
由 推出
∴P'E=2P'D,
,求出BE即可解决问题.
故选B.
11如图,抛物线 与x轴交于A、B两点(A在B的左侧),与y轴交于点C,⊙D过A, B,C三点, P是⊙D上一动点,连接PC , PO,则 的最小值为 .
【答案】3
【解析】如图所示,连接DA,DB,DC,过点D作DE⊥AB交AB于E,
∵抛物线 与x轴交于A,B两点(A在B的左侧),
又∵
故由二次函数的交点式可知A点的坐标为(-1,0),B点的坐标为(3,0).
令x=0,得y=3,则点C的坐标为(0,3),
∵⊙D过A,B两点,
∴由圆的垂径定理可知E点的横坐标为1,D点的坐标为(1,y).
5
∴y=1,
. D点的坐标为(1,1),
∵P在圆上,
延长DO到F使得 连接PF,PO,
∵直线DF经过点D(1,1)、O(0,0),
∴直线DF的解析式是y=x,
设F点坐标为(x,y),
解得
∴点F的坐标为
∴△DOP∽△DPF,
∴当P、C、F三点共线时取最小值,
故答案为:3
12如图,点A、B在圆O上,OA⊥OB,OA=OB=12,点C是OA的中点,点D在OB上,OD=10,点P是圆O上一动点,则 的最小值为 .
【答案】13
【解析】延长OA至Q,使QA=AO=12,连接QP,
∴△COP∽△POQ,
∴PQ=2PC,
当P、Q、D三点共线时,
13如图,正方形ABCD的边长为4,E是BC的中点,F是BE的中点,P点是以B为圆心,BE为半径的圆上任意一点,则 的最小值为 .
【答案】
【解析】设圆与AB交于G点,BG中点为H,连HP、PC、BP.
易证△BHP∽△BPA,△BFP∽△BPC,且相似比均为1:2.
则 为所求.
14.问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连接AP、BP,求 的最小值,
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D使CD=1,则有 又∵∠PCD=∠BCP,∴△PCD∽△BCP ,∴
请你完成余下的思考,并直接写出答案: BP的最小值为
中小学教育资源及组卷应用平台
(2)自主探索:在“问题提出”的条件不变的情况下 的最小值为
【答案】(1)
【解析】(1)如图1,连接AD,
∴当点A, P,D在同一条直线时, AP+PD最小,
日 BP的最小值为AD的长度,
在Rt△ACD中,CD=1,AC=6,
的最小值为
(2)如图2,连接CP,在CA上取点D,使
·∠PCD=∠ACP,
∴△PCD∽△ACP,
∴同(1)的方法得出 的最小值为
【标注】【知识点】阿氏圆问题
15.(1)【问题发现】
如图1,已知线段AC和BC,AC=2,BC=5,则线段AB的最小值为 .
(2)【问题探究】
如图2,在矩形ABCD中,BC=7,AB=9,P为矩形内部一点,分别连接AP. BRCP,且PB-3,延长CP交AB于点F,若BF=1,求 的值.
(3) 【问题解决】
如图3是某街心花园的一角,在扇形AOB中,∠AOB=90°,OA=12米,在矮围墙OA和OB上分别有两个入口C和D,AC=4米,D为OB的中点.现要在AB上找一个出口E,沿CE、DE从入口到出口铺设两条景观小路.已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元,则在AB上是否存在点E,使铺设小路CE和DE的总造价最低 若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.(小路的宽度忽略不计)
【答案】(1)3
(2)5
(3)存在,总造价的最小值为 出口E距直线OB的距离为 米.
【解析】(1)当AC与BC重合时,AB最小,
ABmin=BC-AC=5-2=3.
(2)如图,在AB上截取BF=1,连接PF、CF,
∴AB=9,PB=3,BF=1,
.∠ABP=∠PBF,
.△ABP∽△PBF,
当F、P、C三点共线时. 最小,且为CF的长,
在Rt△BCF中,BF=1,BC=7,
(3) 铺设小路CE和DE总造价为200CE+400DE=200(CE+2DE),如图:连接OE,延长OB到点Q,使BQ=OB=12米,连接EQ,在△EOD与△QOE中,∠EOD=∠QOE,
∴△EOD∽△QOE,
故:QE=2DE,
∴CE+2DE=CE+QE,问题转化为求CE+QE的最小值,
连接CQ,交弧AB于点E',此时CE+QE取得最小值CQ,
在Rt△COQ中,CO=8米,OQ=24米,
米,
故总造价的最小值为1600 元.
作E'H⊥OB,垂足为H ,连接OE',
设E'H=x,则QH=3x,
∵在Rt△E'OH中, 有 解得: (舍) ,
∴总造价的最小值为: 出口E距直线OB的距离为
【标注】 【知识点】圆与最值问题
16.如图,抛物线 c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:
交y轴于点C .点E是直线AB上的动点,过点E作EF⊥x轴交AO于点F,交抛物线于点G.
(1)求抛物线 c的表达式.
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标.
(3)解答下列各题:
① 在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F ,H为顶点的四边形是矩形 求出此时点E,H的坐标.
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求 的最小值.
【答案】(
(2) G(-2,4).
(3)① E(-2,0),H(0,-1).
【解析】(1) ∵点A(-4,-4), B(0,4)在抛物线g
抛物线的解析式为
(2) 设直线AB的解析式为y= kx+n过点A, B,
直线AB的解析式为y=2x+4.
设E(m,2m+4),
∵四边形GEOB是平行四边形,
∴EG=OB=4,
∴m=-2,
∴G(-2,4).
(3)① 如图1,
由(2)知,直线AB的解析式为y=2x+4,
∴设E(a,2a+4).
∵直线
设H(0,p),
∵以点A,E,F,H为顶点的四边形是矩形,
且直线AB的解析式为y=2x+4,直线AC的解析式为
∴AB⊥AC,
∴EF与AH互相平分,
∴a=-2,p=-1,
. E(-2,0), H(0,-1).
②
如图2,
由①知,E(-2,0), H(0,-1),
A(-4,-4).
设AE交⊙E于G ,取EG的中点P,
连接PC交⊙E于M ,连接EM,
∠PEM=∠MEA,
∴△PEM∽△MEA,
的最小值=PC.
设点
∵E(-2,0),
或 由于E(-2,0),所以舍去) ,
∵C(0,-6),
即
【标注】 【知识点】二次函数与圆的综合问题
知识回顾
1. “阿氏圆”问题
我们学过将军饮马模型,知道怎么求解PA+PB的最小值,但是有时候我们还会见到下面这种,即“PB+nPA"的最小值问题(n≠1),这是近几年考试热点也是难点,本讲内容主要来研究这个问题.
“阿氏圆”问题总结
1、特点:①两定一动.点A 、B是定点,点P是动点.②动点P在圆周上运动.
2、解题步骤:
①连接动点P和圆心O .将系数不为1的线段的两个端点分别与圆心连接,如图线段OP、OA
②计算出所连接的这两条线段的长度 .③计算这两条线段的长度比.即
④在线段上取点Q ,使得 得到△OPQ ∽△OAP ,则PQ=n·PA
⑤连接BQ ,与圆交点即为当“PB+nPA”的值最小时,点P的位置.
3、 “阿氏圆”问题本质是构造字母型相似,如图1 .
构造 得 所以.PQ=n·PA
4、特殊情况:如果n值大于1,则要先提取n,再跟据思路2进行求解.
如: 的最小值转化为求
求2PA+3PB的最小值转化为求
品真题精炼
1.二次函数+一次函数+阿氏圆最值——24济南模拟/23烟台+代数综合压轴+初三
如图,抛物线 与x轴交于A,B两点,与y轴交于点C,. 抛物线的对称轴 与经过点A的直线 交于点D,与x轴交于点E .
(1)求直线AD及抛物线的表达式;
(2)以点B为圆心,画半径为2的圆,点P为⊙B上一个动点,请求出 的最小值.
2.三角形+锐角三角函数+隐形圆+阿氏圆最值+定弦定角——24广元+填空压轴+初三如图,在△ABC中, AB=5,tan∠C=2,则 的最大值为
3.等腰直角三角形+弧+阿氏圆最值+中点——22衢州模拟/20桂林+填空压轴+初三如图,在Rt△ABC中, AB= AC=4, 点E, F分别是AB, AC的中点,点P是扇形AEF的 上任意一点,连接BP ,CP ,则 的最小值是 .
4.圆+切线+阿氏圆最值———22南京模拟+填空压轴+初三
如图, AB是⊙O 的直径, CA、DB为⊙O的切线, P是⊙O上一动点, 若( DB=3 ,则 的最小值是
5.直角三角形+圆+阿氏圆最值——23宁波模拟+填空压轴+初三
在△ABC中,. ,以点C为圆心,4为半径的圆上有一动点D ,连接AD,BD,CD,则 的最小值是
6.矩形+圆+阿氏圆最值——23扬州模拟+填空压轴+初三
如图,已知矩形ABCD, AB=8,BC=6,以点A为圆心、5为半径作圆, M为⊙A上一动点,连接CM、DM,则 的最小值为 .
7直角三角形+圆+阿氏圆最值——22温州模拟+填空压轴+初三
如图所示,在△ABC中,. 以点C为圆心、2为半径的圆上有一动点D, 连接AD, BD , CD, 则 的最小值是
8.圆+切线+阿氏圆最值——23盐城模拟+几何解答题+初三
已知⊙O半径为1, AC、BD为切线,. ,P为弧AB上一动点,试求 的最小值.
9.特殊角度+圆+阿氏圆最值——23宿迁模拟+填空压轴+初三
在△ABC中, ,圆A的半径为6 ,P是圆A上的动点,连接PB、PC, 则3PC+2PB的最小值为 .
10.扇形+特殊角度+阿氏圆最值+中点——22眉山模拟+选择压轴+初三
如图,在扇形CAB中, ,D为CA的中点, P为. 上一动点(不与C,B重合),则 的最小值为( )
C. 10
11.二次函数+圆+阿氏圆最值——23广州模拟+填空压轴+初三
如图,抛物线 与x轴交于A、B两点(A在B的左侧) , 与y轴交于点C , ⊙D过A, B,C三点, P是⊙D上一动点, 连接PC , PO , 则 的最小值为
12.圆+中点+阿氏圆最值——22绍兴模拟+填空压轴+初三
如图,点A、B在圆O上,( , 点C是OA的中点, 点D在OB上, 点P是圆O上一动点,则 的最小值为
13.正方形+中点+圆+阿氏圆最值———23无锡模拟+填空压轴+初三如图,正方形ABCD的边长为4,E是BC的中点,F是BE的中点,P点是以B为圆心,BE为半径的圆上任意一点,则 的最小值为 .
14.圆+直角三角形+阿氏圆最值——21淮安模拟+几何综合压轴+初三
问题提出:如图1,在] 中, ⊙C半径为2,P为圆上一动点, 连接AP、BP , 求 的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使 则有 又∵
请你完成余下的思考,并直接写出答案: 的最小值为 .
(2)自主探索:在“问题提出”的条件不变的情况下, 的最小值为 .
15.几何综合+胡不归最值+阿氏圆最值——22陕西+几何综合压轴+初三
(1) 【问题发现】
如图1, 已知线段AC和BC ,. ,则线段AB的最小值为 .
(2) 【问题探究】
如图2,在矩形ABCD中,. P为矩形内部一点 ,分别连接AP、BP、CP,且PB=3,延长CP交AB于点F ,若 求 的值.
(3) 【问题解决】
如图3是某街心花园的一角 ,在扇形AOB中,. 米,在矮围墙OA和OB上分别有两个入口C和D,. 米,D为OB的中点.现要在 上找一个出口E,沿CE、DE从入口到出口铺设两条景观小路.已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元,则在 上是否存在点E ,使铺设小路CE和DE的总造价最低 若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.(小路的宽度忽略不计)
16.二次函数+矩形+圆+阿氏圆最值———21连云港模拟+代数综合压轴+初三
如图,抛物线 与直线AB交于A(-4,-4), B(0,4)两点, 直线AC: 交y轴于点C.点E是直线AB上的动点,过点E作 轴交AC于点F ,交抛物线于点G.
(1)求抛物线 c的表达式.
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标.
(3)解答下列各题:
① 在y轴上存在一点H,连接EH ,HF ,当点E运动到什么位置时,以A,E ,F ,H为顶点的四边形是矩形 求出此时点E ,H的坐标.
② 在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求 的最小值.
1.如图,抛物线y 与x轴交于A,B两点,与y轴交于点C,AB=4.抛物线的对称轴x=3与经过点A的直线y=kx-1交于点D,与x轴交于点E.
(1)求直线AD及抛物线的表达式;
(2)以点B为圆心,画半径为2的圆,点P为⊙B上一个动点,请求出 PA的最小值.
【答案】(1)直线AD的解析式为y=x-1;抛物线解析式为
【解析】(1)解:∵抛物线的对称轴x=3,AB=4,∴A(1,0),B(5,0),将A(1,0)代入直线y= kx-1,得k-1=0,解得k=1,∴直线AD的解析式为y=x-1;将A(1,0),B(5,0)代 得 解得 .抛物线的解析式为
(2)如下图所示,在AB上取点F,使BF=1,连接CF, 又∵∠PBF=∠ABP,∴△PBF∽△ABP,. 即 ∴当点C、P、F三点共线时, A的值最小,即为线段CF的长,∵OC=5,OF=OB-1=5-1=4 A的最小值为
【标注】 【知识点】二次函数解析式
2.如图,在△ABC中,AB=5,tan∠C=2,则 BC的最大值为 .
【答案】5
【解析】
【分析】
过点B作BD⊥AC,垂足为D,如图所示,利用三角函数定义得到 ,延长DC到E,使EC=CD=x,连接BE,如图所示,从而确定
,再由辅助圆-定弦定角模型得到点E在⊙O上运动,AE是⊙O的弦,求 的最大值就是求弦AE的最大值,即AE是直径时,取到最大值,由圆周角定理及勾股定理求解即可得到答案.
【详解】
解:过点B作BD⊥AC,垂足为D,如图所示:
∵tan∠C=2,
∴在Rt△BCD中,设DC=x,则BD=2x,由勾股定理可得
即
延长DC到E,使EC=CD=x,连接BE,如图所示:
∵BD⊥DE,DE=2x=BD,
∴△BDE是等腰直角三角形,则∠E=45°,
在△ABE中,AB=5,∠E=45°,由辅助圆-定弦定角模型,作△ABE的外接圆,如图所示:
∴由圆周角定理可知,点E在⊙O上运动,AE是⊙O的弦,求 的最大值就是求弦AE的最大值,根据圆的性质可知,当弦AE过圆心O,即AE是直径时,弦最大,如图所示:
∵AE是⊙O的直径,
∴∠ABE=90°,
∴△ABE是等腰直角三角形,
∵AB=5,
∴BE=AB=5,则由勾股定理可得 即 C的最大值为5
故答案为:5
【点睛】
本题考查动点最值问题,涉及解三角形、勾股定理、等腰直角三角形的判定与性质、圆的性质、圆周角定理、动点最值问题-定弦定角模型等知识,熟练掌握动点最值问题-定弦定角横型的解法是解决问题的关键.
【标注】 【知识点】圆心角和圆周角
【知识点】等腰三角形的性质与判定综合问题
【知识点】勾股定理
【知识点】正切的定义
3.如图,在Rt△ABC中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的EF上任意一点,连接BP,CP,则 的最小值是 .
【答案】
【解析】在AB上取一点T,使得AT=1,连接PT,PA,CT.
∵PA=2,AT=1,AB=4,
∵∠PAT=∠PAB,
∴△COP∽△POE,
过点E作AB的平行线分别交CA,DB于点F,G,
则
的最小值是
【标注】【知识点】阿氏圆问题
4在△ABC中,∠ACB=90°,BC=8,AC=6,以点O为圆心,4为半径的圆上有一动点D,连接AD,BD,CD,则 的最小值是
【答案】
【解析】如图,在CB上取一点,使得CF=2,连接FD、AF,
在Rt△ACT中,∵∠CAT=90°, AT=1,AC=4,
的最小值为
故答案为:
【标注】 【知识点】阿氏圆问题
5.如图,AB是⊙O的直径,CA、DB为⊙O的切线,P是⊙O上一动点,若CA=1 ,AB=2,DB=3 ,则 的最小值是
【答案】
【解析】如图,连接OC,OP,取OC的中点E,连接DE,PE,
则CA=OA=OP=1,
又∠OOP=∠POE,
∴CD=4,CF=2,CB=8,
·∠FCD=∠DCB,
.△FCD∽△DCB.
的最小值是2
【标注】【知识点】阿氏圆问题
6.如图,已知矩形ABCD,AB=8,BC=6,以点A为圆心、5为半径作圆, M为⊙A上一动点,连接CM、DM,则 的最小值为 .
【答案】
【解析】连接AO交⊙A于点E,取AE的中点N,连接MN,ND,
则 的最小值为DN的长,
∵矩形ABCD中,AB=8,BC=6,
∵AM=5,AN=2.5,
∵∠MAN=∠CAM(公共角) ,
∴△MAN∽△CAM,
即
∴ CM+MD=MN+DM≥DN.
当N、M、D三点共线时等号成立,即 的最小值就是DN的长.
作NH⊥AD,易求得
故答案为:
【标注】【知识点】阿氏圆问题
7如图所示,在△ABC中,∠ACB=90°,BC=4 ,AC=3,以点C为圆心、2为半径的圆上有一动点D,连接AD,BD,CD,则 的最小值是 .
【答案】
【解析】如图,在CB上取一点F,使得CF=1,连接FD, AF.
∴CD=2,CF=1,CB=4,
∵∠FCD=∠DCB,
∴△FCD∽△DCB,
的最小值是
故答案为:
【标注】 【知识点】阿氏圆问题
8已知⊙O半径为1,AC、BD为切线,AC=1,BD=2,P为弧AB上一动点,试求 的最小值.
【答案】
【解析】连接OC ,在线段OC取一点E,使
且∠EOP=∠POC,
的最小值等于EP+PD最小值.
作EM⊥AB于M,EN⊥BD于N,
即 最小值为
【标注】 【知识点】阿氏圆问题
9.在△ABC中,AB=9,BC=8,∠ABC=60°,圆A的半径为6,P是圆A上的动点,连接 PbPC,则3PC+2PB的最小值为
【答案】21
【解析】在AB上取Q点,连接AP、PQ,使得AQ=4.则△AQP∽△APB,且相似比为2:3,则
在△BQC中用余弦定理求得
QC=7,则所求为21.
【标注】 【知识点】阿氏圆问题
10.如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为BC上一动点(不与C,B重合) ,则2PD+PB的最小值为( )
B. 4 C.10 D.4 +4
【答案】B
【解析】方法一:如图,作∠PAP'=120°,则AP'=2AB=8,连接PP',BP',
则∠1=∠2,
∴△APD∽△AP'B,
∴BP'=2PD,
过点P作PE⊥P'A交P'A的延长线于点E,
在Rt△PEP'中,I
∴2PD+PB的最小值为4
方法二:如图,延长AC到E,使得CE=AC,连接BE交⊙A于P',
由 推出
∴P'E=2P'D,
,求出BE即可解决问题.
故选B.
11如图,抛物线 与x轴交于A、B两点(A在B的左侧),与y轴交于点C,⊙D过A, B,C三点, P是⊙D上一动点,连接PC , PO,则 的最小值为 .
【答案】3
【解析】如图所示,连接DA,DB,DC,过点D作DE⊥AB交AB于E,
∵抛物线 与x轴交于A,B两点(A在B的左侧),
又∵
故由二次函数的交点式可知A点的坐标为(-1,0),B点的坐标为(3,0).
令x=0,得y=3,则点C的坐标为(0,3),
∵⊙D过A,B两点,
∴由圆的垂径定理可知E点的横坐标为1,D点的坐标为(1,y).
5
∴y=1,
. D点的坐标为(1,1),
∵P在圆上,
延长DO到F使得 连接PF,PO,
∵直线DF经过点D(1,1)、O(0,0),
∴直线DF的解析式是y=x,
设F点坐标为(x,y),
解得
∴点F的坐标为
∴△DOP∽△DPF,
∴当P、C、F三点共线时取最小值,
故答案为:3
12如图,点A、B在圆O上,OA⊥OB,OA=OB=12,点C是OA的中点,点D在OB上,OD=10,点P是圆O上一动点,则 的最小值为 .
【答案】13
【解析】延长OA至Q,使QA=AO=12,连接QP,
∴△COP∽△POQ,
∴PQ=2PC,
当P、Q、D三点共线时,
13如图,正方形ABCD的边长为4,E是BC的中点,F是BE的中点,P点是以B为圆心,BE为半径的圆上任意一点,则 的最小值为 .
【答案】
【解析】设圆与AB交于G点,BG中点为H,连HP、PC、BP.
易证△BHP∽△BPA,△BFP∽△BPC,且相似比均为1:2.
则 为所求.
14.问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连接AP、BP,求 的最小值,
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D使CD=1,则有 又∵∠PCD=∠BCP,∴△PCD∽△BCP ,∴
请你完成余下的思考,并直接写出答案: BP的最小值为
中小学教育资源及组卷应用平台
(2)自主探索:在“问题提出”的条件不变的情况下 的最小值为
【答案】(1)
【解析】(1)如图1,连接AD,
∴当点A, P,D在同一条直线时, AP+PD最小,
日 BP的最小值为AD的长度,
在Rt△ACD中,CD=1,AC=6,
的最小值为
(2)如图2,连接CP,在CA上取点D,使
·∠PCD=∠ACP,
∴△PCD∽△ACP,
∴同(1)的方法得出 的最小值为
【标注】【知识点】阿氏圆问题
15.(1)【问题发现】
如图1,已知线段AC和BC,AC=2,BC=5,则线段AB的最小值为 .
(2)【问题探究】
如图2,在矩形ABCD中,BC=7,AB=9,P为矩形内部一点,分别连接AP. BRCP,且PB-3,延长CP交AB于点F,若BF=1,求 的值.
(3) 【问题解决】
如图3是某街心花园的一角,在扇形AOB中,∠AOB=90°,OA=12米,在矮围墙OA和OB上分别有两个入口C和D,AC=4米,D为OB的中点.现要在AB上找一个出口E,沿CE、DE从入口到出口铺设两条景观小路.已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元,则在AB上是否存在点E,使铺设小路CE和DE的总造价最低 若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.(小路的宽度忽略不计)
【答案】(1)3
(2)5
(3)存在,总造价的最小值为 出口E距直线OB的距离为 米.
【解析】(1)当AC与BC重合时,AB最小,
ABmin=BC-AC=5-2=3.
(2)如图,在AB上截取BF=1,连接PF、CF,
∴AB=9,PB=3,BF=1,
.∠ABP=∠PBF,
.△ABP∽△PBF,
当F、P、C三点共线时. 最小,且为CF的长,
在Rt△BCF中,BF=1,BC=7,
(3) 铺设小路CE和DE总造价为200CE+400DE=200(CE+2DE),如图:连接OE,延长OB到点Q,使BQ=OB=12米,连接EQ,在△EOD与△QOE中,∠EOD=∠QOE,
∴△EOD∽△QOE,
故:QE=2DE,
∴CE+2DE=CE+QE,问题转化为求CE+QE的最小值,
连接CQ,交弧AB于点E',此时CE+QE取得最小值CQ,
在Rt△COQ中,CO=8米,OQ=24米,
米,
故总造价的最小值为1600 元.
作E'H⊥OB,垂足为H ,连接OE',
设E'H=x,则QH=3x,
∵在Rt△E'OH中, 有 解得: (舍) ,
∴总造价的最小值为: 出口E距直线OB的距离为
【标注】 【知识点】圆与最值问题
16.如图,抛物线 c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:
交y轴于点C .点E是直线AB上的动点,过点E作EF⊥x轴交AO于点F,交抛物线于点G.
(1)求抛物线 c的表达式.
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标.
(3)解答下列各题:
① 在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F ,H为顶点的四边形是矩形 求出此时点E,H的坐标.
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求 的最小值.
【答案】(
(2) G(-2,4).
(3)① E(-2,0),H(0,-1).
【解析】(1) ∵点A(-4,-4), B(0,4)在抛物线g
抛物线的解析式为
(2) 设直线AB的解析式为y= kx+n过点A, B,
直线AB的解析式为y=2x+4.
设E(m,2m+4),
∵四边形GEOB是平行四边形,
∴EG=OB=4,
∴m=-2,
∴G(-2,4).
(3)① 如图1,
由(2)知,直线AB的解析式为y=2x+4,
∴设E(a,2a+4).
∵直线
设H(0,p),
∵以点A,E,F,H为顶点的四边形是矩形,
且直线AB的解析式为y=2x+4,直线AC的解析式为
∴AB⊥AC,
∴EF与AH互相平分,
∴a=-2,p=-1,
. E(-2,0), H(0,-1).
②
如图2,
由①知,E(-2,0), H(0,-1),
A(-4,-4).
设AE交⊙E于G ,取EG的中点P,
连接PC交⊙E于M ,连接EM,
∠PEM=∠MEA,
∴△PEM∽△MEA,
的最小值=PC.
设点
∵E(-2,0),
或 由于E(-2,0),所以舍去) ,
∵C(0,-6),
即
【标注】 【知识点】二次函数与圆的综合问题
同课章节目录
