2024-2025学年山东省济宁市邹城市高一下学期4月期中质量检测数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年山东省济宁市邹城市高一下学期4月期中质量检测数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 259.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-28 00:00:00 | ||
图片预览



文档简介
2024-2025学年山东省济宁市邹城市高一下学期4月期中质量检测
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设是虚数单位,则( )
A. B. C. D.
2.已知单位向量,,且,则( )
A. B. C. D.
3.( )
A. B. C. D.
4.如图,在平面内,不共线向量与构成的四边形中,,分别是,的中点若,则( )
A. B. C. D.
5.已知函数,将函数的图象上各点的横坐标变为原来的倍纵坐标不变,得到函数的图象;再把函数的图象向左平移个单位长度,得到函数的图象,则,的值分别为( )
A. , B. , C. , D. ,
6.已知圆锥的轴截面是三角形,如图,是水平放置的三角形的直观图,若平行于轴,且,则圆锥的侧面积为( )
A. B. C. D.
7.在中,角,,的对边分别为,,,已知,则的形状是( )
A. 等腰三角形或直角三角形 B. 等腰三角形
C. 直角三角形 D. 等腰直角三角形
8.某市居民小区内的重兴塔,在年被列为国家级重点保护单位塔身为八角形楼阁式建筑,九层十檐,最下层为双檐木回廊,檐下系砖雕斗拱上八层为单檐,砖雕仰莲承托,层层紧缩,造型浑厚拙朴,气势雄伟、如图,某校高一学生进行实践活动,选取与塔基在同一水平面内的两个测量基点与,在点测得重兴塔在北偏东的点处,塔顶的仰角为,在点测得重兴塔在北偏西的处,通过测量两个测量基点与之间的距离约为米,则塔高约为 米.
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.在复平面内,若复数,则下列说法正确的是( )
A. 当时,复数的虚部为
B. 当时,
C. 当时,复数对应的点在第一象限
D. 当时,为纯虚数
10.如图,设,是平面内相交成角的两条数轴,和分别是与轴和轴正方向同向的单位向量若向量,则定义有序数对叫做向量的广义坐标若,两点的广义坐标分别为,则下列说法正确的是( )
A. 若,则
B. 若,,三点共线,则
C. 若,则点的广义坐标为
D. 若,,则
11.的内角、、的对边分别为、、,若,则( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,,若,则 .
13.函数的最大值 .
14.已知圆台甲、乙有相同的内切球与圆台的上、下底面及侧面都相切的球叫圆台的内切球,两圆台的高为,圆台的母线长分别为、,则圆台甲与乙的体积之比为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,是同一平面内的两个向量,其中.
若,且与垂直,求与的夹角;
若,且在上的投影向量的坐标为,求实数.
16.本小题分
已知复数为虚数.
若是实数,求复数的模;
若,是关于的方程的一个根,求.
17.本小题分
已知,,其中,.
求;
求.
18.本小题分
的内角、、的对边分别为、、,已知,且.
求;
若的面积为,角的角平分线为,求的长;
若为锐角三角形,为边的中点,求的取值范围.
19.本小题分
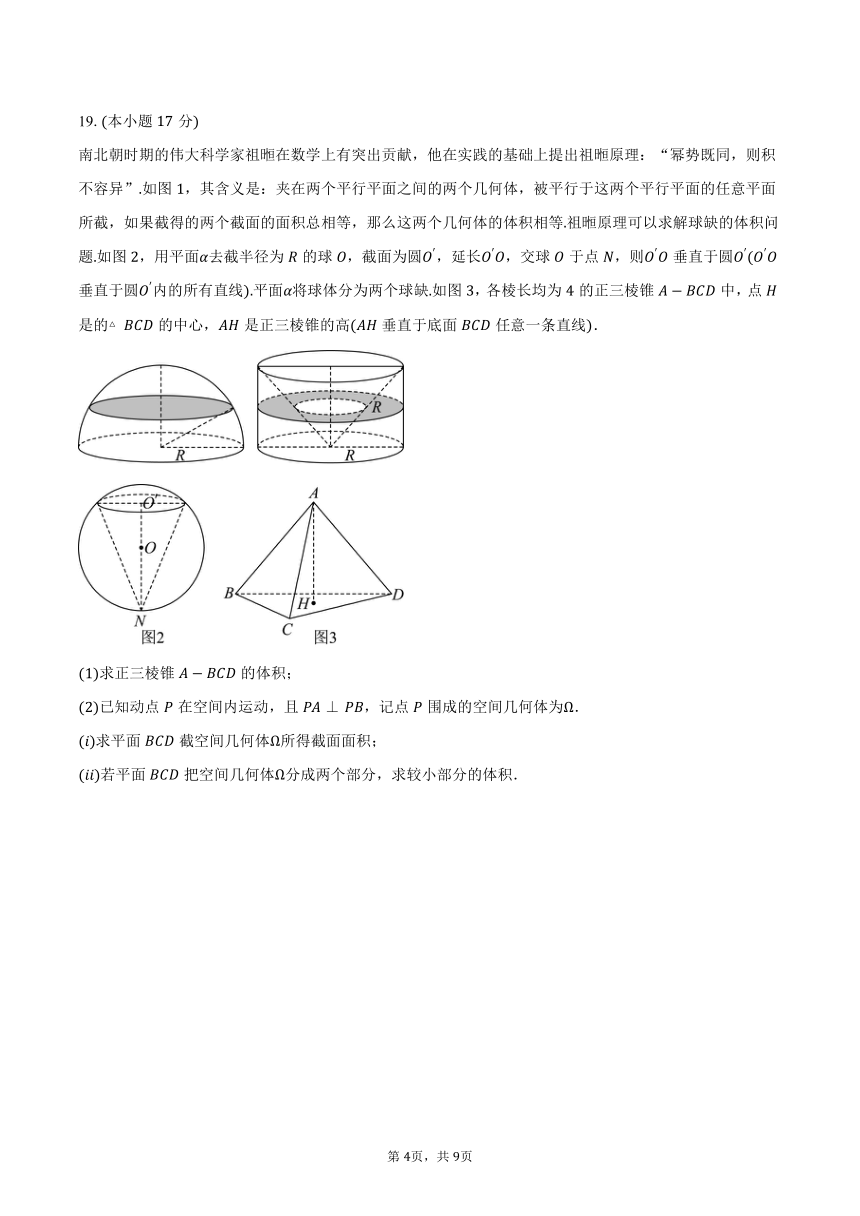
南北朝时期的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”如图,其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等祖暅原理可以求解球缺的体积问题如图,用平面去截半径为的球,截面为圆,延长,交球于点,则垂直于圆垂直于圆内的所有直线平面将球体分为两个球缺如图,各棱长均为的正三棱锥中,点是的的中心,是正三棱锥的高垂直于底面任意一条直线.
求正三棱锥的体积;
已知动点在空间内运动,且,记点围成的空间几何体为.
求平面截空间几何体所得截面面积;
若平面把空间几何体分成两个部分,求较小部分的体积.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.【详解】因为与垂直,
所以,故,又,
所以,
由,可得,
所以,
又,
所以,
因为,,
所以,
因为在上的投影向量的坐标为,
所以,
所以,
所以,
所以.
16.【详解】由复数为虚数,则,
又因为,
因为是实数,所以,即,所以;
由是方程的一个根,所以,即,由,
所以.
17.【详解】因为,,则,,
因为,,
所以,,
,
所以,
.
因为,
,
所以,
,
因此.
18.【详解】设的外接圆半径为,
由正弦定理可得,,,
因为,
所以,
又,
所以,
所以,又,故,
所以,因为,故,
所以,故,
所以;
因为的面积为,又的面积,,
由,所以,
因为为角的角平分线,故,
又,
所以,即,
所以;
所以的长为;
在中由正弦定理可得,
由,又,,
所以,
因为为锐角三角形,所以,,
所以,故,
所以,
在中由余弦定理可得,
又,,,
所以,
所以,
所以的取值范围为.
19.【详解】已知正三棱锥各棱长均为,是正三角形可得.
因为点是的中心,在正三角形中,.
在中,根据勾股定理,,,则.
根据三棱锥体积公式,可得.
因为,所以点的轨迹是以为直径的球,球的半径.
设球心为,为中点,求到平面的距离:
为中心,,则到平面的距离.
设截面圆的半径为,根据勾股定理.
根据圆的面积公式,可得截面面积.
设较小部分为球缺,利用祖暅原理,推导球缺体积公式.
设球半径为,球缺高为.
构造一个底面半径,高为的圆柱,在圆柱里挖去一个同底等高的圆锥.
对于球缺,在距离球缺底面处,由勾股定理可知截面半径,
此截面面积.
对于上述圆柱挖圆锥的组合体,在距离底面处,圆柱截面面积是,
圆锥在该高度处截面半径与高度成正比,其截面面积为,
所以组合体在该高度处截面面积.
可见在任意相同高度处,球缺和组合体的截面面积相等.
圆柱体积,圆锥体积,
组合体体积,故球缺体积也是.
先求球缺的高根据球缺体积公式将,代入可得:
.
第1页,共1页
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设是虚数单位,则( )
A. B. C. D.
2.已知单位向量,,且,则( )
A. B. C. D.
3.( )
A. B. C. D.
4.如图,在平面内,不共线向量与构成的四边形中,,分别是,的中点若,则( )
A. B. C. D.
5.已知函数,将函数的图象上各点的横坐标变为原来的倍纵坐标不变,得到函数的图象;再把函数的图象向左平移个单位长度,得到函数的图象,则,的值分别为( )
A. , B. , C. , D. ,
6.已知圆锥的轴截面是三角形,如图,是水平放置的三角形的直观图,若平行于轴,且,则圆锥的侧面积为( )
A. B. C. D.
7.在中,角,,的对边分别为,,,已知,则的形状是( )
A. 等腰三角形或直角三角形 B. 等腰三角形
C. 直角三角形 D. 等腰直角三角形
8.某市居民小区内的重兴塔,在年被列为国家级重点保护单位塔身为八角形楼阁式建筑,九层十檐,最下层为双檐木回廊,檐下系砖雕斗拱上八层为单檐,砖雕仰莲承托,层层紧缩,造型浑厚拙朴,气势雄伟、如图,某校高一学生进行实践活动,选取与塔基在同一水平面内的两个测量基点与,在点测得重兴塔在北偏东的点处,塔顶的仰角为,在点测得重兴塔在北偏西的处,通过测量两个测量基点与之间的距离约为米,则塔高约为 米.
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.在复平面内,若复数,则下列说法正确的是( )
A. 当时,复数的虚部为
B. 当时,
C. 当时,复数对应的点在第一象限
D. 当时,为纯虚数
10.如图,设,是平面内相交成角的两条数轴,和分别是与轴和轴正方向同向的单位向量若向量,则定义有序数对叫做向量的广义坐标若,两点的广义坐标分别为,则下列说法正确的是( )
A. 若,则
B. 若,,三点共线,则
C. 若,则点的广义坐标为
D. 若,,则
11.的内角、、的对边分别为、、,若,则( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,,若,则 .
13.函数的最大值 .
14.已知圆台甲、乙有相同的内切球与圆台的上、下底面及侧面都相切的球叫圆台的内切球,两圆台的高为,圆台的母线长分别为、,则圆台甲与乙的体积之比为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,是同一平面内的两个向量,其中.
若,且与垂直,求与的夹角;
若,且在上的投影向量的坐标为,求实数.
16.本小题分
已知复数为虚数.
若是实数,求复数的模;
若,是关于的方程的一个根,求.
17.本小题分
已知,,其中,.
求;
求.
18.本小题分
的内角、、的对边分别为、、,已知,且.
求;
若的面积为,角的角平分线为,求的长;
若为锐角三角形,为边的中点,求的取值范围.
19.本小题分
南北朝时期的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”如图,其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等祖暅原理可以求解球缺的体积问题如图,用平面去截半径为的球,截面为圆,延长,交球于点,则垂直于圆垂直于圆内的所有直线平面将球体分为两个球缺如图,各棱长均为的正三棱锥中,点是的的中心,是正三棱锥的高垂直于底面任意一条直线.
求正三棱锥的体积;
已知动点在空间内运动,且,记点围成的空间几何体为.
求平面截空间几何体所得截面面积;
若平面把空间几何体分成两个部分,求较小部分的体积.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.【详解】因为与垂直,
所以,故,又,
所以,
由,可得,
所以,
又,
所以,
因为,,
所以,
因为在上的投影向量的坐标为,
所以,
所以,
所以,
所以.
16.【详解】由复数为虚数,则,
又因为,
因为是实数,所以,即,所以;
由是方程的一个根,所以,即,由,
所以.
17.【详解】因为,,则,,
因为,,
所以,,
,
所以,
.
因为,
,
所以,
,
因此.
18.【详解】设的外接圆半径为,
由正弦定理可得,,,
因为,
所以,
又,
所以,
所以,又,故,
所以,因为,故,
所以,故,
所以;
因为的面积为,又的面积,,
由,所以,
因为为角的角平分线,故,
又,
所以,即,
所以;
所以的长为;
在中由正弦定理可得,
由,又,,
所以,
因为为锐角三角形,所以,,
所以,故,
所以,
在中由余弦定理可得,
又,,,
所以,
所以,
所以的取值范围为.
19.【详解】已知正三棱锥各棱长均为,是正三角形可得.
因为点是的中心,在正三角形中,.
在中,根据勾股定理,,,则.
根据三棱锥体积公式,可得.
因为,所以点的轨迹是以为直径的球,球的半径.
设球心为,为中点,求到平面的距离:
为中心,,则到平面的距离.
设截面圆的半径为,根据勾股定理.
根据圆的面积公式,可得截面面积.
设较小部分为球缺,利用祖暅原理,推导球缺体积公式.
设球半径为,球缺高为.
构造一个底面半径,高为的圆柱,在圆柱里挖去一个同底等高的圆锥.
对于球缺,在距离球缺底面处,由勾股定理可知截面半径,
此截面面积.
对于上述圆柱挖圆锥的组合体,在距离底面处,圆柱截面面积是,
圆锥在该高度处截面半径与高度成正比,其截面面积为,
所以组合体在该高度处截面面积.
可见在任意相同高度处,球缺和组合体的截面面积相等.
圆柱体积,圆锥体积,
组合体体积,故球缺体积也是.
先求球缺的高根据球缺体积公式将,代入可得:
.
第1页,共1页
同课章节目录
