第1单元 观察物体(三)高频易错培优讲练测(讲义)-2024-2025学年五年级下册数学人教版
文档属性
| 名称 | 第1单元 观察物体(三)高频易错培优讲练测(讲义)-2024-2025学年五年级下册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 784.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 14:27:34 | ||
图片预览


文档简介
【思维导图+典型例题+知识精讲+高频真题+答案解析】
1.从不同方向观察物体和几何体 【知识点归纳】 视图定义: 当我们从某一角度观察一个实物时,所看到的图象叫做物体的一个视图. 物体的三视图特指主视图、俯视图、左视图. 主视图:在正面内得到的由前向后观察物体的视图,叫做主视图. 俯视图:在水平面内得到的由上向下观察物体的视图,叫做俯视图. 左视图:在侧面内得到的由左向右观察物体的视图,叫做左视图,有时也叫做侧视图. 人在观察目标时,从眼睛到目标的射线叫做视线,眼睛所在的位置叫做视点,有公共视点的两条视线所称的角叫做视角. 我们把视线不能到达的区域叫做盲区. 2.从不同角度观察多个物体 【知识点归纳】 1、不同角度观察一个物体,看到的面都是两个或三个相邻的面。 2、不可能一次看到长方体或正方体相对的面。 注意点: (1)这里所说的正面、左面和上面,都是相对于观察者而言的。 (2)站在任意一个位置,最多只能看到长方体的3个面。 (3)从不同的位置观察物体,看到的形状可能是不同的。 (4)从一个或两个方向看到的图形是不能确定立体图形的形状的。 (5)同一角度观察不同的立体图形,得到的平面图形可能是相同,也可能是不同的。 (6)如果从物体的右面观察,看到的不一定和从左面看到的完全相同。 3.作简单图形的三视图 【知识点归纳】 在画组合体三视图之前,首先运用形体分析法把组合体分解为若干个形体,确定它们的组合形式,判断形体间邻接表面是否处于共面、相切和相交的特殊位置;然后逐个画出形体的三视图;最后对组合体中的垂直面、一般位置面、邻接表面处于共面、相切或相交位置的面、线进行投影分析.当组合体中出现不完整形体、组合柱或复合形体相贯时,可用恢复原形法进行分析. 画哪个方向上的三视图就想象哪个方向上有光照到物体上,画出投影即可.
一、选择题
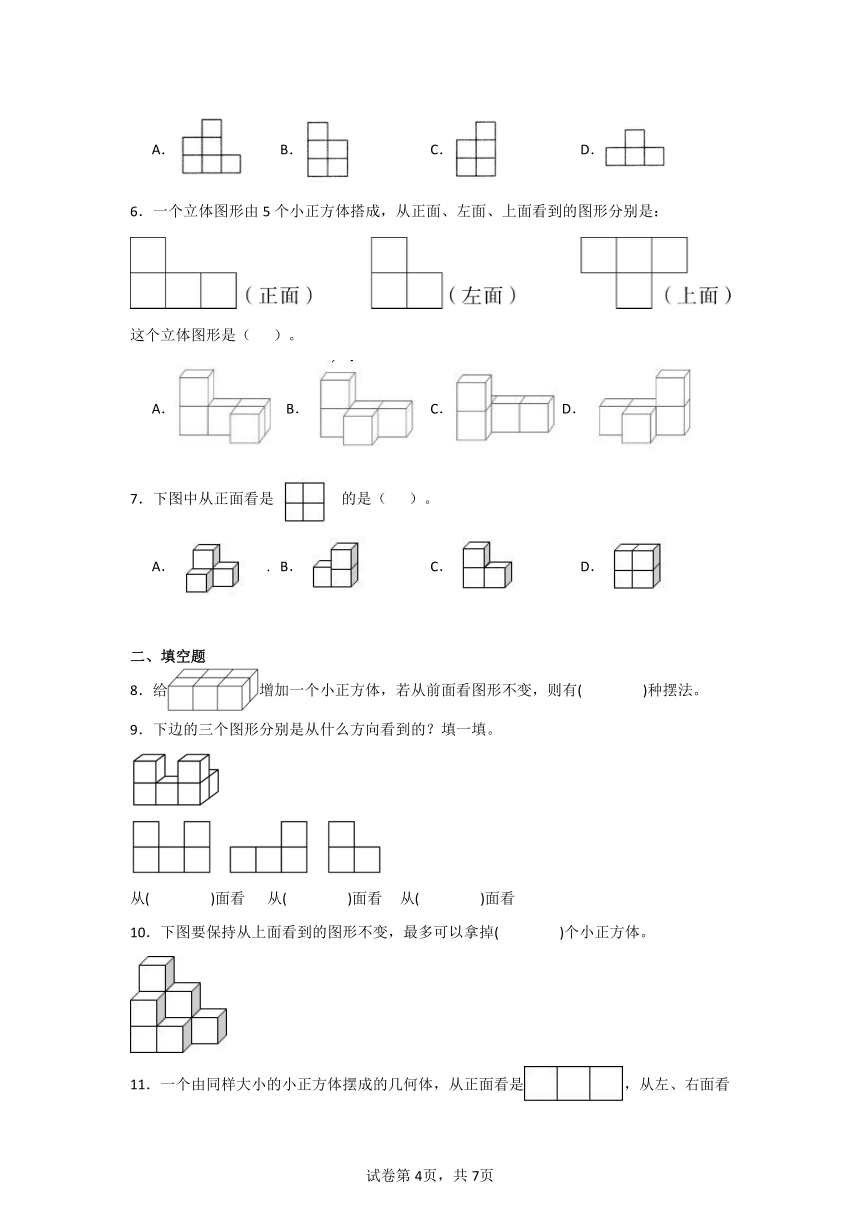
1.一个几何体从上面看是,从前面看是,这个几何体是( )。
A. B. C.
2.从不同的方向观察如下图所示的几何体:有以下4个图案:
其中不可能看到的图案是( )。
A.① B.② C.③ D.④
3.用5个小正方体搭建几何体,要求从正面看到的图形,从左面看到的图形是,那么下列搭法不正确的是( )。
A. B. C. D.
4.由5个小立方块搭成的立体图形,从正面看到的图形是,从左面看到的图形是。这个立体图形的样子是( )。
A. B. C. D.
5.一个几何体从上面看到的形状是,小正方形上面的数字表示在这个位置上所摆小正方体的个数,那么这个几何体从左面看到的是( )。
A. B. C. D.
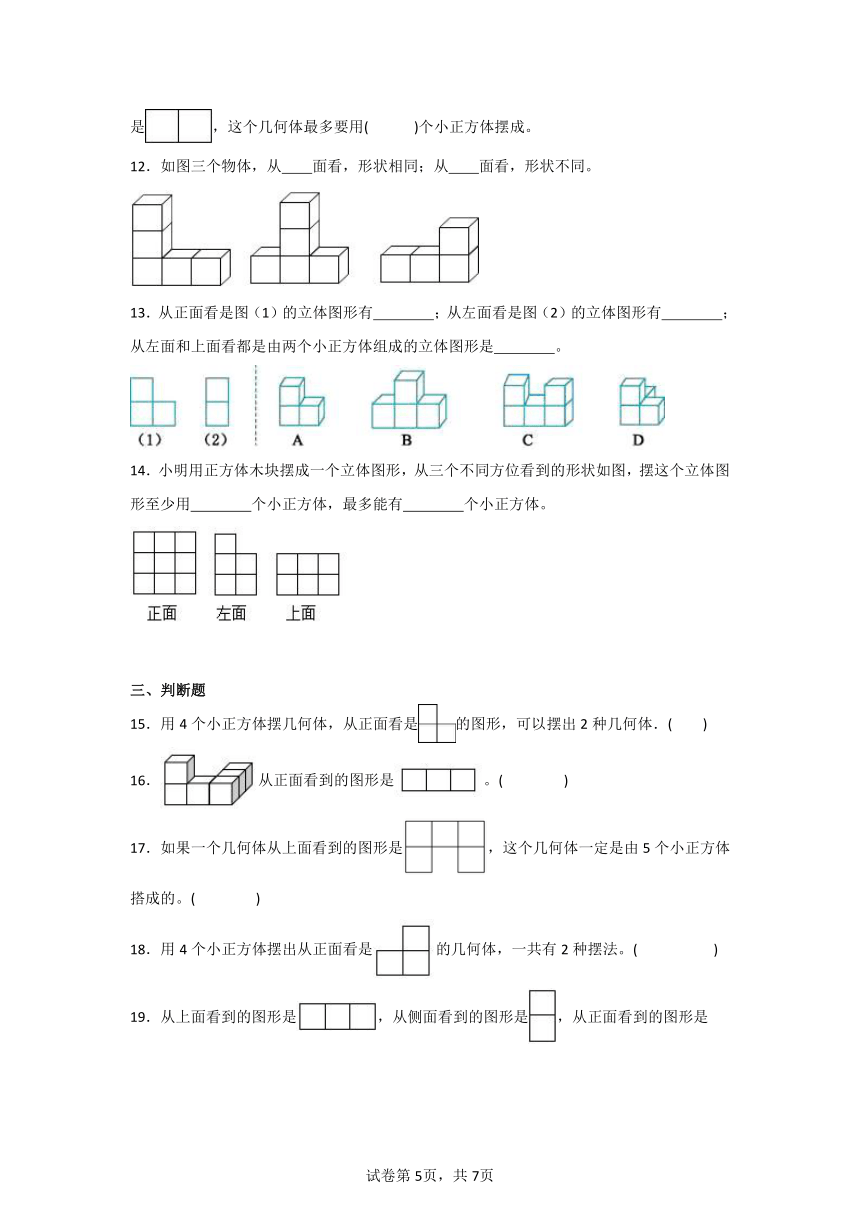
6.一个立体图形由5个小正方体搭成,从正面、左面、上面看到的图形分别是:
这个立体图形是( )。
A.B. C.D.
7.下图中从正面看是的是( )。
A. . B. C. D.
二、填空题
8.给增加一个小正方体,若从前面看图形不变,则有( )种摆法。
9.下边的三个图形分别是从什么方向看到的?填一填。
从( )面看 从( )面看 从( )面看
10.下图要保持从上面看到的图形不变,最多可以拿掉( )个小正方体。
11.一个由同样大小的小正方体摆成的几何体,从正面看是,从左、右面看是,这个几何体最多要用( )个小正方体摆成。
12.如图三个物体,从 面看,形状相同;从 面看,形状不同。
13.从正面看是图(1)的立体图形有 ;从左面看是图(2)的立体图形有 ;从左面和上面看都是由两个小正方体组成的立体图形是 。
14.小明用正方体木块摆成一个立体图形,从三个不同方位看到的形状如图,摆这个立体图形至少用 个小正方体,最多能有 个小正方体。
三、判断题
15.用4个小正方体摆几何体,从正面看是的图形,可以摆出2种几何体.( )
16.从正面看到的图形是。( )
17.如果一个几何体从上面看到的图形是,这个几何体一定是由5个小正方体搭成的。( )
18.用4个小正方体摆出从正面看是的几何体,一共有2种摆法。( )
19.从上面看到的图形是,从侧面看到的图形是,从正面看到的图形是,可以确定这个立体图形的形状是。( )
20.如下图,把一个小正方体放在这个几何体的前面或后面,从正面看到的形状是不变的。 ( )
21.从左面看到的形状是 ,不能确定有多少个小正方体。( )
四、作图题
22.从不同方向看下面的物体,看到的分别是什么,在方格纸上画一画。
五、解答题
23.用一些同样的正方体积木在桌面上摆一个几何体,要求从正面、上面和左面看到的图形都是,至少需要用几块正方体积木?最多呢?
24.计算一下,下面堆起的立体图形中一共用了多少个小正方体积木?
25.从前面观察一个由同样的小正方体组成的几何体,看到的图形如下图,这个几何体可能是怎样摆的?
(1)这个几何体如果是由4个小正方体组成的,可以怎样摆?
(2)这个几何体如果是由5个、6个、7个或更多的小正方体组成的,可以怎样摆?
26.用5个小正方体木块摆一摆。
(1)从正面看到的图形如下,有几种摆法?
(2)如果要同时满足从上面看到的图形如下,有几种摆法?
27.如下图所示,要使从上面看到的图形不变:
(1)如果是5个小正方体,可以有几种不同的摆法?
(2)如果有6个小正方体,可以怎样摆?
(3)最多可以摆几个小正方体?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【分析】根据从不同角度观察立体图形的方法,分别从上面和前面观察各个图形,再进行解答。
【详解】
A.从上面看是,从前面看是,不符合题意,排除;
B.从上面看是,从前面看是,符合题意;
C.从上面看是,从前面看是,不符合题意,排除;
故答案为:B
2.B
【详解】略
3.C
【分析】观察几何体可知:A、B、C、D四个几何体从正面看的图形是一样的,都是最下面一层3个正方形并排,上面一层有一个正方形入在左上角形状如右图:
再从左面观察:A、B、C、D四个几何体,所看到的形状是否和一样。由此判断。
【详解】A、B、C、D四个几何体从正面看的图形是一样的,形状如右图:
从左面观察A、B、D,看到的形状是,而C从左面看到的形状是。
故答案为:C
【点睛】本题考查了根据物体的三视图来确定几何体,注意培养空间想象能力。
4.B
【分析】
根据题意,从正面看到的图形是,第一层3个小正方形,第二层1个小正方形,从左面看到的图形是,第一层2个小正方形,第二层1个小正方形,据此与选项中的图形进行比对,符合则为正确项,据此解答。
【详解】
A.,从正面看到的是,与题意符合,从左面看到的图形是,与题意不符合,选项错误。
B.,从正面看到的是,与题意符合,从左面到的图形是,与题意符合,选项正确。
C. ,从正面看到的是,与题意符合,从左面看到的图形是,与题意不符合,选项错误。
D. ,从正面看到的是,与题意符合,从左面看到的图形是,与题意不符合,选项错误。
故答案为:B
5.B
【分析】根据题意可知,这个几何体由7个小正方体组成;从左面看能看到2列5个小正方体,从左往右,分别是3个、2个,下齐,据此解答。
【详解】
根据分析可知,一个几何体从上面看到的形状是,小正方形上面的数字表示在这个位置上所摆小正方体的个数,那么这个几何体从左面看到的是。
故答案为:B
6.B
【解析】分别将A、B、C、D的正面、左面、上面观察图画出来,和题目中的进行比较即可。
【详解】A从正面、左面、上面看到的图形分别是:
B从正面、左面、上面看到的图形分别是:
C从正面、左面、上面看到的图形分别是:
D从正面、左面、上面看到的图形分别是:
符合题意的是第二个。
故答案为:B
【点睛】本题考查从不同方向观察几何图形,考查的是学生的立体想象能力。
7.D
【详解】略
8.6
【分析】从前面看有一排,3个小正方形,增加一个小正方体,可以摆在任意小正方体的前、后面,放前面有3种方法,放后面有3种方法,一共有3+3=6种摆放。
【详解】3+3=6(种)
给增加一个小正方体,若从前面看图形不变,则有6种摆法。
9. 正 上 右
【分析】由图形可知,从正面(或前面)看,可以看到图形有两层,下面一层是3个连续的正方形,上面是一层是2个正方形,并且中间间隔1个;从上面看,可以看到图形有两排三列,前面一排有3个,后面一排有1个,在最右边一列;从右面看,可以看到图形有两层,下面一层是2个正方形,上面一层是1个正方形,在左面。据此作答。
【详解】由分析可知:
是从正面(或前面)看到的;
是从上面看到的;
是从右面看到的。
10.4
【分析】观察,从上面看到的图形是,要保持从上面看到的图形不变,只能拿第二层和第三层的小正方体,第二层有3个小正方体,第三层有1个小正方体,全部拿走后,从上面看到的图形依然不变,据此解答。
【详解】根据分析得,3+1=4(个)
最多可以拿掉4个小正方体,从上面看到的图形不变。
【点睛】此题主要考查学生的空间想象力,根据观察立体图形的方法,做出正确的解答。
11.6
【分析】从正面看是,,从左、右面看是说明前面第一排最多有3个小正方体,第二排最多可以排3个,据此解答即可。
【详解】这个几何体最多要用6个小正方体摆成。
【点睛】本题考查观察物体,解答本题的关键是掌握根据三视图确定物体的形状的方法。
12. 上 正
【分析】根据观察物体的方法,得出分别从正面、侧面、上面观察看到的图形,再找出形状相同、不同的即可.本题是考查从不同方向观察物体和几何图形,培养学生的观察能力.
【详解】从上面看这三个物体,看到的图形均是一行3个正方形;
从正面看这三个物体,第一个图形是3行5个正方形,下面一行3个,中间、上面均1个靠左对齐;第二个图形是3行5个正方形,下面一行3个,中间、上面均1个居中对齐;
第三个图形是2行4个正方形,下面一行3个,上面均1个靠右对齐;
从侧面看这三个物体,第一、第二图形均是一列3个正方形,第三个图形是一列2个正方形;
所以这三个物体从上面看,形状相同;从正面看,形状不同。
13. A和D A、B、C A
【分析】分别将A、B、C、D四个图形在正面、左面看到的图形画出来,再进行选择即可。
【详解】从正面看是图(1)的立体图形有A和D;
从左面看是图(2)的立体图形有A、B、C;
从左面和上面看都是由两个小正方体组成的立体图形是A。
【点睛】本题主要考查了学生的空间想象能力,一定要能够根据不同方位画出看到的图形。
14. 13 15
【分析】此题主要考查了观察物体的知识,根据从不同的面观察的图形,确定每层的数量及层数,据此数一数最少需要几个小正方体,最多需要几个小正方体。
【详解】根据图分析可得:
此立体图形分为前后两排:后排有3层,每层有3个,共3×3=9个正方体;
①前排有2层,前排至少有4个正方体,最下层3个正方体,上层1个正方体;9+4=13(个)
②前排最多有6个正方体,下层3个,上层3个;9+3+3=15(个)。
【点睛】题目中的三视图有些复杂,看出来小正方体的个数较多。可充分展开想象,把俯视图做基础,上面参考搭建主视图和左视图提供的信息。
15.×
【详解】略
16.×
【分析】从正面观察立体图形,看到的是2层,共4个小正方形,下层3个,上层1个且居左;据此判断。
【详解】
从正面看到的图形是。
原题说法错误。
故答案为:×
【点睛】本题考查从正面观察立体图形得到的平面图,找出从正面看到的小正方形的个数和它们的相对位置是解题的关键。
17.×
【分析】根据从上面看到的图形,只能确定这个几何体的底层是由5个小正方体搭成,不知道上层的情况,所以无法确定是由几个小正方体搭成。
【详解】结合从上面看到的平面图,可以得出下面的几何体:
……
所以,这个几何体不一定是由5个小正方体搭成的。
原题说法错误。
故答案为:×
18.×
【分析】
根据题意,用4个小正方体摆出从正面看是,可知这个几何体的下层有3个小正方体,上层有1个小正方体;
当下层的前一行有2个小正方体,后一行有1个小正方体且居右时,这时上层的小正方体有2种摆法;
当下层的前一行有2个小正方体,后一行有1个小正方体且居左时,这时上层的小正方体有1种摆法;
当下层的前一行有1个小正方体且居右,后一行有2个小正方体时,这时上层的小正方体有2种摆法;
当下层的前一行有1个小正方体且居左,后一行有2个小正方体时,这时上层的小正方体有1种摆法;
所以一共有(2+1+2+1)种摆法。
【详解】如图:
用4个小正方体摆出从正面看是的几何体,一共有6种摆法。
原题说法错误。
故答案为:×
【点睛】本题考查根据部分视图还原立体图形的能力,培养学生的空间想象力和观察能力。
19.√
【分析】此题考查了从不同方向观察物体和几何体,根据空间想象力和抽象思维能力进行解答即可。
【详解】根据从三个方向看到的形状,可以确定立体图形的形状。本题中从上面、侧面、正面看到的图形符合立体图形的形状。
故答案为:√
【点睛】本题考查从不同位置观察立体图形。
20.√
【分析】
根据观察,从正面和后面看到的图形为,把一个小正方体放在这个几何体的前面或后面,看到的图形还是。
【详解】由分析可知:
把一个小正方体放在这个几何体的前面或后面,从正面看到的形状是不变的。表述正确。
故答案为:√
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
21.√
【详解】因为从一个面看到的是,可能有2个正方体,可能有3个正方,所以正方体的个数不能确定。
故答案为:√
22.见详解
【分析】根据物体三视图的画法,结合立体图形,直接分析作图即可。
【详解】
【点睛】本题考查了观察物体,掌握三视图的画法是解题的关键。
23.6块;8块
【分析】根据从上面看到的图形是, 可以知道底层需要4块积木,如图摆放: 。根据从正面看到的图形是 ,可以知道左右两列都有两层;根据从左面看到的图形是 ,可以知道在前后两行也都有两层。综合从正面和左面看到的图形可以知道第二层上至少应摆放2个小正方体,如图摆放: 、 ;最多可摆放4个小正方体,如图摆放:。
【详解】至少需要6块:、。
最多可摆放8个小正方体,如图摆放:。
答:至少需要用6块正方体积木,最多需要用8块正方体积木。
【点睛】本题考查观察物体,解答本题的关键是掌握根据从不同方向看到的图形确定物体形状的方法。
24.76个
【分析】观察图形,每个图形的每层个数加起来即可算出答案。
【详解】第一个图形:第一层9个,第二层6个,第三层4个,所以第一个图形有9+6+4=19个小正方体积木。
第二个图形:第一层9个,第二层6个,第三层3个,所以第二个图形有9+6+3=18个小正方体积木。
第三个图形:第一层11个,第二层6个,第三层3个,所以第三个图形有11+6+3=20个小正方体积木。
第四个图形:第一层9个,第二层7个,第三层3个,所以第四个图形有9+7+3=19个小正方体积木。
即:19+18+20+19
=37+20+19
=57+19
=76(个)
答:下面堆起的立体图形中一共用了76个小正方体积木。
【点睛】本题主要考查学生的观察能力,看清每层的数量。
25.见详解
【分析】
无论用4个、5个、6个、7个或更多的小正方体组成的几何体,从前面看到的形状都是,只要满足这个条件即可。
【详解】(1)这个几何体如果是由4个小正方体组成的,可以这样摆,如图:
(答案不唯一)
(2)这个几何体如果是由5个、6个、7个小正方体或更多的小正方体组成的,可以这样摆,如图:
(答案不唯一)
26.(1)6种 (2)1种
【分析】(1)从正面看到的图形由4个小正方体组成,分两层,则另一个小正方体可以摆在第一层3个小正方体的前面或后面(共6个不同位置),所以有6种不同的搭法;(2)再结合从上面看到的图形分析,只能有一种摆法。
【详解】(1)答:有6种摆法。
(2)答:有1种摆法。
27.(1)4种
(2)10种,摆法见详解
(3)无数个
【分析】(1)根据从上面、正面和侧面看到的图形可知,底层有4个小正方体。如果是5个小正方体,要使从上面看到的图形不变,可以从第二层上任意放一个;
(2)如果有6个小正方体,要使从上面看到的图形不变,可以从第二层上任意放两个;
(3)要使从上面看到的图形不变,可以在底层的4个小正方体的上方加小正方体,可以加无数个。
【详解】(1)如果是5个小正方体,有四种摆法;
(2)有10种摆法
(3)最多可以摆无数个小正方体。
【点睛】本题较易,考虑观察物体的知识点。
1.从不同方向观察物体和几何体 【知识点归纳】 视图定义: 当我们从某一角度观察一个实物时,所看到的图象叫做物体的一个视图. 物体的三视图特指主视图、俯视图、左视图. 主视图:在正面内得到的由前向后观察物体的视图,叫做主视图. 俯视图:在水平面内得到的由上向下观察物体的视图,叫做俯视图. 左视图:在侧面内得到的由左向右观察物体的视图,叫做左视图,有时也叫做侧视图. 人在观察目标时,从眼睛到目标的射线叫做视线,眼睛所在的位置叫做视点,有公共视点的两条视线所称的角叫做视角. 我们把视线不能到达的区域叫做盲区. 2.从不同角度观察多个物体 【知识点归纳】 1、不同角度观察一个物体,看到的面都是两个或三个相邻的面。 2、不可能一次看到长方体或正方体相对的面。 注意点: (1)这里所说的正面、左面和上面,都是相对于观察者而言的。 (2)站在任意一个位置,最多只能看到长方体的3个面。 (3)从不同的位置观察物体,看到的形状可能是不同的。 (4)从一个或两个方向看到的图形是不能确定立体图形的形状的。 (5)同一角度观察不同的立体图形,得到的平面图形可能是相同,也可能是不同的。 (6)如果从物体的右面观察,看到的不一定和从左面看到的完全相同。 3.作简单图形的三视图 【知识点归纳】 在画组合体三视图之前,首先运用形体分析法把组合体分解为若干个形体,确定它们的组合形式,判断形体间邻接表面是否处于共面、相切和相交的特殊位置;然后逐个画出形体的三视图;最后对组合体中的垂直面、一般位置面、邻接表面处于共面、相切或相交位置的面、线进行投影分析.当组合体中出现不完整形体、组合柱或复合形体相贯时,可用恢复原形法进行分析. 画哪个方向上的三视图就想象哪个方向上有光照到物体上,画出投影即可.
一、选择题
1.一个几何体从上面看是,从前面看是,这个几何体是( )。
A. B. C.
2.从不同的方向观察如下图所示的几何体:有以下4个图案:
其中不可能看到的图案是( )。
A.① B.② C.③ D.④
3.用5个小正方体搭建几何体,要求从正面看到的图形,从左面看到的图形是,那么下列搭法不正确的是( )。
A. B. C. D.
4.由5个小立方块搭成的立体图形,从正面看到的图形是,从左面看到的图形是。这个立体图形的样子是( )。
A. B. C. D.
5.一个几何体从上面看到的形状是,小正方形上面的数字表示在这个位置上所摆小正方体的个数,那么这个几何体从左面看到的是( )。
A. B. C. D.
6.一个立体图形由5个小正方体搭成,从正面、左面、上面看到的图形分别是:
这个立体图形是( )。
A.B. C.D.
7.下图中从正面看是的是( )。
A. . B. C. D.
二、填空题
8.给增加一个小正方体,若从前面看图形不变,则有( )种摆法。
9.下边的三个图形分别是从什么方向看到的?填一填。
从( )面看 从( )面看 从( )面看
10.下图要保持从上面看到的图形不变,最多可以拿掉( )个小正方体。
11.一个由同样大小的小正方体摆成的几何体,从正面看是,从左、右面看是,这个几何体最多要用( )个小正方体摆成。
12.如图三个物体,从 面看,形状相同;从 面看,形状不同。
13.从正面看是图(1)的立体图形有 ;从左面看是图(2)的立体图形有 ;从左面和上面看都是由两个小正方体组成的立体图形是 。
14.小明用正方体木块摆成一个立体图形,从三个不同方位看到的形状如图,摆这个立体图形至少用 个小正方体,最多能有 个小正方体。
三、判断题
15.用4个小正方体摆几何体,从正面看是的图形,可以摆出2种几何体.( )
16.从正面看到的图形是。( )
17.如果一个几何体从上面看到的图形是,这个几何体一定是由5个小正方体搭成的。( )
18.用4个小正方体摆出从正面看是的几何体,一共有2种摆法。( )
19.从上面看到的图形是,从侧面看到的图形是,从正面看到的图形是,可以确定这个立体图形的形状是。( )
20.如下图,把一个小正方体放在这个几何体的前面或后面,从正面看到的形状是不变的。 ( )
21.从左面看到的形状是 ,不能确定有多少个小正方体。( )
四、作图题
22.从不同方向看下面的物体,看到的分别是什么,在方格纸上画一画。
五、解答题
23.用一些同样的正方体积木在桌面上摆一个几何体,要求从正面、上面和左面看到的图形都是,至少需要用几块正方体积木?最多呢?
24.计算一下,下面堆起的立体图形中一共用了多少个小正方体积木?
25.从前面观察一个由同样的小正方体组成的几何体,看到的图形如下图,这个几何体可能是怎样摆的?
(1)这个几何体如果是由4个小正方体组成的,可以怎样摆?
(2)这个几何体如果是由5个、6个、7个或更多的小正方体组成的,可以怎样摆?
26.用5个小正方体木块摆一摆。
(1)从正面看到的图形如下,有几种摆法?
(2)如果要同时满足从上面看到的图形如下,有几种摆法?
27.如下图所示,要使从上面看到的图形不变:
(1)如果是5个小正方体,可以有几种不同的摆法?
(2)如果有6个小正方体,可以怎样摆?
(3)最多可以摆几个小正方体?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【分析】根据从不同角度观察立体图形的方法,分别从上面和前面观察各个图形,再进行解答。
【详解】
A.从上面看是,从前面看是,不符合题意,排除;
B.从上面看是,从前面看是,符合题意;
C.从上面看是,从前面看是,不符合题意,排除;
故答案为:B
2.B
【详解】略
3.C
【分析】观察几何体可知:A、B、C、D四个几何体从正面看的图形是一样的,都是最下面一层3个正方形并排,上面一层有一个正方形入在左上角形状如右图:
再从左面观察:A、B、C、D四个几何体,所看到的形状是否和一样。由此判断。
【详解】A、B、C、D四个几何体从正面看的图形是一样的,形状如右图:
从左面观察A、B、D,看到的形状是,而C从左面看到的形状是。
故答案为:C
【点睛】本题考查了根据物体的三视图来确定几何体,注意培养空间想象能力。
4.B
【分析】
根据题意,从正面看到的图形是,第一层3个小正方形,第二层1个小正方形,从左面看到的图形是,第一层2个小正方形,第二层1个小正方形,据此与选项中的图形进行比对,符合则为正确项,据此解答。
【详解】
A.,从正面看到的是,与题意符合,从左面看到的图形是,与题意不符合,选项错误。
B.,从正面看到的是,与题意符合,从左面到的图形是,与题意符合,选项正确。
C. ,从正面看到的是,与题意符合,从左面看到的图形是,与题意不符合,选项错误。
D. ,从正面看到的是,与题意符合,从左面看到的图形是,与题意不符合,选项错误。
故答案为:B
5.B
【分析】根据题意可知,这个几何体由7个小正方体组成;从左面看能看到2列5个小正方体,从左往右,分别是3个、2个,下齐,据此解答。
【详解】
根据分析可知,一个几何体从上面看到的形状是,小正方形上面的数字表示在这个位置上所摆小正方体的个数,那么这个几何体从左面看到的是。
故答案为:B
6.B
【解析】分别将A、B、C、D的正面、左面、上面观察图画出来,和题目中的进行比较即可。
【详解】A从正面、左面、上面看到的图形分别是:
B从正面、左面、上面看到的图形分别是:
C从正面、左面、上面看到的图形分别是:
D从正面、左面、上面看到的图形分别是:
符合题意的是第二个。
故答案为:B
【点睛】本题考查从不同方向观察几何图形,考查的是学生的立体想象能力。
7.D
【详解】略
8.6
【分析】从前面看有一排,3个小正方形,增加一个小正方体,可以摆在任意小正方体的前、后面,放前面有3种方法,放后面有3种方法,一共有3+3=6种摆放。
【详解】3+3=6(种)
给增加一个小正方体,若从前面看图形不变,则有6种摆法。
9. 正 上 右
【分析】由图形可知,从正面(或前面)看,可以看到图形有两层,下面一层是3个连续的正方形,上面是一层是2个正方形,并且中间间隔1个;从上面看,可以看到图形有两排三列,前面一排有3个,后面一排有1个,在最右边一列;从右面看,可以看到图形有两层,下面一层是2个正方形,上面一层是1个正方形,在左面。据此作答。
【详解】由分析可知:
是从正面(或前面)看到的;
是从上面看到的;
是从右面看到的。
10.4
【分析】观察,从上面看到的图形是,要保持从上面看到的图形不变,只能拿第二层和第三层的小正方体,第二层有3个小正方体,第三层有1个小正方体,全部拿走后,从上面看到的图形依然不变,据此解答。
【详解】根据分析得,3+1=4(个)
最多可以拿掉4个小正方体,从上面看到的图形不变。
【点睛】此题主要考查学生的空间想象力,根据观察立体图形的方法,做出正确的解答。
11.6
【分析】从正面看是,,从左、右面看是说明前面第一排最多有3个小正方体,第二排最多可以排3个,据此解答即可。
【详解】这个几何体最多要用6个小正方体摆成。
【点睛】本题考查观察物体,解答本题的关键是掌握根据三视图确定物体的形状的方法。
12. 上 正
【分析】根据观察物体的方法,得出分别从正面、侧面、上面观察看到的图形,再找出形状相同、不同的即可.本题是考查从不同方向观察物体和几何图形,培养学生的观察能力.
【详解】从上面看这三个物体,看到的图形均是一行3个正方形;
从正面看这三个物体,第一个图形是3行5个正方形,下面一行3个,中间、上面均1个靠左对齐;第二个图形是3行5个正方形,下面一行3个,中间、上面均1个居中对齐;
第三个图形是2行4个正方形,下面一行3个,上面均1个靠右对齐;
从侧面看这三个物体,第一、第二图形均是一列3个正方形,第三个图形是一列2个正方形;
所以这三个物体从上面看,形状相同;从正面看,形状不同。
13. A和D A、B、C A
【分析】分别将A、B、C、D四个图形在正面、左面看到的图形画出来,再进行选择即可。
【详解】从正面看是图(1)的立体图形有A和D;
从左面看是图(2)的立体图形有A、B、C;
从左面和上面看都是由两个小正方体组成的立体图形是A。
【点睛】本题主要考查了学生的空间想象能力,一定要能够根据不同方位画出看到的图形。
14. 13 15
【分析】此题主要考查了观察物体的知识,根据从不同的面观察的图形,确定每层的数量及层数,据此数一数最少需要几个小正方体,最多需要几个小正方体。
【详解】根据图分析可得:
此立体图形分为前后两排:后排有3层,每层有3个,共3×3=9个正方体;
①前排有2层,前排至少有4个正方体,最下层3个正方体,上层1个正方体;9+4=13(个)
②前排最多有6个正方体,下层3个,上层3个;9+3+3=15(个)。
【点睛】题目中的三视图有些复杂,看出来小正方体的个数较多。可充分展开想象,把俯视图做基础,上面参考搭建主视图和左视图提供的信息。
15.×
【详解】略
16.×
【分析】从正面观察立体图形,看到的是2层,共4个小正方形,下层3个,上层1个且居左;据此判断。
【详解】
从正面看到的图形是。
原题说法错误。
故答案为:×
【点睛】本题考查从正面观察立体图形得到的平面图,找出从正面看到的小正方形的个数和它们的相对位置是解题的关键。
17.×
【分析】根据从上面看到的图形,只能确定这个几何体的底层是由5个小正方体搭成,不知道上层的情况,所以无法确定是由几个小正方体搭成。
【详解】结合从上面看到的平面图,可以得出下面的几何体:
……
所以,这个几何体不一定是由5个小正方体搭成的。
原题说法错误。
故答案为:×
18.×
【分析】
根据题意,用4个小正方体摆出从正面看是,可知这个几何体的下层有3个小正方体,上层有1个小正方体;
当下层的前一行有2个小正方体,后一行有1个小正方体且居右时,这时上层的小正方体有2种摆法;
当下层的前一行有2个小正方体,后一行有1个小正方体且居左时,这时上层的小正方体有1种摆法;
当下层的前一行有1个小正方体且居右,后一行有2个小正方体时,这时上层的小正方体有2种摆法;
当下层的前一行有1个小正方体且居左,后一行有2个小正方体时,这时上层的小正方体有1种摆法;
所以一共有(2+1+2+1)种摆法。
【详解】如图:
用4个小正方体摆出从正面看是的几何体,一共有6种摆法。
原题说法错误。
故答案为:×
【点睛】本题考查根据部分视图还原立体图形的能力,培养学生的空间想象力和观察能力。
19.√
【分析】此题考查了从不同方向观察物体和几何体,根据空间想象力和抽象思维能力进行解答即可。
【详解】根据从三个方向看到的形状,可以确定立体图形的形状。本题中从上面、侧面、正面看到的图形符合立体图形的形状。
故答案为:√
【点睛】本题考查从不同位置观察立体图形。
20.√
【分析】
根据观察,从正面和后面看到的图形为,把一个小正方体放在这个几何体的前面或后面,看到的图形还是。
【详解】由分析可知:
把一个小正方体放在这个几何体的前面或后面,从正面看到的形状是不变的。表述正确。
故答案为:√
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
21.√
【详解】因为从一个面看到的是,可能有2个正方体,可能有3个正方,所以正方体的个数不能确定。
故答案为:√
22.见详解
【分析】根据物体三视图的画法,结合立体图形,直接分析作图即可。
【详解】
【点睛】本题考查了观察物体,掌握三视图的画法是解题的关键。
23.6块;8块
【分析】根据从上面看到的图形是, 可以知道底层需要4块积木,如图摆放: 。根据从正面看到的图形是 ,可以知道左右两列都有两层;根据从左面看到的图形是 ,可以知道在前后两行也都有两层。综合从正面和左面看到的图形可以知道第二层上至少应摆放2个小正方体,如图摆放: 、 ;最多可摆放4个小正方体,如图摆放:。
【详解】至少需要6块:、。
最多可摆放8个小正方体,如图摆放:。
答:至少需要用6块正方体积木,最多需要用8块正方体积木。
【点睛】本题考查观察物体,解答本题的关键是掌握根据从不同方向看到的图形确定物体形状的方法。
24.76个
【分析】观察图形,每个图形的每层个数加起来即可算出答案。
【详解】第一个图形:第一层9个,第二层6个,第三层4个,所以第一个图形有9+6+4=19个小正方体积木。
第二个图形:第一层9个,第二层6个,第三层3个,所以第二个图形有9+6+3=18个小正方体积木。
第三个图形:第一层11个,第二层6个,第三层3个,所以第三个图形有11+6+3=20个小正方体积木。
第四个图形:第一层9个,第二层7个,第三层3个,所以第四个图形有9+7+3=19个小正方体积木。
即:19+18+20+19
=37+20+19
=57+19
=76(个)
答:下面堆起的立体图形中一共用了76个小正方体积木。
【点睛】本题主要考查学生的观察能力,看清每层的数量。
25.见详解
【分析】
无论用4个、5个、6个、7个或更多的小正方体组成的几何体,从前面看到的形状都是,只要满足这个条件即可。
【详解】(1)这个几何体如果是由4个小正方体组成的,可以这样摆,如图:
(答案不唯一)
(2)这个几何体如果是由5个、6个、7个小正方体或更多的小正方体组成的,可以这样摆,如图:
(答案不唯一)
26.(1)6种 (2)1种
【分析】(1)从正面看到的图形由4个小正方体组成,分两层,则另一个小正方体可以摆在第一层3个小正方体的前面或后面(共6个不同位置),所以有6种不同的搭法;(2)再结合从上面看到的图形分析,只能有一种摆法。
【详解】(1)答:有6种摆法。
(2)答:有1种摆法。
27.(1)4种
(2)10种,摆法见详解
(3)无数个
【分析】(1)根据从上面、正面和侧面看到的图形可知,底层有4个小正方体。如果是5个小正方体,要使从上面看到的图形不变,可以从第二层上任意放一个;
(2)如果有6个小正方体,要使从上面看到的图形不变,可以从第二层上任意放两个;
(3)要使从上面看到的图形不变,可以在底层的4个小正方体的上方加小正方体,可以加无数个。
【详解】(1)如果是5个小正方体,有四种摆法;
(2)有10种摆法
(3)最多可以摆无数个小正方体。
【点睛】本题较易,考虑观察物体的知识点。
