上海市闵行区2024-2025学年七年级下学期期中数学试题(含答案)
文档属性
| 名称 | 上海市闵行区2024-2025学年七年级下学期期中数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 658.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 19:22:54 | ||
图片预览




文档简介
2024-2025学年上海市闵行区七年级(下)期中数学试卷
一、选择题(本大题共有6题,每题2分,满分12分)
1.(2分)已知a<b,下列各式中不正确的是( )
A.2a<2b B.1﹣2a>1﹣2b C.a﹣b<0 D.|a|<|b|
2.(2分)如图,若其中∠1=∠5,则与∠2互补的角有( )
A.4个 B.3个 C.2个 D.1个
3.(2分)已知某个不等式的解集是x<﹣2,下列说法正确的是( )
A.0是这个不等式的解
B.﹣3不是这个不等式的解
C.小于﹣3的数都是这个不等式的解
D.小于﹣1的数都是这个不等式的解
4.(2分)下列各组长度的线段中,能组成三角形的是( )
A.1、2、3 B.6、3、2 C.2、2、3 D.4、2、1
5.(2分)下列语句中真命题的个数是( )
①两直线平行,同旁内角相等;
②三角形的三条高交于三角形内一点;
③若a⊥b,a⊥c,则b∥c;
④在同一平面内,经过一点有且只有一条直线与已知直线垂直;
⑤命题“对顶角相等”的逆命题是真命题;
⑥两条平行直线被第三条直线所截,一组同旁内角的平分线互相垂直.
A.1个 B.2个 C.3个 D.4个
6.(2分)如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=55°,则∠DBC的度数是( )
A.25° B.35° C.45° D.55°
二、填空题(本大题共有12题,每题2分,满分24分)
7.(2分)用不等式表示“x与y的一半的和是非负数”: .
8.(2分)不等式﹣2x+5>﹣3的解集是 .
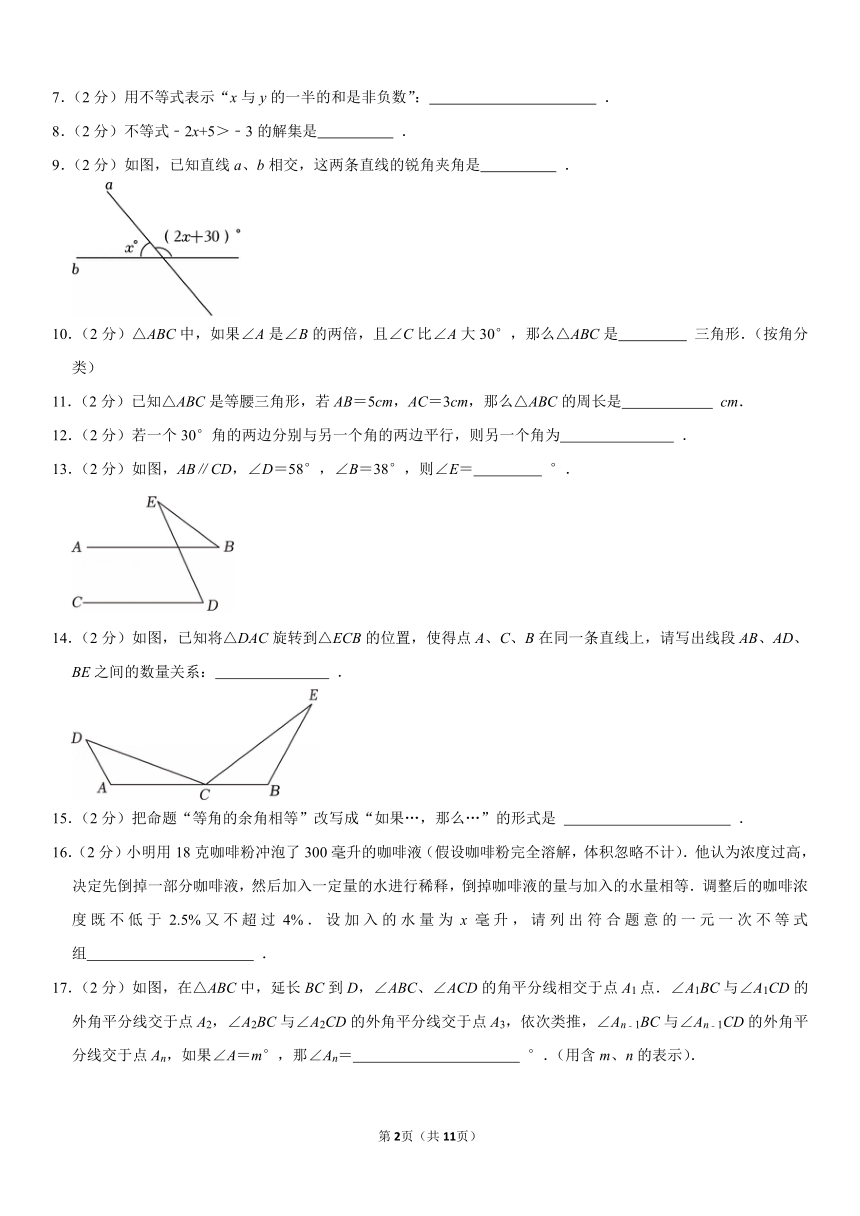
9.(2分)如图,已知直线a、b相交,这两条直线的锐角夹角是 .
10.(2分)△ABC中,如果∠A是∠B的两倍,且∠C比∠A大30°,那么△ABC是 三角形.(按角分类)
11.(2分)已知△ABC是等腰三角形,若AB=5cm,AC=3cm,那么△ABC的周长是 cm.
12.(2分)若一个30°角的两边分别与另一个角的两边平行,则另一个角为 .
13.(2分)如图,AB∥CD,∠D=58°,∠B=38°,则∠E= °.
14.(2分)如图,已知将△DAC旋转到△ECB的位置,使得点A、C、B在同一条直线上,请写出线段AB、AD、BE之间的数量关系: .
15.(2分)把命题“等角的余角相等”改写成“如果…,那么…”的形式是 .
16.(2分)小明用18克咖啡粉冲泡了300毫升的咖啡液(假设咖啡粉完全溶解,体积忽略不计).他认为浓度过高,决定先倒掉一部分咖啡液,然后加入一定量的水进行稀释,倒掉咖啡液的量与加入的水量相等.调整后的咖啡浓度既不低于2.5%又不超过4%.设加入的水量为x毫升,请列出符合题意的一元一次不等式组 .
17.(2分)如图,在△ABC中,延长BC到D,∠ABC、∠ACD的角平分线相交于点A1点.∠A1BC与∠A1CD的外角平分线交于点A2,∠A2BC与∠A2CD的外角平分线交于点A3,依次类推,∠An﹣1BC与∠An﹣1CD的外角平分线交于点An,如果∠A=m°,那∠An= °.(用含m、n的表示).
18.(2分)在△ABC中,∠BAC=50°,点D是边BC上一点,将△ACD沿直线AD翻折,使点C落在直线AB上的点E处,如果△BED是直角三角形,那么∠ACB= °.
三、简答题(本大题共有5题,第19题满分33分,第20题满分33分,第21题满分33分,第22题满分33分,第23题满分33分,共33分)
19.(5分)解不等式:3(2x+1)≤7﹣2(5x﹣6),并把它的解集在数轴上表示出来.
20.(6分)求不等式组:的整数解.
21.(7分)如果关于x的不等式组无解,求a的取值范围.
22.(5分)如图,已知AM∥CN,且∠1=∠2,那么AB∥CD吗?为什么?
解:∵AM∥CN(已知),
∴∠GAM=∠GCN( ).
又∵∠1=∠2,
∴∠ +∠ =∠ +∠ ,
即∠ =∠ ,
∴AB∥CD( ).
23.(10分)(1)反证法是数学中一种常用的证明方法,通常先假设求证的结论是错误的,再由此推导出与已知、公理、定理或条件等相矛盾的结果,从而否定开始的假设,肯定先前求证结论的正确性.在证明“两直线平行,内错角相等”时,采用反证法.
如图1,已知:∠1与∠2是直线AB、CD被直线EF所截得到的一对内错角,AB∥CD,直线AB、CD分别与直线EF相交于点M、N.
求证:∠1=∠2.
证明:假设 ,过点N画一条直线GH,使得∠1=∠ENG,如图2所示,根据 ,可得AB∥GH,又因为AB∥CD,这样直线GH、CD都过点N,这与 矛盾.
说明假设不成立,所以∠1=∠2.
(2)如图3,已知△ABC≌△DEF,∠CFA=∠CAF,∠1=30°,∠D=105°,求∠E的度数.
解:∵△ABC≌△DEF,
∴∠ =∠ ( ).
又:∠D=105°,∠1=30°,
∴∠CAF=∠ ﹣∠ = .
∵∠CFA=∠CAF.
又∵∠CFA=∠ +∠ ( ),
∴∠B=45°.
∵△ABC≌△DEF,
∴∠ =∠ =45°( ).
四、解答题(本大题共有3题,第24、25题满分21分,第26题满分21分,共21分)
24.(6分)小明准备乘坐出租车从商场回家,商场到家的距离为30公里,当地出租车的收费标准是:起步价为12元(3公里以内),超过3公里低于15公里,每公里收费2元,15公里以上每公里单价是在2元的基础上上浮50%,小明发现身上只有75元现金,请问他能直接乘出租车回家吗?
25.(6分)如图,点D、E、H分别在线段AB、BC、AC上,连接DE,过点C画CF交DH的延长线于点F,且满足∠BDE=∠FCA,若BC∥DF,∠B=∠F,求证DE∥AC.
26.(9分)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC.垂足为D,点E在AC上,BE交AD于点F,∠AFE=∠AEB.
(1)点B到直线AD的距离是线段 的长度:若BF=5EF,AE=EC,那么△ABF与△ABC的面积的比值是 .
(2)求证:BE平分∠ABC.
五、综合题(本大题共1题,满分10分)
27.(10分)在一副三角尺中∠B=90°,∠C=90°,∠BPA=45°,∠CPD=60°.
(1)将一副三角尺按如图1所示方式摆放(两条直角边在同一条直线上)
①联结AD.测得∠1=45°,则∠2的度数是多少?
②将三角尺PCD绕点P以每秒3°的速度逆时针旋转,当三角尺PCD的边PD与射线PB重合时停止运动,经历多久使得其中一块三角尺的直角边与另一块三角尺的斜边平行?
(2)若将这幅三角尺按照如图2所示方式摆放(两条斜边在同一条直线MN上),三角尺PCD绕点P以每秒2°的速度逆时针旋转,同时三角尺PAB以每秒3°的速度顺时针旋转,当三角尺PAB的边PB与射线PN重合时两块三角尺都停止运动.运动 秒,使得其中一块三角尺的直角边与另一块三角尺的斜边平行?(只写答案)
2024-2025学年上海市闵行区七年级(下)期中数学试卷
一.选择题(共6小题)
题号 1 2 3 4 5 6
答案 D A C C B B
二、填空题(本大题共有12题,每题2分,满分24分)
7.xy≥0.
8.x<4.
9.50°.
10.直角.
11.13或11.
12.30°或150°.
13.20.
14.AB=AD+BE.
15.如果两个角是等角的余角,那么这两个角相等.
16..
17.,
18.40或90或110.
三、简答题(本大题共有5题,第19题满分33分,第20题满分33分,第21题满分33分,第22题满分33分,第23题满分33分,共33分)
19.解:由题知,
3(2x+1)≤7﹣2(5x﹣6),
6x+3≤7﹣10x+12,
6x+10x≤7+12﹣3,
16x≤16,
x≤1.
数轴表示如下:
.
20.解:由2<x得:x,
由3(x)得:x≤2,
则不等式组的解集为x≤2,
所以不等式组的整数解为﹣1、0、1、2.
21.解:由5x>3(x+a)﹣10得:x,
由3﹣x得:x,
因为不等式组无解,
所以,
解得a>5.
22.解:∵AM∥CN(已知),
∴∠GAM=∠GCN(两直线平行,同位角相等).
又∵∠1=∠2,
∴∠GAM+∠1=∠GCN+∠2,
即∠GAB=∠GCD,
∴AB∥CD(同位角相等,两直线平行).
故答案为:两直线平行,同位角相等;GAM;1;GCN;2;GAB;GCD;同位角相等,两直线平行.
23.(1)证明:假设∠1≠∠2,
过点N画一条直线GH,使得∠1=∠ENG,如图2所示,根据内错角相等,两直线平行,可得AB∥GH,
又因为AB∥CD,这样直线GH、CD都过点N,
这与过直线外一点有且只有一条直线与这条直线平行矛盾.
说明假设不成立,所以∠1=∠2,
故答案为:∠1≠∠2;内错角相等,两直线平行;过直线外一点有且只有一条直线与这条直线平行;
(2)解:∵△ABC≌△DEF,
∴∠BAC=∠D(全等三角形的对应角相等 ).
又:∠D=105°,∠1=30°,
∴∠CAF=∠BAC﹣∠1= 75°.
∵∠CFA=∠CAF.
又∵∠CFA=∠B+∠1( 三角形的外角性质),
∴∠B=45°.
∵△ABC≌△DEF,
∴∠E=∠B=45°(全等三角形的对应角相等),
故答案为:BAC;D;全等三角形的对应角相等;BAC;1;75°;B;1;三角形的外角性质;E;B;全等三角形的对应角相等.
四、解答题(本大题共有3题,第24、25题满分21分,第26题满分21分,共21分)
24.解:他不能直接乘出租车回家,理由如下:
设小明可乘出租车的里程为x公里,
根据题意得:12+2×(15﹣3)+2×(1+50%)(x﹣15)=75,
解得:x=28,
∵28<30,
∴他不能直接乘出租车回家.
25.证明:∵BC∥DF,
∴∠B+∠BDF=180°,∠F+∠BCF=180°,∠ACB=∠AHD,
∵∠B=∠F,
∴∠BDF=∠BCF,
∵∠BDE=∠FCA,∠BDE+∠FDE=∠BDF,∠FCA+∠ACB=∠BCF,
∴∠FDE=∠ACB,
∴∠FDE=∠AHD,
∴DE∥AC.
26.解:从直线外一点到这条直线所作的垂线段的长度,
∴点B到直线AD的距离是线段BD的长度,
连接CF,如图所示,
∵AE=EC,根据等底登高的三角形面积相等,
∴可得S△ABE=S△CBE,S△AEF=S△CEF,
∴S△ABF=S△CBF,
又∵BF=5EF,
∴S△CBF=5S△CEF,
设S△CEF=x,则S△ABF=S△CBF=5x,
则SABE=S△CBE=6x,
则S△ABC=S△ABE+S△CBE=12x,
∴;
故答案为:BD,,
(2)证明:在Rt△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD+∠CAD=90°,∠C+∠CAD=90°,根据同角的余角相等,
∴∠BAD=∠C,
∵∠AFE=∠AEB,且∠AFE=∠BFD(对顶角相等),
∴∠BFD=∠AEB,
在△BDF中,∠BFD+∠FBD=90°,在△ABE中,∠AEB+∠ABE=90°,
由于∠BFD=∠AEB,根据等角的余角相等,
∴可得∠FBD=∠ABE,即BE平分∠ABC.
五、综合题(本大题共1题,满分10分)
27.解:(1)①∠BPA=45°,∠CPD=60°,
∴∠APD=180°﹣∠BPA﹣∠CPD=75°,
∴∠2=180°﹣∠1﹣∠APD=180°﹣45°﹣75°=60°;
②当PD'∥AB时,
则∠D'PC=∠B=90°,
∴∠DPD'=∠D'PC﹣∠DPC=90°﹣60°=30°,
∴t=30÷3=10(秒);
当D'C∥AP时,
∵∠C=90°,∠CPD=60°,
∴∠D=180°﹣∠C﹣∠CPD=30°,
∵旋转,
∴∠D'=∠D=30°,
∵D'C∥AP,
∴∠APD'=∠D'=30°,
∴∠DPD'=∠APD﹣∠APD'=75°﹣30°=45°,
∴t=45÷3=15(秒),
综上所述:当10秒或15秒时,其中一块三角尺的直角边与另一块三角尺的斜边平行;
(2)设旋转时间为t秒,由题意得,∠MPA=3t,∠NPD=2t,
①当PA∥CD时,
则∠APC=∠C=90°,
∵∠MPA+∠APC+∠DPC+∠NPD=180°,
∴3t+90°+60°+2t=180°,
解得:t=6;
②当AB∥PD时,
∴∠BPD=∠B=90°,
∵∠MPA+∠APB+∠DPB+∠NPD=180°,
∴3t+45°+90°+2t=180°,
解得:t=9;
③当CD∥AP时,
则∠APD=∠D=30°,
∵∠MPA+∠NPD﹣∠APD=180°,
∴3t+2t﹣30°=180°,
解得:t=42;
④当AB∥PD时,
则∠APD=∠A,
∵∠B=90°,∠BPA=45°,
∴∠A=180°﹣∠B﹣∠BPA=45°,
∴∠APD=45°,
∴∠MPA+∠NPD﹣∠APD=180°3t+2t﹣45°=180°,
解得:t=45,
综上所述:运动时间为6或9或42或45秒,使得其中一块三角尺的直角边与另一块三角尺的斜边平行.
故答案为:6或9或42或45.
第1页(共1页)
一、选择题(本大题共有6题,每题2分,满分12分)
1.(2分)已知a<b,下列各式中不正确的是( )
A.2a<2b B.1﹣2a>1﹣2b C.a﹣b<0 D.|a|<|b|
2.(2分)如图,若其中∠1=∠5,则与∠2互补的角有( )
A.4个 B.3个 C.2个 D.1个
3.(2分)已知某个不等式的解集是x<﹣2,下列说法正确的是( )
A.0是这个不等式的解
B.﹣3不是这个不等式的解
C.小于﹣3的数都是这个不等式的解
D.小于﹣1的数都是这个不等式的解
4.(2分)下列各组长度的线段中,能组成三角形的是( )
A.1、2、3 B.6、3、2 C.2、2、3 D.4、2、1
5.(2分)下列语句中真命题的个数是( )
①两直线平行,同旁内角相等;
②三角形的三条高交于三角形内一点;
③若a⊥b,a⊥c,则b∥c;
④在同一平面内,经过一点有且只有一条直线与已知直线垂直;
⑤命题“对顶角相等”的逆命题是真命题;
⑥两条平行直线被第三条直线所截,一组同旁内角的平分线互相垂直.
A.1个 B.2个 C.3个 D.4个
6.(2分)如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=55°,则∠DBC的度数是( )
A.25° B.35° C.45° D.55°
二、填空题(本大题共有12题,每题2分,满分24分)
7.(2分)用不等式表示“x与y的一半的和是非负数”: .
8.(2分)不等式﹣2x+5>﹣3的解集是 .
9.(2分)如图,已知直线a、b相交,这两条直线的锐角夹角是 .
10.(2分)△ABC中,如果∠A是∠B的两倍,且∠C比∠A大30°,那么△ABC是 三角形.(按角分类)
11.(2分)已知△ABC是等腰三角形,若AB=5cm,AC=3cm,那么△ABC的周长是 cm.
12.(2分)若一个30°角的两边分别与另一个角的两边平行,则另一个角为 .
13.(2分)如图,AB∥CD,∠D=58°,∠B=38°,则∠E= °.
14.(2分)如图,已知将△DAC旋转到△ECB的位置,使得点A、C、B在同一条直线上,请写出线段AB、AD、BE之间的数量关系: .
15.(2分)把命题“等角的余角相等”改写成“如果…,那么…”的形式是 .
16.(2分)小明用18克咖啡粉冲泡了300毫升的咖啡液(假设咖啡粉完全溶解,体积忽略不计).他认为浓度过高,决定先倒掉一部分咖啡液,然后加入一定量的水进行稀释,倒掉咖啡液的量与加入的水量相等.调整后的咖啡浓度既不低于2.5%又不超过4%.设加入的水量为x毫升,请列出符合题意的一元一次不等式组 .
17.(2分)如图,在△ABC中,延长BC到D,∠ABC、∠ACD的角平分线相交于点A1点.∠A1BC与∠A1CD的外角平分线交于点A2,∠A2BC与∠A2CD的外角平分线交于点A3,依次类推,∠An﹣1BC与∠An﹣1CD的外角平分线交于点An,如果∠A=m°,那∠An= °.(用含m、n的表示).
18.(2分)在△ABC中,∠BAC=50°,点D是边BC上一点,将△ACD沿直线AD翻折,使点C落在直线AB上的点E处,如果△BED是直角三角形,那么∠ACB= °.
三、简答题(本大题共有5题,第19题满分33分,第20题满分33分,第21题满分33分,第22题满分33分,第23题满分33分,共33分)
19.(5分)解不等式:3(2x+1)≤7﹣2(5x﹣6),并把它的解集在数轴上表示出来.
20.(6分)求不等式组:的整数解.
21.(7分)如果关于x的不等式组无解,求a的取值范围.
22.(5分)如图,已知AM∥CN,且∠1=∠2,那么AB∥CD吗?为什么?
解:∵AM∥CN(已知),
∴∠GAM=∠GCN( ).
又∵∠1=∠2,
∴∠ +∠ =∠ +∠ ,
即∠ =∠ ,
∴AB∥CD( ).
23.(10分)(1)反证法是数学中一种常用的证明方法,通常先假设求证的结论是错误的,再由此推导出与已知、公理、定理或条件等相矛盾的结果,从而否定开始的假设,肯定先前求证结论的正确性.在证明“两直线平行,内错角相等”时,采用反证法.
如图1,已知:∠1与∠2是直线AB、CD被直线EF所截得到的一对内错角,AB∥CD,直线AB、CD分别与直线EF相交于点M、N.
求证:∠1=∠2.
证明:假设 ,过点N画一条直线GH,使得∠1=∠ENG,如图2所示,根据 ,可得AB∥GH,又因为AB∥CD,这样直线GH、CD都过点N,这与 矛盾.
说明假设不成立,所以∠1=∠2.
(2)如图3,已知△ABC≌△DEF,∠CFA=∠CAF,∠1=30°,∠D=105°,求∠E的度数.
解:∵△ABC≌△DEF,
∴∠ =∠ ( ).
又:∠D=105°,∠1=30°,
∴∠CAF=∠ ﹣∠ = .
∵∠CFA=∠CAF.
又∵∠CFA=∠ +∠ ( ),
∴∠B=45°.
∵△ABC≌△DEF,
∴∠ =∠ =45°( ).
四、解答题(本大题共有3题,第24、25题满分21分,第26题满分21分,共21分)
24.(6分)小明准备乘坐出租车从商场回家,商场到家的距离为30公里,当地出租车的收费标准是:起步价为12元(3公里以内),超过3公里低于15公里,每公里收费2元,15公里以上每公里单价是在2元的基础上上浮50%,小明发现身上只有75元现金,请问他能直接乘出租车回家吗?
25.(6分)如图,点D、E、H分别在线段AB、BC、AC上,连接DE,过点C画CF交DH的延长线于点F,且满足∠BDE=∠FCA,若BC∥DF,∠B=∠F,求证DE∥AC.
26.(9分)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC.垂足为D,点E在AC上,BE交AD于点F,∠AFE=∠AEB.
(1)点B到直线AD的距离是线段 的长度:若BF=5EF,AE=EC,那么△ABF与△ABC的面积的比值是 .
(2)求证:BE平分∠ABC.
五、综合题(本大题共1题,满分10分)
27.(10分)在一副三角尺中∠B=90°,∠C=90°,∠BPA=45°,∠CPD=60°.
(1)将一副三角尺按如图1所示方式摆放(两条直角边在同一条直线上)
①联结AD.测得∠1=45°,则∠2的度数是多少?
②将三角尺PCD绕点P以每秒3°的速度逆时针旋转,当三角尺PCD的边PD与射线PB重合时停止运动,经历多久使得其中一块三角尺的直角边与另一块三角尺的斜边平行?
(2)若将这幅三角尺按照如图2所示方式摆放(两条斜边在同一条直线MN上),三角尺PCD绕点P以每秒2°的速度逆时针旋转,同时三角尺PAB以每秒3°的速度顺时针旋转,当三角尺PAB的边PB与射线PN重合时两块三角尺都停止运动.运动 秒,使得其中一块三角尺的直角边与另一块三角尺的斜边平行?(只写答案)
2024-2025学年上海市闵行区七年级(下)期中数学试卷
一.选择题(共6小题)
题号 1 2 3 4 5 6
答案 D A C C B B
二、填空题(本大题共有12题,每题2分,满分24分)
7.xy≥0.
8.x<4.
9.50°.
10.直角.
11.13或11.
12.30°或150°.
13.20.
14.AB=AD+BE.
15.如果两个角是等角的余角,那么这两个角相等.
16..
17.,
18.40或90或110.
三、简答题(本大题共有5题,第19题满分33分,第20题满分33分,第21题满分33分,第22题满分33分,第23题满分33分,共33分)
19.解:由题知,
3(2x+1)≤7﹣2(5x﹣6),
6x+3≤7﹣10x+12,
6x+10x≤7+12﹣3,
16x≤16,
x≤1.
数轴表示如下:
.
20.解:由2<x得:x,
由3(x)得:x≤2,
则不等式组的解集为x≤2,
所以不等式组的整数解为﹣1、0、1、2.
21.解:由5x>3(x+a)﹣10得:x,
由3﹣x得:x,
因为不等式组无解,
所以,
解得a>5.
22.解:∵AM∥CN(已知),
∴∠GAM=∠GCN(两直线平行,同位角相等).
又∵∠1=∠2,
∴∠GAM+∠1=∠GCN+∠2,
即∠GAB=∠GCD,
∴AB∥CD(同位角相等,两直线平行).
故答案为:两直线平行,同位角相等;GAM;1;GCN;2;GAB;GCD;同位角相等,两直线平行.
23.(1)证明:假设∠1≠∠2,
过点N画一条直线GH,使得∠1=∠ENG,如图2所示,根据内错角相等,两直线平行,可得AB∥GH,
又因为AB∥CD,这样直线GH、CD都过点N,
这与过直线外一点有且只有一条直线与这条直线平行矛盾.
说明假设不成立,所以∠1=∠2,
故答案为:∠1≠∠2;内错角相等,两直线平行;过直线外一点有且只有一条直线与这条直线平行;
(2)解:∵△ABC≌△DEF,
∴∠BAC=∠D(全等三角形的对应角相等 ).
又:∠D=105°,∠1=30°,
∴∠CAF=∠BAC﹣∠1= 75°.
∵∠CFA=∠CAF.
又∵∠CFA=∠B+∠1( 三角形的外角性质),
∴∠B=45°.
∵△ABC≌△DEF,
∴∠E=∠B=45°(全等三角形的对应角相等),
故答案为:BAC;D;全等三角形的对应角相等;BAC;1;75°;B;1;三角形的外角性质;E;B;全等三角形的对应角相等.
四、解答题(本大题共有3题,第24、25题满分21分,第26题满分21分,共21分)
24.解:他不能直接乘出租车回家,理由如下:
设小明可乘出租车的里程为x公里,
根据题意得:12+2×(15﹣3)+2×(1+50%)(x﹣15)=75,
解得:x=28,
∵28<30,
∴他不能直接乘出租车回家.
25.证明:∵BC∥DF,
∴∠B+∠BDF=180°,∠F+∠BCF=180°,∠ACB=∠AHD,
∵∠B=∠F,
∴∠BDF=∠BCF,
∵∠BDE=∠FCA,∠BDE+∠FDE=∠BDF,∠FCA+∠ACB=∠BCF,
∴∠FDE=∠ACB,
∴∠FDE=∠AHD,
∴DE∥AC.
26.解:从直线外一点到这条直线所作的垂线段的长度,
∴点B到直线AD的距离是线段BD的长度,
连接CF,如图所示,
∵AE=EC,根据等底登高的三角形面积相等,
∴可得S△ABE=S△CBE,S△AEF=S△CEF,
∴S△ABF=S△CBF,
又∵BF=5EF,
∴S△CBF=5S△CEF,
设S△CEF=x,则S△ABF=S△CBF=5x,
则SABE=S△CBE=6x,
则S△ABC=S△ABE+S△CBE=12x,
∴;
故答案为:BD,,
(2)证明:在Rt△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD+∠CAD=90°,∠C+∠CAD=90°,根据同角的余角相等,
∴∠BAD=∠C,
∵∠AFE=∠AEB,且∠AFE=∠BFD(对顶角相等),
∴∠BFD=∠AEB,
在△BDF中,∠BFD+∠FBD=90°,在△ABE中,∠AEB+∠ABE=90°,
由于∠BFD=∠AEB,根据等角的余角相等,
∴可得∠FBD=∠ABE,即BE平分∠ABC.
五、综合题(本大题共1题,满分10分)
27.解:(1)①∠BPA=45°,∠CPD=60°,
∴∠APD=180°﹣∠BPA﹣∠CPD=75°,
∴∠2=180°﹣∠1﹣∠APD=180°﹣45°﹣75°=60°;
②当PD'∥AB时,
则∠D'PC=∠B=90°,
∴∠DPD'=∠D'PC﹣∠DPC=90°﹣60°=30°,
∴t=30÷3=10(秒);
当D'C∥AP时,
∵∠C=90°,∠CPD=60°,
∴∠D=180°﹣∠C﹣∠CPD=30°,
∵旋转,
∴∠D'=∠D=30°,
∵D'C∥AP,
∴∠APD'=∠D'=30°,
∴∠DPD'=∠APD﹣∠APD'=75°﹣30°=45°,
∴t=45÷3=15(秒),
综上所述:当10秒或15秒时,其中一块三角尺的直角边与另一块三角尺的斜边平行;
(2)设旋转时间为t秒,由题意得,∠MPA=3t,∠NPD=2t,
①当PA∥CD时,
则∠APC=∠C=90°,
∵∠MPA+∠APC+∠DPC+∠NPD=180°,
∴3t+90°+60°+2t=180°,
解得:t=6;
②当AB∥PD时,
∴∠BPD=∠B=90°,
∵∠MPA+∠APB+∠DPB+∠NPD=180°,
∴3t+45°+90°+2t=180°,
解得:t=9;
③当CD∥AP时,
则∠APD=∠D=30°,
∵∠MPA+∠NPD﹣∠APD=180°,
∴3t+2t﹣30°=180°,
解得:t=42;
④当AB∥PD时,
则∠APD=∠A,
∵∠B=90°,∠BPA=45°,
∴∠A=180°﹣∠B﹣∠BPA=45°,
∴∠APD=45°,
∴∠MPA+∠NPD﹣∠APD=180°3t+2t﹣45°=180°,
解得:t=45,
综上所述:运动时间为6或9或42或45秒,使得其中一块三角尺的直角边与另一块三角尺的斜边平行.
故答案为:6或9或42或45.
第1页(共1页)
同课章节目录
