2024-2025学年山东省济南历城区七年级第二学期数学期中考试试题(含答案)
文档属性
| 名称 | 2024-2025学年山东省济南历城区七年级第二学期数学期中考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 516.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 20:09:06 | ||
图片预览

文档简介
2024—2025 学年度第二学期期中质量检测七年级数学试题
(满分150分 时间120分钟)
一、选择题(本大题共 10 个题,每题 4 分,共 40 分。在每题给出的四个选项中,只有一项是符合题目要求的。)
1.中国 “二十四节气” 已列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表 “立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )
A. B. C. D.
2.中国科学院近日成功研发出固态深紫外(DUV)激光源,能够发射出 193 纳米波长的相干光,为半导体工艺提升至 3 纳米节点提供了有力支持。已知 193 纳米等于 0.000 000 193 米,那么数字 0.000 000 193 用科学记数法表示为( )
A. 1.93×10 7 B. 1.93×10 8 C. 1.93×107 D. 193×10 9
3.若x2+(2m 6)x+16是一个完全平方式,则 m 的值是( )
A. 4 B. - 1 或 7 C. - 1 或 4 D. 7
4.光线从空气斜射向水中时会发生折射现象。空气中平行的光线斜射向水中,经过折射后在水中的光线也是平行的。如图,AC,BD为入射光线,CE,DF为折射光线,且满足AC∥BD,AB∥CD∥EF,若∠1=43 ,∠2=167 ,则∠3的度数为( )
A. 43 B. 47 C. 56 D. 66
5.下列运算正确的是( )
A. 3x+3y=6xy B. (xy2)3=xy6 C. 3(x+8)=3x+8 D. x2·x3=x5
6.如图,点E,C,F,B在一条直线上,AB∥ED,∠A=∠D,添加下列条件不能判定△ABC △DEF的是( )
A. AC∥DF B. AB=DE C. EC=BF D. AC=DF
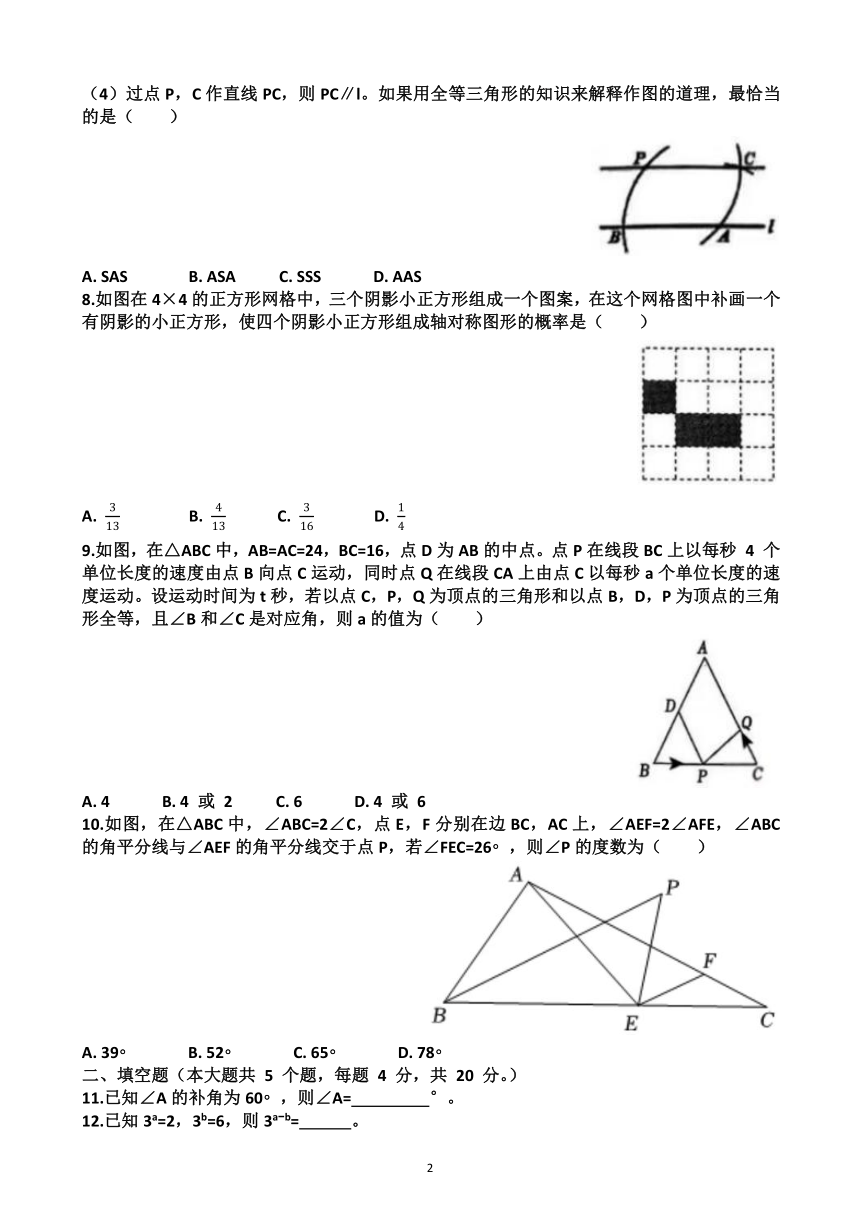
7.我们曾经学习 “过直线外一点P作直线l的平行线” 的一种方法,如图:
(1)在直线l上任取一点A,以点A为圆心,以AP的长为半径作弧,交直线l于点B;
(2)以点P为圆心,以PA的长为半径作弧;
(3)以点A为圆心,以PB的长为半径作弧,交前弧于点C;
(4)过点P,C作直线PC,则PC∥l。如果用全等三角形的知识来解释作图的道理,最恰当的是( )
A. SAS B. ASA C. SSS D. AAS
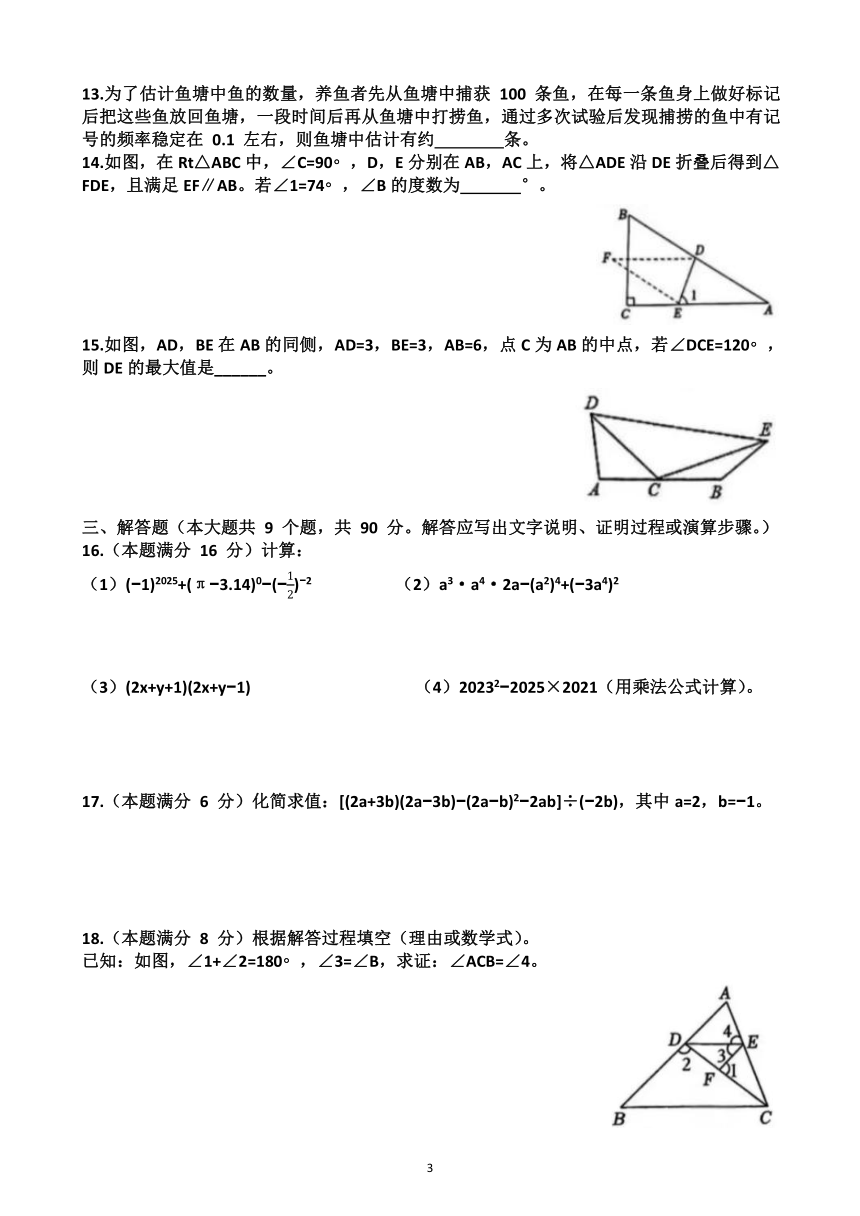
8.如图在4×4的正方形网格中,三个阴影小正方形组成一个图案,在这个网格图中补画一个有阴影的小正方形,使四个阴影小正方形组成轴对称图形的概率是( )
A. B. C. D.
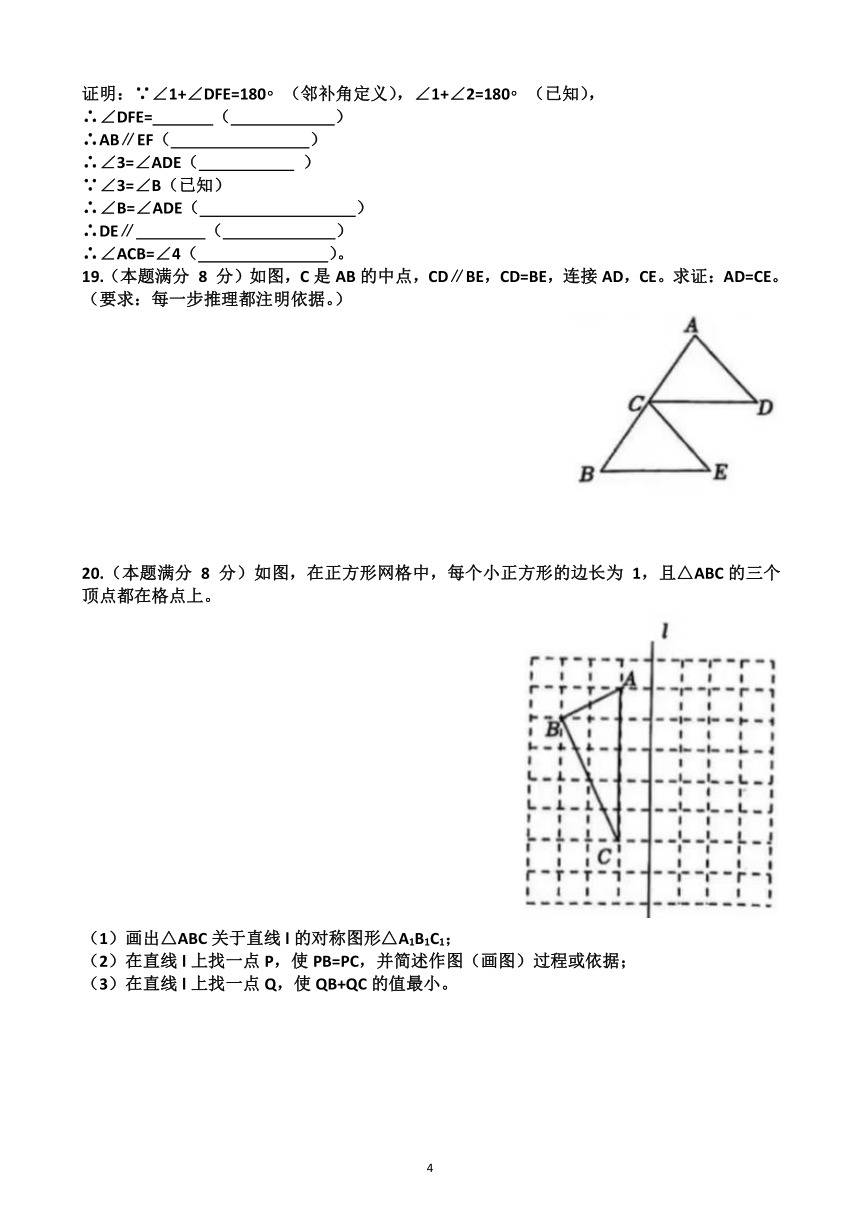
9.如图,在△ABC中,AB=AC=24,BC=16,点D为AB的中点。点P在线段BC上以每秒 4 个单位长度的速度由点B向点C运动,同时点Q在线段CA上由点C以每秒a个单位长度的速度运动。设运动时间为t秒,若以点C,P,Q为顶点的三角形和以点B,D,P为顶点的三角形全等,且∠B和∠C是对应角,则a的值为( )
A. 4 B. 4 或 2 C. 6 D. 4 或 6
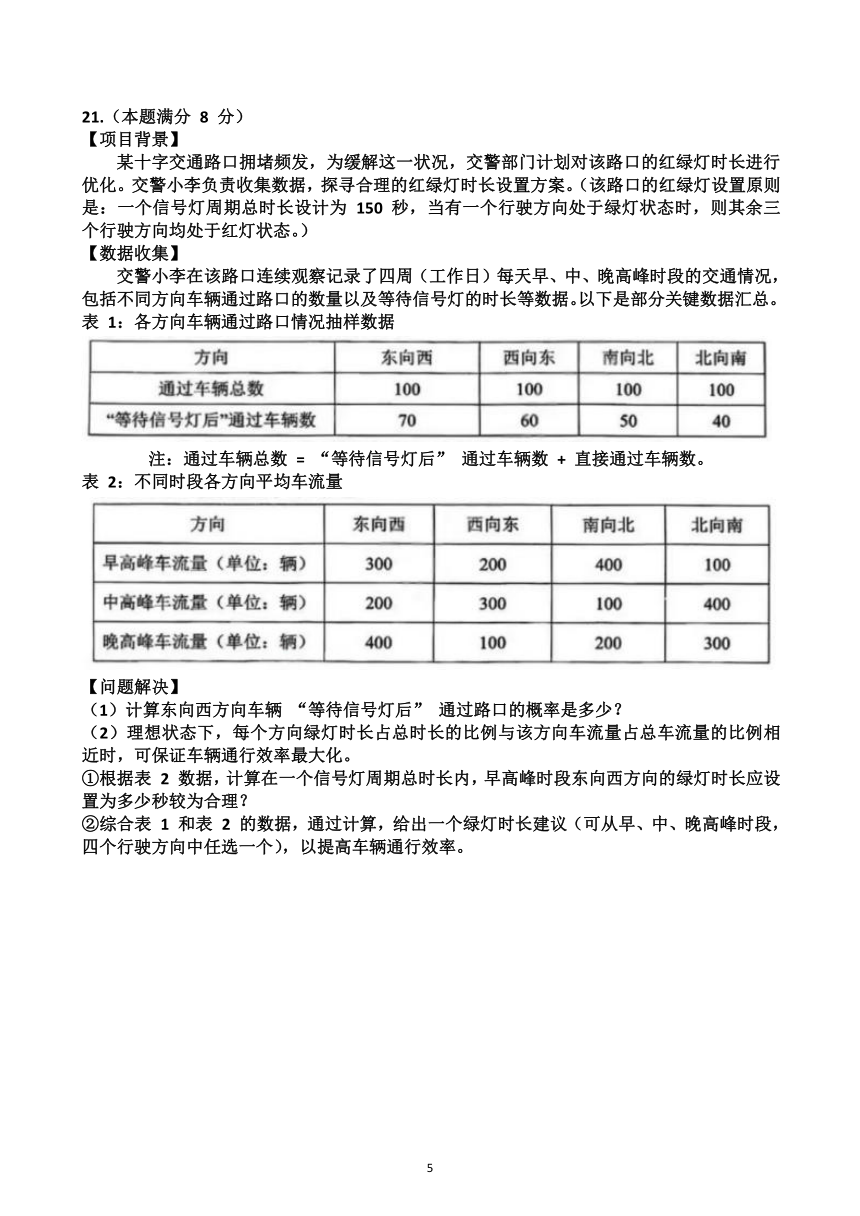
10.如图,在△ABC中,∠ABC=2∠C,点E,F分别在边BC,AC上,∠AEF=2∠AFE,∠ABC的角平分线与∠AEF的角平分线交于点P,若∠FEC=26 ,则∠P的度数为( )
A. 39 B. 52 C. 65 D. 78
二、填空题(本大题共 5 个题,每题 4 分,共 20 分。)
11.已知∠A的补角为60 ,则∠A= °。
12.已知3a=2,3b=6,则3a b= 。
13.为了估计鱼塘中鱼的数量,养鱼者先从鱼塘中捕获 100 条鱼,在每一条鱼身上做好标记后把这些鱼放回鱼塘,一段时间后再从鱼塘中打捞鱼,通过多次试验后发现捕捞的鱼中有记号的频率稳定在 0.1 左右,则鱼塘中估计有约 条。
14.如图,在Rt△ABC中,∠C=90 ,D,E分别在AB,AC上,将△ADE沿DE折叠后得到△FDE,且满足EF∥AB。若∠1=74 ,∠B的度数为 °。
15.如图,AD,BE在AB的同侧,AD=3,BE=3,AB=6,点C为AB的中点,若∠DCE=120 ,则DE的最大值是______。
三、解答题(本大题共 9 个题,共 90 分。解答应写出文字说明、证明过程或演算步骤。)
16.(本题满分 16 分)计算:
(1)( 1)2025+(π 3.14)0 ( ) 2 (2)a3·a4·2a (a2)4+( 3a4)2
(3)(2x+y+1)(2x+y 1) (4)20232 2025×2021(用乘法公式计算)。
17.(本题满分 6 分)化简求值:[(2a+3b)(2a 3b) (2a b)2 2ab]÷( 2b),其中a=2,b= 1。
18.(本题满分 8 分)根据解答过程填空(理由或数学式)。
已知:如图,∠1+∠2=180 ,∠3=∠B,求证:∠ACB=∠4。
证明:∵∠1+∠DFE=180 (邻补角定义),∠1+∠2=180 (已知),
∴∠DFE= ( )
∴AB∥EF( )
∴∠3=∠ADE( )
∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥ ( )
∴∠ACB=∠4( )。
19.(本题满分 8 分)如图,C是AB的中点,CD∥BE,CD=BE,连接AD,CE。求证:AD=CE。(要求:每一步推理都注明依据。)
20.(本题满分 8 分)如图,在正方形网格中,每个小正方形的边长为 1,且△ABC的三个顶点都在格点上。
(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)在直线l上找一点P,使PB=PC,并简述作图(画图)过程或依据;
(3)在直线l上找一点Q,使QB+QC的值最小。
21.(本题满分 8 分)
【项目背景】
某十字交通路口拥堵频发,为缓解这一状况,交警部门计划对该路口的红绿灯时长进行优化。交警小李负责收集数据,探寻合理的红绿灯时长设置方案。(该路口的红绿灯设置原则是:一个信号灯周期总时长设计为 150 秒,当有一个行驶方向处于绿灯状态时,则其余三个行驶方向均处于红灯状态。)
【数据收集】
交警小李在该路口连续观察记录了四周(工作日)每天早、中、晚高峰时段的交通情况,包括不同方向车辆通过路口的数量以及等待信号灯的时长等数据。以下是部分关键数据汇总。
表 1:各方向车辆通过路口情况抽样数据
注:通过车辆总数 = “等待信号灯后” 通过车辆数 + 直接通过车辆数。
表 2:不同时段各方向平均车流量
【问题解决】
(1)计算东向西方向车辆 “等待信号灯后” 通过路口的概率是多少?
(2)理想状态下,每个方向绿灯时长占总时长的比例与该方向车流量占总车流量的比例相近时,可保证车辆通行效率最大化。
①根据表 2 数据,计算在一个信号灯周期总时长内,早高峰时段东向西方向的绿灯时长应设置为多少秒较为合理?
②综合表 1 和表 2 的数据,通过计算,给出一个绿灯时长建议(可从早、中、晚高峰时段,四个行驶方向中任选一个),以提高车辆通行效率。
22.(本题满分 12 分)直线AB∥CD,直线EF与AB,CD分别交于点G,H,∠EHD=α(0 <α<90 ),小明将一个含30 角的直角三角板PMN按如图①放置,使点N,M分别在直线AB,CD上,∠P=90 ,∠PMN=60 。
(1)猜想∠PNB,∠PMD,∠MPN之间的数量关系,并说明理由;
(2)若∠MNG的平分线NO交直线CD于点O。
①如图②,当NO∥EF,PM∥EF时,求α的度数;
②小明将三角板PMN沿直线AB左右移动,保持PM∥EF,请直接写出∠MON的度数。(用含α的式子表示)
23.(本题满分 12 分)
【阅读理解】若x满足(16 x)(x 6)=20,求(16 x)2+(x 6)2的值。
解:设16 x=a,x 6=b,则(16 x)(x 6)=a·b=20
∵a+b=(16 x)+(x 6)=10
∴(16 x)2+(x 6)2=a2+b2=(a+b)2 2ab=102 2×20=60。
我们把解决上述问题的这种方法叫做换元法。利用换元法达到简化运算的目的,体现了转化的数学思想。用换元法解决问题:
(1)若x满足(2025 x)(x 2020)=4,求(2025 x)2+(x 2020)2的值;
【类比应用】
(2)若m满足(2025 m)(2023 m)=2,则(2025 m)4+(2023 m)4的值是______;
【迁移应用】
通过计算几何图形的面积可以表示一些代数恒等式,这种解决数学问题的思想方法叫数形结合,利用这种方法可将抽象的数学知识变得直观起来。例如,图 1 可以得到(a+b)2=a2+2ab+b2。
结合上述阅读材料,解决下列问题:
(3)两块完全相同的直角三角板(∠AOB=∠COD=90 )如图 2 所示放置,其中A,O,D在同一直线上。连接AC,BD,若AD=12,S△AOC+S△BOD=36,求一块直角三角板的面积。
24.(本题满分 12 分)
【模型建立】
(1)如图 1,△ABC,△ADE为等边三角形,连接BD,CE,求证:BD=CE;
探索思路如下:
∵△ABC,△ADE为等边三角形
∴∠BAC=∠DAE=60 ,AB=AC,AD=AE
∴∠BAC -∠DAC -∠DAE -∠DAC .(① )
即∠BAD =∠CAE
在△ABD 与△DACE 中
∴ ABD≌△ACE(② )
∴BD = CE (③ )
请在上面三个( )中填写适当的理由。
【模型应用】
(2)如图2,在△ ABC 与 AADE 中,AB = AC , AD = AE ,∠BAC =∠DAE =90°,B , D , E 三点在一条直线上,AC 与BE 交于点F ,连接EC。
①求∠BEC 的度数;
②若点F 为AC 中点,BD =6,求EF 的长。
图1 图2
答案
一、选择题(本大题共 10 个题,每题 4 分,共 40 分。在每题给出的四个选项中,只有一项是符合题目要求的。)
1.中国 “二十四节气” 已列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表 “立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( D )
A. B. C. D.
2.中国科学院近日成功研发出固态深紫外(DUV)激光源,能够发射出 193 纳米波长的相干光,为半导体工艺提升至 3 纳米节点提供了有力支持。已知 193 纳米等于 0.000 000 193 米,那么数字 0.000 000 193 用科学记数法表示为( A )
A. 1.93×10 7 B. 1.93×10 8 C. 1.93×107 D. 193×10 9
3.若x2+(2m 6)x+16是一个完全平方式,则 m 的值是( B )
A. 4 B. - 1 或 7 C. - 1 或 4 D. 7
4.光线从空气斜射向水中时会发生折射现象。空气中平行的光线斜射向水中,经过折射后在水中的光线也是平行的。如图,AC,BD为入射光线,CE,DF为折射光线,且满足AC∥BD,AB∥CD∥EF,若∠1=43 ,∠2=167 ,则∠3的度数为( C )
A. 43 B. 47 C. 56 D. 66
5.下列运算正确的是( D )
A. 3x+3y=6xy B. (xy2)3=xy6 C. 3(x+8)=3x+8 D. x2·x3=x5
6.如图,点E,C,F,B在一条直线上,AB∥ED,∠A=∠D,添加下列条件不能判定△ABC △DEF的是( A )
A. AC∥DF B. AB=DE C. EC=BF D. AC=DF
7.我们曾经学习 “过直线外一点P作直线l的平行线” 的一种方法,如图:
(1)在直线l上任取一点A,以点A为圆心,以AP的长为半径作弧,交直线l于点B;
(2)以点P为圆心,以PA的长为半径作弧;
(3)以点A为圆心,以PB的长为半径作弧,交前弧于点C;
(4)过点P,C作直线PC,则PC∥l。如果用全等三角形的知识来解释作图的道理,最恰当的是( C )
A. SAS B. ASA C. SSS D. AAS
8.如图在4×4的正方形网格中,三个阴影小正方形组成一个图案,在这个网格图中补画一个有阴影的小正方形,使四个阴影小正方形组成轴对称图形的概率是( B )
A. B. C. D.
9.如图,在△ABC中,AB=AC=24,BC=16,点D为AB的中点。点P在线段BC上以每秒 4 个单位长度的速度由点B向点C运动,同时点Q在线段CA上由点C以每秒a个单位长度的速度运动。设运动时间为t秒,若以点C,P,Q为顶点的三角形和以点B,D,P为顶点的三角形全等,且∠B和∠C是对应角,则a的值为( D )
A. 4 B. 4 或 2 C. 6 D. 4 或 6
10.如图,在△ABC中,∠ABC=2∠C,点E,F分别在边BC,AC上,∠AEF=2∠AFE,∠ABC的角平分线与∠AEF的角平分线交于点P,若∠FEC=26 ,则∠P的度数为( B )
A. 39 B. 52 C. 65 D. 78
二、填空题(本大题共 5 个题,每题 4 分,共 20 分。)
11.已知∠A的补角为60 ,则∠A= 120° °。
12.已知3a=2,3b=6,则3a b= 。
13.为了估计鱼塘中鱼的数量,养鱼者先从鱼塘中捕获 100 条鱼,在每一条鱼身上做好标记后把这些鱼放回鱼塘,一段时间后再从鱼塘中打捞鱼,通过多次试验后发现捕捞的鱼中有记号的频率稳定在 0.1 左右,则鱼塘中估计有约 1000 条。
14.如图,在Rt△ABC中,∠C=90 ,D,E分别在AB,AC上,将△ADE沿DE折叠后得到△FDE,且满足EF∥AB。若∠1=74 ,∠B的度数为 58 °。
15.如图,AD,BE在AB的同侧,AD=3,BE=3,AB=6,点C为AB的中点,若∠DCE=120 ,则DE的最大值是___9___。
三、解答题(本大题共 9 个题,共 90 分。解答应写出文字说明、证明过程或演算步骤。)
16.(本题满分 16 分)计算:
(1)( 1)2025+(π 3.14)0 ( ) 2 (2)a3·a4·2a (a2)4+( 3a4)2
=﹣1+1﹣4 =2a8﹣a8+9a8
=﹣4 =10a8
(3)(2x+y+1)(2x+y 1) (4)20232 2025×2021(用乘法公式计算)。
=(2x+y)2﹣1 =20232﹣(20232﹣4)
=4x2+4xy+y2﹣1 =4
17.(本题满分 6 分)化简求值:[(2a+3b)(2a 3b) (2a b)2 2ab]÷( 2b),其中a=2,b= 1。
解原式=[﹣10b2+2ab]( 2b)
=5b﹣a
将a=2,b= 1代入得﹣5﹣2=﹣7
18.(本题满分 8 分)根据解答过程填空(理由或数学式)。
已知:如图,∠1+∠2=180 ,∠3=∠B,求证:∠ACB=∠4。
证明:∵∠1+∠DFE=180 (邻补角定义),∠1+∠2=180 (已知),
∴∠DFE= ∠2 ( 同角的补交相等 )
∴AB∥EF( 内错角相等,两直线平行 )
∴∠3=∠ADE( 两直线平行,内错角相等 )
∵∠3=∠B(已知)
∴∠B=∠ADE( 等量代换 )
∴DE∥ BC ( 同位角相等,两直线平行 )
∴∠ACB=∠4( 两直线平行,同位角相等 )。
19.(本题满分 8 分)如图,C是AB的中点,CD∥BE,CD=BE,连接AD,CE。求证:AD=CE。(要求:每一步推理都注明依据。)
证明∵C是AB中点(已知)
∴AC=BC(中点的定义)
∵CD∥BE(已知)
∴∠ACD =∠B ,(两直线平行,同位角相等)
在△ADC 与△CEB 中
∴△ADC≌△CEB ( SAS ).
∴AD = CE(全等三角形对应边相等,对应角相等)
20.(本题满分 8 分)如图,在正方形网格中,每个小正方形的边长为 1,且△ABC的三个顶点都在格点上。
(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)在直线l上找一点P,使PB=PC,并简述作图(画图)过程或依据;
(3)在直线l上找一点Q,使QB+QC的值最小。
略
21.(本题满分 8 分)
【项目背景】
某十字交通路口拥堵频发,为缓解这一状况,交警部门计划对该路口的红绿灯时长进行优化。交警小李负责收集数据,探寻合理的红绿灯时长设置方案。(该路口的红绿灯设置原则是:一个信号灯周期总时长设计为 150 秒,当有一个行驶方向处于绿灯状态时,则其余三个行驶方向均处于红灯状态。)
【数据收集】
交警小李在该路口连续观察记录了四周(工作日)每天早、中、晚高峰时段的交通情况,包括不同方向车辆通过路口的数量以及等待信号灯的时长等数据。以下是部分关键数据汇总。
表 1:各方向车辆通过路口情况抽样数据
注:通过车辆总数 = “等待信号灯后” 通过车辆数 + 直接通过车辆数。
表 2:不同时段各方向平均车流量
【问题解决】
(1)计算东向西方向车辆 “等待信号灯后” 通过路口的概率是多少?
(2)理想状态下,每个方向绿灯时长占总时长的比例与该方向车流量占总车流量的比例相近时,可保证车辆通行效率最大化。
①根据表 2 数据,计算在一个信号灯周期总时长内,早高峰时段东向西方向的绿灯时长应设置为多少秒较为合理?
②综合表 1 和表 2 的数据,通过计算,给出一个绿灯时长建议(可从早、中、晚高峰时段,四个行驶方向中任选一个),以提高车辆通行效率。
解:(1)P(东向西方向车辆"等待信号灯后"通过路口)==0.7
①早高峰时段总车流量:300+200+400+100=1000辆。东向西方向车流量占总车流量的比例为0.3
∴早高峰时段东向西方向绿灯时长应为:150x=45秒
②以早高峰东向西方向为例。由(2)可知,早高峰时段东向西方向绿灯时长应为45秒。由(1)知, P(东向西方向车辆在等待信号灯后通过路口)=0.7,此比例相对较高。建议将早高峰东向西方向的绿灯时长在计算结果基础上增加2秒,调整为47秒,以缓解车辆等待压力,提高该方向通行效率,同时相应缩短其他方向绿灯时长,确保信号灯周期总时长仍为150秒。
22.(本题满分 12 分)直线AB∥CD,直线EF与AB,CD分别交于点G,H,∠EHD=α(0 <α<90 ),小明将一个含30 角的直角三角板PMN按如图①放置,使点N,M分别在直线AB,CD上,∠P=90 ,∠PMN=60 。
(1)猜想∠PNB,∠PMD,∠MPN之间的数量关系,并说明理由;
(2)若∠MNG的平分线NO交直线CD于点O。
①如图②,当NO∥EF,PM∥EF时,求α的度数;
②小明将三角板PMN沿直线AB左右移动,保持PM∥EF,请直接写出∠MON的度数。(用含α的式子表示)
解:(1)∠PNB +∠PMD =∠MPN
过P 点作PQ // AB
∵AB // CD
∴AB // PQ // CD .
∴∠PNB =∠NPQ ,∠PMD =∠QPM
∴∠PNB +∠PMD =∠NPQ +∠QPM =∠MPN
(2)①∵NO // EF , PM // EF ,∠PMN =60°
∴NO // PM // EF ,
∴∠ONM =∠PMN =60°, ∠EHD =∠NOM =a
∵NO 平分∠MNG .
∴∠ANO =∠ONM =60°
∵AB // CD
∴∠NOM =∠ANO =60°
∴α=60°
②30°+α或60°﹣α
23.(本题满分 12 分)
【阅读理解】若x满足(16 x)(x 6)=20,求(16 x)2+(x 6)2的值。
解:设16 x=a,x 6=b,则(16 x)(x 6)=a·b=20
∵a+b=(16 x)+(x 6)=10
∴(16 x)2+(x 6)2=a2+b2=(a+b)2 2ab=102 2×20=60。
我们把解决上述问题的这种方法叫做换元法。利用换元法达到简化运算的目的,体现了转化的数学思想。用换元法解决问题:
(1)若x满足(2025 x)(x 2020)=4,求(2025 x)2+(x 2020)2的值;
【类比应用】
(2)若m满足(2025 m)(2023 m)=2,则(2025 m)4+(2023 m)4的值是______;
【迁移应用】
通过计算几何图形的面积可以表示一些代数恒等式,这种解决数学问题的思想方法叫数形结合,利用这种方法可将抽象的数学知识变得直观起来。例如,图 1 可以得到(a+b)2=a2+2ab+b2。
结合上述阅读材料,解决下列问题:
(3)两块完全相同的直角三角板(∠AOB=∠COD=90 )如图 2 所示放置,其中A,O,D在同一直线上。连接AC,BD,若AD=12,S△AOC+S△BOD=36,求一块直角三角板的面积。
解:(1)设2025- x= a , x -2020=b ,则(2025- x)( x -2020)=ab =4
∵a + b =(2025- x )+( x -2020)=5
∴ (2025- x )2+( x -2020)2=a2+b2=( atb )2-2ab=52-2x4=17:
(2)56
(3)设直角三角形的较短的直角边为 a ,较长的直角边为 b ,
由题意可得:a + b=12,a2+b2=36
∴a2+b2=72
∵a + b =12
∴(a +b)2=144,
∴a2+2ab+b2=144
∴2ab=144-(a2+b2)=144-72=72
∴ab =36
∴ab =18,
即一块直角三角板的面积为18。
24.(本题满分 12 分)
【模型建立】
(1)如图 1,△ABC,△ADE为等边三角形,连接BD,CE,求证:BD=CE;
探索思路如下:
∵△ABC,△ADE为等边三角形
∴∠BAC=∠DAE=60 ,AB=AC,AD=AE
∴∠BAC -∠DAC -∠DAE -∠DAC .(① )
即∠BAD =∠CAE
在△ABD 与△DACE 中
∴ ABD≌△ACE(② )
∴BD = CE (③ )
请在上面三个( )中填写适当的理由。
【模型应用】
(2)如图2,在△ ABC 与 AADE 中,AB = AC , AD = AE ,∠BAC =∠DAE =90°,B , D , E 三点在一条直线上,AC 与BE 交于点F ,连接EC。
①求∠BEC 的度数;
②若点F 为AC 中点,BD =6,求EF 的长。
图1 图2
(1)等式的性质 SAS 两全等三角形的对应线段相等
(2)①∵∠BAC =∠DAE =90°
∴∠DAE -∠DAF =∠BAC -∠DAF
即∠BAD =∠CAE
在△ABD 与△ACE 中
∴△ABD≌ △ACE ( SAS )
∴∠ABD =∠ACE
∵∠BAC =90°
∴∠ABD +∠BFA -90°
∴∠ACE +∠CFE -90°
∴∠BEC =90°
②作 AM⊥BE交BE 于点M .
∴∠AME =90°
∵F 为AC 中点
∴AF = FC
∵∠BEC =90°
∴∠AMF =∠CEF =90°
∵∠AFM =∠CFE
∴△AFM≌ CFE
∴MF=EF =ME ,AM=CE
由①知:△ABD≌△ACE
∴CE=BD=6
∴AM =6
∵AD = AE .∠DAE =90°,AM⊥DE
∴∠MAE =45°, ∠AEM =45°
∴∠MAE =∠AEM
∴ME = AM =6
∴EF=ME =3..
(满分150分 时间120分钟)
一、选择题(本大题共 10 个题,每题 4 分,共 40 分。在每题给出的四个选项中,只有一项是符合题目要求的。)
1.中国 “二十四节气” 已列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表 “立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )
A. B. C. D.
2.中国科学院近日成功研发出固态深紫外(DUV)激光源,能够发射出 193 纳米波长的相干光,为半导体工艺提升至 3 纳米节点提供了有力支持。已知 193 纳米等于 0.000 000 193 米,那么数字 0.000 000 193 用科学记数法表示为( )
A. 1.93×10 7 B. 1.93×10 8 C. 1.93×107 D. 193×10 9
3.若x2+(2m 6)x+16是一个完全平方式,则 m 的值是( )
A. 4 B. - 1 或 7 C. - 1 或 4 D. 7
4.光线从空气斜射向水中时会发生折射现象。空气中平行的光线斜射向水中,经过折射后在水中的光线也是平行的。如图,AC,BD为入射光线,CE,DF为折射光线,且满足AC∥BD,AB∥CD∥EF,若∠1=43 ,∠2=167 ,则∠3的度数为( )
A. 43 B. 47 C. 56 D. 66
5.下列运算正确的是( )
A. 3x+3y=6xy B. (xy2)3=xy6 C. 3(x+8)=3x+8 D. x2·x3=x5
6.如图,点E,C,F,B在一条直线上,AB∥ED,∠A=∠D,添加下列条件不能判定△ABC △DEF的是( )
A. AC∥DF B. AB=DE C. EC=BF D. AC=DF
7.我们曾经学习 “过直线外一点P作直线l的平行线” 的一种方法,如图:
(1)在直线l上任取一点A,以点A为圆心,以AP的长为半径作弧,交直线l于点B;
(2)以点P为圆心,以PA的长为半径作弧;
(3)以点A为圆心,以PB的长为半径作弧,交前弧于点C;
(4)过点P,C作直线PC,则PC∥l。如果用全等三角形的知识来解释作图的道理,最恰当的是( )
A. SAS B. ASA C. SSS D. AAS
8.如图在4×4的正方形网格中,三个阴影小正方形组成一个图案,在这个网格图中补画一个有阴影的小正方形,使四个阴影小正方形组成轴对称图形的概率是( )
A. B. C. D.
9.如图,在△ABC中,AB=AC=24,BC=16,点D为AB的中点。点P在线段BC上以每秒 4 个单位长度的速度由点B向点C运动,同时点Q在线段CA上由点C以每秒a个单位长度的速度运动。设运动时间为t秒,若以点C,P,Q为顶点的三角形和以点B,D,P为顶点的三角形全等,且∠B和∠C是对应角,则a的值为( )
A. 4 B. 4 或 2 C. 6 D. 4 或 6
10.如图,在△ABC中,∠ABC=2∠C,点E,F分别在边BC,AC上,∠AEF=2∠AFE,∠ABC的角平分线与∠AEF的角平分线交于点P,若∠FEC=26 ,则∠P的度数为( )
A. 39 B. 52 C. 65 D. 78
二、填空题(本大题共 5 个题,每题 4 分,共 20 分。)
11.已知∠A的补角为60 ,则∠A= °。
12.已知3a=2,3b=6,则3a b= 。
13.为了估计鱼塘中鱼的数量,养鱼者先从鱼塘中捕获 100 条鱼,在每一条鱼身上做好标记后把这些鱼放回鱼塘,一段时间后再从鱼塘中打捞鱼,通过多次试验后发现捕捞的鱼中有记号的频率稳定在 0.1 左右,则鱼塘中估计有约 条。
14.如图,在Rt△ABC中,∠C=90 ,D,E分别在AB,AC上,将△ADE沿DE折叠后得到△FDE,且满足EF∥AB。若∠1=74 ,∠B的度数为 °。
15.如图,AD,BE在AB的同侧,AD=3,BE=3,AB=6,点C为AB的中点,若∠DCE=120 ,则DE的最大值是______。
三、解答题(本大题共 9 个题,共 90 分。解答应写出文字说明、证明过程或演算步骤。)
16.(本题满分 16 分)计算:
(1)( 1)2025+(π 3.14)0 ( ) 2 (2)a3·a4·2a (a2)4+( 3a4)2
(3)(2x+y+1)(2x+y 1) (4)20232 2025×2021(用乘法公式计算)。
17.(本题满分 6 分)化简求值:[(2a+3b)(2a 3b) (2a b)2 2ab]÷( 2b),其中a=2,b= 1。
18.(本题满分 8 分)根据解答过程填空(理由或数学式)。
已知:如图,∠1+∠2=180 ,∠3=∠B,求证:∠ACB=∠4。
证明:∵∠1+∠DFE=180 (邻补角定义),∠1+∠2=180 (已知),
∴∠DFE= ( )
∴AB∥EF( )
∴∠3=∠ADE( )
∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥ ( )
∴∠ACB=∠4( )。
19.(本题满分 8 分)如图,C是AB的中点,CD∥BE,CD=BE,连接AD,CE。求证:AD=CE。(要求:每一步推理都注明依据。)
20.(本题满分 8 分)如图,在正方形网格中,每个小正方形的边长为 1,且△ABC的三个顶点都在格点上。
(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)在直线l上找一点P,使PB=PC,并简述作图(画图)过程或依据;
(3)在直线l上找一点Q,使QB+QC的值最小。
21.(本题满分 8 分)
【项目背景】
某十字交通路口拥堵频发,为缓解这一状况,交警部门计划对该路口的红绿灯时长进行优化。交警小李负责收集数据,探寻合理的红绿灯时长设置方案。(该路口的红绿灯设置原则是:一个信号灯周期总时长设计为 150 秒,当有一个行驶方向处于绿灯状态时,则其余三个行驶方向均处于红灯状态。)
【数据收集】
交警小李在该路口连续观察记录了四周(工作日)每天早、中、晚高峰时段的交通情况,包括不同方向车辆通过路口的数量以及等待信号灯的时长等数据。以下是部分关键数据汇总。
表 1:各方向车辆通过路口情况抽样数据
注:通过车辆总数 = “等待信号灯后” 通过车辆数 + 直接通过车辆数。
表 2:不同时段各方向平均车流量
【问题解决】
(1)计算东向西方向车辆 “等待信号灯后” 通过路口的概率是多少?
(2)理想状态下,每个方向绿灯时长占总时长的比例与该方向车流量占总车流量的比例相近时,可保证车辆通行效率最大化。
①根据表 2 数据,计算在一个信号灯周期总时长内,早高峰时段东向西方向的绿灯时长应设置为多少秒较为合理?
②综合表 1 和表 2 的数据,通过计算,给出一个绿灯时长建议(可从早、中、晚高峰时段,四个行驶方向中任选一个),以提高车辆通行效率。
22.(本题满分 12 分)直线AB∥CD,直线EF与AB,CD分别交于点G,H,∠EHD=α(0 <α<90 ),小明将一个含30 角的直角三角板PMN按如图①放置,使点N,M分别在直线AB,CD上,∠P=90 ,∠PMN=60 。
(1)猜想∠PNB,∠PMD,∠MPN之间的数量关系,并说明理由;
(2)若∠MNG的平分线NO交直线CD于点O。
①如图②,当NO∥EF,PM∥EF时,求α的度数;
②小明将三角板PMN沿直线AB左右移动,保持PM∥EF,请直接写出∠MON的度数。(用含α的式子表示)
23.(本题满分 12 分)
【阅读理解】若x满足(16 x)(x 6)=20,求(16 x)2+(x 6)2的值。
解:设16 x=a,x 6=b,则(16 x)(x 6)=a·b=20
∵a+b=(16 x)+(x 6)=10
∴(16 x)2+(x 6)2=a2+b2=(a+b)2 2ab=102 2×20=60。
我们把解决上述问题的这种方法叫做换元法。利用换元法达到简化运算的目的,体现了转化的数学思想。用换元法解决问题:
(1)若x满足(2025 x)(x 2020)=4,求(2025 x)2+(x 2020)2的值;
【类比应用】
(2)若m满足(2025 m)(2023 m)=2,则(2025 m)4+(2023 m)4的值是______;
【迁移应用】
通过计算几何图形的面积可以表示一些代数恒等式,这种解决数学问题的思想方法叫数形结合,利用这种方法可将抽象的数学知识变得直观起来。例如,图 1 可以得到(a+b)2=a2+2ab+b2。
结合上述阅读材料,解决下列问题:
(3)两块完全相同的直角三角板(∠AOB=∠COD=90 )如图 2 所示放置,其中A,O,D在同一直线上。连接AC,BD,若AD=12,S△AOC+S△BOD=36,求一块直角三角板的面积。
24.(本题满分 12 分)
【模型建立】
(1)如图 1,△ABC,△ADE为等边三角形,连接BD,CE,求证:BD=CE;
探索思路如下:
∵△ABC,△ADE为等边三角形
∴∠BAC=∠DAE=60 ,AB=AC,AD=AE
∴∠BAC -∠DAC -∠DAE -∠DAC .(① )
即∠BAD =∠CAE
在△ABD 与△DACE 中
∴ ABD≌△ACE(② )
∴BD = CE (③ )
请在上面三个( )中填写适当的理由。
【模型应用】
(2)如图2,在△ ABC 与 AADE 中,AB = AC , AD = AE ,∠BAC =∠DAE =90°,B , D , E 三点在一条直线上,AC 与BE 交于点F ,连接EC。
①求∠BEC 的度数;
②若点F 为AC 中点,BD =6,求EF 的长。
图1 图2
答案
一、选择题(本大题共 10 个题,每题 4 分,共 40 分。在每题给出的四个选项中,只有一项是符合题目要求的。)
1.中国 “二十四节气” 已列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表 “立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( D )
A. B. C. D.
2.中国科学院近日成功研发出固态深紫外(DUV)激光源,能够发射出 193 纳米波长的相干光,为半导体工艺提升至 3 纳米节点提供了有力支持。已知 193 纳米等于 0.000 000 193 米,那么数字 0.000 000 193 用科学记数法表示为( A )
A. 1.93×10 7 B. 1.93×10 8 C. 1.93×107 D. 193×10 9
3.若x2+(2m 6)x+16是一个完全平方式,则 m 的值是( B )
A. 4 B. - 1 或 7 C. - 1 或 4 D. 7
4.光线从空气斜射向水中时会发生折射现象。空气中平行的光线斜射向水中,经过折射后在水中的光线也是平行的。如图,AC,BD为入射光线,CE,DF为折射光线,且满足AC∥BD,AB∥CD∥EF,若∠1=43 ,∠2=167 ,则∠3的度数为( C )
A. 43 B. 47 C. 56 D. 66
5.下列运算正确的是( D )
A. 3x+3y=6xy B. (xy2)3=xy6 C. 3(x+8)=3x+8 D. x2·x3=x5
6.如图,点E,C,F,B在一条直线上,AB∥ED,∠A=∠D,添加下列条件不能判定△ABC △DEF的是( A )
A. AC∥DF B. AB=DE C. EC=BF D. AC=DF
7.我们曾经学习 “过直线外一点P作直线l的平行线” 的一种方法,如图:
(1)在直线l上任取一点A,以点A为圆心,以AP的长为半径作弧,交直线l于点B;
(2)以点P为圆心,以PA的长为半径作弧;
(3)以点A为圆心,以PB的长为半径作弧,交前弧于点C;
(4)过点P,C作直线PC,则PC∥l。如果用全等三角形的知识来解释作图的道理,最恰当的是( C )
A. SAS B. ASA C. SSS D. AAS
8.如图在4×4的正方形网格中,三个阴影小正方形组成一个图案,在这个网格图中补画一个有阴影的小正方形,使四个阴影小正方形组成轴对称图形的概率是( B )
A. B. C. D.
9.如图,在△ABC中,AB=AC=24,BC=16,点D为AB的中点。点P在线段BC上以每秒 4 个单位长度的速度由点B向点C运动,同时点Q在线段CA上由点C以每秒a个单位长度的速度运动。设运动时间为t秒,若以点C,P,Q为顶点的三角形和以点B,D,P为顶点的三角形全等,且∠B和∠C是对应角,则a的值为( D )
A. 4 B. 4 或 2 C. 6 D. 4 或 6
10.如图,在△ABC中,∠ABC=2∠C,点E,F分别在边BC,AC上,∠AEF=2∠AFE,∠ABC的角平分线与∠AEF的角平分线交于点P,若∠FEC=26 ,则∠P的度数为( B )
A. 39 B. 52 C. 65 D. 78
二、填空题(本大题共 5 个题,每题 4 分,共 20 分。)
11.已知∠A的补角为60 ,则∠A= 120° °。
12.已知3a=2,3b=6,则3a b= 。
13.为了估计鱼塘中鱼的数量,养鱼者先从鱼塘中捕获 100 条鱼,在每一条鱼身上做好标记后把这些鱼放回鱼塘,一段时间后再从鱼塘中打捞鱼,通过多次试验后发现捕捞的鱼中有记号的频率稳定在 0.1 左右,则鱼塘中估计有约 1000 条。
14.如图,在Rt△ABC中,∠C=90 ,D,E分别在AB,AC上,将△ADE沿DE折叠后得到△FDE,且满足EF∥AB。若∠1=74 ,∠B的度数为 58 °。
15.如图,AD,BE在AB的同侧,AD=3,BE=3,AB=6,点C为AB的中点,若∠DCE=120 ,则DE的最大值是___9___。
三、解答题(本大题共 9 个题,共 90 分。解答应写出文字说明、证明过程或演算步骤。)
16.(本题满分 16 分)计算:
(1)( 1)2025+(π 3.14)0 ( ) 2 (2)a3·a4·2a (a2)4+( 3a4)2
=﹣1+1﹣4 =2a8﹣a8+9a8
=﹣4 =10a8
(3)(2x+y+1)(2x+y 1) (4)20232 2025×2021(用乘法公式计算)。
=(2x+y)2﹣1 =20232﹣(20232﹣4)
=4x2+4xy+y2﹣1 =4
17.(本题满分 6 分)化简求值:[(2a+3b)(2a 3b) (2a b)2 2ab]÷( 2b),其中a=2,b= 1。
解原式=[﹣10b2+2ab]( 2b)
=5b﹣a
将a=2,b= 1代入得﹣5﹣2=﹣7
18.(本题满分 8 分)根据解答过程填空(理由或数学式)。
已知:如图,∠1+∠2=180 ,∠3=∠B,求证:∠ACB=∠4。
证明:∵∠1+∠DFE=180 (邻补角定义),∠1+∠2=180 (已知),
∴∠DFE= ∠2 ( 同角的补交相等 )
∴AB∥EF( 内错角相等,两直线平行 )
∴∠3=∠ADE( 两直线平行,内错角相等 )
∵∠3=∠B(已知)
∴∠B=∠ADE( 等量代换 )
∴DE∥ BC ( 同位角相等,两直线平行 )
∴∠ACB=∠4( 两直线平行,同位角相等 )。
19.(本题满分 8 分)如图,C是AB的中点,CD∥BE,CD=BE,连接AD,CE。求证:AD=CE。(要求:每一步推理都注明依据。)
证明∵C是AB中点(已知)
∴AC=BC(中点的定义)
∵CD∥BE(已知)
∴∠ACD =∠B ,(两直线平行,同位角相等)
在△ADC 与△CEB 中
∴△ADC≌△CEB ( SAS ).
∴AD = CE(全等三角形对应边相等,对应角相等)
20.(本题满分 8 分)如图,在正方形网格中,每个小正方形的边长为 1,且△ABC的三个顶点都在格点上。
(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)在直线l上找一点P,使PB=PC,并简述作图(画图)过程或依据;
(3)在直线l上找一点Q,使QB+QC的值最小。
略
21.(本题满分 8 分)
【项目背景】
某十字交通路口拥堵频发,为缓解这一状况,交警部门计划对该路口的红绿灯时长进行优化。交警小李负责收集数据,探寻合理的红绿灯时长设置方案。(该路口的红绿灯设置原则是:一个信号灯周期总时长设计为 150 秒,当有一个行驶方向处于绿灯状态时,则其余三个行驶方向均处于红灯状态。)
【数据收集】
交警小李在该路口连续观察记录了四周(工作日)每天早、中、晚高峰时段的交通情况,包括不同方向车辆通过路口的数量以及等待信号灯的时长等数据。以下是部分关键数据汇总。
表 1:各方向车辆通过路口情况抽样数据
注:通过车辆总数 = “等待信号灯后” 通过车辆数 + 直接通过车辆数。
表 2:不同时段各方向平均车流量
【问题解决】
(1)计算东向西方向车辆 “等待信号灯后” 通过路口的概率是多少?
(2)理想状态下,每个方向绿灯时长占总时长的比例与该方向车流量占总车流量的比例相近时,可保证车辆通行效率最大化。
①根据表 2 数据,计算在一个信号灯周期总时长内,早高峰时段东向西方向的绿灯时长应设置为多少秒较为合理?
②综合表 1 和表 2 的数据,通过计算,给出一个绿灯时长建议(可从早、中、晚高峰时段,四个行驶方向中任选一个),以提高车辆通行效率。
解:(1)P(东向西方向车辆"等待信号灯后"通过路口)==0.7
①早高峰时段总车流量:300+200+400+100=1000辆。东向西方向车流量占总车流量的比例为0.3
∴早高峰时段东向西方向绿灯时长应为:150x=45秒
②以早高峰东向西方向为例。由(2)可知,早高峰时段东向西方向绿灯时长应为45秒。由(1)知, P(东向西方向车辆在等待信号灯后通过路口)=0.7,此比例相对较高。建议将早高峰东向西方向的绿灯时长在计算结果基础上增加2秒,调整为47秒,以缓解车辆等待压力,提高该方向通行效率,同时相应缩短其他方向绿灯时长,确保信号灯周期总时长仍为150秒。
22.(本题满分 12 分)直线AB∥CD,直线EF与AB,CD分别交于点G,H,∠EHD=α(0 <α<90 ),小明将一个含30 角的直角三角板PMN按如图①放置,使点N,M分别在直线AB,CD上,∠P=90 ,∠PMN=60 。
(1)猜想∠PNB,∠PMD,∠MPN之间的数量关系,并说明理由;
(2)若∠MNG的平分线NO交直线CD于点O。
①如图②,当NO∥EF,PM∥EF时,求α的度数;
②小明将三角板PMN沿直线AB左右移动,保持PM∥EF,请直接写出∠MON的度数。(用含α的式子表示)
解:(1)∠PNB +∠PMD =∠MPN
过P 点作PQ // AB
∵AB // CD
∴AB // PQ // CD .
∴∠PNB =∠NPQ ,∠PMD =∠QPM
∴∠PNB +∠PMD =∠NPQ +∠QPM =∠MPN
(2)①∵NO // EF , PM // EF ,∠PMN =60°
∴NO // PM // EF ,
∴∠ONM =∠PMN =60°, ∠EHD =∠NOM =a
∵NO 平分∠MNG .
∴∠ANO =∠ONM =60°
∵AB // CD
∴∠NOM =∠ANO =60°
∴α=60°
②30°+α或60°﹣α
23.(本题满分 12 分)
【阅读理解】若x满足(16 x)(x 6)=20,求(16 x)2+(x 6)2的值。
解:设16 x=a,x 6=b,则(16 x)(x 6)=a·b=20
∵a+b=(16 x)+(x 6)=10
∴(16 x)2+(x 6)2=a2+b2=(a+b)2 2ab=102 2×20=60。
我们把解决上述问题的这种方法叫做换元法。利用换元法达到简化运算的目的,体现了转化的数学思想。用换元法解决问题:
(1)若x满足(2025 x)(x 2020)=4,求(2025 x)2+(x 2020)2的值;
【类比应用】
(2)若m满足(2025 m)(2023 m)=2,则(2025 m)4+(2023 m)4的值是______;
【迁移应用】
通过计算几何图形的面积可以表示一些代数恒等式,这种解决数学问题的思想方法叫数形结合,利用这种方法可将抽象的数学知识变得直观起来。例如,图 1 可以得到(a+b)2=a2+2ab+b2。
结合上述阅读材料,解决下列问题:
(3)两块完全相同的直角三角板(∠AOB=∠COD=90 )如图 2 所示放置,其中A,O,D在同一直线上。连接AC,BD,若AD=12,S△AOC+S△BOD=36,求一块直角三角板的面积。
解:(1)设2025- x= a , x -2020=b ,则(2025- x)( x -2020)=ab =4
∵a + b =(2025- x )+( x -2020)=5
∴ (2025- x )2+( x -2020)2=a2+b2=( atb )2-2ab=52-2x4=17:
(2)56
(3)设直角三角形的较短的直角边为 a ,较长的直角边为 b ,
由题意可得:a + b=12,a2+b2=36
∴a2+b2=72
∵a + b =12
∴(a +b)2=144,
∴a2+2ab+b2=144
∴2ab=144-(a2+b2)=144-72=72
∴ab =36
∴ab =18,
即一块直角三角板的面积为18。
24.(本题满分 12 分)
【模型建立】
(1)如图 1,△ABC,△ADE为等边三角形,连接BD,CE,求证:BD=CE;
探索思路如下:
∵△ABC,△ADE为等边三角形
∴∠BAC=∠DAE=60 ,AB=AC,AD=AE
∴∠BAC -∠DAC -∠DAE -∠DAC .(① )
即∠BAD =∠CAE
在△ABD 与△DACE 中
∴ ABD≌△ACE(② )
∴BD = CE (③ )
请在上面三个( )中填写适当的理由。
【模型应用】
(2)如图2,在△ ABC 与 AADE 中,AB = AC , AD = AE ,∠BAC =∠DAE =90°,B , D , E 三点在一条直线上,AC 与BE 交于点F ,连接EC。
①求∠BEC 的度数;
②若点F 为AC 中点,BD =6,求EF 的长。
图1 图2
(1)等式的性质 SAS 两全等三角形的对应线段相等
(2)①∵∠BAC =∠DAE =90°
∴∠DAE -∠DAF =∠BAC -∠DAF
即∠BAD =∠CAE
在△ABD 与△ACE 中
∴△ABD≌ △ACE ( SAS )
∴∠ABD =∠ACE
∵∠BAC =90°
∴∠ABD +∠BFA -90°
∴∠ACE +∠CFE -90°
∴∠BEC =90°
②作 AM⊥BE交BE 于点M .
∴∠AME =90°
∵F 为AC 中点
∴AF = FC
∵∠BEC =90°
∴∠AMF =∠CEF =90°
∵∠AFM =∠CFE
∴△AFM≌ CFE
∴MF=EF =ME ,AM=CE
由①知:△ABD≌△ACE
∴CE=BD=6
∴AM =6
∵AD = AE .∠DAE =90°,AM⊥DE
∴∠MAE =45°, ∠AEM =45°
∴∠MAE =∠AEM
∴ME = AM =6
∴EF=ME =3..
同课章节目录
